Update

README.md

@@ -38,6 +38,7 @@
 * [哈希表：map等候多时了](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ)
 * [哈希表：其实需要哈希的地方都能找到map的身影](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)
 * [哈希表：这道题目我做过？](https://mp.weixin.qq.com/s/sYZIR4dFBrw_lr3eJJnteQ)
+* [哈希表：解决了两数之和，那么能解决三数之和么？](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
 * 精选链表相关的面试题
 * 精选字符串相关的面试题
 * 精选栈与队列相关的面试题
@@ -354,11 +355,13 @@ int countNodes(TreeNode* root) {
 |[0027.移除元素](https://github.com/youngyangyang04/leetcode/blob/master/problems/0027.移除元素.md)  |数组 |简单| **暴力** **双指针/快慢指针/双指针**|
 |[0028.实现strStr()](https://github.com/youngyangyang04/leetcode/blob/master/problems/0028.实现strStr().md)  |字符串 |简单| **KMP** |
 |[0035.搜索插入位置](https://github.com/youngyangyang04/leetcode/blob/master/problems/0035.搜索插入位置.md) |数组 |简单| **暴力** **二分**|
+|[0037.解数独](https://github.com/youngyangyang04/leetcode/blob/master/problems/0037.解数独.md) |回溯 |困难| **回溯**|
 |[0039.组合总和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0039.组合总和.md) |数组/回溯 |中等| **回溯**|
 |[0040.组合总和II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0040.组合总和II.md) |数组/回溯 |中等| **回溯**|
 |[0046.全排列](https://github.com/youngyangyang04/leetcode/blob/master/problems/0046.全排列.md) |回溯|中等| **回溯**|
 |[0047.全排列II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0047.全排列II.md) |回溯|中等| **回溯**|
-|[0051.N皇后](https://github.com/youngyangyang04/leetcode/blob/master/problems/0051.N皇后.md) |回溯|中等| **回溯**|
+|[0051.N皇后](https://github.com/youngyangyang04/leetcode/blob/master/problems/0051.N皇后.md) |回溯|困难| **回溯**|
+|[0052.N皇后II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0052.N皇后II.md) |回溯|困难| **回溯**|
 |[0053.最大子序和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0053.最大子序和.md) |数组 |简单|**暴力** **贪心** 动态规划 分治|
 |[0059.螺旋矩阵II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0059.螺旋矩阵II.md) |数组 |中等|**模拟**|
 |[0077.组合](https://github.com/youngyangyang04/leetcode/blob/master/problems/0077.组合.md) |回溯 |中等|**回溯**|
@@ -400,10 +403,11 @@ int countNodes(TreeNode* root) {
 |[0349.两个数组的交集](https://github.com/youngyangyang04/leetcode/blob/master/problems/0349.两个数组的交集.md) |哈希表 |简单|**哈希**|
 |[0350.两个数组的交集II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0350.两个数组的交集II.md) |哈希表 |简单|**哈希**|
 |[0383.赎金信](https://github.com/youngyangyang04/leetcode/blob/master/problems/0383.赎金信.md) |数组 |简单|**暴力** **字典计数** **哈希**|
-|[0450.删除二叉搜索树中的节点](https://github.com/youngyangyang04/leetcode/blob/master/problems/0450.删除二叉搜索树中的节点.md) |树 |中等|**递归**|
 |[0434.字符串中的单词数](https://github.com/youngyangyang04/leetcode/blob/master/problems/0434.字符串中的单词数.md) |字符串 |简单|**模拟**|
+|[0450.删除二叉搜索树中的节点](https://github.com/youngyangyang04/leetcode/blob/master/problems/0450.删除二叉搜索树中的节点.md) |树 |中等|**递归**|
 |[0454.四数相加II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0454.四数相加II.md) |哈希表 |中等| **哈希**|
 |[0459.重复的子字符串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0459.重复的子字符串.md) |字符创 |简单| **KMP**|
+|[0491.递增子序列](https://github.com/youngyangyang04/leetcode/blob/master/problems/0491.递增子序列.md) |深度优先搜索 |中等|**深度优先搜索/回溯**|
 |[0541.反转字符串II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0541.反转字符串II.md) |字符串 |简单| **模拟**|
 |[0575.分糖果](https://github.com/youngyangyang04/leetcode/blob/master/problems/0575.分糖果.md) |哈希表 |简单|**哈希**|
 |[0617.合并二叉树](https://github.com/youngyangyang04/leetcode/blob/master/problems/0617.合并二叉树.md) |树 |简单|**递归** **迭代**|

problems/0018.四数之和.md

@@ -1,19 +1,48 @@
-
-## 题目地址 
+# 题目地址 
 https://leetcode-cn.com/problems/4sum/  
 
-## 思路 
+> 一样的道理，能解决四数之和
 
+> 那么五数之和、六数之和、N数之和呢？
 
-四数之和，和[三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md)是一个思路，都是使用双指针法，但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。
+# 第18题. 四数之和 
 
-三数之和 我们是一层for循环，然后循环内有left和right下表作为指针，四数之和，就可以是两层for循环，依然是循环内有left和right下表作为指针，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。 
+题意：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。
 
-动画如下：
-<video src='../video/15.三数之和.mp4' controls='controls' width='640' height='320' autoplay='autoplay'> Your browser does not support the video tag.</video></div>
+**注意：**
 
+答案中不可以包含重复的四元组。
 
-## C++代码
+示例：   
+给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。   
+满足要求的四元组集合为：    
+[
+  [-1,  0, 0, 1],
+  [-2, -1, 1, 2],
+  [-2,  0, 0, 2]
+]
+
+# 思路 
+
+四数之和，和[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)是一个思路，都是使用双指针法, 基本解法就是在[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A) 的基础上再套一层for循环。 
+
+但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来）
+
+[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
+
+四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下表作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。 
+
+那么一样的道理，五数之和、六数之和等等都采用这种解法。 
+
+对于[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。
+
+之前我们讲过哈希表的经典题目：[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
+
+而[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！
+
+大家解决一下这两道题目就能感受出来难度的差异。
+
+# C++代码
 ```
 class Solution {
 public:
@@ -21,7 +50,7 @@ public:
         vector<vector<int>> result;
         sort(nums.begin(), nums.end());
         for (int k = 0; k < nums.size(); k++) {
-            // 这中剪枝是错误的，这道题目target 是任意值 
+            // 这种剪枝是错误的，这道题目target 是任意值 
             // if (nums[k] > target) {
             //     return result;
             // }

problems/0037.解数独.md

@@ -0,0 +1,60 @@
+# 题目地址 
+
+https://leetcode-cn.com/problems/sudoku-solver/
+
+# 思路 
+
+这道题目和之前递归的方式都不一样，这里相当于两层递归，之前的都是一层递归
+
+# C++代码 
+
+```
+class Solution {
+private:
+bool backtracking(vector<vector<char>>& board) {
+    for (int i = 0; i < board.size(); i++) {
+        for (int j = 0; j < board[0].size(); j++) {
+            if (board[i][j] != '.') continue;
+            for (char k = '1'; k <= '9'; k++) {
+                if (isValid(i, j, k, board)) {
+                    board[i][j] = k;
+                    if (backtracking(board)) return true;
+                    board[i][j] = '.';
+                }
+            }
+            return false;
+        }
+    }
+    return true;
+
+}
+bool isValid(int row, int col, char val, vector<vector<char>>& board) {
+
+    for (int i = 0; i < 9; i++) {
+        if (board[row][i] == val) {
+            return false;
+        }
+    }
+    for (int j = 0; j < 9; j++) {
+        if (board[j][col] == val) {
+            return false;
+        }
+
+    }
+    int startRow = (row / 3) * 3;
+    int startCol = (col / 3) * 3;
+    for (int i = startRow; i < startRow + 3; i++) {
+        for (int j = startCol; j < startCol + 3; j++) {
+            if (board[i][j] == val ) {
+                return false;
+            }
+        }
+    }
+    return true;
+}
+public:
+    void solveSudoku(vector<vector<char>>& board) {
+        backtracking(board);
+    }
+};
+```

problems/0052.N皇后II.md

@@ -0,0 +1,86 @@
+# 题目链接 
+https://leetcode-cn.com/problems/n-queens-ii/ 
+
+# 第51题. N皇后
+
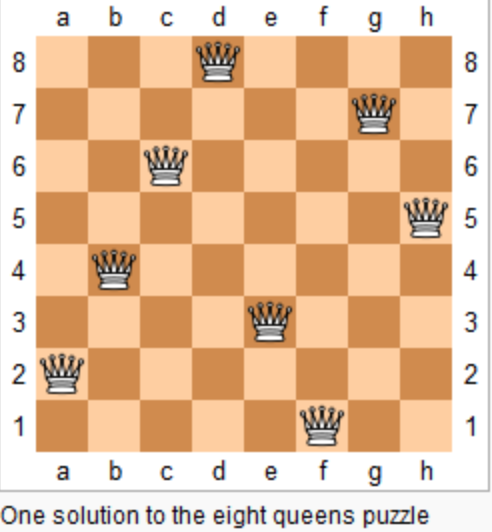
+n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 
+
+上图为 8 皇后问题的一种解法。
+![51n皇后](https://img-blog.csdnimg.cn/20200821152118456.png)
+
+给定一个整数 n，返回 n 皇后不同的解决方案的数量。
+
+示例:
+
+输入: 4
+输出: 2
+解释: 4 皇后问题存在如下两个不同的解法。
+[
+ [".Q..",  // 解法 1
+  "...Q",
+  "Q...",
+  "..Q."],
+
+ ["..Q.",  // 解法 2
+  "Q...",
+  "...Q",
+  ".Q.."]
+]
+# 思路
+
+这道题目和 51.N皇后 基本没有区别
+
+# C++代码
+
+```
+class Solution {
+private:
+int count = 0;
+void backtracking(int n, int row, vector<string>& chessboard, vector<vector<string>>& result) {
+    if (row == n) {
+        count++;
+        return;
+    }
+    for (int col = 0; col < n; col++) {
+        if (isValid(row, col, chessboard, n)) {
+            chessboard[row][col] = 'Q';
+            backtracking(n, row + 1, chessboard, result);
+            chessboard[row][col] = '.';
+        }
+    }
+}
+bool isValid(int row, int col, vector<string>& chessboard, int n) {
+    int count = 0;
+    // 检查列
+    for (int i = 0; i < row; i++) { // 这是一个剪枝
+        if (chessboard[i][col] == 'Q') {
+            return false;
+        }
+    }
+    // 检查 45度角是否有皇后
+    for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
+        if (chessboard[i][j] == 'Q') {
+            return false;
+        }
+    }
+    // 检查 135度角是否有皇后
+    for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
+        if (chessboard[i][j] == 'Q') {
+            return false;
+        }
+    }
+    return true;
+}
+
+public:
+    int totalNQueens(int n) {
+        std::vector<std::string> chessboard(n, std::string(n, '.'));
+        vector<vector<string>> result;
+        backtracking(n, 0, chessboard, result);
+        return count;
+
+    }
+};
+```
+
+> 更多算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。

problems/0053.最大子序和.md

@@ -53,5 +53,5 @@ public:
     }
 };
 ```
-> 更过算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。
+> 更多算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。
 

problems/0459.重复的子字符串.md

@@ -4,6 +4,22 @@ https://leetcode-cn.com/problems/repeated-substring-pattern/
 
 ## 思路 
 
+这是一道标准的KMP的题目。
+
+使用KMP算法，next 数组记录的就是最长公共前后缀， 最后如果 next[len - 1] != -1，说明此时有最长公共前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度），同时如果len % (len - (next[len - 1] + 1)) == 0 ，则说明 (数组长度-最长公共前后缀的长度) 正好可以被 数组的长度整除，说明有重复的子字符串。
+
+**强烈建议大家把next数组打印出来，看看next数组里的规律，有助于理解KMP算法**
+
+如图：
+
+<img src='../pics/459.重复的子字符串_1.png' width=600> </img></div>
+
+此时next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时 字符串asdfasdfasdf的最长公共前后缀的长度。
+
+
+(len - (next[len - 1] + 1)) 也就是： 12(字符串的长度) - 8(最长公共前后缀的长度)   = 4， 4正好可以被 12(字符串的长度) 整除，所以说明有重复的子字符串。
+
+代码如下：
 
 ## C++代码
 

problems/0491.递增子序列.md

@@ -0,0 +1,42 @@
+## 题目地址 
+
+## 思路 
+
+这道题可以说是深度优先搜索，也可以说是回溯法，其实我更倾向于说它用回溯法，因为本题和[90. 子集 II](https://leetcode-cn.com/problems/subsets-ii/)非常像，差别就是[90. 子集 II](https://leetcode-cn.com/problems/subsets-ii/)可以通过排序，在加一个标记数组来达到去重的目的。
+
+去重复的逻辑，关键在于子序列的末尾，如果子序列的末尾重复出现一个元素，那么该序列就是重复的了，如图所示：
+
+<img src='../pics/491. 递增子序列1.jpg' width=600> </img></div>
+
+在递归的过程中 `if ((subseq.empty() || nums[i] >= subseq.back()) && uset.find(nums[i]) == uset.end())` 这个判断条件一定要想清楚， 如果子序列为空或者nums[i]>=子序列尾部数值，**同时** 这个nums[i] 不能出现过， 因为一旦出现过就 是一个重复的递增子序列了。
+
+## C++代码
+
+```
+class Solution {
+private:
+void backtracking(vector<int>& nums, vector<vector<int>>& result, vector<int>& subseq, int startIndex) {
+    if (subseq.size() > 1) {
+        result.push_back(subseq);
+        // 注意这里不要加return，因为要取所有的可能
+    }
+    unordered_set<int> uset; // 使用set来对尾部元素进行去重
+    for (int i = startIndex; i < nums.size(); i++) {
+        if ((subseq.empty() || nums[i] >= subseq.back())
+                && uset.find(nums[i]) == uset.end()) {
+            subseq.push_back(nums[i]);
+            backtracking(nums, result, subseq, i + 1);
+            subseq.pop_back();
+            uset.insert(nums[i]);//在回溯的时候，记录这个元素用过了，后面不能再用了
+        }
+    }
+}
+public:
+    vector<vector<int>> findSubsequences(vector<int>& nums) {
+        vector<vector<int>> result;
+        vector<int> subseq;
+        backtracking(nums, result, subseq, 0);
+        return result;
+    }
+};
+```

problems/面试题02.07.链表相交.md

@@ -7,6 +7,20 @@ https://leetcode-cn.com/problems/intersection-of-two-linked-lists-lcci/
 
 简单来说，就是求两个链表交点节点的**指针**。 这里同学们要注意，交点不是数值相等，而是指针相等。
 
+为了方便举例，假设节点元素数值相等，则节点指针相等。
+
+看如下两个链表，目前curA指向链表A的头结点，curB指向链表B的头结点：
+
+<img src='../pics/面试题02.07.链表相交_1.png' width=600> </img></div>
+
+我们求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB 末尾对齐的位置，如图：
+
+<img src='../pics/面试题02.07.链表相交_2.png' width=600> </img></div>
+
+此时我们就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到焦点。
+
+否则循环退出返回空指针。
+
 ## C++代码 
 
 ```