Update

problems/kamacoder/0058.区间和.md

@@ -0,0 +1,191 @@
+
+# 58. 区间和 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1070)
+
+题目描述
+
+给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。
+
+输入描述
+
+第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。
+
+输出描述
+
+输出每个指定区间内元素的总和。
+
+输入示例
+
+```
+5
+1
+2
+3
+4
+5
+0 1
+1 3
+```
+
+输出示例
+
+```
+3
+9
+```
+
+数据范围：
+
+0 < n <= 100000
+
+## 思路 
+
+本题我们来讲解 数组 上常用的解题技巧：前缀和  
+
+首先来看本题，我们最直观的想法是什么？ 
+
+那就是给一个区间，然后 把这个区间的和都累加一遍不就得了，是一道简单不能再简单的题目。 
+
+代码如下： 
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    int n, a, b;
+    cin >> n;
+    vector<int> vec(n);
+    for (int i = 0; i < n; i++) cin >> vec[i];
+    while (cin >> a >> b) {
+        int sum = 0;
+        // 累加区间 a 到 b 的和
+        for (int i = a; i <= b; i++) sum += vec[i];
+        cout << sum << endl;
+    }
+} 
+```
+
+代码一提交，发现超时了..... 
+
+我在制作本题的时候，特别制作了大数据量查询，卡的就是这种暴力解法。  
+
+来举一个极端的例子，如果我查询m次，每次查询的范围都是从0 到 n - 1 
+
+那么该算法的时间复杂度是 O(n * m)  m 是查询的次数 
+
+如果查询次数非常大的话，这个时间复杂度也是非常大的。 
+
+接下来我们来引入前缀和，看看前缀和如何解决这个问题。 
+
+前缀和的思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。 
+
+**前缀和 在涉及计算区间和的问题时非常有用**！ 
+
+前缀和的思路其实很简单，我给大家举个例子很容易就懂了。 
+
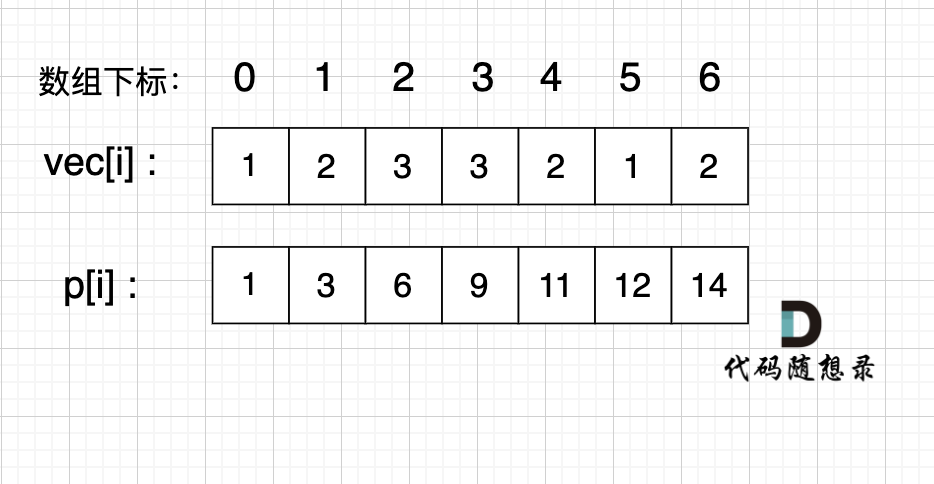
+例如，我们要统计 vec[i] 这个数组上的区间和。
+
+我们先做累加，即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。 
+
+如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240627110604.png)
+
+
+如果，我们想统计，在vec数组上 下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。  
+
+为什么呢？ 
+
+p[1] = vec[0] + vec[1]; 
+
+p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
+
+p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
+
+这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。 
+
+如图所示： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240627111319.png)
+
+p[5] - p[1] 就是 红色部分的区间和。 
+
+而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1)的操作。 
+
+
+
+```CPP
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    int n, a, b;
+    cin >> n;
+    vector<int> vec(n);
+    vector<int> p(n);
+    int presum = 0;
+    for (int i = 0; i < n; i++) {
+        cin >> vec[i];
+        presum += vec[i];
+        p[i] = presum;
+    }
+
+    while (cin >> a >> b) {
+        int sum;
+        if (a == 0) sum = p[b];
+        else sum = p[b] - p[a - 1];
+        cout << sum << endl;
+    }
+}
+
+```
+
+```CPP
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    int n, a, b;
+    cin >> n;
+    vector<int> vec(n);
+    vector<int> p(n);
+    int presum = 0;
+    for (int i = 0; i < n; i++) {
+        scanf("%d", &vec[i]);
+        presum += vec[i];
+        p[i] = presum;
+    }
+
+    while (~scanf("%d%d", &a, &b)) {
+        int sum;
+        if (a == 0) sum = p[b];
+        else sum = p[b] - p[a - 1];
+        printf("%d\n", sum);
+    }
+}
+
+```
+
+```CPP 
+
+#include<bits/stdc++.h>
+using namespace std;
+
+
+int main(){
+    int n, a, b;
+    cin >> n;
+    vector<int> vec(n + 1);
+    vector<int> p(n + 1, 0);
+    for(int i = 1; i <= n; i++) {
+        scanf("%d", &vec[i]);
+        p[i] = p[i - 1] + vec[i];
+    }
+    while(~scanf("%d%d", &a, &b)){
+        printf("%d\n", p[b + 1] - p[a]);
+    }
+    return 0;
+} 
+```

problems/kamacoder/0105.有向图的完全可达性.md

@@ -24,7 +24,7 @@
 1 2
 2 1
 1 3
-3 4
+2 4
 ```
 
 【输出示例】

problems/kamacoder/0126.骑士的攻击astar.md

@@ -7,6 +7,10 @@
 
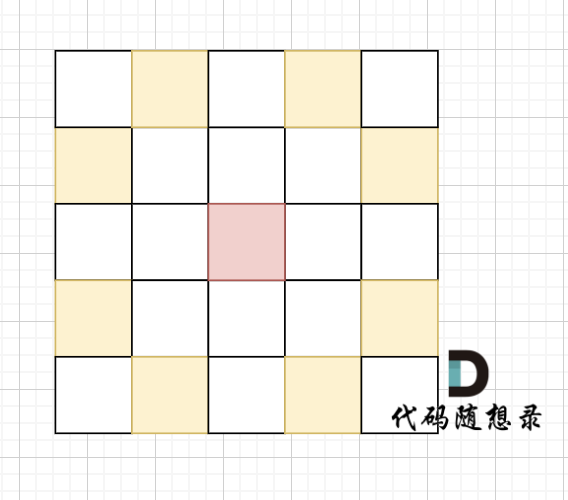
 在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。
 
+骑士移动规则如图，红色是起始位置，黄色是骑士可以走的地方。 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240626104833.png)
+
 棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）
 
 输入描述
@@ -42,6 +46,7 @@
 0
 ```
 
+
 ## 思路 
 
 我们看到这道题目的第一个想法就是广搜，这也是最经典的广搜类型题目。 

problems/kamacoder/0132.夹吃旗.md

@@ -0,0 +1,47 @@
+
+# 132. 夹吃棋 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1209)
+
+这道题是模拟题，但很多录友可能想复杂了。 
+
+行方向，白棋吃，只有这样的布局 `o*o`，黑棋吃，只有这样的布局 `*o*`
+
+列方向也是同理的。 
+
+想到这一点，本题的代码就容易写了， C++代码如下：
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    int n;
+    cin >> n;
+    while (n--) {
+        int black = 0, white = 0;
+        vector<string> grid(3, "");
+        // 判断行
+        for (int i = 0; i < 3; i++) {
+            cin >> grid[i];
+            if (grid[i] == "o*o") white++;
+            if (grid[i] == "*o*") black++;
+        }
+        // 判断列
+        for (int i = 0; i < 3; i++) {
+            string s;
+            s += grid[0][i];
+            s += grid[1][i];
+            s += grid[2][i];
+            if (s == "o*o") white++;
+            if (s == "*o*") black++;
+        }
+        // 如果一个棋盘的局面没有一方被夹吃或者黑白双方都被对面夹吃，则认为是平局
+        if ((!white && !black) || (white && black)) cout << "draw" << endl; 
+        // 白棋赢
+        else if (white && !black) cout << "yukan" << endl;
+        // 黑棋赢
+        else cout << "kou" << endl;
+    }
+}
+```

problems/kamacoder/0133.小红买药.md

@@ -0,0 +1,48 @@
+
+# 133. 小红买药 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1210)
+
+本题是一道直观的模拟题，但也并不简单，很多情况容易漏了，笔试现场可能要多错几次 才能把情况都想到。 
+
+主要是三个情况： 
+
+* 小红没症状，药有副作用，统计加一，同时要给小红标记上症状
+* 小红有症状，药治不了，同时也没副症状 ，这时也要统计加一
+* 小红有症状，药可以治，给小红取消症状标记  
+
+
+```CPP
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    int n, m, q, u;
+    cin >> n;
+    string s;
+    cin >> s;
+    cin >> m;
+    vector<string> a(m + 1); // 因为后面u是从1开始的
+    vector<string> b(m + 1);
+    for (int i = 1; i <= m; i++) {
+        cin >> a[i] >> b[i];
+    }
+    cin >> q;
+    while (q--) {
+        cin >> u;
+        int num = 0;
+        for (int i = 0; i < n; i++) {
+            // s 没症状，但b给了副作用，统计num的同时，要给s标记上症状
+            if (s[i] == '0' && b[u][i] == '1') {
+                num ++;
+                s[i] = '1';
+            } 
+            // s 有症状，但 a治不了，b也没副症状 
+            else if (s[i] == '1' && a[u][i] == '0' && a[u][i] == '0') num++;
+            // s 有症状，a 可以治 
+            else if (s[i] == '1' && a[u][i] == '1') s[i] = '0';
+        }
+        cout << num << endl;
+    }
+}
+```

problems/kamacoder/0134.皇后移动的最小步数.md

@@ -0,0 +1,77 @@
+
+# 134. 皇后移动的最小步数 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1211)
+
+本题和 [代码随想录-不同路径](https://www.programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html) 有一些类似。 
+
+关键是弄清楚递推公式  
+
+一共分三个情况，
+
+情况一，向右移动： 
+
+然后从 (i, j) 再向右走 到 (i, k)。 无论k 多大，步数只加1 ： 
+
+`dp[i][k] = dp[i][j] + 1` 
+
+那么 `dp[i][k]` 也有可能 从其他方向得到，例如 从上到下， 或者斜上方到达 dp[i][k] 
+
+本题我们要求最小步数，所以取最小值：`dp[i][k] = min(dp[i][k], dp[i][j] + 1);` 
+
+情况二，向下移动： 
+
+从 (i, j) 再向下走 到 (k, j)。 无论k 多大，步数只加1 ：
+
+`dp[k][j] = dp[i][j] + 1;` 
+
+同理 `dp[i][k]` 也有可能 从其他方向得到，取最小值：`dp[k][j] = min(dp[k][j], dp[i][j] + 1);` 
+
+情况三，右下方移动： 
+
+从 (i, j) 再向右下方移动 到 (i + k, j + k)。 无论k 多大，步数只加1 ： 
+
+`dp[i + k][j + k] = dp[i][j] + 1`
+
+同理 `dp[i + k][j + k]` 也有可能 从其他方向得到，取最小值：`dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);`
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+const int INF = 4e6; // 最多步数也就是 2000 * 2000
+int main() {
+    int n, m;
+    cin >> n >> m;
+    vector<vector<char>> grid(n, vector<char>(m));
+    for (int i = 0; i < n; i++) {
+        for (int j = 0; j < m; j++) {
+            cin >> grid[i][j];
+        }
+    }
+    vector<vector<int>> dp(n, vector<int>(m, INF));
+    dp[0][0] = 0;
+    for (int i = 0; i < n; i++) {
+        for (int j = 0; j < m; j++) {
+            if (grid[i][j] == '*') continue;
+            // 向右移动k个格子
+            for (int k = j + 1; k < m && grid[i][k] == '.'; k++) {
+                dp[i][k] = min(dp[i][k], dp[i][j] + 1);
+            }
+            // 向下移动 k个格子
+            for (int k = i + 1; k < n && grid[k][j] == '.'; k++) {
+                dp[k][j] = min(dp[k][j], dp[i][j] + 1);
+            }
+            // 向右下移动k个格子
+            for (int k = 1; i + k < n && j + k < m && grid[i + k][j + k] == '.'; k++) {
+                dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);
+            }
+        }
+    }
+    if (dp[n - 1][m - 1] == INF) cout << -1 << endl;
+    else cout << dp[n - 1][m - 1] << endl;
+}
+```
+
+

problems/kamacoder/夹吃旗.md

@@ -1,47 +0,0 @@
-
-#include <bits/stdc++.h>
-
-using namespace std;
-
-int main() {
-    int t = 0;
-
-    cin >> t;
-
-    while(t--) {
-        vector<string> grid(3, "");
-        int a = 0;
-        int b = 0;
-        for(int i = 0; i < 3; i++) {
-            cin >> grid[i];
-            if(grid[i] == "o*o") {
-                a++;
-            } else if(grid[i] == "*o*") {
-                b++;
-            }
-        }
-        // 判断列
-        for(int i = 0; i < 3; i++) {
-            string line(1, grid[0][i]);
-            line += grid[1][i];
-            line += grid[2][i];
-
-            if(line == "o*o") {
-                a++;
-            } else if(line == "*o*") {
-                b++;
-            }
-        }
-        if((a && b) || (!a && !b)) {
-            cout << "draw" << endl;
-        }
-        if(a && !b) {
-            cout << "yukan" << endl;
-        }
-        if(!a && b) {
-            cout << "kou" << endl;
-        }
-    }
-
-    return 0;
-}

problems/kamacoder/字符串处理器.md

@@ -0,0 +1,50 @@
+
+
+```CPP 
+#include<bits/stdc++.h>
+using namespace std;
+ int main() {
+     int index = 0;
+     long long optNum;
+     string s;
+     string cmd;
+     while(cin >> cmd){
+         //cout << s << endl;
+        if(cmd == "insert"){
+            string buff;
+            cin >> buff;
+            s.insert(index, buff);
+            index += buff.size();
+        }
+        else if(cmd == "move"){
+            cin >> optNum;
+            if(optNum > 0 && index + optNum <= s.size()) index += optNum;
+            if(optNum < 0 && index >= -optNum) index += optNum;
+        }
+        else if(cmd == "delete"){
+            cin >> optNum;
+            if(index >= optNum && optNum != 0){
+                s.erase(index - optNum, optNum);
+                index -= optNum;
+            }
+        }
+        else if(cmd == "copy"){
+            if(index > 0) {
+                string tmp = s.substr(0, index);
+                s.insert(index, tmp);
+            }
+        }
+        else if(cmd == "end"){
+            for(int i = 0; i < index; i++) {
+                cout << s[i];
+            }
+            cout << '|';
+            for(int i = index; i < s.size(); i++){
+                cout << s[i];
+            }
+            break;
+        }
+     }
+     return 0;
+ } 
+```

problems/kamacoder/获取连通的相邻节点列表.md

@@ -0,0 +1,47 @@
+
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <algorithm>
+#include <unordered_set>
+using namespace std;
+int main() {
+    unordered_set<int> uset;
+    int n, a;
+    cin >> n;
+    while (n--) {
+        cin >> a;
+        uset.insert(a);
+    }
+    int m, x, vlan_id;
+    long long tb;
+    vector<long long> vecTB;
+    cin >> m;
+    while(m--) {
+        cin >> tb;
+        cin >> x;
+        vector<long long> vecVlan_id(x);
+        for (int i = 0; i < x; i++) {
+            cin >> vecVlan_id[i];
+        }
+        for (int i = 0; i < x; i++) {
+            if (uset.find(vecVlan_id[i]) != uset.end()) {
+                vecTB.push_back(tb);
+                break;
+            }
+        }
+
+    }
+
+    cout << vecTB.size() << endl;
+    if (vecTB.size() != 0) {
+        sort(vecTB.begin(), vecTB.end());
+        for (int i = 0; i < vecTB.size() ; i++) cout << vecTB[i] << " ";
+    }
+
+
+}
+
+```