mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 16:54:50 +08:00
Merge pull request #1799 from juguagua/leetcode-modify-the-code-of-the-BinaryTree
完善更新二叉树部分:从 “最大二叉树” 到 “删除二叉搜索树中的节点”
This commit is contained in:
@ -437,8 +437,6 @@ class Solution:
|
||||
## Go
|
||||
|
||||
```Go
|
||||
import "math"
|
||||
|
||||
func isValidBST(root *TreeNode) bool {
|
||||
// 二叉搜索树也可以是空树
|
||||
if root == nil {
|
||||
|
||||
@ -35,7 +35,7 @@
|
||||
|
||||
因为只要给我们一个有序数组,如果强调平衡,都可以以线性结构来构造二叉搜索树。
|
||||
|
||||
例如 有序数组[-10,-3,0,5,9] 可以就可以构造成这样的二叉搜索树,如图。
|
||||
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。
|
||||
|
||||
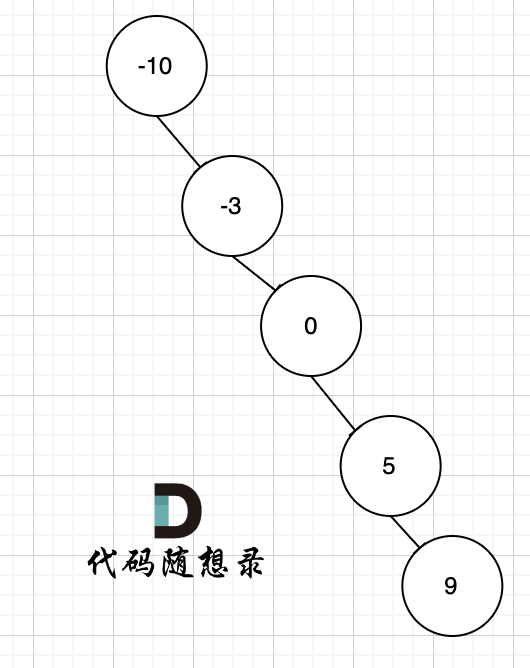
|
||||
|
||||
@ -147,7 +147,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
**注意:在调用traversal的时候为什么传入的left和right为什么是0和nums.size() - 1,因为定义的区间为左闭右闭**。
|
||||
**注意:在调用traversal的时候传入的left和right为什么是0和nums.size() - 1,因为定义的区间为左闭右闭**。
|
||||
|
||||
|
||||
## 迭代法
|
||||
@ -354,10 +354,15 @@ class Solution:
|
||||
|
||||
```go
|
||||
func sortedArrayToBST(nums []int) *TreeNode {
|
||||
if len(nums)==0{return nil}//终止条件,最后数组为空则可以返回
|
||||
root:=&TreeNode{nums[len(nums)/2],nil,nil}//按照BSL的特点,从中间构造节点
|
||||
root.Left=sortedArrayToBST(nums[:len(nums)/2])//数组的左边为左子树
|
||||
root.Right=sortedArrayToBST(nums[len(nums)/2+1:])//数字的右边为右子树
|
||||
if len(nums) == 0 { //终止条件,最后数组为空则可以返回
|
||||
return nil
|
||||
}
|
||||
idx := len(nums)/2
|
||||
root := &TreeNode{Val: nums[idx]}
|
||||
|
||||
root.Left = sortedArrayToBST(nums[:idx])
|
||||
root.Right = sortedArrayToBST(nums[idx+1:])
|
||||
|
||||
return root
|
||||
}
|
||||
```
|
||||
@ -384,33 +389,33 @@ var sortedArrayToBST = function (nums) {
|
||||
迭代
|
||||
```JavaScript
|
||||
var sortedArrayToBST = function(nums) {
|
||||
if(nums.length===0){
|
||||
if(nums.length===0) {
|
||||
return null;
|
||||
}
|
||||
let root=new TreeNode(0); //初始根节点
|
||||
let nodeQue=[root]; //放遍历的节点,并初始化
|
||||
let leftQue=[0]; //放左区间的下标,初始化
|
||||
let rightQue=[nums.length-1]; // 放右区间的下标
|
||||
let root = new TreeNode(0); //初始根节点
|
||||
let nodeQue = [root]; //放遍历的节点,并初始化
|
||||
let leftQue = [0]; //放左区间的下标,初始化
|
||||
let rightQue = [nums.length-1]; // 放右区间的下标
|
||||
|
||||
while(nodeQue.length){
|
||||
let curNode=nodeQue.pop();
|
||||
let left=leftQue.pop();
|
||||
let right=rightQue.pop();
|
||||
let mid=left+Math.floor((right-left)/2);
|
||||
while(nodeQue.length) {
|
||||
let curNode = nodeQue.pop();
|
||||
let left = leftQue.pop();
|
||||
let right = rightQue.pop();
|
||||
let mid = left + Math.floor((right-left)/2);
|
||||
|
||||
curNode.val=nums[mid]; //将下标为mid的元素给中间节点
|
||||
curNode.val = nums[mid]; //将下标为mid的元素给中间节点
|
||||
|
||||
// 处理左区间
|
||||
if(left<=mid-1){
|
||||
curNode.left=new TreeNode(0);
|
||||
if(left <= mid-1) {
|
||||
curNode.left = new TreeNode(0);
|
||||
nodeQue.push(curNode.left);
|
||||
leftQue.push(left);
|
||||
rightQue.push(mid-1);
|
||||
}
|
||||
|
||||
// 处理右区间
|
||||
if(right>=mid+1){
|
||||
curNode.right=new TreeNode(0);
|
||||
if(right >= mid+1) {
|
||||
curNode.right = new TreeNode(0);
|
||||
nodeQue.push(curNode.right);
|
||||
leftQue.push(mid+1);
|
||||
rightQue.push(right);
|
||||
|
||||
@ -303,14 +303,22 @@ class Solution:
|
||||
|
||||
递归法:
|
||||
```go
|
||||
//利用BSL的性质(前序遍历有序)
|
||||
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
|
||||
if root==nil{return nil}
|
||||
if root.Val>p.Val&&root.Val>q.Val{//当前节点的值大于给定的值,则说明满足条件的在左边
|
||||
return lowestCommonAncestor(root.Left,p,q)
|
||||
}else if root.Val<p.Val&&root.Val<q.Val{//当前节点的值小于各点的值,则说明满足条件的在右边
|
||||
return lowestCommonAncestor(root.Right,p,q)
|
||||
}else {return root}//当前节点的值在给定值的中间(或者等于),即为最深的祖先
|
||||
if root == nil {
|
||||
return nil
|
||||
}
|
||||
for {
|
||||
if root.Val > p.Val && root.Val > q.Val {
|
||||
root = root.Left
|
||||
}
|
||||
if root.Val < p.Val && root.Val < q.Val {
|
||||
root = root.Right
|
||||
}
|
||||
if (root.Val - p.Val) * (root.Val - q.Val) <= 0 {
|
||||
return root
|
||||
}
|
||||
}
|
||||
return root
|
||||
}
|
||||
```
|
||||
|
||||
@ -326,11 +334,11 @@ var lowestCommonAncestor = function(root, p, q) {
|
||||
if(root === null) {
|
||||
return root;
|
||||
}
|
||||
if(root.val>p.val&&root.val>q.val) {
|
||||
if(root.val > p.val && root.val > q.val) {
|
||||
// 向左子树查询
|
||||
return root.left = lowestCommonAncestor(root.left,p,q);
|
||||
}
|
||||
if(root.val<p.val&&root.val<q.val) {
|
||||
if(root.val < p.val && root.val < q.val) {
|
||||
// 向右子树查询
|
||||
return root.right = lowestCommonAncestor(root.right,p,q);
|
||||
}
|
||||
@ -343,9 +351,9 @@ var lowestCommonAncestor = function(root, p, q) {
|
||||
var lowestCommonAncestor = function(root, p, q) {
|
||||
// 使用迭代的方法
|
||||
while(root) {
|
||||
if(root.val>p.val&&root.val>q.val) {
|
||||
if(root.val > p.val && root.val > q.val) {
|
||||
root = root.left;
|
||||
}else if(root.val<p.val&&root.val<q.val) {
|
||||
}else if(root.val < p.val && root.val < q.val) {
|
||||
root = root.right;
|
||||
}else {
|
||||
return root;
|
||||
|
||||
@ -48,7 +48,7 @@
|
||||
|
||||
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
|
||||
|
||||
接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。
|
||||
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
|
||||
|
||||
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
|
||||
|
||||
@ -66,9 +66,9 @@
|
||||
|
||||
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
|
||||
|
||||
因为遇到 q 或者 p 就返回,这样也包含了 q 或者 p 本省就是 公共祖先的情况。
|
||||
因为遇到 q 或者 p 就返回,这样也包含了 q 或者 p 本身就是 公共祖先的情况。
|
||||
|
||||
这一点是很多录友容易忽略的,在下面的代码讲解中,可以在去体会。
|
||||
这一点是很多录友容易忽略的,在下面的代码讲解中,可以再去体会。
|
||||
|
||||
递归三部曲:
|
||||
|
||||
@ -86,9 +86,9 @@ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
|
||||
|
||||
* 确定终止条件
|
||||
|
||||
遇到空的话,然后然后空,因为树都是空了,所以返回空。
|
||||
遇到空的话,因为树都是空了,所以返回空。
|
||||
|
||||
那么我们来说一说,如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到,那么中节点处理逻辑,后下面讲解。
|
||||
那么我们来说一说,如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到,那么中节点的处理逻辑,下面讲解。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -167,7 +167,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
|
||||
|
||||
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
|
||||
|
||||
这里点也很重要,可能刷过这道题目的同学,都不清楚结果究竟是如何从底层一层一层传到头结点的。
|
||||
这里也很重要,可能刷过这道题目的同学,都不清楚结果究竟是如何从底层一层一层传到头结点的。
|
||||
|
||||
那么如果left和right都为空,则返回left或者right都是可以的,也就是返回空。
|
||||
|
||||
@ -231,7 +231,7 @@ public:
|
||||
|
||||
**那么我给大家归纳如下三点**:
|
||||
|
||||
1. 求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历(即:回溯)实现从低向上的遍历方式。
|
||||
1. 求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历(即:回溯)实现从底向上的遍历方式。
|
||||
|
||||
2. 在回溯的过程中,必然要遍历整棵二叉树,即使已经找到结果了,依然要把其他节点遍历完,因为要使用递归函数的返回值(也就是代码中的left和right)做逻辑判断。
|
||||
|
||||
@ -332,16 +332,16 @@ var lowestCommonAncestor = function(root, p, q) {
|
||||
// 1. 确定递归的函数
|
||||
const travelTree = function(root,p,q) {
|
||||
// 2. 确定递归终止条件
|
||||
if(root === null || root === p||root === q) {
|
||||
if(root === null || root === p || root === q) {
|
||||
return root;
|
||||
}
|
||||
// 3. 确定递归单层逻辑
|
||||
let left = travelTree(root.left,p,q);
|
||||
let right = travelTree(root.right,p,q);
|
||||
if(left !== null&&right !== null) {
|
||||
if(left !== null && right !== null) {
|
||||
return root;
|
||||
}
|
||||
if(left ===null) {
|
||||
if(left === null) {
|
||||
return right;
|
||||
}
|
||||
return left;
|
||||
|
||||
@ -25,7 +25,7 @@
|
||||
|
||||
# 思路
|
||||
|
||||
搜索树的节点删除要比节点增加复杂的多,有很多情况需要考虑,做好心里准备。
|
||||
搜索树的节点删除要比节点增加复杂的多,有很多情况需要考虑,做好心理准备。
|
||||
|
||||
## 递归
|
||||
|
||||
@ -33,7 +33,7 @@
|
||||
|
||||
* 确定递归函数参数以及返回值
|
||||
|
||||
说道递归函数的返回值,在[二叉树:搜索树中的插入操作](https://programmercarl.com/0701.二叉搜索树中的插入操作.html)中通过递归返回值来加入新节点, 这里也可以通过递归返回值删除节点。
|
||||
说到递归函数的返回值,在[二叉树:搜索树中的插入操作](https://programmercarl.com/0701.二叉搜索树中的插入操作.html)中通过递归返回值来加入新节点, 这里也可以通过递归返回值删除节点。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -66,7 +66,7 @@ if (root == nullptr) return root;
|
||||
|
||||

|
||||
|
||||
动画中棵二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
|
||||
动画中的二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
|
||||
|
||||
将删除节点(元素7)的左孩子放到删除节点(元素7)的右子树的最左面节点(元素8)的左孩子上,就是把5为根节点的子树移到了8的左孩子的位置。
|
||||
|
||||
@ -251,7 +251,7 @@ public:
|
||||
|
||||
**这里最关键的逻辑就是第五种情况(删除一个左右孩子都不为空的节点),这种情况一定要想清楚**。
|
||||
|
||||
而且就算想清楚了,对应的代码也未必可以写出来,所以**这道题目即考察思维逻辑,也考察代码能力**。
|
||||
而且就算想清楚了,对应的代码也未必可以写出来,所以**这道题目既考察思维逻辑,也考察代码能力**。
|
||||
|
||||
递归中我给出了两种写法,推荐大家学会第一种(利用搜索树的特性)就可以了,第二种递归写法其实是比较绕的。
|
||||
|
||||
@ -390,39 +390,39 @@ class Solution:
|
||||
```Go
|
||||
// 递归版本
|
||||
func deleteNode(root *TreeNode, key int) *TreeNode {
|
||||
if root==nil{
|
||||
if root == nil {
|
||||
return nil
|
||||
}
|
||||
if key<root.Val{
|
||||
root.Left=deleteNode(root.Left,key)
|
||||
if key < root.Val {
|
||||
root.Left = deleteNode(root.Left, key)
|
||||
return root
|
||||
}
|
||||
if key>root.Val{
|
||||
root.Right=deleteNode(root.Right,key)
|
||||
if key > root.Val {
|
||||
root.Right = deleteNode(root.Right, key)
|
||||
return root
|
||||
}
|
||||
if root.Right==nil{
|
||||
if root.Right == nil {
|
||||
return root.Left
|
||||
}
|
||||
if root.Left==nil{
|
||||
if root.Left == nil{
|
||||
return root.Right
|
||||
}
|
||||
minnode:=root.Right
|
||||
for minnode.Left!=nil{
|
||||
minnode=minnode.Left
|
||||
minnode := root.Right
|
||||
for minnode.Left != nil {
|
||||
minnode = minnode.Left
|
||||
}
|
||||
root.Val=minnode.Val
|
||||
root.Right=deleteNode1(root.Right)
|
||||
root.Val = minnode.Val
|
||||
root.Right = deleteNode1(root.Right)
|
||||
return root
|
||||
}
|
||||
|
||||
func deleteNode1(root *TreeNode)*TreeNode{
|
||||
if root.Left==nil{
|
||||
pRight:=root.Right
|
||||
root.Right=nil
|
||||
func deleteNode1(root *TreeNode)*TreeNode {
|
||||
if root.Left == nil {
|
||||
pRight := root.Right
|
||||
root.Right = nil
|
||||
return pRight
|
||||
}
|
||||
root.Left=deleteNode1(root.Left)
|
||||
root.Left = deleteNode1(root.Left)
|
||||
return root
|
||||
}
|
||||
// 迭代版本
|
||||
|
||||
@ -54,7 +54,7 @@
|
||||
|
||||
1. 这个树都遍历了,用map统计频率
|
||||
|
||||
至于用前中后序那种遍历也不重要,因为就是要全遍历一遍,怎么个遍历法都行,层序遍历都没毛病!
|
||||
至于用前中后序哪种遍历也不重要,因为就是要全遍历一遍,怎么个遍历法都行,层序遍历都没毛病!
|
||||
|
||||
这里采用前序遍历,代码如下:
|
||||
|
||||
@ -354,7 +354,7 @@ public:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int[] findMode(FindModeInBinarySearchTree.TreeNode root) {
|
||||
public int[] findMode(TreeNode root) {
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
List<Integer> list = new ArrayList<>();
|
||||
if (root == null) return list.stream().mapToInt(Integer::intValue).toArray();
|
||||
@ -375,7 +375,7 @@ class Solution {
|
||||
return list.stream().mapToInt(Integer::intValue).toArray();
|
||||
}
|
||||
|
||||
void searchBST(FindModeInBinarySearchTree.TreeNode curr, Map<Integer, Integer> map) {
|
||||
void searchBST(TreeNode curr, Map<Integer, Integer> map) {
|
||||
if (curr == null) return;
|
||||
map.put(curr.val, map.getOrDefault(curr.val, 0) + 1);
|
||||
searchBST(curr.left, map);
|
||||
@ -556,46 +556,7 @@ class Solution:
|
||||
```
|
||||
## Go
|
||||
|
||||
暴力法(非BSL)
|
||||
|
||||
```go
|
||||
func findMode(root *TreeNode) []int {
|
||||
var history map[int]int
|
||||
var maxValue int
|
||||
var maxIndex int
|
||||
var result []int
|
||||
history=make(map[int]int)
|
||||
traversal(root,history)
|
||||
for k,value:=range history{
|
||||
if value>maxValue{
|
||||
maxValue=value
|
||||
maxIndex=k
|
||||
}
|
||||
}
|
||||
for k,value:=range history{
|
||||
if value==history[maxIndex]{
|
||||
result=append(result,k)
|
||||
}
|
||||
}
|
||||
return result
|
||||
}
|
||||
func traversal(root *TreeNode,history map[int]int){
|
||||
if root.Left!=nil{
|
||||
traversal(root.Left,history)
|
||||
}
|
||||
if value,ok:=history[root.Val];ok{
|
||||
history[root.Val]=value+1
|
||||
}else{
|
||||
history[root.Val]=1
|
||||
}
|
||||
if root.Right!=nil{
|
||||
traversal(root.Right,history)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
计数法,不使用额外空间,利用二叉树性质,中序遍历
|
||||
|
||||
```go
|
||||
func findMode(root *TreeNode) []int {
|
||||
res := make([]int, 0)
|
||||
|
||||
@ -248,28 +248,6 @@ class Solution:
|
||||
## Go:
|
||||
|
||||
中序遍历,然后计算最小差值
|
||||
|
||||
```go
|
||||
func getMinimumDifference(root *TreeNode) int {
|
||||
var res []int
|
||||
findMIn(root,&res)
|
||||
min:=1000000//一个比较大的值
|
||||
for i:=1;i<len(res);i++{
|
||||
tempValue:=res[i]-res[i-1]
|
||||
if tempValue<min{
|
||||
min=tempValue
|
||||
}
|
||||
}
|
||||
return min
|
||||
}
|
||||
//中序遍历
|
||||
func findMIn(root *TreeNode,res *[]int){
|
||||
if root==nil{return}
|
||||
findMIn(root.Left,res)
|
||||
*res=append(*res,root.Val)
|
||||
findMIn(root.Right,res)
|
||||
}
|
||||
```
|
||||
```go
|
||||
// 中序遍历的同时计算最小值
|
||||
func getMinimumDifference(root *TreeNode) int {
|
||||
|
||||
@ -45,11 +45,11 @@
|
||||
|
||||
# 思路
|
||||
|
||||
一看到累加树,相信很多小伙伴都会疑惑:如何累加?遇到一个节点,然后在遍历其他节点累加?怎么一想这么麻烦呢。
|
||||
一看到累加树,相信很多小伙伴都会疑惑:如何累加?遇到一个节点,然后再遍历其他节点累加?怎么一想这么麻烦呢。
|
||||
|
||||
然后再发现这是一棵二叉搜索树,二叉搜索树啊,这是有序的啊。
|
||||
|
||||
那么有序的元素如果求累加呢?
|
||||
那么有序的元素如何求累加呢?
|
||||
|
||||
**其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。**
|
||||
|
||||
@ -233,23 +233,23 @@ class Solution:
|
||||
## Go
|
||||
|
||||
弄一个sum暂存其和值
|
||||
|
||||
```go
|
||||
//右中左
|
||||
func bstToGst(root *TreeNode) *TreeNode {
|
||||
var sum int
|
||||
RightMLeft(root,&sum)
|
||||
return root
|
||||
}
|
||||
func RightMLeft(root *TreeNode,sum *int) *TreeNode {
|
||||
if root==nil{return nil}//终止条件,遇到空节点就返回
|
||||
RightMLeft(root.Right,sum)//先遍历右边
|
||||
temp:=*sum//暂存总和值
|
||||
*sum+=root.Val//将总和值变更
|
||||
root.Val+=temp//更新节点值
|
||||
RightMLeft(root.Left,sum)//遍历左节点
|
||||
var pre int
|
||||
func convertBST(root *TreeNode) *TreeNode {
|
||||
pre = 0
|
||||
traversal(root)
|
||||
return root
|
||||
}
|
||||
|
||||
func traversal(cur *TreeNode) {
|
||||
if cur == nil {
|
||||
return
|
||||
}
|
||||
traversal(cur.Right)
|
||||
cur.Val += pre
|
||||
pre = cur.Val
|
||||
traversal(cur.Left)
|
||||
}
|
||||
```
|
||||
|
||||
## JavaScript
|
||||
|
||||
@ -46,7 +46,7 @@
|
||||
|
||||
1. **确定递归函数的参数和返回值:**
|
||||
|
||||
首先那么要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点。
|
||||
首先要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -56,7 +56,7 @@ TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
|
||||
|
||||
2. **确定终止条件:**
|
||||
|
||||
因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了啊(如果t2也为NULL也无所谓,合并之后就是NULL)。
|
||||
因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了(如果t2也为NULL也无所谓,合并之后就是NULL)。
|
||||
|
||||
反过来如果t2 == NULL,那么两个数合并就是t1(如果t1也为NULL也无所谓,合并之后就是NULL)。
|
||||
|
||||
@ -70,7 +70,7 @@ if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1
|
||||
|
||||
3. **确定单层递归的逻辑:**
|
||||
|
||||
单层递归的逻辑就比较好些了,这里我们用重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
|
||||
单层递归的逻辑就比较好写了,这里我们重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
|
||||
|
||||
那么单层递归中,就要把两棵树的元素加到一起。
|
||||
```
|
||||
@ -144,7 +144,7 @@ public:
|
||||
|
||||
**但是前序遍历是最好理解的,我建议大家用前序遍历来做就OK。**
|
||||
|
||||
如上的方法修改了t1的结构,当然也可以不修改t1和t2的结构,重新定一个树。
|
||||
如上的方法修改了t1的结构,当然也可以不修改t1和t2的结构,重新定义一个树。
|
||||
|
||||
不修改输入树的结构,前序遍历,代码如下:
|
||||
|
||||
@ -214,7 +214,7 @@ public:
|
||||
|
||||
## 拓展
|
||||
|
||||
当然也可以秀一波指针的操作,这是我写的野路子,大家就随便看看就行了,以防带跑遍了。
|
||||
当然也可以秀一波指针的操作,这是我写的野路子,大家就随便看看就行了,以防带跑偏了。
|
||||
|
||||
如下代码中,想要更改二叉树的值,应该传入指向指针的指针。
|
||||
|
||||
@ -252,7 +252,7 @@ public:
|
||||
|
||||
迭代法中,一般一起操作两个树都是使用队列模拟类似层序遍历,同时处理两个树的节点,这种方式最好理解,如果用模拟递归的思路的话,要复杂一些。
|
||||
|
||||
最后拓展中,我给了一个操作指针的野路子,大家随便看看就行了,如果学习C++的话,可以在去研究研究。
|
||||
最后拓展中,我给了一个操作指针的野路子,大家随便看看就行了,如果学习C++的话,可以再去研究研究。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
@ -417,43 +417,7 @@ class Solution:
|
||||
### Go
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
//前序遍历(递归遍历,跟105 106差不多的思路)
|
||||
func mergeTrees(t1 *TreeNode, t2 *TreeNode) *TreeNode {
|
||||
var value int
|
||||
var nullNode *TreeNode//空node,便于遍历
|
||||
nullNode=&TreeNode{
|
||||
Val:0,
|
||||
Left:nil,
|
||||
Right:nil}
|
||||
switch {
|
||||
case t1==nil&&t2==nil: return nil//终止条件
|
||||
default : //如果其中一个节点为空,则将该节点置为nullNode,方便下次遍历
|
||||
if t1==nil{
|
||||
value=t2.Val
|
||||
t1=nullNode
|
||||
}else if t2==nil{
|
||||
value=t1.Val
|
||||
t2=nullNode
|
||||
}else {
|
||||
value=t1.Val+t2.Val
|
||||
}
|
||||
}
|
||||
root:=&TreeNode{//构造新的二叉树
|
||||
Val: value,
|
||||
Left: mergeTrees(t1.Left,t2.Left),
|
||||
Right: mergeTrees(t1.Right,t2.Right)}
|
||||
return root
|
||||
}
|
||||
|
||||
// 前序遍历简洁版
|
||||
// 前序遍历
|
||||
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
|
||||
if root1 == nil {
|
||||
return root2
|
||||
@ -479,28 +443,28 @@ func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
|
||||
queue = append(queue,root1)
|
||||
queue = append(queue,root2)
|
||||
|
||||
for size:=len(queue);size>0;size=len(queue){
|
||||
for size := len(queue); size>0; size=len(queue) {
|
||||
node1 := queue[0]
|
||||
queue = queue[1:]
|
||||
node2 := queue[0]
|
||||
queue = queue[1:]
|
||||
node1.Val += node2.Val
|
||||
// 左子树都不为空
|
||||
if node1.Left != nil && node2.Left != nil{
|
||||
if node1.Left != nil && node2.Left != nil {
|
||||
queue = append(queue,node1.Left)
|
||||
queue = append(queue,node2.Left)
|
||||
}
|
||||
// 右子树都不为空
|
||||
if node1.Right !=nil && node2.Right !=nil{
|
||||
queue = append(queue,node1.Right)
|
||||
queue = append(queue,node2.Right)
|
||||
if node1.Right !=nil && node2.Right !=nil {
|
||||
queue = append(queue, node1.Right)
|
||||
queue = append(queue, node2.Right)
|
||||
}
|
||||
// 树 1 的左子树为 nil,直接接上树 2 的左子树
|
||||
if node1.Left == nil{
|
||||
if node1.Left == nil {
|
||||
node1.Left = node2.Left
|
||||
}
|
||||
// 树 1 的右子树为 nil,直接接上树 2 的右子树
|
||||
if node1.Right == nil{
|
||||
if node1.Right == nil {
|
||||
node1.Right = node2.Right
|
||||
}
|
||||
}
|
||||
|
||||
@ -40,7 +40,7 @@
|
||||
|
||||
* 确定递归函数的参数和返回值
|
||||
|
||||
参数就是传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
|
||||
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -309,30 +309,24 @@ class Solution:
|
||||
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func constructMaximumBinaryTree(nums []int) *TreeNode {
|
||||
if len(nums)<1{return nil}
|
||||
//首选找到最大值
|
||||
index:=findMax(nums)
|
||||
//其次构造二叉树
|
||||
root:=&TreeNode{
|
||||
if len(nums) == 0 {
|
||||
return nil
|
||||
}
|
||||
// 找到最大值
|
||||
index := findMax(nums)
|
||||
// 构造二叉树
|
||||
root := &TreeNode {
|
||||
Val: nums[index],
|
||||
Left:constructMaximumBinaryTree(nums[:index]),//左半边
|
||||
Right:constructMaximumBinaryTree(nums[index+1:]),//右半边
|
||||
Left: constructMaximumBinaryTree(nums[:index]), //左半边
|
||||
Right: constructMaximumBinaryTree(nums[index+1:]),//右半边
|
||||
}
|
||||
return root
|
||||
}
|
||||
func findMax(nums []int) (index int){
|
||||
for i:=0;i<len(nums);i++{
|
||||
if nums[i]>nums[index]{
|
||||
index=i
|
||||
func findMax(nums []int) (index int) {
|
||||
for i, v := range nums {
|
||||
if nums[index] < v {
|
||||
index = i
|
||||
}
|
||||
}
|
||||
return
|
||||
|
||||
@ -59,7 +59,7 @@ public:
|
||||
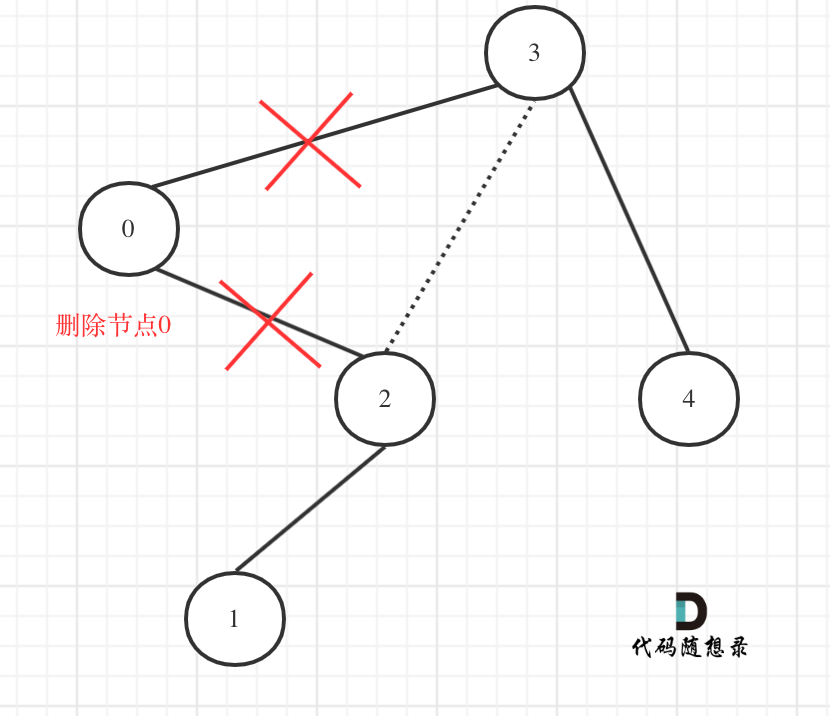
|
||||
|
||||
|
||||
理解了最关键部分了我们在递归三部曲:
|
||||
理解了最关键部分了我们再递归三部曲:
|
||||
|
||||
* 确定递归函数的参数以及返回值
|
||||
|
||||
@ -179,7 +179,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
只看代码,其实不太好理解节点是符合移除的,这一块大家可以自己在模拟模拟!
|
||||
只看代码,其实不太好理解节点是如何移除的,这一块大家可以自己再模拟模拟!
|
||||
|
||||
## 迭代法
|
||||
|
||||
@ -301,19 +301,19 @@ class Solution:
|
||||
|
||||
// 递归
|
||||
func trimBST(root *TreeNode, low int, high int) *TreeNode {
|
||||
if root==nil{
|
||||
if root == nil {
|
||||
return nil
|
||||
}
|
||||
if root.Val<low{//如果该节点值小于最小值,则该节点更换为该节点的右节点值,继续遍历
|
||||
right:=trimBST(root.Right,low,high)
|
||||
if root.Val < low { //如果该节点值小于最小值,则该节点更换为该节点的右节点值,继续遍历
|
||||
right := trimBST(root.Right, low, high)
|
||||
return right
|
||||
}
|
||||
if root.Val>high{//如果该节点的值大于最大值,则该节点更换为该节点的左节点值,继续遍历
|
||||
left:=trimBST(root.Left,low,high)
|
||||
if root.Val > high { //如果该节点的值大于最大值,则该节点更换为该节点的左节点值,继续遍历
|
||||
left := trimBST(root.Left, low, high)
|
||||
return left
|
||||
}
|
||||
root.Left=trimBST(root.Left,low,high)
|
||||
root.Right=trimBST(root.Right,low,high)
|
||||
root.Left = trimBST(root.Left, low, high)
|
||||
root.Right = trimBST(root.Right, low, high)
|
||||
return root
|
||||
}
|
||||
|
||||
@ -323,25 +323,25 @@ func trimBST(root *TreeNode, low int, high int) *TreeNode {
|
||||
return nil
|
||||
}
|
||||
// 处理 root,让 root 移动到[low, high] 范围内,注意是左闭右闭
|
||||
for root != nil && (root.Val<low||root.Val>high){
|
||||
if root.Val < low{
|
||||
for root != nil && (root.Val < low || root.Val > high) {
|
||||
if root.Val < low {
|
||||
root = root.Right
|
||||
}else{
|
||||
} else {
|
||||
root = root.Left
|
||||
}
|
||||
}
|
||||
cur := root
|
||||
// 此时 root 已经在[low, high] 范围内,处理左孩子元素小于 low 的情况(左节点是一定小于 root.Val,因此天然小于 high)
|
||||
for cur != nil{
|
||||
for cur.Left!=nil && cur.Left.Val < low{
|
||||
for cur != nil {
|
||||
for cur.Left != nil && cur.Left.Val < low {
|
||||
cur.Left = cur.Left.Right
|
||||
}
|
||||
cur = cur.Left
|
||||
}
|
||||
cur = root
|
||||
// 此时 root 已经在[low, high] 范围内,处理右孩子大于 high 的情况
|
||||
for cur != nil{
|
||||
for cur.Right!=nil && cur.Right.Val > high{
|
||||
for cur != nil {
|
||||
for cur.Right != nil && cur.Right.Val > high {
|
||||
cur.Right = cur.Right.Left
|
||||
}
|
||||
cur = cur.Right
|
||||
@ -359,24 +359,24 @@ var trimBST = function(root, low, high) {
|
||||
if(root === null) {
|
||||
return null;
|
||||
}
|
||||
while(root !==null &&(root.val<low||root.val>high)) {
|
||||
if(root.val<low) {
|
||||
while(root !== null && (root.val < low || root.val > high)) {
|
||||
if(root.val < low) {
|
||||
root = root.right;
|
||||
}else {
|
||||
root = root.left;
|
||||
}
|
||||
}
|
||||
let cur = root;
|
||||
while(cur!==null) {
|
||||
while(cur.left&&cur.left.val<low) {
|
||||
while(cur !== null) {
|
||||
while(cur.left && cur.left.val < low) {
|
||||
cur.left = cur.left.right;
|
||||
}
|
||||
cur = cur.left;
|
||||
}
|
||||
cur = root;
|
||||
//判断右子树大于high的情况
|
||||
while(cur!==null) {
|
||||
while(cur.right&&cur.right.val>high) {
|
||||
while(cur !== null) {
|
||||
while(cur.right && cur.right.val > high) {
|
||||
cur.right = cur.right.left;
|
||||
}
|
||||
cur = cur.right;
|
||||
@ -391,16 +391,16 @@ var trimBST = function (root,low,high) {
|
||||
if(root === null) {
|
||||
return null;
|
||||
}
|
||||
if(root.val<low) {
|
||||
let right = trimBST(root.right,low,high);
|
||||
if(root.val < low) {
|
||||
let right = trimBST(root.right, low, high);
|
||||
return right;
|
||||
}
|
||||
if(root.val>high) {
|
||||
let left = trimBST(root.left,low,high);
|
||||
if(root.val > high) {
|
||||
let left = trimBST(root.left, low, high);
|
||||
return left;
|
||||
}
|
||||
root.left = trimBST(root.left,low,high);
|
||||
root.right = trimBST(root.right,low,high);
|
||||
root.left = trimBST(root.left, low, high);
|
||||
root.right = trimBST(root.right, low, high);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
@ -24,7 +24,7 @@
|
||||
|
||||
## 思路
|
||||
|
||||
之前我们讲了都是普通二叉树,那么接下来看看二叉搜索树。
|
||||
之前我们讲的都是普通二叉树,那么接下来看看二叉搜索树。
|
||||
|
||||
在[关于二叉树,你该了解这些!](https://programmercarl.com/二叉树理论基础.html)中,我们已经讲过了二叉搜索树。
|
||||
|
||||
@ -269,13 +269,13 @@ class Solution:
|
||||
```go
|
||||
//递归法
|
||||
func searchBST(root *TreeNode, val int) *TreeNode {
|
||||
if root==nil||root.Val==val{
|
||||
if root == nil || root.Val == val {
|
||||
return root
|
||||
}
|
||||
if root.Val>val{
|
||||
return searchBST(root.Left,val)
|
||||
if root.Val > val {
|
||||
return searchBST(root.Left, val)
|
||||
}
|
||||
return searchBST(root.Right,val)
|
||||
return searchBST(root.Right, val)
|
||||
}
|
||||
```
|
||||
|
||||
@ -284,13 +284,13 @@ func searchBST(root *TreeNode, val int) *TreeNode {
|
||||
```go
|
||||
//迭代法
|
||||
func searchBST(root *TreeNode, val int) *TreeNode {
|
||||
for root!=nil{
|
||||
if root.Val>val{
|
||||
root=root.Left
|
||||
}else if root.Val<val{
|
||||
root=root.Right
|
||||
}else{
|
||||
break
|
||||
for root != nil {
|
||||
if root.Val > val {
|
||||
root = root.Left
|
||||
} else if root.Val < val {
|
||||
root = root.Right
|
||||
} else {
|
||||
return root
|
||||
}
|
||||
}
|
||||
return nil
|
||||
|
||||
@ -24,7 +24,7 @@
|
||||
|
||||
# 思路
|
||||
|
||||
其实这道题目其实是一道简单题目,**但是题目中的提示:有多种有效的插入方式,还可以重构二叉搜索树,一下子吓退了不少人**,瞬间感觉题目复杂了很多。
|
||||
这道题目其实是一道简单题目,**但是题目中的提示:有多种有效的插入方式,还可以重构二叉搜索树,一下子吓退了不少人**,瞬间感觉题目复杂了很多。
|
||||
|
||||
其实**可以不考虑题目中提示所说的改变树的结构的插入方式。**
|
||||
|
||||
@ -157,7 +157,7 @@ public:
|
||||
|
||||
我之所以举这个例子,是想说明通过递归函数的返回值完成父子节点的赋值是可以带来便利的。
|
||||
|
||||
**网上千变一律的代码,可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义,其实这里是有优化的!**
|
||||
**网上千篇一律的代码,可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义,其实这里是有优化的!**
|
||||
|
||||
|
||||
## 迭代
|
||||
@ -197,7 +197,7 @@ public:
|
||||
|
||||
首先在二叉搜索树中的插入操作,大家不用恐惧其重构搜索树,其实根本不用重构。
|
||||
|
||||
然后在递归中,我们重点讲了如果通过递归函数的返回值完成新加入节点和其父节点的赋值操作,并强调了搜索树的有序性。
|
||||
然后在递归中,我们重点讲了如何通过递归函数的返回值完成新加入节点和其父节点的赋值操作,并强调了搜索树的有序性。
|
||||
|
||||
最后依然给出了迭代的方法,迭代的方法就需要记录当前遍历节点的父节点了,这个和没有返回值的递归函数实现的代码逻辑是一样的。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user