Merge branch 'master' into master

README.md

@@ -254,7 +254,7 @@
 33. [二叉树：构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
 34. [二叉树：搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
 35. [二叉树：总结篇！（需要掌握的二叉树技能都在这里了）](./problems/二叉树总结篇.md)
- 
+
 ## 回溯算法 
 
 题目分类大纲如下：             

problems/0019.删除链表的倒数第N个节点.md

@@ -39,7 +39,7 @@
 
 分为如下几步：
 
-* 首先这里我推荐大家使用虚拟头结点，这样方面处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://programmercarl.com/0203.移除链表元素.html)
+* 首先这里我推荐大家使用虚拟头结点，这样方便处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://programmercarl.com/0203.移除链表元素.html)
 
 * 定义fast指针和slow指针，初始值为虚拟头结点，如图：
 

problems/0027.移除元素.md

@@ -81,7 +81,7 @@ public:
 
 **双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组、链表、字符串等操作的面试题，都使用双指针法。**
 
-后序都会一一介绍到，本题代码如下：
+后续都会一一介绍到，本题代码如下：
 
 ```CPP
 // 时间复杂度：O(n)

problems/0035.搜索插入位置.md

@@ -318,6 +318,31 @@ func searchInsert(_ nums: [Int], _ target: Int) -> Int {
 ```
 
 
+### PHP 
+
+```php
+// 二分法(1)：[左闭右闭]
+function searchInsert($nums, $target)
+{
+    $n = count($nums);
+    $l = 0;
+    $r = $n - 1;
+    while ($l <= $r) {
+        $mid = floor(($l + $r) / 2);
+        if ($nums[$mid] > $target) {
+            // 下次搜索在左区间：[$l,$mid-1]
+            $r = $mid - 1;
+        } else if ($nums[$mid] < $target) {
+			// 下次搜索在右区间：[$mid+1,$r]
+			$l = $mid + 1;
+		} else {
+			// 命中返回
+			return $mid;
+		}
+    }
+    return $r + 1;
+}
+```
 
 
 -----------------------

problems/0039.组合总和.md

@@ -370,18 +370,17 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int)
 ```js
 var combinationSum = function(candidates, target) {
     const res = [], path = [];
-    candidates.sort(); // 排序
+    candidates.sort((a,b)=>a-b); // 排序
     backtracking(0, 0);
     return res;
     function backtracking(j, sum) {
-        if (sum > target) return;
         if (sum === target) {
             res.push(Array.from(path));
             return;
         }
         for(let i = j; i < candidates.length; i++ ) {
             const n = candidates[i];
-            if(n > target - sum) continue;
+            if(n > target - sum) break;
             path.push(n);
             sum += n;
             backtracking(i, sum);

problems/0040.组合总和II.md

@@ -508,22 +508,27 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int)
  */
 var combinationSum2 = function(candidates, target) {
     const res = []; path = [], len = candidates.length;
-    candidates.sort();
+    candidates.sort((a,b)=>a-b);
     backtracking(0, 0);
     return res;
     function backtracking(sum, i) {
-        if (sum > target) return;
         if (sum === target) {
             res.push(Array.from(path));
             return;
         }
-        let f = -1;
         for(let j = i; j < len; j++) {
             const n = candidates[j];
-            if(n > target - sum || n === f) continue;
+            if(j > i && candidates[j] === candidates[j-1]){
+              //若当前元素和前一个元素相等
+              //则本次循环结束，防止出现重复组合
+              continue;
+            }
+            //如果当前元素值大于目标值-总和的值
+            //由于数组已排序，那么该元素之后的元素必定不满足条件
+            //直接终止当前层的递归
+            if(n > target - sum) break;
             path.push(n);
             sum += n;
-            f = n;
             backtracking(sum, j + 1);
             path.pop();
             sum -= n;

problems/0045.跳跃游戏II.md

@@ -217,18 +217,26 @@ class Solution:
 ### Go
 ```Go
 func jump(nums []int) int {
-	dp:=make([]int ,len(nums))
-	dp[0]=0
+    dp := make([]int, len(nums))
+    dp[0] = 0//初始第一格跳跃数一定为0
 
-	for i:=1;i<len(nums);i++{
-		dp[i]=i
-		for j:=0;j<i;j++{
-			if nums[j]+j>i{
-				dp[i]=min(dp[j]+1,dp[i])
-			}
-		}
-	}
-	return dp[len(nums)-1]
+    for i := 1; i < len(nums); i++ {
+        dp[i] = i
+        for j := 0; j < i; j++ {
+            if nums[j] + j >= i {//nums[j]为起点,j为往右跳的覆盖范围,这行表示从j能跳到i
+                dp[i] = min(dp[j] + 1, dp[i])//更新最小能到i的跳跃次数
+            }
+        }
+    }
+    return dp[len(nums)-1]
+}
+
+func min(a, b int) int {
+    if a < b {
+        return a
+    } else {
+        return b 
+    }
 }
 ```
 

problems/0053.最大子序和.md

@@ -140,7 +140,7 @@ public:
 ## 其他语言版本
 
 
-### Java 
+### Java
 ```java
 class Solution {
     public int maxSubArray(int[] nums) {
@@ -180,7 +180,7 @@ class Solution {
 }
 ```
 
-### Python 
+### Python
 ```python
 class Solution:
     def maxSubArray(self, nums: List[int]) -> int:
@@ -195,7 +195,7 @@ class Solution:
         return result
 ```
 
-### Go 
+### Go
 
 ```go
 func maxSubArray(nums []int) int {
@@ -212,6 +212,20 @@ func maxSubArray(nums []int) int {
 }
 ```
 
+### Rust
+```rust
+pub fn max_sub_array(nums: Vec<i32>) -> i32 {
+    let mut max_sum = i32::MIN;
+    let mut curr = 0;
+    for n in nums.iter() {
+        curr += n;
+        max_sum = max_sum.max(curr);
+        curr = curr.max(0);
+    }
+    max_sum
+}
+```
+
 ### Javascript:
 ```Javascript
 var maxSubArray = function(nums) {

problems/0056.合并区间.md

@@ -112,8 +112,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n\log n)$ ，有一个快排
-* 空间复杂度：$O(1)$，我没有算result数组（返回值所需容器占的空间）
+* 时间复杂度：O(nlog n) ，有一个快排
+* 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
 
 
 ## 总结

problems/0062.不同路径.md

@@ -273,7 +273,7 @@ public:
         return dp[m-1][n-1];
     }
 
-``` 
+```
 
 ### Python 
 ```python
@@ -347,7 +347,35 @@ var uniquePaths = function(m, n) {
 };
 ```
 
+### TypeScript
+
+```typescript
+function uniquePaths(m: number, n: number): number {
+    /**
+        dp[i][j]: 到达(i, j)的路径数
+        dp[0][*]: 1;
+        dp[*][0]: 1;
+        ...
+        dp[i][j]: dp[i - 1][j] + dp[i][j - 1];
+     */
+    const dp: number[][] = new Array(m).fill(0).map(_ => []);
+    for (let i = 0; i < m; i++) {
+        dp[i][0] = 1;
+    }
+    for (let i = 0; i < n; i++) {
+        dp[0][i] = 1;
+    }
+    for (let i = 1; i < m; i++) {
+        for (let j = 1; j < n; j++) {
+            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+        }
+    }
+    return dp[m - 1][n - 1];
+};
+```
+
 ### C
+
 ```c
 //初始化dp数组
 int **initDP(int m, int n) {

problems/0063.不同路径II.md

@@ -352,7 +352,38 @@ var uniquePathsWithObstacles = function(obstacleGrid) {
 };
 ```
 
-C
+### TypeScript
+
+```typescript
+function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
+    /**
+        dp[i][j]: 到达(i, j)的路径数
+        dp[0][*]: 用u表示第一个障碍物下标，则u之前为1，u之后（含u）为0
+        dp[*][0]: 同上
+        ...
+        dp[i][j]: obstacleGrid[i][j] === 1 ? 0 : dp[i-1][j] + dp[i][j-1];
+     */
+    const m: number = obstacleGrid.length;
+    const n: number = obstacleGrid[0].length;
+    const dp: number[][] = new Array(m).fill(0).map(_ => new Array(n).fill(0));
+    for (let i = 0; i < m && obstacleGrid[i][0] === 0; i++) {
+        dp[i][0] = 1;
+    }
+    for (let i = 0; i < n && obstacleGrid[0][i] === 0; i++) {
+        dp[0][i] = 1;
+    }
+    for (let i = 1; i < m; i++) {
+        for (let j = 1; j < n; j++) {
+            if (obstacleGrid[i][j] === 1) continue;
+            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+        }
+    }
+    return dp[m - 1][n - 1];
+};
+```
+
+### C
+
 ```c
 //初始化dp数组
 int **initDP(int m, int n, int** obstacleGrid) {

problems/0070.爬楼梯.md

@@ -308,7 +308,58 @@ var climbStairs = function(n) {
 };
 ```
 
+TypeScript
+
+> 爬2阶
+
+```typescript
+function climbStairs(n: number): number {
+    /**
+        dp[i]: i阶楼梯的方法种数
+        dp[1]: 1;
+        dp[2]: 2;
+        ...
+        dp[i]: dp[i - 1] + dp[i - 2];
+     */
+    const dp: number[] = [];
+    dp[1] = 1;
+    dp[2] = 2;
+    for (let i = 3; i <= n; i++) {
+        dp[i] = dp[i - 1] + dp[i - 2];
+    }
+    return dp[n];
+};
+```
+
+> 爬m阶
+
+```typescript
+function climbStairs(n: number): number {
+    /**
+        一次可以爬m阶
+        dp[i]: i阶楼梯的方法种数
+        dp[1]: 1;
+        dp[2]: 2;
+        dp[3]: dp[2] + dp[1];
+        ...
+        dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; 从i-1加到max(i-m, 1)
+     */
+    const m: number = 2;    // 本题m为2
+    const dp: number[] = new Array(n + 1).fill(0);
+    dp[1] = 1;
+    dp[2] = 2;
+    for (let i = 3; i <= n; i++) {
+        const end: number = Math.max(i - m, 1);
+        for (let j = i - 1; j >= end; j--) {
+            dp[i] += dp[j];
+        }
+    }
+    return dp[n];
+};
+```
+
 ### C
+
 ```c
 int climbStairs(int n){
     //若n<=2，返回n

problems/0070.爬楼梯完全背包版本.md

@@ -199,6 +199,28 @@ var climbStairs = function(n) {
 };
 ```
 
+TypeScript：
+
+```typescript
+function climbStairs(n: number): number {
+    const m: number = 2;    // 本题m为2
+    const dp: number[] = new Array(n + 1).fill(0);
+    dp[0] = 1;
+    // 遍历背包
+    for (let i = 1; i <= n; i++) {
+        // 遍历物品
+        for (let j = 1; j <= m; j++) {
+            if (j <= i) {
+                dp[i] += dp[i - j];
+            }
+        }
+    }
+    return dp[n];
+};
+```
+
+
+
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0077.组合.md

@@ -27,7 +27,7 @@
 
 也可以直接看我的B站视频：[带你学透回溯算法-组合问题（对应力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv#reply3733925949)
 
-# 思路 
+## 思路 
 
 
 本题这是回溯法的经典题目。
@@ -232,7 +232,7 @@ void backtracking(参数) {
 
 **对比一下本题的代码，是不是发现有点像！** 所以有了这个模板，就有解题的大体方向，不至于毫无头绪。 
 
-# 总结 
+## 总结 
 
 组合问题是回溯法解决的经典问题，我们开始的时候给大家列举一个很形象的例子，就是n为100，k为50的话，直接想法就需要50层for循环。
 
@@ -242,7 +242,7 @@ void backtracking(参数) {
 
 接着用回溯法三部曲，逐步分析了函数参数、终止条件和单层搜索的过程。
 
-# 剪枝优化
+## 剪枝优化
 
 我们说过，回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。
 
@@ -324,7 +324,7 @@ public:
 };
 ```
 
-# 剪枝总结
+## 剪枝总结
 
 本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
 
@@ -334,10 +334,10 @@ public:
 
 
 
-# 其他语言版本
+## 其他语言版本
 
 
-## Java：
+### Java：
 ```java
 class Solution {
     List<List<Integer>> result = new ArrayList<>();
@@ -366,6 +366,8 @@ class Solution {
 }
 ```
 
+### Python 
+
 Python2:
 ```python
 class Solution(object):
@@ -395,7 +397,6 @@ class Solution(object):
         return result
 ```
 
-## Python 
 ```python
 class Solution:
     def combine(self, n: int, k: int) -> List[List[int]]:
@@ -432,7 +433,7 @@ class Solution:
 ```
 
 
-## javascript 
+### javascript 
 
 剪枝：
 ```javascript
@@ -456,7 +457,7 @@ const combineHelper = (n, k, startIndex) => {
 }
 ```
 
-## TypeScript
+### TypeScript
 
 ```typescript
 function combine(n: number, k: number): number[][] {
@@ -479,7 +480,7 @@ function combine(n: number, k: number): number[][] {
 
 
 
-## Go 
+### Go 
 ```Go
 var res [][]int 
 func combine(n int, k int) [][]int {
@@ -534,7 +535,7 @@ func backtrack(n,k,start int,track []int){
 }
 ```
 
-## C
+### C
 ```c
 int* path;
 int pathTop;
@@ -642,7 +643,7 @@ int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
 }
 ```
 
-## Swift
+### Swift
 
 ```swift
 func combine(_ n: Int, _ k: Int) -> [[Int]] {

problems/0096.不同的二叉搜索树.md

@@ -227,7 +227,33 @@ const numTrees =(n) => {
 };
 ```
 
-C:
+TypeScript
+
+```typescript
+function numTrees(n: number): number {
+    /**
+        dp[i]: i个节点对应的种树
+        dp[0]: -1; 无意义；
+        dp[1]: 1;
+        ...
+        dp[i]: 2 * dp[i - 1] + 
+            (dp[1] * dp[i - 2] + dp[2] * dp[i - 3] + ... + dp[i - 2] * dp[1]); 从1加到i-2
+     */
+    const dp: number[] = [];
+    dp[0] = -1; // 表示无意义
+    dp[1] = 1;
+    for (let i = 2; i <= n; i++) {
+        dp[i] = 2 * dp[i - 1];
+        for (let j = 1, end = i - 1; j < end; j++) {
+            dp[i] += dp[j] * dp[end - j];
+        }
+    }
+    return dp[n];
+};
+```
+
+### C
+
 ```c
 //开辟dp数组
 int *initDP(int n) {

problems/0101.对称二叉树.md

@@ -238,7 +238,7 @@ public:
 };
 ```
 
-# 总结
+## 总结
 
 这次我们又深度剖析了一道二叉树的“简单题”，大家会发现，真正的把题目搞清楚其实并不简单，leetcode上accept了和真正掌握了还是有距离的。
 
@@ -248,7 +248,7 @@ public:
 
 如果已经做过这道题目的同学，读完文章可以再去看看这道题目，思考一下，会有不一样的发现！
 
-# 相关题目推荐
+## 相关题目推荐
 
 这两道题目基本和本题是一样的，只要稍加修改就可以AC。
 

problems/0112.路径总和.md

@@ -377,22 +377,22 @@ class solution {
 
 ```java
 class solution {
-    public list<list<integer>> pathsum(treenode root, int targetsum) {
-        list<list<integer>> res = new arraylist<>();
+    public List<List<Integer>> pathsum(TreeNode root, int targetsum) {
+        List<List<Integer>> res = new ArrayList<>();
         if (root == null) return res; // 非空判断
-        
-        list<integer> path = new linkedlist<>();
+
+        List<Integer> path = new LinkedList<>();
         preorderdfs(root, targetsum, res, path);
         return res;
     }
 
-    public void preorderdfs(treenode root, int targetsum, list<list<integer>> res, list<integer> path) {
+    public void preorderdfs(TreeNode root, int targetsum, List<List<Integer>> res, List<Integer> path) {
         path.add(root.val);
         // 遇到了叶子节点
         if (root.left == null && root.right == null) {
             // 找到了和为 targetsum 的路径
             if (targetsum - root.val == 0) {
-                res.add(new arraylist<>(path));
+                res.add(new ArrayList<>(path));
             }
             return; // 如果和不为 targetsum，返回
         }

problems/0135.分发糖果.md

@@ -126,11 +126,11 @@ public:
 ## 其他语言版本
 
 
-### Java 
+### Java
 ```java
 class Solution {
-    /** 
-         分两个阶段 
+    /**
+         分两个阶段
          1、起点下标1 从左往右，只要 右边 比 左边 大，右边的糖果=左边 + 1
          2、起点下标 ratings.length - 2 从右往左， 只要左边 比 右边 大，此时 左边的糖果应该 取本身的糖果数（符合比它左边大） 和 右边糖果数 + 1 二者的最大值，这样才符合 它比它左边的大，也比它右边大
     */
@@ -160,7 +160,7 @@ class Solution {
 }
 ```
 
-### Python 
+### Python
 ```python
 class Solution:
     def candy(self, ratings: List[int]) -> int:
@@ -213,6 +213,25 @@ func findMax(num1 int ,num2 int) int{
 }
 ```
 
+### Rust
+```rust
+pub fn candy(ratings: Vec<i32>) -> i32 {
+    let mut candies = vec![1i32; ratings.len()];
+    for i in 1..ratings.len() {
+        if ratings[i - 1] < ratings[i] {
+            candies[i] = candies[i - 1] + 1;
+        }
+    }
+
+    for i in (0..ratings.len()-1).rev() {
+        if ratings[i] > ratings[i + 1] {
+            candies[i] = candies[i].max(candies[i + 1] + 1);
+        }
+    }
+    candies.iter().sum()
+}
+```
+
 ### Javascript:
 ```Javascript
 var candy = function(ratings) {
@@ -229,7 +248,7 @@ var candy = function(ratings) {
             candys[i] = Math.max(candys[i], candys[i + 1] + 1)
         }
     }
-    
+
     let count = candys.reduce((a, b) => {
         return a + b
     })

problems/0139.单词拆分.md

@@ -345,6 +345,48 @@ const wordBreak = (s, wordDict) => {
 }
 ```
 
+TypeScript：
+
+> 动态规划
+
+```typescript
+function wordBreak(s: string, wordDict: string[]): boolean {
+    const dp: boolean[] = new Array(s.length + 1).fill(false);
+    dp[0] = true;
+    for (let i = 1; i <= s.length; i++) {
+        for (let j = 0; j < i; j++) {
+            const tempStr: string = s.slice(j, i);
+            if (wordDict.includes(tempStr) && dp[j] === true) {
+                dp[i] = true;
+                break;
+            }
+        }
+    }
+    return dp[s.length];
+};
+```
+
+> 记忆化回溯
+
+```typescript
+function wordBreak(s: string, wordDict: string[]): boolean {
+    // 只需要记忆结果为false的情况
+    const memory: boolean[] = [];
+    return backTracking(s, wordDict, 0, memory);
+    function backTracking(s: string, wordDict: string[], startIndex: number, memory: boolean[]): boolean {
+        if (startIndex >= s.length) return true;
+        if (memory[startIndex] === false) return false;
+        for (let i = startIndex + 1, length = s.length; i <= length; i++) {
+            const str: string = s.slice(startIndex, i);
+            if (wordDict.includes(str) && backTracking(s, wordDict, i, memory))
+                return true;
+        }
+        memory[startIndex] = false;
+        return false;
+    }
+};
+```
+
 
 
 -----------------------

problems/0279.完全平方数.md

@@ -355,5 +355,24 @@ var numSquares2 = function(n) {
 };
 ```
 
+TypeScript：
+
+```typescript
+function numSquares(n: number): number {
+    const goodsNum: number = Math.floor(Math.sqrt(n));
+    const dp: number[] = new Array(n + 1).fill(Infinity);
+    dp[0] = 0;
+    for (let i = 1; i <= goodsNum; i++) {
+        const tempVal: number = i * i;
+        for (let j = tempVal; j <= n; j++) {
+            dp[j] = Math.min(dp[j], dp[j - tempVal] + 1);
+        }
+    }
+    return dp[n];
+};
+```
+
+
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0300.最长上升子序列.md

@@ -201,6 +201,23 @@ func max(x, y int) int {
 }
 ```
 
+Rust:
+```rust
+pub fn length_of_lis(nums: Vec<i32>) -> i32 {
+    let mut dp = vec![1; nums.len() + 1];
+    let mut result = 1;
+    for i in 1..nums.len() {
+        for j in 0..i {
+            if nums[j] < nums[i] {
+                dp[i] = dp[i].max(dp[j] + 1);
+            }
+            result = result.max(dp[i]);
+        }
+    }
+    result
+}
+```
+
 Javascript
 ```javascript
 const lengthOfLIS = (nums) => {

problems/0322.零钱兑换.md

@@ -220,7 +220,7 @@ class Solution:
             for j in range(coin, amount + 1):
                 dp[j] = min(dp[j], dp[j - coin] + 1)
         return dp[amount] if dp[amount] < amount + 1 else -1
-    
+
     def coinChange1(self, coins: List[int], amount: int) -> int:
         '''版本二'''
         # 初始化
@@ -302,6 +302,24 @@ func min(a, b int) int {
 
 ```
 
+Rust:
+
+```rust
+pub fn coin_change(coins: Vec<i32>, amount: i32) -> i32 {
+    let amount = amount as usize;
+    let mut dp = vec![i32::MAX; amount + 1];
+    dp[0] = 0;
+    for i in 0..coins.len() {
+        for j in coins[i] as usize..=amount {
+            if dp[j - coins[i] as usize] != i32::MAX {
+                dp[j] = dp[j].min(dp[j - coins[i] as usize] + 1);
+            }
+        }
+    }
+    if dp[amount] == i32::MAX { -1 } else { dp[amount] }
+}
+```
+
 Javascript：
 ```javascript
 const coinChange = (coins, amount) => {
@@ -322,7 +340,21 @@ const coinChange = (coins, amount) => {
 }
 ```
 
+TypeScript：
 
+```typescript
+function coinChange(coins: number[], amount: number): number {
+    const dp: number[] = new Array(amount + 1).fill(Infinity);
+    dp[0] = 0;
+    for (let i = 0; i < coins.length; i++) {
+        for (let j = coins[i]; j <= amount; j++) {
+            if (dp[j - coins[i]] === Infinity) continue;
+            dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
+        }
+    }
+    return dp[amount] === Infinity ? -1 : dp[amount];
+};
+```
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0343.整数拆分.md

@@ -274,7 +274,33 @@ var integerBreak = function(n) {
 };
 ```
 
-C:
+### TypeScript
+
+```typescript
+function integerBreak(n: number): number {
+    /**
+        dp[i]: i对应的最大乘积
+        dp[2]: 1;
+        ...
+        dp[i]: max(
+            1 * dp[i - 1], 1 * (i - 1),
+            2 * dp[i - 2], 2 * (i - 2),
+            ..., (i - 2) * dp[2], (i - 2) * 2
+        );
+     */
+    const dp: number[] = new Array(n + 1).fill(0);
+    dp[2] = 1;
+    for (let i = 3; i <= n; i++) {
+        for (let j = 1; j <= i - 2; j++) {
+            dp[i] = Math.max(dp[i], j * dp[i - j], j * (i - j));
+        }
+    }
+    return dp[n];
+};
+```
+
+### C
+
 ```c
 //初始化DP数组
 int *initDP(int num) {

problems/0377.组合总和Ⅳ.md

@@ -221,7 +221,27 @@ const combinationSum4 = (nums, target) => {
 };
 ```
 
+TypeScript：
+
+```typescript
+function combinationSum4(nums: number[], target: number): number {
+    const dp: number[] = new Array(target + 1).fill(0);
+    dp[0] = 1;
+    // 遍历背包
+    for (let i = 1; i <= target; i++) {
+        // 遍历物品
+        for (let j = 0, length = nums.length; j < length; j++) {
+            if (i >= nums[j]) {
+                dp[i] += dp[i - nums[j]];
+            }
+        }
+    }
+    return dp[target];
+};
+```
+
 Rust 
+
 ```Rust
 impl Solution {
     pub fn combination_sum4(nums: Vec<i32>, target: i32) -> i32 {

problems/0383.赎金信.md

@@ -114,23 +114,25 @@ Java：
 ```Java
 class Solution {
     public boolean canConstruct(String ransomNote, String magazine) {
-        //记录杂志字符串出现的次数
-        int[] arr = new int[26];
-        int temp;
-        for (int i = 0; i < magazine.length(); i++) {
-            temp = magazine.charAt(i) - 'a';
-            arr[temp]++;
+        // 定义一个哈希映射数组
+        int[] record = new int[26];
+
+        // 遍历
+        for(char c : magazine.toCharArray()){
+            record[c - 'a'] += 1;
         }
-        for (int i = 0; i < ransomNote.length(); i++) {
-            temp = ransomNote.charAt(i) - 'a';
-            //对于金信中的每一个字符都在数组中查找
-            //找到相应位减一，否则找不到返回false
-            if (arr[temp] > 0) {
-                arr[temp]--;
-            } else {
+
+        for(char c : ransomNote.toCharArray()){
+            record[c - 'a'] -= 1;
+        }
+        
+        // 如果数组中存在负数，说明ransomNote字符串总存在magazine中没有的字符
+        for(int i : record){
+            if(i < 0){
                 return false;
             }
         }
+
         return true;
     }
 }

problems/0416.分割等和子集.md

@@ -416,6 +416,7 @@ var canPartition = function(nums) {
 };
 ```
 
+
 C:
 二维dp：
 ```c
@@ -517,6 +518,62 @@ bool canPartition(int* nums, int numsSize){
 }
 ```
 
+TypeScript:
+
+> 一维数组，简洁
+
+```typescript
+function canPartition(nums: number[]): boolean {
+    const sum: number = nums.reduce((pre, cur) => pre + cur);
+    if (sum % 2 === 1) return false;
+    const bagSize: number = sum / 2;
+    const goodsNum: number = nums.length;
+    const dp: number[] = new Array(bagSize + 1).fill(0);
+    for (let i = 0; i < goodsNum; i++) {
+        for (let j = bagSize; j >= nums[i]; j--) {
+            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
+        }
+    }
+    return dp[bagSize] === bagSize;
+};
+```
+
+> 二维数组，易懂
+
+```typescript
+function canPartition(nums: number[]): boolean {
+    /**
+        weightArr = nums;
+        valueArr = nums;
+        bagSize = sum / 2; (sum为nums各元素总和);
+        按照0-1背包处理
+     */
+    const sum: number = nums.reduce((pre, cur) => pre + cur);
+    if (sum % 2 === 1) return false;
+    const bagSize: number = sum / 2;
+    const weightArr: number[] = nums;
+    const valueArr: number[] = nums;
+    const goodsNum: number = weightArr.length;
+    const dp: number[][] = new Array(goodsNum)
+    	.fill(0)
+    	.map(_ => new Array(bagSize + 1).fill(0));
+    for (let i = weightArr[0]; i <= bagSize; i++) {
+        dp[0][i] = valueArr[0];
+    }
+    for (let i = 1; i < goodsNum; i++) {
+        for (let j = 0; j <= bagSize; j++) {
+            if (j < weightArr[i]) {
+                dp[i][j] = dp[i - 1][j];
+            } else {
+                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weightArr[i]] + valueArr[i]);
+            }
+        }
+    }
+    return dp[goodsNum - 1][bagSize] === bagSize;
+};
+```
+
+
 
 
 -----------------------

problems/0435.无重叠区间.md

@@ -93,7 +93,7 @@ public:
 };
 ```
 * 时间复杂度：O(nlog n) ，有一个快排
-* 空间复杂度：O(1)
+* 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
 
 大家此时会发现如此复杂的一个问题，代码实现却这么简单！
 

problems/0452.用最少数量的箭引爆气球.md

@@ -105,8 +105,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n\log n)$，因为有一个快排
-* 空间复杂度：$O(1)$
+* 时间复杂度：O(nlog n)，因为有一个快排
+* 空间复杂度：O(1)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
 
 可以看出代码并不复杂。
 

problems/0455.分发饼干.md

@@ -106,7 +106,7 @@ public:
 ## 其他语言版本
 
 
-### Java 
+### Java
 ```java
 class Solution {
     // 思路1：优先考虑饼干，小饼干先喂饱小胃口
@@ -145,7 +145,7 @@ class Solution {
 }
 ```
 
-### Python 
+### Python
 ```python
 class Solution:
     # 思路1：优先考虑胃饼干
@@ -166,13 +166,13 @@ class Solution:
         s.sort()
         start, count = len(s) - 1, 0
         for index in range(len(g) - 1, -1, -1): # 先喂饱大胃口
-            if start >= 0 and g[index] <= s[start]: 
+            if start >= 0 and g[index] <= s[start]:
                 start -= 1
                 count += 1
         return count
 ```
 
-### Go 
+### Go
 ```golang
 //排序后，局部最优
 func findContentChildren(g []int, s []int) int {
@@ -191,7 +191,27 @@ func findContentChildren(g []int, s []int) int {
 }
 ```
 
-### Javascript 
+### Rust
+```rust
+pub fn find_content_children(children: Vec<i32>, cookie: Vec<i32>) -> i32 {
+    let mut children = children;
+    let mut cookies = cookie;
+    children.sort();
+    cookies.sort();
+
+    let (mut child, mut cookie) = (0usize, 0usize);
+    while child < children.len() && cookie < cookies.len() {
+        // 优先选择最小饼干喂饱孩子
+        if children[child] <= cookies[cookie] {
+            child += 1;
+        }
+        cookie += 1
+    }
+    child as i32
+}
+```
+
+### Javascript
 ```js
 var findContentChildren = function(g, s) {
     g = g.sort((a, b) => a - b)
@@ -203,7 +223,7 @@ var findContentChildren = function(g, s) {
             result++
             index--
         }
-    } 
+    }
     return result
 };
 
@@ -251,7 +271,7 @@ function findContentChildren(g: number[], s: number[]): number {
 };
 ```
 
-### C 
+### C
 
 ```c
 int cmp(int* a, int* b) {
@@ -261,7 +281,7 @@ int cmp(int* a, int* b) {
 int findContentChildren(int* g, int gSize, int* s, int sSize){
     if(sSize == 0)
         return 0;
-    
+
     //将两个数组排序为升序
     qsort(g, gSize, sizeof(int), cmp);
     qsort(s, sSize, sizeof(int), cmp);

problems/0474.一和零.md

@@ -323,6 +323,129 @@ const findMaxForm = (strs, m, n) => {
 };
 ```
 
+TypeScript：
+
+> 滚动数组，二维数组法
+
+```typescript
+type BinaryInfo = { numOfZero: number, numOfOne: number };
+function findMaxForm(strs: string[], m: number, n: number): number {
+    const goodsNum: number = strs.length;
+    const dp: number[][] = new Array(m + 1).fill(0)
+        .map(_ => new Array(n + 1).fill(0));
+    for (let i = 0; i < goodsNum; i++) {
+        const { numOfZero, numOfOne } = countBinary(strs[i]);
+        for (let j = m; j >= numOfZero; j--) {
+            for (let k = n; k >= numOfOne; k--) {
+                dp[j][k] = Math.max(dp[j][k], dp[j - numOfZero][k - numOfOne] + 1);
+            }
+        }
+    }
+    return dp[m][n];
+};
+function countBinary(str: string): BinaryInfo {
+    let numOfZero: number = 0,
+        numOfOne: number = 0;
+    for (let s of str) {
+        if (s === '0') {
+            numOfZero++;
+        } else {
+            numOfOne++;
+        }
+    }
+    return { numOfZero, numOfOne };
+}
+```
+
+> 传统背包，三维数组法
+
+```typescript
+type BinaryInfo = { numOfZero: number, numOfOne: number };
+function findMaxForm(strs: string[], m: number, n: number): number {
+    /**
+        dp[i][j][k]: 前i个物品中, 背包的0容量为j, 1容量为k, 最多能放的物品数量
+     */
+    const goodsNum: number = strs.length;
+    const dp: number[][][] = new Array(goodsNum).fill(0)
+        .map(_ => new Array(m + 1)
+            .fill(0)
+            .map(_ => new Array(n + 1).fill(0))
+        );
+    const { numOfZero, numOfOne } = countBinary(strs[0]);
+    for (let i = numOfZero; i <= m; i++) {
+        for (let j = numOfOne; j <= n; j++) {
+            dp[0][i][j] = 1;
+        }
+    }
+    for (let i = 1; i < goodsNum; i++) {
+        const { numOfZero, numOfOne } = countBinary(strs[i]);
+        for (let j = 0; j <= m; j++) {
+            for (let k = 0; k <= n; k++) {
+                if (j < numOfZero || k < numOfOne) {
+                    dp[i][j][k] = dp[i - 1][j][k];
+                } else {
+                    dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - numOfZero][k - numOfOne] + 1);
+                }
+            }
+        }
+    }
+    return dp[dp.length - 1][m][n];
+};
+function countBinary(str: string): BinaryInfo {
+    let numOfZero: number = 0,
+        numOfOne: number = 0;
+    for (let s of str) {
+        if (s === '0') {
+            numOfZero++;
+        } else {
+            numOfOne++;
+        }
+    }
+    return { numOfZero, numOfOne };
+}
+```
+
+> 回溯法（会超时）
+
+```typescript
+function findMaxForm(strs: string[], m: number, n: number): number {
+    /**
+        思路：暴力枚举strs的所有子集，记录符合条件子集的最大长度
+     */
+    let resMax: number = 0;
+    backTrack(strs, m, n, 0, []);
+    return resMax;
+    function backTrack(
+        strs: string[], m: number, n: number,
+        startIndex: number, route: string[]
+    ): void {
+        if (startIndex === strs.length) return;
+        for (let i = startIndex, length = strs.length; i < length; i++) {
+            route.push(strs[i]);
+            if (isValidSubSet(route, m, n)) {
+                resMax = Math.max(resMax, route.length);
+                backTrack(strs, m, n, i + 1, route);
+            }
+            route.pop();
+        }
+    }
+};
+function isValidSubSet(strs: string[], m: number, n: number): boolean {
+    let zeroNum: number = 0,
+        oneNum: number = 0;
+    strs.forEach(str => {
+        for (let s of str) {
+            if (s === '0') {
+                zeroNum++;
+            } else {
+                oneNum++;
+            }
+        }
+    });
+    return zeroNum <= m && oneNum <= n;
+}
+```
+
 
 
 -----------------------

problems/0494.目标和.md

@@ -351,6 +351,25 @@ const findTargetSumWays = (nums, target) => {
 };
 ```
 
+TypeScript：
+
+```typescript
+function findTargetSumWays(nums: number[], target: number): number {
+    const sum: number = nums.reduce((pre, cur) => pre + cur);
+    if (Math.abs(target) > sum) return 0;
+    if ((target + sum) % 2 === 1) return 0;
+    const bagSize: number = (target + sum) / 2;
+    const dp: number[] = new Array(bagSize + 1).fill(0);
+    dp[0] = 1;
+    for (let i = 0; i < nums.length; i++) {
+        for (let j = bagSize; j >= nums[i]; j--) {
+            dp[j] += dp[j - nums[i]];
+        }
+    }
+    return dp[bagSize];
+};
+```
+
 
 
 -----------------------

problems/0496.下一个更大元素I.md

@@ -244,6 +244,39 @@ class Solution:
 ```
 
 Go：
+
+> 未精简版本
+```go
+func nextGreaterElement(nums1 []int, nums2 []int) []int {
+    res := make([]int, len(nums1))
+    for i := range res { res[i] = -1 }
+    m := make(map[int]int, len(nums1))
+    for k, v := range nums1 { m[v] = k }
+
+    stack := []int{0}
+    for i := 1; i < len(nums2); i++ {
+        top := stack[len(stack)-1]
+        if nums2[i] < nums2[top] {
+            stack = append(stack, i)
+        } else if nums2[i] == nums2[top] {
+            stack = append(stack, i)
+        } else {
+            for len(stack) != 0 && nums2[i] > nums2[top] {
+                if v, ok := m[nums2[top]]; ok {
+                    res[v] = nums2[i]
+                }
+                stack = stack[:len(stack)-1]
+                if len(stack) != 0 {
+                    top = stack[len(stack)-1]
+                }
+            }
+            stack = append(stack, i)
+        }
+    }
+    return res
+}
+```
+> 精简版本
 ```go
 func nextGreaterElement(nums1 []int, nums2 []int) []int {
     res := make([]int, len(nums1))

problems/0509.斐波那契数.md

@@ -245,7 +245,29 @@ var fib = function(n) {
 };
 ```
 
+TypeScript
+
+```typescript
+function fib(n: number): number {
+    /**
+        dp[i]: 第i个斐波那契数
+        dp[0]: 0;
+        dp[1]：1；
+        ...
+        dp[i] = dp[i - 1] + dp[i - 2];
+     */
+    const dp: number[] = [];
+    dp[0] = 0;
+    dp[1] = 1;
+    for (let i = 2; i <= n; i++) {
+        dp[i] = dp[i - 1] + dp[i - 2];
+    }
+    return dp[n];
+};
+```
+
 ### C
+
 动态规划:
 ```c
 int fib(int n){

problems/0518.零钱兑换II.md

@@ -242,6 +242,22 @@ func change(amount int, coins []int) int {
 }
 ```
 
+Rust:
+```rust
+pub fn change(amount: i32, coins: Vec<i32>) -> i32 {
+    let amount = amount as usize;
+    let coins = coins.iter().map(|&c|c as usize).collect::<Vec<usize>>();
+    let mut dp = vec![0usize; amount + 1];
+    dp[0] = 1;
+    for i in 0..coins.len() {
+        for j in coins[i]..=amount {
+            dp[j] += dp[j - coins[i]];
+        }
+    }
+    dp[amount] as i32
+}
+```
+
 Javascript：
 ```javascript
 const change = (amount, coins) => {
@@ -258,6 +274,21 @@ const change = (amount, coins) => {
 }
 ```
 
+TypeScript：
+
+```typescript
+function change(amount: number, coins: number[]): number {
+    const dp: number[] = new Array(amount + 1).fill(0);
+    dp[0] = 1;
+    for (let i = 0, length = coins.length; i < length; i++) {
+        for (let j = coins[i]; j <= amount; j++) {
+            dp[j] += dp[j - coins[i]];
+        }
+    }
+    return dp[amount];
+};
+```
+
 
 
 -----------------------

problems/0674.最长连续递增序列.md

@@ -218,6 +218,7 @@ class Solution:
         return result
 ```
 
+
 > 贪心法：
 ```python
 class Solution:
@@ -276,6 +277,24 @@ func findLengthOfLCIS(nums []int) int {
 }
 ```
 
+Rust:
+```rust
+pub fn find_length_of_lcis(nums: Vec<i32>) -> i32 {
+    if nums.is_empty() {
+        return 0;
+    }
+    let mut result = 1;
+    let mut dp = vec![1; nums.len()];
+    for i in 1..nums.len() {
+        if nums[i - 1] < nums[i] {
+            dp[i] = dp[i - 1] + 1;
+            result = result.max(dp[i]);
+        }
+    }
+    result
+}
+```
+
 Javascript：
 
 > 动态规划：

problems/0701.二叉搜索树中的插入操作.md

@@ -279,7 +279,7 @@ class Solution:
             root.right = self.insertIntoBST(root.right, val)
 
         # 返回更新后的以当前root为根节点的新树
-        return roo
+        return root
 ```
 
 **递归法** - 无返回值

problems/0739.每日温度.md

@@ -34,7 +34,7 @@
 
 那么单调栈的原理是什么呢？为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢？
 
-单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素的元素，优点是只需要遍历一次。
+单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素大的元素，优点是只需要遍历一次。
 
 
 在使用单调栈的时候首先要明确如下几点：
@@ -233,7 +233,7 @@ class Solution {
 }
 ```
 Python：
-``` Python3
+```python
 class Solution:
     def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
         answer = [0]*len(temperatures)
@@ -277,8 +277,36 @@ func dailyTemperatures(t []int) []int {
 }
 ```
 
-> 单调栈法
+> 单调栈法(未精简版本)
 
+```go
+func dailyTemperatures(temperatures []int) []int {
+    res := make([]int, len(temperatures))
+    // 初始化栈顶元素为第一个下标索引0
+    stack := []int{0}
+
+    for i := 1; i < len(temperatures); i++ {
+        top := stack[len(stack)-1]
+        if temperatures[i] < temperatures[top] {
+            stack = append(stack, i)
+        } else if temperatures[i] ==  temperatures[top] {
+            stack = append(stack, i)
+        } else {
+            for len(stack) != 0 && temperatures[i] > temperatures[top] {
+                res[top] = i - top
+                stack = stack[:len(stack)-1]
+                if len(stack) != 0 {
+                    top = stack[len(stack)-1]
+                }
+            }
+            stack = append(stack, i)
+        }
+    }
+    return res
+}
+```
+
+> 单调栈法(精简版本)
 ```go
 // 单调递减栈
 func dailyTemperatures(num []int) []int {

problems/0746.使用最小花费爬楼梯.md

@@ -266,7 +266,30 @@ var minCostClimbingStairs = function(cost) {
 };
 ```
 
+### TypeScript
+
+```typescript
+function minCostClimbingStairs(cost: number[]): number {
+    /**
+        dp[i]: 走到第i阶需要花费的最少金钱
+        dp[0]: cost[0];
+        dp[1]: cost[1];
+        ...
+        dp[i]: min(dp[i - 1], dp[i - 2]) + cost[i];
+     */
+    const dp: number[] = [];
+    const length: number = cost.length;
+    dp[0] = cost[0];
+    dp[1] = cost[1];
+    for (let i = 2; i <= length; i++) {
+        dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
+    }
+    return Math.min(dp[length - 1], dp[length - 2]);
+};
+```
+
 ### C
+
 ```c
 int minCostClimbingStairs(int* cost, int costSize){
     //开辟dp数组，大小为costSize

problems/1005.K次取反后最大化的数组和.md

@@ -209,6 +209,22 @@ var largestSumAfterKNegations = function(nums, k) {
         return a + b
     })
 };
+
+// 版本二 (优化: 一次遍历)
+var largestSumAfterKNegations = function(nums, k) {
+    nums.sort((a, b) => Math.abs(b) - Math.abs(a)); // 排序
+    let sum = 0;
+    for(let i = 0; i < nums.length; i++) {
+        if(nums[i] < 0 && k-- > 0) { // 负数取反（k 数量足够时）
+            nums[i] = -nums[i];
+        }
+        sum += nums[i]; // 求和
+    }
+    if(k % 2 > 0) { // k 有多余的（k若消耗完则应为 -1）
+        sum -= 2 * nums[nums.length - 1]; // 减去两倍的最小值（因为之前加过一次）
+    }
+    return sum;
+};
 ```
 
 

problems/1035.不相交的线.md

@@ -111,7 +111,6 @@ class Solution:
 Golang:
 
 ```go
-
 func maxUncrossedLines(A []int, B []int) int {
 	m, n := len(A), len(B)
 	dp := make([][]int, m+1)
@@ -140,7 +139,26 @@ func max(a, b int) int {
 }
 ```
 
+Rust:
 
+```rust
+pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
+    let (n, m) = (nums1.len(), nums2.len());
+    let mut last = vec![0; m + 1]; // 记录滚动数组
+    let mut dp = vec![0; m + 1];
+    for i in 1..=n {
+        dp.swap_with_slice(&mut last);
+        for j in 1..=m {
+            if nums1[i - 1] == nums2[j - 1] {
+                dp[j] = last[j - 1] + 1;
+            } else {
+                dp[j] = last[j].max(dp[j - 1]);
+            }
+        }
+    }
+    dp[m]
+}
+```
 
 JavaScript：
 

problems/1049.最后一块石头的重量II.md

@@ -277,5 +277,26 @@ var lastStoneWeightII = function (stones) {
 };
 ```
 
+TypeScript：
+
+```typescript
+function lastStoneWeightII(stones: number[]): number {
+    const sum: number = stones.reduce((pre, cur) => pre + cur);
+    const bagSize: number = Math.floor(sum / 2);
+    const weightArr: number[] = stones;
+    const valueArr: number[] = stones;
+    const goodsNum: number = weightArr.length;
+    const dp: number[] = new Array(bagSize + 1).fill(0);
+    for (let i = 0; i < goodsNum; i++) {
+        for (let j = bagSize; j >= weightArr[i]; j--) {
+            dp[j] = Math.max(dp[j], dp[j - weightArr[i]] + valueArr[i]);
+        }
+    }
+    return sum - dp[bagSize] * 2;
+};
+```
+
+
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/1143.最长公共子序列.md

@@ -4,40 +4,40 @@
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
 
-## 1143.最长公共子序列 
+## 1143.最长公共子序列
 
 [力扣题目链接](https://leetcode-cn.com/problems/longest-common-subsequence/)
 
-给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。  
+给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
 
-一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。     
+一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
 
-例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。   
+例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
 
-若这两个字符串没有公共子序列，则返回 0。        
+若这两个字符串没有公共子序列，则返回 0。
 
-示例 1:    
+示例 1:
 
-输入：text1 = "abcde", text2 = "ace"      
-输出：3          
-解释：最长公共子序列是 "ace"，它的长度为 3。     
+输入：text1 = "abcde", text2 = "ace"
+输出：3
+解释：最长公共子序列是 "ace"，它的长度为 3。
 
-示例 2:      
-输入：text1 = "abc", text2 = "abc"    
-输出：3       
-解释：最长公共子序列是 "abc"，它的长度为 3。    
+示例 2:
+输入：text1 = "abc", text2 = "abc"
+输出：3
+解释：最长公共子序列是 "abc"，它的长度为 3。
 
-示例 3:     
-输入：text1 = "abc", text2 = "def"      
-输出：0        
-解释：两个字符串没有公共子序列，返回 0。    
+示例 3:
+输入：text1 = "abc", text2 = "def"
+输出：0
+解释：两个字符串没有公共子序列，返回 0。
 
-提示:       
+提示:
 * 1 <= text1.length <= 1000
 * 1 <= text2.length <= 1000
 输入的字符串只含有小写英文字符。
 
-## 思路 
+## 思路
 
 本题和[动态规划：718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html)区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
 
@@ -45,21 +45,21 @@
 
 1. 确定dp数组（dp table）以及下标的含义
 
-dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j] 
+dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
 
-有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？ 
+有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？
 
 这样定义是为了后面代码实现方便，如果非要定义为为长度为[0, i]的字符串text1也可以，大家可以试一试！
 
 2. 确定递推公式
 
-主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同 
+主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
 
-如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1; 
+如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
 
 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
 
-即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); 
+即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
 
 代码如下：
 
@@ -71,9 +71,9 @@ if (text1[i - 1] == text2[j - 1]) {
 }
 ```
 
-3. dp数组如何初始化  
+3. dp数组如何初始化
 
-先看看dp[i][0]应该是多少呢？ 
+先看看dp[i][0]应该是多少呢？
 
 test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
 
@@ -101,7 +101,7 @@ vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
 
 ![1143.最长公共子序列1](https://img-blog.csdnimg.cn/20210210150215918.jpg)
 
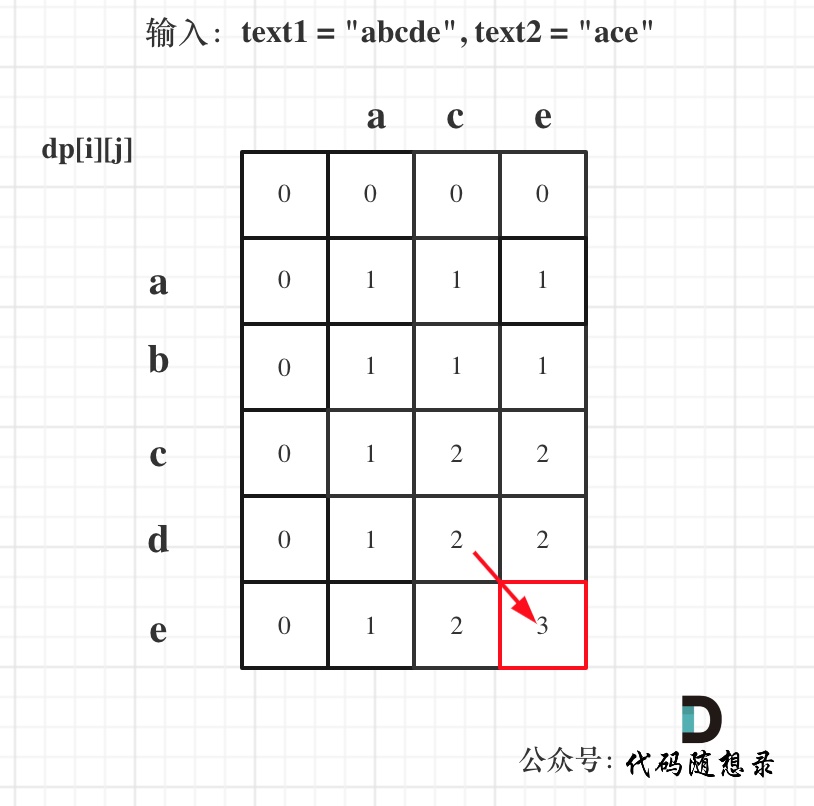
-最后红框dp[text1.size()][text2.size()]为最终结果 
+最后红框dp[text1.size()][text2.size()]为最终结果
 
 以上分析完毕，C++代码如下：
 
@@ -158,7 +158,7 @@ class Solution:
         for i in range(1, len2):
             for j in range(1, len1): # 开始列出状态转移方程
                 if text1[j-1] == text2[i-1]:
-                    dp[i][j] = dp[i-1][j-1]+1 
+                    dp[i][j] = dp[i-1][j-1]+1
                 else:
                     dp[i][j] = max(dp[i-1][j], dp[i][j-1])
         return dp[-1][-1]
@@ -189,10 +189,32 @@ func longestCommonSubsequence(text1 string, text2 string) int {
 
 func max(a,b int)int  {
 	if a>b{
-		return a 
+		return a
 	}
 	return b
 }
+
+```
+
+Rust:
+```rust
+pub fn longest_common_subsequence(text1: String, text2: String) -> i32 {
+    let (n, m) = (text1.len(), text2.len());
+    let (s1, s2) = (text1.as_bytes(), text2.as_bytes());
+    let mut dp = vec![0; m + 1];
+    let mut last = vec![0; m + 1];
+    for i in 1..=n {
+        dp.swap_with_slice(&mut last);
+        for j in 1..=m {
+            dp[j] = if s1[i - 1] == s2[j - 1] {
+                last[j - 1] + 1
+            } else {
+                last[j].max(dp[j - 1])
+            };
+        }
+    }
+    dp[m]
+}
 ```
 
 Javascript：

problems/背包理论基础01背包-1.md

@@ -432,6 +432,7 @@ function test () {
 test();
 ```
 
+
 ### C
 ```c
 #include <stdio.h>
@@ -478,5 +479,48 @@ int main(int argc, char* argv[]) {
 }
 ```
 
+
+### TypeScript
+
+```typescript
+function testWeightBagProblem(
+  weight: number[],
+  value: number[],
+  size: number
+): number {
+  /**
+   * dp[i][j]: 前i个物品，背包容量为j，能获得的最大价值
+   * dp[0][*]: u=weight[0],u之前为0，u之后（含u）为value[0]
+   * dp[*][0]: 0
+   * ...
+   * dp[i][j]: max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
+   */
+  const goodsNum: number = weight.length;
+  const dp: number[][] = new Array(goodsNum)
+    .fill(0)
+    .map((_) => new Array(size + 1).fill(0));
+  for (let i = weight[0]; i <= size; i++) {
+    dp[0][i] = value[0];
+  }
+  for (let i = 1; i < goodsNum; i++) {
+    for (let j = 1; j <= size; j++) {
+      if (j < weight[i]) {
+        dp[i][j] = dp[i - 1][j];
+      } else {
+        dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
+      }
+    }
+  }
+  return dp[goodsNum - 1][size];
+}
+// test
+const weight = [1, 3, 4];
+const value = [15, 20, 30];
+const size = 4;
+console.log(testWeightBagProblem(weight, value, size));
+```
+
+
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/背包理论基础01背包-2.md

@@ -137,6 +137,8 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
 
 因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
 
+倒序遍历的原因是，本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。
+
 （这里如果读不懂，就在回想一下dp[j]的定义，或者就把两个for循环顺序颠倒一下试试！）
 
 **所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的！**，这一点大家一定要注意。
@@ -349,6 +351,31 @@ int main(int argc, char** argv) {
 }
 ```
 
+### TypeScript
+
+```typescript
+function testWeightBagProblem(
+  weight: number[],
+  value: number[],
+  size: number
+): number {
+  const goodsNum: number = weight.length;
+  const dp: number[] = new Array(size + 1).fill(0);
+  for (let i = 0; i < goodsNum; i++) {
+    for (let j = size; j >= weight[i]; j--) {
+      dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+  }
+  return dp[size];
+}
+const weight = [1, 3, 4];
+const value = [15, 20, 30];
+const size = 4;
+console.log(testWeightBagProblem(weight, value, size));
+
+```
+
+
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/背包问题理论基础完全背包.md

@@ -340,6 +340,27 @@ function test_completePack2() {
 }
 ```
 
+TypeScript：
+
+```typescript
+// 先遍历物品，再遍历背包容量
+function test_CompletePack(): void {
+  const weight: number[] = [1, 3, 4];
+  const value: number[] = [15, 20, 30];
+  const bagSize: number = 4;
+  const dp: number[] = new Array(bagSize + 1).fill(0);
+  for (let i = 0; i < weight.length; i++) {
+    for (let j = weight[i]; j <= bagSize; j++) {
+      dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+  }
+  console.log(dp);
+}
+test_CompletePack();
+```
+
+
+
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/面试题 02.07. 解法更新.md

@@ -1,41 +0,0 @@
-# 双指针，不计算链表长度
-设置指向headA和headB的指针pa、pb，分别遍历两个链表，每次循环同时更新pa和pb。
-* 当链表A遍历完之后，即pa为空时，将pa指向headB；
-* 当链表B遍历完之后，即pa为空时，将pb指向headA；
-* 当pa与pb相等时，即指向同一个节点，该节点即为相交起始节点。
-* 若链表不相交，则pa、pb同时为空时退出循环，即如果链表不相交，pa与pb在遍历过全部节点后同时指向结尾空节点，此时退出循环，返回空。
-# 证明思路
-设链表A不相交部分长度为a，链表B不相交部分长度为b，两个链表相交部分长度为c。<br>
-在pa指向链表A时，即pa为空之前，pa经过链表A不相交部分和相交部分，走过的长度为a+c；<br>
-pa指向链表B后，在移动相交节点之前经过链表B不相交部分，走过的长度为b，总合为a+c+b。<br>
-同理，pb走过长度的总合为b+c+a。二者相等，即pa与pb可同时到达相交起始节点。 <br>
-该方法可避免计算具体链表长度。
-```cpp
-class Solution {
-public:
-    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
-        //链表为空时，返回空指针
-        if(headA == nullptr || headB == nullptr) return nullptr;
-        ListNode* pa = headA;
-        ListNode* pb = headB;
-        //pa与pb在遍历过全部节点后,同时指向结尾空节点时退出循环
-        while(pa != nullptr || pb != nullptr){
-            //pa为空时，将pa指向headB
-            if(pa == nullptr){
-                pa = headB;
-            }
-            //pa为空时，将pb指向headA
-            if(pb == nullptr){
-                pb = headA;
-            }
-            //pa与pb相等时，返回相交起始节点
-            if(pa == pb){
-                return pa;
-            }
-            pa = pa->next;
-            pb = pb->next;
-        }
-        return nullptr;
-    }
-};
-```