Update

README.md

@@ -114,7 +114,10 @@
     * [本周小结！（二叉树系列三）](https://mp.weixin.qq.com/s/JLLpx3a_8jurXcz6ovgxtg) 
     * [二叉树：合并两个二叉树](https://mp.weixin.qq.com/s/3f5fbjOFaOX_4MXzZ97LsQ)
     * [二叉树：二叉搜索树登场！](https://mp.weixin.qq.com/s/vsKrWRlETxCVsiRr8v_hHg)
+    * [二叉树：我是不是一棵二叉搜索树](https://mp.weixin.qq.com/s/8odY9iUX5eSi0eRFSXFD4Q)
     * [二叉树：搜索树的最小绝对差](https://mp.weixin.qq.com/s/Hwzml6698uP3qQCC1ctUQQ)
+    * [二叉树：我的众数是多少？](https://mp.weixin.qq.com/s/KSAr6OVQIMC-uZ8MEAnGHg)
+    * [二叉树：公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)
 
  
 
@@ -172,6 +175,7 @@
     * [0015.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
     * [0018.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
     * [0026.删除排序数组中的重复项](https://github.com/youngyangyang04/leetcode/blob/master/problems/0026.删除排序数组中的重复项.md) 
+    * [19.删除链表的倒数第N个节点](https://github.com/youngyangyang04/leetcode/blob/master/problems/19.删除链表的倒数第N个节点) 
     * [0206.翻转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
     * [0142.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
     * [0344.反转字符串](https://mp.weixin.qq.com/s/X02S61WCYiCEhaik6VUpFA)
@@ -237,6 +241,7 @@
 |[0015.三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md) | 数组 |中等|**双指针** **哈希**| 
 |[0017.电话号码的字母组合](https://github.com/youngyangyang04/leetcode/blob/master/problems/0017.电话号码的字母组合.md) | 回溯 |中等|**回溯**| 
 |[0018.四数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0018.四数之和.md) | 数组 |中等|**双指针**| 
+|[0019.删除链表的倒数第N个节点](https://github.com/youngyangyang04/leetcode/blob/master/problems/0019.删除链表的倒数第N个节点.md) | 链表 |中等|**双指针**| 
 |[0020.有效的括号](https://github.com/youngyangyang04/leetcode/blob/master/problems/0020.有效的括号.md) | 栈 |简单|**栈**| 
 |[0021.合并两个有序链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0021.合并两个有序链表.md)  |链表 |简单|**模拟** |
 |[0024.两两交换链表中的节点](https://github.com/youngyangyang04/leetcode/blob/master/problems/0024.两两交换链表中的节点.md)  |链表 |中等|**模拟** |

problems/0019.删除链表的倒数第N个节点.md

@@ -0,0 +1,49 @@
+
+
+## 思路 
+
+双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。
+
+思路是这样的，但要注意一些细节。
+
+分为如下几步：
+
+* 首先这里我推荐大家使用虚拟头结点，这样方面处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://mp.weixin.qq.com/s/slM1CH5Ew9XzK93YOQYSjA)
+
+
+* 定义fast指针和slow指针，初始值为虚拟头结点，如图：
+
+<img src='../pics/19.删除链表的倒数第N个节点.png' width=600> </img></div>
+
+* fast首先走n + 1步 ，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：
+<img src='../pics/19.删除链表的倒数第N个节点1.png' width=600> </img></div>
+
+* fast和slow同时移动，之道fast指向末尾，如题： 
+<img src='../pics/19.删除链表的倒数第N个节点2.png' width=600> </img></div>
+
+* 删除slow指向的下一个节点，如图：
+<img src='../pics/19.删除链表的倒数第N个节点3.png' width=600> </img></div>
+
+此时不难写出如下C++代码：
+
+```
+class Solution {
+public:
+    ListNode* removeNthFromEnd(ListNode* head, int n) {
+        ListNode* dummyHead = new ListNode(0);
+        dummyHead->next = head;
+        ListNode* slow = dummyHead;
+        ListNode* fast = dummyHead;
+        while(n-- && fast != NULL) {
+            fast = fast->next;
+        }
+        fast = fast->next; // fast再提前走一步，因为需要让slow指向删除节点的上一个节点
+        while (fast != NULL) {
+            fast = fast->next;
+            slow = slow->next;
+        }
+        slow->next = slow->next->next;
+        return dummyHead->next;
+    }
+};
+```

problems/0052.N皇后II.md

@@ -43,9 +43,9 @@ void backtracking(int n, int row, vector<string>& chessboard, vector<vector<stri
     }
     for (int col = 0; col < n; col++) {
         if (isValid(row, col, chessboard, n)) {
-            chessboard[row][col] = 'Q';
+            chessboard[row][col] = 'Q'; // 放置皇后
             backtracking(n, row + 1, chessboard, result);
-            chessboard[row][col] = '.';
+            chessboard[row][col] = '.'; // 回溯
         }
     }
 }

problems/0235.二叉搜索树的最近公共祖先.md

@@ -1,85 +1,198 @@
 ## 链接 
 https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
 
+> 二叉搜索树的最近公共祖先问题如约而至
+
+# 235. 二叉搜索树的最近公共祖先 
+
+链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/ 
+
+给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
+
+百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
+
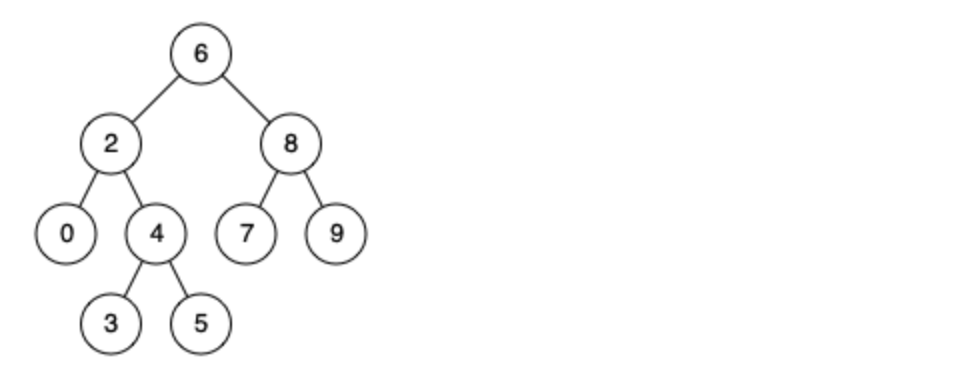
+例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]
+
+![235. 二叉搜索树的最近公共祖先](https://img-blog.csdnimg.cn/20201018172243602.png)
+
+示例 1:
+
+输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
+输出: 6
+解释: 节点 2 和节点 8 的最近公共祖先是 6。
+示例 2:
+
+输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
+输出: 2
+解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
+ 
+
+说明:
+
+* 所有节点的值都是唯一的。
+* p、q 为不同节点且均存在于给定的二叉搜索树中。
+
 ## 思路 
 
-
-遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了，可惜二叉树只能自上向低。
-
-那么自上相下查找的话，如何记录祖先呢？
-
-做过[236. 二叉树的最近公共祖先](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/)题目的同学，应该知道，只要判断一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。
+做过[二叉树：公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)题目的同学应该知道，利用回溯从底向上搜索，遇到一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。
 
 那么本题是二叉搜索树，二叉搜索树是有序的，那得好好利用一下这个特点。
 
 在有序树里，如果判断一个节点的左子树里有p，右子树里有q呢？
 
-其实只要从上到下遍历的时候，如果 (p->val <= cur->val && cur->val <= q->val)则说明该节点cur就是最近公共祖先了。
+其实只要从上到下遍历的时候，cur节点是数值在[p, q]区间中则说明该节点cur就是最近公共祖先了。
 
-理解这一点，本题就很好解了。
+理解这一点，本题就很好解了。 
 
-如图所示
+和[二叉树：公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)不同，普通二叉树求最近公共祖先需要使用回溯，从底向上来查找，二叉搜索树就不用了，因为搜索树有序（相当于自带方向），那么只要从上向下遍历就可以了。 
+
+那么我们可以采用前序遍历（其实这里没有中节点的处理逻辑，遍历顺序无所谓了）。
+
+如图所示：p为节点3，q为节点5
 
 <img src='../pics/235.二叉搜索树的最近公共祖先.png' width=600> </img></div>
 
+可以看出直接按照指定的方向，就可以找到节点4，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！
+
+
+递归三部曲如下：
+
+* 确定递归函数返回值以及参数
+
+参数就是当前节点，以及两个结点 p、q。
+
+返回值是要返回最近公共祖先，所以是TreeNode *  。
+
+代码如下：
+
+```
+TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) 
+```
+
+* 确定终止条件 
+
+遇到空返回就可以了，代码如下：
+
+```
+if (cur == NULL) return cur;
+```
+
+其实都不需要这个终止条件，因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的，所以并不存在遇到空的情况。
+
+* 确定单层递归的逻辑 
+
 在遍历二叉搜索树的时候就是寻找区间[p->val, q->val]（注意这里是左闭又闭）
 
-那么如果 cur->val 大于 p->val，同时 cur->val 大于q->val，那么就应该向左遍历。（因为我们此时不知道p和q谁大，所以两个都要判断）
+那么如果 cur->val 大于 p->val，同时 cur->val 大于q->val，那么就应该向左遍历（说明目标区间在左子树上）。
+
+**需要注意的是此时不知道p和q谁大，所以两个都要判断** 
 
 代码如下：
 
 ```
-        if (cur->val > p->val && cur->val > q->val) {
-            return traversal(cur->left, p, q);
-        }
+if (cur->val > p->val && cur->val > q->val) {
+    TreeNode* left = traversal(cur->left, p, q);
+    if (left != NULL) {
+        return left;
+    }
+}
 ```
 
-如果 cur->val 小于 p->val，同时 cur->val 小于 q->val，那么就应该向右遍历。
+**细心的同学会发现，在这里调用递归函数的地方，把递归函数的返回值left，直接return**。 
+
+
+在[二叉树：公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)中，如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树。 
+
+搜索一条边的写法：
 
 ```
-        } else if (cur->val < p->val && cur->val < q->val) {
-            return traversal(cur->right, p, q);
-        }
+if (递归函数(root->left)) return ;
+
+if (递归函数(root->right)) return ;
 ```
 
-剩下的情况，我们就找到了区间使（p->val <=  cur->val && cur->val <= q->val）或者是 （q->val <=  cur->val && cur->val <= p->val）
+搜索整个树写法：
+
+```
+left = 递归函数(root->left);
+right = 递归函数(root->right);
+left与right的逻辑处理;
+```
+
+本题就是标准的搜索一条边的写法，遇到递归函数的返回值，如果不为空，立刻返回。
+
+
+如果 cur->val 小于 p->val，同时 cur->val 小于 q->val，那么就应该向右遍历（目标区间在右子树）。
+
+```
+if (cur->val < p->val && cur->val < q->val) {
+    TreeNode* right = traversal(cur->right, p, q);
+    if (right != NULL) {
+        return right;
+    }
+}
+```
+
+剩下的情况，就是cur节点在区间（p->val <=  cur->val && cur->val <= q->val）或者 （q->val <=  cur->val && cur->val <= p->val）中，那么cur就是最近公共祖先了，直接返回cur。
 
 代码如下：
 ```
-        else {
-            return cur;
-        }
+return cur;
 
 ```
 
 那么整体递归代码如下:
 
-## C++递归代码
-
-（我这里特意把递归的过程抽出一个函数traversal，这样代码更清晰，有助于读者理解。）
-
 ```
 class Solution {
 private:
     TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {
-        if (cur->val > p->val && cur->val > q->val) {
-            return traversal(cur->left, p, q);
-        } else if (cur->val < p->val && cur->val < q->val) {
-            return traversal(cur->right, p, q);
-        } else return cur;
+        if (cur == NULL) return cur;
+                                                        // 中
+        if (cur->val > p->val && cur->val > q->val) {   // 左
+            TreeNode* left = traversal(cur->left, p, q);
+            if (left != NULL) {
+                return left;
+            }
+        }
+
+        if (cur->val < p->val && cur->val < q->val) {   // 右
+            TreeNode* right = traversal(cur->right, p, q);
+            if (right != NULL) {
+                return right;
+            }
+        }
+        return cur;
     }
 public:
     TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
-
         return traversal(root, p, q);
     }
 };
 ```
 
+精简后代码如下：
 
-## C++迭代法代码
+```
+class Solution {
+public:
+    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+        if (root->val > p->val && root->val > q->val) {
+            return lowestCommonAncestor(root->left, p, q);
+        } else if (root->val < p->val && root->val < q->val) {
+            return lowestCommonAncestor(root->right, p, q);
+        } else return root;
+    }
+};
+```
 
-同时给出一个迭代的版本，思想是一样的，代码如下：
+## 迭代法
+
+对于二叉搜索树的迭代法，大家应该在[二叉树：二叉搜索树登场！](https://mp.weixin.qq.com/s/vsKrWRlETxCVsiRr8v_hHg)就了解了。
+
+利用其有序性，迭代的方式还是比较简单的，解题思路在递归中已经分析了。
+
+迭代代码如下：
 
 ```
 class Solution {
@@ -96,3 +209,15 @@ public:
     }
 };
 ```
+
+灵魂拷问：是不是又被简单的迭代法感动到痛哭流涕？
+
+# 总结 
+
+对于二叉搜索树的最近祖先问题，其实要比[普通二叉树公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)简单的多。
+
+不用使用回溯，二叉搜索树自带方向性，可以方便的从上向下查找目标区间，遇到目标区间内的节点，直接返回。
+
+最后给出了对应的迭代法，二叉搜索树的迭代法甚至比递归更容易理解，也是因为其有序性（自带方向性），按照目标区间找就行了。
+
+**就酱，学到了，就转发给身边需要学习的同学吧！**

problems/0844.比较含退格的字符串.md

@@ -0,0 +1,120 @@
+感觉像是使用栈
+
+## 思路 
+
+本文将给出 空间复杂度O(n)的栈模拟方法 以及空间复杂度是O(1)的双指针方法。
+
+### 普通方法（使用栈的思路）
+
+这道题目一看就是要使用栈的节奏，这种匹配（消除）问题也是栈的擅长所在，跟着一起刷题的同学应该知道，在[栈与队列：匹配问题都是栈的强项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)，我就已经提过了一次使用栈来做类似的事情了。
+
+**那么本题，确实可以使用栈的思路，但是没有必要使用栈，因为最后比较的时候还要比较栈里的元素，有点麻烦**。
+
+这里直接使用字符串string，来作为栈，末尾添加和弹出，string都有相应的接口，最后比较的时候，只要比较两个字符串就可以了，比比较栈里的元素方便一些。
+
+代码如下：
+
+```
+class Solution {
+public:
+    bool backspaceCompare(string S, string T) {
+        string s; // 当栈来用
+        string t; // 当栈来用
+        for (int i = 0; i < S.size(); i++) {
+            if (S[i] != '#') s += S[i];
+            else if (!s.empty()) {
+                s.pop_back();
+            
+        }
+        for (int i = 0; i < T.size(); i++) {
+            if (T[i] != '#') t += T[i];
+            else if (!t.empty()) {
+                t.pop_back();
+            }
+        }
+        if (s == t) return true; // 直接比较两个字符串是否相等，比用栈来比较方便多了
+        return false;
+    }
+};
+```
+* 时间复杂度:O(n + m)， n为S的长度，m为T的长度 ，也可以理解是O(n)的时间复杂度
+* 空间复杂度:O(n + m)
+
+当然以上代码，大家可以发现有重复的逻辑处理S，处理T，可以把这块公共逻辑抽离出来，代码精简如下：
+
+```
+class Solution {
+private:
+string getString(const string& S) {
+    string s;
+    for (int i = 0; i < S.size(); i++) {
+        if (S[i] != '#') s += S[i];
+        else if (!s.empty()) {
+            s.pop_back();
+        }
+    }
+    return s;
+}
+public:
+    bool backspaceCompare(string S, string T) {
+        return getString(S) == getString(T);
+    }
+};
+```
+性能依然是：
+* 时间复杂度:O(n + m)
+* 空间复杂度:O(n + m)
+
+### 优化方法（从后向前双指针）
+
+当然还可以有使用 O(1) 的空间复杂度来解决该问题。 
+
+同时从后向前遍历S和T（i初始为S末尾，j初始为T末尾），记录#的数量，模拟消除的操作，如果#用完了，就开始比较S[i]和S[j]。 
+
+动画如下：
+
+<img src='../video/844.比较含退格的字符串.gif' width=600> </img></div>
+
+如果S[i]和S[j]不相同返回false，如果有一个指针（i或者j）先走到的字符串头部位置，也返回false。
+
+代码如下：
+
+```
+class Solution {
+public:
+    bool backspaceCompare(string S, string T) {
+        int sSkipNum = 0; // 记录S的#数量
+        int tSkipNum = 0; // 记录T的#数量
+        int i = S.size() - 1;
+        int j = T.size() - 1;
+        while (1) {
+            while (i >= 0) { // 从后向前，消除S的#
+                if (S[i] == '#') sSkipNum++;
+                else {
+                    if (sSkipNum > 0) sSkipNum--;
+                    else break;
+                }
+                i--;
+            }
+            while (j >= 0) { // 从后向前，消除T的#
+                if (T[j] == '#') tSkipNum++;
+                else {
+                    if (tSkipNum > 0) tSkipNum--;
+                    else break;
+                }
+                j--;
+            }
+            // 后半部分#消除完了，接下来比较S[i] != T[j]
+            if (i < 0 || j < 0) break; // S 或者T 遍历到头了
+            if (S[i] != T[j]) return false;
+            i--;j--;
+        }
+        // 说明S和T同时遍历完毕
+        if (i == -1 && j == -1) return true;
+        return false;
+    }
+};
+```
+
+* 时间复杂度：O(n + m) 
+* 空间复杂度：O(1)