Merge branch 'master' into master

.gitignore

@@ -0,0 +1 @@
+**/.DS_Store

README.md

@@ -62,7 +62,7 @@
 如果你是算法老手，这篇攻略也是复习的最佳资料，如果把每个系列对应的总结篇，快速过一遍，整个算法知识体系以及各种解法就重现脑海了。
 
 
-目前「代码随想录」刷题攻略更新了：**200多篇文章，精讲了200道经典算法题目，共60w字的详细图解，部分难点题目还搭配了20分钟左右的视频讲解**。
+目前「代码随想录」刷题攻略更新了：**200多篇文章，精讲了200道经典算法题目，共60w字的详细图解，大部分题目都搭配了20分钟左右的视频讲解**，视频质量很好，口碑很好，大家可以去看看，视频列表：[代码随想录视频讲解](https://www.bilibili.com/video/BV1fA4y1o715)。
 
 **这里每一篇题解，都是精品，值得仔细琢磨**。
 

problems/0001.两数之和.md

@@ -41,7 +41,7 @@
 
 那么我们就应该想到使用哈希法了。
 
-因为本地，我们不仅要知道元素有没有遍历过，还有知道这个元素对应的下标，**需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适**。 
+因为本地，我们不仅要知道元素有没有遍历过，还要知道这个元素对应的下标，**需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适**。 
 
 再来看一下使用数组和set来做哈希法的局限。
 

problems/0017.电话号码的字母组合.md

@@ -183,6 +183,8 @@ public:
     }
 };
 ```
+* 时间复杂度: O(3^m * 4^n)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数
+* 空间复杂度: O(3^m * 4^n)
 
 一些写法，是把回溯的过程放在递归函数里了，例如如下代码，我可以写成这样：（注意注释中不一样的地方）
 

problems/0028.实现strStr.md

@@ -1293,7 +1293,6 @@ impl Solution {
 
     pub fn str_str(haystack: String, needle: String) -> i32 {
         let (haystack_len, needle_len) = (haystack.len(), needle.len());
-        if haystack_len == 0 { return 0; }
         if haystack_len < needle_len { return -1;}
         let (haystack, needle) = (haystack.chars().collect::<Vec<char>>(), needle.chars().collect::<Vec<char>>());
         let mut next: Vec<usize> = vec![0; haystack_len];
@@ -1334,9 +1333,6 @@ impl Solution {
         next
     }
     pub fn str_str(haystack: String, needle: String) -> i32 {
-        if needle.is_empty() {
-            return 0;
-        }
         if haystack.len() < needle.len() {
             return -1;
         }

problems/0035.搜索插入位置.md

@@ -191,8 +191,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(\log n)$
-* 时间复杂度：$O(1)$
+* 时间复杂度：O(log n)
+* 空间复杂度：O(1)
 
 ## 总结
 
@@ -274,7 +274,7 @@ func searchInsert(nums []int, target int) int {
 			left = mid + 1
 		}
 	}
-	return len(nums)
+	return right+1
 }
 ```
 

problems/0039.组合总和.md

@@ -214,6 +214,8 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此
+* 空间复杂度: O(target)
 
 # 总结
 

problems/0040.组合总和II.md

@@ -214,6 +214,8 @@ public:
 };
 
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
 
 ## 补充
 

problems/0046.全排列.md

@@ -136,6 +136,8 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n!)
+* 空间复杂度: O(n)
 
 ## 总结
 

problems/0047.全排列II.md

@@ -99,6 +99,8 @@ public:
 };
 
 ```
+* 时间复杂度: O(n)
+* 空间复杂度: O(n)
 
 ## 拓展
 
@@ -158,6 +160,19 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
 
 所以我通过举[1,1,1]的例子，把这两个去重的逻辑分别抽象成树形结构，大家可以一目了然：为什么两种写法都可以以及哪一种效率更高！
 
+这里可能大家又有疑惑，既然 `used[i - 1] == false`也行而`used[i - 1] == true`也行，那为什么还要写这个条件呢？ 
+
+直接这样写 不就完事了？ 
+
+```cpp
+if (i > 0 && nums[i] == nums[i - 1]) {
+    continue;
+}
+``` 
+
+其实并不行，一定要加上  `used[i - 1] == false`或者`used[i - 1] == true`，因为 used[i - 1] 要一直是 true 或者一直是false 才可以，而不是 一会是true 一会又是false。 所以这个条件要写上。
+
+
 是不是豁然开朗了！！
 
 ## 其他语言版本

problems/0051.N皇后.md

@@ -208,6 +208,9 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n!)
+* 空间复杂度: O(n)
+
 
 可以看出，除了验证棋盘合法性的代码，省下来部分就是按照回溯法模板来的。
 

problems/0053.最大子序和.md

@@ -124,7 +124,7 @@ public:
 
 ## 动态规划
 
-当然本题还可以用动态规划来做，当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列，后续到动态规划系列的时候会详细讲解本题的 dp 方法。
+当然本题还可以用动态规划来做，在代码随想录动态规划章节我会详细介绍，如果大家想在想看，可以直接跳转：[动态规划版本详解](https://programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html#%E6%80%9D%E8%B7%AF)
 
 那么先给出我的 dp 代码如下，有时间的录友可以提前做一做：
 

problems/0053.最大子序和（动态规划）.md

@@ -139,8 +139,6 @@ Python：
 ```python
 class Solution:
     def maxSubArray(self, nums: List[int]) -> int:
-        if len(nums) == 0:
-            return 0
         dp = [0] * len(nums)
         dp[0] = nums[0]
         result = dp[0]

problems/0055.跳跃游戏.md

@@ -50,7 +50,8 @@
 
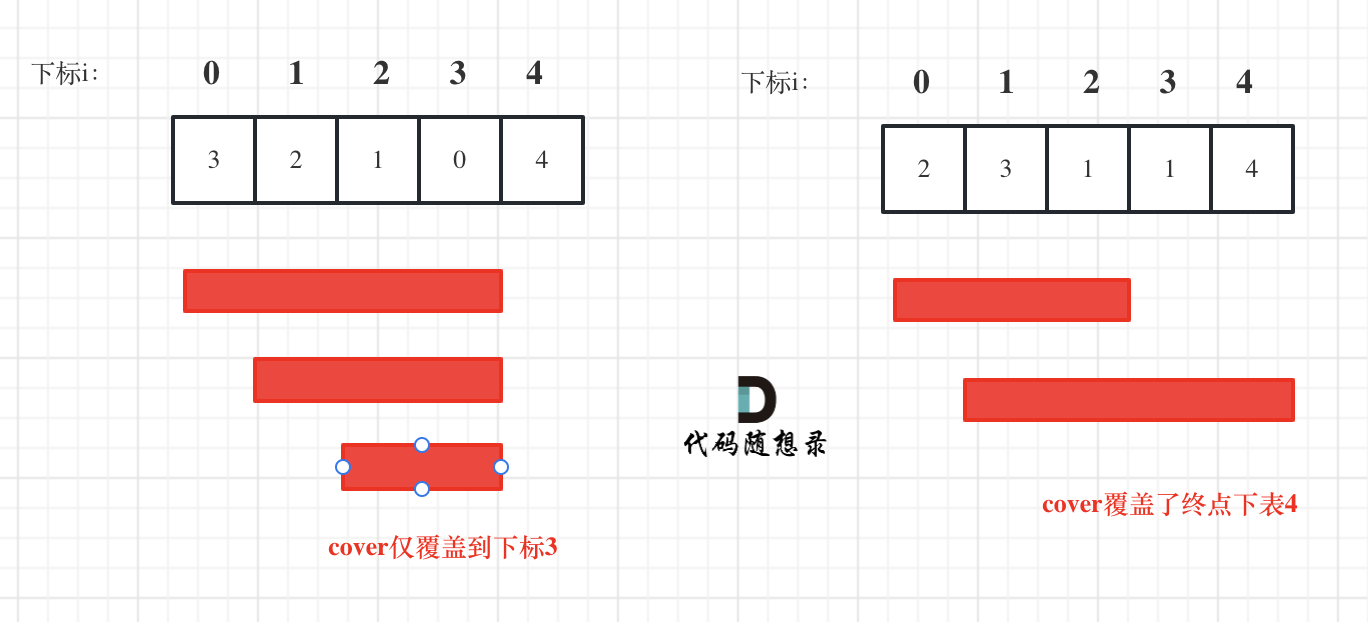
 如图：
 
-![55.跳跃游戏](https://code-thinking-1253855093.file.myqcloud.com/pics/20201124154758229-20230310135019977.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230203105634.png)
+
 
 i 每次移动只能在 cover 的范围内移动，每移动一个元素，cover 得到该元素数值（新的覆盖范围）的补充，让 i 继续移动下去。
 

problems/0056.合并区间.md

@@ -113,7 +113,6 @@ class Solution {
     }
 }
 
-}
 ```
 ```java
 // 版本2

problems/0062.不同路径.md

@@ -448,21 +448,14 @@ function uniquePaths(m: number, n: number): number {
 ```Rust
 impl Solution {
     pub fn unique_paths(m: i32, n: i32) -> i32 {
-            let m = m as usize;
-            let n = n as usize;
-            let mut dp = vec![vec![0; n]; m];
-            for i in 0..m {
-                dp[i][0] = 1;
+        let (m, n) = (m as usize, n as usize);
+        let mut dp = vec![vec![1; n]; m];
+        for i in 1..m {
+            for j in 1..n {
+                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
             }
-            for j in 0..n {
-                dp[0][j] = 1;
-            }
-            for i in 1..m {
-                for j in 1..n {
-                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
-                }
-            }
-        dp[m-1][n-1]
+        }
+        dp[m - 1][n - 1]
     }
 }
 ```

problems/0063.不同路径II.md

@@ -135,7 +135,7 @@ for (int i = 1; i < m; i++) {
 
 ![63.不同路径II2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210104114610256.png)
 
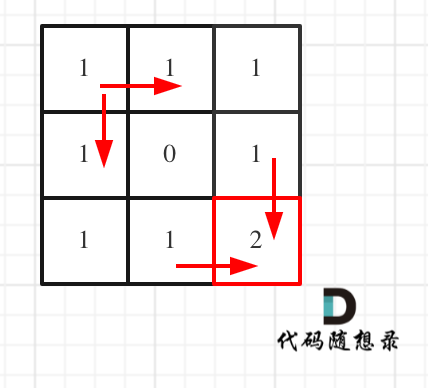
-如果这个图看不同，建议在理解一下递归公式，然后照着文章中说的遍历顺序，自己推导一下！
+如果这个图看不懂，建议再理解一下递归公式，然后照着文章中说的遍历顺序，自己推导一下！
 
 动规五部分分析完毕，对应C++代码如下：
 
@@ -554,6 +554,33 @@ impl Solution {
 }
 ```
 
+空间优化：
+
+```rust
+impl Solution {
+    pub fn unique_paths_with_obstacles(obstacle_grid: Vec<Vec<i32>>) -> i32 {
+        let mut dp = vec![0; obstacle_grid[0].len()];
+        for (i, &v) in obstacle_grid[0].iter().enumerate() {
+            if v == 0 {
+                dp[i] = 1;
+            } else {
+                break;
+            }
+        }
+        for rows in obstacle_grid.iter().skip(1) {
+            for j in 0..rows.len() {
+                if rows[j] == 1 {
+                    dp[j] = 0;
+                } else if j != 0 {
+                    dp[j] += dp[j - 1];
+                }
+            }
+        }
+        dp.pop().unwrap()
+    }
+}
+```
+
 ### C
 
 ```c

problems/0070.爬楼梯.md

@@ -488,18 +488,32 @@ public class Solution {
 ```rust
 impl Solution {
     pub fn climb_stairs(n: i32) -> i32 {
-        if n <= 2 {
+        if n <= 1 {
             return n;
         }
-        let mut a = 1;
-        let mut b = 2;
-        let mut f = 0;
-        for i in 2..n {
+        let (mut a, mut b, mut f) = (1, 1, 0);
+        for _ in 2..=n {
             f = a + b;
             a = b;
             b = f;
         }
-        return f;
+        f
+}
+```
+
+dp 数组
+
+```rust
+impl Solution {
+    pub fn climb_stairs(n: i32) -> i32 {
+        let n = n as usize;
+        let mut dp = vec![0; n + 1];
+        dp[0] = 1;
+        dp[1] = 1;
+        for i in 2..=n {
+            dp[i] = dp[i - 1] + dp[i - 2];
+        }
+        dp[n]
     }
 }
 ```

problems/0077.组合.md

@@ -218,6 +218,10 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
+
+
 
 还记得我们在[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中给出的回溯法模板么？
 

problems/0077.组合优化.md

@@ -130,6 +130,10 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
+
+
 
 # 总结
 

problems/0078.子集.md

@@ -149,6 +149,8 @@ public:
 };
 
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
 
 在注释中，可以发现可以不写终止条件，因为本来我们就要遍历整棵树。
 

problems/0084.柱状图中最大的矩形.md

@@ -307,6 +307,33 @@ class Solution {
     }
 }
 ```
+单调栈精简
+```java
+class Solution {
+    public int largestRectangleArea(int[] heights) {
+        int[] newHeight = new int[heights.length + 2];
+        System.arraycopy(heights, 0, newHeight, 1, heights.length);
+        newHeight[heights.length+1] = 0;
+        newHeight[0] = 0;
+
+        Stack<Integer> stack = new Stack<>();
+        stack.push(0);
+
+        int res = 0;
+        for (int i = 1; i < newHeight.length; i++) {
+            while (newHeight[i] < newHeight[stack.peek()]) {
+                int mid = stack.pop();
+                int w = i - stack.peek() - 1;
+                int h = newHeight[mid];
+                res = Math.max(res, w * h);
+            }
+            stack.push(i);
+
+        }
+        return res;
+    }
+}
+```
 
 Python3:
 

problems/0090.子集II.md

@@ -83,6 +83,9 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
+
 
 使用set去重的版本。
 ```CPP

problems/0093.复原IP地址.md

@@ -244,6 +244,8 @@ public:
 };
 
 ```
+* 时间复杂度: O(3^4)，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式，则搜索树的最大深度为4，每个节点最多有3个子节点。
+* 空间复杂度: O(n)
 
 # 总结
 
@@ -314,6 +316,47 @@ class Solution {
         return true;
     }
 }
+//方法一：但使用stringBuilder，故优化时间、空间复杂度，因为向字符串插入字符时无需复制整个字符串，从而减少了操作的时间复杂度，也不用开新空间存subString，从而减少了空间复杂度。
+class Solution {
+    List<String> result = new ArrayList<>();
+    public List<String> restoreIpAddresses(String s) {
+        StringBuilder sb = new StringBuilder(s);
+        backTracking(sb, 0, 0);
+        return result;
+    }
+    private void backTracking(StringBuilder s, int startIndex, int dotCount){
+        if(dotCount == 3){
+            if(isValid(s, startIndex, s.length() - 1)){
+                result.add(s.toString());
+            }
+            return;
+        }
+        for(int i = startIndex; i < s.length(); i++){
+            if(isValid(s, startIndex, i)){
+                s.insert(i + 1, '.');
+                backTracking(s, i + 2, dotCount + 1);
+                s.deleteCharAt(i + 1);
+            }else{
+                break;
+            }
+        }
+    }
+    //[start, end]
+    private boolean isValid(StringBuilder s, int start, int end){
+        if(start > end)
+            return false;
+        if(s.charAt(start) == '0' && start != end)
+            return false;
+        int num = 0;
+        for(int i = start; i <= end; i++){
+            int digit = s.charAt(i) - '0';
+            num = num * 10 + digit;
+            if(num > 255)
+                return false;
+        }
+        return true;
+    }
+}
 
 //方法二：比上面的方法时间复杂度低，更好地剪枝，优化时间复杂度
 class Solution {
@@ -358,6 +401,7 @@ class Solution {
 }
 ```
 
+
 ## python
 
 回溯（版本一）

problems/0098.验证二叉搜索树.md

@@ -259,6 +259,36 @@ public:
 
 ## Java 
 
+```Java
+//使用統一迭代法
+class Solution {
+    public boolean isValidBST(TreeNode root) {
+        Stack<TreeNode> stack = new Stack<>();
+        TreeNode pre = null;
+        if(root != null)
+            stack.add(root);        
+        while(!stack.isEmpty()){
+            TreeNode curr = stack.peek();
+            if(curr != null){
+                stack.pop();
+                if(curr.right != null)
+                    stack.add(curr.right);
+                stack.add(curr);
+                stack.add(null);
+                if(curr.left != null)
+                    stack.add(curr.left);
+            }else{
+                stack.pop();
+                TreeNode temp = stack.pop();
+                if(pre != null && pre.val >= temp.val)
+                    return false;
+                pre = temp;
+            }
+        }
+        return true;
+    }
+}
+```
 ```Java
 class Solution {
     // 递归

problems/0101.对称二叉树.md

@@ -88,7 +88,7 @@ else if (left->val != right->val) return false; // 注意这里我没有
 
 
 * 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
-* 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
+* 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
 * 如果左右都对称就返回true ，有一侧不对称就返回false 。
 
 代码如下：
@@ -157,7 +157,7 @@ public:
 
 **这个代码就很简洁了，但隐藏了很多逻辑，条理不清晰，而且递归三部曲，在这里完全体现不出来。**
 
-**所以建议大家做题的时候，一定要想清楚逻辑，每一步做什么。把道题目所有情况想到位，相应的代码写出来之后，再去追求简洁代码的效果。**
+**所以建议大家做题的时候，一定要想清楚逻辑，每一步做什么。把题目所有情况想到位，相应的代码写出来之后，再去追求简洁代码的效果。**
 
 ## 迭代法
 

problems/0104.二叉树的最大深度.md

@@ -38,7 +38,7 @@
 本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
 
 * 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
-* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
+* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
 
 **而根节点的高度就是二叉树的最大深度**，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
 

problems/0106.从中序与后序遍历序列构造二叉树.md

@@ -620,7 +620,42 @@ class Solution {
     }
 }
 ```
+```java
+class Solution {
+    public TreeNode buildTree(int[] inorder, int[] postorder) {
+        if(postorder.length == 0 || inorder.length == 0)
+            return null;
+        return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);
+    
+    }
+    private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd){
+        if(postorderStart == postorderEnd)
+            return null;
+        int rootVal = postorder[postorderEnd - 1];
+        TreeNode root = new TreeNode(rootVal);
+        int middleIndex;
+        for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){
+            if(inorder[middleIndex] == rootVal)
+                break;
+        }
 
+        int leftInorderStart = inorderStart; 
+        int leftInorderEnd = middleIndex;
+        int rightInorderStart = middleIndex + 1;
+        int rightInorderEnd = inorderEnd;
+
+
+        int leftPostorderStart = postorderStart;
+        int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);
+        int rightPostorderStart = leftPostorderEnd;
+        int rightPostorderEnd = postorderEnd - 1;
+        root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd,  postorder, leftPostorderStart, leftPostorderEnd);
+        root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);
+
+        return root;
+    }  
+}
+```
 105.从前序与中序遍历序列构造二叉树
 
 ```java

problems/0111.二叉树的最小深度.md

@@ -170,11 +170,14 @@ class Solution {
 private:
     int result;
     void getdepth(TreeNode* node, int depth) {
-        if (node->left == NULL && node->right == NULL) {
-            result = min(depth, result);  
+        // 函数递归终止条件
+        if (root == nullptr) {
             return;
         }
-        // 中 只不过中没有处理的逻辑
+        // 中，处理逻辑：判断是不是叶子结点
+        if (root -> left == nullptr && root->right == nullptr) {
+            res = min(res, depth);
+        }
         if (node->left) { // 左
             getdepth(node->left, depth + 1);
         }
@@ -186,7 +189,9 @@ private:
 
 public:
     int minDepth(TreeNode* root) {
-        if (root == NULL) return 0;
+        if (root == nullptr) {
+            return 0;
+        }
         result = INT_MAX;
         getdepth(root, 1);
         return result;

problems/0112.路径总和.md

@@ -17,7 +17,7 @@
 示例:
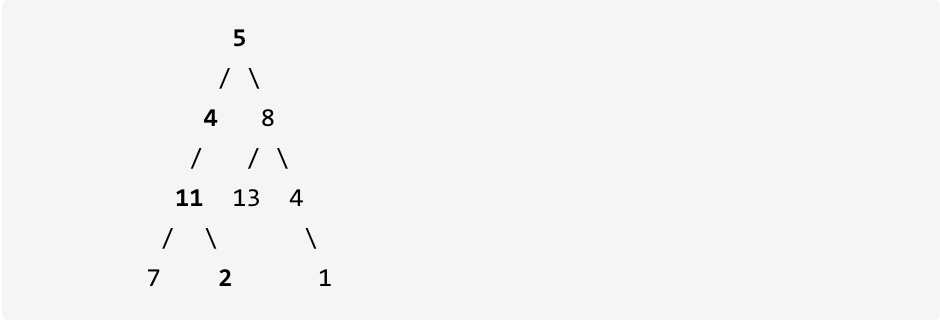
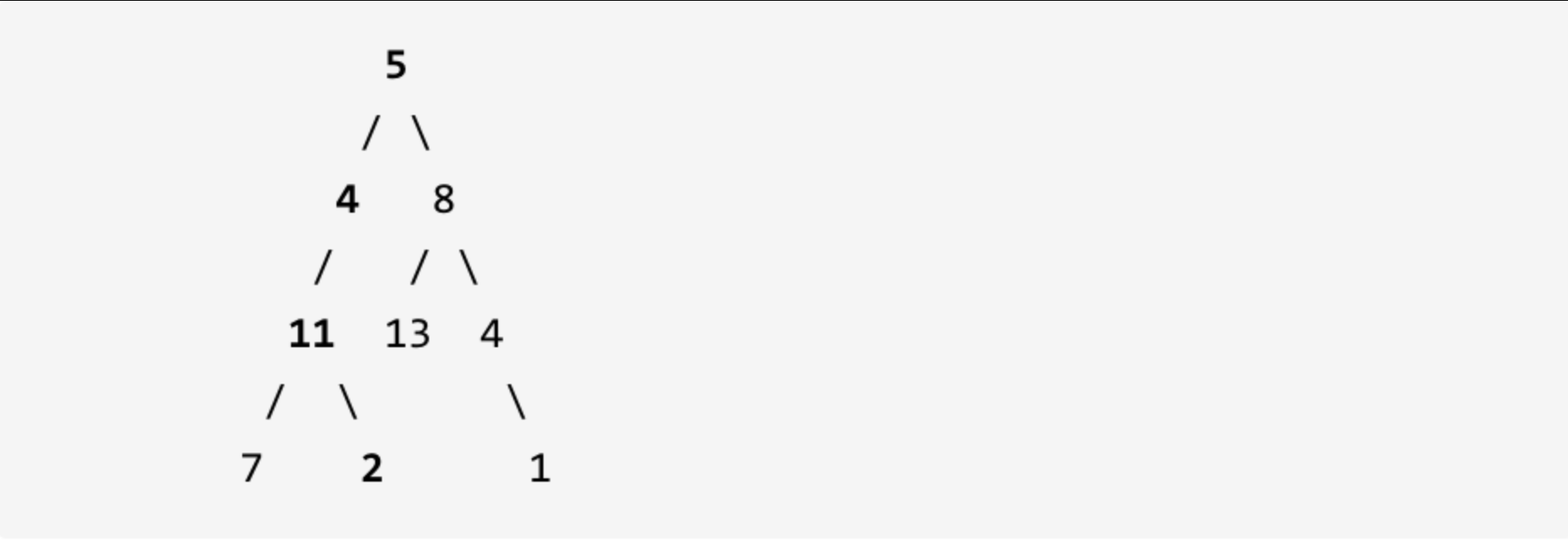
 给定如下二叉树，以及目标和 sum = 22，
 
-![112.路径总和1](https://img-blog.csdnimg.cn/20210203160355234.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230407210247.png)
 
 返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
 
@@ -385,6 +385,42 @@ class solution {
     }
 }
 ```
+```Java 統一迭代法
+    public boolean hasPathSum(TreeNode root, int targetSum) {
+        Stack<TreeNode> treeNodeStack = new Stack<>();
+        Stack<Integer> sumStack = new Stack<>();
+
+        if(root == null)
+            return false;
+        treeNodeStack.add(root);
+        sumStack.add(root.val);
+
+        while(!treeNodeStack.isEmpty()){
+            TreeNode curr = treeNodeStack.peek();
+            int tempsum = sumStack.pop();
+            if(curr != null){
+                treeNodeStack.pop();
+                treeNodeStack.add(curr);
+                treeNodeStack.add(null);
+                sumStack.add(tempsum);
+                if(curr.right != null){
+                    treeNodeStack.add(curr.right);
+                    sumStack.add(tempsum + curr.right.val);
+                }
+                if(curr.left != null){
+                    treeNodeStack.add(curr.left);
+                    sumStack.add(tempsum + curr.left.val);
+                }
+            }else{
+                treeNodeStack.pop();
+                TreeNode temp = treeNodeStack.pop();
+                if(temp.left == null && temp.right == null && tempsum == targetSum)
+                    return true;
+            }
+        }
+        return false;
+    }
+```
 
 ### 0113.路径总和-ii
 
@@ -446,6 +482,52 @@ class Solution {
     }
 }
 ```
+```java
+// 解法3 DFS统一迭代法
+class Solution {
+    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
+        List<List<Integer>> result = new ArrayList<>();
+        Stack<TreeNode> nodeStack = new Stack<>();
+        Stack<Integer> sumStack = new Stack<>();
+        Stack<ArrayList<Integer>> pathStack = new Stack<>();
+        if(root == null)
+            return result;
+        nodeStack.add(root);
+        sumStack.add(root.val);
+        pathStack.add(new ArrayList<>());
+
+        while(!nodeStack.isEmpty()){
+            TreeNode currNode = nodeStack.peek();
+            int currSum = sumStack.pop();
+            ArrayList<Integer> currPath = pathStack.pop();
+            if(currNode != null){
+                nodeStack.pop();
+                nodeStack.add(currNode);
+                nodeStack.add(null);
+                sumStack.add(currSum);
+                currPath.add(currNode.val);
+                pathStack.add(new ArrayList(currPath));
+                if(currNode.right != null){
+                    nodeStack.add(currNode.right);
+                    sumStack.add(currSum + currNode.right.val);
+                    pathStack.add(new ArrayList(currPath));
+                }
+                if(currNode.left != null){
+                    nodeStack.add(currNode.left);
+                    sumStack.add(currSum + currNode.left.val);
+                    pathStack.add(new ArrayList(currPath));
+                }
+            }else{
+                nodeStack.pop();
+                TreeNode temp = nodeStack.pop();
+                if(temp.left == null && temp.right == null && currSum == targetSum)
+                    result.add(new ArrayList(currPath));
+            }
+        }
+        return result;
+    }
+}
+```
 
 ## python
 

problems/0121.买卖股票的最佳时机.md

@@ -14,16 +14,21 @@
 
 返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
 
-示例 1：   
-输入：[7,1,5,3,6,4]   
-输出：5    
+* 示例 1：   
+* 输入：[7,1,5,3,6,4]   
+* 输出：5    
 解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
 
-示例 2：   
-输入：prices = [7,6,4,3,1]  
-输出：0    
+* 示例 2：   
+* 输入：prices = [7,6,4,3,1]  
+* 输出：0    
 解释：在这种情况下, 没有交易完成, 所以最大利润为 0。
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划之 LeetCode：121.买卖股票的最佳时机1](https://www.bilibili.com/video/BV1Xe4y1u77q)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 
 ## 思路
 

problems/0122.买卖股票的最佳时机II.md

@@ -102,7 +102,7 @@ public:
 
 ### 动态规划
 
-动态规划将在下一个系列详细讲解，本题解先给出我的 C++代码（带详细注释），感兴趣的同学可以自己先学习一下。
+动态规划将在下一个系列详细讲解，本题解先给出我的 C++代码（带详细注释），想先学习的话，可以看本篇：[122.买卖股票的最佳时机II（动态规划）](https://programmercarl.com/0122.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAII%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html#%E6%80%9D%E8%B7%AF)
 
 ```CPP
 class Solution {

problems/0122.买卖股票的最佳时机II（动态规划）.md

@@ -15,25 +15,30 @@
 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
 
-示例 1:         
-输入: [7,1,5,3,6,4]    
-输出: 7                   
+* 示例 1:         
+* 输入: [7,1,5,3,6,4]    
+* 输出: 7                   
 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。         
 
-示例 2:           
-输入: [1,2,3,4,5]        
-输出: 4                         
+* 示例 2:           
+* 输入: [1,2,3,4,5]        
+* 输出: 4                         
 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
 
-示例 3:           
-输入: [7,6,4,3,1]        
-输出: 0         
+* 示例 3:           
+* 输入: [7,6,4,3,1]        
+* 输出: 0         
 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。       
 
 提示：    
 * 1 <= prices.length <= 3 * 10 ^ 4
 * 0 <= prices[i] <= 10 ^ 4
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，股票问题第二弹 | LeetCode：122.买卖股票的最佳时机II](https://www.bilibili.com/video/BV1D24y1Q7Ls)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路 
 
 本题我们在讲解贪心专题的时候就已经讲解过了[贪心算法：买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html)，只不过没有深入讲解动态规划的解法，那么这次我们再好好分析一下动规的解法。

problems/0123.买卖股票的最佳时机III.md

@@ -15,23 +15,23 @@
 
 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
-示例 1:
-输入：prices = [3,3,5,0,0,3,1,4]
-输出：6
+* 示例 1:
+* 输入：prices = [3,3,5,0,0,3,1,4]
+* 输出：6
 解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3。
 
-示例 2：
-输入：prices = [1,2,3,4,5]
-输出：4
+* 示例 2：
+* 输入：prices = [1,2,3,4,5]
+* 输出：4
 解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
 
-示例 3：
-输入：prices = [7,6,4,3,1]
-输出：0
+* 示例 3：
+* 输入：prices = [7,6,4,3,1]
+* 输出：0
 解释：在这个情况下, 没有交易完成, 所以最大利润为0。
 
-示例 4：
-输入：prices = [1]
+* 示例 4：
+* 输入：prices = [1]
 输出：0
 
 提示：
@@ -39,6 +39,11 @@
 * 1 <= prices.length <= 10^5
 * 0 <= prices[i] <= 10^5
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，股票至多买卖两次，怎么求？ | LeetCode：123.买卖股票最佳时机III](https://www.bilibili.com/video/BV1WG411K7AR)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 

problems/0131.分割回文串.md

@@ -209,6 +209,9 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n^2)
+
 # 优化
 
 上面的代码还存在一定的优化空间, 在于如何更高效的计算一个子字符串是否是回文字串。上述代码```isPalindrome```函数运用双指针的方法来判定对于一个字符串```s```, 给定起始下标和终止下标, 截取出的子字符串是否是回文字串。但是其中有一定的重复计算存在:

problems/0139.单词拆分.md

@@ -351,7 +351,17 @@ class Solution:
                     dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
         return dp[len(s)]
 ```
-
+```python
+class Solution: # 和视频中写法一致（和最上面C++写法一致）
+    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
+        dp = [False]*(len(s)+1)
+        dp[0]=True
+        for j in range(1,len(s)+1):
+            for i in range(j):
+                word = s[i:j]
+                if word in wordDict and dp[i]: dp[j]=True
+        return dp[-1]
+```
 
 
 

problems/0188.买卖股票的最佳时机IV.md

@@ -14,14 +14,14 @@
 
 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
-示例 1：
-输入：k = 2, prices = [2,4,1]
-输出：2
+* 示例 1：
+* 输入：k = 2, prices = [2,4,1]
+* 输出：2
 解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2。
 
-示例 2：
-输入：k = 2, prices = [3,2,6,5,0,3]
-输出：7
+* 示例 2：
+* 输入：k = 2, prices = [3,2,6,5,0,3]
+* 输出：7
 解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
 
 
@@ -31,6 +31,11 @@
 * 0 <= prices.length <= 1000
 * 0 <= prices[i] <= 1000
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划来决定最佳时机，至多可以买卖K次！| LeetCode：188.买卖股票最佳时机4](https://www.bilibili.com/video/BV16M411U7XJ)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 这道题目可以说是[动态规划：123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)的进阶版，这里要求至多有k次交易。
@@ -328,6 +333,42 @@ func max(a, b int) int {
 }
 ```
 
+版本二: 三维 dp数组
+```go
+func maxProfit(k int, prices []int) int {
+	length := len(prices)
+	if length == 0 {
+		return 0
+	}
+	// [天数][交易次数][是否持有股票]
+	// 1表示不持有/卖出, 0表示持有/买入
+	dp := make([][][]int, length)
+	for i := 0; i < length; i++ {
+		dp[i] = make([][]int, k+1)
+		for j := 0; j <= k; j++ {
+			dp[i][j] = make([]int, 2)
+		}
+	}
+	for j := 0; j <= k; j++ {
+		dp[0][j][0] = -prices[0]
+	}
+	for i := 1; i < length; i++ {
+		for j := 1; j <= k; j++ {
+			dp[i][j][0] = max188(dp[i-1][j][0], dp[i-1][j-1][1]-prices[i])
+			dp[i][j][1] = max188(dp[i-1][j][1], dp[i-1][j][0]+prices[i])
+		}
+	}
+	return dp[length-1][k][1]
+}
+
+func max188(a, b int) int {
+	if a > b {
+		return a
+	}
+	return b
+}
+```
+
 Javascript:
 
 ```javascript

problems/0198.打家劫舍.md

@@ -31,6 +31,10 @@
 * 0 <= nums.length <= 100
 * 0 <= nums[i] <= 400
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍](https://www.bilibili.com/video/BV1Te411N7SX)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 ## 思路
 
@@ -136,6 +140,29 @@ class Solution {
 		return dp[nums.length - 1];
 	}
 }
+
+// 空间优化 dp数组只存与计算相关的两次数据
+class Solution {
+    public int rob(int[] nums) {
+        if (nums.length == 1)  {
+            return nums[0];
+        }
+        // 初始化dp数组
+        // 优化空间 dp数组只用2格空间 只记录与当前计算相关的前两个结果
+        int[] dp = new int[2];
+        dp[0] = nums[0];
+        dp[1] = nums[0] > nums[1] ? nums[0] : nums[1];
+        int res = 0;
+        // 遍历
+        for (int i = 2; i < nums.length; i++) {
+            res = (dp[0] + nums[i]) > dp[1] ? (dp[0] + nums[i]) : dp[1];
+            dp[0] = dp[1];
+            dp[1] = res;
+        }
+        // 输出结果
+        return dp[1];
+    }
+}
 ```
 
 Python：
@@ -153,7 +180,17 @@ class Solution:
             dp[i] = max(dp[i-2]+nums[i], dp[i-1])
         return dp[-1]
 ```
-
+```python
+class Solution: # 二维dp数组写法
+    def rob(self, nums: List[int]) -> int:
+        dp = [[0,0] for _ in range(len(nums))]
+        dp[0][1] = nums[0]
+        for i in range(1,len(nums)):
+            dp[i][0] = max(dp[i-1][1],dp[i-1][0])
+            dp[i][1] = dp[i-1][0]+nums[i]
+        print(dp)            
+        return max(dp[-1])
+```
 Go：
 ```Go
 func rob(nums []int) int {
@@ -220,3 +257,4 @@ function rob(nums: number[]): number {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0213.打家劫舍II.md

@@ -14,23 +14,28 @@
 
 示例 1：
 
-输入：nums = [2,3,2]
-输出：3
-解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。
+* 输入：nums = [2,3,2]
+* 输出：3
+* 解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。
 
-示例 2：
-输入：nums = [1,2,3,1]
-输出：4
-解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。偷窃到的最高金额 = 1 + 3 = 4 。
+* 示例 2：
+* 输入：nums = [1,2,3,1]
+* 输出：4
+* 解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。偷窃到的最高金额 = 1 + 3 = 4 。
 
-示例 3：
-输入：nums = [0]
-输出：0
+* 示例 3：
+* 输入：nums = [0]
+* 输出：0
 
 提示：
 * 1 <= nums.length <= 100
 * 0 <= nums[i] <= 1000
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，房间连成环了那还偷不偷呢？| LeetCode：213.打家劫舍II](https://www.bilibili.com/video/BV1oM411B7xq)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 这道题目和[198.打家劫舍](https://programmercarl.com/0198.打家劫舍.html)是差不多的，唯一区别就是成环了。
@@ -147,7 +152,20 @@ class Solution:
                 dp[i]=max(dp[i-1],dp[i-2]+nums[i])
         return dp[-1]
 ```
-
+```python
+class Solution: # 二维dp数组写法
+    def rob(self, nums: List[int]) -> int:
+        if len(nums)<3: return max(nums)
+        return max(self.default(nums[:-1]),self.default(nums[1:]))
+    def default(self,nums):
+        dp = [[0,0] for _ in range(len(nums))]
+        dp[0][1] = nums[0]
+        for i in range(1,len(nums)):
+            dp[i][0] = max(dp[i-1])
+            dp[i][1] = dp[i-1][0] + nums[i]
+        return max(dp[-1])
+        
+```
 Go：
 
 ```go

problems/0216.组合总和III.md

@@ -235,6 +235,8 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
 
 # 总结
 

problems/0225.用队列实现栈.md

@@ -166,7 +166,7 @@ public:
 
 Java：
 
-使用两个 Queue 实现
+使用两个 Queue 实现方法1
 ```java
 class MyStack {
 
@@ -208,6 +208,42 @@ class MyStack {
 }
 
 ```
+使用两个 Queue 实现方法2
+```java
+class MyStack {
+    //q1作为主要的队列，其元素排列顺序和出栈顺序相同
+    Queue<Integer> q1 = new ArrayDeque<>();
+    //q2仅作为临时放置
+    Queue<Integer> q2 = new ArrayDeque<>();
+
+    public MyStack() {
+
+    }
+    //在加入元素时先将q1中的元素依次出栈压入q2，然后将新加入的元素压入q1，再将q2中的元素依次出栈压入q1
+    public void push(int x) {
+        while (q1.size() > 0) {
+            q2.add(q1.poll());
+        }
+        q1.add(x);
+        while (q2.size() > 0) {
+            q1.add(q2.poll());
+        }
+    }
+
+    public int pop() {
+        return q1.poll();
+    }
+
+    public int top() {
+        return q1.peek();
+    }
+
+    public boolean empty() {
+        return q1.isEmpty();
+    }
+}
+```
+
 使用两个 Deque 实现
 ```java
 class MyStack {
@@ -329,6 +365,43 @@ class MyStack {
     }
 }
 
+```
+优化，使用一个 Queue 实现，但用卡哥的逻辑实现
+```Java
+class MyStack {
+    Queue<Integer> queue;
+    
+    public MyStack() {
+        queue = new LinkedList<>();
+    }
+    
+    public void push(int x) {
+        queue.add(x);
+    }
+    
+    public int pop() {
+        rePosition();
+        return queue.poll();
+    }
+    
+    public int top() {
+        rePosition();
+        int result = queue.poll();
+        queue.add(result);
+        return result;
+    }
+    
+    public boolean empty() {
+        return queue.isEmpty();
+    }
+
+    public void rePosition(){
+        int size = queue.size();
+        size--;
+        while(size-->0)
+            queue.add(queue.poll());
+    }
+}
 ```
 
 Python：

problems/0226.翻转二叉树.md

@@ -991,6 +991,53 @@ impl Solution {
 }
 ```
 
+### C#
+
+```csharp
+//递归
+public class Solution {
+    public TreeNode InvertTree(TreeNode root) {
+    if (root == null) return root;
+    
+    swap(root);
+    InvertTree(root.left);
+    InvertTree(root.right);
+    return root;
+    }
+   
+    public void swap(TreeNode node) {
+        TreeNode temp = node.left;
+        node.left = node.right;
+        node.right = temp;
+    }
+}
+```
+
+```csharp
+//迭代
+public class Solution {
+    public TreeNode InvertTree(TreeNode root) {
+          if (root == null) return null;
+        Stack<TreeNode> stack=new Stack<TreeNode>();
+        stack.Push(root);
+        while(stack.Count>0)
+        {
+            TreeNode node = stack.Pop();   
+            swap(node);
+            if(node.right!=null) stack.Push(node.right);   
+            if(node.left!=null) stack.Push(node.left);     
+        }
+        return root;
+    }
+
+    public void swap(TreeNode node) {
+        TreeNode temp = node.left;
+        node.left = node.right;
+        node.right = temp;
+    }
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0242.有效的字母异位词.md

@@ -202,6 +202,19 @@ var isAnagram = function(s, t) {
     }
     return true;
 };
+
+var isAnagram = function(s, t) {
+  if(s.length !== t.length) return false;
+  let char_count = new Map();
+  for(let item of s) {
+    char_count.set(item, (char_count.get(item) || 0) + 1) ;
+  }
+  for(let item of t) {
+    if(!char_count.get(item)) return false;
+    char_count.set(item, char_count.get(item)-1);
+  }
+  return true;
+};
 ```
 
 TypeScript：

problems/0300.最长上升子序列.md

@@ -149,7 +149,7 @@ class Solution:
         if len(nums) <= 1:
             return len(nums)
         dp = [1] * len(nums)
-        result = 0
+        result = 1
         for i in range(1, len(nums)):
             for j in range(0, i):
                 if nums[i] > nums[j]:

problems/0309.最佳买卖股票时机含冷冻期.md

@@ -20,6 +20,10 @@
 * 输出: 3
 * 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划来决定最佳时机，这次有冷冻期！| LeetCode：309.买卖股票的最佳时机含冷冻期](https://www.bilibili.com/video/BV1rP4y1D7ku)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 ## 思路
 

problems/0337.打家劫舍III.md

@@ -16,6 +16,11 @@
 
 ![337.打家劫舍III](https://code-thinking-1253855093.file.myqcloud.com/pics/20210223173849619.png)
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，房间连成树了，偷不偷呢？| LeetCode：337.打家劫舍3](https://www.bilibili.com/video/BV1H24y1Q7sY)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 这道题目和 [198.打家劫舍](https://programmercarl.com/0198.打家劫舍.html)，[213.打家劫舍II](https://programmercarl.com/0213.打家劫舍II.html)也是如出一辙，只不过这个换成了树。

problems/0343.整数拆分.md

@@ -367,6 +367,29 @@ pub fn integer_break(n: i32) -> i32 {
 }
 ```
 
+贪心：
+
+```rust
+impl Solution {
+    pub fn integer_break(mut n: i32) -> i32 {
+        match n {
+            2 => 1,
+            3 => 2,
+            4 => 4,
+            5.. => {
+                let mut res = 1;
+                while n > 4 {
+                    res *= 3;
+                    n -= 3;
+                }
+                res * n
+            }
+            _ => panic!("Error"),
+        }
+    }
+}
+```
+
 ### TypeScript
 
 ```typescript
@@ -392,27 +415,6 @@ function integerBreak(n: number): number {
 };
 ```
 
-### Rust
-
-```Rust
-impl Solution {
-    fn max(a: i32, b: i32) -> i32{
-        if a > b { a } else { b }
-    }
-    pub fn integer_break(n: i32) -> i32 {
-        let n = n as usize;
-        let mut dp = vec![0; n + 1];
-        dp[2] = 1;
-        for i in 3..=n {
-            for j in 1..i - 1 {
-                dp[i] = Self::max(dp[i], Self::max(((i - j) * j) as i32, dp[i - j] * j as i32));
-            }
-        }
-        dp[n]
-    }
-}
-```
-
 ### C
 
 ```c

problems/0347.前K个高频元素.md

@@ -188,7 +188,33 @@ class Solution {
     }
 }
 ```
-
+简化版代码：
+```java
+class Solution {
+    public int[] topKFrequent(int[] nums, int k) {
+        // 优先级队列，为了避免复杂 api 操作，pq 存储数组
+        // lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从大到小，o2 - o1 反之
+        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
+        int[] res = new int[k]; // 答案数组为 k 个元素
+        Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数
+        for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
+        for(var x : map.entrySet()) { // entrySet 获取 k-v Set 集合
+            // 将 kv 转化成数组
+            int[] tmp = new int[2];
+            tmp[0] = x.getKey();
+            tmp[1] = x.getValue();
+            pq.offer(tmp);
+            if(pq.size() > k) {
+                pq.poll();
+            }
+        }
+        for(int i = 0; i < k; i ++) {
+            res[i] = pq.poll()[0]; // 获取优先队列里的元素
+        }
+        return res;
+    }
+}
+```
 
 Python：
 ```python

problems/0376.摆动序列.md

@@ -99,7 +99,7 @@
 
 这里我们可以写死，就是 如果只有两个元素，且元素不同，那么结果为 2。
 
-不写死的话，如果和我们的判断规则结合在一起呢？
+不写死的话，如何和我们的判断规则结合在一起呢？
 
 可以假设，数组最前面还有一个数字，那这个数字应该是什么呢？
 

problems/0377-组合总和IV(完全背包的排列问题二维迭代理解).md

@@ -1,145 +0,0 @@
-# 完全背包的排列问题模拟
-
-#### Problem
-
-1. 排列问题是完全背包中十分棘手的问题。
-2. 其在迭代过程中需要先迭代背包容量，再迭代物品个数，使得其在代码理解上较难入手。
-
-#### Contribution
-
-本文档以力扣上[组合总和IV](https://leetcode.cn/problems/combination-sum-iv/)为例，提供一个二维dp的代码例子，并提供模拟过程以便于理解
-
-#### Code
-
-```cpp
-int combinationSum4(vector<int>& nums, int target) {
-	// 定义背包容量为target，物品个数为nums.size()的dp数组	
-	// dp[i][j]表示将第0-i个物品添加入排列中，和为j的排列方式
-	vector<vector<int>> dp (nums.size(), vector(target+1,0));
-
-	// 表示有0,1,...,n个物品可选择的情况下，和为0的选择方法为1：什么都不取
-	for(int i = 0; i < nums.size(); i++) dp[i][0] = 1;
-
-	// 必须按列遍历，因为右边数组需要知道左边数组最低部的信息（排列问题）
-	// 后面的模拟可以更清楚的表现这么操作的原因
-	for(int i = 1; i <= target; i++){
-		for(int j = 0; j < nums.size(); j++){
-			// 只有nums[j]可以取的情况
-			if(j == 0){
-				if(nums[j] > i) dp[j][i] = 0;
-				// 如果背包容量放不下 那么此时没有排列方式
-				else dp[j][i] = dp[nums.size()-1][i-nums[j]];
-				// 如果背包容量放的下 全排列方式为dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]
-			}
-			// 有多个nums数可以取
-			else{
-				// 如果背包容量放不下 那么沿用0-j-1个物品的排列方式
-				if(nums[j] > i) dp[j][i] = dp[j-1][i];
-				// 如果背包容量放得下 在dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]后面放个nums[j]
-				// INT_MAX避免溢出
-				else if(i >= nums[j] && dp[j-1][i] < INT_MAX - dp[nums.size()-1][i-nums[j]]) 
-					dp[j][i] = dp[j-1][i] + dp[nums.size()-1][i-nums[j]];
-				}
-			}
-		}
-	// 打印dp数组
-	for(int i = 0; i < nums.size(); i++){
-		for(int j = 0; j <= target; j++){
-			cout<<dp[i][j]<<" ";
-		}
-		cout<<endl;
-	}
-	return dp[nums.size()-1][target];
-}
-```
-
-#### Simulation
-
-##### 样例 nums = [2,3,4], target = 6
-
-##### 1. 初始化一个3x7的dp数组
-
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-
-dp\[0-2\]\[0\] = 1，含义是有nums[0-2]物品时使得背包容量为0的取法为1，作用是在取到nums[i]物品使得背包容量为nums[i]时取法为1。
-
-##### 2.迭代方式
-
-必须列优先，因为右边的数组在迭代时需要最左下的数组最终结果。
-
-##### 3. 模拟过程
-
-i = 1, j = 0	dp\[0\]\[1\] = 0，表示在物品集合{2}中无法组成和为1
-i = 1, j = 1	dp\[1\]\[1\] = 0，表示在物品集合{2,3}中无法组成和为1
-i = 1, j = 2	dp\[2\]\[1\] = 0，表示在物品集合{2,3,4}中无法组成和为1
-
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-1 **0** 0 0 0 0 0
-
-此时dp\[2\]\[1\]作为第1列最底部的元素，表示所有物品都有的情况下组成和为1的排列方式为0
-
-————————————————————————————
-
-i = 2, j = 0	dp\[0\]\[2\] = 1，表示在物品集合{2}中取出和为2的排列有{2}
-i = 2, j = 1	dp\[1\]\[2\] = 1，表示在物品集合{2,3}中取出和为2的排列有{2}
-i = 2, j = 2	dp\[2\]\[2\] = 1，表示在物品集合{2,3,4}中取出和为2的排列有{2}
-
-1 0 1 0 0 0 0
-1 0 1 0 0 0 0
-1 0 **1** 0 0 0 0
-
-此时dp\[2\]\[2\]作为第2列最底部的元素，表示所有物品都有的情况下和为2的排列方式有1个 （类比成一维dp即dp[2]=dp[0]）
-
-————————————————————————————
-
-i = 3, j = 0	dp\[0\]\[3\] = 0，表示在物品集合{2}中无法取出和为3
-i = 3, j = 1	dp\[1\]\[3\] = 1，表示在物品集合{2,3}中取出和为3的排列有{3}
-i = 3, j = 2	dp\[2\]\[3\] = 1，表示在物品集合{2,3,4}中取出和为3的排列有{3}
-
-1 0 1 0 0 0 0
-1 0 1 1 0 0 0
-1 0 1 **1** 0 0 0
-
-此时dp\[2\]\[3\]作为第3列最底部的元素，表示所有物品都有的情况下和为3的排列方式有1个（类比成一维dp即dp[3]=dp[0]）
-
-————————————————————————————
-
-i = 4, j = 0	dp\[0\]\[4\] = 1，表示在物品集合{2}中取出和为4的排列有在原有的排列{2}后添加一个2成为{2,2}（从第2列底部信息继承获得）
-i = 4, j = 1	dp\[1\]\[4\] = 1，表示在物品集合{2,3}中取出和为4的排列有{2,2}
-i = 4, j = 2	dp\[2\]\[4\] = 2，表示在物品集合{2,3,4}中取出和为4的排列有{{2,2},{4}}（{2,2}的信息从该列头上获得）
-
-1 0 1 0 1 0 0
-1 0 1 1 1 0 0
-1 0 1 1 **2** 0 0
-
-此时dp\[2\]\[4\]作为第4列最底部的元素，表示所有物品都有的情况下和为4的排列方式有2个
-
-————————————————————————————
-
-i = 5, j = 0	dp\[0\]\[5\] = 1，表示在物品集合{2}中取出和为5的排列有{3,2} **(3的信息由dp[2]\[3]获得，即将2放在3的右边)**
-i = 5, j = 1	dp\[1\]\[5\] = 2，表示在物品集合{2,3}中取出和为5的排列有{{2,3},{3,2}} **({3,2}由上一行信息继承，{2,3}是从dp[2] [2]获得，将3放在2的右边)**
-i = 5, j = 2	dp\[2\]\[5\] = 2，表示在物品集合{2,3,4}中取出和为5的排列有{{2,3},{3,2}}
-
-1 0 1 0 1 1 0
-1 0 1 1 1 2 0
-1 0 1 1 2 **2** 0
-
-此时dp\[2\]\[5\]作为第5列最底部的元素，表示所有物品都有的情况下和为5的排列方式有2个
-
-————————————————————————————
-
-i = 6, j = 0	dp\[0\]\[6\] = 2，表示在物品集合{2}中取出和为6的排列有{{2,2,2},{4,2}} **(信息由dp[2]\[4]获得，即将2放在{2,2}和{4}的右边)**
-i = 6, j = 1	dp\[1\]\[6\] = 3，表示在物品集合{2,3}中取出和为6的排列有{{2,2,2},{4,2},{3,3}} **({2,2,2},{4,2}由上一行信息继承，{3,3}是从dp[2] [3]获得，将3放在3的右边)**
-i = 6, j = 2	dp\[2\]\[6\] = 4，表示在物品集合{2,3,4}中取出和为6的排列有{{2,2,2},{4,2},{3,3},{2,4}} **({2,2,2},{4,2},{3,3}由上一行继承，{2,4}从dp[2]获得，将4放在2的右边)**
-
-1 0 1 0 1 1 2
-1 0 1 1 1 2 3
-1 0 1 1 2 2 **4**
-
-此时dp\[2\]\[6\]作为第6列最底部的元素，表示所有物品都有的情况下和为6的排列方式有4个，为{2,2,2}，{4,2}，{3,3}，{2,4}。
-
-
-

problems/0377.组合总和IV二维dp数组.md

@@ -1,145 +0,0 @@
-# 完全背包的排列问题模拟
-
-#### Problem
-
-1. 排列问题是完全背包中十分棘手的问题。
-2. 其在迭代过程中需要先迭代背包容量，再迭代物品个数，使得其在代码理解上较难入手。
-
-#### Contribution
-
-本文档以力扣上[组合总和IV](https://leetcode.cn/problems/combination-sum-iv/)为例，提供一个二维dp的代码例子，并提供模拟过程以便于理解
-
-#### Code
-
-```cpp
-int combinationSum4(vector<int>& nums, int target) {
-	// 定义背包容量为target，物品个数为nums.size()的dp数组	
-	// dp[i][j]表示将第0-i个物品添加入排列中，和为j的排列方式
-	vector<vector<int>> dp (nums.size(), vector(target+1,0));
-
-	// 表示有0,1,...,n个物品可选择的情况下，和为0的选择方法为1：什么都不取
-	for(int i = 0; i < nums.size(); i++) dp[i][0] = 1;
-
-	// 必须按列遍历，因为右边数组需要知道左边数组最低部的信息（排列问题）
-	// 后面的模拟可以更清楚的表现这么操作的原因
-	for(int i = 1; i <= target; i++){
-		for(int j = 0; j < nums.size(); j++){
-			// 只有nums[j]可以取的情况
-			if(j == 0){
-				if(nums[j] > i) dp[j][i] = 0;
-				// 如果背包容量放不下 那么此时没有排列方式
-				else dp[j][i] = dp[nums.size()-1][i-nums[j]];
-				// 如果背包容量放的下 全排列方式为dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]
-			}
-			// 有多个nums数可以取
-			else{
-				// 如果背包容量放不下 那么沿用0-j-1个物品的排列方式
-				if(nums[j] > i) dp[j][i] = dp[j-1][i];
-				// 如果背包容量放得下 在dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]后面放个nums[j]
-				// INT_MAX避免溢出
-				else if(i >= nums[j] && dp[j-1][i] < INT_MAX - dp[nums.size()-1][i-nums[j]]) 
-					dp[j][i] = dp[j-1][i] + dp[nums.size()-1][i-nums[j]];
-				}
-			}
-		}
-	// 打印dp数组
-	for(int i = 0; i < nums.size(); i++){
-		for(int j = 0; j <= target; j++){
-			cout<<dp[i][j]<<" ";
-		}
-		cout<<endl;
-	}
-	return dp[nums.size()-1][target];
-}
-```
-
-#### Simulation
-
-##### 样例 nums = [2,3,4], target = 6
-
-##### 1. 初始化一个3x7的dp数组
-
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-
-dp\[0-2\]\[0\] = 1，含义是有nums[0-2]物品时使得背包容量为0的取法为1，作用是在取到nums[i]物品使得背包容量为nums[i]时取法为1。
-
-##### 2.迭代方式
-
-必须列优先，因为右边的数组在迭代时需要最左下的数组最终结果。
-
-##### 3. 模拟过程
-
-i = 1, j = 0	dp\[0\]\[1\] = 0，表示在物品集合{2}中无法组成和为1
-i = 1, j = 1	dp\[1\]\[1\] = 0，表示在物品集合{2,3}中无法组成和为1
-i = 1, j = 2	dp\[2\]\[1\] = 0，表示在物品集合{2,3,4}中无法组成和为1
-
-1 0 0 0 0 0 0
-1 0 0 0 0 0 0
-1 **0** 0 0 0 0 0
-
-此时dp\[2\]\[1\]作为第1列最底部的元素，表示所有物品都有的情况下组成和为1的排列方式为0
-
-————————————————————————————
-
-i = 2, j = 0	dp\[0\]\[2\] = 1，表示在物品集合{2}中取出和为2的排列有{2}
-i = 2, j = 1	dp\[1\]\[2\] = 1，表示在物品集合{2,3}中取出和为2的排列有{2}
-i = 2, j = 2	dp\[2\]\[2\] = 1，表示在物品集合{2,3,4}中取出和为2的排列有{2}
-
-1 0 1 0 0 0 0
-1 0 1 0 0 0 0
-1 0 **1** 0 0 0 0
-
-此时dp\[2\]\[2\]作为第2列最底部的元素，表示所有物品都有的情况下和为2的排列方式有1个 （类比成一维dp即dp[2]=dp[0]）
-
-————————————————————————————
-
-i = 3, j = 0	dp\[0\]\[3\] = 0，表示在物品集合{2}中无法取出和为3
-i = 3, j = 1	dp\[1\]\[3\] = 1，表示在物品集合{2,3}中取出和为3的排列有{3}
-i = 3, j = 2	dp\[2\]\[3\] = 1，表示在物品集合{2,3,4}中取出和为3的排列有{3}
-
-1 0 1 0 0 0 0
-1 0 1 1 0 0 0
-1 0 1 **1** 0 0 0
-
-此时dp\[2\]\[3\]作为第3列最底部的元素，表示所有物品都有的情况下和为3的排列方式有1个（类比成一维dp即dp[3]=dp[0]）
-
-————————————————————————————
-
-i = 4, j = 0	dp\[0\]\[4\] = 1，表示在物品集合{2}中取出和为4的排列有在原有的排列{2}后添加一个2成为{2,2}（从第2列底部信息继承获得）
-i = 4, j = 1	dp\[1\]\[4\] = 1，表示在物品集合{2,3}中取出和为4的排列有{2,2}
-i = 4, j = 2	dp\[2\]\[4\] = 2，表示在物品集合{2,3,4}中取出和为4的排列有{{2,2},{4}}（{2,2}的信息从该列头上获得）
-
-1 0 1 0 1 0 0
-1 0 1 1 1 0 0
-1 0 1 1 **2** 0 0
-
-此时dp\[2\]\[4\]作为第4列最底部的元素，表示所有物品都有的情况下和为4的排列方式有2个
-
-————————————————————————————
-
-i = 5, j = 0	dp\[0\]\[5\] = 1，表示在物品集合{2}中取出和为5的排列有{3,2} **(3的信息由dp[2]\[3]获得，即将2放在3的右边)**
-i = 5, j = 1	dp\[1\]\[5\] = 2，表示在物品集合{2,3}中取出和为5的排列有{{2,3},{3,2}} **({3,2}由上一行信息继承，{2,3}是从dp[2] [2]获得，将3放在2的右边)**
-i = 5, j = 2	dp\[2\]\[5\] = 2，表示在物品集合{2,3,4}中取出和为5的排列有{{2,3},{3,2}}
-
-1 0 1 0 1 1 0
-1 0 1 1 1 2 0
-1 0 1 1 2 **2** 0
-
-此时dp\[2\]\[5\]作为第5列最底部的元素，表示所有物品都有的情况下和为5的排列方式有2个
-
-————————————————————————————
-
-i = 6, j = 0	dp\[0\]\[6\] = 2，表示在物品集合{2}中取出和为6的排列有{{2,2,2},{4,2}} **(信息由dp[2]\[4]获得，即将2放在{2,2}和{4}的右边)**
-i = 6, j = 1	dp\[1\]\[6\] = 3，表示在物品集合{2,3}中取出和为6的排列有{{2,2,2},{4,2},{3,3}} **({2,2,2},{4,2}由上一行信息继承，{3,3}是从dp[2] [3]获得，将3放在3的右边)**
-i = 6, j = 2	dp\[2\]\[6\] = 4，表示在物品集合{2,3,4}中取出和为6的排列有{{2,2,2},{4,2},{3,3},{2,4}} **({2,2,2},{4,2},{3,3}由上一行继承，{2,4}从dp[2]获得，将4放在2的右边)**
-
-1 0 1 0 1 1 2
-1 0 1 1 1 2 3
-1 0 1 1 2 2 **4**
-
-此时dp\[2\]\[6\]作为第6列最底部的元素，表示所有物品都有的情况下和为6的排列方式有4个，为{2,2,2}，{4,2}，{3,3}，{2,4}。
-
-
-

problems/0383.赎金信.md

@@ -117,6 +117,10 @@ Java：
 ```Java
 class Solution {
     public boolean canConstruct(String ransomNote, String magazine) {
+        // shortcut
+        if (ransomNote.length() > magazine.length()) {
+            return false;
+        }
         // 定义一个哈希映射数组
         int[] record = new int[26];
 

problems/0406.根据身高重建队列.md

@@ -191,14 +191,14 @@ class Solution {
     public int[][] reconstructQueue(int[][] people) {
         // 身高从大到小排（身高相同k小的站前面）
         Arrays.sort(people, (a, b) -> {
-            if (a[0] == b[0]) return a[1] - b[1];
-            return b[0] - a[0];
+            if (a[0] == b[0]) return a[1] - b[1];   // a - b 是升序排列，故在a[0] == b[0]的狀況下，會根據k值升序排列
+            return b[0] - a[0];   //b - a 是降序排列，在a[0] != b[0]，的狀況會根據h值降序排列
         });
 
         LinkedList<int[]> que = new LinkedList<>();
 
         for (int[] p : people) {
-            que.add(p[1],p);
+            que.add(p[1],p);   //Linkedlist.add(index, value)，會將value插入到指定index裡。
         }
 
         return que.toArray(new int[people.length][]);
@@ -295,19 +295,19 @@ var reconstructQueue = function(people) {
 
 ```Rust
 impl Solution {
-    pub fn reconstruct_queue(people: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
-        let mut people = people;
+    pub fn reconstruct_queue(mut people: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
+        let mut queue = vec![];
         people.sort_by(|a, b| {
-            if a[0] == b[0] { return a[1].cmp(&b[1]); }
+            if a[0] == b[0] {
+                return a[1].cmp(&b[1]);
+            }
             b[0].cmp(&a[0])
         });
-        let mut que: Vec<Vec<i32>> = Vec::new();
-        que.push(people[0].clone());
-        for i in 1..people.len() {
-            let position = people[i][1];
-            que.insert(position as usize, people[i].clone());
+        queue.push(people[0].clone());
+        for v in people.iter().skip(1) {
+            queue.insert(v[1] as usize, v.clone());
         }
-        que
+        queue
     }
 }
 ```

problems/0416.分割等和子集.md

@@ -406,24 +406,21 @@ var canPartition = function(nums) {
 
 ```Rust
 impl Solution {
-    fn max(a: usize, b: usize) -> usize {
-        if a > b { a } else { b }
-    }
     pub fn can_partition(nums: Vec<i32>) -> bool {
-        let nums = nums.iter().map(|x| *x as usize).collect::<Vec<usize>>();
-        let mut sum = 0;
-        let mut dp: Vec<usize> = vec![0; 10001];
-        for i in 0..nums.len() {
-            sum += nums[i];
+        let sum = nums.iter().sum::<i32>() as usize;
+        if sum % 2 == 1 {
+            return false;
         }
-        if sum % 2 == 1 { return false; }
         let target = sum / 2;
-        for i in 0..nums.len() {
-            for j in (nums[i]..=target).rev() {
-                dp[j] = Self::max(dp[j], dp[j - nums[i]] + nums[i]);
+        let mut dp = vec![0; target + 1];
+        for n in nums {
+            for j in (n as usize..=target).rev() {
+                dp[j] = dp[j].max(dp[j - n as usize] + n)
             }
         }
-        if dp[target] == target { return true; }
+        if dp[target] == target as i32 {
+            return true;
+        }
         false
     }
 }

problems/0450.删除二叉搜索树中的节点.md

@@ -682,6 +682,40 @@ object Solution {
 }
 ```
 
+## rust
+
+```rust
+impl Solution {
+    pub fn delete_node(
+        root: Option<Rc<RefCell<TreeNode>>>,
+        key: i32,
+    ) -> Option<Rc<RefCell<TreeNode>>> {
+        root.as_ref()?;
+
+        let mut node = root.as_ref().unwrap().borrow_mut();
+        match node.val.cmp(&key) {
+            std::cmp::Ordering::Less => node.right = Self::delete_node(node.right.clone(), key),
+            std::cmp::Ordering::Equal => match (node.left.clone(), node.right.clone()) {
+                (None, None) => return None,
+                (None, Some(r)) => return Some(r),
+                (Some(l), None) => return Some(l),
+                (Some(l), Some(r)) => {
+                    let mut cur = Some(r.clone());
+                    while let Some(n) = cur.clone().unwrap().borrow().left.clone() {
+                        cur = Some(n);
+                    }
+                    cur.unwrap().borrow_mut().left = Some(l);
+                    return Some(r);
+                }
+            },
+            std::cmp::Ordering::Greater => node.left = Self::delete_node(node.left.clone(), key),
+        }
+        drop(node);
+        root
+    }
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0454.四数相加II.md

@@ -102,21 +102,14 @@ class Solution {
         //统计两个数组中的元素之和，同时统计出现的次数，放入map
         for (int i : nums1) {
             for (int j : nums2) {
-                int tmp = map.getOrDefault(i + j, 0);
-                if (tmp == 0) {
-                    map.put(i + j, 1);
-                } else {
-                    map.replace(i + j, tmp + 1);
-                }
+                int sum = i + j;
+                map.put(sum, map.getOrDefault(sum, 0) + 1);
             }
         }
         //统计剩余的两个元素的和，在map中找是否存在相加为0的情况，同时记录次数
         for (int i : nums3) {
             for (int j : nums4) {
-                int tmp = map.getOrDefault(0 - i - j, 0);
-                if (tmp != 0) {
-                    res += tmp;
-                }
+                res += map.getOrDefault(0 - i - j, 0);
             }
         }
         return res;

problems/0455.分发饼干.md

@@ -48,7 +48,7 @@
 
 如图：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230203105634.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230405225628.png)
 
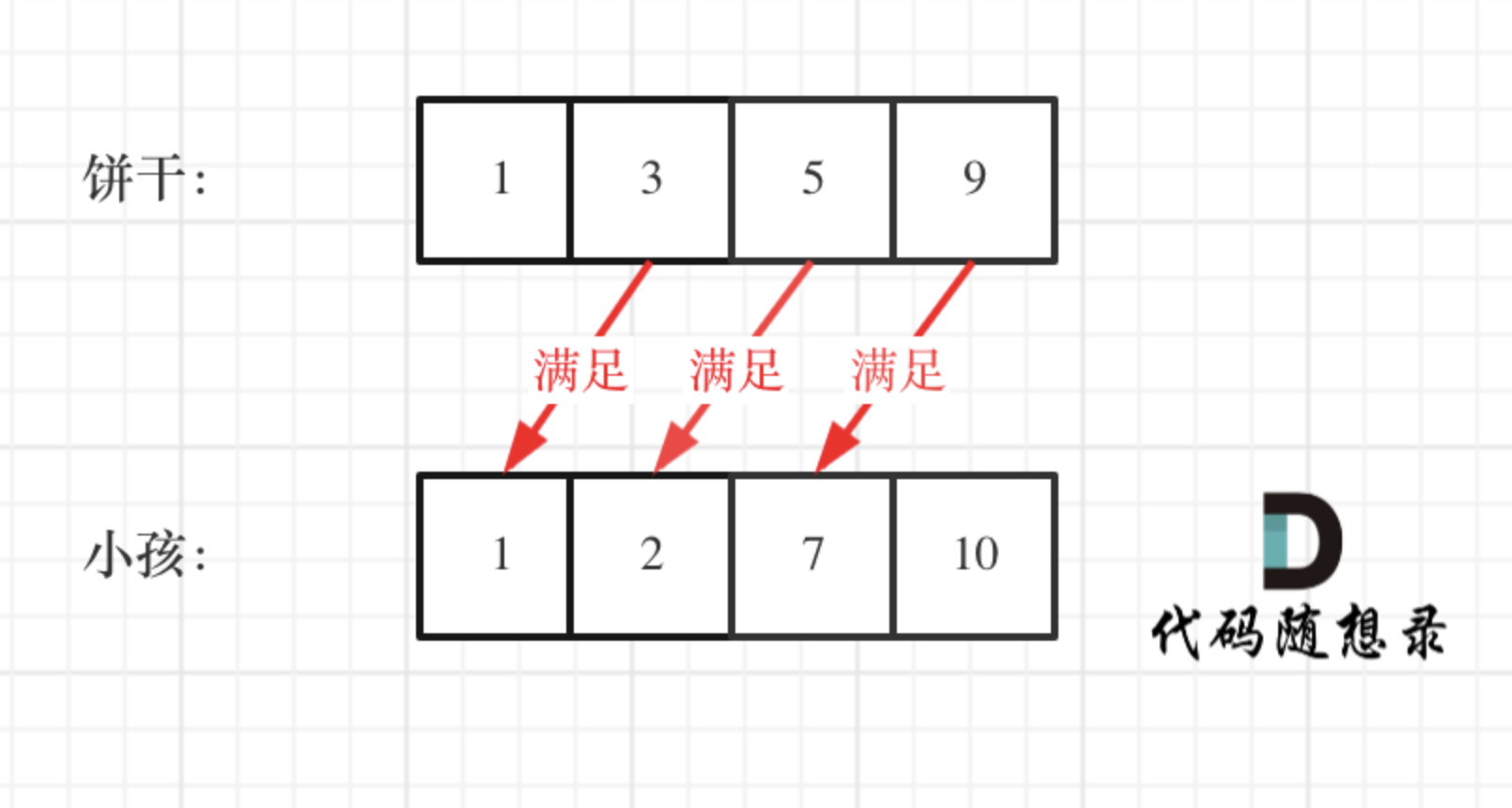
 这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩，这样才是整体最优解，并想不出反例，那么就可以撸代码了。
 

problems/0491.递增子序列.md

@@ -139,6 +139,8 @@ public:
     }
 };
 ```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
 
 ## 优化
 

problems/0494.目标和.md

@@ -417,6 +417,31 @@ object Solution {
 }
 ```
 
+### Rust
+
+```rust
+impl Solution {
+    pub fn find_target_sum_ways(nums: Vec<i32>, target: i32) -> i32 {
+        let sum = nums.iter().sum::<i32>();
+        if target.abs() > sum {
+            return 0;
+        }
+        if (target + sum) % 2 == 1 {
+            return 0;
+        }
+        let size = (sum + target) as usize / 2;
+        let mut dp = vec![0; size + 1];
+        dp[0] = 1;
+        for n in nums {
+            for s in (n as usize..=size).rev() {
+                dp[s] += dp[s - n as usize];
+            }
+        }
+        dp[size]
+    }
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0501.二叉搜索树中的众数.md

@@ -472,6 +472,59 @@ class Solution {
     }
 }
 ```
+統一迭代法
+```Java
+class Solution {
+    public int[] findMode(TreeNode root) {
+        int count = 0;
+        int maxCount = 0;
+        TreeNode pre = null;
+        LinkedList<Integer> res = new LinkedList<>();
+        Stack<TreeNode> stack = new Stack<>();
+
+        if(root != null)
+            stack.add(root);
+        
+        while(!stack.isEmpty()){
+            TreeNode curr = stack.peek();
+            if(curr != null){
+                stack.pop();
+                if(curr.right != null)
+                    stack.add(curr.right);
+                stack.add(curr);
+                stack.add(null);
+                if(curr.left != null)
+                    stack.add(curr.left);
+            }else{
+                stack.pop();
+                TreeNode temp = stack.pop();
+                if(pre == null)
+                    count = 1;
+                else if(pre != null && pre.val == temp.val)
+                    count++;
+                else
+                    count = 1;
+                pre = temp;
+                if(count == maxCount)
+                    res.add(temp.val);
+                if(count > maxCount){
+                    maxCount = count;
+                    res.clear();
+                    res.add(temp.val);
+                }
+            }
+        }
+        int[] result = new int[res.size()];
+        int i = 0;
+        for (int x : res){
+            result[i] = x;
+            i++;
+        }
+        return result;    
+    }
+}
+```
+
 
 ## Python 
 

problems/0503.下一个更大元素II.md

@@ -164,6 +164,7 @@ class Solution {
 
 Python: 
 ```python
+# 方法 1:
 class Solution:
     def nextGreaterElements(self, nums: List[int]) -> List[int]:
         dp = [-1] * len(nums)
@@ -174,6 +175,26 @@ class Solution:
                     stack.pop()
             stack.append(i%len(nums))
         return dp
+
+# 方法 2:
+class Solution:
+    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
+        stack = []
+        # 创建答案数组
+        ans = [-1] * len(nums1)
+        for i in range(len(nums2)):
+            while len(stack) > 0 and nums2[i] > nums2[stack[-1]]:
+                # 判断 num1 是否有 nums2[stack[-1]]。如果没有这个判断会出现指针异常
+                if nums2[stack[-1]] in nums1:
+                    # 锁定 num1 检索的 index
+                    index = nums1.index(nums2[stack[-1]])
+                    # 更新答案数组
+                    ans[index] = nums2[i]
+                # 弹出小元素
+                # 这个代码一定要放在 if 外面。否则单调栈的逻辑就不成立了
+                stack.pop()
+            stack.append(i)
+        return ans
 ```
 Go:
 ```go

problems/0509.斐波那契数.md

@@ -379,26 +379,32 @@ int fib(int n){
 ### Rust
 动态规划:
 ```Rust
-pub fn fib(n: i32) -> i32 {
-    let n = n as usize;
-    let mut dp = vec![0; 31];
-    dp[1] = 1;
-    for i in 2..=n {
-        dp[i] = dp[i - 1] + dp[i - 2];
+impl Solution {
+    pub fn fib(n: i32) -> i32 {
+        if n <= 1 {
+            return n;
+        }
+        let n = n as usize;
+        let mut dp = vec![0; n + 1];
+        dp[1] = 1;
+        for i in 2..=n {
+            dp[i] = dp[i - 2] + dp[i - 1];
+        }
+        dp[n]
     }
-    dp[n]
 }
 ```
 
 递归实现：
 ```Rust
-pub fn fib(n: i32) -> i32 {
-    //若n小于等于1，返回n
-    f n <= 1 {
-        return n;
+impl Solution {
+    pub fn fib(n: i32) -> i32 {
+        if n <= 1 {
+            n
+        } else {
+            Self::fib(n - 1) + Self::fib(n - 2)
+        }
     }
-    //否则返回fib(n-1) + fib(n-2)
-    return fib(n - 1) + fib(n - 2);
 }
 ```
 

problems/0530.二叉搜索树的最小绝对差.md

@@ -174,6 +174,39 @@ class Solution {
     }
 }
 ```
+統一迭代法-中序遍历
+```Java
+class Solution {
+    public int getMinimumDifference(TreeNode root) {
+        Stack<TreeNode> stack = new Stack<>();
+        TreeNode pre = null;
+        int result = Integer.MAX_VALUE;
+
+        if(root != null)
+            stack.add(root);
+        while(!stack.isEmpty()){
+            TreeNode curr = stack.peek();
+            if(curr != null){
+                stack.pop();
+                if(curr.right != null)
+                    stack.add(curr.right);
+                stack.add(curr);
+                stack.add(null);
+                if(curr.left != null)
+                    stack.add(curr.left);
+            }else{
+                stack.pop();
+                TreeNode temp = stack.pop();
+                if(pre != null)
+                    result = Math.min(result, temp.val - pre.val);
+                pre = temp;
+            }
+        }
+        return result;
+    }
+}
+```
+
 迭代法-中序遍历
 
 ```java

problems/0538.把二叉搜索树转换为累加树.md

@@ -177,6 +177,8 @@ public:
 
 
 ## Java 
+**递归**
+
 ```Java
 class Solution {
     int sum;
@@ -198,6 +200,42 @@ class Solution {
     }
 }
 ```
+**迭代**
+
+```Java
+class Solution {
+    //DFS iteraion統一迭代法
+    public TreeNode convertBST(TreeNode root) {
+        int pre = 0;
+        Stack<TreeNode> stack = new Stack<>();
+        if(root == null) //edge case check
+            return null;
+
+        stack.add(root);
+
+        while(!stack.isEmpty()){
+            TreeNode curr = stack.peek();
+            //curr != null的狀況，只負責存node到stack中
+            if(curr != null){ 
+                stack.pop();
+                if(curr.left != null)       //左
+                    stack.add(curr.left);
+                stack.add(curr);            //中
+                stack.add(null);
+                if(curr.right != null)      //右
+                    stack.add(curr.right);
+            }else{
+            //curr == null的狀況，只負責做單層邏輯
+                stack.pop();
+                TreeNode temp = stack.pop();
+                temp.val += pre;
+                pre = temp.val;
+            }
+        }
+        return root;
+    }
+}
+```
 
 ## Python 
 递归法(版本一)

problems/0647.回文子串.md

@@ -238,33 +238,45 @@ Java：
 ```java
 class Solution {
     public int countSubstrings(String s) {
-        int len, ans = 0;
-        if (s == null || (len = s.length()) < 1) return 0;
-        //dp[i][j]：s字符串下标i到下标j的字串是否是一个回文串，即s[i, j]
+        char[] chars = s.toCharArray();
+        int len = chars.length;
         boolean[][] dp = new boolean[len][len];
-        for (int j = 0; j < len; j++) {
-            for (int i = 0; i <= j; i++) {
-                //当两端字母一样时，才可以两端收缩进一步判断
-                if (s.charAt(i) == s.charAt(j)) {
-                    //i++，j--，即两端收缩之后i,j指针指向同一个字符或者i超过j了,必然是一个回文串
-                    if (j - i < 3) {
+        int result = 0;
+        for (int i = len - 1; i >= 0; i--) {
+            for (int j = i; j < len; j++) {
+                if (chars[i] == chars[j]) {
+                    if (j - i <= 1) { // 情况一 和 情况二
+                        result++;
+                        dp[i][j] = true;
+                    } else if (dp[i + 1][j - 1]) { //情况三
+                        result++;
                         dp[i][j] = true;
-                    } else {
-                        //否则通过收缩之后的字串判断
-                        dp[i][j] = dp[i + 1][j - 1];
                     }
-                } else {//两端字符不一样，不是回文串
-                    dp[i][j] = false;
                 }
             }
         }
-        //遍历每一个字串，统计回文串个数
-        for (int i = 0; i < len; i++) {
-            for (int j = 0; j < len; j++) {
-                if (dp[i][j]) ans++;
+        return result;
+    }
+}
+
+```
+
+动态规划：简洁版
+```java
+class Solution {
+    public int countSubstrings(String s) {
+        boolean[][] dp = new boolean[s.length()][s.length()];
+        
+        int res = 0;
+        for (int i = s.length() - 1; i >= 0; i--) {
+            for (int j = i; j < s.length(); j++) {
+                if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
+                    res++;
+                    dp[i][j] = true;
+                }
             }
         }
-        return ans;
+        return res;
     }
 }
 ```

problems/0669.修剪二叉搜索树.md

@@ -248,6 +248,8 @@ public:
 
 ## Java
 
+**递归**
+
 ```Java
 class Solution {
     public TreeNode trimBST(TreeNode root, int low, int high) {
@@ -269,6 +271,46 @@ class Solution {
 
 ```
 
+**迭代**
+
+```Java
+class Solution {
+    //iteration
+    public TreeNode trimBST(TreeNode root, int low, int high) {
+        if(root == null)
+            return null;
+        while(root != null && (root.val < low || root.val > high)){
+            if(root.val < low)
+                root = root.right;
+            else
+                root = root.left;
+        }
+
+        TreeNode curr = root;
+        
+        //deal with root's left sub-tree, and deal with the value smaller than low.
+        while(curr != null){
+            while(curr.left != null && curr.left.val < low){
+                curr.left = curr.left.right;
+            }
+            curr = curr.left;
+        }
+        //go back to root;
+        curr = root;
+
+        //deal with root's righg sub-tree, and deal with the value bigger than high.
+        while(curr != null){
+            while(curr.right != null && curr.right.val > high){
+                curr.right = curr.right.left;
+            }
+            curr = curr.right;
+        }
+        return root;
+    }
+}
+
+````
+
 ## Python
 
 递归法（版本一）

problems/0714.买卖股票的最佳时机含手续费（动态规划）.md

@@ -32,6 +32,11 @@
 * 0 < prices[i] < 50000.
 * 0 <= fee < 50000.
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划来决定最佳时机，这次含手续费！| LeetCode：714.买卖股票的最佳时机含手续费](https://www.bilibili.com/video/BV1z44y1Z7UR)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 本题贪心解法：[贪心算法：买卖股票的最佳时机含手续费](https://programmercarl.com/0714.买卖股票的最佳时机含手续费.html) 

problems/0746.使用最小花费爬楼梯.md

@@ -328,17 +328,30 @@ func min(a, b int) int {
 ```
 
 
-### Javascript 
-```Javascript
+### JavaScript 
+
+```JavaScript
 var minCostClimbingStairs = function(cost) {
-    const n = cost.length;
-    const dp = new Array(n + 1);
-    dp[0] = dp[1] = 0;
-    for (let i = 2; i <= n; ++i) {
-        dp[i] = Math.min(dp[i -1] + cost[i - 1], dp[i - 2] + cost[i - 2])
+  const dp = [0, 0]
+  for (let i = 2; i <= cost.length; ++i) {
+    dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
+  }
+  return dp[cost.length]
+};
+```
+
+不使用 dp 数组
+
+```JavaScript
+var minCostClimbingStairs = function(cost) {
+  let dpBefore = 0,
+    dpAfter = 0
+    for(let i = 2;i <= cost.length;i++){
+        let dpi = Math.min(dpBefore + cost[i - 2],dpAfter + cost[i - 1])
+        dpBefore = dpAfter
+        dpAfter = dpi
     }
-    
-    return dp[n]
+    return dpAfter
 };
 ```
 
@@ -346,38 +359,55 @@ var minCostClimbingStairs = function(cost) {
 
 ```typescript
 function minCostClimbingStairs(cost: number[]): number {
-    /**
-        dp[i]: 走到第i阶需要花费的最少金钱
-        dp[0]: 0;
-        dp[1]: 0;
-        ...
-        dp[i]: min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
-     */
-    const dp = [];
-    const length = cost.length;
-    dp[0] = 0;
-    dp[1] = 0;
-    for (let i = 2; i <= length; i++) {
-        dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
-    }
-    return dp[length];
-};
+  const dp = [0, 0]
+  for (let i = 2; i <= cost.length; i++) {
+    dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
+  }
+  return dp[cost.length]
+}
+```
+
+不使用 dp 数组
+
+```typescript
+function minCostClimbingStairs(cost: number[]): number {
+  let dpBefore = 0,
+    dpAfter = 0
+  for (let i = 2; i <= cost.length; i++) {
+    let dpi = Math.min(dpBefore + cost[i - 2], dpAfter + cost[i - 1])
+    dpBefore = dpAfter
+    dpAfter = dpi
+  }
+  return dpAfter
+}
 ```
 
 ### Rust
 
 ```Rust
-use std::cmp::min;
 impl Solution {
     pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
-        let len = cost.len();
-        let mut dp = vec![0; len];
-        dp[0] = cost[0];
-        dp[1] = cost[1];
-        for i in 2..len {
-            dp[i] = min(dp[i-1], dp[i-2]) + cost[i];
+        let mut dp = vec![0; cost.len() + 1];
+        for i in 2..=cost.len() {
+            dp[i] = (dp[i - 1] + cost[i - 1]).min(dp[i - 2] + cost[i - 2]);
         }
-        min(dp[len-1], dp[len-2])
+        dp[cost.len()]
+    }
+}
+```
+
+不使用 dp 数组
+
+```rust
+impl Solution {
+    pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
+        let (mut dp_before, mut dp_after) = (0, 0);
+        for i in 2..=cost.len() {
+            let dpi = (dp_before + cost[i - 2]).min(dp_after + cost[i - 1]);
+            dp_before = dp_after;
+            dp_after = dpi;
+        }
+        dp_after
     }
 }
 ```
@@ -385,18 +415,29 @@ impl Solution {
 ### C
 
 ```c
-int minCostClimbingStairs(int* cost, int costSize){
-    //开辟dp数组，大小为costSize
-    int *dp = (int *)malloc(sizeof(int) * costSize);
-    //初始化dp[0] = cost[0], dp[1] = cost[1]
-    dp[0] = cost[0], dp[1] = cost[1];
+#include <math.h>
+int minCostClimbingStairs(int *cost, int costSize) {
+  int dp[costSize + 1];
+  dp[0] = dp[1] = 0;
+  for (int i = 2; i <= costSize; i++) {
+    dp[i] = fmin(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
+  }
+  return dp[costSize];
+}
+```
 
-    int i;
-    for(i = 2; i < costSize; ++i) {
-        dp[i] = (dp[i-1] < dp[i-2] ? dp[i-1] : dp[i-2]) + cost[i];
-    }
-    //选出倒数2层楼梯中较小的
-    return dp[i-1] < dp[i-2] ? dp[i-1] : dp[i-2];
+不使用 dp 数组
+
+```c
+#include <math.h>
+int minCostClimbingStairs(int *cost, int costSize) {
+  int dpBefore = 0, dpAfter = 0;
+  for (int i = 2; i <= costSize; i++) {
+    int dpi = fmin(dpBefore + cost[i - 2], dpAfter + cost[i - 1]);
+    dpBefore = dpAfter;
+    dpAfter = dpi;
+  }
+  return dpAfter;
 }
 ```
 

problems/1002.查找常用字符.md

@@ -252,6 +252,36 @@ var commonChars = function (words) {
 	}
 	return res
 };
+
+// 方法二：map()
+var commonChars = function(words) {
+  let min_count = new Map()
+  // 统计字符串中字符出现的最小频率,以第一个字符串初始化
+  for(let str of words[0]) {
+    min_count.set(str, ((min_count.get(str) || 0) + 1))
+  }
+  // 从第二个单词开始统计字符出现次数
+  for(let i = 1; i < words.length; i++) {
+    let char_count = new Map()
+    for(let str of words[i]) { // 遍历字母
+      char_count.set(str, (char_count.get(str) || 0) + 1)
+    }
+    // 比较出最小的字符次数
+    for(let value of min_count) { // 注意这里遍历min_count!而不是单词
+      min_count.set(value[0], Math.min((min_count.get(value[0]) || 0), (char_count.get(value[0]) || 0)))
+    }
+  }
+  // 遍历map
+  let res = []
+  min_count.forEach((value, key) => {
+    if(value) {
+      for(let i=0; i<value; i++) {
+        res.push(key)
+      }
+    }
+  })
+  return res
+}
 ```
 
 TypeScript

problems/1005.K次取反后最大化的数组和.md

@@ -130,30 +130,6 @@ class Solution {
 }
 ```
 
-```java
-class Solution {
-    public int largestSumAfterKNegations(int[] A, int K) {
-        if (A.length == 1) return k % 2 == 0 ? A[0] : -A[0];
-        Arrays.sort(A);
-        int sum = 0;
-        int idx = 0;
-        for (int i = 0; i < K; i++) {
-            if (i < A.length - 1 && A[idx] < 0) {
-                A[idx] = -A[idx];
-                if (A[idx] >= Math.abs(A[idx + 1])) idx++;
-                continue;
-            }
-            A[idx] = -A[idx];
-        }
-
-        for (int i = 0; i < A.length; i++) {
-            sum += A[i];
-        }
-        return sum;
-    }
-}
-```
-
 ### Python
 贪心
 ```python

problems/1047.删除字符串中的所有相邻重复项.md

@@ -264,14 +264,15 @@ javaScript:
 
 ```js
 var removeDuplicates = function(s) {
-    const stack = [];
-    for(const x of s) {
-        let c = null;
-        if(stack.length && x === (c = stack.pop())) continue;
-        c && stack.push(c);
-        stack.push(x);
+    const result = []
+    for(const i of s){
+        if(i === result[result.length-1]){
+            result.pop()
+        }else{
+            result.push(i)
+        }
     }
-    return stack.join("");
+    return result.join('')
 };
 ```
 

problems/1049.最后一块石头的重量II.md

@@ -379,8 +379,23 @@ object Solution {
 }
 ```
 
+### Rust
 
-
+```rust
+impl Solution {
+    pub fn last_stone_weight_ii(stones: Vec<i32>) -> i32 {
+        let sum = stones.iter().sum::<i32>();
+        let target = sum as usize / 2;
+        let mut dp = vec![0; target + 1];
+        for s in stones {
+            for j in (s as usize..=target).rev() {
+                dp[j] = dp[j].max(dp[j - s as usize] + s);
+            }
+        }
+        sum - dp[target] * 2
+    }
+}
+```
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">

problems/二叉树理论基础.md

@@ -195,15 +195,16 @@ Java：
 ```java
 public class TreeNode {
     int val;
-  	TreeNode left;
-  	TreeNode right;
-  	TreeNode() {}
-  	TreeNode(int val) { this.val = val; }
-  	TreeNode(int val, TreeNode left, TreeNode right) {
-    		this.val = val;
-    		this.left = left;
-    		this.right = right;
-  	}
+    TreeNode left;
+    TreeNode right;
+
+    TreeNode() {}
+    TreeNode(int val) { this.val = val; }
+    TreeNode(int val, TreeNode left, TreeNode right) {
+        this.val = val;
+        this.left = left;
+        this.right = right;
+    }
 }
 ```
 
@@ -212,10 +213,10 @@ Python：
 
 ```python
 class TreeNode:
-    def __init__(self, value):
-        self.value = value
-        self.left = None
-        self.right = None
+    def __init__(self, val, left = None, right = None):
+        self.val = val
+        self.left = left
+        self.right = right
 ```
 
 Go：

problems/前序/刷力扣用不用库函数.md

@@ -24,5 +24,5 @@
 
 例如for循环里套一个字符串的insert，erase之类的操作，你说时间复杂度是多少呢，很明显是O(n^2)的时间复杂度了。
 
-在刷题的时候本着我说的标准来使用库函数，详细对大家回有所帮助！
+在刷题的时候本着我说的标准来使用库函数，相信对大家会有所帮助！
 

problems/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.md

@@ -54,9 +54,9 @@ int function2(int x, int n) {
 
 ```CPP
 int function3(int x, int n) {
-    if (n == 0) {
-        return 1;
-    }
+    if (n == 0) return 1;
+    if (n == 1) return x;
+
     if (n % 2 == 1) {
         return function3(x, n / 2) * function3(x, n / 2)*x;
     }
@@ -93,9 +93,8 @@ int function3(int x, int n) {
 
 ```CPP
 int function4(int x, int n) {
-    if (n == 0) {
-        return 1;
-    }
+    if (n == 0) return 1;
+    if (n == 1) return x;
     int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
     if (n % 2 == 1) {
         return t * t * x;
@@ -124,9 +123,8 @@ int function4(int x, int n) {
 
 ```CPP
 int function3(int x, int n) {
-    if (n == 0) {
-        return 1;
-    }
+    if (n == 0) return 1;
+    if (n == 1) return x;
     if (n % 2 == 1) {
         return function3(x, n / 2) * function3(x, n / 2)*x;
     }

problems/动态规划理论基础.md

@@ -10,6 +10,11 @@
 
 <img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-总结大纲1.jpg' width=600> </img>
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划理论基础](https://www.bilibili.com/video/BV13Q4y197Wg)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 什么是动态规划
 
 动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

problems/周总结/20210204动规周末总结.md

@@ -146,7 +146,7 @@ public:
 
 **这也体现了刷题顺序的重要性**。
 
-先遍历背包，在遍历物品：
+先遍历背包，再遍历物品：
 
 ```CPP
 // 版本一
@@ -165,7 +165,7 @@ public:
 };
 ```
 
-先遍历物品，在遍历背包：
+先遍历物品，再遍历背包：
 
 ```CPP
 // 版本二

problems/哈希表理论基础.md

@@ -89,7 +89,7 @@
 在C++中，set 和 map 分别提供以下三种数据结构，其底层实现以及优劣如下表所示：
 
 | 集合               | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
-| ------------------ | -------- | -------- | ---------------- | ------------ | -------- | -------- |
+| --- | --- | ---- | --- | --- | --- | --- |
 | std::set           | 红黑树   | 有序     | 否               | 否           | O(log n) | O(log n) |
 | std::multiset      | 红黑树   | 有序     | 是               | 否           | O(logn)  | O(logn)  |
 | std::unordered_set | 哈希表   | 无序     | 否               | 否           | O(1)     | O(1)     |
@@ -97,11 +97,12 @@
 std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。
 
 | 映射               | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
-| ------------------ | -------- | -------- | ---------------- | ------------ | -------- | -------- |
+| --- | --- | --- | --- | --- | --- | --- |
 | std::map           | 红黑树   | key有序  | key不可重复      | key不可修改  | O(logn)  | O(logn)  |
 | std::multimap      | 红黑树   | key有序  | key可重复        | key不可修改  | O(log n) | O(log n) |
 | std::unordered_map | 哈希表   | key无序  | key不可重复      | key不可修改  | O(1)     | O(1)     |
 
+
 std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。
 
 当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的，如果需要集合是有序的，那么就用set，如果要求不仅有序还要有重复数据的话，那么就用multiset。

problems/背包理论基础01背包-1.md

@@ -573,6 +573,39 @@ object Solution {
 }
 ```
 
+### Rust
+
+```rust
+pub struct Solution;
+
+impl Solution {
+    pub fn wei_bag_problem1(weight: Vec<usize>, value: Vec<usize>, bag_size: usize) -> usize {
+        let mut dp = vec![vec![0; bag_size + 1]; weight.len()];
+        for j in weight[0]..=weight.len() {
+            dp[0][j] = value[0];
+        }
+
+        for i in 1..weight.len() {
+            for j in 0..=bag_size {
+                match j < weight[i] {
+                    true => dp[i][j] = dp[i - 1][j],
+                    false => dp[i][j] = dp[i - 1][j].max(dp[i - 1][j - weight[i]] + value[i]),
+                }
+            }
+        }
+        dp[weight.len() - 1][bag_size]
+    }
+}
+
+#[test]
+fn test_wei_bag_problem1() {
+    println!(
+        "{}",
+        Solution::wei_bag_problem1(vec![1, 3, 4], vec![15, 20, 30], 4)
+    );
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/背包理论基础01背包-2.md

@@ -406,6 +406,34 @@ object Solution {
 }
 ```
 
+### Rust
+
+```rust
+pub struct Solution;
+
+impl Solution {
+    pub fn wei_bag_problem2(weight: Vec<usize>, value: Vec<usize>, bag_size: usize) -> usize {
+        let mut dp = vec![0; bag_size + 1];
+        for i in 0..weight.len() {
+            for j in (weight[i]..=bag_size).rev() {
+                if j >= weight[i] {
+                    dp[j] = dp[j].max(dp[j - weight[i]] + value[i]);
+                }
+            }
+        }
+        dp[dp.len() - 1]
+    }
+}
+
+#[test]
+fn test_wei_bag_problem2() {
+    println!(
+        "{}",
+        Solution::wei_bag_problem2(vec![1, 3, 4], vec![15, 20, 30], 4)
+    );
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/面试题02.07.链表相交.md

@@ -101,8 +101,8 @@ public:
 
 ## 其他语言版本
 
+Java：
 
-### Java
 ```Java
 public class Solution {
     public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
@@ -150,9 +150,13 @@ public class Solution {
 }
 ```
 
-### Python
+
+Python：
+
 ```python
+
 （版本一）求长度，同时出发
+
 class Solution:
     def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
         lenA, lenB = 0, 0
@@ -255,6 +259,7 @@ class Solution:
 #         self.val = x
 #         self.next = None
 
+
 class Solution:
     def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
         # 处理边缘情况
@@ -274,7 +279,8 @@ class Solution:
         # 如果相交，指针将位于交点节点，如果没有交点，值为None
         return pointerA
 ```
-### Go
+
+Go:
 
 ```go
 func getIntersectionNode(headA, headB *ListNode) *ListNode {
@@ -335,7 +341,7 @@ func getIntersectionNode(headA, headB *ListNode) *ListNode {
 }
 ```
 
-### javaScript
+JavaScript：
 
 ```js
 var getListLen = function(head) {
@@ -447,6 +453,7 @@ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
 ```
 
 Scala:
+
 ```scala
 object Solution {
   def getIntersectionNode(headA: ListNode, headB: ListNode): ListNode = {