algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-06 15:09:40 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
youngyangyang04
2021-07-14 15:45:42 +08:00
parent 0597ad9ba3
commit 3957e9583d
3 changed files with 381 additions and 22 deletions
Download Patch File Download Diff File Expand all files Collapse all files

44
README.md
View File

@ -275,10 +275,10 @@
16. [回溯算法：排列问题（二）](./problems/0047.全排列II.md)
17. [本周小结！（回溯算法系列三）](./problems/周总结/20201112回溯周末总结.md)
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
23. [回溯算法：重新安排行程](./problems/0332.重新安排行程.md)
24. [回溯算法：N皇后问题](./problems/0051.N皇后.md)
25. [回溯算法：解数独](./problems/0037.解数独.md)
26. [一篇总结带你彻底搞透回溯算法！](./problems/回溯总结.md)
19. [回溯算法：重新安排行程](./problems/0332.重新安排行程.md)
20. [回溯算法：N皇后问题](./problems/0051.N皇后.md)
21. [回溯算法：解数独](./problems/0037.解数独.md)
22. [一篇总结带你彻底搞透回溯算法！](./problems/回溯总结.md)
## 贪心算法
@ -365,41 +365,43 @@
32. [动态规划：买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
33. [动态规划：本周我们都讲了这些（系列六）](./problems/周总结/20210225动规周末总结.md)
33. [动态规划：买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II（动态规划）.md)
34. [动态规划：买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
35. [动态规划：买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
36. [动态规划：最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
37. [动态规划：本周我们都讲了这些（系列七）](./problems/周总结/20210304动规周末总结.md)
38. [动态规划：买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费（动态规划）.md)
39. [动态规划：股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
34. [动态规划：买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II（动态规划）.md)
35. [动态规划：买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
36. [动态规划：买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
37. [动态规划：最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
38. [动态规划：本周我们都讲了这些（系列七）](./problems/周总结/20210304动规周末总结.md)
39. [动态规划：买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费（动态规划）.md)
40. [动态规划：股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列：
<img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-子序列问题总结.jpg' width=500 alt=''> </img></div>
40. [动态规划：最长递增子序列](./problems/0300.最长上升子序列.md)
41. [动态规划：最长连续递增序列](./problems/0674.最长连续递增序列.md)
42. [动态规划：最长重复子数组](./problems/0718.最长重复子数组.md)
43. [动态规划：最长公共子序列](./problems/1143.最长公共子序列.md)
41. [动态规划：最长递增子序列](./problems/0300.最长上升子序列.md)
42. [动态规划：最长连续递增序列](./problems/0674.最长连续递增序列.md)
43. [动态规划：最长重复子数组](./problems/0718.最长重复子数组.md)
44. [动态规划：最长公共子序列](./problems/1143.最长公共子序列.md)
45. [动态规划：不相交的线](./problems/1035.不相交的线.md)
46. [动态规划：最大子序和](./problems/0053.最大子序和（动态规划）.md)
47. [动态规划：判断子序列](./problems/0392.判断子序列.md)
48. [动态规划：不同的子序列](./problems/0115.不同的子序列.md)
49. [动态规划：两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
51. [动态规划：编辑距离](./problems/0072.编辑距离.md)
52. [为了绝杀编辑距离，Carl做了三步铺垫，你都知道么？](./problems/为了绝杀编辑距离，卡尔做了三步铺垫.md)
53. [动态规划：回文子串](./problems/0647.回文子串.md)
54. [动态规划：最长回文子序列](./problems/0516.最长回文子序列.md)
55. [动态规划总结篇](./problems/动态规划总结篇.md)
50. [动态规划：编辑距离](./problems/0072.编辑距离.md)
51. [为了绝杀编辑距离，Carl做了三步铺垫，你都知道么？](./problems/为了绝杀编辑距离，卡尔做了三步铺垫.md)
52. [动态规划：回文子串](./problems/0647.回文子串.md)
53. [动态规划：最长回文子序列](./problems/0516.最长回文子序列.md)
54. [动态规划总结篇](./problems/动态规划总结篇.md)
（持续更新中....）
## 单调栈
1. [单调栈：每日温度](./problems/0739.每日温度.md)
2. [单调栈：下一个更大元素I](./problems/0496.下一个更大元素I.md)
3. [单调栈：下一个更大元素II](./problems/0503.下一个更大元素II.md)
4. [单调栈：接雨水](./problems/0042.接雨水.md)
（持续更新中....）
## 图论

357
problems/0042.接雨水.md Normal file
View File

@ -0,0 +1,357 @@
# 42. 接雨水
题目链接：https://leetcode-cn.com/problems/trapping-rain-water/
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：
![](https://code-thinking-1253855093.cos.ap-guangzhou.myqcloud.com/pics/20210713205038.png)
* 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
* 输出：6
* 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：
* 输入：height = [4,2,0,3,2,5]
* 输出：9
 
# 思路
接雨水问题在面试中还是常见题目的，有必要好好讲一讲。
本文深度讲解如下三种方法：
* 双指针法
* 动态规划
* 单调栈
## 双指针解法
这道题目使用双指针法并不简单，我们来看一下思路。
首先要明确，要按照行来计算，还是按照列来计算。
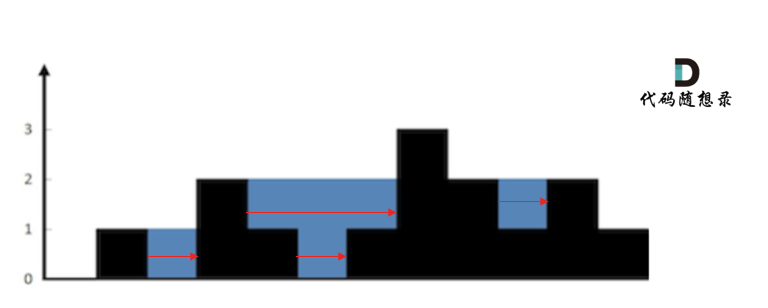
按照行来计算如图：
![42.接雨水2](https://img-blog.csdnimg.cn/20210402091118927.png)
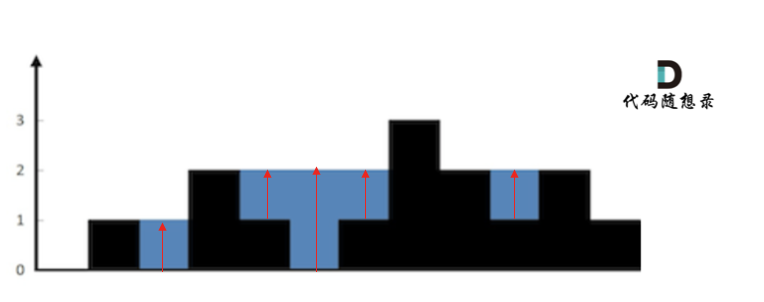
按照列来计算如图：
![42.接雨水1](https://img-blog.csdnimg.cn/20210402091208445.png)
一些同学在实现的时候，很容易一会按照行来计算一会按照列来计算，这样就会越写越乱。
我个人倾向于按照列来计算，比较容易理解，接下来看一下按照列如何计算。
首先，**如果按照列来计算的话，宽度一定是1了，我们再把每一列的雨水的高度求出来就可以了。**
可以看出每一列雨水的高度，取决于，该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
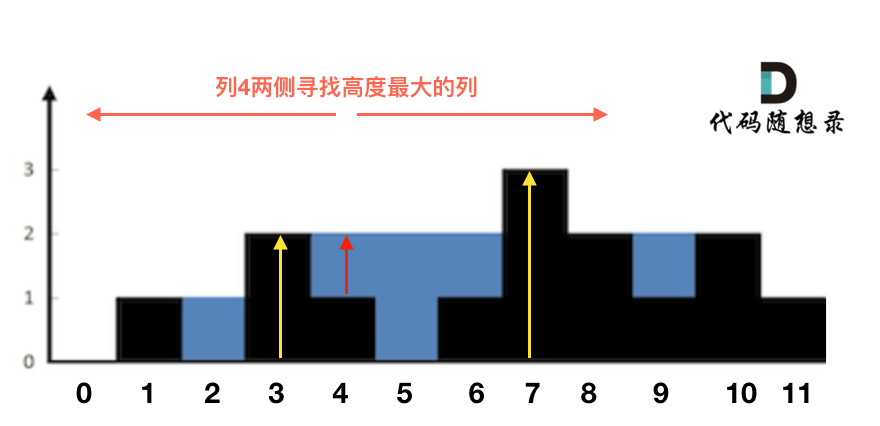
这句话可以有点绕，来举一个理解，例如求列4的雨水高度，如图：
![42.接雨水3](https://img-blog.csdnimg.cn/20210223092732301.png)
列4 左侧最高的柱子是列3，高度为2（以下用lHeight表示）。
列4 右侧最高的柱子是列7，高度为3（以下用rHeight表示）。
列4 柱子的高度为1（以下用height表示）
那么列4的雨水高度为 列3和列7的高度最小值减列4高度，即： min(lHeight, rHeight) - height。
列4的雨水高度求出来了，宽度为1，相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法，只要从头遍历一遍所有的列，然后求出每一列雨水的体积，相加之后就是总雨水的体积了。
首先从头遍历所有的列，并且**要注意第一个柱子和最后一个柱子不接雨水**，代码如下：
```C++
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
}
```
在for循环中求左右两边最高柱子，代码如下：
```C++
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
```
最后，计算该列的雨水高度，代码如下：
```C++
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // 注意只有h大于零的时候，在统计到总和中
```
整体代码如下：
```C++
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};
```
因为每次遍历列的时候，还要向两边寻找最高的列，所以时间复杂度为O(n^2)。
空间复杂度为O(1)。
## 动态规划解法
在上一节的双指针解法中，我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度，就可以计算当前位置的雨水面积，这就是通过列来计算。
当前列雨水面积：min(左边柱子的最高高度，记录右边柱子的最高高度) - 当前柱子高度。
为了的到两边的最高高度，使用了双指针来遍历，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight）。这样就避免了重复计算，这就用到了动态规划。
当前位置，左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
即从左向右遍历：maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历：maxRight[i] = max(height[i], maxRight[i + 1]);
这样就找到递推公式。
代码如下：
```C++
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0;
vector<int> maxLeft(height.size(), 0);
vector<int> maxRight(height.size(), 0);
int size = maxRight.size();
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// 求和
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
};
```
## 单调栈解法
这个解法可以说是最不好理解的了，所以下面我花了大量的篇幅来介绍这种方法。
单调栈就是保持栈内元素有序。和[栈与队列：单调队列](https://mp.weixin.qq.com/s/Xgcqx5eBa3xZabt_LurnNQ)一样，需要我们自己维持顺序，没有现成的容器可以用。
### 准备工作
那么本题使用单调栈有如下几个问题：
1. 首先单调栈是按照行方向来计算雨水，如图：
![42.接雨水2](https://img-blog.csdnimg.cn/20210223092629946.png)
知道这一点，后面的就可以理解了。
2. 使用单调栈内元素的顺序
从大到小还是从小打到呢？
从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。
如图：
![42.接雨水4](https://img-blog.csdnimg.cn/2021022309321229.png)
3. 遇到相同高度的柱子怎么办。
遇到相同的元素，更新栈内下标，就是将栈里元素（旧下标）弹出，将新元素（新下标）加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出，把第二个5添加到栈中。
**因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度**。
如图所示：
![42.接雨水5](https://img-blog.csdnimg.cn/20210223094619398.png)
4. 栈里要保存什么数值
是用单调栈，其实是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算，宽是通过柱子之间的下标来计算，
那么栈里有没有必要存一个pair<int, int>类型的元素，保存柱子的高度和下标呢。
其实不用，栈里就存放int类型的元素就行了，表示下标，想要知道对应的高度，通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下：
```
stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
```
明确了如上几点，我们再来看处理逻辑。
### 单调栈处理逻辑
先将下标0的柱子加入到栈中，`st.push(0);`。
然后开始从下标1开始遍历所有的柱子，`for (int i = 1; i < height.size(); i++)`。
如果当前遍历的元素（柱子）高度小于栈顶元素的高度，就把这个元素加入栈中，因为栈里本来就要保持从小到大的顺序（从栈头到栈底）。
代码如下：
```
if (height[i] < height[st.top()]) st.push(i);
```
如果当前遍历的元素（柱子）高度等于栈顶元素的高度，要跟更新栈顶元素，因为遇到相相同高度的柱子，需要使用最右边的柱子来计算宽度。
代码如下：
```
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
st.pop();
st.push(i);
}
```
如果当前遍历的元素（柱子）高度大于栈顶元素的高度，此时就出现凹槽了，如图所示：
![42.接雨水4](https://img-blog.csdnimg.cn/2021022309321229.png)
取栈顶元素，将栈顶元素弹出，这个就是凹槽的底部，也就是中间位置，下标记为mid，对应的高度为height[mid]（就是图中的高度1）。
此时的栈顶元素st.top()，就是凹槽的左边位置，下标为st.top()，对应的高度为height[st.top()]（就是图中的高度2）。
当前遍历的元素i，就是凹槽右边的位置，下标为i，对应的高度为height[i]（就是图中的高度3）。
此时大家应该可以发现其实就是**栈顶和栈顶的下一个元素以及要入栈的三个元素来接水！**
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度，代码为：`int h = min(height[st.top()], height[i]) - height[mid];`
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1（因为只求中间宽度），代码为：`int w = i - st.top() - 1 ;`
当前凹槽雨水的体积就是：`h * w`。
求当前凹槽雨水的体积代码如下：
```C++
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while，持续跟新栈顶元素
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一，只求中间宽度
sum += h * w;
}
}
```
关键部分讲完了，整体代码如下：
```C++
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0; // 可以不加
stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // 情况一
st.push(i);
} if (height[i] == height[st.top()]) { // 情况二
st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一，只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
```
以上代码冗余了一些，但是思路是清晰的，下面我将代码精简一下，如下：
```C++
class Solution {
public:
int trap(vector<int>& height) {
stack<int> st;
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
}
};
```
精简之后的代码，大家就看不出去三种情况的处理了，貌似好像只处理的情况三，其实是把情况一和情况二融合了。 这样的代码不太利于理解。
## 其他语言版本

2
problems/0583.两个字符串的删除操作.md
View File

@ -73,7 +73,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
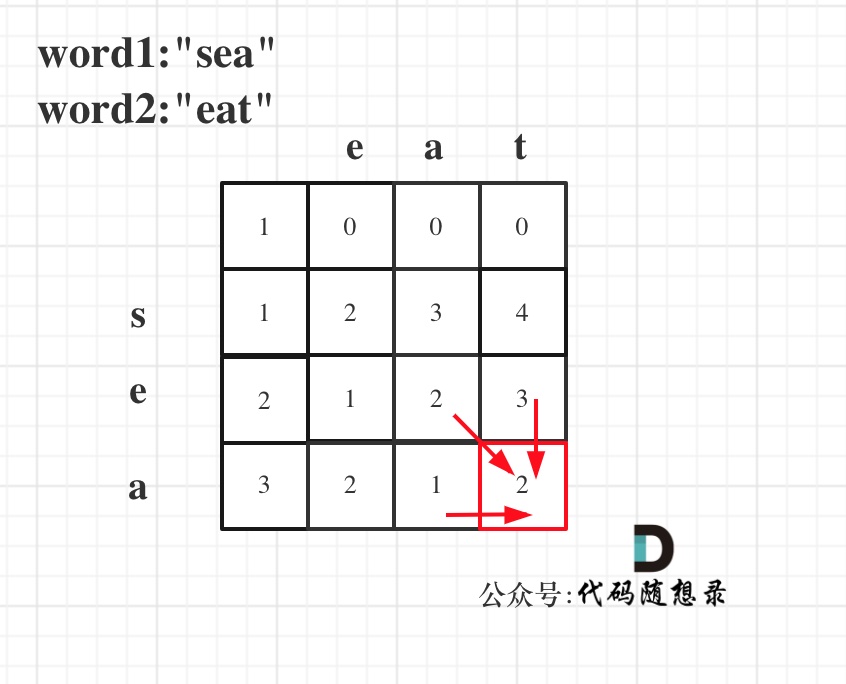
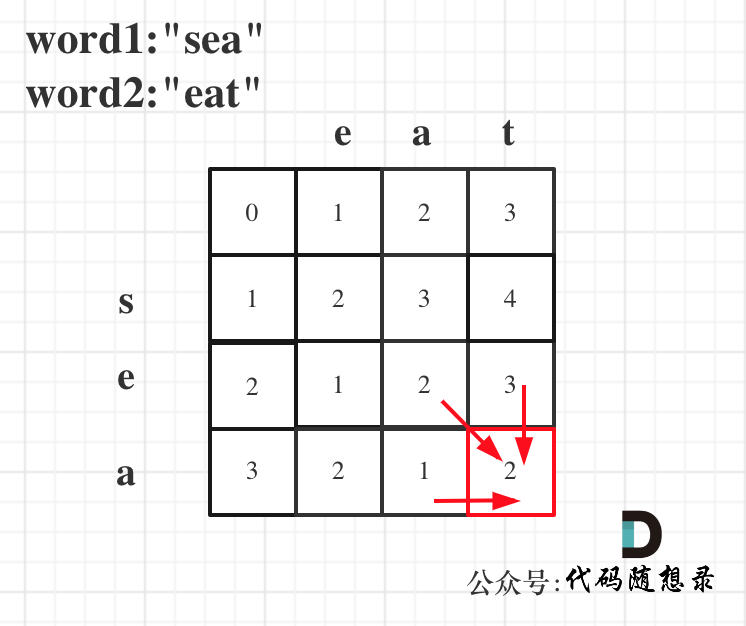
以word1:"sea"，word2:"eat"为例，推导dp数组状态图如下：
![583.两个字符串的删除操作](https://img-blog.csdnimg.cn/20210118163801914.jpg)
![583.两个字符串的删除操作1](https://img-blog.csdnimg.cn/20210714101750205.png)
以上分析完毕，代码如下：