Update

problems/0108.将有序数组转换为二叉搜索树.md

@@ -248,7 +248,7 @@ class Solution {
 		return root;
 	}
 
-	// 左闭右闭区间[left, right)
+	// 左闭右闭区间[left, right]
 	private TreeNode traversal(int[] nums, int left, int right) {
 		if (left > right) return null;
 

problems/0139.单词拆分.md

@@ -6,7 +6,7 @@
 
 
 
-## 139.单词拆分
+# 139.单词拆分
 
 [力扣题目链接](https://leetcode.cn/problems/word-break/)
 
@@ -19,19 +19,19 @@
 你可以假设字典中没有重复的单词。
 
 示例 1：
-输入: s = "leetcode", wordDict = ["leet", "code"]
+* 输入: s = "leetcode", wordDict = ["leet", "code"]
-输出: true
+* 输出: true
-解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
+* 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
 
 示例 2：
-输入: s = "applepenapple", wordDict = ["apple", "pen"]
+* 输入: s = "applepenapple", wordDict = ["apple", "pen"]
-输出: true
+* 输出: true
-解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
+* 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
-     注意你可以重复使用字典中的单词。
+* 注意你可以重复使用字典中的单词。
 
 示例 3：
-输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
+* 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
-输出: false
+* 输出: false
 
 ## 思路
 
@@ -158,24 +158,19 @@ dp[0]表示如果字符串为空的话，说明出现在字典里。
 
 **如果求排列数就是外层for遍历背包，内层for循环遍历物品**。
 
-对这个结论还有疑问的同学可以看这篇[本周小结！（动态规划系列五）](https://programmercarl.com/%E5%91%A8%E6%80%BB%E7%BB%93/20210204动规周末总结.html)，这篇本周小节中，我做了如下总结：
+我在这里做一个一个总结：
 
 求组合数：[动态规划：518.零钱兑换II](https://programmercarl.com/0518.零钱兑换II.html)
 求排列数：[动态规划：377. 组合总和 Ⅳ](https://programmercarl.com/0377.组合总和.html)、[动态规划：70. 爬楼梯进阶版（完全背包）](https://programmercarl.com/0070.爬楼梯完全背包版本.html)
 求最小数：[动态规划：322. 零钱兑换](https://programmercarl.com/0322.零钱兑换.html)、[动态规划：279.完全平方数](https://programmercarl.com/0279.完全平方数.html)
 
-本题最终要求的是是否都出现过，所以对出现单词集合里的元素是组合还是排列，并不在意！
+而本题其实我们求的是排列数，为什么呢。 拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。 
 
-**那么本题使用求排列的方式，还是求组合的方式都可以**。
+"apple", "pen" 是物品，那么我们要求 物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。 
 
-即：外层for循环遍历物品，内层for遍历背包 或者 外层for遍历背包，内层for循环遍历物品 都是可以的。
+"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的，那么我们就是强调物品之间顺序。 
-
-但本题还有特殊性，因为是要求子串，最好是遍历背包放在外循环，将遍历物品放在内循环。
-
-如果要是外层for循环遍历物品，内层for遍历背包，就需要把所有的子串都预先放在一个容器里。（如果不理解的话，可以自己尝试这么写一写就理解了）
-
-**所以最终我选择的遍历顺序为：遍历背包放在外循环，将遍历物品放在内循环。内循环从前到后**。
 
+所以说，本题一定是 先遍历 背包，在遍历物品。 
 
 5. 举例推导dp[i]
 
@@ -210,22 +205,51 @@ public:
 * 时间复杂度：O(n^3)，因为substr返回子串的副本是O(n)的复杂度（这里的n是substring的长度）
 * 空间复杂度：O(n)
 
+## 拓展 
+
+关于遍历顺序，再给大家讲一下为什么 先遍历物品再遍历背包不行。 
+
+这里可以给出先遍历物品在遍历背包的代码： 
+
+```CPP
+class Solution {
+public:
+    bool wordBreak(string s, vector<string>& wordDict) {
+        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
+        vector<bool> dp(s.size() + 1, false);
+        dp[0] = true;
+        for (int j = 0; j < wordDict.size(); j++) { // 物品
+            for (int i = wordDict[j].size(); i <= s.size(); i++) { // 背包
+                string word = s.substr(i - wordDict[j].size(), wordDict[j].size());
+                // cout << word << endl;
+                if ( word == wordDict[j] && dp[i - wordDict[j].size()]) {
+                    dp[i] = true;
+                }
+                // for (int k = 0; k <= s.size(); k++) cout << dp[k] << " "; //这里打印 dp数组的情况 
+                // cout << endl;
+            }
+        }
+        return dp[s.size()];
+
+    }
+};
+``` 
+
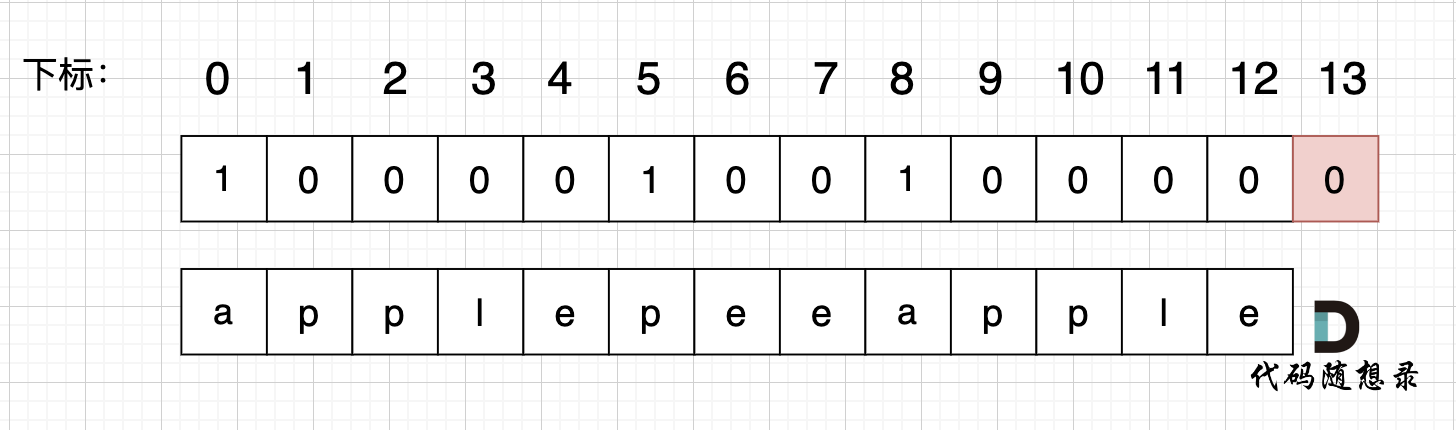
+使用用例：s = "applepenapple", wordDict = ["apple", "pen"]，对应的dp数组状态如下： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20221123205105.png) 
+
+最后dp[s.size()] = 0 即 dp[13] = 0 ，而不是1，因为先用 "apple" 去遍历的时候，dp[8]并没有被赋值为1 （还没用"pen"），所以 dp[13]也不能变成1。 
+
+除非是先用 "apple" 遍历一遍，在用  "pen" 遍历，此时 dp[8]已经是1，最后再用  "apple" 去遍历，dp[13]才能是1。 
+
+如果大家对这里不理解，建议可以把我上面给的代码，拿去力扣上跑一跑，把dp数组打印出来，对着递推公式一步一步去看，思路就清晰了。 
 
 ## 总结
 
 本题和我们之前讲解回溯专题的[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)非常像，所以我也给出了对应的回溯解法。
 
-稍加分析，便可知道本题是完全背包，而且是求能否组成背包，所以遍历顺序理论上来讲 两层for循环谁先谁后都可以！
+稍加分析，便可知道本题是完全背包，是求能否组成背包，而且这里要求物品是要有顺序的。
-
-但因为分割子串的特殊性，遍历背包放在外循环，将遍历物品放在内循环更方便一些。
-
-本题其实递推公式都不是重点，遍历顺序才是重点，如果我直接把代码贴出来，估计同学们也会想两个for循环的顺序理所当然就是这样，甚至都不会想为什么遍历背包的for循环在外层。
-
-不分析透彻不是Carl的风格啊，哈哈
-
-
-
-
 
 ## 其他语言版本
 

problems/0198.打家劫舍.md

@@ -12,15 +12,16 @@
 
 给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
 
-示例 1：
+* 示例 1：
-输入：[1,2,3,1]
+* 输入：[1,2,3,1]
-输出：4
+* 输出：4
+
 解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
      偷窃到的最高金额 = 1 + 3 = 4 。
 
-示例 2：
+* 示例 2：
-输入：[2,7,9,3,1]
+* 输入：[2,7,9,3,1]
-输出：12
+* 输出：12
 解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
      偷窃到的最高金额 = 2 + 9 + 1 = 12 。
 
@@ -33,7 +34,13 @@
 
 ## 思路
 
-打家劫舍是dp解决的经典问题，动规五部曲分析如下：
+大家如果刚接触这样的题目，会有点困惑，当前的状态我是偷还是不偷呢？ 
+
+仔细一想，当前房屋偷与不偷取决于  前一个房屋和前两个房屋是否被偷了。 
+
+所以这里就更感觉到，当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式。
+
+当然以上是大概思路，打家劫舍是dp解决的经典问题，接下来我们来动规五部曲分析如下：
 
 1. 确定dp数组（dp table）以及下标的含义
 

problems/0279.完全平方数.md

@@ -131,10 +131,8 @@ public:
         vector<int> dp(n + 1, INT_MAX);
         dp[0] = 0;
         for (int i = 1; i * i <= n; i++) { // 遍历物品
-            for (int j = 1; j <= n; j++) { // 遍历背包
+            for (int j = i * i; j <= n; j++) { // 遍历背包
-                if (j - i * i >= 0) {
+                dp[j] = min(dp[j - i * i] + 1, dp[j]);
-                    dp[j] = min(dp[j - i * i] + 1, dp[j]);
-                }
             }
         }
         return dp[n];

problems/0322.零钱兑换.md

@@ -53,8 +53,6 @@
 
 2. 确定递推公式
 
-得到dp[j]（考虑coins[i]），只有一个来源，dp[j - coins[i]]（没有考虑coins[i]）。
-
 凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）
 
 所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。

problems/0337.打家劫舍III.md

@@ -50,8 +50,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n^2)$，这个时间复杂度不太标准，也不容易准确化，例如越往下的节点重复计算次数就越多
+* 时间复杂度：O(n^2)，这个时间复杂度不太标准，也不容易准确化，例如越往下的节点重复计算次数就越多
-* 空间复杂度：$O(\log n)$，算上递推系统栈的空间
+* 空间复杂度：O(log n)，算上递推系统栈的空间
 
 当然以上代码超时了，这个递归的过程中其实是有重复计算了。
 
@@ -84,8 +84,8 @@ public:
 
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(\log n)$，算上递推系统栈的空间
+* 空间复杂度：O(log n)，算上递推系统栈的空间
 
 
 ### 动态规划

problems/0377.组合总和Ⅳ.md

@@ -4,9 +4,8 @@
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
 
-# 动态规划：Carl称它为排列总和！
 
-## 377. 组合总和 Ⅳ
+# 377. 组合总和 Ⅳ
 
 [力扣题目链接](https://leetcode.cn/problems/combination-sum-iv/)
 

problems/0416.分割等和子集.md

@@ -79,7 +79,17 @@
 
 01背包中，dp[j] 表示： 容量为j的背包，所背的物品价值可以最大为dp[j]。
 
-**套到本题，dp[j]表示 背包总容量是j，最大可以凑成j的子集总和为dp[j]**。
+本题中每一个元素的数值即是重量，也是价值。
+
+**套到本题，dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]**。
+
+那么如果背包容量为target， dp[target]就是装满 背包之后的重量，所以 当 dp[target] == target 的时候，背包就装满了。
+
+有录友可能想，那还有装不满的时候？ 
+
+拿输入数组 [1, 5, 11, 5]，距离， dp[7] 只能等于 6，因为 只能放进 1 和 5。
+
+而dp[6] 就可以等于6了，放进1 和 5，那么dp[6] == 6，说明背包装满了。
 
 2. 确定递推公式
 

problems/0474.一和零.md

@@ -3,9 +3,8 @@
   <img src="../pics/训练营.png" width="1000"/>
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
-# 动态规划：一和零！
 
-## 474.一和零
+# 474.一和零
 
 [力扣题目链接](https://leetcode.cn/problems/ones-and-zeroes/)
 
@@ -42,7 +41,7 @@
 * [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
 * [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)
 
-这道题目，还是比较难的，也有点像程序员自己给自己出个脑筋急转弯，程序员何苦为难程序员呢哈哈。
+这道题目，还是比较难的，也有点像程序员自己给自己出个脑筋急转弯，程序员何苦为难程序员呢。
 
 来说题，本题不少同学会认为是多重背包，一些题解也是这么写的。
 
@@ -82,7 +81,7 @@ dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
 
 对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。
 
-**这就是一个典型的01背包！** 只不过物品的重量有了两个维度而已。
+**这就是一个典型的01背包！** 只不过物品的重量有了两个维度而已。 
 
 
 3. dp数组如何初始化
@@ -155,8 +154,15 @@ public:
 
 不少同学刷过这道提，可能没有总结这究竟是什么背包。
 
-这道题的本质是有两个维度的01背包，如果大家认识到这一点，对这道题的理解就比较深入了。
+此时我们讲解了0-1背包的多种应用，
 
+* [纯 0 - 1 背包](https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-2.html) 是求 给定背包容量 装满背包 的最大价值是多少。 
+* [416. 分割等和子集](https://programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html) 是求 给定背包容量，能不能装满这个背包。 
+* [1049. 最后一块石头的重量 II](https://programmercarl.com/1049.%E6%9C%80%E5%90%8E%E4%B8%80%E5%9D%97%E7%9F%B3%E5%A4%B4%E7%9A%84%E9%87%8D%E9%87%8FII.html)   是求 给定背包容量，尽可能装，最多能装多少 
+* [494. 目标和](https://programmercarl.com/0494.%E7%9B%AE%E6%A0%87%E5%92%8C.html) 是求 给定背包容量，装满背包有多少种方法。 
+* 本题是求 给定背包容量，装满背包最多有多少个物品。
+
+所以在代码随想录中所列举的题目，都是 0-1背包不同维度上的应用，大家可以细心体会！
 
 
 

problems/0494.目标和.md

@@ -3,9 +3,11 @@
   <img src="../pics/训练营.png" width="1000"/>
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
-# 动态规划：目标和！
 
-## 494. 目标和
+
+
+
+# 494. 目标和
 
 [力扣题目链接](https://leetcode.cn/problems/target-sum/)
 
@@ -52,9 +54,9 @@
 
 既然为target，那么就一定有 left组合 - right组合 = target。
 
-left + right等于sum，而sum是固定的。
+left + right = sum，而sum是固定的。right = sum - left  
 
-公式来了， left - (sum - left) = target ->  left = (target + sum)/2 。
+公式来了， left - (sum - left) = target 推导出  left = (target + sum)/2 。
 
 target是固定的，sum是固定的，left就可以求出来。
 
@@ -117,22 +119,26 @@ public:
 
 假设加法的总和为x，那么减法对应的总和就是sum - x。
 
-所以我们要求的是 x - (sum - x) = S
+所以我们要求的是 x - (sum - x) = target
 
-x = (S + sum) / 2
+x = (target + sum) / 2
 
 **此时问题就转化为，装满容量为x背包，有几种方法**。
 
-大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
+这里的x，就是bagSize，也就是我们后面要求的背包容量。
+
+大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。
 
 这么担心就对了，例如sum 是5，S是2的话其实就是无解的，所以：
 
-```CPP
+```CPP 
+（C++代码中，输入的S 就是题目描述的 target）
 if ((S + sum) % 2 == 1) return 0; // 此时没有方案
 ```
 
 同时如果 S的绝对值已经大于sum，那么也是没有方案的。
 ```CPP
+（C++代码中，输入的S 就是题目描述的 target）
 if (abs(S) > sum) return 0; // 此时没有方案
 ```
 
@@ -156,17 +162,15 @@ dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法
 
 有哪些来源可以推出dp[j]呢？
 
-不考虑nums[i]的情况下，填满容量为j的背包，有dp[j]种方法。
+只要搞到nums[i]），凑成dp[j]就有dp[j - nums[i]] 种方法。
-
-那么考虑nums[i]的话（只要搞到nums[i]），凑成dp[j]就有dp[j - nums[i]] 种方法。
 
 例如：dp[j]，j 为5， 
 
-* 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
+* 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
-* 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
+* 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
-* 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]
+* 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
-* 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]
+* 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
-* 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 dp[5] 
+* 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包
 
 那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。
 
@@ -182,9 +186,19 @@ dp[j] += dp[j - nums[i]]
 
 从递归公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递归结果将都是0。
 
-dp[0] = 1，理论上也很好解释，装满容量为0的背包，有1种方法，就是装0件物品。
+这里有录友可能认为从dp数组定义来说 dp[0] 应该是0，也有录友认为dp[0]应该是1。 
 
-dp[j]其他下标对应的数值应该初始化为0，从递归公式也可以看出，dp[j]要保证是0的初始值，才能正确的由dp[j - nums[i]]推导出来。
+其实不要硬去解释它的含义，咱就把 dp[0]的情况带入本题看看就是应该等于多少。 
+
+如果数组[0] ，target = 0，那么 bagSize =  (target + sum) / 2 = 0。 dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。 
+
+所以本题我们应该初始化 dp[0] 为 1。
+
+可能有同学想了，那 如果是 数组[0,0,0,0,0] target = 0 呢。 
+
+其实 此时最终的dp[0] = 32，也就是这五个零 子集的所有组合情况，但此dp[0]非彼dp[0]，dp[0]能算出32，其基础是因为dp[0] = 1 累加起来的。 
+
+dp[j]其他下标对应的数值也应该初始化为0，从递归公式也可以看出，dp[j]要保证是0的初始值，才能正确的由dp[j - nums[i]]推导出来。
 
 
 4. 确定遍历顺序
@@ -213,7 +227,6 @@ public:
         if (abs(S) > sum) return 0; // 此时没有方案
         if ((S + sum) % 2 == 1) return 0; // 此时没有方案
         int bagSize = (S + sum) / 2;
-	if (bagsize < 0) return 0;
         vector<int> dp(bagSize + 1, 0);
         dp[0] = 1;
         for (int i = 0; i < nums.size(); i++) {
@@ -238,7 +251,7 @@ public:
 
 本题还是有点难度，大家也可以记住，在求装满背包有几种方法的情况下，递推公式一般为：
 
-```
+```CPP
 dp[j] += dp[j - nums[i]];
 ```
 

problems/0518.零钱兑换II.md

@@ -3,9 +3,10 @@
   <img src="../pics/训练营.png" width="1000"/>
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
-# 动态规划：给你一些零钱，你要怎么凑？
 
-## 518. 零钱兑换 II
+
+
+# 518. 零钱兑换 II
 
 [力扣题目链接](https://leetcode.cn/problems/coin-change-ii/)
 
@@ -15,22 +16,25 @@
 
 示例 1:
 
-输入: amount = 5, coins = [1, 2, 5]
+* 输入: amount = 5, coins = [1, 2, 5]
-输出: 4
+* 输出: 4
+
 解释: 有四种方式可以凑成总金额:
-5=5
+
-5=2+2+1
+* 5=5
-5=2+1+1+1
+* 5=2+2+1
-5=1+1+1+1+1
+* 5=2+1+1+1
+* 5=1+1+1+1+1
 
 示例 2:
-输入: amount = 3, coins = [2]
+
-输出: 0
+* 输入: amount = 3, coins = [2]
-解释: 只用面额2的硬币不能凑成总金额3。
+* 输出: 0
+* 解释: 只用面额2的硬币不能凑成总金额3。
 
 示例 3:
-输入: amount = 10, coins = [10]
+* 输入: amount = 10, coins = [10]
-输出: 1
+* 输出: 1
 
 注意，你可以假设：
 
@@ -47,7 +51,7 @@
 
 对完全背包还不了解的同学，可以看这篇：[动态规划：关于完全背包，你该了解这些！](https://programmercarl.com/背包问题理论基础完全背包.html)
 
-但本题和纯完全背包不一样，**纯完全背包是能否凑成总金额，而本题是要求凑成总金额的个数！**
+但本题和纯完全背包不一样，**纯完全背包是凑成背包最大价值是多少，而本题是要求凑成总金额的物品组合个数！**
 
 注意题目描述中是凑成总金额的硬币组合数，为什么强调是组合数呢？
 
@@ -73,17 +77,21 @@ dp[j]：凑成总金额j的货币组合数为dp[j]
 
 2. 确定递推公式
 
-dp[j] （考虑coins[i]的组合总和） 就是所有的dp[j - coins[i]]（不考虑coins[i]）相加。
+dp[j]  就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加。
 
 所以递推公式：dp[j] += dp[j - coins[i]];
 
-**这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[动态规划：目标和！](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，一般公式都是：dp[j] += dp[j - nums[i]];**
+**这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[494. 目标和](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，公式都是：dp[j] += dp[j - nums[i]];**
 
 3. dp数组如何初始化
 
-首先dp[0]一定要为1，dp[0] = 1是 递归公式的基础。
+首先dp[0]一定要为1，dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话，后面所有推导出来的值都是0了。 
 
-从dp[i]的含义上来讲就是，凑成总金额0的货币组合数为1。
+那么 dp[0] = 1 有没有含义，其实既可以说 凑成总金额0的货币组合数为1，也可以说 凑成总金额0的货币组合数为0，好像都没有毛病。
+
+但题目描述中，也没明确说 amount = 0 的情况，结果应该是多少。 
+
+这里我认为题目描述还是要说明一下，因为后台测试数据是默认，amount = 0 的情况，组合数为1的。 
 
 下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
 
@@ -96,9 +104,9 @@ dp[j] （考虑coins[i]的组合总和） 就是所有的dp[j - coins[i]]（不
 
 **但本题就不行了！**
 
-因为纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！
+因为纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！
 
-而本题要求凑成总和的组合数，元素之间要求没有顺序。
+而本题要求凑成总和的组合数，元素之间明确要求没有顺序。
 
 所以纯完全背包是能凑成总和就行，不用管怎么凑的。
 
@@ -126,7 +134,7 @@ for (int i = 0; i < coins.size(); i++) { // 遍历物品
 
 如果把两个for交换顺序，代码如下：
 
-```
+```CPP
 for (int j = 0; j <= amount; j++) { // 遍历背包容量
     for (int i = 0; i < coins.size(); i++) { // 遍历物品
         if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
@@ -169,7 +177,7 @@ public:
 
 ## 总结
 
-本题的递推公式，其实我们在[动态规划：目标和！](https://programmercarl.com/0494.目标和.html)中就已经讲过了，**而难点在于遍历顺序！**
+本题的递推公式，其实我们在[494. 目标和](https://programmercarl.com/0494.目标和.html)中就已经讲过了，**而难点在于遍历顺序！**
 
 在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。
 
@@ -181,8 +189,6 @@ public:
 
 
 
-
-
 ## 其他语言版本
 
 

problems/1049.最后一块石头的重量II.md

@@ -15,17 +15,20 @@
 每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
 
 如果 x == y，那么两块石头都会被完全粉碎；
+
 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
+
 最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。
 
 示例：
-输入：[2,7,4,1,8,1]
+* 输入：[2,7,4,1,8,1]
-输出：1
+* 输出：1
+
 解释：
-组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
+* 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
-组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
+* 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
-组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
+* 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
-组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。
+* 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。
 
 提示：
 
@@ -51,7 +54,11 @@
 
 1. 确定dp数组以及下标的含义
 
-**dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背dp[j]这么重的石头**。
+**dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]**。
+
+可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。
+
+相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”
 
 2. 确定递推公式
 
@@ -61,7 +68,7 @@
 
 一些同学可能看到这dp[j - stones[i]] + stones[i]中 又有- stones[i] 又有+stones[i]，看着有点晕乎。
 
-还是要牢记dp[j]的含义，要知道dp[j - stones[i]]为 容量为j - stones[i]的背包最大所背重量。
+大家可以再去看 dp[j]的含义。
 
 3. dp数组如何初始化
 

problems/哈希表理论基础.md

@@ -108,7 +108,7 @@ std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底
 
 其他语言例如：java里的HashMap ，TreeMap 都是一样的原理。可以灵活贯通。
 
-虽然std::set、std::multiset 的底层实现是红黑树，不是哈希表，但是std::set、std::multiset 依然使用哈希函数来做映射，只不过底层的符号表使用了红黑树来存储数据，所以使用这些数据结构来解决映射问题的方法，我们依然称之为哈希法。 map也是一样的道理。
+虽然std::set、std::multiset 的底层实现是红黑树，不是哈希表，std::set、std::multiset 使用红黑树来索引和存储，不过给我们的使用方式，还是哈希法的使用方式，即key和value。所以使用这些数据结构来解决映射问题的方法，我们依然称之为哈希法。 map也是一样的道理。
 
 这里在说一下，一些C++的经典书籍上 例如STL源码剖析，说到了hash_set hash_map，这个与unordered_set，unordered_map又有什么关系呢？
 

problems/图论深搜理论基础.md

@@ -6,10 +6,18 @@
 
 # 深度优先搜索理论基础 
 
-提到深度优先搜索（dfs），就不得不说和广度优先有什么区别（bfs）
+录友们期待图论内容已久了，为什么鸽了这么久，主要是最近半年开始更新[代码随想录算法公开课](https://mp.weixin.qq.com/s/xncn6IHJGs45sJOChN6V_g)，是开源在B站的算法视频，已经帮助非常多基础不好的录友学习算法。 
+
+录视频其实是非常累的，也要花很多时间，所以图论这边就没抽出时间来。 
+
+后面计划先给大家讲图论里大家特别需要的深搜和广搜。 
+
+以下，开始讲解深度优先搜索理论基础：
 
 ## dfs 与 bfs 区别 
 
+提到深度优先搜索（dfs），就不得不说和广度优先有什么区别（bfs）
+
 先来了解dfs的过程，很多录友可能对dfs（深度优先搜索），bfs（广度优先搜索）分不清。
 
 先给大家说一下两者大概的区别：
@@ -35,7 +43,7 @@
 
 ![图三](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094011.png) 
 
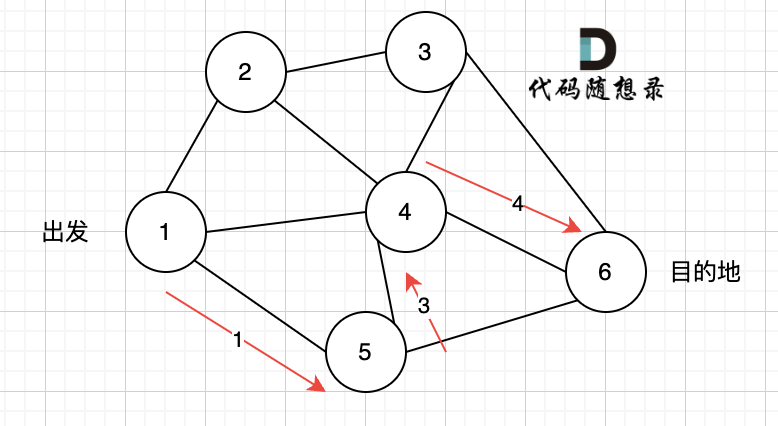
-路径2撤销了，改变了方向，走路径3（红色线）， 接着也找到终点6。 那么撤销路径2，改为路径3，在dfs中其实就是回溯的过程（这一点很重要，很多录友，都不理解dfs代码中回溯是用来干什么的）
+路径2撤销了，改变了方向，走路径3（红色线）， 接着也找到终点6。 那么撤销路径2，改为路径3，在dfs中其实就是回溯的过程（这一点很重要，很多录友不理解dfs代码中回溯是用来干什么的）
 
 又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图四中，路径4撤销（回溯的过程），改为路径5。
 
@@ -55,7 +63,6 @@
 * 搜索方向，是认准一个方向搜，直到碰壁之后在换方向 
 * 换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程。  
 
-
 ## 代码框架 
 
 正式因为dfs搜索可一个方向，并需要回溯，所以用递归的方式来实现是最方便的。 
@@ -65,6 +72,7 @@
 有递归的地方就有回溯，那么回溯在哪里呢？ 
 
 就地递归函数的下面，例如如下代码： 
+
 ```
 void dfs(参数) {
     处理节点
@@ -160,8 +168,6 @@ if (终止条件) {
 终止添加不仅是结束本层递归，同时也是我们收获结果的时候。 
 
 另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。
-* 841.钥匙和房间 
-* 200. 岛屿数量
 
 3. 处理目前搜索节点出发的路径 
 
@@ -190,6 +196,9 @@ for (选择：本节点所连接的其他节点) {
 
 以上如果大家都能理解了，其实搜索的代码就很好写，具体题目套用具体场景就可以了。
 
+后面我也会给大家安排具体练习的题目，依旧是代码随想录的风格，循序渐进由浅入深！
+
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/背包问题理论基础完全背包.md

@@ -82,7 +82,7 @@ dp状态图如下：
 
 就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
 
-**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！**
+**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！**
 
 因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。