mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 15:09:40 +08:00
Update
This commit is contained in:
@ -132,6 +132,7 @@
|
||||
8. [计算机专业要不要读研!](https://mp.weixin.qq.com/s/c9v1L3IjqiXtkNH7sOMAdg)
|
||||
9. [秋招和提前批都越来越提前了....](https://mp.weixin.qq.com/s/SNFiRDx8CKyjhTPlys6ywQ)
|
||||
10. [你的简历里「专业技能」写的够专业么?](https://mp.weixin.qq.com/s/bp6y-e5FVN28H9qc8J9zrg)
|
||||
11. [对于秋招,实习生也有烦恼....](https://mp.weixin.qq.com/s/ka07IPryFnfmIjByFFcXDg)
|
||||
|
||||
|
||||
## 数组
|
||||
@ -398,6 +399,7 @@
|
||||
|
||||
1. [单调栈:每日温度](./problems/0739.每日温度.md)
|
||||
2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
|
||||
3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
|
||||
|
||||
## 图论
|
||||
|
||||
|
||||
@ -32,7 +32,7 @@
|
||||
|
||||
可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
vector<int> vec;
|
||||
void traversal(TreeNode* root) {
|
||||
if (root == NULL) return;
|
||||
@ -44,7 +44,7 @@ void traversal(TreeNode* root) {
|
||||
|
||||
然后只要比较一下,这个数组是否是有序的,**注意二叉搜索树中不能有重复元素**。
|
||||
|
||||
```
|
||||
```C++
|
||||
traversal(root);
|
||||
for (int i = 1; i < vec.size(); i++) {
|
||||
// 注意要小于等于,搜索树里不能有相同元素
|
||||
@ -55,7 +55,7 @@ return true;
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<int> vec;
|
||||
@ -162,7 +162,8 @@ return left && right;
|
||||
```
|
||||
|
||||
整体代码如下:
|
||||
```
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
|
||||
@ -188,7 +189,7 @@ public:
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
TreeNode* pre = NULL; // 用来记录前一个节点
|
||||
@ -213,7 +214,7 @@ public:
|
||||
|
||||
迭代法中序遍历稍加改动就可以了,代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
bool isValidBST(TreeNode* root) {
|
||||
|
||||
@ -35,7 +35,7 @@
|
||||
|
||||
## 题外话
|
||||
|
||||
咋眼一看这道题目和[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)很像,其实有很大区别。
|
||||
咋眼一看这道题目和[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)很像,其实有很大区别。
|
||||
|
||||
这里强调一波概念:
|
||||
|
||||
@ -50,11 +50,11 @@
|
||||
|
||||
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
|
||||
|
||||
有的同学一定疑惑,为什么[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中求的是二叉树的最大深度,也用的是后序遍历。
|
||||
有的同学一定疑惑,为什么[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中求的是二叉树的最大深度,也用的是后序遍历。
|
||||
|
||||
**那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这颗树的最大深度,所以才可以使用后序遍历。**
|
||||
|
||||
在[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
|
||||
在[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
@ -227,7 +227,7 @@ public:
|
||||
|
||||
### 迭代
|
||||
|
||||
在[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
|
||||
在[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
|
||||
|
||||
本题的迭代方式可以先定义一个函数,专门用来求高度。
|
||||
|
||||
@ -448,7 +448,6 @@ class Solution {
|
||||
/**
|
||||
* 优化迭代法,针对暴力迭代法的getHeight方法做优化,利用TreeNode.val来保存当前结点的高度,这样就不会有重复遍历
|
||||
* 获取高度算法时间复杂度可以降到O(1),总的时间复杂度降为O(n)。
|
||||
* <p>
|
||||
* 时间复杂度:O(n)
|
||||
*/
|
||||
public boolean isBalanced(TreeNode root) {
|
||||
@ -493,7 +492,6 @@ class Solution {
|
||||
return height;
|
||||
}
|
||||
}
|
||||
// LeetCode题解链接:https://leetcode-cn.com/problems/balanced-binary-tree/solution/110-ping-heng-er-cha-shu-di-gui-fa-bao-l-yqr3/
|
||||
```
|
||||
|
||||
Python:
|
||||
@ -590,6 +588,7 @@ func abs(a int)int{
|
||||
return a
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
var isBalanced = function(root) {
|
||||
|
||||
@ -173,7 +173,7 @@ return {val2, val1};
|
||||
|
||||
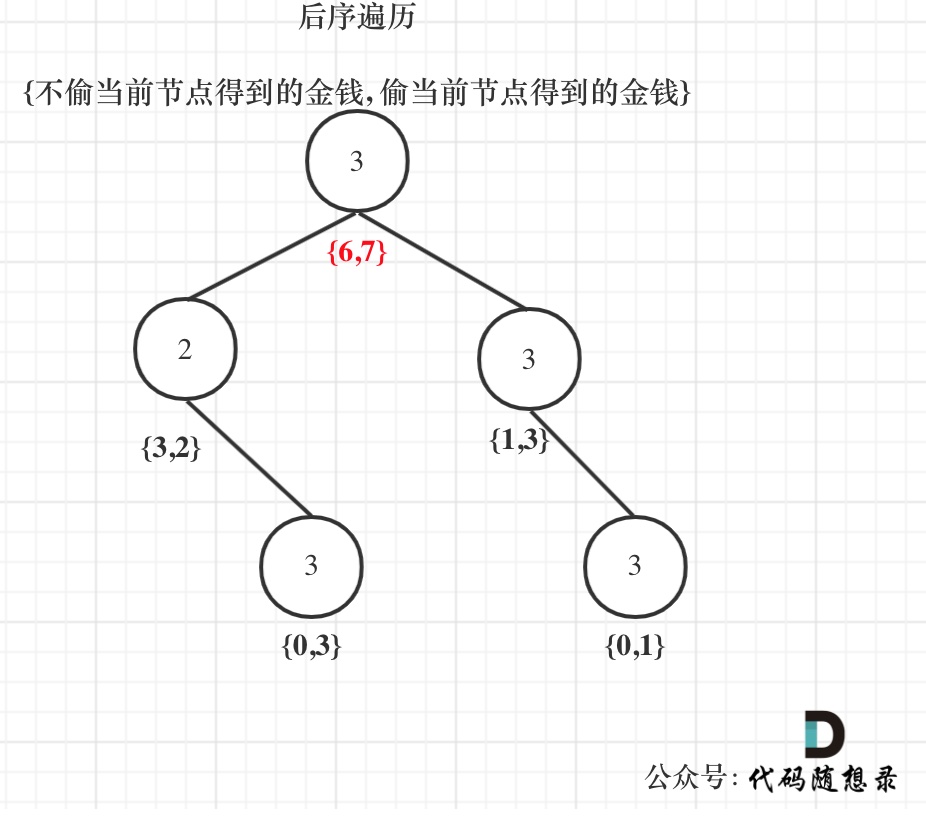
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||
|
||||
|
||||

|
||||
|
||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||
|
||||
|
||||
@ -18,18 +18,18 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
|
||||
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
|
||||
|
||||
示例 1:
|
||||
输入: nums = [1,1,1,2,2,3], k = 2
|
||||
输出: [1,2]
|
||||
* 输入: nums = [1,1,1,2,2,3], k = 2
|
||||
* 输出: [1,2]
|
||||
|
||||
示例 2:
|
||||
输入: nums = [1], k = 1
|
||||
输出: [1]
|
||||
* 输入: nums = [1], k = 1
|
||||
* 输出: [1]
|
||||
|
||||
提示:
|
||||
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
|
||||
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
|
||||
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
|
||||
你可以按任意顺序返回答案。
|
||||
* 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
|
||||
* 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
|
||||
* 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
|
||||
* 你可以按任意顺序返回答案。
|
||||
|
||||
# 思路
|
||||
|
||||
@ -70,7 +70,7 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
|
||||
|
||||
寻找前k个最大元素流程如图所示:(图中的频率只有三个,所以正好构成一个大小为3的小顶堆,如果频率更多一些,则用这个小顶堆进行扫描)
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
我们来看一下C++代码:
|
||||
@ -126,10 +126,7 @@ public:
|
||||
优先级队列的定义正好反过来了,可能和优先级队列的源码实现有关(我没有仔细研究),我估计是底层实现上优先队列队首指向后面,队尾指向最前面的缘故!
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
103
problems/0503.下一个更大元素II.md
Normal file
103
problems/0503.下一个更大元素II.md
Normal file
@ -0,0 +1,103 @@
|
||||
|
||||
# 503.下一个更大元素II
|
||||
|
||||
链接:https://leetcode-cn.com/problems/next-greater-element-ii/
|
||||
|
||||
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
|
||||
|
||||
示例 1:
|
||||
|
||||
* 输入: [1,2,1]
|
||||
* 输出: [2,-1,2]
|
||||
* 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
|
||||
|
||||
|
||||
# 思路
|
||||
|
||||
做本题之前建议先做[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q) 和 [496.下一个更大元素 I](https://mp.weixin.qq.com/s/U0O6XkFOe-RMXthPS16sWQ)。
|
||||
|
||||
这道题和[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)也几乎如出一辙。
|
||||
|
||||
不同的时候本题要循环数组了。
|
||||
|
||||
关于单调栈的讲解我在题解[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)中已经详细讲解了。
|
||||
|
||||
本篇我侧重与说一说,如何处理循环数组。
|
||||
|
||||
相信不少同学看到这道题,就想那我直接把两个数组拼接在一起,然后使用单调栈求下一个最大值不就行了!
|
||||
|
||||
确实可以!
|
||||
|
||||
讲两个nums数组拼接在一起,使用单调栈计算出每一个元素的下一个最大值,最后再把结果集即result数组resize到原数组大小就可以了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElements(vector<int>& nums) {
|
||||
// 拼接一个新的nums
|
||||
vector<int> nums1(nums.begin(), nums.end());
|
||||
nums.insert(nums.end(), nums1.begin(), nums1.end());
|
||||
// 用新的nums大小来初始化result
|
||||
vector<int> result(nums.size(), -1);
|
||||
if (nums.size() == 0) return result;
|
||||
|
||||
// 开始单调栈
|
||||
stack<int> st;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
while (!st.empty() && nums[i] > nums[st.top()]) {
|
||||
result[st.top()] = nums[i];
|
||||
st.pop();
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
// 最后再把结果集即result数组resize到原数组大小
|
||||
result.resize(nums.size() / 2);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
这种写法确实比较直观,但做了很多无用操作,例如修改了nums数组,而且最后还要把result数组resize回去。
|
||||
|
||||
resize倒是不费时间,是O(1)的操作,但扩充nums数组相当于多了一个O(n)的操作。
|
||||
|
||||
其实也可以不扩充nums,而是在遍历的过程中模拟走了两边nums。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElements(vector<int>& nums) {
|
||||
vector<int> result(nums.size(), -1);
|
||||
if (nums.size() == 0) return result;
|
||||
stack<int> st;
|
||||
for (int i = 0; i < nums.size() * 2; i++) {
|
||||
// 模拟遍历两边nums,注意一下都是用i % nums.size()来操作
|
||||
while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {
|
||||
result[st.top()] = nums[i % nums.size()];
|
||||
st.pop();
|
||||
}
|
||||
st.push(i % nums.size());
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
可以版本二不仅代码精简了,也比版本一少做了无用功!
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
Java:
|
||||
|
||||
Python:
|
||||
|
||||
Go:
|
||||
|
||||
JavaScript:
|
||||
@ -37,7 +37,7 @@
|
||||
|
||||
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行。
|
||||
|
||||
如果对二叉树深度和高度还有点疑惑的话,请看:[二叉树:我平衡么?](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)。
|
||||
如果对二叉树深度和高度还有点疑惑的话,请看:[110.平衡二叉树](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)。
|
||||
|
||||
所以要找深度最大的叶子节点。
|
||||
|
||||
@ -207,7 +207,7 @@ public:
|
||||
|
||||
本题涉及如下几点:
|
||||
|
||||
* 递归求深度的写法,我们在[二叉树:我平衡么?](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)中详细的分析了深度应该怎么求,高度应该怎么求。
|
||||
* 递归求深度的写法,我们在[110.平衡二叉树](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)中详细的分析了深度应该怎么求,高度应该怎么求。
|
||||
* 递归中其实隐藏了回溯,在[二叉树:以为使用了递归,其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)中讲解了究竟哪里使用了回溯,哪里隐藏了回溯。
|
||||
* 层次遍历,在[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)深度讲解了二叉树层次遍历。
|
||||
所以本题涉及到的点,我们之前都讲解过,这些知识点需要同学们灵活运用,这样就举一反三了。
|
||||
|
||||
@ -5,6 +5,7 @@
|
||||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||||
</p>
|
||||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 二叉树理论基础篇
|
||||
|
||||
我们要开启新的征程了,大家跟上!
|
||||
|
||||
@ -111,7 +111,7 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
@ -125,7 +125,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
|
||||
|
||||
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是又左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
|
||||
|
||||
初始-1,初始-2,初始100,都可以!
|
||||
**初始-1,初始-2,初始100,都可以!**
|
||||
|
||||
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user