Merge pull request #2658 from nineninee/km0053

修正 卡码网0053.寻宝-Kruskal 表述错误

problems/kamacoder/0053.寻宝-Kruskal.md

@@ -38,7 +38,7 @@
 5 6 2
 5 7 1
 6 7 1
-``` 
+```
 
 输出示例： 
 
@@ -79,7 +79,7 @@ kruscal的思路：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240111114204.png)
 
--------- 
+--------
 
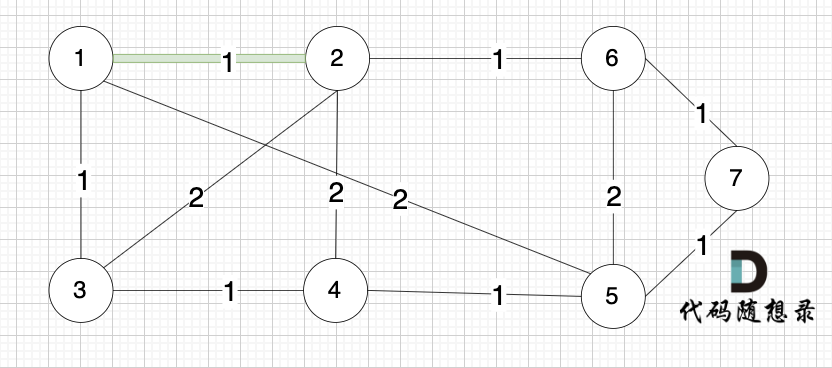
 选边(4,5)，节点4 和 节点 5 不在同一个集合，生成树可以添加边(4,5) ，并将节点4，节点5 放到同一个集合。 
 
@@ -87,7 +87,7 @@ kruscal的思路：
 
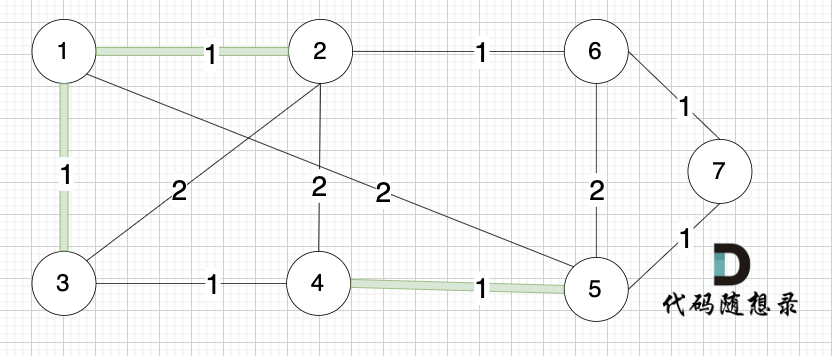
 **大家判断两个节点是否在同一个集合，就看图中两个节点是否有绿色的粗线连着就行**
 
------- 
+------
 
 （这里在强调一下，以下选边是按照上面排序好的边的数组来选择的）
 
@@ -95,13 +95,13 @@ kruscal的思路：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112105834.png) 
 
---------- 
+---------
 
 选边(2,6)，节点2 和 节点6 不在同一个集合，生成树添加边(2,6)，并将节点2，节点6 放到同一个集合。
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112110214.png) 
 
--------- 
+--------
 
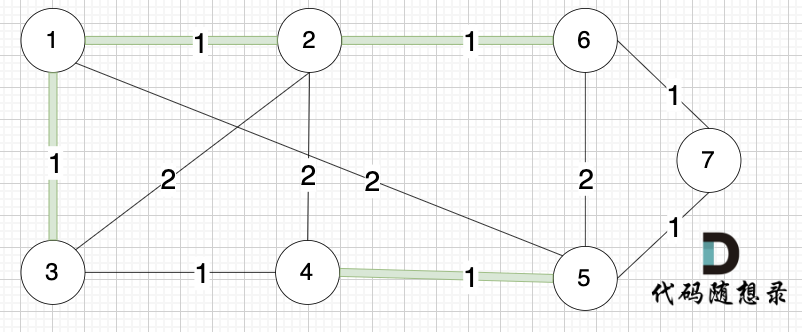
 选边(3,4)，节点3 和 节点4 不在同一个集合，生成树添加边(3,4)，并将节点3，节点4 放到同一个集合。 
 
@@ -113,7 +113,7 @@ kruscal的思路：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112110637.png) 
 
------------ 
+-----------
 
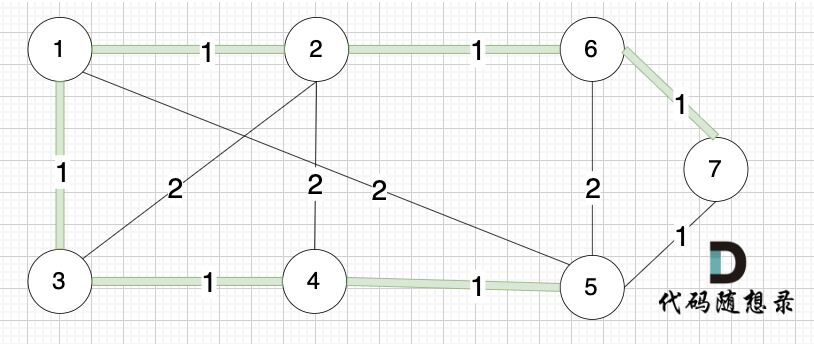
 选边(5,7)，节点5 和 节点7 在同一个集合，不做计算。 
 
@@ -122,7 +122,7 @@ kruscal的思路：
 后面遍历 边(3,2)，(2,4)，(5,6) 同理，都因两个节点已经在同一集合，不做计算。
 
 
-------- 
+-------
 
 此时 我们就已经生成了一个最小生成树，即： 
 
@@ -230,7 +230,7 @@ int main() {
 
 如果题目要求将最小生成树的边输出的话，应该怎么办呢？ 
 
-Kruskal 算法 输出边的话，相对prim 要容易很多，因为 Kruskal 本来就是直接操作边，边的结构自然清晰，不用像 prim一样 需要再节点练成线输出边 （因为prim是对节点操作，而 Kruskal是对边操作，这是本质区别） 
+Kruskal 算法 输出边的话，相对prim 要容易很多，因为 Kruskal 本来就是直接操作边，边的结构自然清晰，不用像 prim一样 需要再将节点连成线输出边 （因为prim是对节点操作，而 Kruskal是对边操作，这是本质区别） 
 
 本题中，边的结构为：