mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
1035.不相交的线题目描述及参数名更新
This commit is contained in:
@ -8,11 +8,16 @@
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/uncrossed-lines/)
|
||||
|
||||
我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
|
||||
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
|
||||
|
||||
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
|
||||
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
|
||||
|
||||
以这种方法绘制线条,并返回我们可以绘制的最大连线数。
|
||||
* nums1[i] == nums2[j]
|
||||
* 且绘制的直线不与任何其他连线(非水平线)相交。
|
||||
|
||||
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
|
||||
|
||||
以这种方法绘制线条,并返回可以绘制的最大连线数。
|
||||
|
||||
|
||||

|
||||
@ -26,16 +31,16 @@
|
||||
|
||||
相信不少录友看到这道题目都没啥思路,我们来逐步分析一下。
|
||||
|
||||
绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且直线不能相交!
|
||||
绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,只要 nums1[i] == nums2[j],且直线不能相交!
|
||||
|
||||
直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
|
||||
直线不能相交,这就是说明在字符串nums1中 找到一个与字符串nums2相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,连接相同数字的直线就不会相交。
|
||||
|
||||
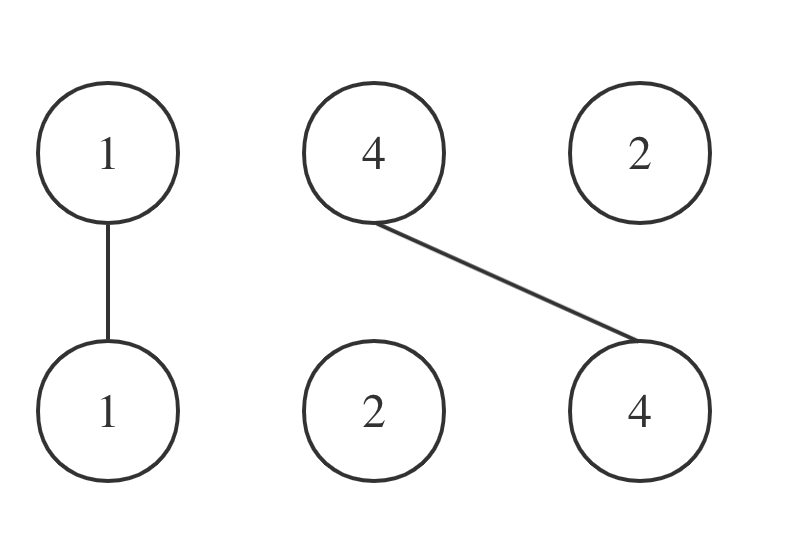
拿示例一A = [1,4,2], B = [1,2,4]为例,相交情况如图:
|
||||
拿示例一nums1 = [1,4,2], nums2 = [1,2,4]为例,相交情况如图:
|
||||
|
||||
|
||||
|
||||
|
||||
其实也就是说A和B的最长公共子序列是[1,4],长度为2。 这个公共子序列指的是相对顺序不变(即数字4在字符串A中数字1的后面,那么数字4也应该在字符串B数字1的后面)
|
||||
其实也就是说nums1和nums2的最长公共子序列是[1,4],长度为2。 这个公共子序列指的是相对顺序不变(即数字4在字符串nums1中数字1的后面,那么数字4也应该在字符串nums2数字1的后面)
|
||||
|
||||
这么分析完之后,大家可以发现:**本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!**
|
||||
|
||||
@ -52,18 +57,18 @@
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
int maxUncrossedLines(vector<int>& A, vector<int>& B) {
|
||||
vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
|
||||
for (int i = 1; i <= A.size(); i++) {
|
||||
for (int j = 1; j <= B.size(); j++) {
|
||||
if (A[i - 1] == B[j - 1]) {
|
||||
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
|
||||
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
|
||||
for (int i = 1; i <= nums1.size(); i++) {
|
||||
for (int j = 1; j <= nums2.size(); j++) {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[A.size()][B.size()];
|
||||
return dp[nums1.size()][nums2.size()];
|
||||
}
|
||||
};
|
||||
```
|
||||
@ -110,11 +115,11 @@ public:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxUncrossedLines(self, A: List[int], B: List[int]) -> int:
|
||||
dp = [[0] * (len(B)+1) for _ in range(len(A)+1)]
|
||||
for i in range(1, len(A)+1):
|
||||
for j in range(1, len(B)+1):
|
||||
if A[i-1] == B[j-1]:
|
||||
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
|
||||
dp = [[0] * (len(nums2)+1) for _ in range(len(nums1)+1)]
|
||||
for i in range(1, len(nums1)+1):
|
||||
for j in range(1, len(nums2)+1):
|
||||
if nums1[i-1] == nums2[j-1]:
|
||||
dp[i][j] = dp[i-1][j-1] + 1
|
||||
else:
|
||||
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
|
||||
@ -124,23 +129,22 @@ class Solution:
|
||||
### Go:
|
||||
|
||||
```go
|
||||
func maxUncrossedLines(A []int, B []int) int {
|
||||
m, n := len(A), len(B)
|
||||
dp := make([][]int, m+1)
|
||||
func maxUncrossedLines(nums1 []int, nums2 []int) int {
|
||||
dp := make([][]int, len(nums1) + 1)
|
||||
for i := range dp {
|
||||
dp[i] = make([]int, n+1)
|
||||
dp[i] = make([]int, len(nums2) + 1)
|
||||
}
|
||||
|
||||
for i := 1; i <= len(A); i++ {
|
||||
for j := 1; j <= len(B); j++ {
|
||||
if (A[i - 1] == B[j - 1]) {
|
||||
for i := 1; i <= len(nums1); i++ {
|
||||
for j := 1; j <= len(nums2); j++ {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[m][n]
|
||||
return dp[len(nums1)][len(nums2)]
|
||||
|
||||
}
|
||||
|
||||
|
||||
Reference in New Issue
Block a user