添加1035.不相交的线和1143.最长公共子序列

problems/1035.不相交的线.md

@@ -111,7 +111,6 @@ class Solution:
 Golang:
 
 ```go
-
 func maxUncrossedLines(A []int, B []int) int {
 	m, n := len(A), len(B)
 	dp := make([][]int, m+1)
@@ -140,7 +139,26 @@ func max(a, b int) int {
 }
 ```
 
+Rust:
 
+```rust
+pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
+    let (n, m) = (nums1.len(), nums2.len());
+    let mut last = vec![0; m + 1]; // 记录滚动数组
+    let mut dp = vec![0; m + 1];
+    for i in 1..=n {
+        dp.swap_with_slice(&mut last);
+        for j in 1..=m {
+            if nums1[i - 1] == nums2[j - 1] {
+                dp[j] = last[j - 1] + 1;
+            } else {
+                dp[j] = last[j].max(dp[j - 1]);
+            }
+        }
+    }
+    dp[m]
+}
+```
 
 JavaScript：
 

problems/1143.最长公共子序列.md

@@ -4,40 +4,40 @@
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
 
-## 1143.最长公共子序列 
+## 1143.最长公共子序列
 
 [力扣题目链接](https://leetcode-cn.com/problems/longest-common-subsequence/)
 
-给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。  
+给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
 
-一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。     
+一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
 
-例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。   
+例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
 
-若这两个字符串没有公共子序列，则返回 0。        
+若这两个字符串没有公共子序列，则返回 0。
 
-示例 1:    
+示例 1:
 
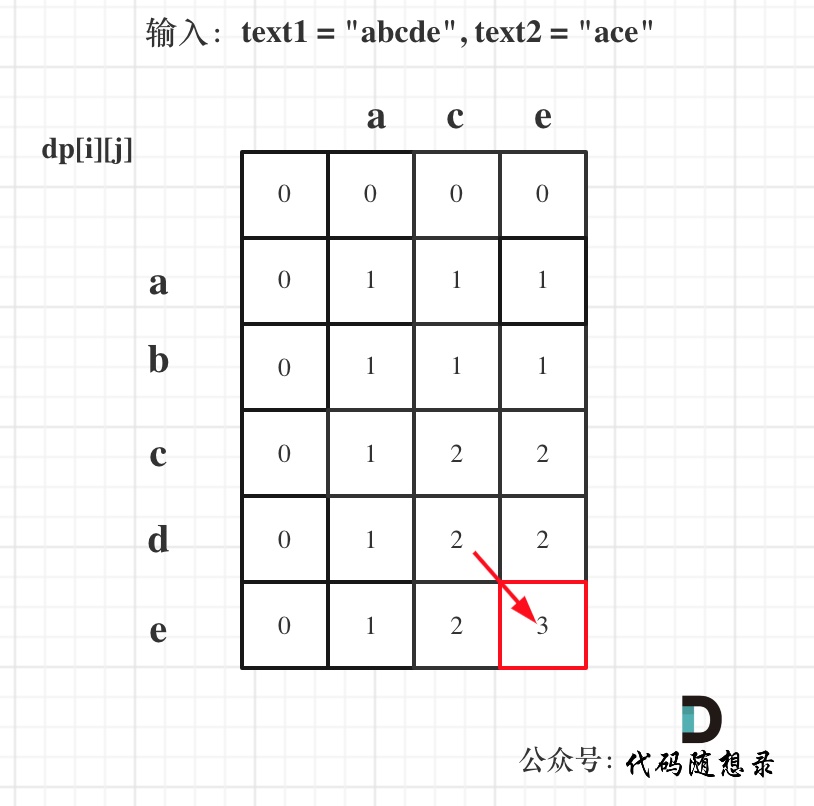
-输入：text1 = "abcde", text2 = "ace"      
+输入：text1 = "abcde", text2 = "ace"
-输出：3          
+输出：3
-解释：最长公共子序列是 "ace"，它的长度为 3。     
+解释：最长公共子序列是 "ace"，它的长度为 3。
 
-示例 2:      
+示例 2:
-输入：text1 = "abc", text2 = "abc"    
+输入：text1 = "abc", text2 = "abc"
-输出：3       
+输出：3
-解释：最长公共子序列是 "abc"，它的长度为 3。    
+解释：最长公共子序列是 "abc"，它的长度为 3。
 
-示例 3:     
+示例 3:
-输入：text1 = "abc", text2 = "def"      
+输入：text1 = "abc", text2 = "def"
-输出：0        
+输出：0
-解释：两个字符串没有公共子序列，返回 0。    
+解释：两个字符串没有公共子序列，返回 0。
 
-提示:       
+提示:
 * 1 <= text1.length <= 1000
 * 1 <= text2.length <= 1000
 输入的字符串只含有小写英文字符。
 
-## 思路 
+## 思路
 
 本题和[动态规划：718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html)区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
 
@@ -45,21 +45,21 @@
 
 1. 确定dp数组（dp table）以及下标的含义
 
-dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j] 
+dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
 
-有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？ 
+有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？
 
 这样定义是为了后面代码实现方便，如果非要定义为为长度为[0, i]的字符串text1也可以，大家可以试一试！
 
 2. 确定递推公式
 
-主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同 
+主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
 
-如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1; 
+如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
 
 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
 
-即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); 
+即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
 
 代码如下：
 
@@ -71,9 +71,9 @@ if (text1[i - 1] == text2[j - 1]) {
 }
 ```
 
-3. dp数组如何初始化  
+3. dp数组如何初始化
 
-先看看dp[i][0]应该是多少呢？ 
+先看看dp[i][0]应该是多少呢？
 
 test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
 
@@ -101,7 +101,7 @@ vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
 
 ![1143.最长公共子序列1](https://img-blog.csdnimg.cn/20210210150215918.jpg)
 
-最后红框dp[text1.size()][text2.size()]为最终结果 
+最后红框dp[text1.size()][text2.size()]为最终结果
 
 以上分析完毕，C++代码如下：
 
@@ -158,7 +158,7 @@ class Solution:
         for i in range(1, len2):
             for j in range(1, len1): # 开始列出状态转移方程
                 if text1[j-1] == text2[i-1]:
-                    dp[i][j] = dp[i-1][j-1]+1 
+                    dp[i][j] = dp[i-1][j-1]+1
                 else:
                     dp[i][j] = max(dp[i-1][j], dp[i][j-1])
         return dp[-1][-1]
@@ -189,10 +189,32 @@ func longestCommonSubsequence(text1 string, text2 string) int {
 
 func max(a,b int)int  {
 	if a>b{
-		return a 
+		return a
 	}
 	return b
 }
+
+```
+
+Rust:
+```rust
+pub fn longest_common_subsequence(text1: String, text2: String) -> i32 {
+    let (n, m) = (text1.len(), text2.len());
+    let (s1, s2) = (text1.as_bytes(), text2.as_bytes());
+    let mut dp = vec![0; m + 1];
+    let mut last = vec![0; m + 1];
+    for i in 1..=n {
+        dp.swap_with_slice(&mut last);
+        for j in 1..=m {
+            dp[j] = if s1[i - 1] == s2[j - 1] {
+                last[j - 1] + 1
+            } else {
+                last[j].max(dp[j - 1])
+            };
+        }
+    }
+    dp[m]
+}
 ```
 
 Javascript：