Adds Portuguese (pt-BR) translation (#340)

* create portuguese translations

* renames `Lista Ligada` to `Lista Encadeada`

* revert changes on package-lock.json

README.pt-BR.md

@@ -29,23 +29,23 @@ os dados.
 
 `B` - Iniciante, `A` - Avançado
 
-* `B` [Linked List](src/data-structures/linked-list)
-* `B` [Doubly Linked List](src/data-structures/doubly-linked-list)
-* `B` [Queue](src/data-structures/queue)
-* `B` [Stack](src/data-structures/stack)
-* `B` [Hash Table](src/data-structures/hash-table)
-* `B` [Heap](src/data-structures/heap)
-* `B` [Priority Queue](src/data-structures/priority-queue)
-* `A` [Trie](src/data-structures/trie)
-* `A` [Tree](src/data-structures/tree)
-  * `A` [Binary Search Tree](src/data-structures/tree/binary-search-tree)
-  * `A` [AVL Tree](src/data-structures/tree/avl-tree)
-  * `A` [Red-Black Tree](src/data-structures/tree/red-black-tree)
-  * `A` [Segment Tree](src/data-structures/tree/segment-tree) - com exemplos de consultas min / max / sum range
-  * `A` [Fenwick Tree](src/data-structures/tree/fenwick-tree) (Árvore indexada binária)
-* `A` [Graph](src/data-structures/graph) (ambos dirigidos e não direcionados)
-* `A` [Disjoint Set](src/data-structures/disjoint-set)
-* `A` [Bloom Filter](src/data-structures/bloom-filter)
+* `B` [Lista Encadeada (Linked List)](src/data-structures/linked-list.pt-BR)
+* `B` [Lista Duplamente Ligada (Doubly Linked List)](src/data-structures/doubly-linked-list.pt-BR)
+* `B` [Fila (Queue)](src/data-structures/queue.pt-BR)
+* `B` [Stack](src/data-structures/stack.pt-BR)
+* `B` [Tabela de Hash (Hash Table)](src/data-structures/hash-table.pt-BR)
+* `B` [Heap](src/data-structures/heap.pt-BR)
+* `B` [Fila de Prioridade (Priority Queue)](src/data-structures/priority-queue.pt-BR)
+* `A` [Trie](src/data-structures/trie.pt-BR)
+* `A` [Árvore (Tree)](src/data-structures/tree.pt-BR)
+  * `A` [Árvore de Pesquisa Binária (Binary Search Tree)](src/data-structures/tree/binary-search-tree.pt-BR)
+  * `A` [Árvore AVL (AVL Tree)](src/data-structures/tree/avl-tree.pt-BR)
+  * `A` [Árvore Vermelha-Preta (Red-Black Tree)](src/data-structures/tree/red-black-tree.pt-BR)
+  * `A` [Árvore de Segmento (Segment Tree)](src/data-structures/tree/segment-tree.pt-BR) - com exemplos de consultas min / max / sum range
+  * `A` [Árvore Fenwick (Fenwick Tree)](src/data-structures/tree/fenwick-tree.pt-BR) (Árvore indexada binária)
+* `A` [Gráfico (Graph)](src/data-structures/graph.pt-BR) (ambos dirigidos e não direcionados)
+* `A` [Conjunto Disjuntor (Disjoint Set)](src/data-structures/disjoint-set.pt-BR)
+* `A` [Filtro Bloom (Bloom Filter)](src/data-structures/bloom-filter.pt-BR)
 
 ## Algoritmos
 

src/data-structures/bloom-filter/README.md

@@ -1,7 +1,7 @@
 # Bloom Filter
 
 _Read this in other languages:_
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md) | [_Português_](README.pt-BR.md)
 
 A **bloom filter** is a space-efficient probabilistic 
 data structure designed to test whether an element 

src/data-structures/bloom-filter/README.pt-BR.md

@@ -0,0 +1,132 @@
+# Filtro Bloom (Bloom Filter)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_Русский_](README.ru-RU.md) 
+
+O **bloom filter** é uma estrutura de dados probabilística
+espaço-eficiente designada para testar se um elemento está
+ou não presente em um conjunto de dados. Foi projetado para ser
+incrivelmente rápido e utilizar o mínimo de memória ao 
+potencial custo de um falso-positivo. Correspondências 
+_falsas positivas_ são possíveis, contudo _falsos negativos_ 
+não são - em outras palavras, a consulta retorna 
+"possivelmente no conjunto" ou "definitivamente não no conjunto".
+
+Bloom propôs a técnica para aplicações onde a quantidade 
+de entrada de dados exigiria uma alocação de memória
+impraticavelmente grande se as "convencionais" técnicas
+error-free hashing fossem aplicado.
+
+## Descrição do algoritmo
+
+Um filtro Bloom vazio é um _bit array_ de `m` bits, todos
+definidos como `0`. Também deverá haver diferentes funções
+de hash `k` definidas, cada um dos quais mapeia e produz hash
+para um dos elementos definidos em uma das posições `m` da
+ _array_, gerando uma distribuição aleatória e uniforme.
+Normalmente, `k` é uma constante, muito menor do que `m`,
+pelo qual é proporcional ao número de elements a ser adicionado;
+a escolha precisa de `k` e a constante de proporcionalidade de `m`
+são determinadas pela taxa de falsos positivos planejado do filtro.
+
+Aqui está um exemplo de um filtro Bloom, representando o
+conjunto `{x, y, z}`. As flechas coloridas demonstram as
+posições no _bit array_ em que cada elemento é mapeado.
+O elemento `w` não está definido dentro de `{x, y, z}`,
+porque este produz hash para uma posição de array de bits
+contendo `0`. Para esta imagem: `m = 18` e `k = 3`.
+
+![Bloom Filter](https://upload.wikimedia.org/wikipedia/commons/a/ac/Bloom_filter.svg)
+
+## Operações
+
+Existem duas operações principais que o filtro Bloom pode operar:
+_inserção_ e _pesquisa_. A pesquisa pode resultar em falsos
+positivos. Remoção não é possível.
+
+Em outras palavras, o filtro pode receber itens. Quando
+vamos verificar se um item já foi anteriormente
+inserido, ele poderá nos dizer "não" ou "talvez".
+
+Ambas as inserções e pesquisas são operações `O(1)`.
+
+## Criando o filtro
+
+Um filtro Bloom é criado ao alocar um certo tamanho.
+No nosso exemplo, nós utilizamos `100` como tamanho padrão.
+Todas as posições são initializadas como `false`.
+
+### Inserção
+
+Durante a inserção, um número de função hash, no nosso caso `3`
+funções de hash, são utilizadas para criar hashes de uma entrada.
+Estas funções de hash emitem saída de índices. A cada índice
+recebido, nós simplismente trocamos o valor de nosso filtro
+Bloom para `true`.
+
+### Pesquisa
+
+Durante a pesquisa, a mesma função de hash é chamada
+e usada para emitir hash da entrada. Depois nós checamos
+se _todos_ os indices recebidos possuem o valor `true`
+dentro de nosso filtro Bloom. Caso _todos_ possuam o valor
+`true`, nós sabemos que o filtro Bloom pode ter tido
+o valor inserido anteriormente.
+
+Contudo, isto não é certeza, porque é possível que outros
+valores anteriormente inseridos trocaram o valor para `true`.
+Os valores não são necessariamente `true` devido ao ítem
+atualmente sendo pesquisado. A certeza absoluta é impossível,
+a não ser que apenas um item foi inserido anteriormente.
+
+Durante a checagem do filtro Bloom para índices retornados
+pela nossa função de hash, mesmo que apenas um deles possua
+valor como `false`, nós definitivamente sabemos que o ítem
+não foi anteriormente inserido.
+
+## Falso Positivos
+
+A probabilidade de falso positivos é determinado por
+três fatores: o tamanho do filtro de Bloom, o número de 
+funções de hash que utilizados, e o número de itens que
+foram inseridos dentro do filtro.
+
+A formula para calcular a probabilidade de um falso positivo é:
+
+( 1 - e <sup>-kn/m</sup> ) <sup>k</sup>
+
+`k` = número de funções de hash
+
+`m` = tamanho do filtro
+
+`n` = número de itens inserido
+
+Estas variáveis, `k`, `m` e `n`, devem ser escolhidas baseado
+em quanto aceitável são os falsos positivos. Se os valores
+escolhidos resultam em uma probabilidade muito alta, então
+os valores devem ser ajustados e a probabilidade recalculada.
+
+## Aplicações
+
+Um filtro Bloom pode ser utilizado em uma página de Blog.
+Se o objetivo é mostrar aos leitores somente os artigos
+em que eles nunca viram, então o filtro Bloom é perfeito 
+para isso. Ele pode armazenar hashes baseados nos artigos.
+Depois que um usuário lê alguns artigos, eles podem ser
+inseridos dentro do filtro. Na próxima vez que o usuário
+visitar o Blog, aqueles artigos poderão ser filtrados (eliminados) 
+do resultado.
+
+Alguns artigos serão inevitavelmente filtrados (eliminados) 
+por engano, mas o custo é aceitável. Tudo bem se um usuário nunca
+ver alguns poucos artigos, desde que tenham outros novos
+para ver toda vez que eles visitam o site. 
+
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Bloom_filter)
+- [Bloom Filters by Example](http://llimllib.github.io/bloomfilter-tutorial/)
+- [Calculating False Positive Probability](https://hur.st/bloomfilter/?n=4&p=&m=18&k=3)
+- [Bloom Filters on Medium](https://blog.medium.com/what-are-bloom-filters-1ec2a50c68ff)
+- [Bloom Filters on YouTube](https://www.youtube.com/watch?v=bEmBh1HtYrw)

src/data-structures/disjoint-set/README.md

@@ -1,7 +1,8 @@
 # Disjoint Set
 
 _Read this in other languages:_
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md) | [_Português_](README.pt-BR.md)
+
 
 **Disjoint-set** data structure (also called a union–find data structure or merge–find set) is a data 
 structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. 

src/data-structures/disjoint-set/README.pt-BR.md

@@ -0,0 +1,32 @@
+# Conjunto Disjuntor (Disjoint Set)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_Русский_](README.ru-RU.md) 
+
+**Conjunto Disjuntor**
+
+**Conjunto Disjuntor** é uma estrutura de dados (também chamado de
+estrutura de dados de union–find ou merge–find) é uma estrutura de dados
+que rastreia um conjunto de elementos particionados em um número de
+subconjuntos separados (sem sobreposição).
+Ele fornece operações de tempo quase constante (limitadas pela função
+inversa de Ackermann) para *adicionar novos conjuntos*, para 
+*mesclar/fundir conjuntos existentes* e para *determinar se os elementos
+estão no mesmo conjunto*.
+Além de muitos outros usos (veja a seção Applications), conjunto disjuntor
+desempenham um papel fundamental no algoritmo de Kruskal para encontrar a
+árvore geradora mínima de um gráfico (graph).
+
+
+![disjoint set](https://upload.wikimedia.org/wikipedia/commons/6/67/Dsu_disjoint_sets_init.svg)
+
+*MakeSet* cria 8 singletons.
+
+![disjoint set](https://upload.wikimedia.org/wikipedia/commons/a/ac/Dsu_disjoint_sets_final.svg)
+
+Depois de algumas operações de *Uniões*, alguns conjuntos são agrupados juntos.
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)
+- [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/doubly-linked-list/README.md

@@ -1,9 +1,7 @@
 # Doubly Linked List
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_Русский_](README.ru-RU.md) | [_简体中文_](README.zh-CN.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **doubly linked list** is a linked data structure that 
 consists of a set of sequentially linked records called nodes. Each node contains 

src/data-structures/doubly-linked-list/README.pt-BR.md

@@ -0,0 +1,114 @@
+# Lista Duplamente Ligada (Doubly Linked List)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, uma **lista duplamente conectada** é uma estrutura
+de dados vinculada que se consistem em um conjunto de registros
+sequencialmente vinculados chamados de nós (nodes). Em cada nó contém dois
+campos, chamados de ligações, que são referenciados ao nó anterior e posterior
+de uma sequência de nós. O começo e o fim dos nós anteriormente e posteiormente
+ligados, respectiviamente, apontam para algum tipo de terminação, normalmente
+um nó sentinela ou nulo, para facilitar a travessia da lista. Se existe
+somente um nó sentinela, então a lista é ligada circularmente através do nó
+sentinela. Ela pode ser conceitualizada como duas listas individualmente ligadas
+e formadas a partir dos mesmos itens, mas em ordem sequencial opostas.
+
+![Doubly Linked List](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg)
+
+Os dois nós ligados permitem a travessia da lista em qualquer direção.
+Enquanto adicionar ou remover um nó de uma lista duplamente vinculada requer
+alterar mais ligações (conexões) do que em uma lista encadeada individualmente
+(singly linked list), as operações são mais simples e potencialmente mais
+eficientes (para nós que não sejam nós iniciais) porque não há necessidade
+de se manter rastreamento do nó anterior durante a travessia ou não há
+necessidade de percorrer a lista para encontrar o nó anterior, para que
+então sua ligação/conexão possa ser modificada.
+
+## Pseudocódigo para Operações Básicas
+
+### Inserir
+
+```text
+Add(value)
+  Pre: value is the value to add to the list
+  Post: value has been placed at the tail of the list
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    n.previous ← tail
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+    
+### Deletar
+
+```text
+Remove(head, value)
+  Pre: head is the head node in the list
+       value is the value to remove from the list
+  Post: value is removed from the list, true; otherwise false
+  if head = ø
+    return false
+  end if
+  if value = head.value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+      head.previous ← ø
+    end if
+    return true
+  end if
+  n ← head.next
+  while n = ø and value !== n.value
+    n ← n.next
+  end while
+  if n = tail
+    tail ← tail.previous
+    tail.next ← ø
+    return true
+  else if n = ø
+    n.previous.next ← n.next
+    n.next.previous ← n.previous
+    return true
+  end if
+  return false
+end Remove
+```
+    
+### Travessia reversa
+
+```text
+ReverseTraversal(tail)
+  Pre: tail is the node of the list to traverse
+  Post: the list has been traversed in reverse order
+  n ← tail
+  while n = ø
+    yield n.value
+    n ← n.previous
+  end while
+end Reverse Traversal
+```
+    
+## Complexidades
+
+## Complexidade de Tempo
+
+| Acesso    | Pesquisa    | Inserção | Remoção  |
+| :-------: | :---------: | :------: | :------: |
+| O(n)      | O(n)        | O(1)     | O(n)     |
+
+### Complexidade de Espaço
+
+O(n)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
+- [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/graph/README.md

@@ -1,8 +1,7 @@
 # Graph
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **graph** is an abstract data type 
 that is meant to implement the undirected graph and 

src/data-structures/graph/README.pt-BR.md

@@ -0,0 +1,29 @@
+# Gráfico (Graph)
+
+_Read this in other languages:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, um **gráfico** é uma abstração de estrutura
+de dados que se destina a implementar os conceitos da matemática de
+gráficos direcionados e não direcionados, especificamente o campo da
+teoria dos gráficos.
+
+Uma estrutura de dados gráficos consiste em um finito (e possivelmente
+mutável) conjunto de vértices, nós ou pontos, juntos com um
+conjunto de pares não ordenados desses vértices para um gráfico não
+direcionado ou para um conjunto de pares ordenados para um gráfico
+direcionado. Esses pares são conhecidos como arestas, arcos
+ou linhas diretas para um gráfico não direcionado e como setas,
+arestas direcionadas, arcos direcionados ou linhas direcionadas
+para um gráfico direcionado.
+
+Os vértices podem fazer parte a estrutura do gráfico, ou podem
+ser entidades externas representadas por índices inteiros ou referências.
+
+![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg)
+
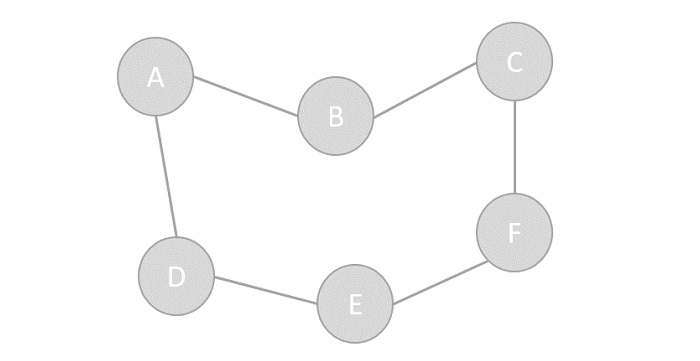
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type))
+- [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/hash-table/README.md

@@ -1,9 +1,7 @@
 # Hash Table
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
  
 In computing, a **hash table** (hash map) is a data 
 structure which implements an *associative array* 

src/data-structures/hash-table/README.pt-BR.md

@@ -0,0 +1,28 @@
+# Tabela de Hash (Hash Table)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md)
+ 
+Na ciência da computação, uma **tabela de hash** (hash map) é uma
+estrutura de dados pela qual implementa um tipo de dado abstrado de
+*array associativo*, uma estrutura que pode *mapear chaves para valores*.
+Uma tabela de hash utiliza uma *função de hash* para calcular um índice
+em um _array_ de buckets ou slots, a partir do qual o valor desejado
+pode ser encontrado.
+
+Idealmente, a função de hash irá atribuir a cada chave a um bucket único,
+mas a maioria dos designs de tabela de hash emprega uma função de hash
+imperfeita, pela qual poderá causar colisões de hashes onde a função de hash
+gera o mesmo índice para mais de uma chave.Tais colisões devem ser
+acomodados de alguma forma.
+
+![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg)
+
+Colisão de hash resolvida por encadeamento separado.
+
+![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Hash_table)
+- [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/heap/README.md

@@ -1,9 +1,7 @@
 # Heap (data-structure)
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **heap** is a specialized tree-based 
 data structure that satisfies the heap property described

src/data-structures/heap/README.pt-BR.md

@@ -0,0 +1,24 @@
+# Heap (estrutura de dados)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md)
+
+Na ciência da computação, um **heap** é uma estrutura de dados
+baseada em uma árvore especializada que satisfaz a propriedade _heap_ descrita abaixo.
+
+Em um *heap mínimo* (min heap), caso `P` é um nó pai de `C`, então a chave
+(o valor) de `P` é menor ou igual a chave de `C`.
+
+![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png)
+
+Em uma *heap máximo* (max heap), a chave de `P` é maior ou igual
+a chave de `C`.
+
+![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg)
+
+O nó no "topo" do _heap_, cujo não possui pais, é chamado de nó raiz.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure))
+- [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/linked-list/README.md

@@ -1,10 +1,7 @@
 # Linked List
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_Português_](README.pt-BR.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **linked list** is a linear collection 
 of data elements, in which linear order is not given by 

src/data-structures/linked-list/README.pt-BR.md

@@ -1,15 +1,25 @@
-# Lista encadeada
+# Lista Encadeada (Linked List)
 
-Em ciência da computação, uma **lista encadeada** é uma coleção linear
-de elementos de dados, em que a ordem linear não é fornecida pelo seu
-posicionamento físico na memória. Em vez disso, cada elemento aponta para o próximo.
-É uma estrutura de dados consistente de um grupo de nós que juntos
-representam uma sequência. De forma simples, cada nó é composto de dado
-e uma referência (em outras palavras, um link) para o próximo nó na sequência.
-Essa estrutura permite uma inserção eficiente ou uma remoção de elementos
-apartir de qualquer posição na sequência durante a iteração. Variantes
-mais complexas adicionam links adicionais, permitindo inserção eficiente ou remoção
-arbitrária de referências do elemento. Uma desvantagem da lista encadeada é que o tempo de acesso é linear (e dificulta para pipeline) Acesso rápido, assim como acesso randômico, não é viável. Arrays têm um melhor cache de localidade quando comparado com listas encadeadas.
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, uma **lista encadeada** é uma coleção linear de
+elementos de dado, em que a ordem linear não é dada por sua locação
+física na memória. Em vez disso, cada elemento aponta para o próximo.
+É uma estrutura de dados consistindo em um grupo de nós
+que juntos representam uma sequência. Sob a forma mais simples,
+cada nó é composto de dados e uma referência (em outras palavras,
+uma ligação/conexão) para o próximo nó na sequência. Esta estrutua
+permite uma eficiente inserção e remoção de elementos de qualquer
+posição na sequência durante a iteração.
+
+Variantes mais complexas adicionam ligações adicionais, permitindo
+uma inserção ou remoção mais eficiente a partir de referências
+de elementos arbitrárias. Uma desvantagem das listas vinculadas
+é que o tempo de acesso é linear (e difícil de inserir em uma
+pipeline). Acessos mais rápidos, como acesso aleatório, não é viável.
+Arrays possuem uma melhor localização de cache em comparação
+com lista encadeada (linked list).
 
 ![Linked List](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg)
 
@@ -45,7 +55,7 @@ Prepend(value)
 end Prepend
 ```
 
-### Busca
+### Pesquisa
 
 ```text
 Contains(head, value)
@@ -63,7 +73,7 @@ Contains(head, value)
 end Contains
 ```
 
-### Deleção
+### Remoção
 
 ```text
 Remove(head, value)
@@ -97,7 +107,7 @@ Remove(head, value)
 end Remove
 ```
 
-### Traverse
+### Travessia
 
 ```text
 Traverse(head)
@@ -111,7 +121,7 @@ Traverse(head)
 end Traverse
 ```
 
-### Traverse in Reverse
+### Travessia Reversa
 
 ```text
 ReverseTraversal(head, tail)
@@ -134,13 +144,19 @@ end ReverseTraversal
 
 ## Complexidades
 
-### Tempo de complexidade
+### Complexidade de Tempo
 
+<<<<<<< HEAD
 | Acesso | Busca | Inserção | Deleção |
 | :----: | :---: | :------: | :-----: |
 |  O(n)  | O(n)  |   O(1)   |  O(n)   |
+=======
+| Acesso | Pesquisa | Inserção | Remoção |
+| :----: | :------: | :------: | :-----: |
+|  O(n)  |  O(n)    |  O(1)    |  O(n)   |
+>>>>>>> create portuguese translations
 
-### Spaço de complexidade
+### Complexidade de Espaçø
 
 O(n)
 

src/data-structures/priority-queue/README.md

@@ -1,9 +1,7 @@
 # Priority Queue
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **priority queue** is an abstract data type 
 which is like a regular queue or stack data structure, but where 

src/data-structures/priority-queue/README.pt-BR.md

@@ -0,0 +1,26 @@
+# Fila de Prioridade (Priority Queue)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, uma **fila de prioridade** é um tipo de dados
+abastrato que é como uma fila regular (regular queue) ou estrutura de
+dados de pilha (stack), mas adicionalmente cada elemento possui uma
+"prioridade" associada.
+
+Em uma fila de prioridade, um elemento com uma prioridade alta é servido
+antes de um elemento com baixa prioridade. Caso dois elementos posusam a
+mesma prioridade, eles serão servidos de acordo com sua ordem na fila.
+
+Enquanto as filas de prioridade são frequentemente implementadas com
+pilhas (heaps), elas são conceitualmente distintas das pilhas (heaps).
+A fila de prioridade é um conceito abstrato como uma "lista" (list) ou
+um "mapa" (map); assim como uma lista pode ser implementada com uma
+lista encadeada (liked list) ou um array, a fila de prioridade pode ser
+implementada com uma pilha (heap) ou com uima variedade de outros métodos,
+como um array não ordenado (unordered array).
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue)
+- [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6)

src/data-structures/queue/README.md

@@ -1,9 +1,7 @@
 # Queue
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **queue** is a particular kind of abstract data 
 type or collection in which the entities in the collection are 

src/data-structures/queue/README.pt-BR.md

@@ -0,0 +1,31 @@
+# Fila (Queue)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, uma **fila** é um tipo particular de abstração
+de tipo de dado ou coleção em que as entidades na coleção são mantidas em
+ordem e a causa primária (ou única) de operações na coleção são a
+adição de entidades à posição final da coleção, conhecido como enfileiramento
+(enqueue) e a remoção de entidades do posição inicial, conhecida como desenfileirar
+(dequeue).Isto torna a fila uma estrutura de dados tipo First-In-First-Out (FIFO).
+
+Em uma estrutura de dados FIFO, o primeiro elemento adicionado a fila
+será o primeiro a ser removido. Isso é equivalente ao requisito em que uma vez
+que um novo elemento é adicionado, todos os elementos que foram adicionados
+anteriormente devem ser removidos antes que o novo elemento possa ser removido.
+
+Muitas vezes uma espiada (peek) ou uma operação de frente é iniciada,
+retornando o valor do elemento da frente, sem desenfileira-lo. Uma lista é
+um exemplo de uma estrutura de dados linear, ou mais abstratamente uma
+coleção seqüencial.
+
+
+Representação de uma file FIFO (first in, first out)
+
+![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg)
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)

src/data-structures/stack/README.md

@@ -1,9 +1,7 @@
 # Stack
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md),
-[_日本語_](README.ja-JP.md)
+[_简体中文_](README.zh-CN.md), | [_Русский_](README.ru-RU.md) | [_日本語_](README.ja-JP.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **stack** is an abstract data type that serves 
 as a collection of elements, with two principal operations:

src/data-structures/stack/README.pt-BR.md

@@ -0,0 +1,29 @@
+# Stack
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md)
+
+Na ciência da computação, um **stack** é uma estrutura de dados abstrata
+que serve como uma coleção de elementos com duas operações principais:
+
+* **push**, pela qual adiciona um elemento à coleção, e
+* **pop**, pela qual remove o último elemento adicionado.
+
+A ordem em que os elementos saem de um _stack_ dá origem ao seu
+nome alternativo, LIFO (last in, first out). Adicionalmente, uma
+espiar a operação pode dar acesso ao topo sem modificar o _stack_.
+O nome "stack" para este tipo de estrutura vem da analogia de
+um conjunto de itens físicos empilhados uns sobre os outros,
+o que facilita retirar um item do topo da pilha, enquanto para chegar a
+um item mais profundo na pilha pode exigir a retirada de
+vários outros itens primeiro.
+
+Representação simples de um tempo de execução de pilha com operações
+_push_ e _pop_.
+
+![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)

src/data-structures/tree/README.md

@@ -1,5 +1,8 @@
 # Tree
 
+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md) | [_Português_](README.pt-BR.md)
+
 * [Binary Search Tree](binary-search-tree)
 * [AVL Tree](avl-tree)
 * [Red-Black Tree](red-black-tree)

src/data-structures/tree/README.pt-BR.md

@@ -0,0 +1,33 @@
+# Árvore (Tree)
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md)
+ 
+* [Árvore de Pesquisa Binária (Binary Search Tree)](binary-search-tree/README.pt-BR.md)
+* [Árvore AVL (AVL Tree)](avl-tree/README.pt-BR.md)
+* [Árvore Vermelha-Preta (Red-Black Tree)](red-black-tree/README.pt-BR.md)
+* [Árvore de Segmento (Segment Tree)](segment-tree/README.pt-BR.md) - com exemplos de consulta de intervalores min/max/sum
+* [Árvorem Fenwick (Fenwick Tree)](fenwick-tree/README.pt-BR.md) (Árvore Binária Indexada / Binary Indexed Tree)
+
+Na ciência da computação, uma **árvore** é uma estrutura de dados
+abstrada (ADT) amplamente utilizada - ou uma estrutura de dados
+implementando este ADT que simula uma estrutura hierarquica de árvore,
+com valor raíz e sub-árvores de filhos com um nó pai, representado
+como um conjunto de nós conectados.
+
+Uma estrutura de dados em árvore pode ser definida recursivamente como
+(localmente) uma coleção de nós (começando no nó raíz), aonde cada nó
+é uma estrutura de dados consistindo de um valor, junto com uma lista
+de referências aos nós (os "filhos"), com as restrições de que nenhuma
+referência é duplicada e nenhuma aponta para a raiz.
+
+Uma árvore não ordenada simples; neste diagrama, o nó rotulado como `7`
+possui dois filhos, rotulados como `2` e `6`, e um pai, rotulado como `2`.
+O nó raíz, no topo, não possui nenhum pai.
+
+![Tree](https://upload.wikimedia.org/wikipedia/commons/f/f7/Binary_tree.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Tree_(data_structure))
+- [YouTube](https://www.youtube.com/watch?v=oSWTXtMglKE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=8)

src/data-structures/tree/avl-tree/README.md

@@ -1,5 +1,8 @@
 # AVL Tree
 
+_Read this in other languages:_
+[_Português_](README.pt-BR.md)
+
 In computer science, an **AVL tree** (named after inventors 
 Adelson-Velsky and Landis) is a self-balancing binary search 
 tree. It was the first such data structure to be invented. 

src/data-structures/tree/avl-tree/README.pt-BR.md

@@ -0,0 +1,53 @@
+# Árvore AVL (AVL Tree)
+
+_Leia em outro idioma:_
+[_English_](README.md) 
+
+Na ciência da computação, uma **árvore AVL** (em homenagem aos
+inventores Adelson-Velsky e Landis) é uma árvore de pesquisa
+binária auto balanceada. Foi a primeira estrutura de dados a
+ser inventada.
+Em uma árvore AVL, as alturas de duas sub-árvores filhas
+de qualquer nó diferem no máximo em um; se a qualquer momento
+diferirem por em mais de um, um rebalanceamento é feito para
+restaurar esta propriedade.
+Pesquisa, inserção e exclusão possuem tempo `O(log n)` tanto na
+média quanto nos piores casos, onde `n` é o número de nós na
+árvore antes da operação. Inserções e exclusões podem exigir
+que a árvore seja reequilibrada por uma ou mais rotações.
+
+
+Animação mostrando a inserção de vários elementos em uma árvore AVL.
+Inclui as rotações de esquerda, direita, esquerda-direita e direita-esquerda.
+
+![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/f/fd/AVL_Tree_Example.gif)
+
+Árvore AVL com fatores de equilíbrio (verde)
+
+![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/a/ad/AVL-tree-wBalance_K.svg)
+
+### Rotações de Árvores AVL
+
+**Rotação Esquerda-Esquerda**
+
+![Left-Left Rotation](http://btechsmartclass.com/data_structures/ds_images/LL%20Rotation.png)
+
+**Rotação direita-direita**
+
+![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RR%20Rotation.png)
+
+**Rotação Esquerda-Direita**
+
+![Left-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/LR%20Rotation.png)
+
+**Rotação Direita-Esquerda**
+
+![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RL%20Rotation.png)
+
+## Referências
+
+* [Wikipedia](https://en.wikipedia.org/wiki/AVL_tree)
+* [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm)
+* [BTech](http://btechsmartclass.com/data_structures/avl-trees.html)
+* [AVL Tree Insertion on YouTube](https://www.youtube.com/watch?v=rbg7Qf8GkQ4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=12&)
+* [AVL Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html)

src/data-structures/tree/binary-search-tree/README.md

@@ -1,5 +1,8 @@
 # Binary Search Tree
 
+_Read this in other languages:_
+[_Português_](README.pt-BR.md)
+
 In computer science, **binary search trees** (BST), sometimes called 
 ordered or sorted binary trees, are a particular type of container: 
 data structures that store "items" (such as numbers, names etc.) 

src/data-structures/tree/binary-search-tree/README.pt-BR.md

@@ -0,0 +1,280 @@
+# Árvore de Pesquisa Binária (Binary Search Tree)
+
+_Leia em outro idioma:_
+[_English_](README.md) 
+
+Na ciência da computação **binary search trees** (BST), algumas vezes
+chamadas de árvores binárias ordenadas (_ordered or sorted binary trees_),
+é um tipo particular de container: estruturas de dados que armazenam
+"itens" (como números, nomes, etc.) na memória. Permite pesquisa rápida,
+adição e remoção de itens além de poder ser utilizado para implementar
+tanto conjuntos dinâmicos de itens ou, consultar tabelas que permitem
+encontrar um item por seu valor chave. E.g. encontrar o número de
+telefone de uma pessoa pelo seu nome.
+
+Árvore de Pesquisa Binária mantem seus valores chaves ordenados, para
+que uma pesquisa e outras operações possam usar o princípio da pesquisa
+binária: quando pesquisando por um valor chave na árvore (ou um lugar
+para inserir uma nova chave), eles atravessam a árvore da raiz para a folha,
+fazendo comparações com chaves armazenadas nos nós da árvore e decidindo então,
+com base nas comparações, continuar pesquisando nas sub-árvores a direita ou
+a esquerda. Em média isto significa que cara comparação permite as operações
+pular metade da árvore, para que então, cada pesquisa, inserção ou remoção
+consuma tempo proporcional ao logaritmo do número de itens armazenados na
+árvore. Isto é muito melhor do que um tempo linear necessário para encontrar
+itens por seu valor chave em um array (desorndenado - _unsorted_), mas muito
+mais lento do que operações similares em tableas de hash (_hash tables_).
+
+Uma pesquisa de árvore binária de tamanho 9 e profundidade 3, com valor 8
+na raíz.
+As folhas não foram desenhadas.
+
+
+![Binary Search Tree](https://upload.wikimedia.org/wikipedia/commons/d/da/Binary_search_tree.svg)
+
+## Pseudocódigo para Operações Básicas
+
+### Inserção
+
+```text
+insert(value)
+  Pre: value has passed custom type checks for type T
+  Post: value has been placed in the correct location in the tree
+  if root = ø
+    root ← node(value)
+  else
+    insertNode(root, value)
+  end if
+end insert
+```
+    
+```text
+insertNode(current, value)
+  Pre: current is the node to start from
+  Post: value has been placed in the correct location in the tree
+  if value < current.value
+    if current.left = ø
+      current.left ← node(value)
+    else
+      InsertNode(current.left, value)
+    end if
+  else
+    if current.right = ø
+      current.right ← node(value)
+    else
+      InsertNode(current.right, value)
+    end if
+  end if
+end insertNode
+```
+
+### Pesquisa
+
+```text
+contains(root, value)
+  Pre: root is the root node of the tree, value is what we would like to locate
+  Post: value is either located or not
+  if root = ø
+    return false
+  end if
+  if root.value = value
+    return true
+  else if value < root.value
+    return contains(root.left, value)
+  else
+    return contains(root.right, value)
+  end if
+end contains
+```
+    
+     
+### Remoção
+
+```text
+remove(value)
+  Pre: value is the value of the node to remove, root is the node of the BST
+      count is the number of items in the BST
+  Post: node with value is removed if found in which case yields true, otherwise false
+  nodeToRemove ← findNode(value)
+  if nodeToRemove = ø
+    return false
+  end if
+  parent ← findParent(value)
+  if count = 1
+    root ← ø
+  else if nodeToRemove.left = ø and nodeToRemove.right = ø
+    if nodeToRemove.value < parent.value
+      parent.left ←  nodeToRemove.right
+    else
+      parent.right ← nodeToRemove.right
+    end if
+  else if nodeToRemove.left != ø and nodeToRemove.right != ø
+    next ← nodeToRemove.right
+    while next.left != ø
+      next ← next.left
+    end while
+    if next != nodeToRemove.right
+      remove(next.value)
+      nodeToRemove.value ← next.value
+    else
+      nodeToRemove.value ← next.value
+      nodeToRemove.right ← nodeToRemove.right.right
+    end if
+  else
+    if nodeToRemove.left = ø
+      next ← nodeToRemove.right
+    else
+      next ← nodeToRemove.left
+    end if
+    if root = nodeToRemove
+      root = next
+    else if parent.left = nodeToRemove
+      parent.left = next
+    else if parent.right = nodeToRemove
+      parent.right = next
+    end if
+  end if
+  count ← count - 1
+  return true
+end remove
+```
+
+### Encontrar o Nó Pai
+
+```text
+findParent(value, root)
+  Pre: value is the value of the node we want to find the parent of
+       root is the root node of the BST and is != ø
+  Post: a reference to the prent node of value if found; otherwise ø
+  if value = root.value
+    return ø
+  end if
+  if value < root.value
+    if root.left = ø
+      return ø
+    else if root.left.value = value
+      return root
+    else
+      return findParent(value, root.left)
+    end if
+  else
+    if root.right = ø
+      return ø
+    else if root.right.value = value
+      return root
+    else
+      return findParent(value, root.right)
+    end if
+  end if
+end findParent
+```
+
+### Encontrar um Nó
+
+```text
+findNode(root, value)
+  Pre: value is the value of the node we want to find the parent of
+       root is the root node of the BST
+  Post: a reference to the node of value if found; otherwise ø
+  if root = ø
+    return ø
+  end if
+  if root.value = value
+    return root
+  else if value < root.value
+    return findNode(root.left, value)
+  else
+    return findNode(root.right, value)
+  end if
+end findNode
+```
+    
+### Encontrar Mínimo
+
+```text
+findMin(root)
+  Pre: root is the root node of the BST
+    root = ø
+  Post: the smallest value in the BST is located
+  if root.left = ø
+    return root.value
+  end if
+  findMin(root.left)
+end findMin
+```
+    
+### Encontrar Máximo
+
+```text
+findMax(root)
+  Pre: root is the root node of the BST
+    root = ø
+  Post: the largest value in the BST is located
+  if root.right = ø
+    return root.value
+  end if
+  findMax(root.right)
+end findMax
+```
+    
+### Traversal
+
+#### Na Ordem Traversal (InOrder Traversal)
+
+```text
+inorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in inorder
+  if root = ø
+    inorder(root.left)
+    yield root.value
+    inorder(root.right)
+  end if
+end inorder
+```
+
+#### Pré Ordem Traversal (PreOrder Traversal)
+
+```text
+preorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in preorder
+  if root = ø
+    yield root.value
+    preorder(root.left)
+    preorder(root.right)
+  end if
+end preorder
+```
+   
+#### Pós Ordem Traversal (PostOrder Traversal)
+
+```text
+postorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in postorder
+  if root = ø
+    postorder(root.left)
+    postorder(root.right)
+    yield root.value
+  end if
+end postorder
+```
+     
+## Complexidades
+
+### Complexidade de Tempo
+
+| Access    | Search    | Insertion | Deletion  |
+| :-------: | :-------: | :-------: | :-------: |
+| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
+
+### Complexidade de Espaço
+
+O(n)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Binary_search_tree)
+- [Inserting to BST on YouTube](https://www.youtube.com/watch?v=wcIRPqTR3Kc&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=9&t=0s)
+- [BST Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/BST.html)

src/data-structures/tree/fenwick-tree/README.md

@@ -1,5 +1,8 @@
 # Fenwick Tree / Binary Indexed Tree
 
+_Leia em outro idioma:_
+[_English_](README.pt-BR.md) 
+
 A **Fenwick tree** or **binary indexed tree** is a data 
 structure that can efficiently update elements and 
 calculate prefix sums in a table of numbers.

src/data-structures/tree/fenwick-tree/README.pt-BR.md

@@ -0,0 +1,45 @@
+# Árvore Fenwick / Árvore Binária Indexada (Fenwick Tree / Binary Indexed Tree)
+
+_Read this in other languages:_
+[_Português_](README.md)
+
+Uma **árvore Fenwick** ou **árvore binária indexada** é um tipo de
+estrutura de dados que consegue eficiemente atualizar elementos e
+calcular soma dos prefixos em uma tabela de números.
+
+Quando comparado com um _flat array_ de números, a árvore Fenwick
+alcança um balanceamento muito melhor entre duas operações: atualização
+(_update_) do elemento e cálculo da soma do prefíxo. Em uma _flar array_
+de `n` números, você pode tanto armazenar elementos quando a soma dos
+prefixos. Em ambos os casos, computar a soma dos prefixos requer ou 
+atualizar um array de elementos também requerem um tempo linear, contudo,
+a demais operações podem ser realizadas com tempo constante.
+A árvore Fenwick permite ambas as operações serem realizadas com tempo
+`O(log n)`.
+
+Isto é possível devido a representação dos números como uma árvore, aonde
+os valores de cada nó é a soma dos números naquela sub-árvore. A estrutura
+de árvore permite operações a serem realizadas consumindo somente acessos
+a nós em `O(log n)`.
+
+## Implementação de Nós
+
+Árvore Binária Indexada é representada como um _array_. Em cada nó da Árvore
+Binária Indexada armazena a soma de alguns dos elementos de uma _array_
+fornecida. O tamanho da Árvore Binária Indexada é igual a `n` aonde `n` é o
+tamanho do _array_ de entrada. Na presente implementação nós utilizados o
+tamanho `n+1` para uma implementação fácil. Todos os índices são baseados em 1. 
+
+![Binary Indexed Tree](https://www.geeksforgeeks.org/wp-content/uploads/BITSum.png)
+
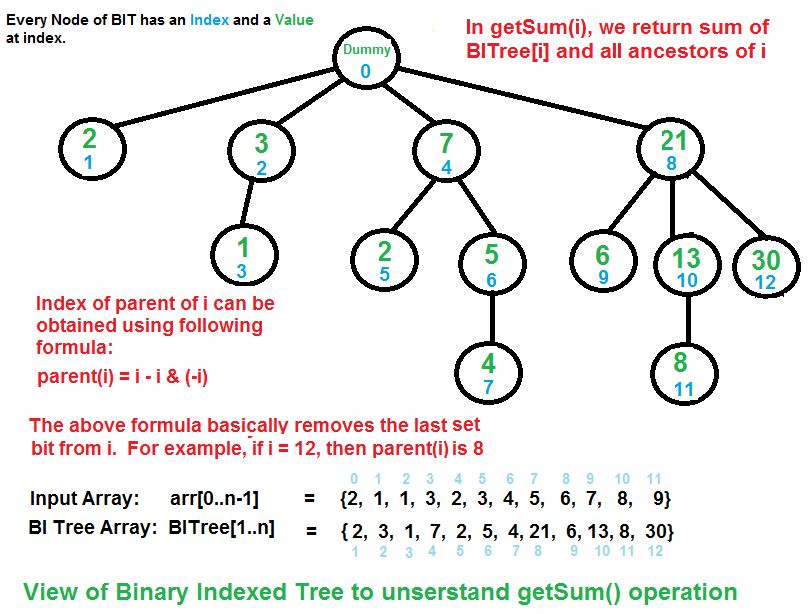
+Na imagem abaixo você pode ver o exemplo animado da criação de uma árvore
+binária indexada para o _array_ `[1, 2, 3, 4, 5]`, sendo inseridos um após
+o outro.
+
+![Fenwick Tree](https://upload.wikimedia.org/wikipedia/commons/d/dc/BITDemo.gif)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Fenwick_tree)
+- [GeeksForGeeks](https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/)
+- [YouTube](https://www.youtube.com/watch?v=CWDQJGaN1gY&index=18&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/tree/red-black-tree/README.md

@@ -1,5 +1,8 @@
 # Red–Black Tree
 
+_Leia em outro idioma:_
+[_English_](README.pt-BR.md) 
+
 A **red–black tree** is a kind of self-balancing binary search 
 tree in computer science. Each node of the binary tree has 
 an extra bit, and that bit is often interpreted as the 

src/data-structures/tree/red-black-tree/README.pt-BR.md

@@ -0,0 +1,95 @@
+# Árvore Vermelha-Preta (Red-Black Tree)
+
+_Read this in other languages:_
+[_Português_](README.md)
+
+Uma **árvore vermelha-preta** é um tipo de árvore de pesquisa
+binária auto balanceada na ciência da computação. Cada nó da 
+árvore binária possui um _bit_ extra, e este _bit_ é frequentemente
+interpretado com a cor (vermelho ou preto) do nó. Estas cores de _bits_
+são utilizadas para garantir que a árvore permanece aproximadamente
+equilibrada durante as operações de inserções e remoções.
+
+O equilíbrio é preservado através da pintura de cada nó da árvore com
+uma das duas cores, de maneira que satisfaça certas propriedades, das
+quais restringe nos piores dos casos, o quão desequilibrada a árvore
+pode se tornar. Quando a árvore é modificada, a nova árvore é
+subsequentemente reorganizada e repintada para restaurar as
+propriedades de coloração. As propriedades são designadas de tal modo que
+esta reorganização e nova pintura podem ser realizadas eficientemente.
+
+O balanceamento de uma árvore não é perfeito, mas é suficientemente bom
+para permitir e garantir uma pesquisa no tempo `O(log n)`, aonde `n` é o
+número total de elementos na árvore.
+Operações de inserções e remoções, juntamente com a reorganização e 
+repintura da árvore, também são executados no tempo `O (log n)`.
+
+Um exemplo de uma árvore vermalha-preta:
+
+![red-black tree](https://upload.wikimedia.org/wikipedia/commons/6/66/Red-black_tree_example.svg)
+
+## Propriedades
+
+Em adição aos requerimentos impostos pela árvore de pesquisa binária,
+as seguintes condições devem ser satisfeitas pela árvore vermelha-preta:
+
+- Cada nó é tanto vermelho ou preto.
+- O nó raíz é preto. Esta regra algumas vezes é omitida.
+Tendo em vista que a raíz pode sempre ser alterada de vermelho para preto,
+mas não de preto para vermelho, esta regra tem pouco efeito na análise.
+- Todas as folhas (Nulo/NIL) são pretas.
+- Caso um nó é vermelho, então seus filhos serão pretos.
+- Cada caminho de um determinado nó para qualquer um dos seus nós nulos (NIL)
+descendentes contém o mesmo número de nós pretos.
+
+Algumas definições: o número de nós pretos da raiz até um nó é a
+**profundidade preta**(_black depth_) do nó; o número uniforme de nós pretos
+em todos os caminhos da raíz até as folhas são chamados de **altura negra**
+(_black-height_) da árvore vermelha-preta.
+
+Essas restrições impõem uma propriedade crítica de árvores vermelhas e pretas:
+_o caminho da raiz até a folha mais distante não possui mais que o dobro do
+comprimento do caminho da raiz até a folha mais próxima_.
+O resultado é que a árvore é grosseiramente balanceada na altura.
+
+Tendo em vista que operações como inserções, remoção e pesquisa de valores
+requerem nos piores dos casos um tempo proporcional a altura da ávore,
+este limite superior teórico na altura permite que as árvores vermelha-preta
+sejam eficientes no pior dos casos, ao contrário das árvores de busca binária
+comuns.
+
+## Balanceamento durante a inserção
+
+### Se o tio é VERMELHO
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase2.png)
+
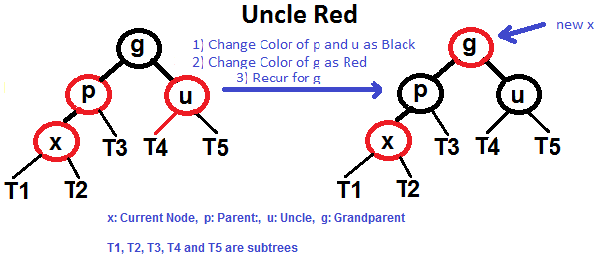
+### Se o tio é PRETO
+
+- Caso Esquerda Esquerda (`p` é o filho a esquerda de `g` e `x`, é o filho a esquerda de `p`)
+- Caso Esquerda Direita (`p` é o filho a esquerda de `g` e `x`, é o filho a direita de `p`)
+- Caso Direita Direita (`p` é o filho a direita de `g` e `x`, é o filho da direita de `p`)
+- Caso Direita Esqueda (`p` é o filho a direita de `g` e `x`, é o filho a esquerda de `p`)
+
+#### Caso Esquerda Esquerda (Veja g, p e x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3a1.png)
+
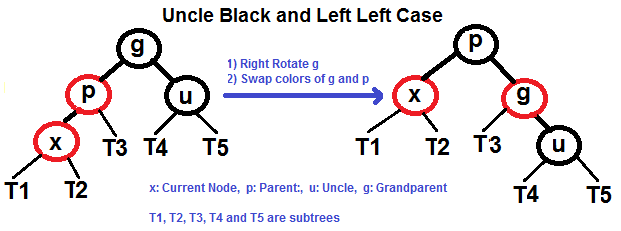
+#### Caso Esquerda Direita (Veja g, p e x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3b.png)
+
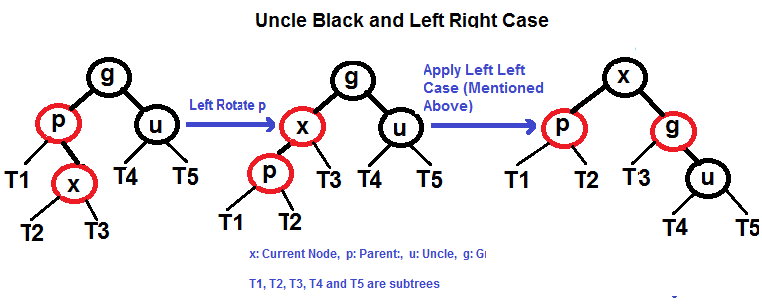
+#### Caso Direita Direita (Veja g, p e x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3c.png)
+
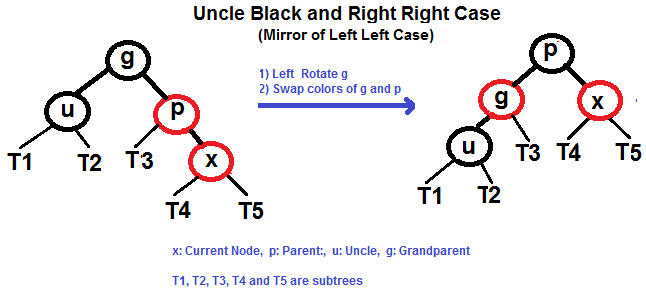
+#### Caso Direita Esquerda (Veja g, p e x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3d.png)
+
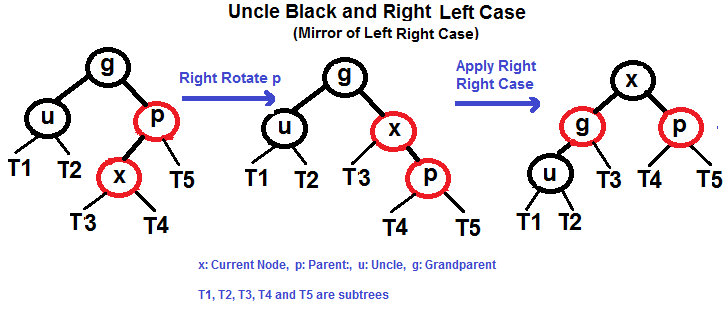
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree)
+- [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63)
+- [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64)
+- [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/)
+- [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)

src/data-structures/tree/segment-tree/README.md

@@ -1,5 +1,8 @@
 # Segment Tree
 
+_Leia em outro idioma:_
+[_English_](README.pt-BR.md) 
+
 In computer science, a **segment tree** also known as a statistic tree 
 is a tree data structure used for storing information about intervals, 
 or segments. It allows querying which of the stored segments contain 

src/data-structures/tree/segment-tree/README.pt-BR.md

@@ -0,0 +1,51 @@
+# Árvore de Segmento (Segment Tree)
+
+_Read this in other languages:_
+[_Português_](README.md)
+
+Na ciência da computação, uma **árvore de segmento** também conhecida como
+árvore estatística é uma árvore de estrutura de dados utilizadas para
+armazenar informações sobre intervalores ou segmentos. Ela permite pesquisas
+no qual os segmentos armazenados contém um ponto fornecido. Isto é,
+em princípio, uma estrutura estática; ou seja, é uma estrutura que não pode
+ser modificada depois de inicializada. Uma estrutura de dados similar é a
+árvore de intervalos.
+
+Uma árvore de segmento é uma árvore binária. A raíz da árvore representa a
+_array_ inteira. Os dois filhos da raíz representam a primeira e a segunda
+metade da _array_. Similarmente, os filhos de cada nó correspondem ao número
+das duas metadas da _array_ correspondente do nó.
+
+Nós construímos a árvore debaixo para cima, com o valor de cada nó sendo o 
+"mínimo" (ou qualquer outra função) dos valores de seus filhos. Isto consumirá
+tempo `O(n log n)`. O número de oprações realizadas é equivalente a altura da
+árvore, pela qual consome tempo `O(log n)`. Para fazer consultas de intervalos,
+cada nó divide a consulta em duas partes, sendo uma sub consulta para cada filho.
+Se uma pesquisa contém todo o _subarray_ de um nó, nós podemos utilizar do valor
+pré-calculado do nó. Utilizando esta otimização, nós podemos provar que somente
+operações mínimas `O(log n)` são realizadas.
+
+![Min Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/RangeMinimumQuery.png)
+
+![Sum Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/segment-tree1.png)
+
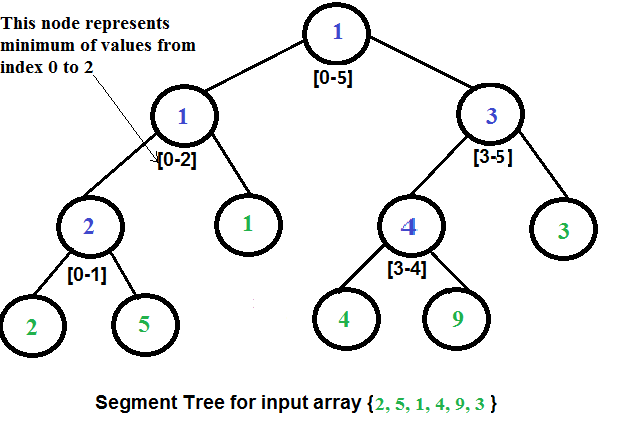
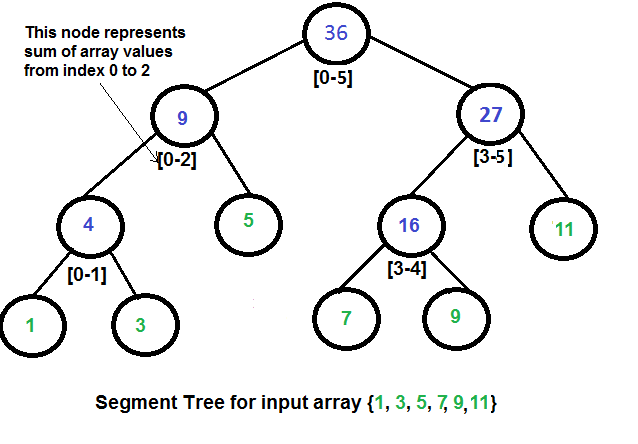
+## Aplicação
+
+Uma árvore de segmento é uma estrutura de dados designada a realizar
+certas operações de _array_ eficientemente, especialmente aquelas envolvendo
+consultas de intervalos.
+
+Aplicações da árvore de segmentos são nas áreas de computação geométrica e
+sistemas de informação geográficos.
+
+A implementação atual da Árvore de Segmentos implica que você pode passar
+qualquer função binária (com dois parâmetros de entradas) e então, você
+será capaz de realizar consultas de intervalos para uma variedade de funções.
+Nos testes você poderá encontrar exemplos realizando `min`, `max` e consultas de
+intervalo `sam` na árvore segmentada (SegmentTree).
+ 
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Segment_tree)
+- [YouTube](https://www.youtube.com/watch?v=ZBHKZF5w4YU&index=65&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [GeeksForGeeks](https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/)

src/data-structures/trie/README.md

@@ -1,8 +1,7 @@
 # Trie
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | [_Português_](README.pt-BR.md)
 
 In computer science, a **trie**, also called digital tree and sometimes 
 radix tree or prefix tree (as they can be searched by prefixes), 

src/data-structures/trie/README.pt-BR.md

@@ -0,0 +1,28 @@
+# Trie
+
+_Leia em outro idioma:_
+[_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) 
+
+Na ciência da computação, uma **trie**, também chamada de árvore digital (digital tree)
+e algumas vezes de _radix tree_ ou _prefix tree_ (tendo em vista que eles
+podem ser pesquisados por prefixos), é um tipo de árvore de pesquisa, uma
+uma estrutura de dados de árvore ordenada que é usado para armazenar um 
+conjunto dinâmico ou matriz associativa onde as chaves são geralmente _strings_.
+Ao contrário de uma árvore de pesquisa binária (binary search tree),
+nenhum nó na árvore armazena a chave associada a esse nó; em vez disso,
+sua posição na árvore define a chave com a qual ela está associada.
+Todos os descendentes de um nó possuem em comum o prefixo de uma _string_
+associada com aquele nó, e a raiz é associada com uma _string_ vazia.
+Valores não são necessariamente associados a todos nós. Em vez disso,
+os valores tendem a ser associados apenas a folhas e com alguns nós
+internos que correspondem a chaves de interesse.
+
+Para a apresentação otimizada do espaço da árvore de prefixo (_prefix tree_),
+veja árvore de prefixo compacto.
+
+![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Trie)
+- [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s)