mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-08-01 08:46:25 +08:00
111 lines
3.8 KiB
Markdown
111 lines
3.8 KiB
Markdown
# [1738. Find Kth Largest XOR Coordinate Value](https://leetcode.com/problems/find-kth-largest-xor-coordinate-value/)
|
||
|
||
|
||
## 题目
|
||
|
||
You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
|
||
|
||
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
|
||
|
||
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
|
||
|
||
**Example 1:**
|
||
|
||
```
|
||
Input: matrix = [[5,2],[1,6]], k = 1
|
||
Output: 7
|
||
Explanation: The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
|
||
```
|
||
|
||
**Example 2:**
|
||
|
||
```
|
||
Input: matrix = [[5,2],[1,6]], k = 2
|
||
Output: 5
|
||
Explanation:The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
|
||
```
|
||
|
||
**Example 3:**
|
||
|
||
```
|
||
Input: matrix = [[5,2],[1,6]], k = 3
|
||
Output: 4
|
||
Explanation: The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
|
||
```
|
||
|
||
**Example 4:**
|
||
|
||
```
|
||
Input: matrix = [[5,2],[1,6]], k = 4
|
||
Output: 0
|
||
Explanation: The value of coordinate (1,1) is 5 XOR 2 XOR 1 XOR 6 = 0, which is the 4th largest value.
|
||
```
|
||
|
||
**Constraints:**
|
||
|
||
- `m == matrix.length`
|
||
- `n == matrix[i].length`
|
||
- `1 <= m, n <= 1000`
|
||
- `0 <= matrix[i][j] <= 10^6`
|
||
- `1 <= k <= m * n`
|
||
|
||
## 题目大意
|
||
|
||
给你一个二维矩阵 matrix 和一个整数 k ,矩阵大小为 m x n 由非负整数组成。矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j](下标从 0 开始计数)执行异或运算得到。请你找出 matrix 的所有坐标中第 k 大的值(k 的值从 1 开始计数)。
|
||
|
||
## 解题思路
|
||
|
||
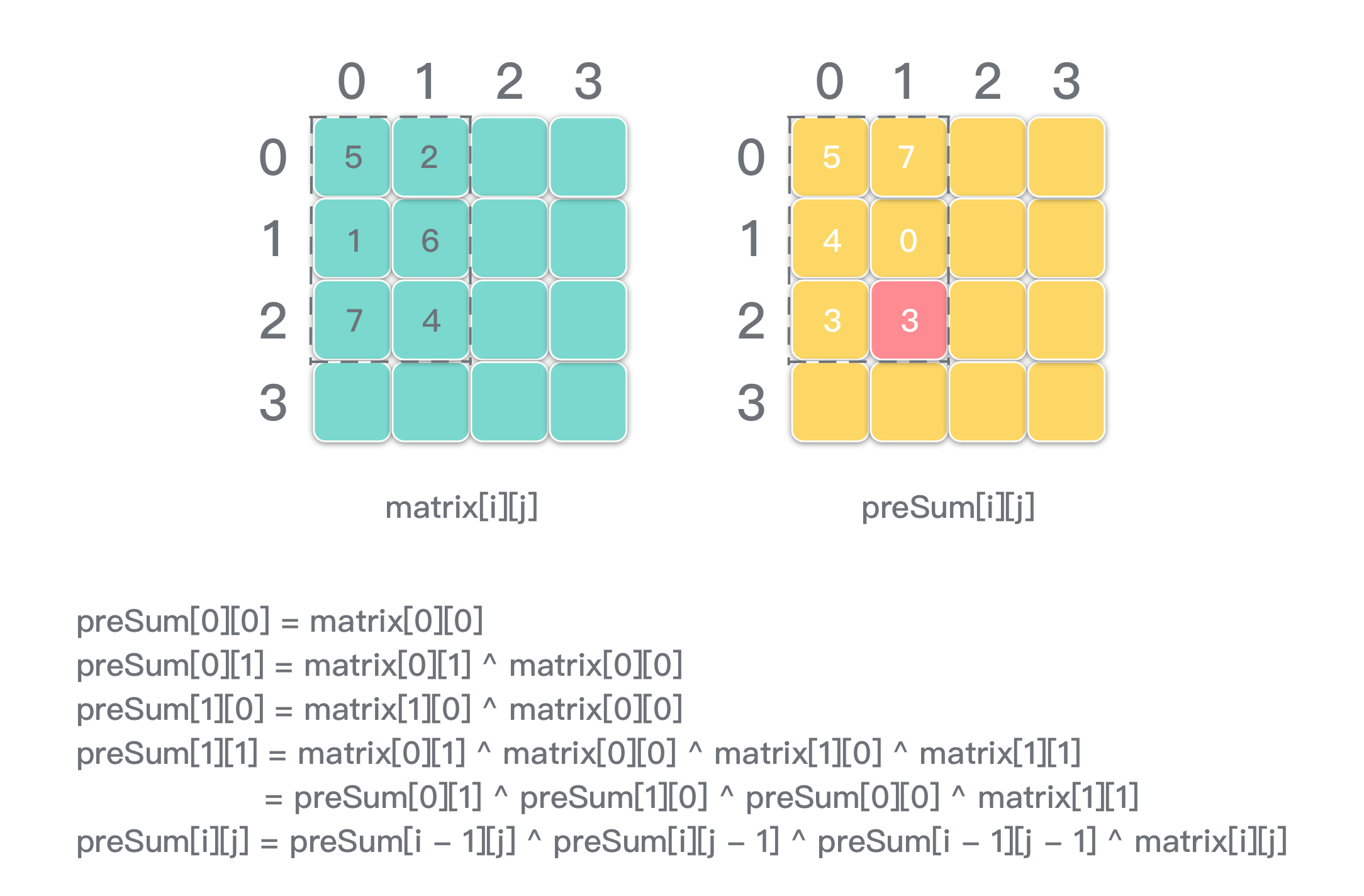
- 区间异或结果类比于区间二维前缀和。只不过需要注意 x^x = 0 这一性质。举例:
|
||
|
||
|
||
|
||
通过简单推理,可以得出区间二维前缀和 preSum 的递推式。具体代码见解法二。
|
||
|
||
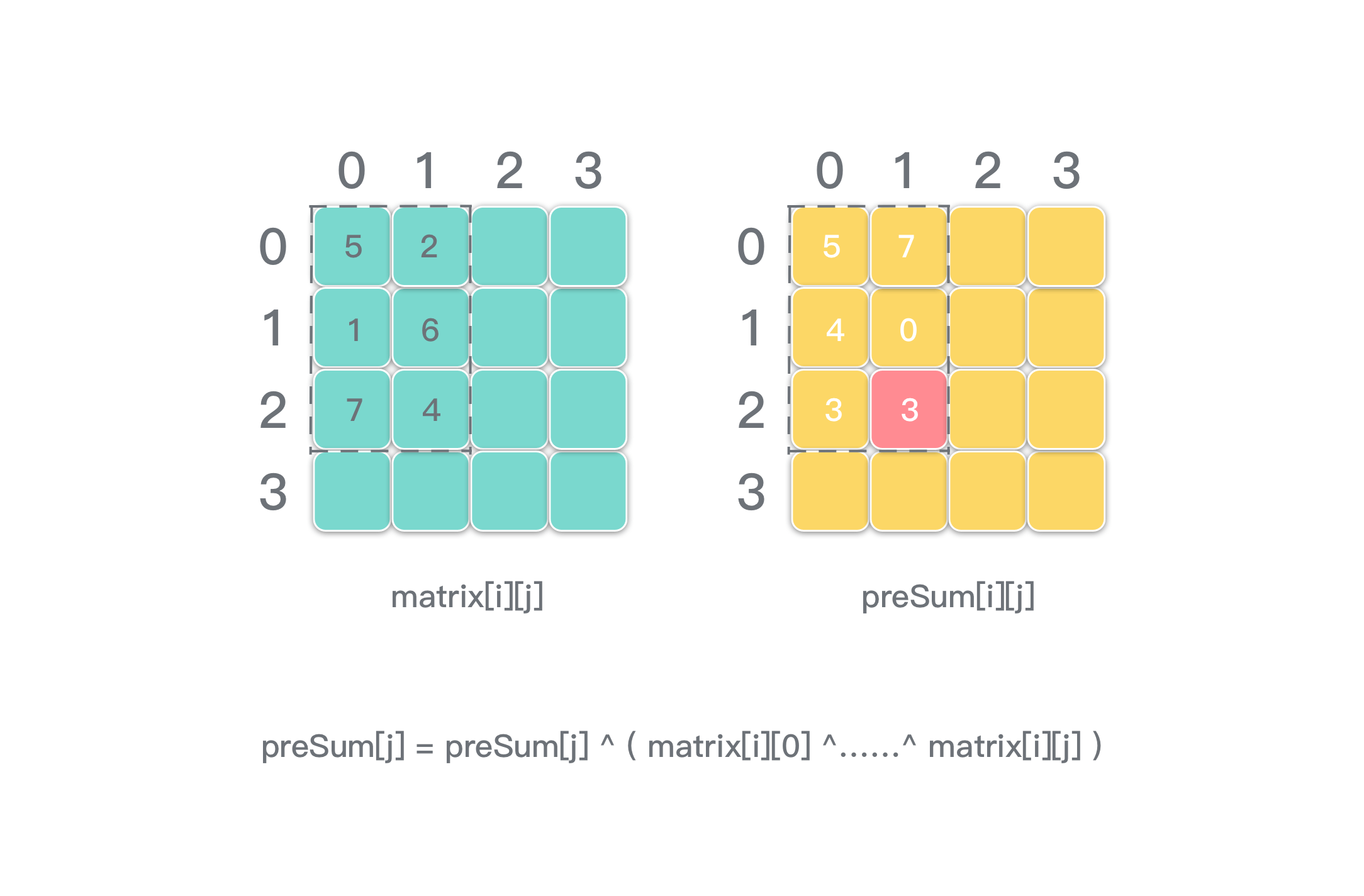
- 上面的解法中,preSum 用二维数组计算的。能否再优化空间复杂度,降低成 O(n)?答案是可以的。通过观察可以发现。preSum 可以按照一行一行来生成。先生成 preSum 前一行,下一行生成过程中会用到前一行的信息,异或计算以后,可以覆盖原数据(前一行的信息),对之后的计算没有影响。这个优化空间复杂度的方法和优化 DP 空间复杂度是完全一样的思路和方法。
|
||
|
||
|
||
|
||
具体代码见解法一。
|
||
|
||
- 计算出了 preSum,还需要考虑如何输出第 k 大的值。有 3 种做法,第一种是排序,第二种是优先队列,第三种是第 215 题中的 O(n) 的 partition 方法。时间复杂度最低的当然是 O(n)。但是经过实际测试,runtime 最优的是排序的方法。所以笔者以下两种方法均采用了排序的方法。
|
||
|
||
## 代码
|
||
|
||
```go
|
||
package leetcode
|
||
|
||
import "sort"
|
||
|
||
// 解法一 压缩版的前缀和
|
||
func kthLargestValue(matrix [][]int, k int) int {
|
||
if len(matrix) == 0 || len(matrix[0]) == 0 {
|
||
return 0
|
||
}
|
||
res, prefixSum := make([]int, 0, len(matrix)*len(matrix[0])), make([]int, len(matrix[0]))
|
||
for i := range matrix {
|
||
line := 0
|
||
for j, v := range matrix[i] {
|
||
line ^= v
|
||
prefixSum[j] ^= line
|
||
res = append(res, prefixSum[j])
|
||
}
|
||
}
|
||
sort.Ints(res)
|
||
return res[len(res)-k]
|
||
}
|
||
|
||
// 解法二 前缀和
|
||
func kthLargestValue1(matrix [][]int, k int) int {
|
||
nums, prefixSum := []int{}, make([][]int, len(matrix)+1)
|
||
prefixSum[0] = make([]int, len(matrix[0])+1)
|
||
for i, row := range matrix {
|
||
prefixSum[i+1] = make([]int, len(matrix[0])+1)
|
||
for j, val := range row {
|
||
prefixSum[i+1][j+1] = prefixSum[i+1][j] ^ prefixSum[i][j+1] ^ prefixSum[i][j] ^ val
|
||
nums = append(nums, prefixSum[i+1][j+1])
|
||
}
|
||
}
|
||
sort.Ints(nums)
|
||
return nums[len(nums)-k]
|
||
}
|
||
``` |