LeetCode-Go/website/content/ChapterTwo/Backtracking.md

---
title: Backtracking
type: docs
---

# Backtracking

![](https://img.halfrost.com/Leetcode/Backtracking.png)

- 排列问题 Permutations。第 46 题，第 47 题。第 60 题，第 526 题，第 996 题。
- 组合问题 Combination。第 39 题，第 40 题，第 77 题，第 216 题。
- 排列和组合杂交问题。第 1079 题。
- N 皇后终极解法(二进制解法)。第 51 题，第 52 题。
- 数独问题。第 37 题。
- 四个方向搜索。第 79 题，第 212 题，第 980 题。
- 子集合问题。第 78 题，第 90 题。
- Trie。第 208 题，第 211 题。
- BFS 优化。第 126 题，第 127 题。
- DFS 模板。(只是一个例子，不对应任何题)

```go
func combinationSum2(candidates []int, target int) [][]int {
	if len(candidates) == 0 {
		return [][]int{}
	}
	c, res := []int{}, [][]int{}
	sort.Ints(candidates)
	findcombinationSum2(candidates, target, 0, c, &res)
	return res
}

func findcombinationSum2(nums []int, target, index int, c []int, res *[][]int) {
	if target == 0 {
		b := make([]int, len(c))
		copy(b, c)
		*res = append(*res, b)
		return
	}
	for i := index; i < len(nums); i++ {
		if i > index && nums[i] == nums[i-1] { // 这里是去重的关键逻辑
			continue
		}
		if target >= nums[i] {
			c = append(c, nums[i])
			findcombinationSum2(nums, target-nums[i], i+1, c, res)
			c = c[:len(c)-1]
		}
	}
}
```
- BFS 模板。(只是一个例子，不对应任何题)

```go
func updateMatrix_BFS(matrix [][]int) [][]int {
	res := make([][]int, len(matrix))
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return res
	}
	queue := make([][]int, 0)
	for i, _ := range matrix {
		res[i] = make([]int, len(matrix[0]))
		for j, _ := range res[i] {
			if matrix[i][j] == 0 {
				res[i][j] = -1
				queue = append(queue, []int{i, j})
			}
		}
	}
	level := 1
	for len(queue) > 0 {
		size := len(queue)
		for size > 0 {
			size -= 1
			node := queue[0]
			queue = queue[1:]
			i, j := node[0], node[1]
			for _, direction := range [][]int{{-1, 0}, {1, 0}, {0, 1}, {0, -1}} {
				x := i + direction[0]
				y := j + direction[1]
				if x < 0 || x >= len(matrix) || y < 0 || y >= len(matrix[0]) || res[x][y] < 0 || res[x][y] > 0 {
					continue
				}
				res[x][y] = level
				queue = append(queue, []int{x, y})
			}
		}
		level++
	}
	for i, row := range res {
		for j, cell := range row {
			if cell == -1 {
				res[i][j] = 0
			}
		}
	}
	return res
}
```

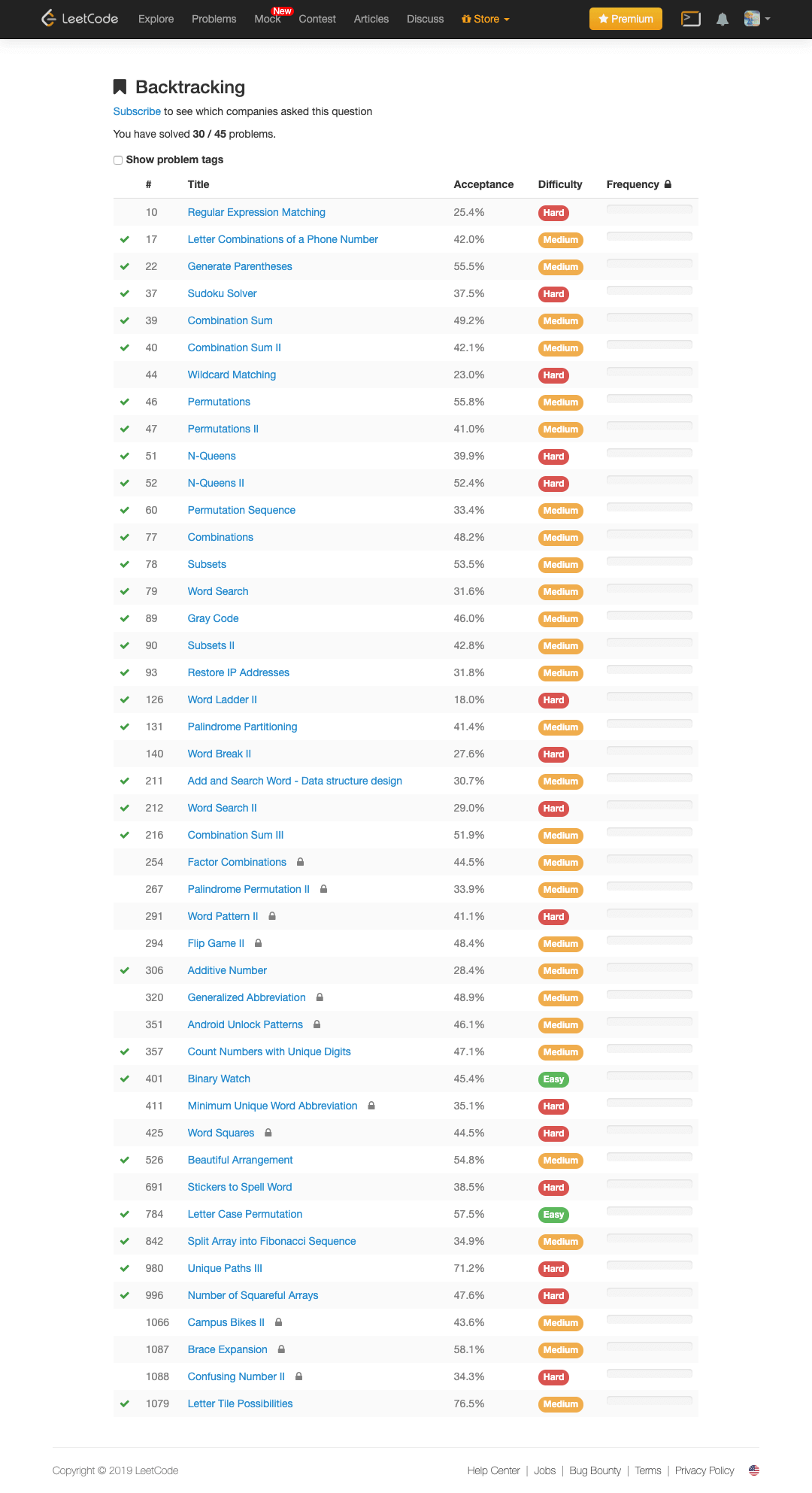
| Title | Solution | Difficulty | Time | Space |收藏| 
| ----- | :--------: | :----------: | :----: | :-----: | :-----: |
|17. Letter Combinations of a Phone Number | [Go]({{< relref "/ChapterFour/0017.Letter-Combinations-of-a-Phone-Number.md" >}})| Medium | O(log n)| O(1)||
|22. Generate Parentheses| [Go]({{< relref "/ChapterFour/0022.Generate-Parentheses.md" >}})| Medium | O(log n)| O(1)||
|37. Sudoku Solver  | [Go]({{< relref "/ChapterFour/0037.Sudoku-Solver.md" >}})| Hard | O(n^2)| O(n^2)|❤️|
|39. Combination Sum | [Go]({{< relref "/ChapterFour/0039.Combination-Sum.md" >}})| Medium | O(n log n)| O(n)||
|40. Combination Sum II | [Go]({{< relref "/ChapterFour/0040.Combination-Sum-II.md" >}})| Medium | O(n log n)| O(n)||
|46. Permutations | [Go]({{< relref "/ChapterFour/0046.Permutations.md" >}})| Medium | O(n)| O(n)|❤️|
|47. Permutations II | [Go]({{< relref "/ChapterFour/0047.Permutations-II.md" >}})| Medium | O(n^2)| O(n)|❤️|
|51. N-Queens | [Go]({{< relref "/ChapterFour/0051.N-Queens.md" >}})| Hard | O(n^2)| O(n)|❤️|
|52. N-Queens II  | [Go]({{< relref "/ChapterFour/0052.N-Queens-II.md" >}})| Hard | O(n^2)| O(n)|❤️|
|60. Permutation Sequence  | [Go]({{< relref "/ChapterFour/0060.Permutation-Sequence.md" >}})| Medium | O(n log n)| O(1)||
|77. Combinations  | [Go]({{< relref "/ChapterFour/0077.Combinations.md" >}})| Medium | O(n)| O(n)|❤️|
|78. Subsets   | [Go]({{< relref "/ChapterFour/0078.Subsets.md" >}})| Medium | O(n^2)| O(n)|❤️|
|79. Word Search  | [Go]({{< relref "/ChapterFour/0079.Word-Search.md" >}})| Medium | O(n^2)| O(n^2)|❤️|
|89. Gray Codes | [Go]({{< relref "/ChapterFour/0089.Gray-Code.md" >}})| Medium | O(n)| O(1)||
|90. Subsets II  | [Go]({{< relref "/ChapterFour/0090.Subsets-II.md" >}})| Medium | O(n^2)| O(n)|❤️|
|93. Restore IP Addresses | [Go]({{< relref "/ChapterFour/0093.Restore-IP-Addresses.md" >}})| Medium | O(n)| O(n)|❤️|
|126. Word Ladder II | [Go]({{< relref "/ChapterFour/0126.Word-Ladder-II.md" >}})| Hard | O(n)| O(n^2)|❤️|
|131. Palindrome Partitioning | [Go]({{< relref "/ChapterFour/0131.Palindrome-Partitioning.md" >}})| Medium | O(n)| O(n^2)|❤️|
|211. Add and Search Word - Data structure design | [Go]({{< relref "/ChapterFour/0211.Add-and-Search-Word---Data-structure-design.md" >}})| Medium | O(n)| O(n)|❤️|
|212. Word Search II | [Go]({{< relref "/ChapterFour/0212.Word-Search-II.md" >}})| Hard | O(n^2)| O(n^2)|❤️|
|216. Combination Sum III | [Go]({{< relref "/ChapterFour/0216.Combination-Sum-III.md" >}})| Medium | O(n)| O(1)|❤️|
|306. Additive Number  | [Go]({{< relref "/ChapterFour/0306.Additive-Number.md" >}})| Medium | O(n^2)| O(1)|❤️|
|357. Count Numbers with Unique Digits  | [Go]({{< relref "/ChapterFour/0357.Count-Numbers-with-Unique-Digits.md" >}})| Medium | O(1)| O(1)||
|401. Binary Watch | [Go]({{< relref "/ChapterFour/0401.Binary-Watch.md" >}})| Easy | O(1)| O(1)||
|526. Beautiful Arrangement | [Go]({{< relref "/ChapterFour/0526.Beautiful-Arrangement.md" >}})| Medium | O(n^2)| O(1)|❤️|
|784. Letter Case Permutation | [Go]({{< relref "/ChapterFour/0784.Letter-Case-Permutation.md" >}})| Easy | O(n)| O(n)||
|842. Split Array into Fibonacci Sequence  | [Go]({{< relref "/ChapterFour/0842.Split-Array-into-Fibonacci-Sequence.md" >}})| Medium | O(n^2)| O(1)|❤️|
|980. Unique Paths III | [Go]({{< relref "/ChapterFour/0980.Unique-Paths-III.md" >}})| Hard | O(n log n)| O(n)||
|996. Number of Squareful Arrays | [Go]({{< relref "/ChapterFour/0996.Number-of-Squareful-Arrays.md" >}})| Hard | O(n log n)| O(n) ||
|1079. Letter Tile Possibilities | [Go]({{< relref "/ChapterFour/1079.Letter-Tile-Possibilities.md" >}})| Medium | O(n^2)| O(1)|❤️|
|---------------------------------------|---------------------------------|--------------------------|-----------------------|-----------|--------|