LeetCode-Go/website/content/ChapterFour/0069.Sqrtx.md

69. Sqrt(x)

题目

Implement int sqrt(int x).

Compute and return the square root of x, where x is guaranteed to be a non-negative integer.

Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.

Example 1:

Input: 4
Output: 2

Example 2:

Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since 
             the decimal part is truncated, 2 is returned.

题目大意

实现 int sqrt(int x) 函数。计算并返回 x 的平方根，其中 x 是非负整数。由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

解题思路

• 题目要求求出根号 x

• 根据题意，根号 x 的取值范围一定在 [0,x] 之间，这个区间内的值是递增有序的，有边界的，可以用下标访问的，满足这三点正好也就满足了二分搜索的 3 大条件。所以解题思路一，二分搜索。

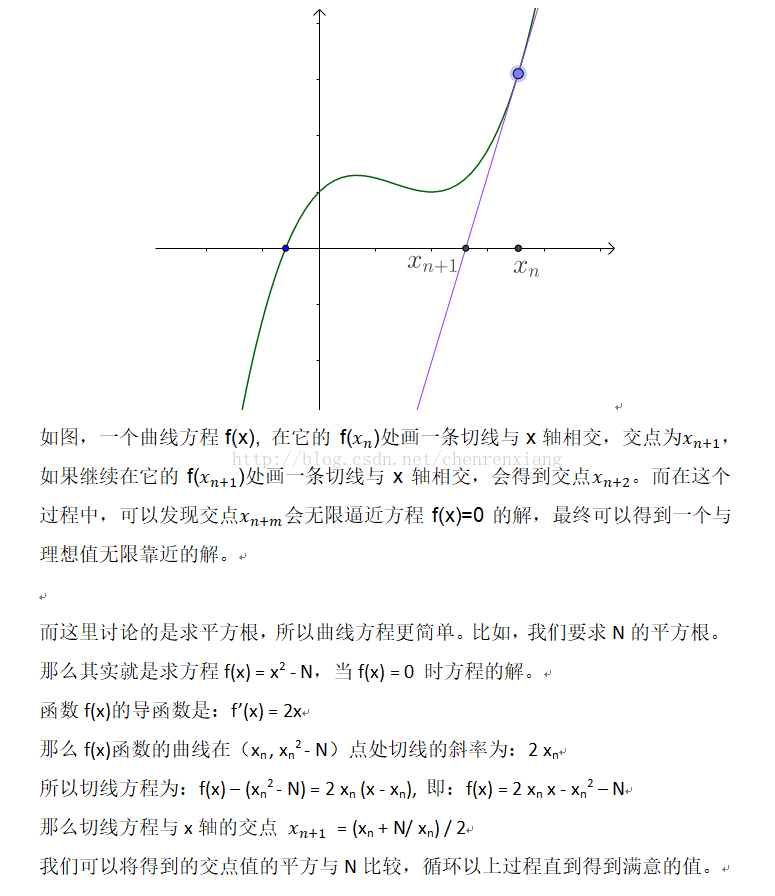
• 解题思路二，牛顿迭代法。求根号 x，即求满足 x^2 - n = 0 方程的所有解。

  

代码

package leetcode

// 解法一 二分
func mySqrt(x int) int {
	if x == 0 {
		return 0
	}
	left, right, res := 1, x, 0
	for left <= right {
		mid := left + ((right - left) >> 1)
		if mid < x/mid {
			left = mid + 1
			res = mid
		} else if mid == x/mid {
			return mid
		} else {
			right = mid - 1
		}
	}
	return res
}

// 解法二 牛顿迭代法 https://en.wikipedia.org/wiki/Integer_square_root
func mySqrt1(x int) int {
	r := x
	for r*r > x {
		r = (r + x/r) / 2
	}
	return r
}

// 解法三 Quake III 游戏引擎中有一种比 STL 的 sqrt 快 4 倍的实现 https://en.wikipedia.org/wiki/Fast_inverse_square_root
// float Q_rsqrt( float number )
// {
// 	long i;
// 	float x2, y;
// 	const float threehalfs = 1.5F;

// 	x2 = number * 0.5F;
// 	y  = number;
// 	i  = * ( long * ) &y;                       // evil floating point bit level hacking
// 	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
// 	y  = * ( float * ) &i;
// 	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
// //	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed
// 	return y;
// }