mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-22 17:02:21 +08:00
275 lines
13 KiB
Markdown
275 lines
13 KiB
Markdown
---
|
||
title: 3.5 Binary Indexed Tree
|
||
type: docs
|
||
weight: 5
|
||
---
|
||
|
||
# 树状数组 Binary Indexed Tree (二叉索引树)
|
||
|
||
树状数组或二叉索引树(英语:Binary Indexed Tree),又以其发明者命名为 Fenwick 树,最早由 Peter M. Fenwick 于 1994 年以 A New Data Structure for Cumulative Frequency Tables 为题发表在 SOFTWARE PRACTICE AND EXPERIENCE 上。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和,区间和。针对区间问题,除了常见的线段树解法,还可以考虑树状数组。它可以以 O(log n) 的时间得到任意前缀和{{< katex >}} \sum_{i=1}^{j}A[i],1<=j<=N {{< /katex >}},并同时支持在 O(log n)时间内支持动态单点值的修改(增加或者减少)。空间复杂度 O(n)。
|
||
|
||
> 利用数组实现前缀和,查询本来是 O(1),但是对于频繁更新的数组,每次重新计算前缀和,时间复杂度 O(n)。此时树状数组的优势便立即显现。
|
||
|
||
## 一. 一维树状数组概念
|
||
|
||
|
||
|
||
|
||
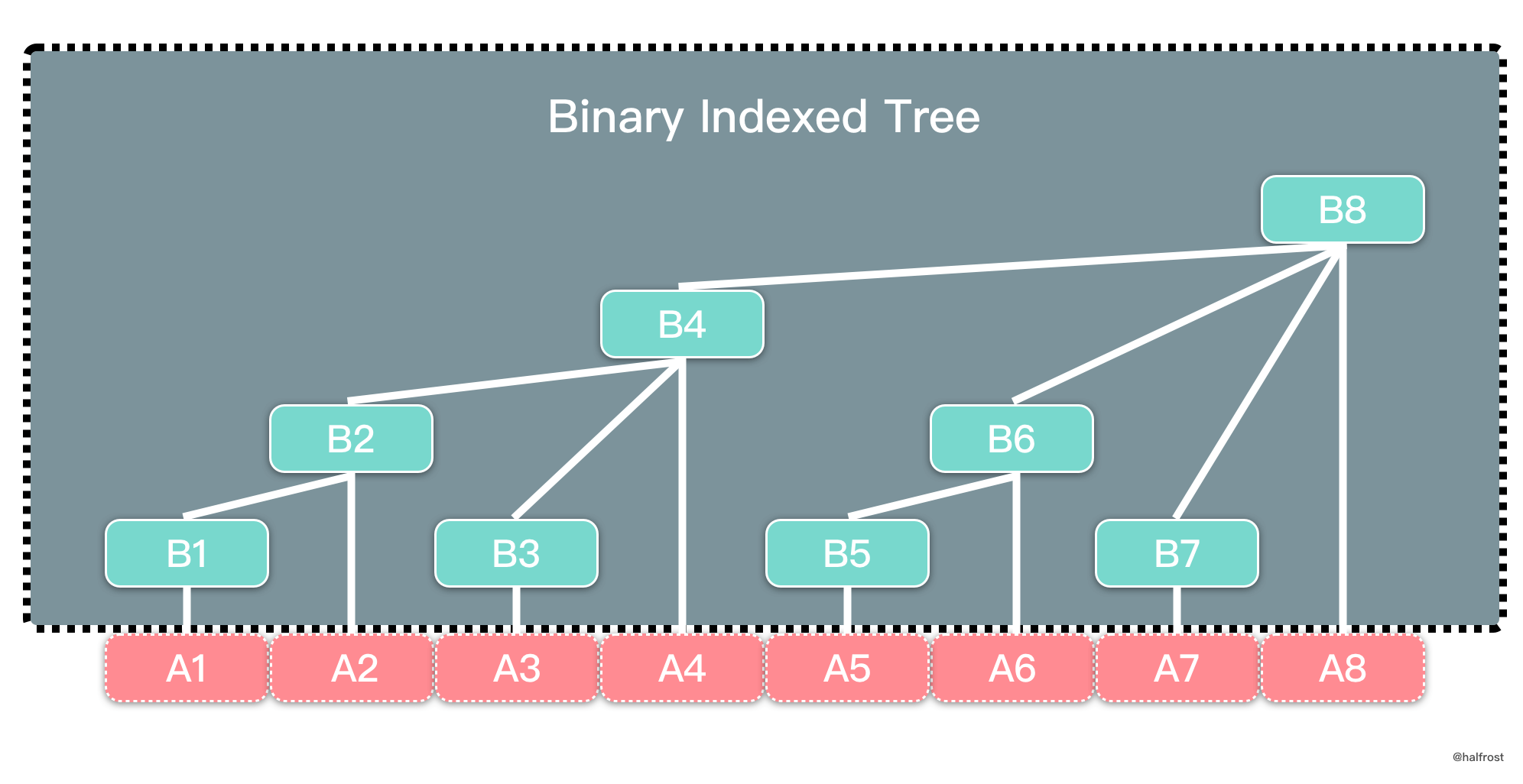
树状数组名字虽然又有树,又有数组,但是它实际上物理形式还是数组,不过每个节点的含义是树的关系,如上图。树状数组中父子节点下标关系是 {{< katex >}}parent = son + 2^{k}{{< /katex >}},其中 k 是子节点下标对应二进制末尾 0 的个数。
|
||
|
||
例如上图中 A 和 B 都是数组。A 数组正常存储数据,B 数组是树状数组。B4,B6,B7 是 B8 的子节点。4 的二进制是 100,4 + {{< katex >}}2^{2}{{< /katex >}} = 8,所以 8 是 4 的父节点。同理,7 的二进制 111,7 + {{< katex >}}2^{0}{{< /katex >}} = 8,8 也是 7 的父节点。
|
||
|
||
|
||
## 1. 节点意义
|
||
|
||
在树状数组中,所有的奇数下标的节点的含义是叶子节点,表示单点,它存的值是原数组相同下标存的值。例如上图中 B1,B3,B5,B7 分别存的值是 A1,A3,A5,A7。所有的偶数下标的节点均是父节点。父节点内存的是区间和。例如 B4 内存的是 B1 + B2 + B3 + A4 = A1 + A2 + A3 + A4。这个区间的左边界是该父节点最左边叶子节点对应的下标,右边界就是自己的下标。例如 B8 表示的区间左边界是 B1,右边界是 B8,所以它表示的区间和是 A1 + A2 + …… + A8。
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
B_{1} &= A_{1} \\
|
||
B_{2} &= B_{1} + A_{2} = A_{1} + A_{2} \\
|
||
B_{3} &= A_{3} \\
|
||
B_{4} &= B_{2} + B_{3} + A_{4} = A_{1} + A_{2} + A_{3} + A_{4} \\
|
||
B_{5} &= A_{5} \\
|
||
B_{6} &= B_{5} + A_{6} = A_{5} + A_{6} \\
|
||
B_{7} &= A_{7} \\
|
||
B_{8} &= B_{4} + B_{6} + B_{7} + A_{8} = A_{1} + A_{2} + A_{3} + A_{4} + A_{5} + A_{6} + A_{7} + A_{8} \\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
|
||
由数学归纳法可以得出,左边界的下标一定是 {{< katex >}}i - 2^{k} + 1{{< /katex >}},其中 i 为父节点的下标,k 为 i 的二进制中末尾 0 的个数。用数学方式表达偶数节点的区间和:
|
||
|
||
{{< katex display >}}
|
||
B_{i} = \sum_{j = i - 2^{k} + 1}^{i} A_{j}
|
||
{{< /katex >}}
|
||
|
||
初始化树状数组的代码如下:
|
||
|
||
```go
|
||
// BinaryIndexedTree define
|
||
type BinaryIndexedTree struct {
|
||
tree []int
|
||
capacity int
|
||
}
|
||
|
||
// Init define
|
||
func (bit *BinaryIndexedTree) Init(nums []int) {
|
||
bit.tree, bit.capacity = make([]int, len(nums)+1), len(nums)+1
|
||
for i := 1; i <= len(nums); i++ {
|
||
bit.tree[i] += nums[i-1]
|
||
for j := i - 2; j >= i-lowbit(i); j-- {
|
||
bit.tree[i] += nums[j]
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
lowbit(i) 函数返回 i 转换成二进制以后,末尾最后一个 1 代表的数值,即 {{< katex >}}2^{k}{{< /katex >}},k 为 i 末尾 0 的个数。我们都知道,在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。利用补码,可以 O(1) 算出 lowbit(i)。负数的补码等于正数的原码每位取反再 + 1,加一会使得负数的补码末尾的 0 和正数原码末尾的 0 一样。这两个数进行 & 运算以后,结果即为 lowbit(i):
|
||
|
||
```go
|
||
func lowbit(x int) int {
|
||
return x & -x
|
||
}
|
||
```
|
||
|
||
如果还想不通的读者,可以看这个例子,34 的二进制是 {{< katex >}}(0010 0010)_{2} {{< /katex >}},它的补码是 {{< katex >}}(1101 1110)_{2} {{< /katex >}}。
|
||
|
||
{{< katex display >}}
|
||
(0010 0010)_{2} \& (1101 1110)_{2} = (0000 0010)_{2}
|
||
{{< /katex >}}
|
||
|
||
lowbit(34) 结果是 {{< katex >}}2^{k} = 2^{1} = 2 {{< /katex >}}
|
||
|
||
## 2. 插入操作
|
||
|
||
树状数组上的父子的下标满足 {{< katex >}}parent = son + 2^{k}{{< /katex >}} 关系,所以可以通过这个公式从叶子结点不断往上递归,直到访问到最大节点值为止,祖先结点最多为 logn 个。插入操作可以实现节点值的增加或者减少,代码实现如下:
|
||
|
||
```go
|
||
// Add define
|
||
func (bit *BinaryIndexedTree) Add(index int, val int) {
|
||
for index <= bit.capacity {
|
||
bit.tree[index] += val
|
||
index += lowbit(index)
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
## 3. 查询操作
|
||
|
||
|
||
树状数组中查询 [1, i] 区间内的和。按照节点的含义,可以得出下面的关系:
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
Query(i) &= A_{1} + A_{2} + ...... + A_{i} \\
|
||
&= A_{1} + A_{2} + A_{i-2^{k}} + A_{i-2^{k}+1} + ...... + A_{i} \\
|
||
&= A_{1} + A_{2} + A_{i-2^{k}} + B_{i} \\
|
||
&= Query(i-2^{k}) + B_{i} \\
|
||
&= Query(i-lowbit(i)) + B_{i} \\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
{{< katex >}}B_{i}{{< /katex >}} 是树状数组存的值。Query 操作实际是一个递归的过程。lowbit(i) 表示 {{< katex >}}2^{k}{{< /katex >}},其中 k 是 i 的二进制表示中末尾 0 的个数。i - lowbit(i) 将 i 的二进制中末尾的 1 去掉,最多有 {{< katex >}}log(i){{< /katex >}} 个 1,所以查询操作最坏的时间复杂度是 O(log n)。查询操作实现代码如下:
|
||
|
||
```go
|
||
// Query define
|
||
func (bit *BinaryIndexedTree) Query(index int) int {
|
||
sum := 0
|
||
for index >= 1 {
|
||
sum += bit.tree[index]
|
||
index -= lowbit(index)
|
||
}
|
||
return sum
|
||
}
|
||
```
|
||
|
||
## 二. 不同场景下树状数组的功能
|
||
|
||
根据节点维护的数据含义不同,树状数组可以提供不同的功能来满足各种各样的区间场景。下面我们先以上例中讲述的区间和为例,进而引出 RMQ 的使用场景。
|
||
|
||
## 1. 单点增减 + 区间求和
|
||
|
||
这种场景是树状数组最经典的场景。单点增减分别调用 add(i,v) 和 add(i,-v)。区间求和,利用前缀和的思想,求 [m,n] 区间和,即 query(n) - query(m-1)。query(n) 代表 [1,n] 区间内的和,query(m-1) 代表 [1,m-1] 区间内的和,两者相减,即 [m,n] 区间内的和。
|
||
|
||
## 2. 区间增减 + 单点查询
|
||
|
||
这种情况需要做一下转化。定义差分数组 {{< katex >}}C_{i}{{< /katex >}} 代表 {{< katex >}}C_{i} = A_{i} - A_{i-1}{{< /katex >}}。那么:
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
C_{0} &= A_{0} \\
|
||
C_{1} &= A_{1} - A_{0}\\
|
||
C_{2} &= A_{2} - A_{1}\\
|
||
......\\
|
||
C_{n} &= A_{n} - A_{n-1}\\
|
||
\sum_{j=1}^{n}C_{j} &= A_{n}\\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
区间增减:在 [m,n] 区间内每一个数都增加 v,只影响 2 个单点的值:
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
C_{m} &= (A_{m} + v) - A_{m-1}\\
|
||
C_{m+1} &= (A_{m+1} + v) - (A_{m} + v)\\
|
||
C_{m+2} &= (A_{m+2} + v) - (A_{m+1} + v)\\
|
||
......\\
|
||
C_{n} &= (A_{n} + v) - (A_{n-1} + v)\\
|
||
C_{n+1} &= A_{n+1} - (A_{n} + v)\\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
|
||
可以观察看,{{< katex >}}C_{m+1}, C_{m+2}, ......, C_{n}{{< /katex >}} 值都不变,变化的是 {{< katex >}}C_{m}, C_{n+1}{{< /katex >}}。所以在这种情况下,区间增加只需要执行 add(m,v) 和 add(n+1,-v) 即可。
|
||
|
||
单点查询这时就是求前缀和了,{{< katex >}}A_{n} = \sum_{j=1}^{n}C_{j}{{< /katex >}},即 query(n)。
|
||
|
||
## 3. 区间增减 + 区间求和
|
||
|
||
这种情况是上面一种情况的增强版。区间增减的做法和上面做法一致,构造差分数组。这里主要说明区间查询怎么做。先来看 [1,n] 区间和如何求:
|
||
|
||
|
||
|
||
{{< katex display >}}
|
||
A_{1} + A_{2} + A_{3} + ...... + A_{n}\\
|
||
\begin{aligned}
|
||
&= (C_{1}) + (C_{1} + C_{2}) + (C_{1} + C_{2} + C_{3}) + ...... + \sum_{1}^{n}C_{n}\\
|
||
&= n * C_{1} + (n-1) * C_{2} + ...... + C_{n}\\
|
||
&= n * (C_{1} + C_{2} + C_{3} + ...... + C_{n}) - (0 * C_{1} + 1 * C_{2} + 2 * C_{3} + ...... + (n - 1) * C_{n})\\
|
||
&= n * \sum_{1}^{n}C_{n} - (D_{1} + D_{2} + D_{3} + ...... + D_{n})\\
|
||
&= n * \sum_{1}^{n}C_{n} - \sum_{1}^{n}D_{n}\\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
其中 {{< katex >}}D_{n} = (n - 1) * C_{n}{{< /katex >}}
|
||
|
||
所以求区间和,只需要再构造一个 {{< katex >}}D_{n}{{< /katex >}} 即可。
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
\sum_{1}^{n}A_{n} &= A_{1} + A_{2} + A_{3} + ...... + A_{n} \\
|
||
&= n * \sum_{1}^{n}C_{n} - \sum_{1}^{n}D_{n}\\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
以此类推,推到更一般的情况:
|
||
|
||
{{< katex display >}}
|
||
\begin{aligned}
|
||
\sum_{m}^{n}A_{n} &= A_{m} + A_{m+1} + A_{m+2} + ...... + A_{n} \\
|
||
&= \sum_{1}^{n}A_{n} - \sum_{1}^{m-1}A_{n}\\
|
||
&= (n * \sum_{1}^{n}C_{n} - \sum_{1}^{n}D_{n}) - ((m-1) * \sum_{1}^{m-1}C_{m-1} - \sum_{1}^{m-1}D_{m-1})\\
|
||
\end{aligned}
|
||
{{< /katex >}}
|
||
|
||
至此区间查询问题得解。
|
||
|
||
## 4. 单点更新 + 区间最值
|
||
|
||
线段树最基础的运用是区间求和,但是将 sum 操作换成 max 操作以后,也可以求区间最值,并且时间复杂度完全没有变。那树状数组呢?也可以实现相同的功能么?答案是可以的,不过时间复杂度会下降一点。
|
||
|
||
线段树求区间和,把每个小区间的和计算好,然后依次 pushUp,往上更新。把 sum 换成 max 操作,含义完全相同:取出小区间的最大值,然后依次 pushUp 得到整个区间的最大值。
|
||
|
||
树状数组求区间和,是将单点增减的增量影响更新到固定区间 {{< katex >}}[i-2^{k}+1, i]{{< /katex >}}。但是把 sum 换成 max 操作,含义就变了。此时单点的增量和区间 max 值并无直接联系。暴力的方式是将该点与区间内所有值比较大小,取出最大值,时间复杂度 O(n * log n)。仔细观察树状数组的结构,可以发现不必枚举所有区间。例如更新 {{< katex >}}A_{i}{{< /katex >}} 的值,那么受到影响的树状数组下标为 {{< katex >}}i-2^{0}, i-2^{1}, i-2^{2}, i-2^{3}, ......, i-2^{k}{{< /katex >}},其中 {{< katex >}}2^{k} < lowbit(i) <= 2^{k+1}{{< /katex >}}。需要更新至多 k 个下标,外层循环由 O(n) 降为了 O(log n)。区间内部每次都需要重新比较,需要 O(log n) 的复杂度,总的时间复杂度为 {{< katex >}}(O(log n))^2 {{< /katex >}}。
|
||
|
||
```go
|
||
func (bit *BinaryIndexedTree) Add(index int, val int) {
|
||
for index <= bit.capacity {
|
||
bit.tree[index] = val
|
||
for i := 1; i < lowbit(index); i = i << 1 {
|
||
bit.tree[index] = max(bit.tree[index], bit.tree[index-i])
|
||
}
|
||
index += lowbit(index)
|
||
}
|
||
}
|
||
```
|
||
|
||
上面解决了单点更新的问题,再来看区间最值。线段树划分区间是均分,对半分,而树状数组不是均分。在树状数组中 {{< katex >}}B_{i} {{< /katex >}} 表示的区间是 {{< katex >}}[i-2^{k}+1, i]{{< /katex >}},据此划分“不规则区间”。对于树状数组求 [m,n] 区间内最值,
|
||
|
||
- 如果 {{< katex >}} m < n - 2^{k} {{< /katex >}},那么 {{< katex >}} query(m,n) = max(query(m,n-2^{k}), B_{n}){{< /katex >}}
|
||
- 如果 {{< katex >}} m >= n - 2^{k} {{< /katex >}},那么 {{< katex >}} query(m,n) = max(query(m,n-1), A_{n}){{< /katex >}}
|
||
|
||
|
||
```go
|
||
func (bit *BinaryIndexedTree) Query(m, n int) int {
|
||
res := 0
|
||
for n >= m {
|
||
res = max(nums[n], res)
|
||
n--
|
||
for ; n-lowbit(n) >= m; n -= lowbit(n) {
|
||
res = max(bit.tree[n], res)
|
||
}
|
||
}
|
||
return res
|
||
}
|
||
```
|
||
|
||
n 最多经过 {{< katex >}}(O(log n))^2 {{< /katex >}} 变化,最终 n < m。时间复杂度为 {{< katex >}}(O(log n))^2 {{< /katex >}}。
|
||
|
||
## 三. 常见应用
|
||
|
||
这一章节来谈谈树状数组的常见应用。
|
||
|
||
## 1. 求逆序对
|
||
|
||
给定 {{< katex >}} n {{< /katex >}} 个数 {{< katex >}} A[n] \in [1,n] {{< /katex >}} 的排列 P,求满足 {{< katex >}}i < j {{< /katex >}} 且 {{< katex >}} A[i] > A[j] {{< /katex >}} 的数对 {{< katex >}} (i,j) {{< /katex >}} 的个数。
|
||
|
||
|
||
这个问题就是经典的逆序数问题,如果采用朴素算法,就是枚举 i 和 j,并且判断 A[i] 和 A[j] 的值进行数值统计,如果 A[i] > A[j] 则计数器加一,统计完后计数器的值就是答案。时间复杂度为 {{< katex >}} O(n^{2}) {{< /katex >}},这个时间复杂度太高,是否存在 {{< katex >}} O(log n) {{< /katex >}} 的解法呢?
|
||
|
||
先把数列中的数按大小顺序转化成 1 到 n 的整数,使得原数列成为一个 1,2,...,n 的数组 B,创建一个树状数组,用来记录这样一个数组 C(下标从1算起)的前缀和:若排列中的数 i 当前已经出现,则 C[i] 的值为 1 ,否则为 0。初始时数组 C 的值均为 0,从排列中的最后一个数开始遍历,每次在树状数组中查询有多少个数小于当前的数 B[j](即用树状数组查询数组 C 中的 [1,B[j]-1] 区间前缀和)并加入计数器,之后对树状数组执行修改数组 C 的第 B[j] 个数值加 1 的操作。
|
||
|
||
|
||
> 如果题目换成 {{< katex >}} A[n] \in [1,10^{10}] {{< /katex >}},解题思路不变,只不过一开始再多加一步,离散化的操作。
|
||
|
||
## 2. 求区间逆序对
|
||
|
||
## 3. 求树上逆序对
|
||
|
||
## 4. 求第 K 大数
|
||
|
||
## 四. 二维树状数组 |