mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 09:23:19 +08:00
106 lines
3.9 KiB
Markdown
106 lines
3.9 KiB
Markdown
# [1691. Maximum Height by Stacking Cuboids](https://leetcode.com/problems/maximum-height-by-stacking-cuboids/)
|
||
|
||
## 题目
|
||
|
||
Given `n` `cuboids` where the dimensions of the `ith` cuboid is `cuboids[i] = [widthi, lengthi, heighti]` (**0-indexed**). Choose a **subset** of `cuboids` and place them on each other.
|
||
|
||
You can place cuboid `i` on cuboid `j` if `widthi <= widthj` and `lengthi <= lengthj` and `heighti <= heightj`. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.
|
||
|
||
Return *the **maximum height** of the stacked* `cuboids`.
|
||
|
||
**Example 1:**
|
||
|
||
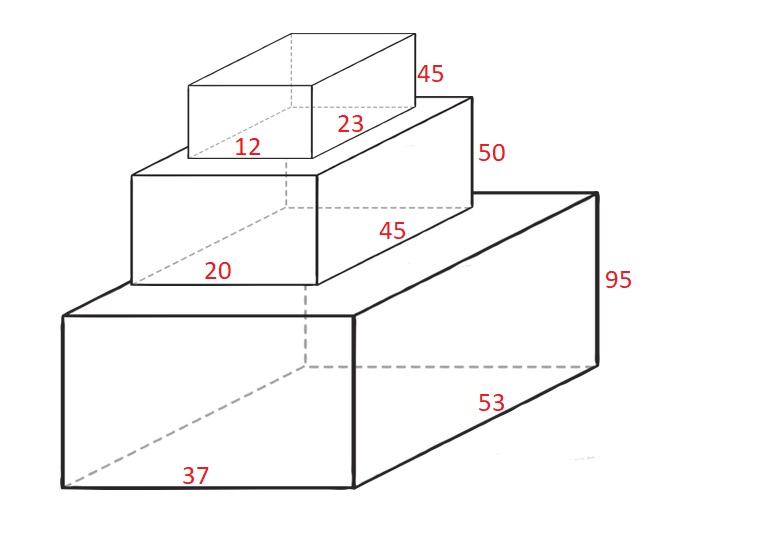
|
||
|
||
```
|
||
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
|
||
Output: 190
|
||
Explanation:
|
||
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
|
||
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
|
||
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
|
||
The total height is 95 + 50 + 45 = 190.
|
||
```
|
||
|
||
**Example 2:**
|
||
|
||
```
|
||
Input: cuboids = [[38,25,45],[76,35,3]]
|
||
Output: 76
|
||
Explanation:
|
||
You can't place any of the cuboids on the other.
|
||
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.
|
||
```
|
||
|
||
**Example 3:**
|
||
|
||
```
|
||
Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
|
||
Output: 102
|
||
Explanation:
|
||
After rearranging the cuboids, you can see that all cuboids have the same dimension.
|
||
You can place the 11x7 side down on all cuboids so their heights are 17.
|
||
The maximum height of stacked cuboids is 6 * 17 = 102.
|
||
```
|
||
|
||
**Constraints:**
|
||
|
||
- `n == cuboids.length`
|
||
- `1 <= n <= 100`
|
||
- `1 <= widthi, lengthi, heighti <= 100`
|
||
|
||
## 题目大意
|
||
|
||
给你 n 个长方体 cuboids ,其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti](下标从 0 开始)。请你从 cuboids 选出一个 子集 ,并将它们堆叠起来。如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ,你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列,以将它放在另一个长方体上。返回 堆叠长方体 cuboids 可以得到的 最大高度 。
|
||
|
||
## 解题思路
|
||
|
||
- 这一题是 LIS 最长递增子序列系列问题的延续。一维 LIS 问题是第 300 题。二维 LIS 问题是 354 题。这一题是三维的 LIS 问题。
|
||
- 题目要求最终摞起来的长方体尽可能的高,那么把长宽高中最大的值旋转为高。这是针对单个方块的排序。多个方块间还要排序,因为他们摞起来有要求,大的方块必须放在下面。所以针对多个方块,按照长,宽,高的顺序进行排序。两次排序完成以后,可以用动态规划找出最大值了。定义 `dp[i]` 为以 `i` 为最后一块砖块所能堆叠的最高高度。由于长和宽已经排好序了。所以只需要在 [0, i - 1] 这个区间内动态更新 dp 最大值。
|
||
|
||
## 代码
|
||
|
||
```go
|
||
package leetcode
|
||
|
||
import "sort"
|
||
|
||
func maxHeight(cuboids [][]int) int {
|
||
n := len(cuboids)
|
||
for i := 0; i < n; i++ {
|
||
sort.Ints(cuboids[i]) // 立方体三边内部排序
|
||
}
|
||
// 立方体排序,先按最短边,再到最长边
|
||
sort.Slice(cuboids, func(i, j int) bool {
|
||
if cuboids[i][0] != cuboids[j][0] {
|
||
return cuboids[i][0] < cuboids[j][0]
|
||
}
|
||
if cuboids[i][1] != cuboids[j][1] {
|
||
return cuboids[i][1] < cuboids[j][1]
|
||
}
|
||
return cuboids[i][2] < cuboids[j][2]
|
||
})
|
||
res := 0
|
||
dp := make([]int, n)
|
||
for i := 0; i < n; i++ {
|
||
dp[i] = cuboids[i][2]
|
||
res = max(res, dp[i])
|
||
}
|
||
for i := 1; i < n; i++ {
|
||
for j := 0; j < i; j++ {
|
||
if cuboids[j][0] <= cuboids[i][0] && cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] {
|
||
dp[i] = max(dp[i], dp[j]+cuboids[i][2])
|
||
}
|
||
}
|
||
res = max(res, dp[i])
|
||
}
|
||
return res
|
||
}
|
||
|
||
func max(x, y int) int {
|
||
if x > y {
|
||
return x
|
||
}
|
||
return y
|
||
}
|
||
``` |