mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 09:23:19 +08:00
74 lines
2.4 KiB
Markdown
Executable File
74 lines
2.4 KiB
Markdown
Executable File
# [1266. Minimum Time Visiting All Points](https://leetcode.com/problems/minimum-time-visiting-all-points/)
|
||
|
||
|
||
## 题目
|
||
|
||
On a plane there are `n` points with integer coordinates `points[i] = [xi, yi]`. Your task is to find the minimum time in seconds to visit all points.
|
||
|
||
You can move according to the next rules:
|
||
|
||
- In one second always you can either move vertically, horizontally by one unit or diagonally (it means to move one unit vertically and one unit horizontally in one second).
|
||
- You have to visit the points in the same order as they appear in the array.
|
||
|
||
**Example 1:**
|
||
|
||
|
||
|
||
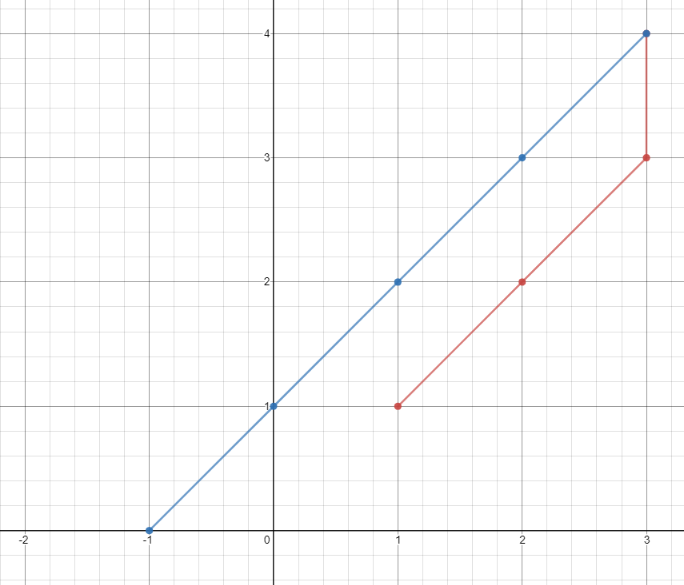
Input: points = [[1,1],[3,4],[-1,0]]
|
||
Output: 7
|
||
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
|
||
Time from [1,1] to [3,4] = 3 seconds
|
||
Time from [3,4] to [-1,0] = 4 seconds
|
||
Total time = 7 seconds
|
||
|
||
**Example 2:**
|
||
|
||
Input: points = [[3,2],[-2,2]]
|
||
Output: 5
|
||
|
||
**Constraints:**
|
||
|
||
- `points.length == n`
|
||
- `1 <= n <= 100`
|
||
- `points[i].length == 2`
|
||
- `-1000 <= points[i][0], points[i][1] <= 1000`
|
||
|
||
## 题目大意
|
||
|
||
|
||
平面上有 n 个点,点的位置用整数坐标表示 points[i] = [xi, yi]。请你计算访问所有这些点需要的最小时间(以秒为单位)。你可以按照下面的规则在平面上移动:
|
||
|
||
- 每一秒沿水平或者竖直方向移动一个单位长度,或者跨过对角线(可以看作在一秒内向水平和竖直方向各移动一个单位长度)。
|
||
- 必须按照数组中出现的顺序来访问这些点。
|
||
|
||
提示:
|
||
|
||
- points.length == n
|
||
- 1 <= n <= 100
|
||
- points[i].length == 2
|
||
- -1000 <= points[i][0], points[i][1] <= 1000
|
||
|
||
|
||
|
||
|
||
|
||
## 解题思路
|
||
|
||
- 在直角坐标系上给出一个数组,数组里面的点是飞机飞行经过的点。飞机飞行只能沿着水平方向、垂直方向、45°方向飞行。问飞机经过所有点的最短时间。
|
||
- 简单的数学问题。依次遍历数组,分别计算 x 轴和 y 轴上的差值,取最大值即是这两点之间飞行的最短时间。最后累加每次计算的最大值就是最短时间。
|
||
|
||
## 代码
|
||
|
||
```go
|
||
|
||
package leetcode
|
||
|
||
func minTimeToVisitAllPoints(points [][]int) int {
|
||
res := 0
|
||
for i := 1; i < len(points); i++ {
|
||
res += max(abs(points[i][0]-points[i-1][0]), abs(points[i][1]-points[i-1][1]))
|
||
}
|
||
return res
|
||
}
|
||
|
||
``` |