mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-05 00:25:22 +08:00
60 lines
3.8 KiB
Markdown
Executable File
60 lines
3.8 KiB
Markdown
Executable File
# [920. Number of Music Playlists](https://leetcode.com/problems/number-of-music-playlists/)
|
||
|
||
|
||
## 题目
|
||
|
||
Your music player contains `N` different songs and she wants to listen to `L` ****(not necessarily different) songs during your trip. You create a playlist so that:
|
||
|
||
- Every song is played at least once
|
||
- A song can only be played again only if `K` other songs have been played
|
||
|
||
Return the number of possible playlists. **As the answer can be very large, return it modulo `10^9 + 7`**.
|
||
|
||
**Example 1:**
|
||
|
||
Input: N = 3, L = 3, K = 1
|
||
Output: 6
|
||
Explanation: There are 6 possible playlists. [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1].
|
||
|
||
**Example 2:**
|
||
|
||
Input: N = 2, L = 3, K = 0
|
||
Output: 6
|
||
Explanation: There are 6 possible playlists. [1, 1, 2], [1, 2, 1], [2, 1, 1], [2, 2, 1], [2, 1, 2], [1, 2, 2]
|
||
|
||
**Example 3:**
|
||
|
||
Input: N = 2, L = 3, K = 1
|
||
Output: 2
|
||
Explanation: There are 2 possible playlists. [1, 2, 1], [2, 1, 2]
|
||
|
||
**Note:**
|
||
|
||
1. `0 <= K < N <= L <= 100`
|
||
|
||
## 题目大意
|
||
|
||
你的音乐播放器里有 N 首不同的歌,在旅途中,你的旅伴想要听 L 首歌(不一定不同,即,允许歌曲重复)。请你为她按如下规则创建一个播放列表:
|
||
|
||
- 每首歌至少播放一次。
|
||
- 一首歌只有在其他 K 首歌播放完之后才能再次播放。
|
||
|
||
返回可以满足要求的播放列表的数量。由于答案可能非常大,请返回它模 10^9 + 7 的结果。
|
||
|
||
提示:
|
||
|
||
- 0 <= K < N <= L <= 100
|
||
|
||
|
||
|
||
|
||
## 解题思路
|
||
|
||
- 简化抽象一下题意,给 N 个数,要求从这 N 个数里面组成一个长度为 L 的序列,并且相同元素的间隔不能小于 K 个数。问总共有多少组组成方法。
|
||
- 一拿到题,会觉得这一题是三维 DP,因为存在 3 个变量,但是实际考虑一下,可以降一维。我们先不考虑 K 的限制,只考虑 N 和 L。定义 `dp[i][j]` 代表播放列表里面有 `i` 首歌,其中包含 `j` 首不同的歌曲,那么题目要求的最终解存在 `dp[L][N]` 中。考虑 `dp[i][j]` 的递归公式,音乐列表当前需要组成 `i` 首歌,有 2 种方式可以得到,由 `i - 1` 首歌的列表中添加一首列表中**不存在**的新歌曲,或者由 `i - 1` 首歌的列表中添加一首列表中**已经存在**的歌曲。即,`dp[i][j]` 可以由 `dp[i - 1][j - 1]` 得到,也可以由 `dp[i - 1][j]` 得到。如果是第一种情况,添加一首新歌,那么新歌有 N - ( j - 1 ) 首,如果是第二种情况,添加一首已经存在的歌,歌有 j 首,所以状态转移方程是 `dp[i][j] = dp[i - 1][j - 1] * ( N - ( j - 1 ) ) + dp[i - 1][j] * j` 。但是这个方程是在不考虑 K 的限制条件下得到的,距离满足题意还差一步。接下来需要考虑加入 K 这个限制条件以后,状态转移方程该如何推导。
|
||
- 如果是添加一首新歌,是不受 K 限制的,所以 `dp[i - 1][j - 1] * ( N - ( j - 1 ) )` 这里不需要变化。如果是添加一首存在的歌曲,这个时候就会受到 K 的限制了。如果当前播放列表里面的歌曲有 `j` 首,并且 `j > K`,那么选择歌曲只能从 `j - K` 里面选,因为不能选择 `j - 1` 到 `j - k` 的这些歌,选择了就不满足重复的歌之间间隔不能小于 `K` 的限制条件了。那 j ≤ K 呢?这个时候一首歌都不能选,因为歌曲数都没有超过 K,当然不能再选择重复的歌曲。(选择了就再次不满足重复的歌之间间隔不能小于 `K` 的限制条件了)。经过上述分析,可以得到最终的状态转移方程:
|
||
|
||
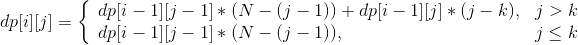
|
||
|
||
- 上面的式子可以合并简化成下面这个式子:`dp[i][j] = dp[i - 1][j - 1]*(N - (j - 1)) + dp[i-1][j]*max(j-K, 0)`,递归初始值 `dp[0][0] = 1`。
|