mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-05 00:25:22 +08:00
100 lines
5.6 KiB
Markdown
Executable File
100 lines
5.6 KiB
Markdown
Executable File
# [850. Rectangle Area II](https://leetcode.com/problems/rectangle-area-ii/)
|
||
|
||
|
||
## 题目
|
||
|
||
We are given a list of (axis-aligned) `rectangles`. Each `rectangle[i] = [x1, y1, x2, y2]` , where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the `i`th rectangle.
|
||
|
||
Find the total area covered by all `rectangles` in the plane. Since the answer may be too large, **return it modulo 10^9 + 7**.
|
||
|
||
|
||
|
||
**Example 1:**
|
||
|
||
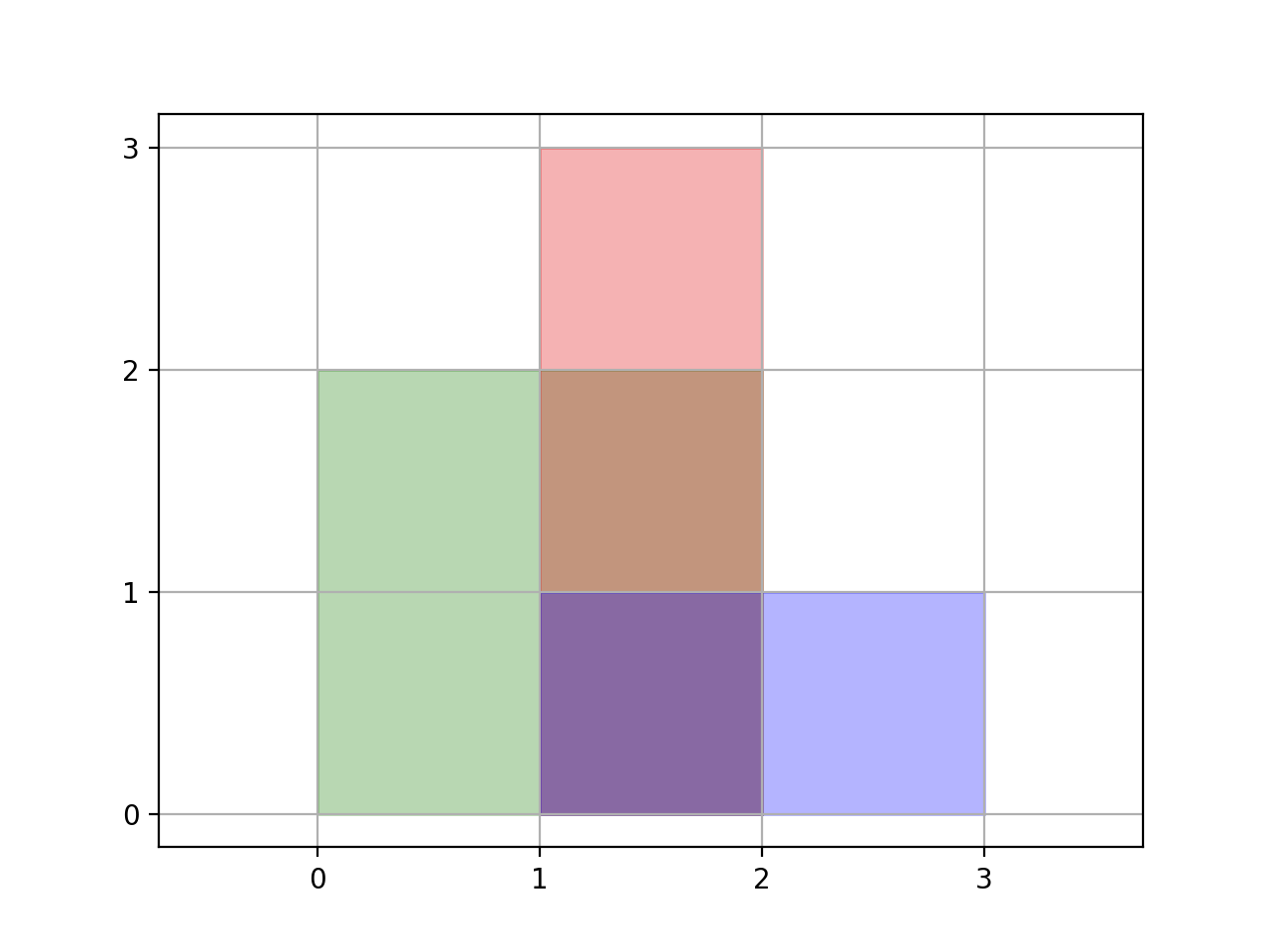
Input: [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
|
||
Output: 6
|
||
Explanation: As illustrated in the picture.
|
||
|
||
**Example 2:**
|
||
|
||
Input: [[0,0,1000000000,1000000000]]
|
||
Output: 49
|
||
Explanation: The answer is 10^18 modulo (10^9 + 7), which is (10^9)^2 = (-7)^2 = 49.
|
||
|
||
**Note:**
|
||
|
||
- `1 <= rectangles.length <= 200`
|
||
- `rectanges[i].length = 4`
|
||
- `0 <= rectangles[i][j] <= 10^9`
|
||
- The total area covered by all rectangles will never exceed `2^63 - 1` and thus will fit in a 64-bit signed integer.
|
||
|
||
|
||
## 题目大意
|
||
|
||
我们给出了一个(轴对齐的)矩形列表 rectangles。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标,(x2,y2)是该矩形右上角的坐标。找出平面中所有矩形叠加覆盖后的总面积。由于答案可能太大,请返回它对 10 ^ 9 + 7 取模的结果。
|
||
|
||
提示:
|
||
|
||
- 1 <= rectangles.length <= 200
|
||
- rectanges[i].length = 4
|
||
- 0 <= rectangles[i][j] <= 10^9
|
||
- 矩形叠加覆盖后的总面积不会超越 2^63 - 1 ,这意味着可以用一个 64 位有符号整数来保存面积结果。
|
||
|
||
|
||
## 解题思路
|
||
|
||
|
||
- 在二维坐标系中给出一些矩形,要求这些矩形合并之后的面积。由于矩形有重叠,所以需要考虑合并以后的面积。矩形的坐标值也会很大。
|
||
- 这一题给人的感觉很像第 218 题,求天际线的过程也是有楼挡楼,重叠的情况。不过那一题只用求天际线的拐点,所以我们可以对区间做“右边界减一”的处理,防止两个相邻区间因为共点,而导致结果错误。但是这一题如果还是用相同的做法,就会出错,因为“右边界减一”以后,面积会少一部分,最终得到的结果也是偏小的。所以这一题要将线段树改造一下。
|
||
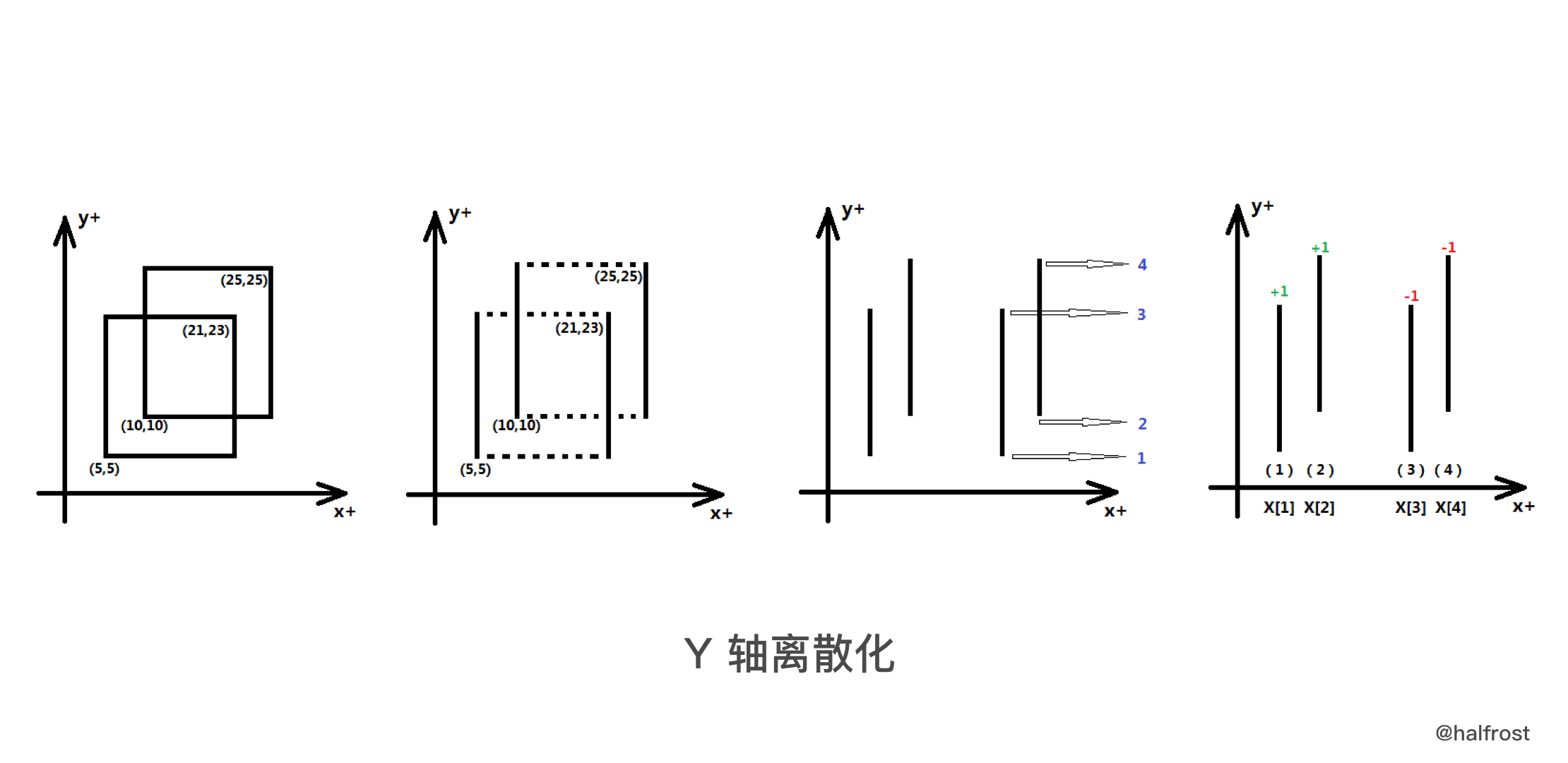
- 思路是先讲 Y 轴上的坐标离线化,转换成线段树。将矩形的 2 条边变成扫描线,左边是入边,右边是出边。
|
||
|
||
|
||
|
||
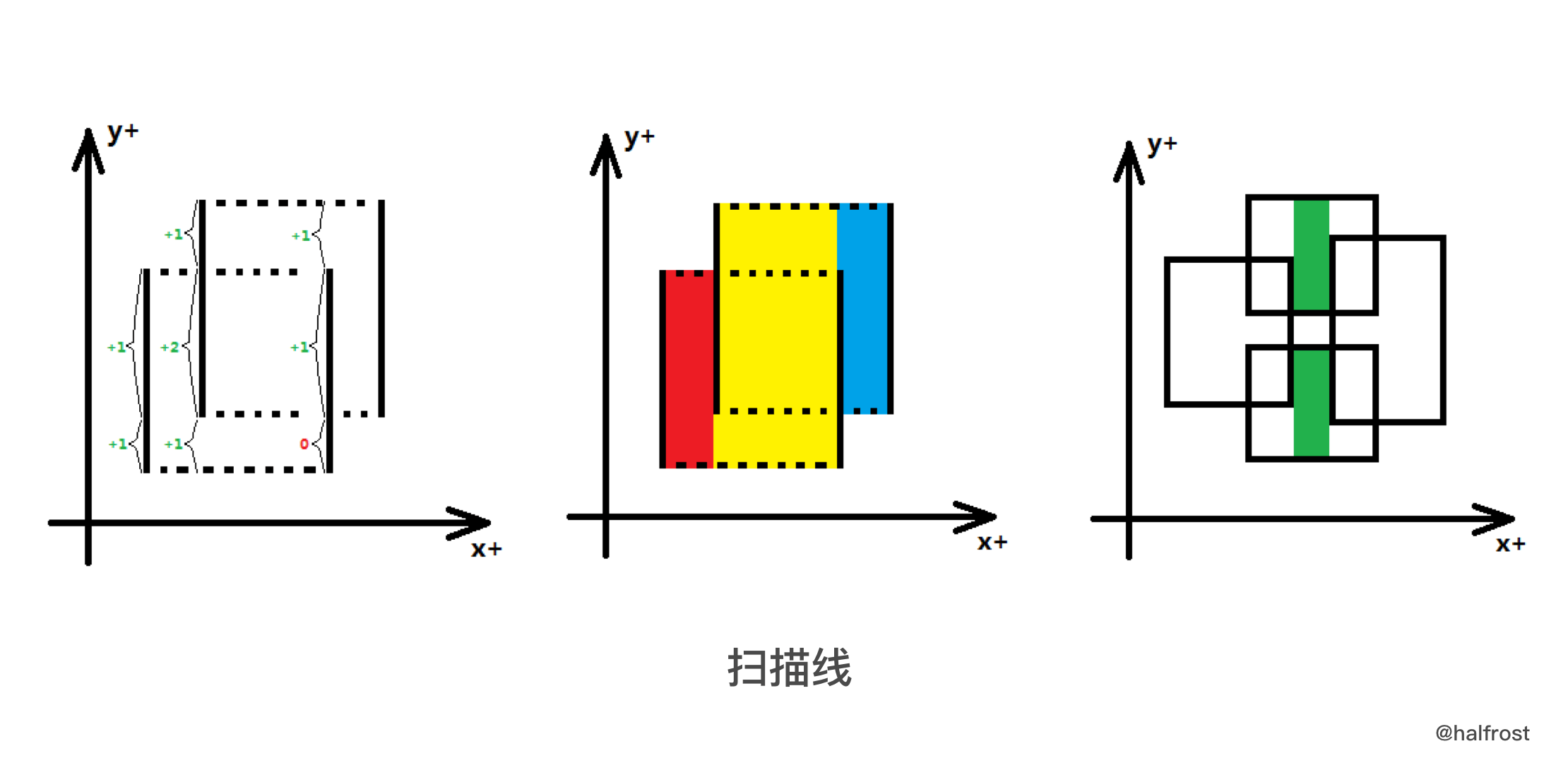
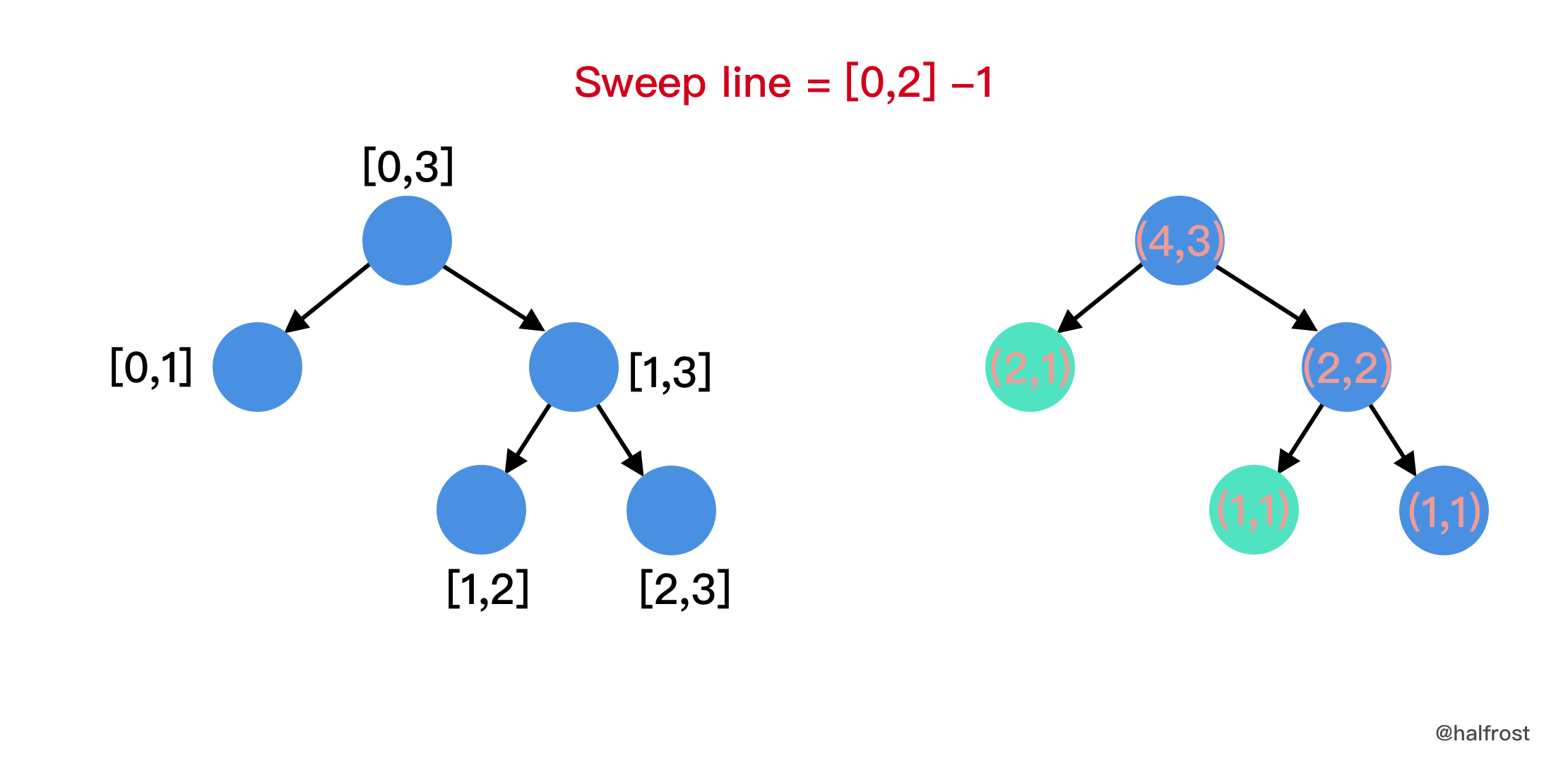
- 再从左往右遍历每条扫描线,并对 Y 轴上的线段树进行 update。X 轴上的每个坐标区间 * query 线段树总高度的结果 = 区间面积。最后将 X 轴对应的每个区间面积加起来,就是最终矩形合并以后的面积。如下图中间的图。
|
||
|
||
|
||
|
||
需要注意的一点是,**每次 query 的结果并不一定是连续线段**。如上图最右边的图,中间有一段是可能出现镂空的。这种情况看似复杂,其实很简单,因为每段线段树的线段代表的权值高度是不同的,每次 query 最大高度得到的结果已经考虑了中间可能有镂空的情况了。
|
||
|
||
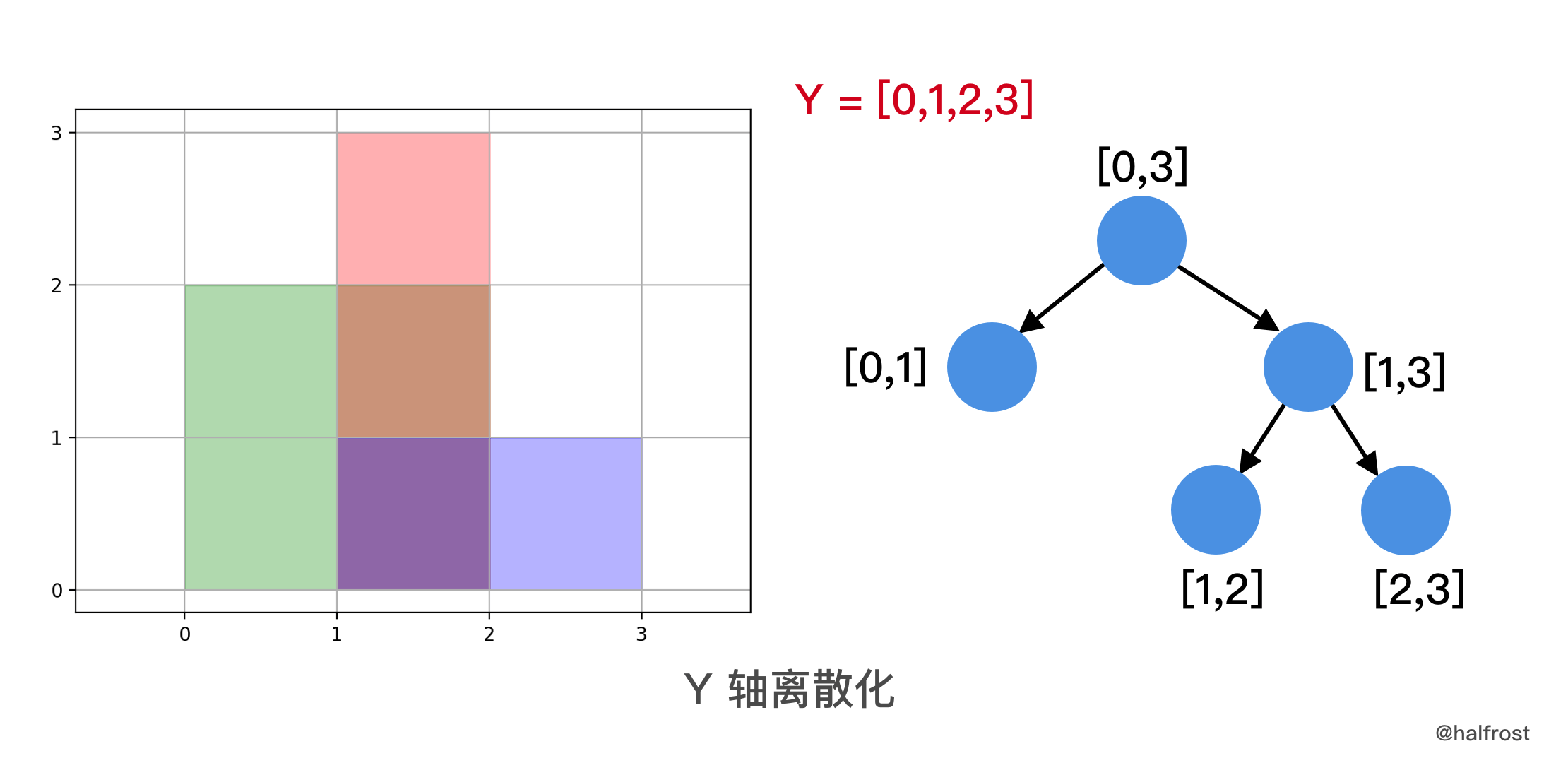
- 具体做法,先把各个矩形在 Y 轴方向上离散化,这里的**线段树叶子节点不再是一个点了,而是一个区间长度为 1 的区间段**。
|
||
|
||
|
||
|
||
每个叶子节点也不再是存储一个 int 值,而是存 2 个值,一个是 count 值,用来记录这条区间被覆盖的次数,另一个值是 val 值,用来反映射该线段长度是多少,因为 Y 轴被离散化了,区间坐标间隔都是 1,但是实际 Y 轴的高度并不是 1 ,所以用 val 来反映射原来的高度。
|
||
|
||
- 初始化线段树,叶子节点的 count = 0,val 根据题目给的 Y 坐标进行计算。
|
||
|
||
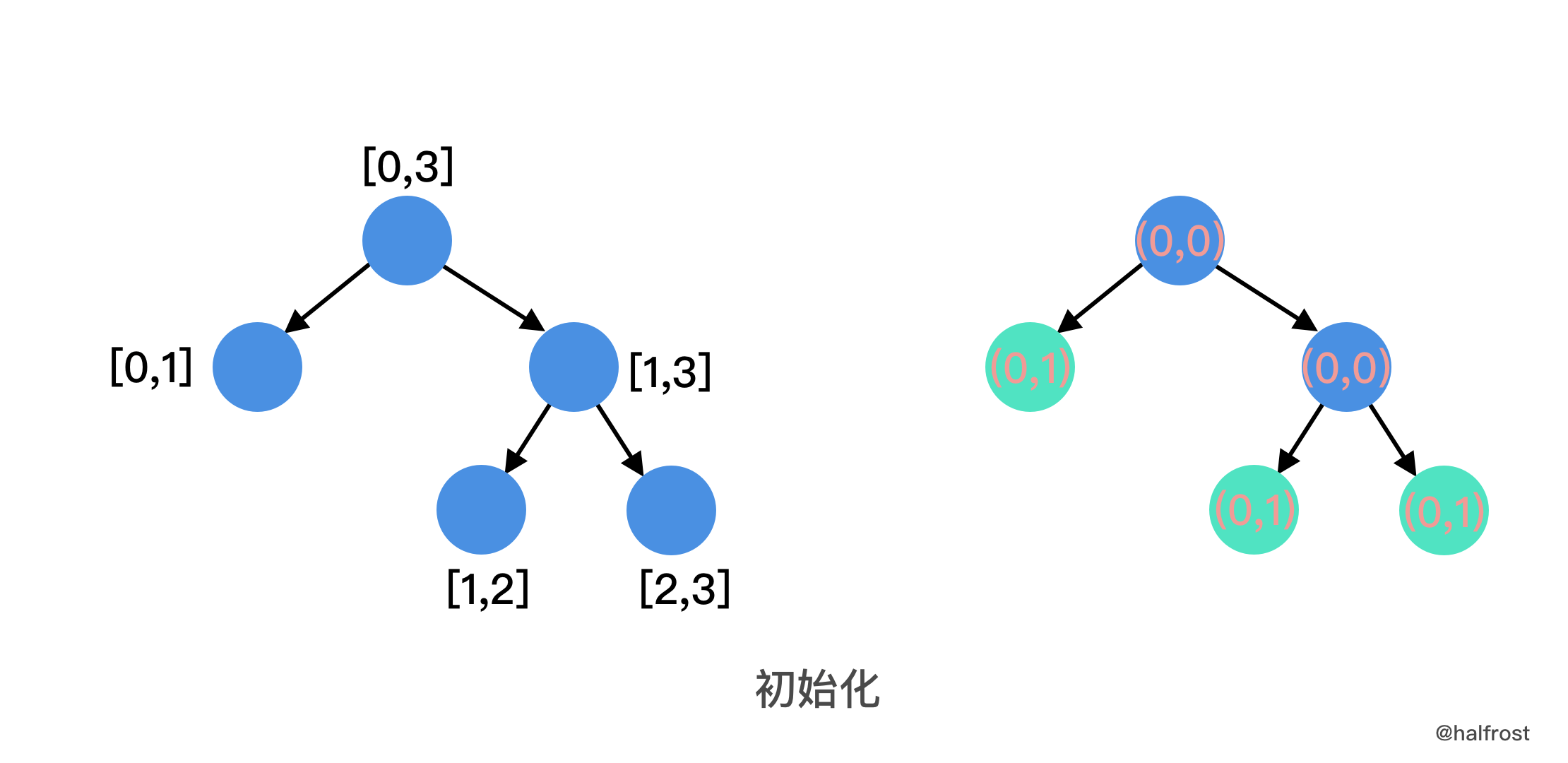
|
||
|
||
- 从左往右遍历每个扫描线。每条扫面线都把对应 update 更新到叶子节点。pushUp 的时候需要合并每个区间段的高度 val 值。如果有区间没有被覆盖,那么这个区间高度 val 为 0,这也就处理了可能“中间镂空”的情况。
|
||
|
||
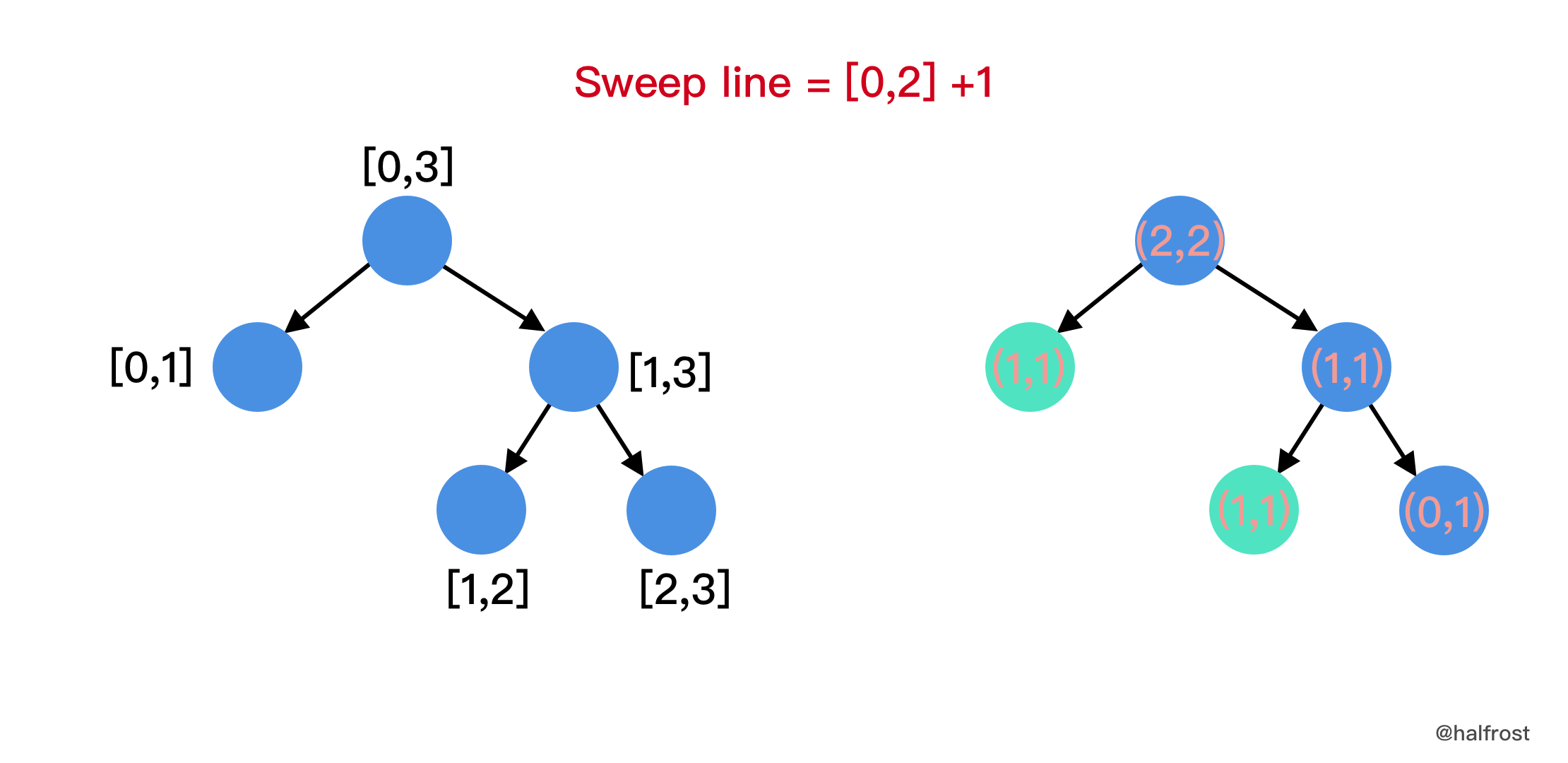
|
||
|
||
func (sat *SegmentAreaTree) pushUp(treeIndex, leftTreeIndex, rightTreeIndex int) {
|
||
newCount, newValue := sat.merge(sat.tree[leftTreeIndex].count, sat.tree[rightTreeIndex].count), 0
|
||
if sat.tree[leftTreeIndex].count > 0 && sat.tree[rightTreeIndex].count > 0 {
|
||
newValue = sat.merge(sat.tree[leftTreeIndex].val, sat.tree[rightTreeIndex].val)
|
||
} else if sat.tree[leftTreeIndex].count > 0 && sat.tree[rightTreeIndex].count == 0 {
|
||
newValue = sat.tree[leftTreeIndex].val
|
||
} else if sat.tree[leftTreeIndex].count == 0 && sat.tree[rightTreeIndex].count > 0 {
|
||
newValue = sat.tree[rightTreeIndex].val
|
||
}
|
||
sat.tree[treeIndex] = SegmentItem{count: newCount, val: newValue}
|
||
}
|
||
|
||
- 扫描每一个扫描线,先 pushDown 到叶子节点,再 pushUp 到根节点。
|
||
|
||
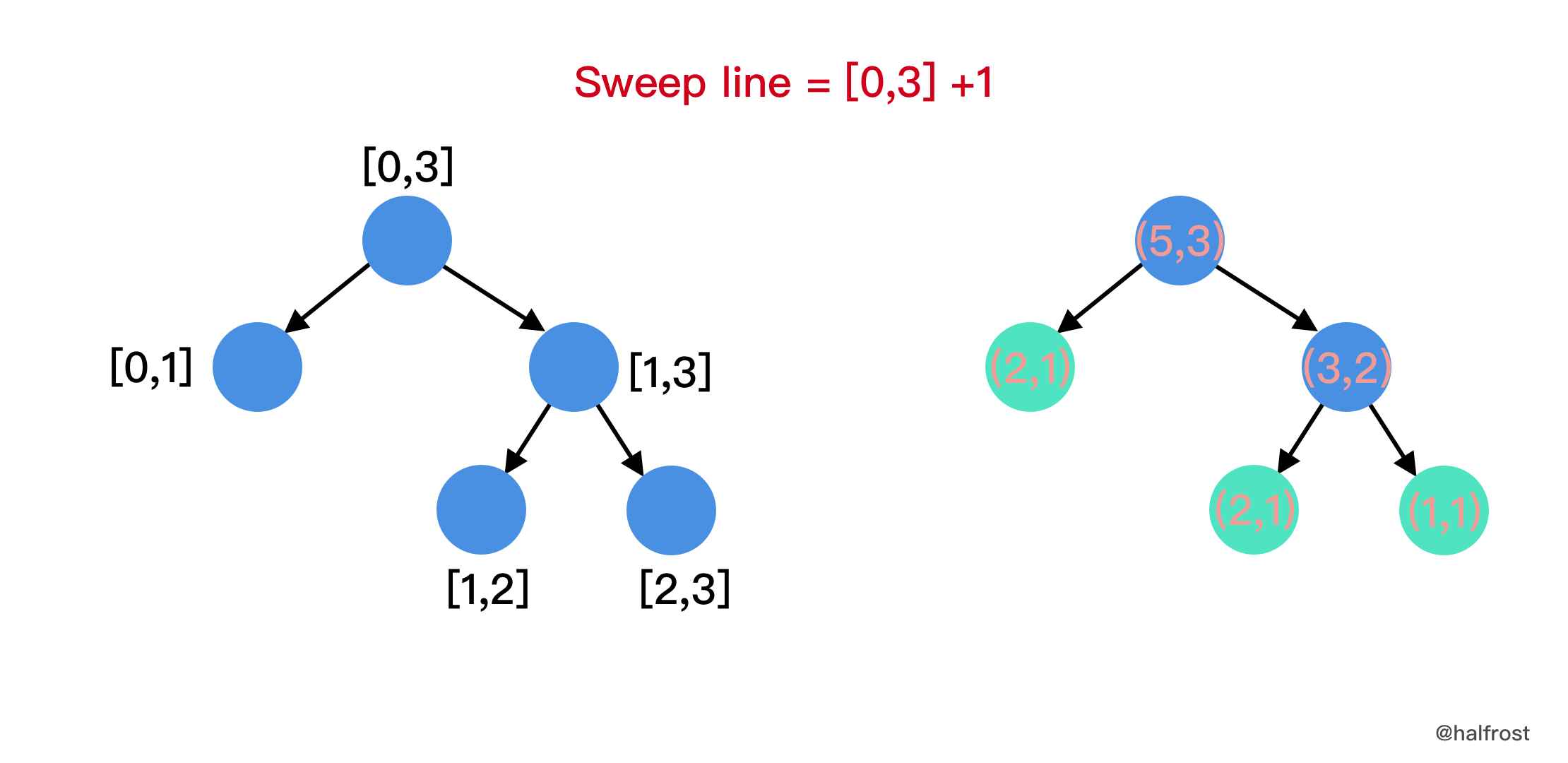
|
||
|
||
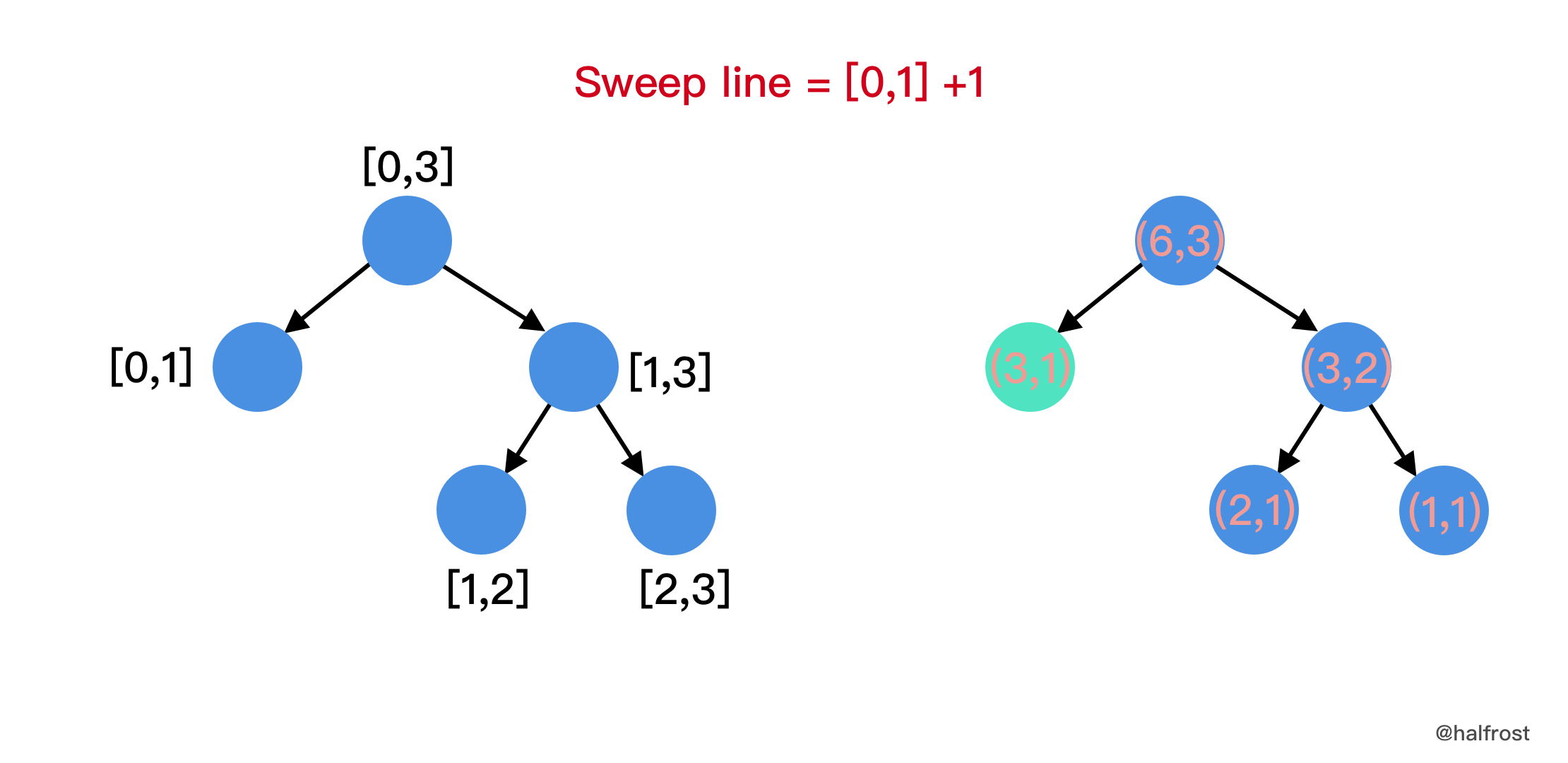
|
||
|
||
|
||
|
||
|
||
|
||
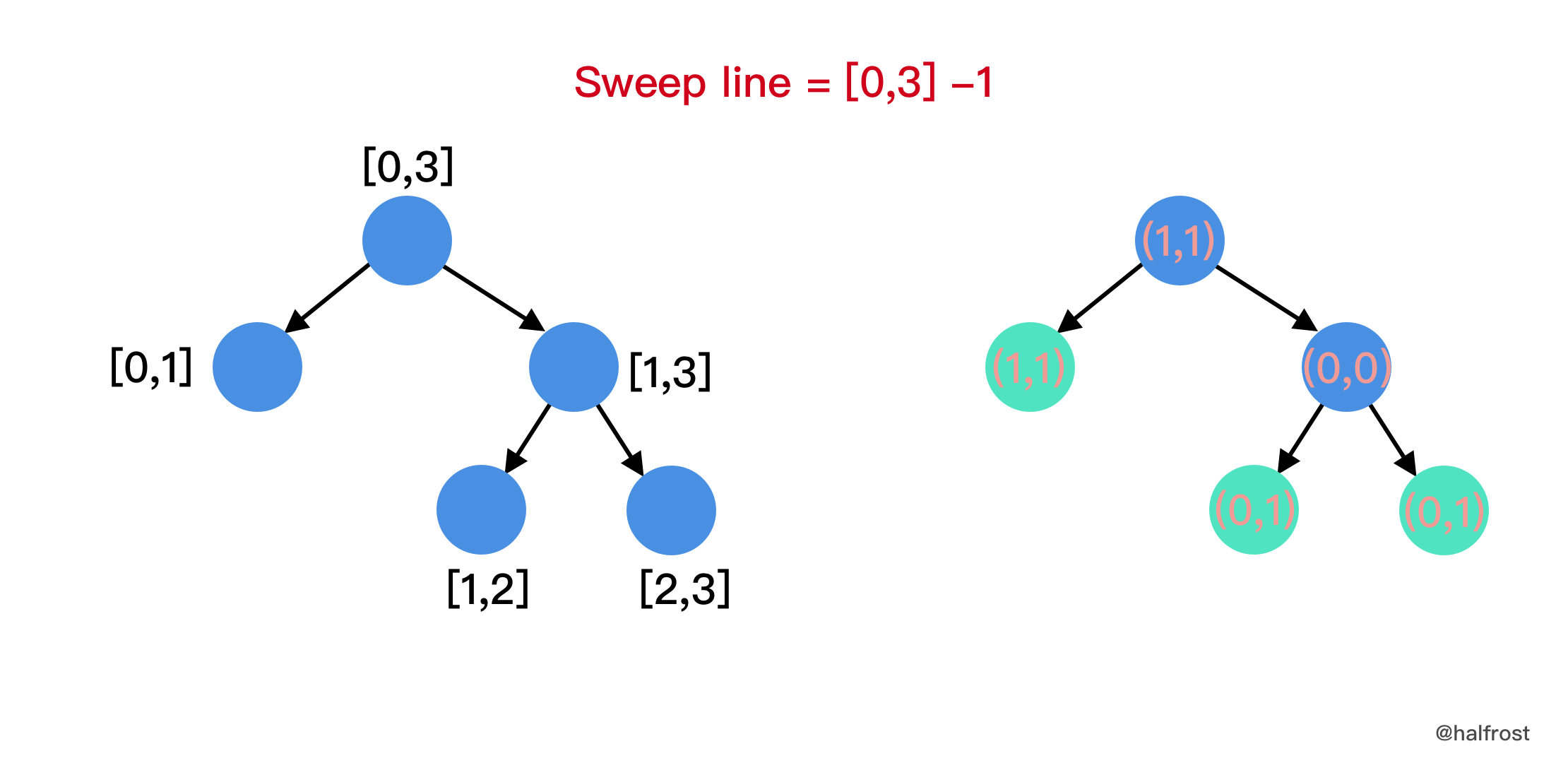
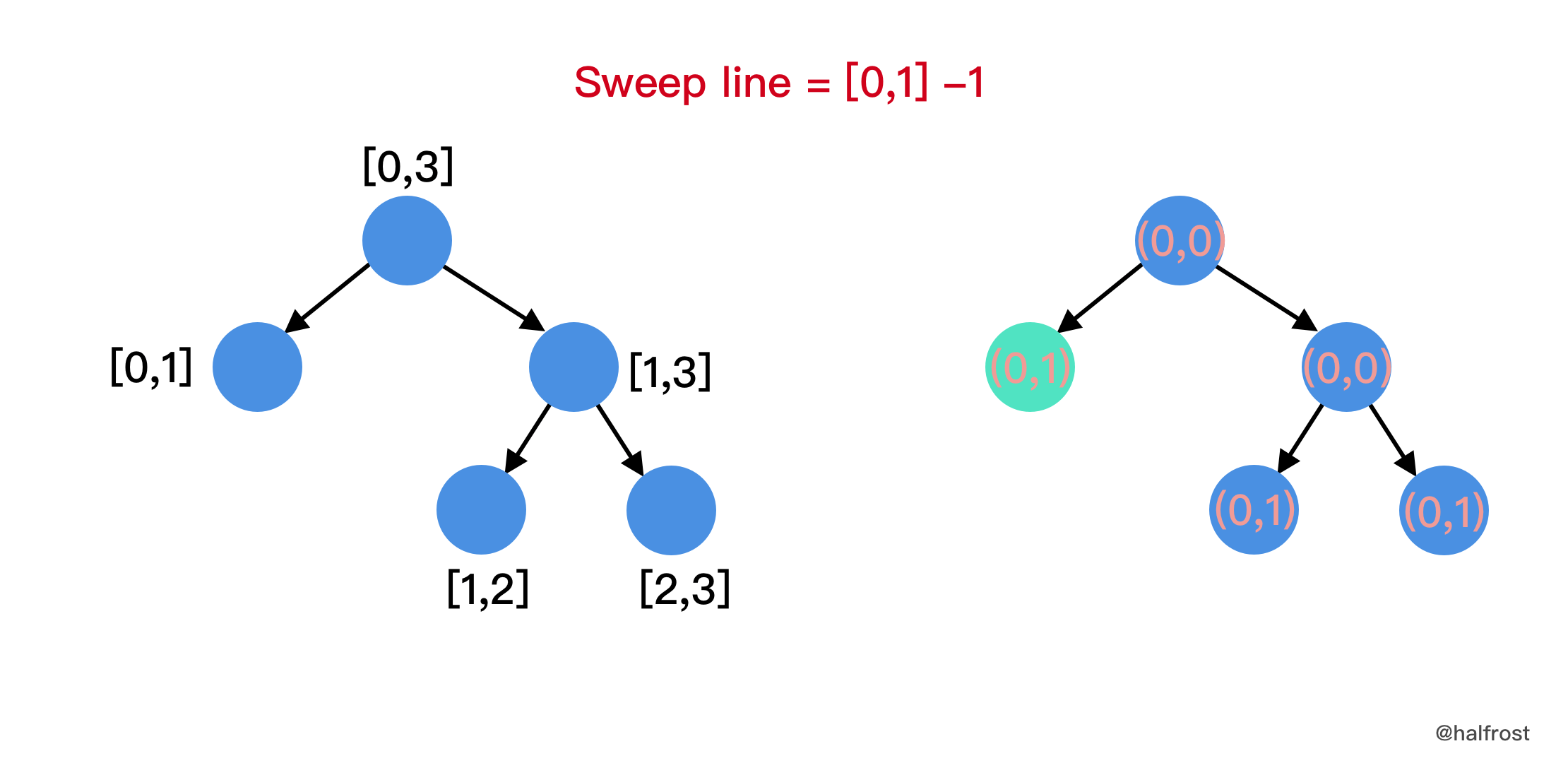
- 遍历到倒数第 2 根扫描线的时候就能得到结果了。因为最后一根扫描线 update 以后,整个线段树全部都归为初始化状态了。
|
||
|
||
|
||
|
||
- 这一题是线段树扫面线解法的经典题。
|