mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-05 16:36:41 +08:00
48 lines
2.8 KiB
Markdown
Executable File
48 lines
2.8 KiB
Markdown
Executable File
# [4. Median of Two Sorted Arrays](https://leetcode.com/problems/median-of-two-sorted-arrays/)
|
||
|
||
|
||
## 题目
|
||
|
||
There are two sorted arrays **nums1** and **nums2** of size m and n respectively.
|
||
|
||
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
|
||
|
||
You may assume **nums1** and **nums2** cannot be both empty.
|
||
|
||
**Example 1:**
|
||
|
||
nums1 = [1, 3]
|
||
nums2 = [2]
|
||
|
||
The median is 2.0
|
||
|
||
**Example 2:**
|
||
|
||
nums1 = [1, 2]
|
||
nums2 = [3, 4]
|
||
|
||
The median is (2 + 3)/2 = 2.5
|
||
|
||
|
||
## 题目大意
|
||
|
||
|
||
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
|
||
|
||
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
|
||
|
||
你可以假设 nums1 和 nums2 不会同时为空。
|
||
|
||
|
||
|
||
## 解题思路
|
||
|
||
|
||
- 给出两个有序数组,要求找出这两个数组合并以后的有序数组中的中位数。要求时间复杂度为 O(log (m+n))。
|
||
- 这一题最容易想到的办法是把两个数组合并,然后取出中位数。但是合并有序数组的操作是 `O(m+n)` 的,不符合题意。看到题目给的 `log` 的时间复杂度,很容易联想到二分搜索。
|
||
- 由于要找到最终合并以后数组的中位数,两个数组的总大小也知道,所以中间这个位置也是知道的。只需要二分搜索一个数组中切分的位置,另一个数组中切分的位置也能得到。为了使得时间复杂度最小,所以二分搜索两个数组中长度较小的那个数组。
|
||
- 关键的问题是如何切分数组 1 和数组 2 。其实就是如何切分数组 1 。先随便二分产生一个 `midA`,切分的线何时算满足了中位数的条件呢?即,线左边的数都小于右边的数,即,`nums1[midA-1] ≤ nums2[midB] && nums2[midB-1] ≤ nums1[midA]` 。如果这些条件都不满足,切分线就需要调整。如果 `nums1[midA] < nums2[midB-1]`,说明 `midA` 这条线划分出来左边的数小了,切分线应该右移;如果 `nums1[midA-1] > nums2[midB]`,说明 midA 这条线划分出来左边的数大了,切分线应该左移。经过多次调整以后,切分线总能找到满足条件的解。
|
||
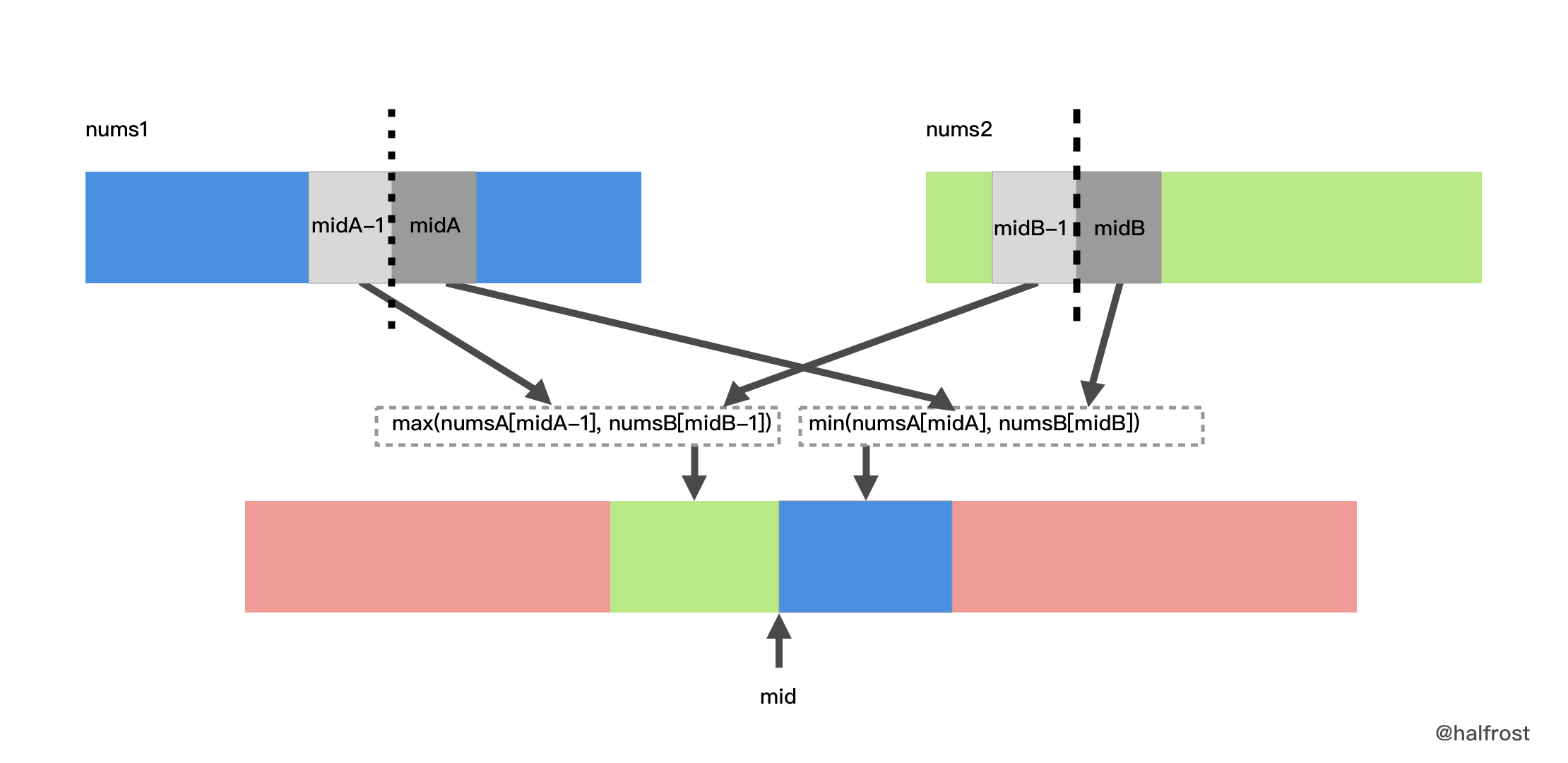
- 假设现在找到了切分的两条线了,`数组 1` 在切分线两边的下标分别是 `midA - 1` 和 `midA`。`数组 2` 在切分线两边的下标分别是 `midB - 1` 和 `midB`。最终合并成最终数组,如果数组长度是奇数,那么中位数就是 `max(nums1[midA-1], nums2[midB-1])`。如果数组长度是偶数,那么中间位置的两个数依次是:`max(nums1[midA-1], nums2[midB-1])` 和 `min(nums1[midA], nums2[midB])`,那么中位数就是 `(max(nums1[midA-1], nums2[midB-1]) + min(nums1[midA], nums2[midB])) / 2`。图示见下图:
|
||
|
||
|