mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 17:44:10 +08:00
79 lines
5.7 KiB
Markdown
Executable File
79 lines
5.7 KiB
Markdown
Executable File
# [1157. Online Majority Element In Subarray](https://leetcode.com/problems/online-majority-element-in-subarray/)
|
||
|
||
|
||
## 题目
|
||
|
||
Implementing the class `MajorityChecker`, which has the following API:
|
||
|
||
- `MajorityChecker(int[] arr)` constructs an instance of MajorityChecker with the given array `arr`;
|
||
- `int query(int left, int right, int threshold)` has arguments such that:
|
||
- `0 <= left <= right < arr.length` representing a subarray of `arr`;
|
||
- `2 * threshold > right - left + 1`, ie. the threshold is always a strict majority of the length of the subarray
|
||
|
||
Each `query(...)` returns the element in `arr[left], arr[left+1], ..., arr[right]` that occurs at least `threshold` times, or `-1` if no such element exists.
|
||
|
||
**Example:**
|
||
|
||
MajorityChecker majorityChecker = new MajorityChecker([1,1,2,2,1,1]);
|
||
majorityChecker.query(0,5,4); // returns 1
|
||
majorityChecker.query(0,3,3); // returns -1
|
||
majorityChecker.query(2,3,2); // returns 2
|
||
|
||
**Constraints:**
|
||
|
||
- `1 <= arr.length <= 20000`
|
||
- `1 <= arr[i] <= 20000`
|
||
- For each query, `0 <= left <= right < len(arr)`
|
||
- For each query, `2 * threshold > right - left + 1`
|
||
- The number of queries is at most `10000`
|
||
|
||
|
||
## 题目大意
|
||
|
||
实现一个 MajorityChecker 的类,它应该具有下述几个 API:
|
||
|
||
- MajorityChecker(int[] arr) 会用给定的数组 arr 来构造一个 MajorityChecker 的实例。
|
||
- int query(int left, int right, int threshold) 有这么几个参数:
|
||
- 0 <= left <= right < arr.length 表示数组 arr 的子数组的长度。
|
||
- 2 * threshold > right - left + 1,也就是说阈值 threshold 始终比子序列长度的一半还要大。
|
||
|
||
每次查询 query(...) 会返回在 arr[left], arr[left+1], ..., arr[right] 中至少出现阈值次数 threshold 的元素,如果不存在这样的元素,就返回 -1。
|
||
|
||
提示:
|
||
|
||
- 1 <= arr.length <= 20000
|
||
- 1 <= arr[i] <= 20000
|
||
- 对于每次查询,0 <= left <= right < len(arr)
|
||
- 对于每次查询,2 * threshold > right - left + 1
|
||
- 查询次数最多为 10000
|
||
|
||
|
||
|
||
|
||
## 解题思路
|
||
|
||
|
||
- 设计一个数据结构,能在任意的一个区间内,查找是否存在众数,众数的定义是:该数字出现的次数大于区间的一半。如果存在众数,一定唯一。如果在给定的区间内找不到众数,则输出 -1 。
|
||
- 这一题有一个很显眼的“暗示”,`2 * threshold > right - left + 1`,这个条件就是摩尔投票算法的前提条件。摩尔投票的思想可以见第 169 题。这一题又要在区间内查询,所以选用线段树这个数据结构来实现。经过分析,可以确定此题的解题思路,摩尔投票 + 线段树。
|
||
- 摩尔投票的思想是用两个变量,candidate 和 count,用来记录待被投票投出去的元素,和候选人累积没被投出去的轮数。如果候选人累积没有被投出去的轮数越多,那么最终成为众数的可能越大。从左往右扫描整个数组,先去第一个元素为 candidate,如果遇到相同的元素就累加轮数,如果遇到不同的元素,就把 candidate 和不同的元素一起投出去。当轮数变成 0 了,再选下一个元素作为 candidate。从左扫到右,就能找到众数了。那怎么和线段树结合起来呢?
|
||
- 线段树是把一个大的区间拆分成很多个小区间,那么考虑这样一个问题。每个小区间内使用摩尔投票,最终把所有小区间合并起来再用一次摩尔投票,得到的结果和对整个区间使用一次摩尔投票的结果是一样的么?答案是一样的。可以这样想,众数总会在一个区间内被选出来,那么其他区间的摩尔投票都是起“中和”作用的,即两两元素一起出局。这个问题想通以后,说明摩尔投票具有可加的性质。既然满足可加,就可以和线段树结合,因为线段树每个线段就是加起来,最终合并成大区间的。
|
||
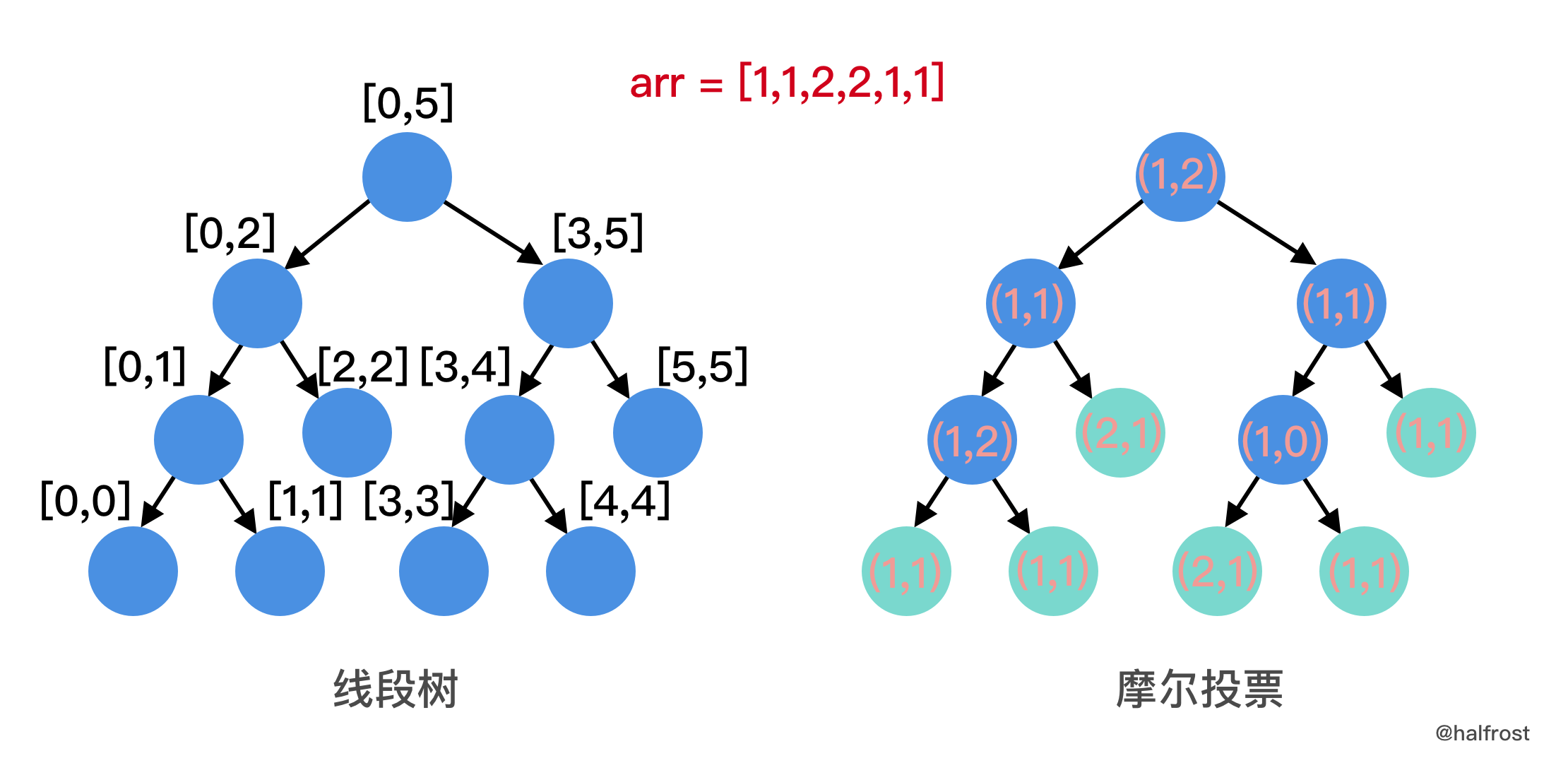
- 举个例子,arr = [1,1,2,2,1,1],先构造线段树,如下左图。
|
||
|
||
|
||
|
||
现在每个线段树的节点不是只存一个 int 数字了,而是存 candidate 和 count。每个节点的 candidate 和 count 分别代表的是该区间内摩尔投票的结果。初始化的时候,先把每个叶子都填满,candidate 是自己,count = 1 。即右图绿色节点。然后在 pushUp 的时候,进行摩尔投票:
|
||
|
||
mc.merge = func(i, j segmentItem) segmentItem {
|
||
if i.candidate == j.candidate {
|
||
return segmentItem{candidate: i.candidate, count: i.count + j.count}
|
||
}
|
||
if i.count > j.count {
|
||
return segmentItem{candidate: i.candidate, count: i.count - j.count}
|
||
}
|
||
return segmentItem{candidate: j.candidate, count: j.count - i.count}
|
||
}
|
||
|
||
直到根节点的 candidate 和 count 都填满。**注意,这里的 count 并不是元素出现的总次数,而是摩尔投票中坚持没有被投出去的轮数**。当线段树构建完成以后,就可以开始查询任意区间内的众数了,candidate 即为众数。接下来还要确定众数是否满足 `threshold` 的条件。
|
||
|
||
- 用一个字典记录每个元素在数组中出现位置的下标,例如上述这个例子,用 map 记录下标:count = map[1:[0 1 4 5] 2:[2 3]]。由于下标在记录过程中是递增的,所以满足二分查找的条件。利用这个字典就可以查出在任意区间内,指定元素出现的次数。例如这里要查找 1 在 [0,5] 区间内出现的个数,那么利用 2 次二分查找,分别找到 `lowerBound` 和 `upperBound`,在 [lowerBound,upperBound) 区间内,都是元素 1 ,那么区间长度即是该元素重复出现的次数,和 `threshold` 比较,如果 ≥ `threshold` 说明找到了答案,否则没有找到就输出 -1 。
|