Use Katex in solution markdown

leetcode/0125.Valid-Palindrome/125. Valid Palindrome.go

@@ -5,9 +5,7 @@ import (
 )
 
 func isPalindrome(s string) bool {
-
 	s = strings.ToLower(s)
-
 	i, j := 0, len(s)-1
 	for i < j {
 		for i < j && !isChar(s[i]) {
@@ -22,7 +20,6 @@ func isPalindrome(s string) bool {
 		i++
 		j--
 	}
-
 	return true
 }
 

leetcode/1203.Sort-Items-by-Groups-Respecting-Dependencies/README.md

@@ -14,7 +14,7 @@ Return any solution if there is more than one solution and return an **empty li
 
 **Example 1:**
 
-![https://assets.leetcode.com/uploads/2019/09/11/1359_ex1.png](https://assets.leetcode.com/uploads/2019/09/11/1359_ex1.png)
+![](https://assets.leetcode.com/uploads/2019/09/11/1359_ex1.png)
 
 ```
 Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
@@ -56,11 +56,11 @@ Explanation: This is the same as example 1 except that 4 needs to be before 6 i
 
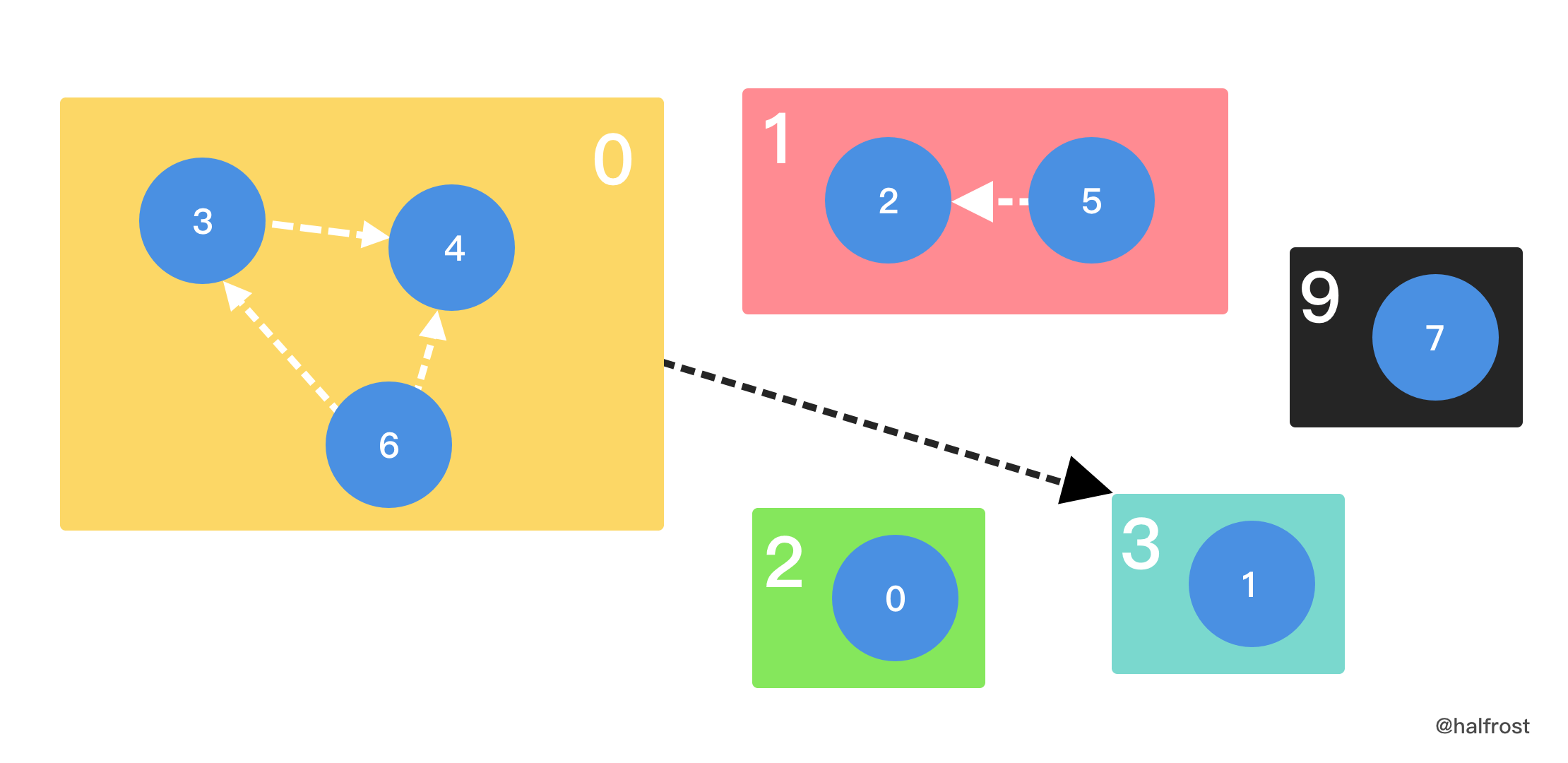
 - 读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是，同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序，第二次拓扑排序排出组内的顺序。为了实现方便，用 map 给虚拟分组标记编号。如下图，将 3，4，6 三个任务打包到 0 号分组里面，将 2，5 两个任务打包到 1 号分组里面，其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里，所以 3 号分组依赖 0 号分组。先组间排序，确定分组顺序，再组内拓扑排序，排出最终顺序。
 
-    ![https://img.halfrost.com/Leetcode/leetcode_1203_1.png](https://img.halfrost.com/Leetcode/leetcode_1203_1.png)
+    ![](https://img.halfrost.com/Leetcode/leetcode_1203_1.png)
 
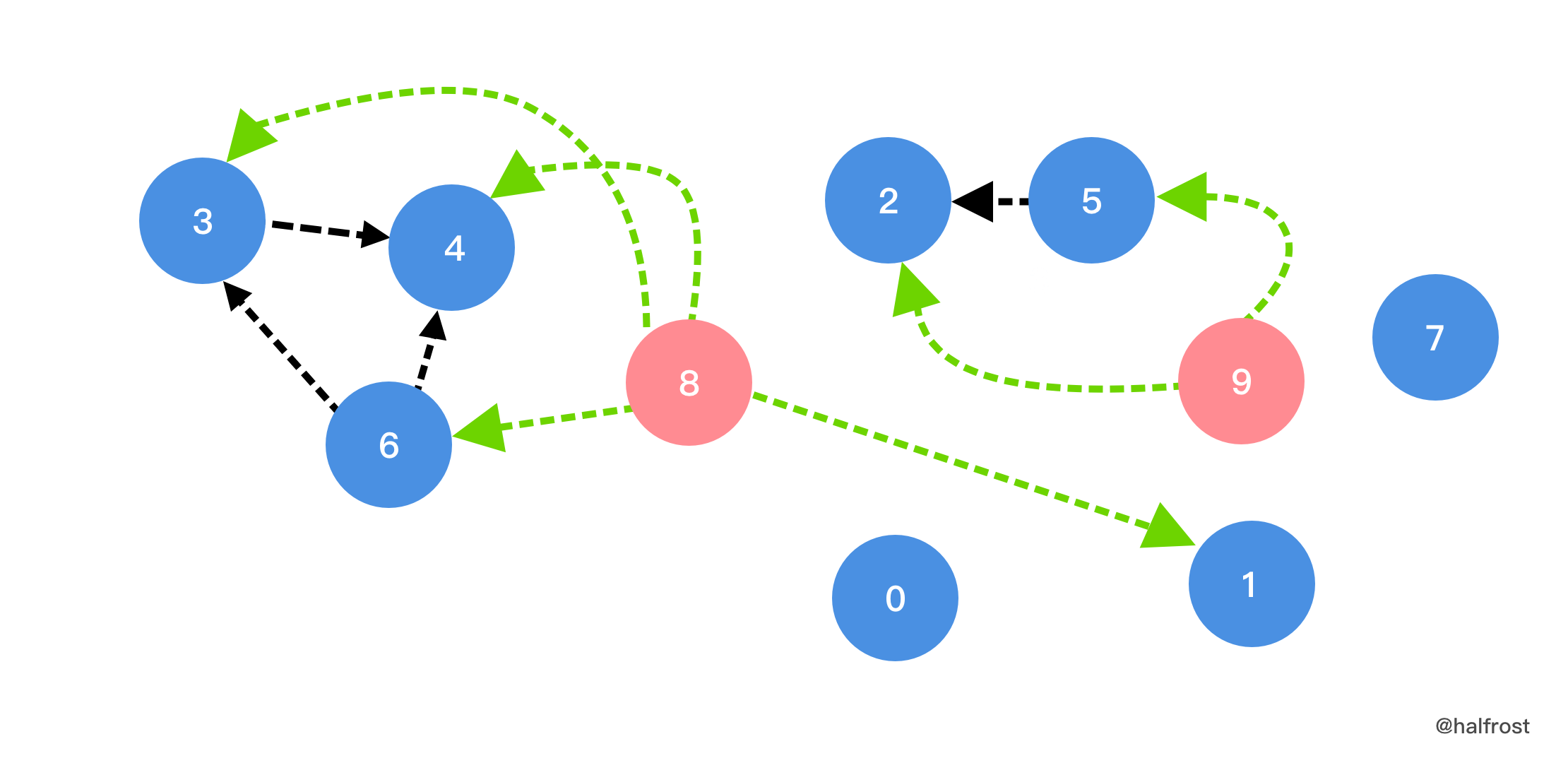
 - 上面的解法可以 AC，但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢？将必须要在一起的结点统一依赖一个虚拟结点，例如下图中的虚拟结点 8 和 9 。3，4，6 都依赖 8 号任务，2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务，由于 6 由依赖 8 ，所以添加 1 依赖 8 的边。通过增加虚拟结点，增加了需要打包在一起结点的入度。构建出以上关系以后，按照入度为 0 的原则，依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ，对它们进行 DFS，必定会使得与它关联的节点都被安排在一起，这样就满足了题意：同一小组的项目，排序后在列表中彼此相邻。一遍扫完，满足题意的顺序就排出来了。这个解法 beat 100%！
 
-    ![https://img.halfrost.com/Leetcode/leetcode_1203_2.png](https://img.halfrost.com/Leetcode/leetcode_1203_2.png)
+    ![](https://img.halfrost.com/Leetcode/leetcode_1203_2.png)
 
 ## 代码