Add BIT

website/content/ChapterThree/Binary_Indexed_Tree.md

@@ -0,0 +1,76 @@
+---
+title: 3.5 Binary Indexed Tree 
+type: docs
+weight: 5
+---
+
+# 树状数组 Binary Indexed Tree (二叉索引树)
+
+针对区间问题，除了常见的线段树解法，还可以考虑树状数组。树状数组也能满足区间内插入数据，删除数据，一段区间内的查询的需求，并且这些操作的时间复杂度能在 O(log n) 或者 O(1) 内完成。
+
+
+## 一. 一维树状数组概念
+
+
+![](https://img.halfrost.com/Blog/ArticleImage/152_0.png)
+
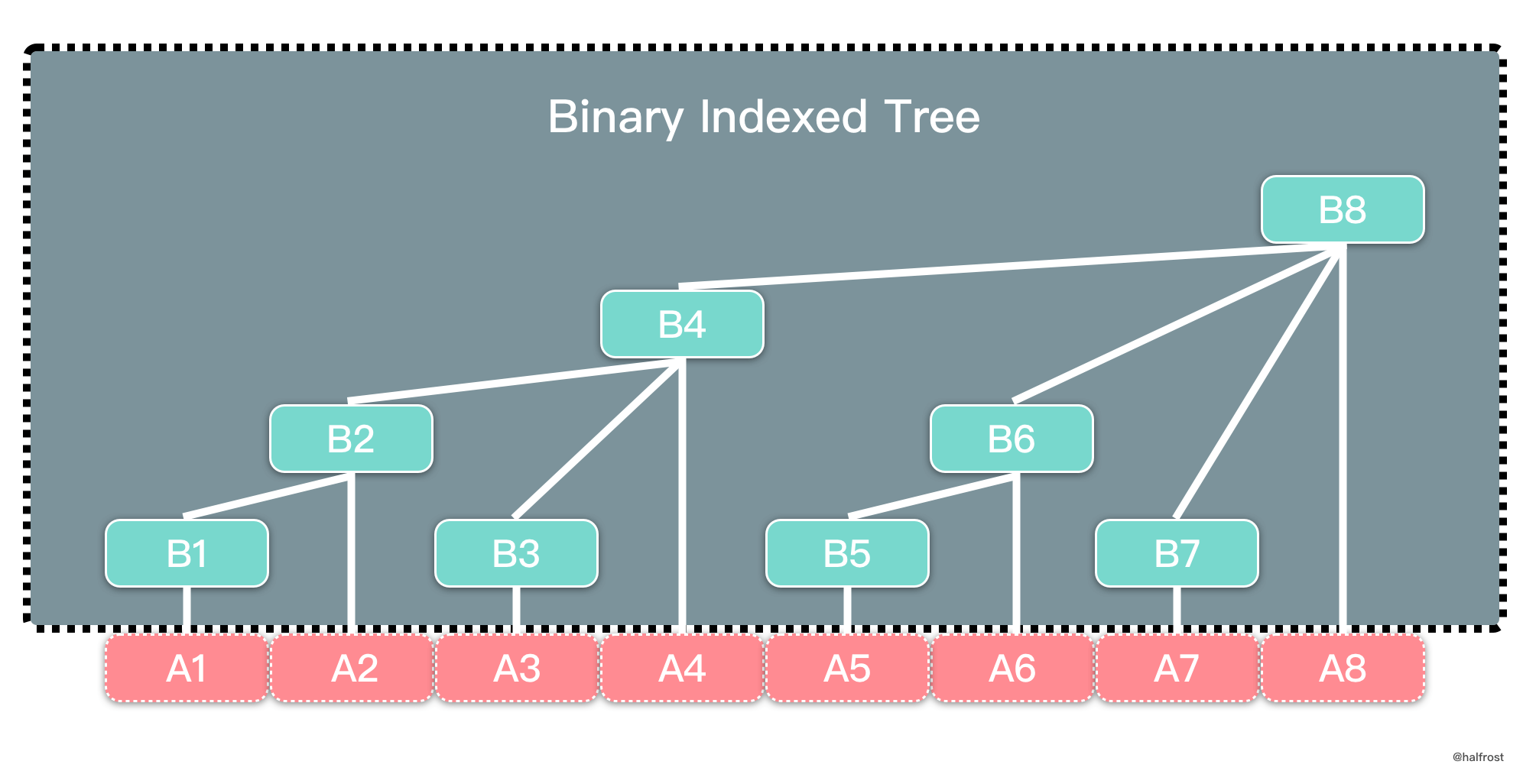
+树状数组名字虽然又有树，又有数组，但是它实际上物理形式还是数组，不过每个节点的含义是树的关系，如上图。树状数组中父子节点下标关系是 p = s + 2^k，其中 k 是子节点下标对应二进制末尾 0 的个数。
+
+例如上图中 A 和 B 都是数组。A 数组正常存储数据，B 数组是树状数组。B4，B6，B7 是 B8 的子节点。4 的二进制是 100，4 + 2^2 = 8，所以 8 是 4 的父节点。同理，7 的二进制 111，7 + 2^0 = 8，8 也是 7 的父节点。
+
+
+## 1. 节点意义
+
+在树状数组中，所有的奇数下标的节点的含义是叶子节点，表示单点，它存的值是原数组相同下标存的值。例如上图中 B1，B3，B5，B7 分别存的值是 A1，A3，A5，A7。所有的偶数下标的节点均是父节点。父节点内存的是区间和。例如 B4 内存的是 B1 + B2 + B3 + A4 = A1 + A2 + A3 + A4。这个区间的左边界是该父节点最左边叶子节点对应的下标，右边界就是自己的下标。例如 B8 表示的区间左边界是 B1，右边界是 B8，所以它表示的区间和是 A1 + A2 + …… + A8。
+
+由数学归纳法可以得出，左边界的下标一定是 i - 2^k + 1，其中 i 为父节点的下标，k 为 i 的二进制中末尾 0 的个数。用数学方式表达偶数节点的区间和：
+
+{{< katex display >}}
+B_{i} = \sum_{j = i - 2^{k} + 1}^{i} A_{j}
+{{< /katex >}}
+
+## 2. 插入操作
+
+## 3. 查询操作
+
+	
+树状数组中查询 [1, i] 区间内的和。按照节点的含义，可以得出下面的关系：
+
+{{< katex display >}}
+\begin{aligned}
+Query(i) &= A_{1} + A_{2} + ...... + A_{i} \\
+&= A_{1} + A_{2} + A_{i-2^{k}} + A_{i-2^{k}+1} + ...... + A_{i} \\
+&= A_{1} + A_{2} + A_{i-2^{k}} + B_{i} \\
+&= Query(i-2^{k}) + B_{i} \\
+&= Query(i-lowbit(i)) + B_{i} \\
+\end{aligned}
+{{< /katex >}}
+
+Bi 是树状数组存的值。Query 操作实际是一个递归的过程。lowbit(i) 表示 2^k，其中 k 是 i 的二进制表示中末尾 0 的个数。i - lowbit(i) 将 i 的二进制中末尾的 1 去掉，最多有 logi 个 1，所以查询操作最坏的时间复杂度是 O(log n)。查询操作实现代码如下：
+
+```go
+
+
+```
+
+## 二. 不同场景下树状数组的功能
+
+根据节点维护的数据含义不同，树状数组可以提供不同的功能来满足各种各样的区间场景。下面我们先以上例中讲述的区间和为例，进而引出 RMQ 的使用场景。
+
+## 1. 单点增减 + 区间求和
+
+## 2. 区间增减 + 单点查询
+
+## 3. 区间增减 + 区间查询
+
+## 三. 常见应用
+
+## 1. 求逆序对
+
+## 2. 求区间逆序对
+
+## 3. 求区间逆序对
+
+## 4. 求第 K 大数
+
+## 四. 二维树状数组