mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 01:15:57 +08:00
Update bit
This commit is contained in:
@ -6,8 +6,83 @@ import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树 Segment Tree,时间复杂度 O(n log n)
|
||||
// 解法一 树状数组,时间复杂度 O(n log n)
|
||||
const LEFTSIDE = 1
|
||||
const RIGHTSIDE = 2
|
||||
|
||||
type Point struct {
|
||||
xAxis int
|
||||
side int
|
||||
index int
|
||||
}
|
||||
|
||||
func getSkyline(buildings [][]int) [][]int {
|
||||
res := [][]int{}
|
||||
if len(buildings) == 0 {
|
||||
return res
|
||||
}
|
||||
allPoints, bit := make([]Point, 0), BinaryIndexedTree{}
|
||||
// [x-axis (value), [1 (left) | 2 (right)], index (building number)]
|
||||
for i, b := range buildings {
|
||||
allPoints = append(allPoints, Point{xAxis: b[0], side: LEFTSIDE, index: i})
|
||||
allPoints = append(allPoints, Point{xAxis: b[1], side: RIGHTSIDE, index: i})
|
||||
}
|
||||
sort.Slice(allPoints, func(i, j int) bool {
|
||||
if allPoints[i].xAxis == allPoints[j].xAxis {
|
||||
return allPoints[i].side < allPoints[j].side
|
||||
}
|
||||
return allPoints[i].xAxis < allPoints[j].xAxis
|
||||
})
|
||||
bit.Init(len(allPoints))
|
||||
kth := make(map[Point]int)
|
||||
for i := 0; i < len(allPoints); i++ {
|
||||
kth[allPoints[i]] = i
|
||||
}
|
||||
for i := 0; i < len(allPoints); i++ {
|
||||
pt := allPoints[i]
|
||||
if pt.side == LEFTSIDE {
|
||||
bit.Add(kth[Point{xAxis: buildings[pt.index][1], side: RIGHTSIDE, index: pt.index}], buildings[pt.index][2])
|
||||
}
|
||||
currHeight := bit.Query(kth[pt] + 1)
|
||||
if len(res) == 0 || res[len(res)-1][1] != currHeight {
|
||||
if len(res) > 0 && res[len(res)-1][0] == pt.xAxis {
|
||||
res[len(res)-1][1] = currHeight
|
||||
} else {
|
||||
res = append(res, []int{pt.xAxis, currHeight})
|
||||
}
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
type BinaryIndexedTree struct {
|
||||
tree []int
|
||||
capacity int
|
||||
}
|
||||
|
||||
// Init define
|
||||
func (bit *BinaryIndexedTree) Init(capacity int) {
|
||||
bit.tree, bit.capacity = make([]int, capacity+1), capacity
|
||||
}
|
||||
|
||||
// Add define
|
||||
func (bit *BinaryIndexedTree) Add(index int, val int) {
|
||||
for ; index > 0; index -= index & -index {
|
||||
bit.tree[index] = max(bit.tree[index], val)
|
||||
}
|
||||
}
|
||||
|
||||
// Query define
|
||||
func (bit *BinaryIndexedTree) Query(index int) int {
|
||||
sum := 0
|
||||
for ; index <= bit.capacity; index += index & -index {
|
||||
sum = max(sum, bit.tree[index])
|
||||
}
|
||||
return sum
|
||||
}
|
||||
|
||||
// 解法三 线段树 Segment Tree,时间复杂度 O(n log n)
|
||||
func getSkyline1(buildings [][]int) [][]int {
|
||||
st, ans, lastHeight, check := template.SegmentTree{}, [][]int{}, 0, false
|
||||
posMap, pos := discretization218(buildings)
|
||||
tmp := make([]int, len(posMap))
|
||||
@ -54,8 +129,8 @@ func max(a int, b int) int {
|
||||
return b
|
||||
}
|
||||
|
||||
// 解法二 扫描线 Sweep Line,时间复杂度 O(n log n)
|
||||
func getSkyline1(buildings [][]int) [][]int {
|
||||
// 解法三 扫描线 Sweep Line,时间复杂度 O(n log n)
|
||||
func getSkyline2(buildings [][]int) [][]int {
|
||||
size := len(buildings)
|
||||
es := make([]E, 0)
|
||||
for i, b := range buildings {
|
||||
|
||||
@ -30,6 +30,16 @@ func Test_Problem218(t *testing.T) {
|
||||
para218{[][]int{{2, 9, 10}, {3, 7, 15}, {5, 12, 12}, {15, 20, 10}, {19, 24, 8}}},
|
||||
ans218{[][]int{{2, 10}, {3, 15}, {7, 12}, {12, 0}, {15, 10}, {20, 8}, {24, 0}}},
|
||||
},
|
||||
|
||||
{
|
||||
para218{[][]int{{1, 2, 1}, {1, 2, 2}, {1, 2, 3}, {2, 3, 1}, {2, 3, 2}, {2, 3, 3}}},
|
||||
ans218{[][]int{{1, 3}, {3, 0}}},
|
||||
},
|
||||
|
||||
{
|
||||
para218{[][]int{{4, 9, 10}, {4, 9, 15}, {4, 9, 12}, {10, 12, 10}, {10, 12, 8}}},
|
||||
ans218{[][]int{{4, 15}, {9, 0}, {10, 10}, {12, 0}}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 218------------------------\n")
|
||||
|
||||
@ -6,7 +6,7 @@ weight: 5
|
||||
|
||||
# 树状数组 Binary Indexed Tree (二叉索引树)
|
||||
|
||||
树状数组或二叉索引树(英语:Binary Indexed Tree),又以其发明者命名为 Fenwick 树,最早由 Peter M. Fenwick 于 1994 年以 A New Data Structure for Cumulative Frequency Tables 为题发表在 SOFTWARE PRACTICE AND EXPERIENCE 上。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和,区间和。针对区间问题,除了常见的线段树解法,还可以考虑树状数组。它可以以 O(log n) 的时间得到任意前缀和{{< katex >}} \sum_{i=1}^{j}A[i],1<=j<=N {{< /katex >}},并同时支持在 O(log n)时间内支持动态单点值的修改(增加或者减少)。空间复杂度 O(n)。
|
||||
树状数组或二叉索引树(Binary Indexed Tree),又以其发明者命名为 Fenwick 树,最早由 Peter M. Fenwick 于 1994 年以 A New Data Structure for Cumulative Frequency Tables 为题发表在 SOFTWARE PRACTICE AND EXPERIENCE 上。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和,区间和。针对区间问题,除了常见的线段树解法,还可以考虑树状数组。它可以以 O(log n) 的时间得到任意前缀和{{< katex >}} \sum_{i=1}^{j}A[i],1<=j<=N {{< /katex >}},并同时支持在 O(log n)时间内支持动态单点值的修改(增加或者减少)。空间复杂度 O(n)。
|
||||
|
||||
> 利用数组实现前缀和,查询本来是 O(1),但是对于频繁更新的数组,每次重新计算前缀和,时间复杂度 O(n)。此时树状数组的优势便立即显现。
|
||||
|
||||
@ -135,6 +135,8 @@ func (bit *BinaryIndexedTree) Query(index int) int {
|
||||
|
||||
这种场景是树状数组最经典的场景。单点增减分别调用 add(i,v) 和 add(i,-v)。区间求和,利用前缀和的思想,求 [m,n] 区间和,即 query(n) - query(m-1)。query(n) 代表 [1,n] 区间内的和,query(m-1) 代表 [1,m-1] 区间内的和,两者相减,即 [m,n] 区间内的和。
|
||||
|
||||
> LeetCode 对应题目是 [307. Range Sum Query - Mutable](https://books.halfrost.com/leetcode/ChapterFour/0300~0399/0307.Range-Sum-Query-Mutable/)、[327. Count of Range Sum](https://books.halfrost.com/leetcode/ChapterFour/0300~0399/0327.Count-of-Range-Sum/)
|
||||
|
||||
### 2. 区间增减 + 单点查询
|
||||
|
||||
这种情况需要做一下转化。定义差分数组 {{< katex >}}C_{i}{{< /katex >}} 代表 {{< katex >}}C_{i} = A_{i} - A_{i-1}{{< /katex >}}。那么:
|
||||
@ -381,7 +383,7 @@ int main()
|
||||
|
||||
具体做法,将 x 轴上的各个区间排序,按照 x 值大小从小到大排序。从左往右依次遍历各个区间。Add() 操作含义是加入每个区间右边界代表后缀区间的最值。这样不需要考虑“移除”最值的问题了。细心的读者可能又有疑问了:能否从右往左遍历区间,Query() 的含义继续延续前缀区间?这样做是可行的,解决第一个问题(维护最值)是可以的。但是这种处理办法解决第二个问题(维护转折点)会遇到麻烦。
|
||||
|
||||
再解决第二个问题(维护转折点)。如果用前缀含义的 Query(),在单点 i 上除了考虑以这个点为结束点的区间,还需要考虑以这个单点 i 为起点的区间。如果是后缀含义的 Query() 就没有这个问题了,{{< katex >}}[i+1,+\infty){{< /katex >}} 这个区间内不用考虑以单点 i 为结束点的区间。
|
||||
再解决第二个问题(维护转折点)。如果用前缀含义的 Query(),在单点 i 上除了考虑以这个点为结束点的区间,还需要考虑以这个单点 i 为起点的区间。如果是后缀含义的 Query() 就没有这个问题了,{{< katex >}}[i+1,+\infty){{< /katex >}} 这个区间内不用考虑以单点 i 为结束点的区间。此题用树状数组代码实现如下:
|
||||
|
||||
|
||||
```go
|
||||
@ -461,6 +463,8 @@ func (bit *BinaryIndexedTree) Query(index int) int {
|
||||
|
||||
```
|
||||
|
||||
> 此题还可以用线段树和扫描线解答。扫描线和树状数组解答此题,非常快。线段树稍微慢一些。
|
||||
|
||||
|
||||
## 三. 常见应用
|
||||
|
||||
@ -534,6 +538,11 @@ func reversePairs(nums []int) int {
|
||||
|
||||
> 注意,计算逆序对的时候不要算重复了。比如,计算当前 j 下标前面比 B[j] 值大的数,又算上 j 下标后面比 B[j] 值小的数。这样计算出现了很多重复。因为 j 下标前面的下标 k,也会寻找 k 下标后面比 B[k] 值小的数,重复计算了。那么统一找比自己下标小,但是值大的元素,那么统一找比自己下标大,但是值小的元素。切勿交叉计算。
|
||||
|
||||
|
||||
> LeetCode 对应题目是 [315. Count of Smaller Numbers After Self](https://books.halfrost.com/leetcode/ChapterFour/0300~0399/0315.Count-of-Smaller-Numbers-After-Self/)、[493. Reverse Pairs](https://books.halfrost.com/leetcode/ChapterFour/0400~0499/0493.Reverse-Pairs/)、[1649. Create Sorted Array through Instructions](https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1649.Create-Sorted-Array-through-Instructions/)
|
||||
|
||||
|
||||
|
||||
### 2. 求区间逆序对
|
||||
|
||||
给定 {{< katex >}} n {{< /katex >}} 个数的序列 {{< katex >}} A[n] \in [1,2^{31}-1] {{< /katex >}},然后给出 {{< katex >}} n \in [1,10^{5}] {{< /katex >}} 次询问 {{< katex >}} [L,R] {{< /katex >}},每次询问区间 {{< katex >}} [L,R] {{< /katex >}} 中满足 {{< katex >}} L \leqslant i < j \leqslant R {{< /katex >}} 且 {{< katex >}} A[i] > A[j] {{< /katex >}} 的下标 {{< katex >}} (i,j) {{< /katex >}} 的对数。
|
||||
@ -617,3 +626,12 @@ func (bit2 *BinaryIndexedTree2D) Query(i, j int) int {
|
||||
return sum
|
||||
}
|
||||
```
|
||||
|
||||
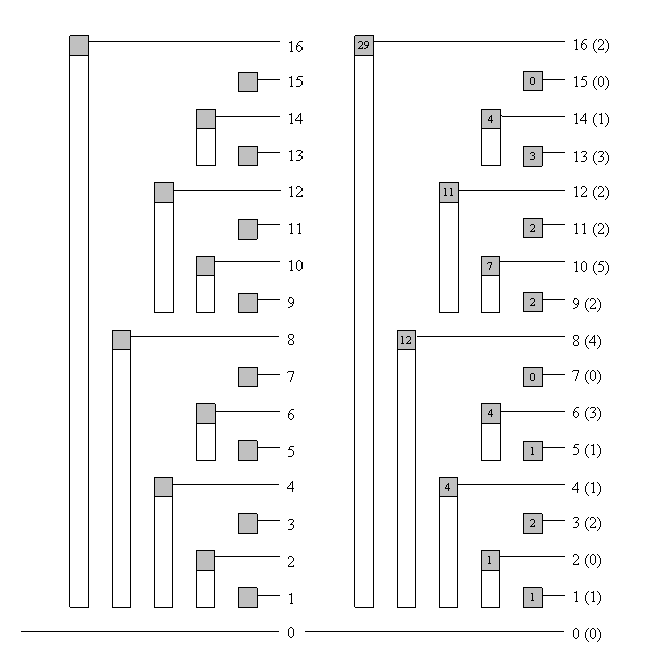
如果把一维树状数组维护的是数轴上的统计问题,
|
||||
|
||||
|
||||
|
||||
|
||||
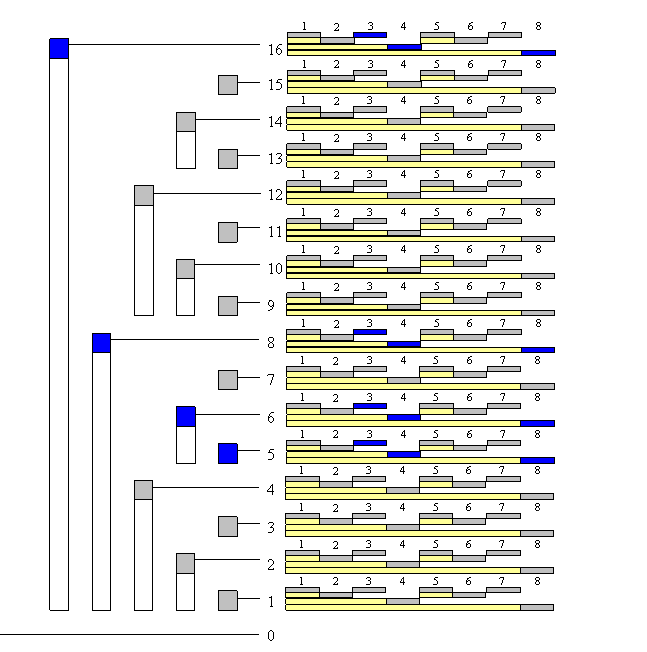
那么二维数组维护的是二维坐标系下的统计问题。X 和 Y 分别都满足一维树状数组的性质。
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user