
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 70. 爬楼梯
[力扣题目链接](https://leetcode.cn/problems/climbing-stairs/)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
* 输入: 2
* 输出: 2
* 解释: 有两种方法可以爬到楼顶。
* 1 阶 + 1 阶
* 2 阶
示例 2:
* 输入: 3
* 输出: 3
* 解释: 有三种方法可以爬到楼顶。
* 1 阶 + 1 阶 + 1 阶
* 1 阶 + 2 阶
* 2 阶 + 1 阶
# 视频讲解
**《代码随想录》算法视频公开课:[带你学透动态规划-爬楼梯|LeetCode:70.爬楼梯)](https://www.bilibili.com/video/BV17h411h7UH),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
## 思路
本题大家如果没有接触过的话,会感觉比较难,多举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
1. 确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
2. 确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!
3. dp数组如何初始化
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层,也有一种方法,什么都不做也就是一种方法即:dp[0] = 1,相当于直接站在楼顶。
但总有点牵强的成分。
那还这么理解呢:我就认为跑到第0层,方法就是0啊,一步只能走一个台阶或者两个台阶,然而楼层是0,直接站楼顶上了,就是不用方法,dp[0]就应该是0.
**其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1**。
从dp数组定义的角度上来说,dp[0] = 0 也能说得通。
需要注意的是:题目中说了n是一个正整数,题目根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4. 确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5. 举例推导dp数组
举例当n为5的时候,dp table(dp数组)应该是这样的
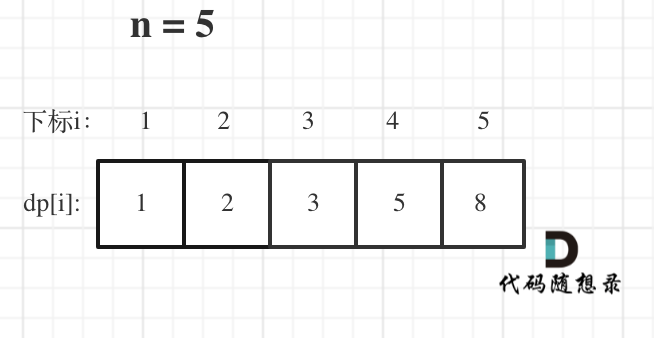
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
**此时大家应该发现了,这不就是斐波那契数列么!**
唯一的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
以上五部分析完之后,C++代码如下:
```CPP
// 版本一
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针
vector dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
```
* 时间复杂度:$O(n)$
* 空间复杂度:$O(n)$
当然依然也可以,优化一下空间复杂度,代码如下:
```CPP
// 版本二
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
int dp[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
};
```
* 时间复杂度:$O(n)$
* 空间复杂度:$O(1)$
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,**但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化**。
因为版本一才能体现出动规的思想精髓,递推的状态变化。
## 拓展
这道题目还可以继续深化,就是一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。
这又有难度了,这其实是一个完全背包问题,但力扣上没有这种题目,所以后续我在讲解背包问题的时候,今天这道题还会从背包问题的角度上来再讲一遍。 如果想提前看一下,可以看这篇:[70.爬楼梯完全背包版本](https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html)
这里我先给出我的实现代码:
```CPP
class Solution {
public:
int climbStairs(int n) {
vector dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // 把m换成2,就可以AC爬楼梯这道题
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
```
代码中m表示最多可以爬m个台阶。
**以上代码不能运行哈,我主要是为了体现只要把m换成2,粘过去,就可以AC爬楼梯这道题,不信你就粘一下试试**。
**此时我就发现一个绝佳的大厂面试题**,第一道题就是单纯的爬楼梯,然后看候选人的代码实现,如果把dp[0]的定义成1了,就可以发难了,为什么dp[0]一定要初始化为1,此时可能候选人就要强行给dp[0]应该是1找各种理由。那这就是一个考察点了,对dp[i]的定义理解的不深入。
然后可以继续发难,如果一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。这道题目leetcode上并没有原题,绝对是考察候选人算法能力的绝佳好题。
这一连套问下来,候选人算法能力如何,面试官心里就有数了。
**其实大厂面试最喜欢的问题就是这种简单题,然后慢慢变化,在小细节上考察候选人**。
## 总结
这道题目和[动态规划:斐波那契数](https://programmercarl.com/0509.斐波那契数.html)题目基本是一样的,但是会发现本题相比[动态规划:斐波那契数](https://programmercarl.com/0509.斐波那契数.html)难多了,为什么呢?
关键是 [动态规划:斐波那契数](https://programmercarl.com/0509.斐波那契数.html) 题目描述就已经把动规五部曲里的递归公式和如何初始化都给出来了,剩下几部曲也自然而然的推出来了。
而本题,就需要逐个分析了,大家现在应该初步感受出[关于动态规划,你该了解这些!](https://programmercarl.com/动态规划理论基础.html)里给出的动规五部曲了。
简单题是用来掌握方法论的,例如昨天斐波那契的题目够简单了吧,但昨天和今天可以使用一套方法分析出来的,这就是方法论!
所以不要轻视简单题,那种凭感觉就刷过去了,其实和没掌握区别不大,只有掌握方法论并说清一二三,才能触类旁通,举一反三哈!
就酱,循序渐进学算法,认准「代码随想录」!
## 其他语言版本
### Java
```java
// 常规方式
public int climbStairs(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
```
```Java
// 用变量记录代替数组
class Solution {
public int climbStairs(int n) {
if(n <= 2) return n;
int a = 1, b = 2, sum = 0;
for(int i = 3; i <= n; i++){
sum = a + b; // f(i - 1) + f(i - 2)
a = b; // 记录f(i - 1),即下一轮的f(i - 2)
b = sum; // 记录f(i),即下一轮的f(i - 1)
}
return b;
}
}
```
### Python
动态规划(版本一)
```python
# 空间复杂度为O(n)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
```
动态规划(版本二)
```python
# 空间复杂度为O(3)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * 3
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
total = dp[1] + dp[2]
dp[1] = dp[2]
dp[2] = total
return dp[2]
```
动态规划(版本三)
```python
# 空间复杂度为O(1)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
prev1 = 1
prev2 = 2
for i in range(3, n + 1):
total = prev1 + prev2
prev1 = prev2
prev2 = total
return prev2
```
### Go
```Go
func climbStairs(n int) int {
if n == 1 {
return 1
}
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 2
for i := 3; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
```
### Javascript
```Javascript
var climbStairs = function(n) {
// dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
// dp[i] = dp[i - 1] + dp[i - 2]
let dp = [1 , 2]
for(let i = 2; i < n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n - 1]
};
```
### TypeScript
> 爬2阶
```typescript
function climbStairs(n: number): number {
/**
dp[i]: i阶楼梯的方法种数
dp[1]: 1;
dp[2]: 2;
...
dp[i]: dp[i - 1] + dp[i - 2];
*/
const dp: number[] = [];
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
```
> 爬m阶
```typescript
function climbStairs(n: number): number {
/**
一次可以爬m阶
dp[i]: i阶楼梯的方法种数
dp[1]: 1;
dp[2]: 2;
dp[3]: dp[2] + dp[1];
...
dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; 从i-1加到max(i-m, 1)
*/
const m: number = 2; // 本题m为2
const dp: number[] = new Array(n + 1).fill(0);
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
const end: number = Math.max(i - m, 1);
for (let j = i - 1; j >= end; j--) {
dp[i] += dp[j];
}
}
return dp[n];
};
```
### C
```c
int climbStairs(int n){
//若n<=2,返回n
if(n <= 2)
return n;
//初始化dp数组,数组大小为n+1
int *dp = (int *)malloc(sizeof(int) * (n + 1));
dp[0] = 0, dp[1] = 1, dp[2] = 2;
//从前向后遍历数组,dp[i] = dp[i-1] + dp[i-2]
int i;
for(i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
//返回dp[n]
return dp[n];
}
```
优化空间复杂度:
```c
int climbStairs(int n){
//若n<=2,返回n
if(n <= 2)
return n;
//初始化dp数组,数组大小为3
int *dp = (int *)malloc(sizeof(int) * 3);
dp[1] = 1, dp[2] = 2;
//只记录前面两个台阶的状态
int i;
for(i = 3; i <= n; ++i) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
//返回dp[2]
return dp[2];
}
```
### Scala
```scala
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var dp = new Array[Int](n + 1)
dp(1) = 1
dp(2) = 2
for (i <- 3 to n) {
dp(i) = dp(i - 1) + dp(i - 2)
}
dp(n)
}
}
```
优化空间复杂度:
```scala
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var (a, b) = (1, 2)
for (i <- 3 to n) {
var tmp = a + b
a = b
b = tmp
}
b // 最终返回b
}
}
```
### C#
```c#
public class Solution {
public int ClimbStairs(int n) {
if(n<=2) return n;
int[] dp = new int[2] { 1, 2 };
for (int i = 3; i <= n; i++)
{
int temp = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = temp;
}
return dp[1];
}
}
```
### Rust
```rust
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
if n <= 1 {
return n;
}
let (mut a, mut b, mut f) = (1, 1, 0);
for _ in 2..=n {
f = a + b;
a = b;
b = f;
}
f
}
```
dp 数组
```rust
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![0; n + 1];
dp[0] = 1;
dp[1] = 1;
for i in 2..=n {
dp[i] = dp[i - 1] + dp[i - 2];
}
dp[n]
}
}
```

