



欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 39. 组合总和
[力扣题目链接](https://leetcode-cn.com/problems/combination-sum/)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
* 所有数字(包括 target)都是正整数。
* 解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
# 思路
[B站视频讲解-组合总和](https://www.bilibili.com/video/BV1KT4y1M7HJ)
题目中的**无限制重复被选取,吓得我赶紧想想 出现0 可咋办**,然后看到下面提示:1 <= candidates[i] <= 200,我就放心了。
本题和[77.组合](https://programmercarl.com/0077.组合.html),[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
本题搜索的过程抽象成树形结构如下:

注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
而在[77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html) 中都可以知道要递归K层,因为要取k个元素的组合。
## 回溯三部曲
* 递归函数参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
首先是题目中给出的参数,集合candidates, 和目标值target。
此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
**本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?**
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:[77.组合](https://programmercarl.com/0077.组合.html),[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:[17.电话号码的字母组合](https://programmercarl.com/0017.电话号码的字母组合.html)
**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我再讲解排列的时候就重点介绍**。
代码如下:
```CPP
vector> result;
vector path;
void backtracking(vector& candidates, int target, int sum, int startIndex)
```
* 递归终止条件
在如下树形结构中:

从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
sum等于target的时候,需要收集结果,代码如下:
```CPP
if (sum > target) {
return;
}
if (sum == target) {
result.push_back(path);
return;
}
```
* 单层搜索的逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。
**注意本题和[77.组合](https://programmercarl.com/0077.组合.html)、[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)的一个区别是:本题元素为可重复选取的**。
如何重复选取呢,看代码,注释部分:
```CPP
for (int i = startIndex; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 关键点:不用i+1了,表示可以重复读取当前的数
sum -= candidates[i]; // 回溯
path.pop_back(); // 回溯
}
```
按照[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中给出的模板,不难写出如下C++完整代码:
```CPP
// 版本一
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& candidates, int target, int sum, int startIndex) {
if (sum > target) {
return;
}
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数
sum -= candidates[i];
path.pop_back();
}
}
public:
vector> combinationSum(vector& candidates, int target) {
result.clear();
path.clear();
backtracking(candidates, target, 0, 0);
return result;
}
};
```
## 剪枝优化
在这个树形结构中:

以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
那么可以在for循环的搜索范围上做做文章了。
**对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历**。
如图:
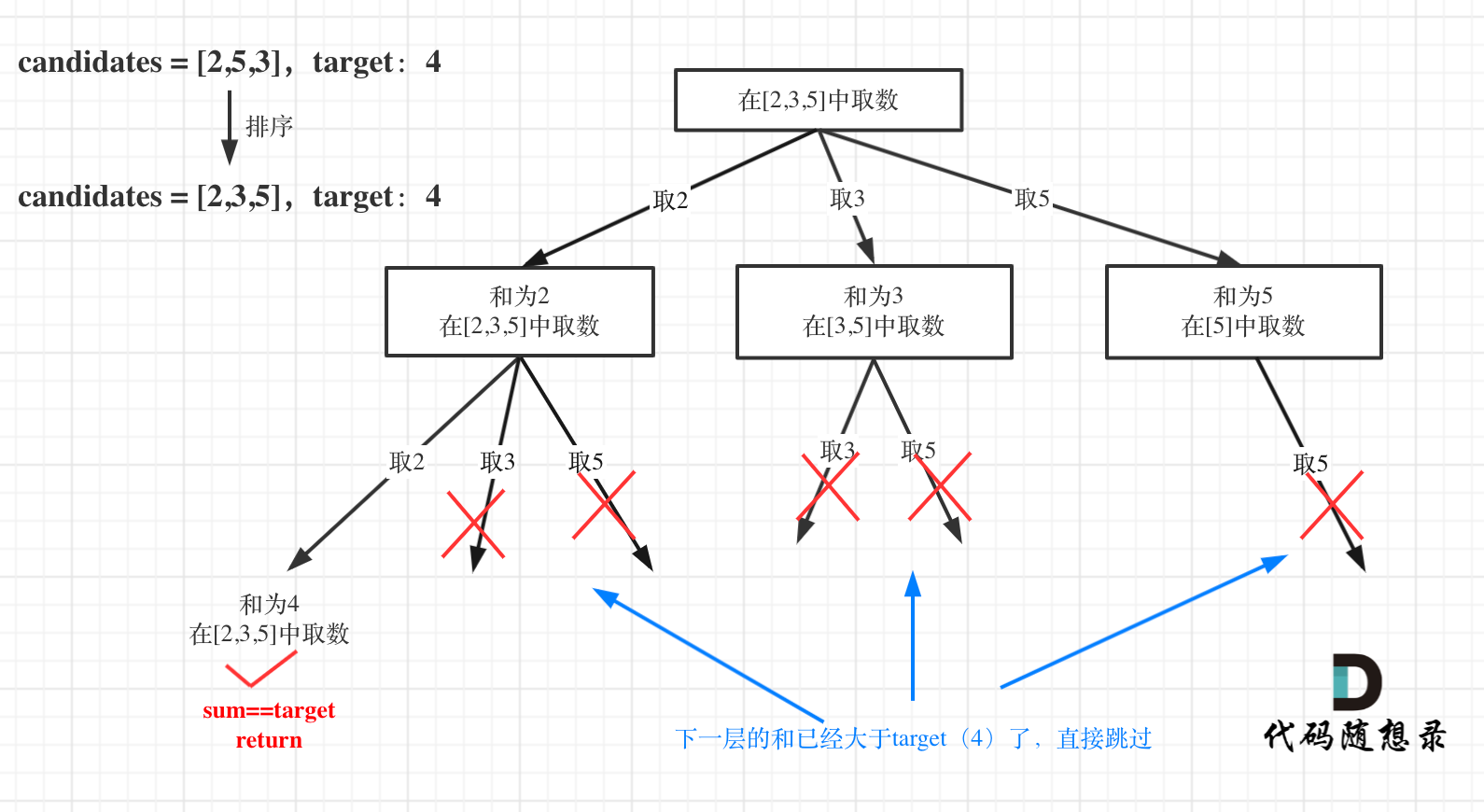
for循环剪枝代码如下:
```
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
```
整体代码如下:(注意注释的部分)
```CPP
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
// 如果 sum + candidates[i] > target 就终止遍历
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i);
sum -= candidates[i];
path.pop_back();
}
}
public:
vector> combinationSum(vector& candidates, int target) {
result.clear();
path.clear();
sort(candidates.begin(), candidates.end()); // 需要排序
backtracking(candidates, target, 0, 0);
return result;
}
};
```
# 总结
本题和我们之前讲过的[77.组合](https://programmercarl.com/0077.组合.html)、[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)有两点不同:
* 组合没有数量要求
* 元素可无限重复选取
针对这两个问题,我都做了详细的分析。
并且给出了对于组合问题,什么时候用startIndex,什么时候不用,并用[17.电话号码的字母组合](https://programmercarl.com/0017.电话号码的字母组合.html)做了对比。
最后还给出了本题的剪枝优化,这个优化如果是初学者的话并不容易想到。
**在求和问题中,排序之后加剪枝是常见的套路!**
可以看出我写的文章都会大量引用之前的文章,就是要不断作对比,分析其差异,然后给出代码解决的方法,这样才能彻底理解题目的本质与难点。
# 其他语言版本
## Java
```Java
// 剪枝优化
class Solution {
public List> combinationSum(int[] candidates, int target) {
List> res = new ArrayList<>();
Arrays.sort(candidates); // 先进行排序
backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
return res;
}
public void backtracking(List> res, List path, int[] candidates, int target, int sum, int idx) {
// 找到了数字和为 target 的组合
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = idx; i < candidates.length; i++) {
// 如果 sum + candidates[i] > target 就终止遍历
if (sum + candidates[i] > target) break;
path.add(candidates[i]);
backtracking(res, path, candidates, target, sum + candidates[i], i);
path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素
}
}
}
```
## Python
```python3
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
path = []
def backtrack(candidates,target,sum,startIndex):
if sum > target: return
if sum == target: return res.append(path[:])
for i in range(startIndex,len(candidates)):
if sum + candidates[i] >target: return #如果 sum + candidates[i] > target 就终止遍历
sum += candidates[i]
path.append(candidates[i])
backtrack(candidates,target,sum,i) #startIndex = i:表示可以重复读取当前的数
sum -= candidates[i] #回溯
path.pop() #回溯
candidates = sorted(candidates) #需要排序
backtrack(candidates,target,0,0)
return res
```
## Go
主要在于递归中传递下一个数字
```go
func combinationSum(candidates []int, target int) [][]int {
var trcak []int
var res [][]int
backtracking(0,0,target,candidates,trcak,&res)
return res
}
func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int){
//终止条件
if sum==target{
tmp:=make([]int,len(trcak))
copy(tmp,trcak)//拷贝
*res=append(*res,tmp)//放入结果集
return
}
if sum>target{return}
//回溯
for i:=startIndex;i target) return;
if (sum === target) {
res.push(Array.from(path));
return;
}
for(let i = j; i < candidates.length; i++ ) {
const n = candidates[i];
if(n > target - sum) continue;
path.push(n);
sum += n;
backtracking(i, sum);
path.pop();
sum -= n;
}
}
};
```
## C
```c
int* path;
int pathTop;
int** ans;
int ansTop;
//记录每一个和等于target的path数组长度
int* length;
void backTracking(int target, int index, int* candidates, int candidatesSize, int sum) {
//若sum>=target就应该终止遍历
if(sum >= target) {
//若sum等于target,将当前的组合放入ans数组中
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
ans[ansTop] = tempPath;
length[ansTop++] = pathTop;
}
return ;
}
int i;
for(i = index; i < candidatesSize; i++) {
//将当前数字大小加入sum
sum+=candidates[i];
path[pathTop++] = candidates[i];
backTracking(target, i, candidates, candidatesSize, sum);
sum-=candidates[i];
pathTop--;
}
}
int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
//初始化变量
path = (int*)malloc(sizeof(int) * 50);
ans = (int**)malloc(sizeof(int*) * 200);
length = (int*)malloc(sizeof(int) * 200);
ansTop = pathTop = 0;
backTracking(target, 0, candidates, candidatesSize, 0);
//设置返回的数组大小
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}
```
-----------------------
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)




