diff --git a/problems/0015.三数之和.md b/problems/0015.三数之和.md
index f336be5b..da319866 100644
--- a/problems/0015.三数之和.md
+++ b/problems/0015.三数之和.md
@@ -29,6 +29,8 @@
# 思路
+针对本题，我录制了视频讲解：[梦破碎的地方！| LeetCode：15.三数之和](https://www.bilibili.com/video/BV1GW4y127qo)，结合本题解一起看，事半功倍！
+
**注意[0， 0， 0， 0] 这组数据**
## 哈希解法
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
index 3813424a..d6b55fd6 100644
--- a/problems/0018.四数之和.md
+++ b/problems/0018.四数之和.md
@@ -29,6 +29,8 @@
# 思路
+针对本题，我录制了视频讲解：[难在去重和剪枝！| LeetCode：18. 四数之和](https://www.bilibili.com/video/BV1DS4y147US)，结合本题解一起看，事半功倍！
+
四数之和，和[15.三数之和](https://programmercarl.com/0015.三数之和.html)是一个思路，都是使用双指针法, 基本解法就是在[15.三数之和](https://programmercarl.com/0015.三数之和.html) 的基础上再套一层for循环。
但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。比如：数组是`[-4, -3, -2, -1]`，`target`是`-10`，不能因为`-4 > -10`而跳过。但是我们依旧可以去做剪枝，逻辑变成`nums[i] > target && (nums[i] >=0 || target >= 0)`就可以了。
diff --git a/problems/0027.移除元素.md b/problems/0027.移除元素.md
index e99fee91..12f88c75 100644
--- a/problems/0027.移除元素.md
+++ b/problems/0027.移除元素.md
@@ -28,7 +28,7 @@
## 思路
-[本题B站视频讲解](https://www.bilibili.com/video/BV12A4y1Z7LP)
+针对本题，我录制了视频讲解：[数组中移除元素并不容易！LeetCode：27. 移除元素](https://www.bilibili.com/video/BV12A4y1Z7LP)，结合本题解一起看，事半功倍！
有的同学可能说了，多余的元素，删掉不就得了。
diff --git a/problems/0059.螺旋矩阵II.md b/problems/0059.螺旋矩阵II.md
index bf0a279e..aa3c848d 100644
--- a/problems/0059.螺旋矩阵II.md
+++ b/problems/0059.螺旋矩阵II.md
@@ -24,7 +24,7 @@
## 思路
-为了利于录友们理解，我特意录制了视频，[拿下螺旋矩阵，《代码随想录》第五题！](https://www.bilibili.com/video/BV1SL4y1N7mV)，结合本篇文章一起看，效果更佳。
+为了利于录友们理解，我特意录制了视频，[拿下螺旋矩阵！LeetCode：59.螺旋矩阵II](https://www.bilibili.com/video/BV1SL4y1N7mV)，结合视频一起看，事半功倍！
这道题目可以说在面试中出现频率较高的题目，**本题并不涉及到什么算法，就是模拟过程，但却十分考察对代码的掌控能力。**
diff --git a/problems/0134.加油站.md b/problems/0134.加油站.md
index e5d50a9b..7e4f74f0 100644
--- a/problems/0134.加油站.md
+++ b/problems/0134.加油站.md
@@ -77,10 +77,9 @@ public:
};
```
-* 时间复杂度：$O(n^2)$
-* 空间复杂度：$O(1)$
+* 时间复杂度：O(n^2)
+* 空间复杂度：O(1)
-C++暴力解法在leetcode上提交也可以过。
## 贪心算法（方法一）
diff --git a/problems/0151.翻转字符串里的单词.md b/problems/0151.翻转字符串里的单词.md
index d0719469..a848d6a3 100644
--- a/problems/0151.翻转字符串里的单词.md
+++ b/problems/0151.翻转字符串里的单词.md
@@ -31,8 +31,9 @@
# 思路
-**这道题目可以说是综合考察了字符串的多种操作。**
+针对本题，我录制了视频讲解：[字符串复杂操作拿捏了！ | LeetCode:151.翻转字符串里的单词](https://www.bilibili.com/video/BV1uT41177fX)，结合本题解一起看，事半功倍！
+**这道题目可以说是综合考察了字符串的多种操作。**
一些同学会使用split库函数，分隔单词，然后定义一个新的string字符串，最后再把单词倒序相加，那么这道题题目就是一道水题了，失去了它的意义。
@@ -81,17 +82,14 @@ void removeExtraSpaces(string& s) {
如果不仔细琢磨一下erase的时间复杂度，还以为以上的代码是O(n)的时间复杂度呢。
-想一下真正的时间复杂度是多少，一个erase本来就是O(n)的操作，erase实现原理题目：[数组：就移除个元素很难么？](https://programmercarl.com/0027.移除元素.html)，最优的算法来移除元素也要O(n)。
+想一下真正的时间复杂度是多少，一个erase本来就是O(n)的操作。
erase操作上面还套了一个for循环，那么以上代码移除冗余空格的代码时间复杂度为O(n^2)。
那么使用双指针法来去移除空格，最后resize（重新设置）一下字符串的大小，就可以做到O(n)的时间复杂度。
-如果对这个操作比较生疏了，可以再看一下这篇文章：[数组：就移除个元素很难么？](https://programmercarl.com/0027.移除元素.html)是如何移除元素的。
-
-那么使用双指针来移除冗余空格代码如下： fastIndex走的快，slowIndex走的慢，最后slowIndex就标记着移除多余空格后新字符串的长度。
-
```CPP
+//版本一
void removeExtraSpaces(string& s) {
int slowIndex = 0, fastIndex = 0; // 定义快指针，慢指针
// 去掉字符串前面的空格
@@ -121,13 +119,37 @@ void removeExtraSpaces(string& s) {
1. leetcode上的测试集里，字符串的长度不够长，如果足够长，性能差距会非常明显。
2. leetcode的测程序耗时不是很准确的。
+版本一的代码是比较如何一般思考过程，就是 先移除字符串钱的空格，在移除中间的，在移除后面部分。
+
+不过其实还可以优化，这部分和[27.移除元素](https://programmercarl.com/0027.移除元素.html)的逻辑是一样一样的，本题是移除空格，而 27.移除元素 就是移除元素。
+
+所以代码可以写的很精简，大家可以看 如下 代码 removeExtraSpaces 函数的实现：
+
+```CPP
+// 版本二
+void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
+ int slow = 0; //整体思想参考https://programmercarl.com/0027.移除元素.html
+ for (int i = 0; i < s.size(); ++i) { //
+ if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
+ if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
+ while (i < s.size() && s[i] != ' ') { //补上该单词，遇到空格说明单词结束。
+ s[slow++] = s[i++];
+ }
+ }
+ }
+ s.resize(slow); //slow的大小即为去除多余空格后的大小。
+}
+```
+
+如果以上代码看不懂，建议先把 [27.移除元素](https://programmercarl.com/0027.移除元素.html)这道题目做了，或者看视频讲解：[数组中移除元素并不容易！LeetCode：27. 移除元素](https://www.bilibili.com/video/BV12A4y1Z7LP) 。
+
此时我们已经实现了removeExtraSpaces函数来移除冗余空格。
还做实现反转字符串的功能，支持反转字符串子区间，这个实现我们分别在[344.反转字符串](https://programmercarl.com/0344.反转字符串.html)和[541.反转字符串II](https://programmercarl.com/0541.反转字符串II.html)里已经讲过了。
代码如下：
-```
+```CPP
// 反转字符串s中左闭又闭的区间[start, end]
void reverse(string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
@@ -136,105 +158,19 @@ void reverse(string& s, int start, int end) {
}
```
-本题C++整体代码
-
+整体代码如下：
```CPP
-// 版本一
class Solution {
public:
- // 反转字符串s中左闭又闭的区间[start, end]
- void reverse(string& s, int start, int end) {
- for (int i = start, j = end; i < j; i++, j--) {
- swap(s[i], s[j]);
- }
- }
-
- // 移除冗余空格：使用双指针（快慢指针法）O(n)的算法
- void removeExtraSpaces(string& s) {
- int slowIndex = 0, fastIndex = 0; // 定义快指针，慢指针
- // 去掉字符串前面的空格
- while (s.size() > 0 && fastIndex < s.size() && s[fastIndex] == ' ') {
- fastIndex++;
- }
- for (; fastIndex < s.size(); fastIndex++) {
- // 去掉字符串中间部分的冗余空格
- if (fastIndex - 1 > 0
- && s[fastIndex - 1] == s[fastIndex]
- && s[fastIndex] == ' ') {
- continue;
- } else {
- s[slowIndex++] = s[fastIndex];
- }
- }
- if (slowIndex - 1 > 0 && s[slowIndex - 1] == ' ') { // 去掉字符串末尾的空格
- s.resize(slowIndex - 1);
- } else {
- s.resize(slowIndex); // 重新设置字符串大小
- }
- }
-
- string reverseWords(string s) {
- removeExtraSpaces(s); // 去掉冗余空格
- reverse(s, 0, s.size() - 1); // 将字符串全部反转
- int start = 0; // 反转的单词在字符串里起始位置
- int end = 0; // 反转的单词在字符串里终止位置
- bool entry = false; // 标记枚举字符串的过程中是否已经进入了单词区间
- for (int i = 0; i < s.size(); i++) { // 开始反转单词
- if (!entry) {
- start = i; // 确定单词起始位置
- entry = true; // 进入单词区间
- }
- // 单词后面有空格的情况，空格就是分词符
- if (entry && s[i] == ' ' && s[i - 1] != ' ') {
- end = i - 1; // 确定单词终止位置
- entry = false; // 结束单词区间
- reverse(s, start, end);
- }
- // 最后一个结尾单词之后没有空格的情况
- if (entry && (i == (s.size() - 1)) && s[i] != ' ' ) {
- end = i;// 确定单词终止位置
- entry = false; // 结束单词区间
- reverse(s, start, end);
- }
- }
- return s;
- }
-
- // 当然这里的主函数reverseWords写的有一些冗余的，可以精简一些，精简之后的主函数为：
- /* 主函数简单写法
- string reverseWords(string s) {
- removeExtraSpaces(s);
- reverse(s, 0, s.size() - 1);
- for(int i = 0; i < s.size(); i++) {
- int j = i;
- // 查找单词间的空格，翻转单词
- while(j < s.size() && s[j] != ' ') j++;
- reverse(s, i, j - 1);
- i = j;
- }
- return s;
- }
- */
-};
-```
-
-效率：
-
-
-```CPP
-//版本二：
-//原理同版本1，更简洁实现。
-class Solution {
-public:
- void reverse(string& s, int start, int end){ //翻转，区间写法：闭区间 []
+ void reverse(string& s, int start, int end){ //翻转，区间写法：左闭又闭 []
for (int i = start, j = end; i < j; i++, j--) {
swap(s[i], s[j]);
}
}
void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
- int slow = 0; //整体思想参考Leetcode: 27. 移除元素：https://leetcode.cn/problems/remove-element/
+ int slow = 0; //整体思想参考https://programmercarl.com/0027.移除元素.html
for (int i = 0; i < s.size(); ++i) { //
if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
@@ -261,6 +197,7 @@ public:
};
```
+
## 其他语言版本
diff --git a/problems/0200.岛屿数量.md b/problems/0200.岛屿数量.md
new file mode 100644
index 00000000..b88e5fd2
--- /dev/null
+++ b/problems/0200.岛屿数量.md
@@ -0,0 +1,249 @@
+
+# 200. 岛屿数量
+
+[题目链接](https://leetcode.cn/problems/number-of-islands/)
+
+给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
+
+岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
+
+此外，你可以假设该网格的四条边均被水包围。
+
+
+
+提示：
+
+* m == grid.length
+* n == grid[i].length
+* 1 <= m, n <= 300
+* grid[i][j] 的值为 '0' 或 '1'
+
+## 思路
+
+注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
+
+也就是说斜角度链接是不算了， 例如示例二，是三个岛屿，如图：
+
+
+
+这道题题目是 DFS，BFS，并查集，基础题目。
+
+本题思路，是用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。
+
+在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
+
+那么如果把节点陆地所能遍历到的陆地都标记上呢，就可以使用 DFS，BFS或者并查集。
+
+### 深度优先搜索
+
+以下代码使用dfs实现，如果对dfs不太了解的话，建议先看这篇题解：[797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)，
+
+C++代码如下：
+
+```CPP
+// 版本一
+class Solution {
+private:
+ int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+ void dfs(vector>& grid, vector>& visited, int x, int y) {
+ for (int i = 0; i < 4; i++) {
+ int nextx = x + dir[i][0];
+ int nexty = y + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 没有访问过的 同时 是陆地的
+
+ visited[nextx][nexty] = true;
+ dfs(grid, visited, nextx, nexty);
+ }
+ }
+ }
+public:
+ int numIslands(vector>& grid) {
+ int n = grid.size(), m = grid[0].size();
+ vector> visited = vector>(n, vector(m, false));
+
+ int result = 0;
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j < m; j++) {
+ if (!visited[i][j] && grid[i][j] == '1') {
+ visited[i][j] = true;
+ result++; // 遇到没访问过的陆地，+1
+ dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
+ }
+ }
+ }
+ return result;
+ }
+};
+```
+
+很多录友可能有疑惑，为什么 以上代码中的dfs函数，没有终止条件呢？ 感觉递归没有终止很危险。
+
+其实终止条件 就写在了，调用dfs的地方，如果遇到不合法的方向，直接不会去调用dfs。
+
+当然，也可以这么写：
+
+```CPP
+// 版本二
+class Solution {
+private:
+ int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+ void dfs(vector>& grid, vector>& visited, int x, int y) {
+ if (visited[x][y] || grid[x][y] == '0') return; // 终止条件：访问过的节点 或者 遇到海水
+ visited[x][y] = true; // 标记访问过
+ for (int i = 0; i < 4; i++) {
+ int nextx = x + dir[i][0];
+ int nexty = y + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ dfs(grid, visited, nextx, nexty);
+ }
+ }
+public:
+ int numIslands(vector>& grid) {
+ int n = grid.size(), m = grid[0].size();
+ vector> visited = vector>(n, vector(m, false));
+
+ int result = 0;
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j < m; j++) {
+ if (!visited[i][j] && grid[i][j] == '1') {
+ result++; // 遇到没访问过的陆地，+1
+ dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
+ }
+ }
+ }
+ return result;
+ }
+};
+```
+
+这里大家应该能看出区别了，无疑就是版本一中 调用dfs 的条件，放在了 版本二 的 终止条件位置上。
+
+**版本一的写法**是 ：下一个节点是否能合法已经判断完了，只要调用dfs就是可以合法的节点。
+
+**版本二的写法**是：不管节点是否合法，上来就dfs，然后在终止条件的地方进行判断，不合法再return。
+
+**理论上来讲，版本一的效率更高一些**，因为避免了 没有意义的递归调用，在调用dfs之前，就做合法性判断。 但从写法来说，可能版本二 更利于理解一些。（不过其实都差不太多）
+
+很多同学看了同一道题目，都是dfs，写法却不一样，有时候有终止条件，有时候连终止条件都没有，其实这就是根本原因，两种写法而已。
+
+
+### 广度优先搜索
+
+不少同学用广搜做这道题目的时候，超时了。 这里有一个广搜中很重要的细节：
+
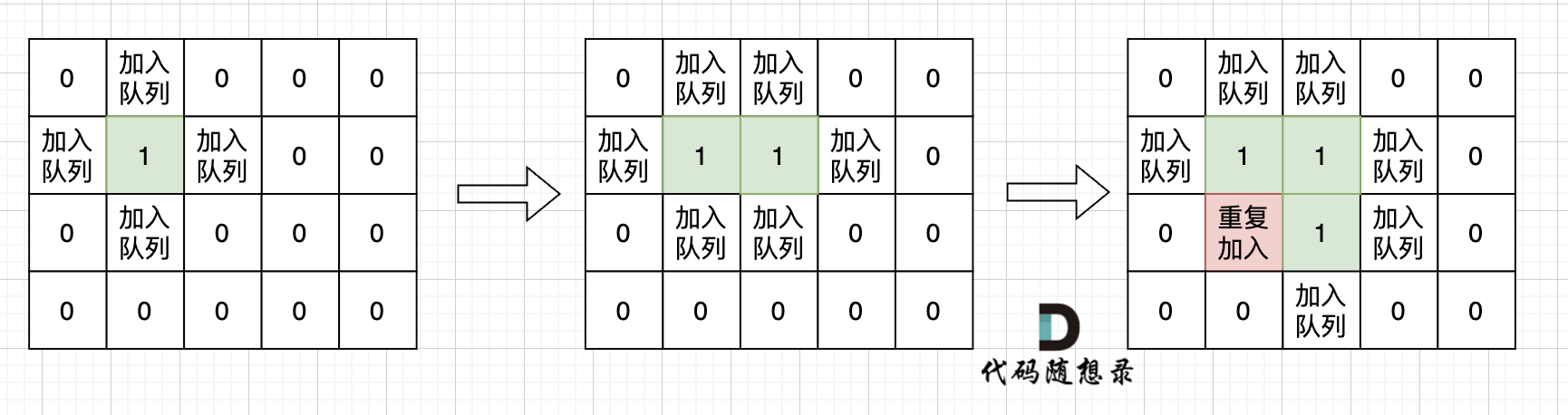
+根本原因是**只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过**。
+
+很多同学可能感觉这有区别吗？
+
+如果从队列拿出节点，再去标记这个节点走过，就会发生下图所示的结果，会导致很多节点重复加入队列。
+
+
+
+超时写法 （从队列中取出节点再标记）
+
+```CPP
+int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+void bfs(vector>& grid, vector>& visited, int x, int y) {
+ queue> que;
+ que.push({x, y});
+ while(!que.empty()) {
+ pair cur = que.front(); que.pop();
+ int curx = cur.first;
+ int cury = cur.second;
+ visited[curx][cury] = true; // 从队列中取出在标记走过
+ for (int i = 0; i < 4; i++) {
+ int nextx = curx + dir[i][0];
+ int nexty = cury + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
+ que.push({nextx, nexty});
+ }
+ }
+ }
+
+}
+```
+
+加入队列 就代表走过，立刻标记，正确写法：
+
+```CPP
+int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+void bfs(vector>& grid, vector>& visited, int x, int y) {
+ queue> que;
+ que.push({x, y});
+ visited[x][y] = true; // 只要加入队列，立刻标记
+ while(!que.empty()) {
+ pair cur = que.front(); que.pop();
+ int curx = cur.first;
+ int cury = cur.second;
+ for (int i = 0; i < 4; i++) {
+ int nextx = curx + dir[i][0];
+ int nexty = cury + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
+ que.push({nextx, nexty});
+ visited[nextx][nexty] = true; // 只要加入队列立刻标记
+ }
+ }
+ }
+
+}
+```
+
+以上两个版本其实，其实只有细微区别，就是 `visited[x][y] = true;` 放在的地方，着去取决于我们对 代码中队列的定义，队列中的节点就表示已经走过的节点。 **所以只要加入队列，理解标记该节点走过**。
+
+本题完整广搜代码：
+
+```CPP
+class Solution {
+private:
+int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+void bfs(vector>& grid, vector>& visited, int x, int y) {
+ queue> que;
+ que.push({x, y});
+ visited[x][y] = true; // 只要加入队列，立刻标记
+ while(!que.empty()) {
+ pair cur = que.front(); que.pop();
+ int curx = cur.first;
+ int cury = cur.second;
+ for (int i = 0; i < 4; i++) {
+ int nextx = curx + dir[i][0];
+ int nexty = cury + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
+ que.push({nextx, nexty});
+ visited[nextx][nexty] = true; // 只要加入队列立刻标记
+ }
+ }
+ }
+}
+public:
+ int numIslands(vector>& grid) {
+ int n = grid.size(), m = grid[0].size();
+ vector> visited = vector>(n, vector(m, false));
+
+ int result = 0;
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j < m; j++) {
+ if (!visited[i][j] && grid[i][j] == '1') {
+ result++; // 遇到没访问过的陆地，+1
+ bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
+ }
+ }
+ }
+ return result;
+ }
+};
+
+```
+
+## 总结
+
+其实本题是 dfs，bfs 模板题，但正是因为是模板题，所以大家或者一些题解把重要的细节都很忽略了，我这里把大家没注意的但以后会踩的坑 都给列出来了。
+
+
+
+
+
+## 其他语言版本
diff --git a/problems/0203.移除链表元素.md b/problems/0203.移除链表元素.md
index 8af8675b..6fd9b66f 100644
--- a/problems/0203.移除链表元素.md
+++ b/problems/0203.移除链表元素.md
@@ -28,7 +28,7 @@
# 思路
-为了方便大家理解，我特意录制了视频：[手把手带你学会操作链表，移除链表元素](https://www.bilibili.com/video/BV18B4y1s7R9)，结合视频在看本题解，事半功倍。
+为了方便大家理解，我特意录制了视频：[链表基础操作| LeetCode：203.移除链表元素](https://www.bilibili.com/video/BV18B4y1s7R9)，结合视频在看本题解，事半功倍。
这里以链表 1 4 2 4 来举例，移除元素4。
diff --git a/problems/0206.翻转链表.md b/problems/0206.翻转链表.md
index a6f4382a..e97befee 100644
--- a/problems/0206.翻转链表.md
+++ b/problems/0206.翻转链表.md
@@ -31,7 +31,7 @@
那么接下来看一看是如何反转的呢？
-我们拿有示例中的链表来举例，如动画所示：
+我们拿有示例中的链表来举例，如动画所示：（纠正：动画应该是先移动pre，在移动cur）
@@ -408,6 +408,7 @@ def reverse(pre, cur)
reverse(cur, tem) # 通过递归实现双指针法中的更新操作
end
```
+
Kotlin:
```Kotlin
fun reverseList(head: ListNode?): ListNode? {
diff --git a/problems/0209.长度最小的子数组.md b/problems/0209.长度最小的子数组.md
index 570242f9..2a018736 100644
--- a/problems/0209.长度最小的子数组.md
+++ b/problems/0209.长度最小的子数组.md
@@ -19,11 +19,11 @@
# 思路
-为了易于大家理解，我特意录制了B站视频[拿下滑动窗口！ | LeetCode 209 长度最小的子数组](https://www.bilibili.com/video/BV1tZ4y1q7XE)
+为了易于大家理解，我特意录制了B站视频[拿下滑动窗口！ | LeetCode 209 长度最小的子数组](https://www.bilibili.com/video/BV1tZ4y1q7XE)，结合视频看本题解，事半功倍！
## 暴力解法
-这道题目暴力解法当然是 两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)。
+这道题目暴力解法当然是 两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)。
代码如下：
@@ -51,7 +51,9 @@ public:
};
```
* 时间复杂度：O(n^2)
-* 空间复杂度：O(1)
+* 空间复杂度：O(1)
+
+后面力扣更新了数据，暴力解法已经超时了。
## 滑动窗口
diff --git a/problems/0232.用栈实现队列.md b/problems/0232.用栈实现队列.md
index 4662e2f2..c8374a61 100644
--- a/problems/0232.用栈实现队列.md
+++ b/problems/0232.用栈实现队列.md
@@ -111,7 +111,7 @@ public:
## 拓展
-可以看出peek()的实现，直接复用了pop()。
+可以看出peek()的实现，直接复用了pop()， 要不然，对stOut判空的逻辑又要重写一遍。
再多说一些代码开发上的习惯问题，在工业级别代码开发中，最忌讳的就是 实现一个类似的函数，直接把代码粘过来改一改就完事了。
diff --git a/problems/0344.反转字符串.md b/problems/0344.反转字符串.md
index ebadc044..5b3d72d8 100644
--- a/problems/0344.反转字符串.md
+++ b/problems/0344.反转字符串.md
@@ -29,6 +29,8 @@
# 思路
+针对本题，我录制了视频讲解：[字符串基础操作！ | LeetCode：344.反转字符串](https://www.bilibili.com/video/BV1fV4y17748)，结合本题解一起看，事半功倍！
+
先说一说题外话：
对于这道题目一些同学直接用C++里的一个库函数 reverse，调一下直接完事了， 相信每一门编程语言都有这样的库函数。
diff --git a/problems/0417.太平洋大西洋水流问题.md b/problems/0417.太平洋大西洋水流问题.md
index 7efee80a..fa2f573f 100644
--- a/problems/0417.太平洋大西洋水流问题.md
+++ b/problems/0417.太平洋大西洋水流问题.md
@@ -2,6 +2,8 @@
[题目链接](https://leetcode.cn/problems/pacific-atlantic-water-flow/)
+## 思路
+
不少同学可能被这道题的题目描述迷惑了，其实就是找到哪些点 可以同时到达太平洋和大西洋。 流动的方式只能从高往低流。
那么一个比较直白的想法，其实就是 遍历每个点，然后看这个点 能不能同时到达太平洋和大西洋。
@@ -197,3 +199,7 @@ for (int j = 0; j < m; j++) {
空间复杂度为：O(n * m) 这个就不难理解了。开了几个 n * m 的数组。
+
+## 其他语言版本
+
+
diff --git a/problems/0459.重复的子字符串.md b/problems/0459.重复的子字符串.md
index 4f45f4d7..f7898ae0 100644
--- a/problems/0459.重复的子字符串.md
+++ b/problems/0459.重复的子字符串.md
@@ -31,21 +31,106 @@
# 思路
-这又是一道标准的KMP的题目。
+暴力的解法， 就是一个for循环获取 子串的终止位置， 然后判断子串是否能重复构成字符串，又嵌套一个for循环，所以是O(n^2)的时间复杂度。
-如果KMP还不够了解，可以看我的B站：
+有的同学可以想，怎么一个for循环就可以获取子串吗？ 至少得一个for获取子串起始位置，一个for获取子串结束位置吧。
-* [帮你把KMP算法学个通透！（理论篇）](https://www.bilibili.com/video/BV1PD4y1o7nd/)
-* [帮你把KMP算法学个通透！（求next数组代码篇）](https://www.bilibili.com/video/BV1M5411j7Xx)
+其实我们只需要判断，以第一个字母为开始的子串就可以，所以一个for循环获取子串的终止位置就行了。 而且遍历的时候 都不用遍历结束，只需要遍历到中间位置，因为子串结束位置大于中间位置的话，一定不能重复组成字符串。
+
+暴力的解法，这里就不讲了。
+
+主要讲一讲移动匹配 和 KMP两种方法。
+
+## 移动匹配
+
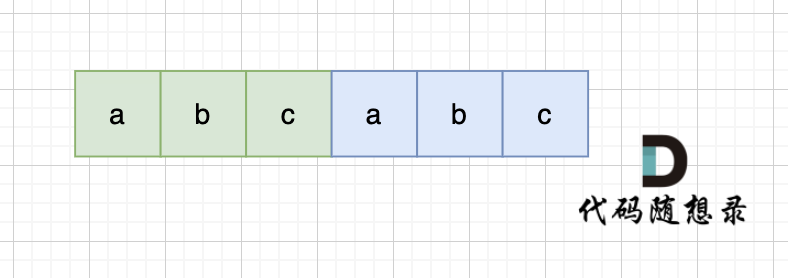
+当一个字符串s：abcabc，内部又重复的子串组成，那么这个字符串的结构一定是这样的：
+
+
+
+也就是又前后又相同的子串组成。
+
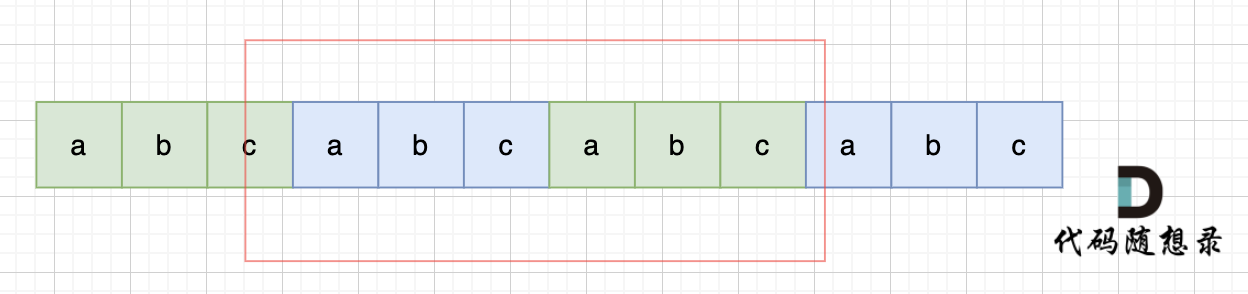
+那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前后的子串做后串，就一定还能组成一个s，如图：
+
+
+
+所以判断字符串s是否有重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是又重复子串组成。
+
+当然，我们在判断 s + s 拼接的字符串里是否出现一个s的的时候，**要刨除 s + s 的首字符和尾字符**，这样避免在s+s中搜索出原来的s，我们要搜索的是中间拼接出来的s。
+
+代码如下：
+
+```CPP
+class Solution {
+public:
+ bool repeatedSubstringPattern(string s) {
+ string t = s + s;
+ t.erase(t.begin()); t.erase(t.end() - 1); // 掐头去尾
+ if (t.find(s) != std::string::npos) return true; // r
+ return false;
+ }
+};
+```
+
+不过这种解法还有一个问题，就是 我们最终还是要判断 一个字符串（s + s）是否出现过 s 的过程，大家可能直接用contains，find 之类的库函数。 却忽略了实现这些函数的时间复杂度（暴力解法是m * n，一般库函数实现为 O(m + n)）。
+
+如果我们做过 [28.实现strStr](https://programmercarl.com/0028.实现strStr.html) 题目的话，其实就知道，**实现一个 高效的算法来判断 一个字符串中是否出现另一个字符串是很复杂的**，这里就涉及到了KMP算法。
+
+## KMP
+
+### 为什么会使用KMP
+以下使用KMP方式讲解，强烈建议大家先把一下两个视频看了，理解KMP算法，在来看下面讲解，否则会很懵。
+
+* [视频讲解版：帮你把KMP算法学个通透！（理论篇）](https://www.bilibili.com/video/BV1PD4y1o7nd/)
+* [视频讲解版：帮你把KMP算法学个通透！（求next数组代码篇）](https://www.bilibili.com/video/BV1M5411j7Xx)
+* [文字讲解版：KMP算法](https://programmercarl.com/0028.实现strStr.html)
+
+在一个串中查找是否出现过另一个串，这是KMP的看家本领。那么寻找重复子串怎么也涉及到KMP算法了呢？
+
+KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配，靠的是有计算好的前缀表。 前缀表里，统计了各个位置为终点字符串的最长相同前后缀的长度。
+
+那么 最长相同前后缀和重复子串的关系又有什么关系呢。
+
+可能很多录友又忘了 前缀和后缀的定义，在回顾一下：
+
+* 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；
+* 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
+
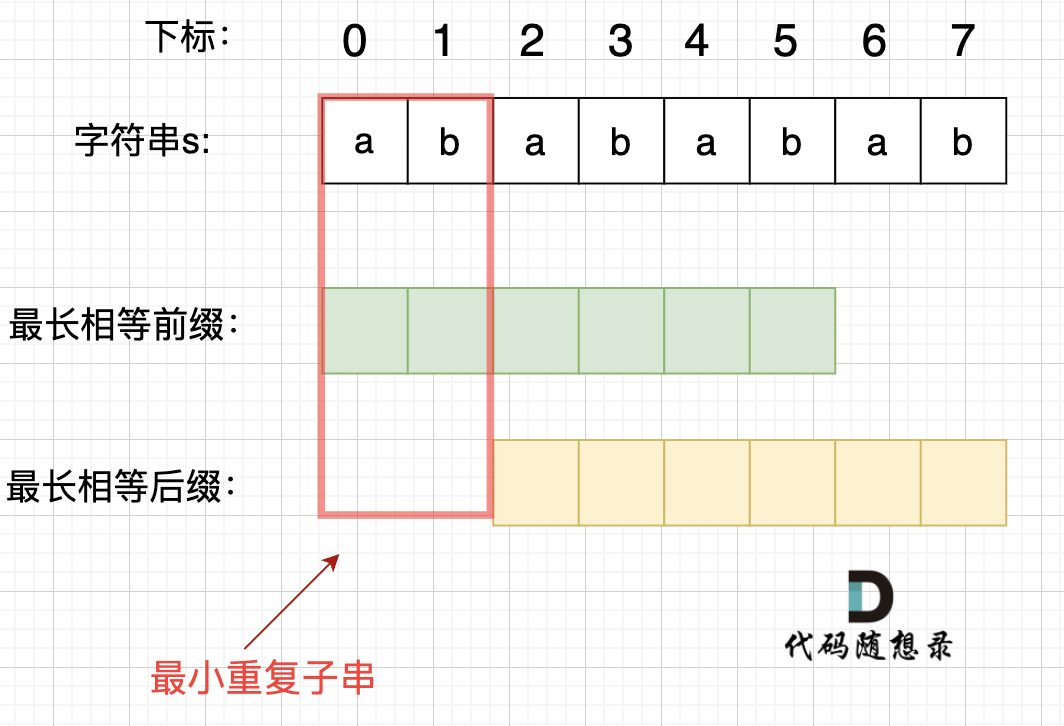
+在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串，这里那字符串s：abababab 来举例，ab就是最小重复单位，如图所示：
+
+
-我们在[字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html)里提到了，在一个串中查找是否出现过另一个串，这是KMP的看家本领。
+### 如何找到最小重复子串
-那么寻找重复子串怎么也涉及到KMP算法了呢？
+这里有同学就问了，为啥一定是开头的ab呢。 其实最关键还是要理解 最长相等前后缀，如图：
-这里就要说一说next数组了，next 数组记录的就是最长相同前后缀( [字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html) 这里介绍了什么是前缀，什么是后缀，什么又是最长相同前后缀)， 如果 next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。
+
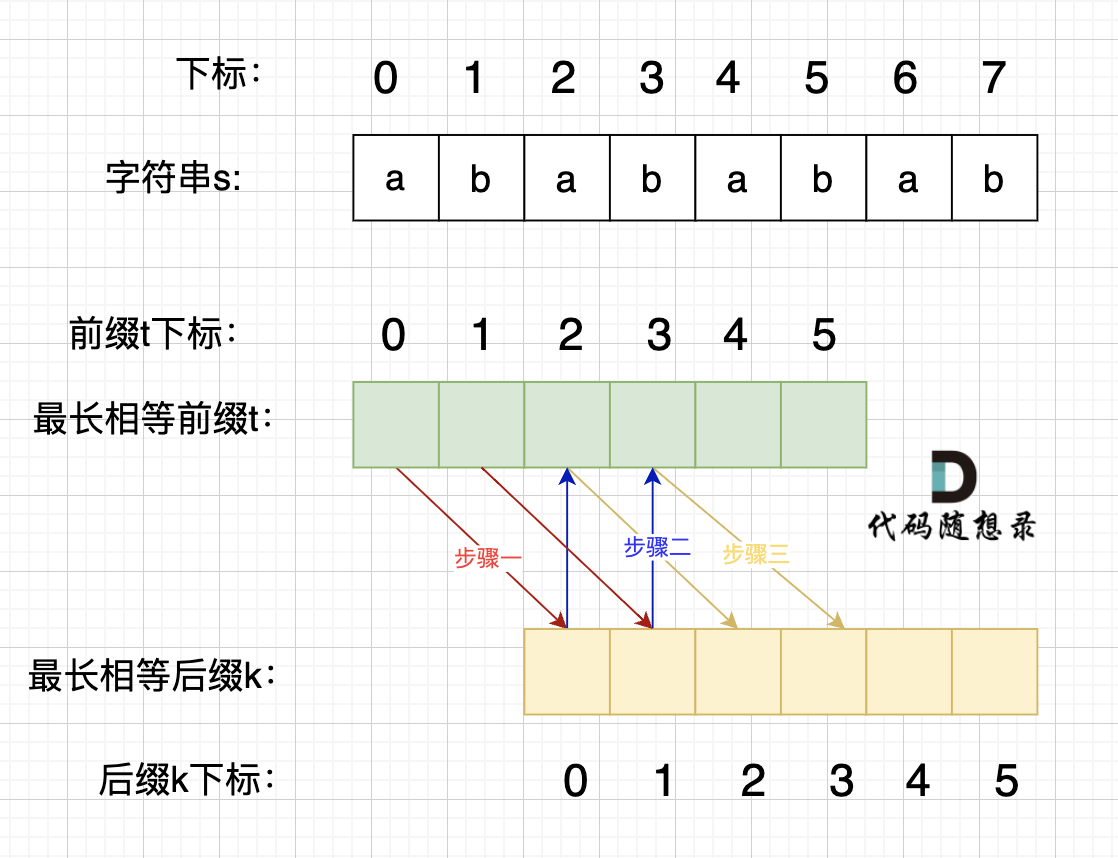
-最长相等前后缀的长度为：next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的，因此需要+1)
+步骤一：因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同 。
+
+步骤二： 因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。
+
+步骤三： 因为 这是相等的前缀和后缀，t[2] 与 k[2]相同 ，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。
+
+步骤四：循环往复。
+
+所以字符串s，s[0]s[1]与s[2]s[3]相同， s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同。
+
+正是因为 最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。
+
+### 简单推理
+
+这里在给出一个数推导，就容易理解很多。
+
+假设字符串s使用多个重复子串构成（这个子串是最小重复单位），重复出现的子字符串长度是x，所以s是由n * x组成。
+
+因为字符串s的最长相同前后缀的的长度一定是不包含s本身，所以 最长相同前后缀长度必然是m * x，而且 n - m = 1，（这里如果不懂，看上面的推理）
+
+所以如果 nx % (n - m)x = 0，就可以判定有重复出现的子字符串。
+
+next 数组记录的就是最长相同前后缀 [字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html) 这里介绍了什么是前缀，什么是后缀，什么又是最长相同前后缀)， 如果 next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。
+
+最长相等前后缀的长度为：next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的，因此需要+1，两种计算next数组的具体区别看这里：[字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html))
数组长度为：len。
@@ -62,7 +147,6 @@
next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
-
(len - (next[len - 1] + 1)) 也就是： 12(字符串的长度) - 8(最长公共前后缀的长度) = 4， 4正好可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。
@@ -75,10 +159,10 @@ public:
next[0] = -1;
int j = -1;
for(int i = 1;i < s.size(); i++){
- while(j >= 0 && s[i] != s[j+1]) {
+ while(j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
- if(s[i] == s[j+1]) {
+ if(s[i] == s[j + 1]) {
j++;
}
next[i] = j;
@@ -100,7 +184,7 @@ public:
```
-前缀表（不减一）的C++代码实现
+前缀表（不减一）的C++代码实现：
```CPP
class Solution {
@@ -133,14 +217,6 @@ public:
};
```
-# 拓展
-
-在[字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html)中讲解KMP算法的基础理论，给出next数组究竟是如何来了，前缀表又是怎么回事，为什么要选择前缀表。
-
-讲解一道KMP的经典题目，力扣：28. 实现 strStr()，判断文本串里是否出现过模式串，这里涉及到构造next数组的代码实现，以及使用next数组完成模式串与文本串的匹配过程。
-
-后来很多同学反馈说：搞不懂前后缀，什么又是最长相同前后缀（最长公共前后缀我认为这个用词不准确），以及为什么前缀表要统一减一（右移）呢，不减一行不行？针对这些问题，我在[字符串：KMP算法精讲](https://programmercarl.com/0028.实现strStr.html)给出了详细的讲解。
-
## 其他语言版本
diff --git a/problems/0541.反转字符串II.md b/problems/0541.反转字符串II.md
index 7ef6463e..a8bf3804 100644
--- a/problems/0541.反转字符串II.md
+++ b/problems/0541.反转字符串II.md
@@ -25,6 +25,8 @@
# 思路
+针对本题，我录制了视频讲解：[字符串操作进阶！ | LeetCode：541. 反转字符串II](https://www.bilibili.com/video/BV1dT411j7NN)，结合本题解一起看，事半功倍！
+
这道题目其实也是模拟，实现题目中规定的反转规则就可以了。
一些同学可能为了处理逻辑：每隔2k个字符的前k的字符，写了一堆逻辑代码或者再搞一个计数器，来统计2k，再统计前k个字符。
diff --git a/problems/0695.岛屿的最大面积.md b/problems/0695.岛屿的最大面积.md
new file mode 100644
index 00000000..b0945292
--- /dev/null
+++ b/problems/0695.岛屿的最大面积.md
@@ -0,0 +1,96 @@
+# 695. 岛屿的最大面积
+
+给你一个大小为 m x n 的二进制矩阵 grid 。
+
+岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
+
+岛屿的面积是岛上值为 1 的单元格的数目。
+
+计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。
+
+
+
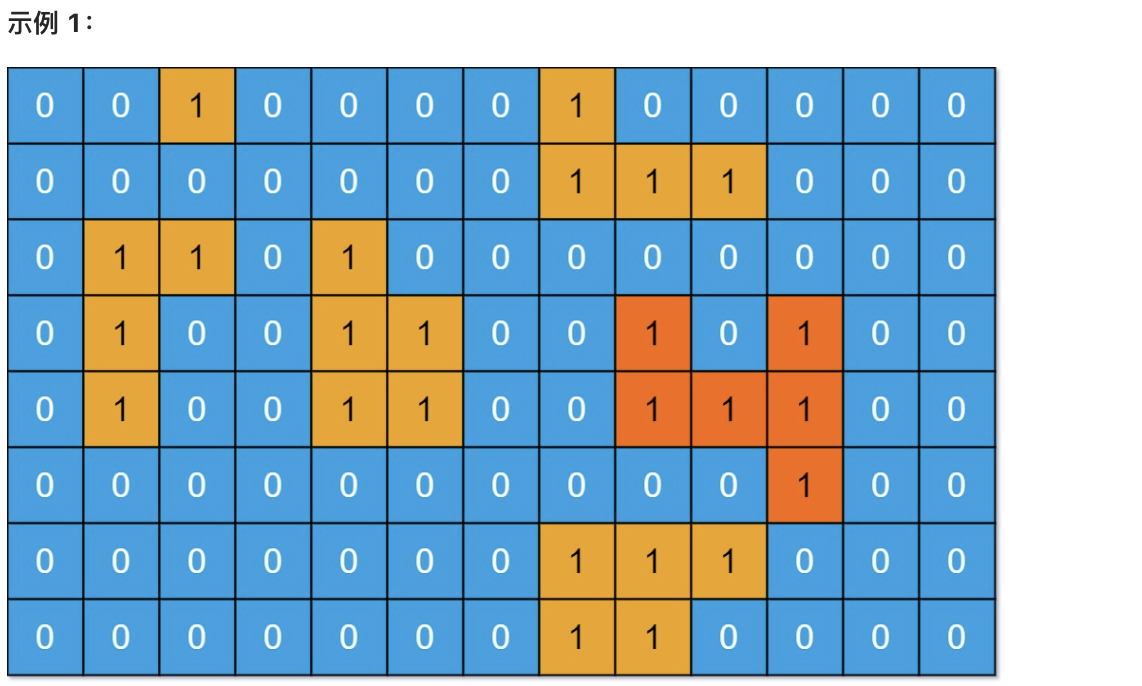
+输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
+输出：6
+解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
+
+# 思路
+
+写法一，dfs只处理下一个节点
+```CPP
+class Solution {
+private:
+ int count;
+ int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+ void dfs(vector>& grid, vector>& visited, int x, int y) {
+ for (int i = 0; i < 4; i++) {
+ int nextx = x + dir[i][0];
+ int nexty = y + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
+
+ visited[nextx][nexty] = true;
+ count++;
+ dfs(grid, visited, nextx, nexty);
+ }
+ }
+ }
+
+public:
+ int maxAreaOfIsland(vector>& grid) {
+ int n = grid.size(), m = grid[0].size();
+ vector> visited = vector>(n, vector(m, false));
+
+ int result = 0;
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j < m; j++) {
+ if (!visited[i][j] && grid[i][j] == 1) {
+ count = 1;
+ visited[i][j] = true;
+ dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
+ result = max(result, count);
+ }
+ }
+ }
+ return result;
+ }
+};
+```
+
+写法二，dfs处理当前节点
+dfs
+```CPP
+class Solution {
+private:
+ int count;
+ int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+ void dfs(vector>& grid, vector>& visited, int x, int y) {
+ if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
+ visited[x][y] = true; // 标记访问过
+ count++;
+ for (int i = 0; i < 4; i++) {
+ int nextx = x + dir[i][0];
+ int nexty = y + dir[i][1];
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
+ dfs(grid, visited, nextx, nexty);
+ }
+ }
+
+public:
+ int maxAreaOfIsland(vector>& grid) {
+ int n = grid.size(), m = grid[0].size();
+ vector> visited = vector>(n, vector(m, false));
+ int result = 0;
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j < m; j++) {
+ if (!visited[i][j] && grid[i][j] == 1) {
+ count = 0;
+ dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
+ result = max(result, count);
+ }
+ }
+ }
+ return result;
+ }
+};
+```
diff --git a/problems/0797.所有可能的路径.md b/problems/0797.所有可能的路径.md
index b990053e..a51590f2 100644
--- a/problems/0797.所有可能的路径.md
+++ b/problems/0797.所有可能的路径.md
@@ -158,6 +158,10 @@ if (终止条件) {
终止添加不仅是结束本层递归，同时也是我们收获结果的时候。
+另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。
+* 841.钥匙和房间
+* 200. 岛屿数量
+
3. 处理目前搜索节点出发的路径
一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。
diff --git a/problems/0977.有序数组的平方.md b/problems/0977.有序数组的平方.md
index 7bc84e85..eb9f42b1 100644
--- a/problems/0977.有序数组的平方.md
+++ b/problems/0977.有序数组的平方.md
@@ -23,7 +23,7 @@
# 思路
-为了易于大家理解，我还特意录制了视频，[本题视频讲解](https://www.bilibili.com/video/BV1QB4y1D7ep)
+针对本题，我录制了视频讲解：[双指针法经典题目!LeetCode:977.有序数组的平方](https://www.bilibili.com/video/BV1QB4y1D7ep)，结合本题解一起看，事半功倍！
## 暴力排序
diff --git a/problems/前序/代码风格.md b/problems/前序/代码风格.md
index 4ab94a51..196f4027 100644
--- a/problems/前序/代码风格.md
+++ b/problems/前序/代码风格.md
@@ -51,7 +51,7 @@
匈牙利命名法是：变量名 = 属性 + 类型 + 对象描述，例如：`int iMyAge`，这种命名是一个来此匈牙利的程序员在微软内部推广起来，然后推广给了全世界的Windows开发人员。
-这种命名方式在没有IDE的时代，可以很好的提醒开发人员遍历的意义，例如看到iMyAge，就知道它是一个int型的变量，而不用找它的定义，缺点是一旦该变量的属性，那么整个项目里这个变量名字都要改动，所以带来代码维护困难。
+这种命名方式在没有IDE的时代，可以很好的提醒开发人员遍历的意义，例如看到iMyAge，就知道它是一个int型的变量，而不用找它的定义，缺点是一旦改变变量的属性，那么整个项目里这个变量名字都要改动，所以带来代码维护困难。
**目前IDE已经很发达了，都不用标记变量属性了，IDE就会帮我们识别了，所以基本没人用匈牙利命名法了**，虽然我不用IDE，VIM大法好。
@@ -89,7 +89,7 @@ while (n) {
}
```
-控制语句（while，if，for）前都有一个空格，例如：
+控制语句（while，if，for）后都有一个空格，例如：
```
while (n) {
if (k > 0) return 9;