Update

problems/0039.组合总和.md

@@ -39,8 +39,7 @@ candidates 中的数字可以无限制重复被选取。
 
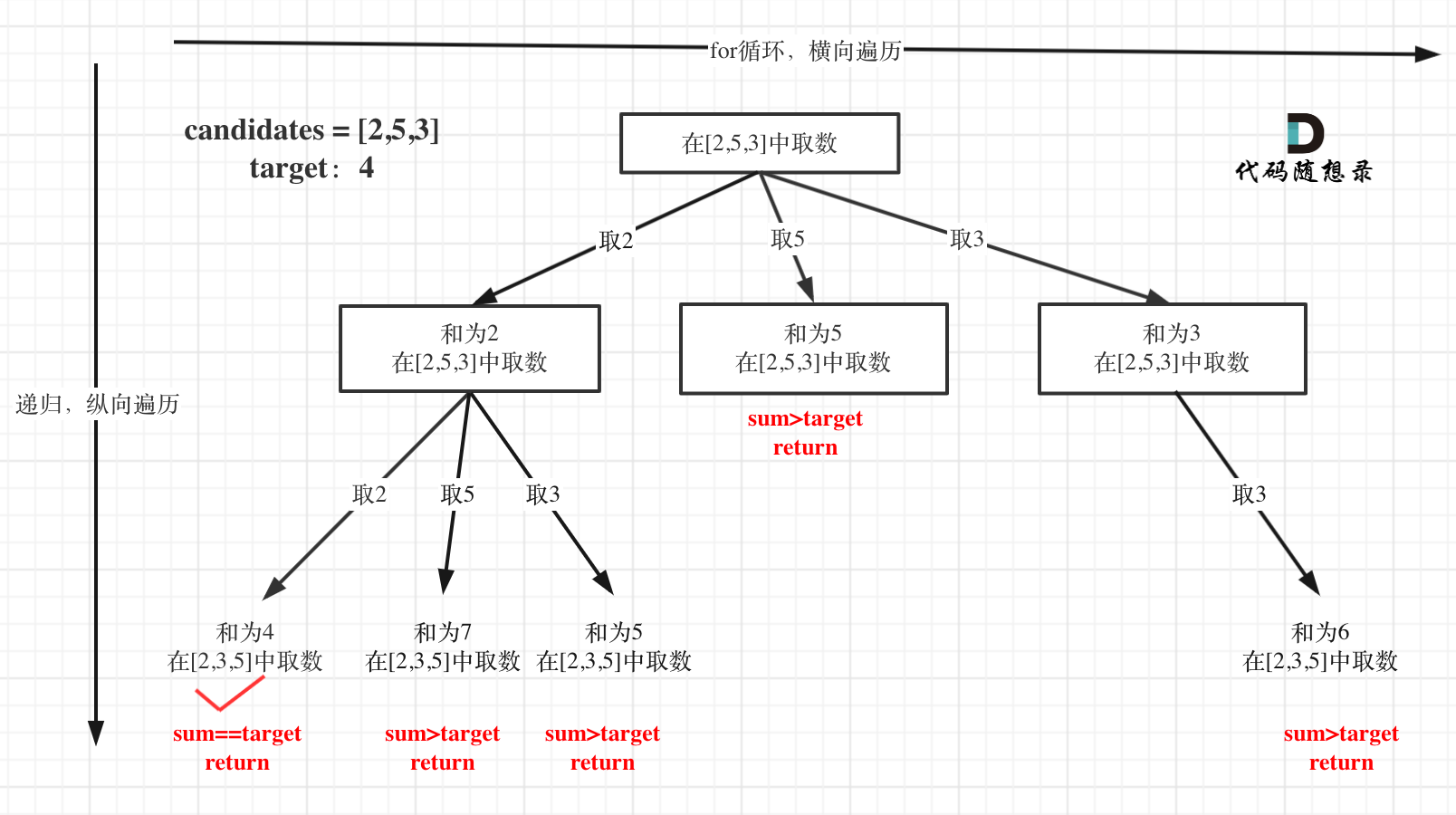
 本题搜索的过程抽象成树形结构如下：
 
-![39.组合总和](https://img-blog.csdnimg.cn/20201123202227835.png)
-
+![39.组合总和](https://img-blog.csdnimg.cn/20201223170730367.png)
 注意图中叶子节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！
 
 而在[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w) 中都可以知道要递归K层，因为要取k个元素的组合。
@@ -75,7 +74,7 @@ void backtracking(vector<int>& candidates, int target, int sum, int startIndex)
 
 在如下树形结构中：
 
-![39.组合总和](https://img-blog.csdnimg.cn/20201123202227835.png)
+![39.组合总和](https://img-blog.csdnimg.cn/20201223170730367.png)
 
 从叶子节点可以清晰看到，终止只有两种情况，sum大于target和sum等于target。
 
@@ -148,7 +147,7 @@ public:
 
 在这个树形结构中：
 
-![39.组合总和](https://img-blog.csdnimg.cn/20201123202227835.png)
+![39.组合总和](https://img-blog.csdnimg.cn/20201223170730367.png)
 
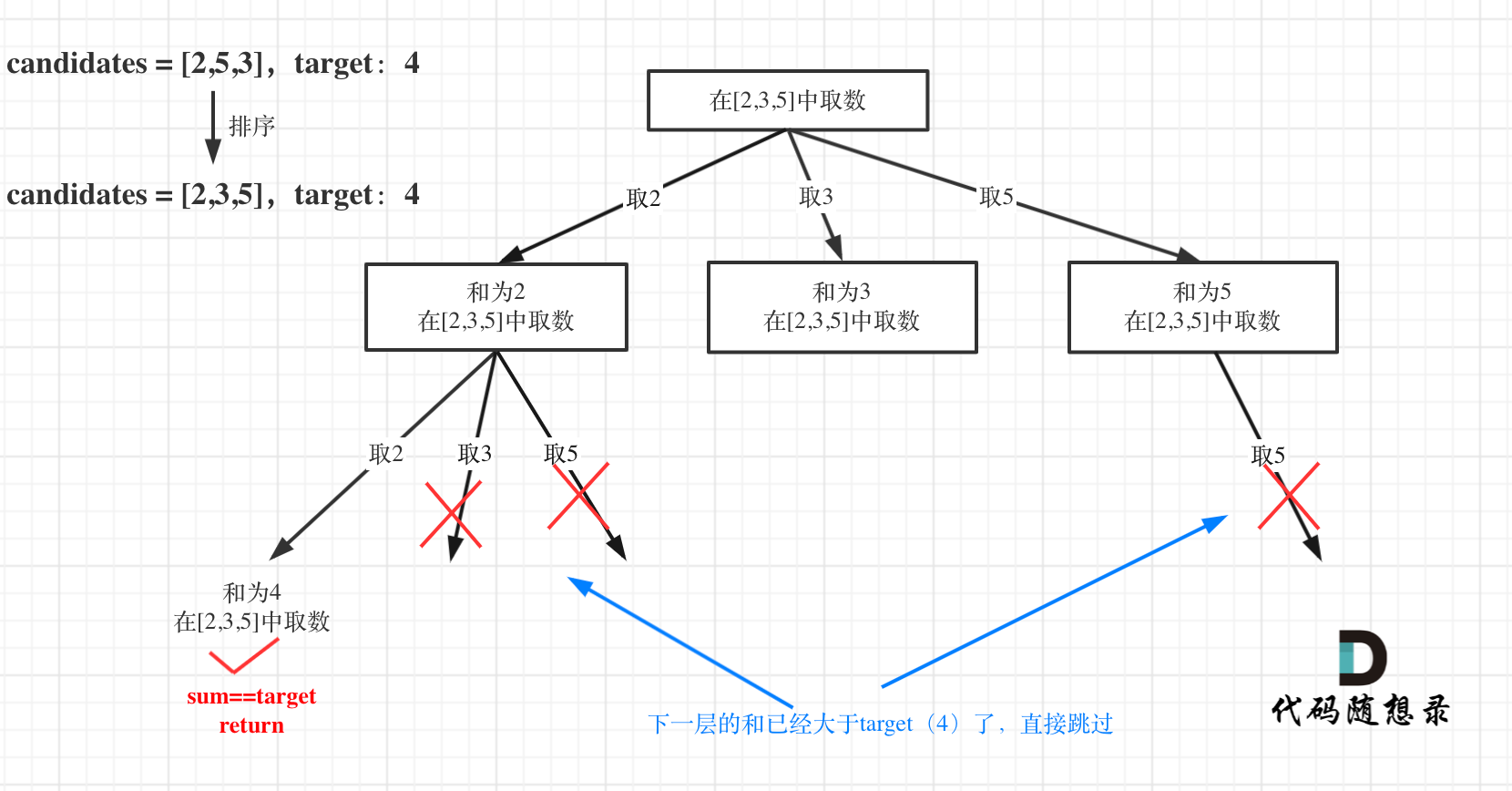
 以及上面的版本一的代码大家可以看到，对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。
 
@@ -160,8 +159,8 @@ public:
 
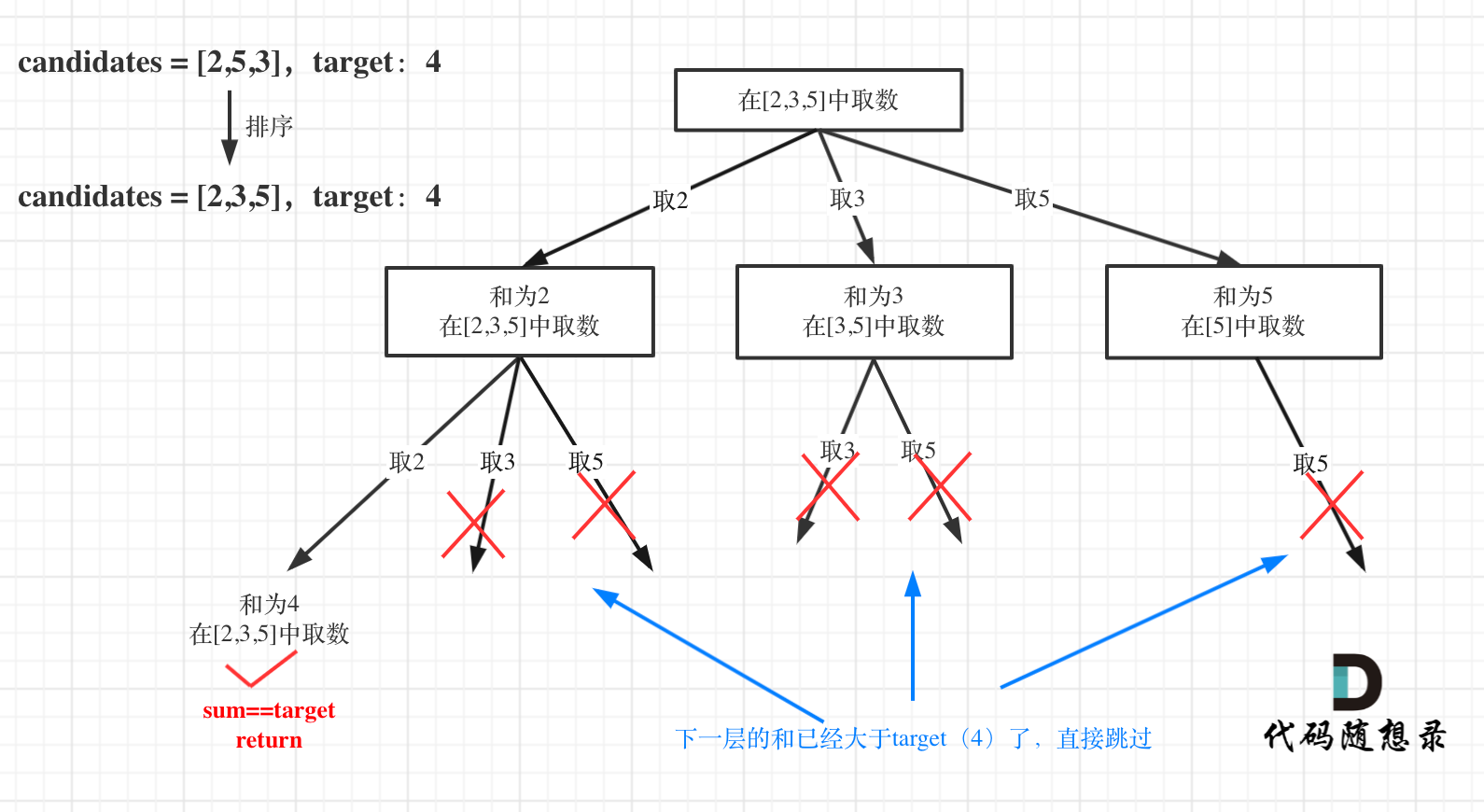
 如图：
 
-![39.组合总和1](https://img-blog.csdnimg.cn/20201123202349897.png)
 
+![39.组合总和1](https://img-blog.csdnimg.cn/20201223170809182.png)
 
 for循环剪枝代码如下：
 

problems/0056.合并区间.md

@@ -1,33 +1,61 @@
-## 题目链接
-https://leetcode-cn.com/problems/merge-intervals/
+> 「代码随想录」出品，毕竟精品！ 
 
-## 思路 
-这道题目看起来就是一道模拟类的题，但其实是一道贪心题目！
+# 56. 合并区间 
 
-按照左区间排序之后，每次合并都取最大的右区间，这样就可以合并更多的区间了。
+题目链接：https://leetcode-cn.com/problems/merge-intervals/
 
-那有同学问了，这不是废话么？ 当然要取最大的右区间啊。
+给出一个区间的集合，请合并所有重叠的区间。
 
-**是的，一想就是这么个道理，但它就是贪心的思想，局部最优推导出整体最优**。
+示例 1:     
+输入: intervals = [[1,3],[2,6],[8,10],[15,18]]     
+输出: [[1,6],[8,10],[15,18]]      
+解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].    
 
-这也就是为什么很多同学刷题的时候都没有发现自己用了贪心。
+示例 2:       
+输入: intervals = [[1,4],[4,5]]     
+输出: [[1,5]]        
+解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。      
+注意：输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。   
 
-合并思路：如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]起始位置 < intervals[i - 1]终止位置，则一定有重复，需要合并。
+提示：
 
-如图所示：
+* intervals[i][0] <= intervals[i][1]
 
-<img src='../pics/56.合并区间.png' width=600> </img></div>
+# 思路 
+
+大家应该都感觉到了，此题一定要排序，那么按照左边界排序，还是右边界排序呢？
+
+都可以！ 
+
+那么我按照左边界排序，排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间。
+
+局部最优可以推出全局最优，找不出反例，试试贪心。
+
+那有同学问了，本来不就应该合并最大右边界么，这和贪心有啥关系？
+
+有时候贪心就是常识！哈哈
+
+按照左边界从小到大排序之后，如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
+
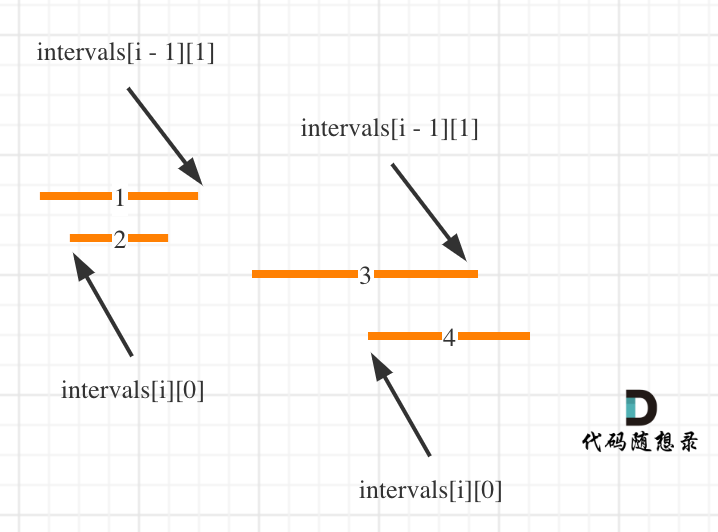
+即：intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内，那么一定有重复！
+
+这么说有点抽象，看图：（**注意图中区间都是按照左边界排序之后了**）
+
+![56.合并区间](https://img-blog.csdnimg.cn/20201223200632791.png)
+
+知道如何判断重复之后，剩下的就是合并了，如何去模拟合并区间呢？
+
+其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
 
 C++代码如下：
 
-```
+```C++
 class Solution {
 public:
-    // 按照区间左边界排序
+    // 按照区间左边界从小到大排序
     static bool cmp (const vector<int>& a, const vector<int>& b) {
         return a[0] < b[0];
     }
-
     vector<vector<int>> merge(vector<vector<int>>& intervals) {
         vector<vector<int>> result;
         if (intervals.size() == 0) return result;
@@ -36,13 +64,14 @@ public:
         int length = intervals.size();
 
         for (int i = 1; i < length; i++) {
-            int start = intervals[i - 1][0];
-            int end = intervals[i - 1][1];
+            int start = intervals[i - 1][0];    // 初始为i-1区间的左边界
+            int end = intervals[i - 1][1];      // 初始i-1区间的右边界
             while (i < length && intervals[i][0] <= end) { // 合并区间
-                end = max(end, intervals[i][1]);
+                end = max(end, intervals[i][1]);    // 不断更新右区间
                 if (i == length - 1) flag = true;   // 最后一个区间也合并了
-                i++;
+                i++;                                // 继续合并下一个区间
             }
+            // start和end是表示intervals[i - 1]的左边界右边界，所以最优intervals[i]区间是否合并了要标记一下
             result.push_back({start, end}); 
         }
         // 如果最后一个区间没有合并，将其加入result
@@ -53,3 +82,47 @@ public:
     }
 };
 ```
+
+当然以上代码有冗余一些，可以优化一下，如下：（思路是一样的）
+
+```C++
+class Solution {
+public:
+    vector<vector<int>> merge(vector<vector<int>>& intervals) {
+        vector<vector<int>> result;
+        if (intervals.size() == 0) return result;
+        // 排序的参数使用了lamda表达式
+        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});
+
+        result.push_back(intervals[0]);
+        for (int i = 1; i < intervals.size(); i++) {
+            if (result.back()[1] >= intervals[i][0]) { // 合并区间
+                result.back()[1] = max(result.back()[1], intervals[i][1]);
+            } else {
+                result.push_back(intervals[i]);
+            }
+        }
+        return result;
+    }
+};
+```
+
+* 时间复杂度：O(nlogn) ，有一个快排
+* 空间复杂度：O(1)，我没有算result数组（返回值所需容器占的空间）
+
+
+# 总结 
+
+对于贪心算法，很多同学都是：**如果能凭常识直接做出来，就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
+
+跟着「代码随想录」刷题的录友应该感受过，贪心难起来，真的难。
+
+那应该怎么办呢？
+
+正如我贪心系列开篇词[关于贪心算法，你该了解这些！](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)中讲解的一样，贪心本来就没有套路，也没有框架，所以各种常规解法需要多接触多练习，自然而然才会想到。
+
+「代码随想录」会把贪心常见的经典题目覆盖到，大家只要认真学习打卡就可以了。
+
+就酱，学算法，就在「代码随想录」，值得介绍给身边的朋友同学们！
+
+

problems/0070.爬楼梯.md

@@ -1,4 +1,43 @@
 
+# 思路 
+
+本题大家多举一个例子，就发现这其实就是斐波那契数列。
+
+题目509. 斐波那契数中的代码初始化部分稍加改动，就可以过了本题。
+
+C++代码如下：
+```
+class Solution {
+public:
+    int climbStairs(int n) {
+        if (n <= 1) return n;
+        vector<int> dp(n + 1);
+        dp[0] = 1;
+        dp[1] = 1;
+        for (int i = 2; i <= n; i++) {
+            dp[i] = dp[i - 1] + dp[i - 2];
+        }
+        return dp[n];
+
+    }
+};
+```
+
+既然这么简单为什么还要讲呢，其实本题稍加改动就是一道面试好题，如果每次可以爬 1 或 2或3或者m 个台阶呢，走到楼顶有几种方法？ 
+
+
+
+* 确定dp数组以及下标的含义
+
+dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法
+
+* 确定递推公式 
+
+dp[i]有几种来源，dp[i - 1]，dp[i - 2]
+
+* dp数组如何初始化
+* 确定遍历顺序
+
 dp里求排列，1 2 步  和 2 1 步都是上三个台阶，但不一样！
 
 这是求排列
@@ -17,3 +56,19 @@ public:
     }
 };
 ```
+
+# 总结 
+
+如果我来面试的话，我就会想给候选人出一个 本题原题，看其表现，如果顺利写出来，进而在要求每次可以爬[1 - m]个台阶应该怎么写。
+
+顺便再考察一下两个for循环的嵌套顺序，为什么target放外面，nums放里面。这就能反馈出对背包问题本质的掌握程度，是不是刷题背公式，一眼就看出来。
+
+这么一连套下来，如果候选人都能答出来，相信任何一位面试官都是非常满意的。
+
+**本题代码不长，题目也很普通，当稍稍一进阶就可以考察本质问题，而且题目进阶的内容在leetcode上并没有，一定程度上就可以排除掉刷题党了，简直是面试题目的绝佳选择！**
+
+相信通过这道简单的斐波那契数列题目，大家能感受到大厂面试官最喜欢什么样的面试题目了，并不是手撕红黑树！
+
+
+所以本题是一道非常好的题目。
+

problems/0322.零钱兑换.md

@@ -1,5 +1,103 @@
 
-[1]  0  ，输出的是0，不是-1啊，这颗真是天坑j
+# 思路 
+* 确定dp数组以及下标的含义
+dp[j]：凑足总额为j所需钱币的最少个数为dp[j] 
+
+* 确定递推公式
+
+得到dp[j]（有考虑coins[i]），有两个来源，一个是dp[j - coins[i]]，一个是dp[j] （没有考虑coins[i]）自己。
+
+凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）
+
+所以dp[j]（有考虑coins[i]）有两个选择，dp[j]（没有考虑coins[i]）和dp[j - coins[i]] + 1（考虑coins[i]），一定是取最小的。
+
+dp[j] =  min(dp[j - coins[i]] + 1, dp[j]);
+
+* dp数组如何初始化
+
+首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;
+
+其他下标对应的数值呢？
+
+考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中比初始值覆盖。
+
+所以下标非0的元素都是应该是最大值。
+
+代码如下：
+
+```
+vector<int> dp(amount + 1, INT_MAX);
+dp[0] = 0;
+```
+
+* 确定遍历顺序
+
+求钱币最小个数，那么钱币有顺序，和钱币没有顺序都可以，都不影响钱币的最小个数。可以用背包组合方式或者排列方式来求。
+
+如果本题要是求组成amount的有几种方式，那么钱币循序就有影响了。
+
+所以两个for循环的关系是：coins放在外循环，target在内循环、或者target放在外循环，coins在内循环都是可以的！
+
+那么我采用coins放在外循环，target在内循环的方式。
+
+本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序
+
+综上所述，遍历顺序为：coins放在外循环，target在内循环。且内循环正序。
+
+
+C++ 代码如下：
+
+```
+class Solution {
+public:
+    int coinChange(vector<int>& coins, int amount) {
+        vector<int> dp(amount + 1, INT_MAX);
+        dp[0] = 0;
+        for (int i = 0 ;i < coins.size(); i++) { // 遍历钱币
+            for (int j = coins[i]; j <= amount; j++) { // 遍历target
+                if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过
+                    dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
+                }
+            }
+        }
+        if (dp[amount] == INT_MAX) return -1;
+        return dp[amount];
+    }
+};
+```
+
+# 拓展 
+
+对于遍历方式target放在外循环，coins在内循环都是可以的，只不过对应的初始化操作有点微调，我就直接给出代码了
+
+```C++
+class Solution {
+public:
+    int coinChange(vector<int>& coins, int amount) {
+        vector<int> dp(amount + 1, INT_MAX);
+        dp[0] = 0;
+        for (int i = 1; i <= amount; i++) {
+            for (int j = 0; j < coins.size(); j++) {
+                if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {
+                    dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
+                }
+            }
+        }
+        if (dp[amount] == INT_MAX) return -1;
+        return dp[amount];
+    }
+};
+```
+
+# 总结 
+
+相信大家看网上的题解，一篇是遍历amount的for循环放外面，一篇是遍历amount的for循环放里面，看多了都看晕了，能把 遍历顺序讲明白的文章非常少。
+
+这也是大多数同学学习动态规划的苦恼所在，有的时候递推公式其实很简单，但遍历顺序很难把握！
+
+那么Carl就把遍历顺序分析的清清楚楚，相信大家看完之后，对背包问题又了更深的理解了。
+
+# tmp
 
 ```
 // dp初始化很重要
@@ -33,40 +131,17 @@ public:
 };
 ```
 
-我用求组合的思路也过了，
 ```
 class Solution {
 public:
     int coinChange(vector<int>& coins, int amount) {
         //int dp[10003] = {0}; // 并没有给所有元素赋值0
-        //if (amount == 0) return 0;
-        vector<int> dp(10003, INT_MAX);
-        dp[0] = 0;
-        for (int i = 0 ;i < coins.size(); i++) { // 求组合
-            for (int j = 1; j <= amount; j++) {
-                if (j - coins[i] >= 0 && dp[j - coins[i]] != INT_MAX) {
-                    dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
-                }
-            }
-        }
-        if (dp[amount] == INT_MAX) return -1;
-        return dp[amount];
-    }
-};
-```
-
-这种标记d代码简短，但思路有点绕
-```
-class Solution {
-public:
-    int coinChange(vector<int>& coins, int amount) {
-        //int dp[10003] = {0}; // 并没有给所有元素赋值0
-        // if (amount == 0) return 0; 这个都可以省略了，但很多同学不知道 还需要注意这个
-        vector<int> dp(10003, 0);
+        if (amount == 0) return 0; // 这个要注意
+        vector<int> dp(amount + 1, 0);
         for (int i = 1; i <= amount; i++) {
             dp[i] = INT_MAX;
             for (int j = 0; j < coins.size(); j++) {
-                if (i - coins[j] >= 0 && dp[i - coins[j]]!=INT_MAX ) {
+                if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX) {
                     dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
                 }
             }
@@ -76,3 +151,5 @@ public:
     }
 };
 ```
+
+

problems/0406.根据身高重建队列.md

@@ -162,6 +162,8 @@ public:
 
 大家可以把两个版本的代码提交一下试试，就可以发现其差别了！
 
+关于本题使用数组还是使用链表的性能差异，我在[贪心算法：根据身高重建队列（续集）](https://mp.weixin.qq.com/s/K-pRN0lzR-iZhoi-1FgbSQ)中详细讲解了一波
+
 # 总结 
 
 关于出现两个维度一起考虑的情况，我们已经做过两道题目了，另一道就是[贪心算法：分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)。

problems/0494.目标和.md

@@ -94,7 +94,7 @@ if ((S + sum) % 2 == 1) return 0; // 此时没有方案，两个int相加的时
 
 这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。
 
-本题是装满有几种方法。
+本题则是装满有几种方法。其实这就是一个组合问题了。
 
 * 确定dp数组以及下标的含义
 
@@ -102,13 +102,50 @@ dp[j] 表示：填满j（包括j）这么大容积的包，有dp[i]种方法
 
 * 确定递推公式
 
-有哪些来源可以推出dp[j]呢，只有dp[j - nums[i]]。
+有哪些来源可以推出dp[j]呢？
 
-那么dp[j] 应该是 dp[j] + dp[j - nums[i]]   （**这块需要好好讲讲**）
+不考虑nums[i]的情况下，填满容量为j - nums[i]的背包，有dp[j - nums[i]]中方法。
+
+那么如果考虑nums[i]呢，dp[j] = dp[j] + dp[j - nums[i]];
+
+公式右面的dp[j]：填满容量为j的背包（没有考虑nums[i]）有dp[j]种方法，
+
+公式右面的dp[j - nums[i]]：填满容量为j - nums[i]的背包有dp[j - nums[i]]种方法
+
+那么只要搞到nums[i]的话，就应该dp[j]（考虑nums[i]）=  dp[j]（没考虑nums[i]） + dp[j - nums[i]] 
+
+
+举一个例子,nums[i] = 2： dp[5] = dp[5] + dp[3]，公式右边的dp[5]没考虑这个2，就有dp[5]种方法。
+
+填满背包容量为3的话，有dp[3]种方法。
+
+那么只需要搞到一个2（nums[i]），有dp[3]方法可以凑齐容量为3的背包，相应的就有多少种方法可以凑齐容量为5的背包。
+
+所以 dp[5]（考虑2） = dp[5]（没考虑2） + dp[3]。
+
+所以求组合类问题的公式，都是类似这种：
+
+```
+dp[j] += dp[j - num[i]]
+```
+
+**这个公式在后面在讲解背包解决排列组合问题的时候还会用到！**
 
 * dp数组如何初始化
+
+从递归公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递归结果将都是0。
+
+dp[0] = 1，理论上也很好解释，装满容量为0的背包，有1中方法，就是装0件物品。
+
+dp[j]其他下标对应的数值应该初始化为0，从递归公式也可以看出，dp[j]要保证是0的初始值，才能正确的由dp[j - nums[i]]推导出来。
+
+
 * 确定遍历顺序
 
+对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。
+
+C++代码如下：
+
 ```
 class Solution {
 public:
@@ -119,7 +156,7 @@ public:
         if ((S + sum) % 2 == 1) return 0; // 此时没有方案，两个int相加的时候要各位小心数值溢出的问题
 
         int bagSize = (S + sum) / 2;
-        int dp[1001] = {1};
+        int dp[1001] = {1}; // 注意这个语法是第一个元素为1，其他都是0
         for (int i = 0; i < nums.size(); i++) {
             for (int j = bagSize; j >= nums[i]; j--) {
                 dp[j] += dp[j - nums[i]];

problems/动态规划理论基础.md

@@ -10,16 +10,17 @@
 
 动态规划中dp[j]是又dp[j-weight[i]]推导出来的。
 
-但如果是贪心呢，dp[j]每次选一个最大的或者最小的就完事了。
+但如果是贪心呢，每次拿物品选一个最大的或者最小的就完事了。
 
 所以贪心解决不了动态规划的问题，这也是最大的区别。
 
-很多讲解动态规划的文章都会讲最优子结构啊和重叠子问题啊这些，这些东西都是教科书的上定义，晦涩难懂而且不实用。
+大家也不用死扣动规和贪心的理论区别，后面做做题目自然就知道了。
 
-大家只要知道，动规是由前一个状态推导出来的，而贪心是局部直接算最优的，就够用了。
+而且很多讲解动态规划的文章都会讲最优子结构啊和重叠子问题啊这些，这些东西都是教科书的上定义，晦涩难懂而且不实用。
 
-对于上述提到的背包问题，后序会详细讲解。
+大家知道动规是由前一个状态推导出来的，而贪心是局部直接选最优的，对于刷题来说就够用了。
 
+上述提到的背包问题，后序会详细讲解。
 
 # 动态规划的解题步骤
 
@@ -80,7 +81,18 @@
 
 然后在问问题，目的性就很强了，回答问题的同学也可以快速知道提问者的疑惑了。
 
-# 动态规划可以解决哪一类问题 
+
+# 总结 
+
+这一篇是动态规划的整体概述，讲解了什么是动态规划，动态规划的解题步骤，以及如何debug。
+
+动态规划是一个很大的领域，今天这一篇讲解的内容是整个动态规划系列里都会使用到的一些理论基础。
+
+在后序讲解中针对某一具体问题，还会讲解其对应的理论基础，例如背包问题中的01背包，leetcode上的题目都是01背包的应用，而没有纯01背包的问题，那么就需要在把对应的理论知识讲解一下。
+
+一些同学可能着急想刷题，这个我很理解，我写的理论基础篇已经是非常偏实用的了，还是需要一点基础的。新加入的录友可能不了解，可以在「算法汇总」中看到每一个系列开始的时候都有对应的理论基础篇，都是特别实用的理论基础了。
+
+今天我们开始新的征程了，你准备好了么？ 
 
 
 

problems/背包总结篇.md

@@ -0,0 +1,19 @@
+
+组合问题公式:dp[i] += dp[i-num]
+True、False问题公式:dp[i] = dp[i] or dp[i-num]
+最大最小问题公式:dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)
+
+
+接下来讲一下背包问题的判定
+背包问题具备的特征：给定一个target，target可以是数字也可以是字符串，再给定一个数组nums，nums中装的可能是数字，也可能是字符串，问：能否使用nums中的元素做各种排列组合得到target。
+背包问题技巧：
+1.如果是0-1背包，即数组中的元素不可重复使用，nums放在外循环，target在内循环，且内循环倒序；
+for num in nums:
+    for i in range(target, nums-1, -1):
+2.如果是完全背包，即数组中的元素可重复使用，nums放在外循环，target在内循环。且内循环正序。
+for num in nums:
+    for i in range(nums, target+1):
+3.如果组合问题需考虑元素之间的顺序，需将target放在外循环，将nums放在内循环。
+for i in range(1, target+1):
+    for num in nums:
+