mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-09 19:44:45 +08:00
Update
This commit is contained in:
@ -44,7 +44,7 @@
|
||||
|
||||
[N皇后问题](https://programmercarl.com/0051.N皇后.html)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
|
||||
|
||||
本题就不一样了,**本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
|
||||
本题就不一样了,**本题中棋盘的每一个位置都要放一个数字(而N换后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
|
||||
|
||||
因为这个树形结构太大了,我抽取一部分,如图所示:
|
||||
|
||||
@ -57,7 +57,7 @@
|
||||
|
||||
**递归函数的返回值需要是bool类型,为什么呢?**
|
||||
|
||||
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值,这一点在[回溯算法:N皇后问题](https://programmercarl.com/0051.N皇后.html)中已经介绍过了,一样的道理。
|
||||
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -157,7 +157,7 @@ private:
|
||||
bool backtracking(vector<vector<char>>& board) {
|
||||
for (int i = 0; i < board.size(); i++) { // 遍历行
|
||||
for (int j = 0; j < board[0].size(); j++) { // 遍历列
|
||||
if (board[i][j] != '.') continue;
|
||||
if (board[i][j] == '.') {
|
||||
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
|
||||
if (isValid(i, j, k, board)) {
|
||||
board[i][j] = k; // 放置k
|
||||
@ -168,6 +168,7 @@ bool backtracking(vector<vector<char>>& board) {
|
||||
return false; // 9个数都试完了,都不行,那么就返回false
|
||||
}
|
||||
}
|
||||
}
|
||||
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
|
||||
}
|
||||
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
|
||||
@ -197,6 +198,7 @@ public:
|
||||
backtracking(board);
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
@ -131,8 +131,16 @@ if (sum == target) {
|
||||
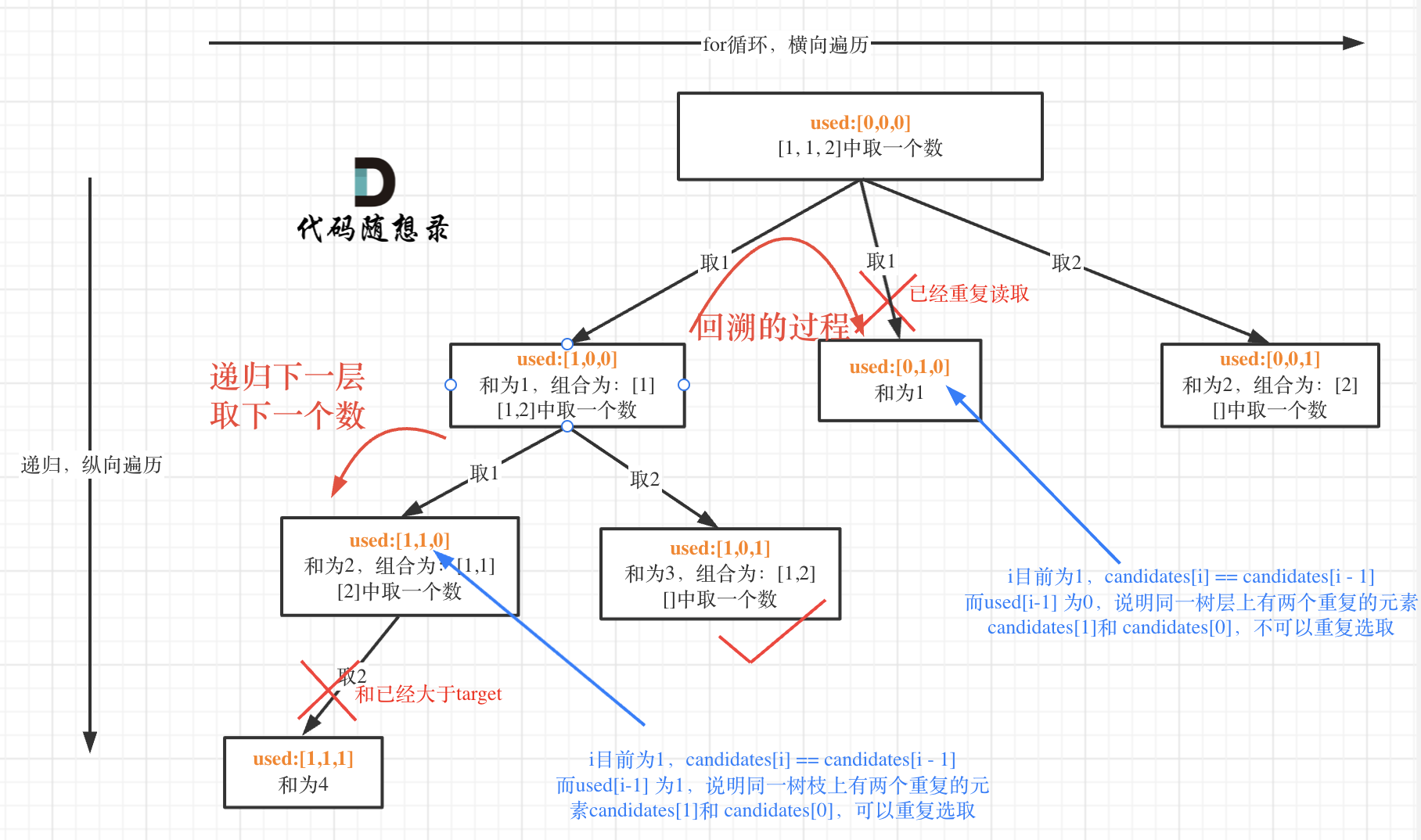
* used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
|
||||
* used[i - 1] == false,说明同一树层candidates[i - 1]使用过
|
||||
|
||||
可能有的录友想,为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
|
||||
|
||||
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
|
||||
|
||||
|
||||
那么单层搜索的逻辑代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
@ -114,7 +114,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
|
||||
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
|
||||
|
||||
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
|
||||
|
||||
|
||||
@ -28,6 +28,10 @@
|
||||
* 1 阶 + 2 阶
|
||||
* 2 阶 + 1 阶
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[带你学透动态规划-爬楼梯|LeetCode:70.爬楼梯)](https://www.bilibili.com/video/BV17h411h7UH),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -3,13 +3,8 @@
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
# 动态规划:以前我没得选,现在我选择再爬一次!
|
||||
|
||||
之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。
|
||||
|
||||
**这次终于讲到了背包问题,我选择带录友们再爬一次楼梯!**
|
||||
|
||||
## 70. 爬楼梯
|
||||
# 70. 爬楼梯
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/climbing-stairs/)
|
||||
|
||||
@ -36,6 +31,10 @@
|
||||
|
||||
## 思路
|
||||
|
||||
之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。
|
||||
|
||||
**这次终于讲到了背包问题,我选择带录友们再爬一次楼梯!**
|
||||
|
||||
这道题目 我们在[动态规划:爬楼梯](https://programmercarl.com/0070.爬楼梯.html) 中已经讲过一次了,原题其实是一道简单动规的题目。
|
||||
|
||||
既然这么简单为什么还要讲呢,其实本题稍加改动就是一道面试好题。
|
||||
|
||||
@ -426,8 +426,8 @@ class Solution:
|
||||
st.append(root.left)
|
||||
st.append(root.right)
|
||||
while st:
|
||||
leftNode = st.pop()
|
||||
rightNode = st.pop()
|
||||
leftNode = st.pop()
|
||||
if not leftNode and not rightNode:
|
||||
continue
|
||||
if not leftNode or not rightNode or leftNode.val != rightNode.val:
|
||||
|
||||
@ -2073,26 +2073,6 @@ class Solution:
|
||||
if curnode.right: queue.append(curnode.right)
|
||||
return root
|
||||
|
||||
# 链表解法
|
||||
class Solution:
|
||||
def connect(self, root: 'Node') -> 'Node':
|
||||
if not root:
|
||||
return None
|
||||
first = root
|
||||
while first: # 遍历每一层
|
||||
dummyHead = Node(None) # 为下一行创建一个虚拟头节点,相当于下一行所有节点链表的头结点(每一层都会创建);
|
||||
tail = dummyHead # 为下一行维护一个尾节点指针(初始化是虚拟节点)
|
||||
cur = first
|
||||
while cur: # 遍历当前层的节点
|
||||
if cur.left: # 链接下一行的节点
|
||||
tail.next = cur.left
|
||||
tail = tail.next
|
||||
if cur.right:
|
||||
tail.next = cur.right
|
||||
tail = tail.next
|
||||
cur = cur.next # cur同层移动到下一节点
|
||||
first = dummyHead.next # 此处为换行操作,更新到下一行
|
||||
return root
|
||||
```
|
||||
JavaScript:
|
||||
```javascript
|
||||
|
||||
@ -89,12 +89,8 @@ C++代码如下:
|
||||
class Solution {
|
||||
public:
|
||||
int evalRPN(vector<string>& tokens) {
|
||||
<<<<<<< HEAD
|
||||
stack<long long> st;
|
||||
=======
|
||||
// 力扣修改了后台测试数据,需要用longlong
|
||||
stack<long long> st;
|
||||
>>>>>>> 28f3b52a82e3cc650290fb02030a53900e122f43
|
||||
for (int i = 0; i < tokens.size(); i++) {
|
||||
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
|
||||
long long num1 = st.top();
|
||||
|
||||
@ -361,7 +361,7 @@ C#:
|
||||
|
||||
## 相关题目
|
||||
|
||||
* 383.赎金信
|
||||
* [383.赎金信](https://programmercarl.com/0383.%E8%B5%8E%E9%87%91%E4%BF%A1.html)
|
||||
* 49.字母异位词分组
|
||||
* 438.找到字符串中所有字母异位词
|
||||
|
||||
|
||||
@ -3,9 +3,9 @@
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
# 动态规划:一样的套路,再求一次完全平方数
|
||||
|
||||
## 279.完全平方数
|
||||
|
||||
# 279.完全平方数
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/perfect-squares/)
|
||||
|
||||
|
||||
@ -3,9 +3,8 @@
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
# 动态规划: 给我个机会,我再兑换一次零钱
|
||||
|
||||
## 322. 零钱兑换
|
||||
# 322. 零钱兑换
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/coin-change/)
|
||||
|
||||
|
||||
@ -32,6 +32,9 @@ F(n) = F(n - 1) + F(n - 2),其中 n > 1
|
||||
|
||||
* 0 <= n <= 30
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[手把手带你入门动态规划 | leetcode:509.斐波那契数](https://www.bilibili.com/video/BV1f5411K7mo),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -4,10 +4,15 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
|
||||
|
||||
# 746. 使用最小花费爬楼梯
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/min-cost-climbing-stairs/)
|
||||
|
||||
**旧题目描述**:
|
||||
|
||||
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
|
||||
|
||||
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
|
||||
@ -30,21 +35,32 @@
|
||||
* cost 的长度范围是 [2, 1000]。
|
||||
* cost[i] 将会是一个整型数据,范围为 [0, 999] 。
|
||||
|
||||
-----------------
|
||||
|
||||
本题之前的题目描述是很模糊的,看不出来,第一步需要花费体力值,最后一步不用花费,还是说 第一步不花费体力值,最后一步花费。
|
||||
|
||||
后来力扣改了题目描述,**新题目描述**:
|
||||
|
||||
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
|
||||
|
||||
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
|
||||
|
||||
请你计算并返回达到楼梯顶部的最低花费。
|
||||
|
||||

|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目可以说是昨天[动态规划:爬楼梯](https://programmercarl.com/0070.爬楼梯.html)的花费版本。
|
||||
(**在力扣修改了题目描述下,我又重新修改了题解**)
|
||||
|
||||
**注意题目描述:每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯**
|
||||
|
||||
所以示例1中只花费一个15 就可以到阶梯顶,最后一步可以理解为 不用花费。
|
||||
|
||||
读完题大家应该知道指定需要动态规划的,贪心是不可能了。
|
||||
修改之后的题意就比较明确了,题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
|
||||
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
|
||||
|
||||
**dp[i]的定义:到达第i个台阶所花费的最少体力为dp[i]**。(注意这里认为是第一步一定是要花费)
|
||||
**dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]**。
|
||||
|
||||
**对于dp数组的定义,大家一定要清晰!**
|
||||
|
||||
@ -52,25 +68,27 @@
|
||||
|
||||
**可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]**。
|
||||
|
||||
那么究竟是选dp[i-1]还是dp[i-2]呢?
|
||||
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
|
||||
|
||||
一定是选最小的,所以dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
|
||||
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
|
||||
|
||||
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
|
||||
|
||||
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
|
||||
|
||||
**注意这里为什么是加cost[i],而不是cost[i-1],cost[i-2]之类的**,因为题目中说了:每当你爬上一个阶梯你都要花费对应的体力值
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
根据dp数组的定义,dp数组初始化其实是比较难的,因为不可能初始化为第i台阶所花费的最少体力。
|
||||
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
|
||||
|
||||
那么看一下递归公式,dp[i]由dp[i-1],dp[i-2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
|
||||
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
|
||||
|
||||
所以初始化代码为:
|
||||
这里就要说名了,本题力扣为什么改题意了,而且修改题意之后 就清晰很多的原因了。
|
||||
|
||||
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 从 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
|
||||
|
||||
所以初始化 dp[0] = 0,dp[1] = 0;
|
||||
|
||||
```CPP
|
||||
vector<int> dp(cost.size());
|
||||
dp[0] = cost[0];
|
||||
dp[1] = cost[1];
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
@ -78,11 +96,10 @@ dp[1] = cost[1];
|
||||
|
||||
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
|
||||
|
||||
因为是模拟台阶,而且dp[i]又dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
|
||||
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
|
||||
|
||||
**但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来**。
|
||||
|
||||
例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
|
||||
> **但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来**。
|
||||
> 例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
|
||||
|
||||
**这些都是遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!**
|
||||
|
||||
@ -90,79 +107,12 @@ dp[1] = cost[1];
|
||||
|
||||
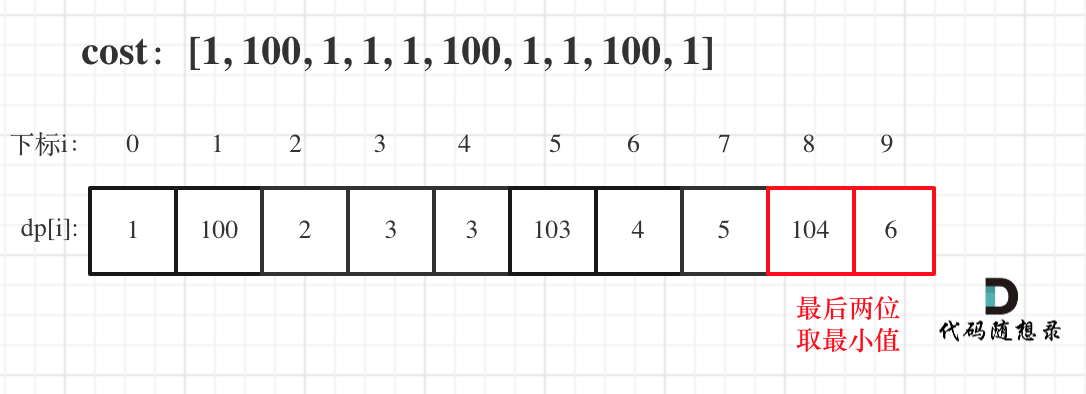
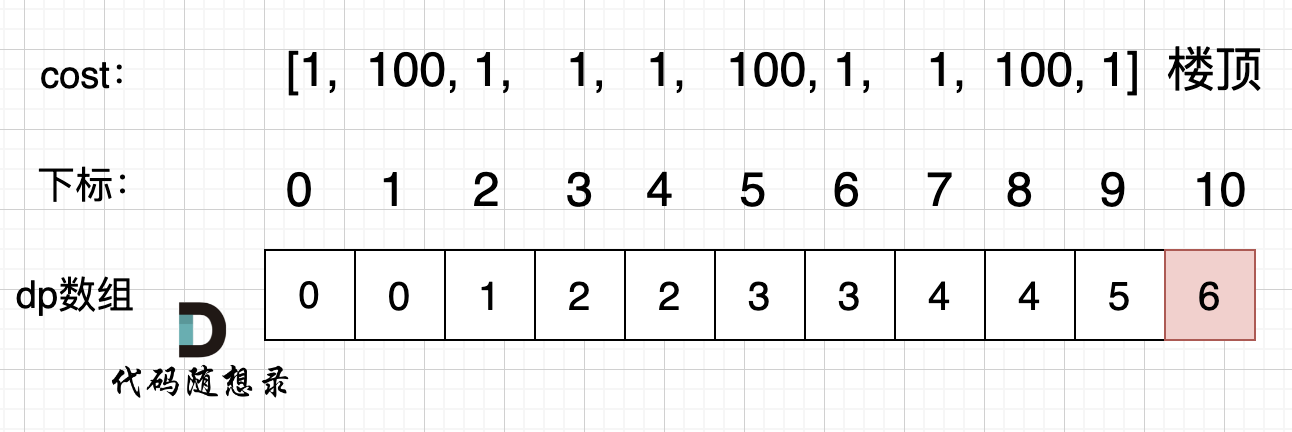
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
|
||||
|
||||
|
||||
|
||||
|
||||
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
|
||||
|
||||
以上分析完毕,整体C++代码如下:
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
int minCostClimbingStairs(vector<int>& cost) {
|
||||
vector<int> dp(cost.size());
|
||||
dp[0] = cost[0];
|
||||
dp[1] = cost[1];
|
||||
for (int i = 2; i < cost.size(); i++) {
|
||||
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
|
||||
}
|
||||
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
|
||||
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
|
||||
还可以优化空间复杂度,因为dp[i]就是由前两位推出来的,那么也不用dp数组了,C++代码如下:
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
int minCostClimbingStairs(vector<int>& cost) {
|
||||
int dp0 = cost[0];
|
||||
int dp1 = cost[1];
|
||||
for (int i = 2; i < cost.size(); i++) {
|
||||
int dpi = min(dp0, dp1) + cost[i];
|
||||
dp0 = dp1; // 记录一下前两位
|
||||
dp1 = dpi;
|
||||
}
|
||||
return min(dp0, dp1);
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
**当然我不建议这么写,能写出版本一就可以了,直观简洁!**
|
||||
|
||||
在后序的讲解中,可能我会忽略这种版本二的写法,大家只要知道有这么个写法就可以了哈。
|
||||
|
||||
## 拓展
|
||||
|
||||
这道题描述也确实有点魔幻。
|
||||
|
||||
题目描述为:每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
|
||||
|
||||
示例1:
|
||||
|
||||
输入:cost = [10, 15, 20]
|
||||
输出:15
|
||||
|
||||
|
||||
**从题目描述可以看出:要不是第一步不需要花费体力,要不就是第最后一步不需要花费体力,我个人理解:题意说的其实是第一步是要支付费用的!**。因为是当你爬上一个台阶就要花费对应的体力值!
|
||||
|
||||
所以我定义的dp[i]意思是也是第一步是要花费体力的,最后一步不用花费体力了,因为已经支付了。
|
||||
|
||||
当然也可以样,定义dp[i]为:第一步是不花费体力,最后一步是花费体力的。
|
||||
|
||||
所以代码这么写:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
@ -177,9 +127,58 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
|
||||
这么写看上去比较顺,但是就是感觉和题目描述的不太符。哈哈,也没有必要这么细扣题意了,大家只要知道,题目的意思反正就是要不是第一步不花费,要不是最后一步不花费,都可以。
|
||||
还可以优化空间复杂度,因为dp[i]就是由前两位推出来的,那么也不用dp数组了,C++代码如下:
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
int minCostClimbingStairs(vector<int>& cost) {
|
||||
int dp0 = 0;
|
||||
int dp1 = 0;
|
||||
for (int i = 2; i <= cost.size(); i++) {
|
||||
int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
|
||||
dp0 = dp1; // 记录一下前两位
|
||||
dp1 = dpi;
|
||||
}
|
||||
return dp1;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
当然如果在面试中,能写出版本一就行,除非面试官额外要求 空间复杂度,那么再去思考版本二,因为版本二还是有点绕。版本一才是正常思路。
|
||||
|
||||
|
||||
## 拓展
|
||||
|
||||
旧力扣描述,如果按照 第一步是花费的,最后一步不花费,那么代码是这么写的,提交也可以通过
|
||||
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
int minCostClimbingStairs(vector<int>& cost) {
|
||||
vector<int> dp(cost.size());
|
||||
dp[0] = cost[0]; // 第一步有花费
|
||||
dp[1] = cost[1];
|
||||
for (int i = 2; i < cost.size(); i++) {
|
||||
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
|
||||
}
|
||||
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
|
||||
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
当然如果对 动态规划 理解不够深入的话,拓展内容就别看了,容易越看越懵。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -193,17 +192,18 @@ public:
|
||||
|
||||
但我也可以随便选来一道难题讲呗,这其实是最省事的,不用管什么题目顺序,看心情找一道就讲。
|
||||
|
||||
难的是把题目按梯度排好,循序渐进,再按照统一方法论把这些都串起来,哈哈,所以大家不要催我哈,按照我的节奏一步一步来就行啦。
|
||||
难的是把题目按梯度排好,循序渐进,再按照统一方法论把这些都串起来,所以大家不要催我哈,按照我的节奏一步一步来就行了。
|
||||
|
||||
学算法,认准「代码随想录」,没毛病!
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
以下版本其他语言版本,大多是按照旧力扣题解来写的,欢迎大家在[Github](https://github.com/youngyangyang04/leetcode-master)上[提交pr](https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A),修正一波。
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
// 方式一:第一步支付费用
|
||||
// 方式一:第一步不支付费用
|
||||
class Solution {
|
||||
public int minCostClimbingStairs(int[] cost) {
|
||||
int len = cost.length;
|
||||
@ -224,7 +224,7 @@ class Solution {
|
||||
```
|
||||
|
||||
```Java
|
||||
// 方式二:第一步不支付费用
|
||||
// 方式二:第一步支付费用
|
||||
class Solution {
|
||||
public int minCostClimbingStairs(int[] cost) {
|
||||
int[] dp = new int[cost.length];
|
||||
|
||||
@ -1,4 +1,6 @@
|
||||
# 人生苦短,我用VIM!
|
||||
# 人生苦短,我用VIM!| 最强vim配置
|
||||
|
||||
> Github地址:[https://github.com/youngyangyang04/PowerVim](https://github.com/youngyangyang04/PowerVim)
|
||||
|
||||
熟悉我的录友,应该都知道我是vim流,无论是写代码还是写文档(Markdown),都是vim,都没用IDE。
|
||||
|
||||
@ -53,7 +55,7 @@ IDE那么很吃内存,打开个IDE卡半天,用VIM就很轻便了,秒开
|
||||
|_| \___/ \_/\_/ \___|_| \/ |_|_| |_| |_|
|
||||
```
|
||||
|
||||
这个配置我开源在Github上,地址:https://github.com/youngyangyang04/PowerVim
|
||||
这个配置我开源在Github上,地址:[https://github.com/youngyangyang04/PowerVim](https://github.com/youngyangyang04/PowerVim)
|
||||
|
||||
|
||||
|
||||
@ -92,6 +94,7 @@ sh install.sh
|
||||
|
||||

|
||||
|
||||
Github地址:[https://github.com/youngyangyang04/PowerVim](https://github.com/youngyangyang04/PowerVim)
|
||||
|
||||
最后,因为这个vim配置因为我一直没有宣传,所以star数量很少,哈哈哈,录友们去给个star吧,真正的开发利器,值得顶起来!
|
||||
|
||||
|
||||
@ -4,6 +4,9 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 贪心算法总结篇
|
||||
|
||||
|
||||
我刚刚开始讲解贪心系列的时候就说了,贪心系列并不打算严格的从简单到困难这么个顺序来讲解。
|
||||
|
||||
因为贪心的简单题可能往往过于简单甚至感觉不到贪心,如果我连续几天讲解简单的贪心,估计录友们一定会不耐烦了,会感觉贪心有啥好学的。
|
||||
|
||||
Reference in New Issue
Block a user