Update

README.md

@@ -1,6 +1,6 @@
 # 算法面试思维导图:
 
-![算法面试知识大纲](https://img-blog.csdnimg.cn/2020073016244490.png)
+![算法面试知识大纲](https://img-blog.csdnimg.cn/20200810145343521.png)
 
 # 算法文章精选：   
 
@@ -125,6 +125,17 @@ void kmp(int* next, const string& s){
 
 ## 二叉树 
 
+二叉树的定义：
+
+```
+struct TreeNode {
+    int val;
+    TreeNode *left;
+    TreeNode *right;
+    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
+};
+```
+
 ### 深度优先遍历（递归） 
 
 前序遍历（中左右）
@@ -261,6 +272,15 @@ vector<vector<int>> levelOrder(TreeNode* root) {
 
 ```
 
+可以直接解决如下题目：
+
+* [0102.二叉树的层序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0102.二叉树的层序遍历.md)
+* [0199.二叉树的右视图](https://github.com/youngyangyang04/leetcode/blob/master/problems/0199.二叉树的右视图.md)
+* [0104.二叉树的最大深度 （迭代法的版本）](https://github.com/youngyangyang04/leetcode/blob/master/problems/0104.二叉树的最大深度.md)
+
+* 0111.二叉树的最小深度（迭代法的版本）
+* 0222.完全二叉树的节点个数（迭代法的版本）
+
 ### 二叉树深度
 
 ```

problems/0015.三数之和.md

@@ -5,13 +5,22 @@ https://leetcode-cn.com/problems/3sum/
 
 ### 哈希解法
 
-去重的过程不好处理，有很多小细节，如果在面试中很难想到位
+
+两层for循环就可以确定 a 和b 的数值了，可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过，其实这个思路是正确的，但是我们有一个非常棘手的问题，就是题目中说的不可以包含重复的三元组。
+
+把符合条件的三元组放进vector中，然后在去去重，这样是非常费时的，很容易超时，也是这道题目通过率如此之低的根源所在。
+
+去重的过程不好处理，有很多小细节，如果在面试中很难想到位。
 
 时间复杂度：O(n^2)，但是运行时间很长，不好做剪枝操作
 
 ### 双指针
 
-推荐使用这个方法，排序后用双指针前后操作，比较容易达到去重的目的，但也有一些细节需要注意，我在如下代码详细注释了需要注意的点 
+推荐使用这个方法，排序后用双指针前后操作，比较容易达到去重的目的，但也有一些细节需要注意，我在如下代码详细注释了需要注意的点。
+
+动画效果如下：
+
+<video src='../video/15.三数之和.mp4' controls='controls' width='640' height='320' autoplay='autoplay'> Your browser does not support the video tag.</video></div>
 
 时间复杂度：O(n^2)
 

problems/0102.二叉树的层序遍历.md

@@ -7,7 +7,7 @@ https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
 
 层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
 
-需要借用一个辅助数据结构队列来实现，**队列先进后出，符合一层一层遍历的逻辑，而是用栈先进先出适合模拟深度优先遍历也就是递归的逻辑。**
+需要借用一个辅助数据结构队列来实现，**队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
 
 使用队列实现广度优先遍历，动画如下：
 

problems/0104.二叉树的最大深度.md

@@ -3,6 +3,59 @@ https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
 
 ## 思路 
 
+### 递归法
+按照递归三部曲，来看看如何来写。
+
+1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
+
+代码如下：
+```
+int getDepth(TreeNode* node)
+```
+2. 确定终止条件：如果为空节点的话，就返回0，表示高度为0。
+
+代码如下： 
+```
+if (node == NULL) return 0;
+```
+
+3. 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后去左右深度最大的数值+1 就是目前节点为根节点的树的深度。
+
+代码如下：
+
+```
+int leftDepth = getDepth(node->left);
+int rightDepth = getDepth(node->right);
+int depth = 1 + max(leftDepth, rightDepth);
+return depth;
+```
+
+所以整体代码如下：
+
+```
+class Solution {
+public:
+    int getDepth(TreeNode* node) {
+        if (node == NULL) return 0;
+        return 1 + max(getDepth(node->left), getDepth(node->right));
+    }
+    int maxDepth(TreeNode* root) {
+        return getDepth(root);
+    }
+};
+```
+
+### 迭代法 
+
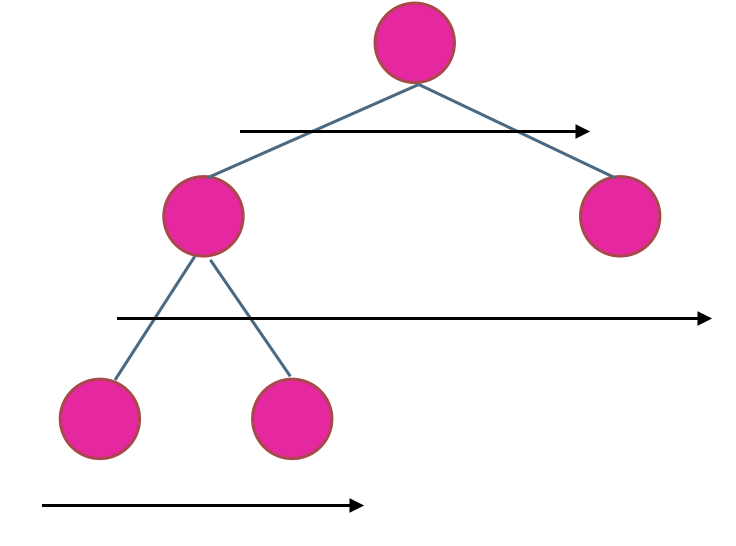
+在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：
+
+![层序遍历](https://img-blog.csdnimg.cn/20200810193056585.png)
+
+所以这道题依然是一道模板题，依然可以使用二叉树层序遍历的模板来解决的。
+
+我总结的算法模板会放到这里[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)，大家可以去看一下。
+
+代码如下：
 
 ## C++代码
 
@@ -33,7 +86,7 @@ public:
         que.push(root);
         while(!que.empty()) {
             int size = que.size(); // 必须要这么写，要固定size大小
-            depth++;
+            depth++;    // 记录深度
             for (int i = 0; i < size; i++) {
                 TreeNode* node = que.front();
                 que.pop();

problems/0111.二叉树的最小深度.md

@@ -11,22 +11,23 @@ https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
 ```
 class Solution {
 public:
-    int process(TreeNode* node) {
+    int getDepth(TreeNode* node) {
         if (node == NULL) return 0;
-        if (node->left == NULL && node->right != NULL) { // 当一个左右其中一个孩子为空的时候并不是最低点
-            return 1 + process(node->right);
+        // 当一个左子树为空，右不为空，这时并不是最低点
+        if (node->left == NULL && node->right != NULL) {
+            return 1 + getDepth(node->right);
         }
-        if (node->left != NULL && node->right == NULL) { // 当一个左右其中一个孩子为空的时候并不是最低点
-            return 1 + process(node->left);
+        // 当一个右子树为空，左不为空，这时并不是最低点
+        if (node->left != NULL && node->right == NULL) {
+            return 1 + getDepth(node->left);
         }
-        return 1 + min(process(node->left), process(node->right));
+        return 1 + min(getDepth(node->left), getDepth(node->right));
     }
 
     int minDepth(TreeNode* root) {
-        return process(root);
+        return getDepth(root);
     }
 };
-
 ```
 
 ### 迭代法

problems/0222.完全二叉树的节点个数.md

@@ -3,7 +3,13 @@ https://leetcode-cn.com/problems/count-complete-tree-nodes/
 
 ## 思路 
 
-递归题目
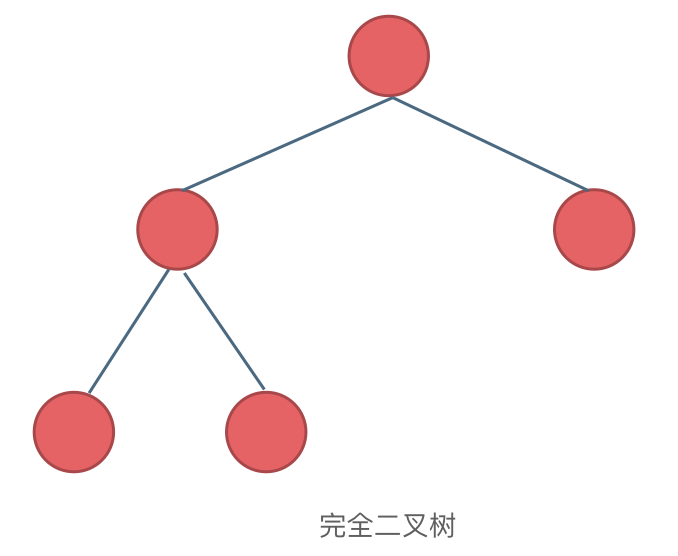
+没有必要强调是完全二叉树，就是求二叉树节点的个数，当然还是递归法和迭代法。
+
+这道题目的递归法和求二叉树的深度写法类似， 而迭代法：二叉树广度优先遍历模板稍稍修改一下，记录遍历的节点数量就可以了。
+
+![完全二叉树](https://img-blog.csdnimg.cn/20200810164440999.png)
+
+代码如下：
 
 ## C++代码
 
@@ -20,6 +26,8 @@ public:
 
 ### 迭代-广度优先
 
+二叉树层序遍历模板详解：[0102.二叉树的层序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0102.二叉树的层序遍历.md)
+
 ```
 class Solution {
 public:
@@ -33,7 +41,7 @@ public:
             for (int i = 0; i < size; i++) {
                 TreeNode* node = que.front();
                 que.pop();
-                result++;
+                result++;   // 记录遍历的层数
                 if (node->left) que.push(node->left);
                 if (node->right) que.push(node->right);
             }

problems/0383.赎金信.md

@@ -21,13 +21,15 @@ public:
     bool canConstruct(string ransomNote, string magazine) {
         for (int i = 0; i < magazine.length(); i++) {
             for (int j = 0; j < ransomNote.length(); j++) {
-                if (magazine[i] == ransomNote[j]) {  // 在ransomNote中找到和magazine相同的字符
+                // 在ransomNote中找到和magazine相同的字符
+                if (magazine[i] == ransomNote[j]) { 
                     ransomNote.erase(ransomNote.begin() + j); // ransomNote删除这个字符
                     break;
                 }
             }
         }
-        if (ransomNote.length() == 0) { // 如果ransomNote为空，则说明magazine的字符可以组成ransomNote
+        // 如果ransomNote为空，则说明magazine的字符可以组成ransomNote
+        if (ransomNote.length() == 0) { 
             return true;
         }
         return false;
@@ -52,11 +54,14 @@ public:
     bool canConstruct(string ransomNote, string magazine) {
         int record[26] = {0};
         for (int i = 0; i < magazine.length(); i++) {
-            record[magazine[i]-'a'] ++;  // 通过recode数据记录 magazine里各个字符出现次数
+            // 通过recode数据记录 magazine里各个字符出现次数
+            record[magazine[i]-'a'] ++; 
         }
         for (int j = 0; j < ransomNote.length(); j++) {
-            record[ransomNote[j]-'a']--; // 遍历ransomNote，在record里对应的字符个数做--操作
-            if(record[ransomNote[j]-'a'] < 0) { // 如果小于零说明 magazine里出现的字符，ransomNote没有
+            // 遍历ransomNote，在record里对应的字符个数做--操作
+            record[ransomNote[j]-'a']--; 
+            // 如果小于零说明 magazine里出现的字符，ransomNote没有
+            if(record[ransomNote[j]-'a'] < 0) {
                 return false;
             }
         }