update 0404.左叶子之和: 修改 go 代码，优化 js 代码风格

problems/0404.左叶子之和.md

@@ -35,7 +35,7 @@
 
 ![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902165805.png)
 
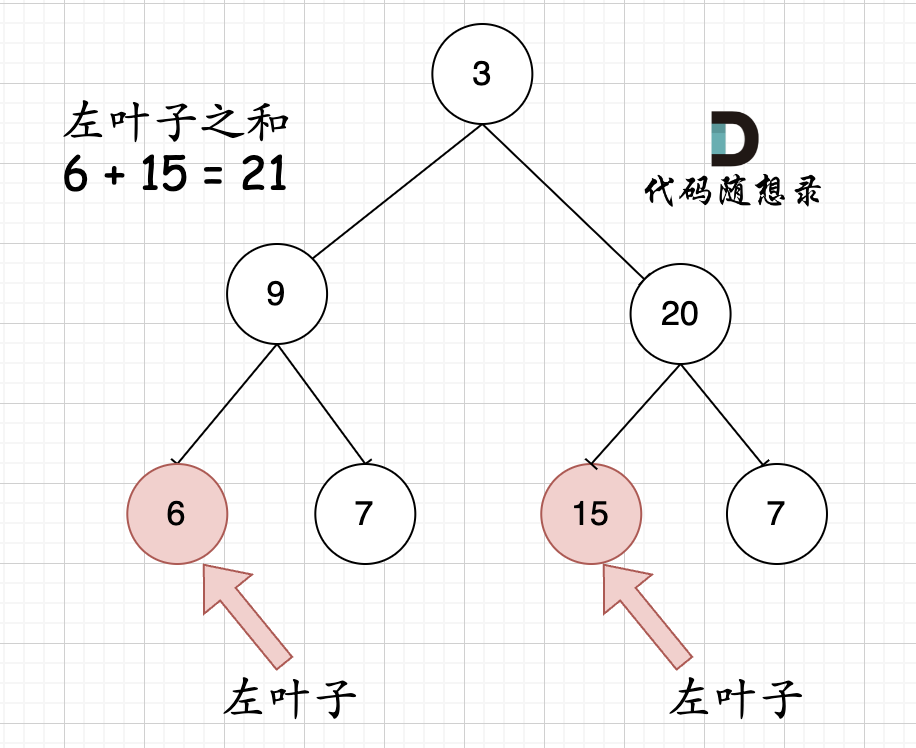
-相信通过这两个图，大家可以最左叶子的定义有明确理解了。 
+相信通过这两个图，大家对最左叶子的定义有明确理解了。 
 
 那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。**
 
@@ -298,48 +298,49 @@ class Solution:
 
 ```go
 func sumOfLeftLeaves(root *TreeNode) int {
-    var  res int
-    findLeft(root,&res)
-    return res
-}
-func findLeft(root *TreeNode,res *int){
-    //左节点
-    if root.Left!=nil&&root.Left.Left==nil&&root.Left.Right==nil{
-        *res=*res+root.Left.Val
+    if root == nil {
+        return 0
     }
-    if root.Left!=nil{
-        findLeft(root.Left,res)
-    }
-    if root.Right!=nil{
-        findLeft(root.Right,res)
+    leftValue := sumOfLeftLeaves(root.Left)   // 左
+
+    if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
+        leftValue = root.Left.Val             // 中
     }
+
+    rightValue := sumOfLeftLeaves(root.Right) // 右
+
+    return leftValue + rightValue
 }
 ```
 
-**迭代法**
+**迭代法(前序遍历)**
 
 ```go
 func sumOfLeftLeaves(root *TreeNode) int {
-    var  res int
-    queue:=list.New()
-    queue.PushBack(root)
-    for queue.Len()>0{
-        length:=queue.Len()
-        for i:=0;i<length;i++{
-            node:=queue.Remove(queue.Front()).(*TreeNode)
-            if node.Left!=nil&&node.Left.Left==nil&&node.Left.Right==nil{
-                res=res+node.Left.Val
+        st := make([]*TreeNode, 0)
+        if root == nil {
+            return 0
+        }
+        st = append(st, root)
+        result := 0
+
+        for len(st) != 0 {
+            node := st[len(st)-1]
+            st = st[:len(st)-1]
+            if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
+                result += node.Left.Val
             }
-            if node.Left!=nil{
-                queue.PushBack(node.Left)
+            if node.Right != nil {
+                st = append(st, node.Right)
             }
-            if node.Right!=nil{
-                queue.PushBack(node.Right)
+            if node.Left != nil {
+                st = append(st, node.Left)
             } 
         }
-    }
-    return res
+
+        return result
 }
+
 ```
 
 
@@ -351,16 +352,16 @@ func sumOfLeftLeaves(root *TreeNode) int {
 var sumOfLeftLeaves = function(root) {
     //采用后序遍历 递归遍历
     // 1. 确定递归函数参数
-    const nodesSum = function(node){
+    const nodesSum = function(node) {
         // 2. 确定终止条件
-        if(node===null){
+        if(node === null) {
             return 0;
         }
         let leftValue = nodesSum(node.left);
         let rightValue = nodesSum(node.right);
         // 3. 单层递归逻辑
         let midValue = 0;
-        if(node.left&&node.left.left===null&&node.left.right===null){
+        if(node.left && node.left.left === null && node.left.right === null) {
             midValue = node.left.val;
         }
         let sum = midValue + leftValue + rightValue;
@@ -374,19 +375,19 @@ var sumOfLeftLeaves = function(root) {
 ```javascript
 var sumOfLeftLeaves = function(root) {
    //采用层序遍历
-   if(root===null){
+   if(root === null) {
        return null;
    }
    let queue = [];
    let sum = 0;
    queue.push(root);
-   while(queue.length){
+   while(queue.length) {
      let node = queue.shift();
-     if(node.left!==null&&node.left.left===null&&node.left.right===null){
+     if(node.left !== null && node.left.left === null && node.left.right === null) {
          sum+=node.left.val;
      }
-     node.left&&queue.push(node.left);
-     node.right&&queue.push(node.right);
+     node.left && queue.push(node.left);
+     node.right && queue.push(node.right);
    }
    return sum;
 };