algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-09 03:34:02 +08:00
Code Issues Packages Projects Releases Wiki Activity

修改错别字“下表”->“下标”

Browse Source 
Signed-off-by: bqlin <bqlins@163.com>
This commit is contained in:
bqlin
2021-12-10 13:45:56 +08:00
parent 94e5dea6f0
commit e12257efc7
23 changed files with 52 additions and 52 deletions
Download Patch File Download Diff File Expand all files Collapse all files

4
problems/0001.两数之和.md
View File

@ -35,9 +35,9 @@
本题呢，则要使用map，那么来看一下使用数组和set来做哈希法的局限。
* 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
* set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下表位置，因为要返回x 和 y的下表。所以set 也不能用。
* set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。
此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value在保存数值所在的下表。
此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value在保存数值所在的下标。
C++中map，有三种类型：

4
problems/0018.四数之和.md
View File

@ -33,9 +33,9 @@
但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来）
[15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
[15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下标作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下表作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
那么一样的道理，五数之和、六数之和等等都采用这种解法。

2
problems/0027.移除元素.md
View File

@ -58,7 +58,7 @@ public:
for (int j = i + 1; j < size; j++) {
nums[j - 1] = nums[j];
}
i--; // 因为下表i以后的数值都向前移动了一位，所以i也向前移动一位
i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
size--; // 此时数组的大小-1
}
}

2
problems/0035.搜索插入位置.md
View File

@ -90,7 +90,7 @@ public:
以后大家**只要看到面试题里给出的数组是有序数组，都可以想一想是否可以使用二分法。**
同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下表可能不是唯一的。
同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的。
大体讲解一下二分法的思路，这里来举一个例子，例如在这个数组中，使用二分法寻找元素为5的位置，并返回其下标。

2
problems/0062.不同路径.md
View File

@ -243,7 +243,7 @@ public:
Java：
```java
/**
* 1. 确定dp数组下表含义 dp[i][j] 到每一个坐标可能的路径种类
* 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
* 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
* 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
* 4. 遍历顺序 一行一行遍历

8
problems/0084.柱状图中最大的矩形.md
View File

@ -140,9 +140,9 @@ public:
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
// 第一个元素已经入栈，从下表1开始
// 第一个元素已经入栈，从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下表
// 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
@ -251,9 +251,9 @@ class Solution {
st.push(0);
int result = 0;
// 第一个元素已经入栈，从下表1开始
// 第一个元素已经入栈，从下标1开始
for (int i = 1; i < heights.length; i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下表
// 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
if (heights[i] > heights[st.peek()]) {
st.push(i);
} else if (heights[i] == heights[st.peek()]) {

2
problems/0106.从中序与后序遍历序列构造二叉树.md
View File

@ -272,7 +272,7 @@ public:
**此时应该发现了，如上的代码性能并不好，应为每层递归定定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。**
下面给出用下表索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下表索引来分割）
下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）
### C++优化版本
```CPP

16
problems/0108.将有序数组转换为二叉搜索树.md
View File

@ -70,7 +70,7 @@
那么本题要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子。
再来看参数，首先是传入数组，然后就是左下表left和右下表right，我们在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中提过，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下表来操作原数组。
再来看参数，首先是传入数组，然后就是左下标left和右下标right，我们在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中提过，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组。
所以代码如下：
@ -144,7 +144,7 @@ public:
## 迭代法
迭代法可以通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下表，一个队列放右区间下表。
迭代法可以通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下标，一个队列放右区间下标。
模拟的就是不断分割的过程，C++代码如下：（我已经详细注释）
@ -156,11 +156,11 @@ public:
TreeNode* root = new TreeNode(0); // 初始根节点
queue<TreeNode*> nodeQue; // 放遍历的节点
queue<int> leftQue; // 保存左区间下表
queue<int> rightQue; // 保存右区间下表
queue<int> leftQue; // 保存左区间下标
queue<int> rightQue; // 保存右区间下标
nodeQue.push(root); // 根节点入队列
leftQue.push(0); // 0为左区间下表初始位置
rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下表初始位置
leftQue.push(0); // 0为左区间下标初始位置
rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下标初始位置
while (!nodeQue.empty()) {
TreeNode* curNode = nodeQue.front();
@ -267,9 +267,9 @@ class Solution {
// 根节点入队列
nodeQueue.offer(root);
// 0为左区间下表初始位置
// 0为左区间下标初始位置
leftQueue.offer(0);
// nums.size() - 1为右区间下表初始位置
// nums.size() - 1为右区间下标初始位置
rightQueue.offer(nums.length - 1);
while (!nodeQueue.isEmpty()) {

2
problems/0242.有效的字母异位词.md
View File

@ -45,7 +45,7 @@
定义一个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下表上，**因为字符a到字符z的ASCII是26个连续的数值，所以字符a映射为下表0，相应的字符z映射为下表25。**
需要把字符映射到数组也就是哈希表的索引下标上，**因为字符a到字符z的ASCII是26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。**
再遍历 字符串s的时候，**只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可，并不需要记住字符a的ASCII，只要求出一个相对数值就可以了。** 这样就将字符串s中字符出现的次数，统计出来了。

2
problems/0344.反转字符串.md
View File

@ -63,7 +63,7 @@
如果对数组和链表原理不清楚的同学，可以看这两篇，[关于链表，你该了解这些！](https://programmercarl.com/链表理论基础.html)，[必须掌握的数组理论知识](https://programmercarl.com/数组理论基础.html)。
对于字符串，我们定义两个指针（也可以说是索引下表），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。
对于字符串，我们定义两个指针（也可以说是索引下标），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。
以字符串`hello`为例，过程如下：

2
problems/0455.分发饼干.md
View File

@ -59,7 +59,7 @@ public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int index = s.size() - 1; // 饼干数组的下表
int index = s.size() - 1; // 饼干数组的下标
int result = 0;
for (int i = g.size() - 1; i >= 0; i--) {
if (index >= 0 && s[index] >= g[i]) {

14
problems/0496.下一个更大元素I.md
View File

@ -70,7 +70,7 @@ C++中，当我们要使用集合来解决哈希问题的时候，优先使用un
那么预处理代码如下:
```CPP
unordered_map<int, int> umap; // key:下表元素，value：下表
unordered_map<int, int> umap; // key:下标元素，value：下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
@ -108,7 +108,7 @@ for (int i = 0; i < nums1.size(); i++) {
```CPP
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
@ -128,7 +128,7 @@ public:
vector<int> result(nums1.size(), -1);
if (nums1.size() == 0) return result;
unordered_map<int, int> umap; // key:下表元素，value：下表
unordered_map<int, int> umap; // key:下标元素，value：下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
@ -141,7 +141,7 @@ public:
} else { // 情况三
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
@ -166,7 +166,7 @@ public:
vector<int> result(nums1.size(), -1);
if (nums1.size() == 0) return result;
unordered_map<int, int> umap; // key:下表元素，value：下表
unordered_map<int, int> umap; // key:下标元素，value：下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
@ -174,7 +174,7 @@ public:
for (int i = 1; i < nums2.size(); i++) {
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
@ -264,7 +264,7 @@ func nextGreaterElement(nums1 []int, nums2 []int) []int {
top := stack[len(stack)-1]
if _, ok := mp[nums2[top]]; ok { // 看map里是否存在这个元素
index := mp[nums2[top]]; // 根据map找到nums2[top] 在 nums1中的下表
index := mp[nums2[top]]; // 根据map找到nums2[top] 在 nums1中的下标
res[index] = nums2[i]
}

18
problems/0654.最大二叉树.md
View File

@ -63,7 +63,7 @@ if (nums.size() == 1) {
这里有三步工作
1. 先要找到数组中最大的值和对应的下表， 最大的值构造根节点，下表用来下一步分割数组。
1. 先要找到数组中最大的值和对应的下标， 最大的值构造根节点，下标用来下一步分割数组。
代码如下：
```CPP
@ -79,7 +79,7 @@ TreeNode* node = new TreeNode(0);
node->val = maxValue;
```
2. 最大值所在的下表左区间 构造左子树
2. 最大值所在的下标左区间 构造左子树
这里要判断maxValueIndex > 0，因为要保证左区间至少有一个数值。
@ -91,7 +91,7 @@ if (maxValueIndex > 0) {
}
```
3. 最大值所在的下表右区间 构造右子树
3. 最大值所在的下标右区间 构造右子树
判断maxValueIndex < (nums.size() - 1)，确保右区间至少有一个数值。
@ -114,7 +114,7 @@ public:
node->val = nums[0];
return node;
}
// 找到数组中最大的值和对应的下表
// 找到数组中最大的值和对应的下标
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {
@ -124,12 +124,12 @@ public:
}
}
node->val = maxValue;
// 最大值所在的下表左区间 构造左子树
// 最大值所在的下标左区间 构造左子树
if (maxValueIndex > 0) {
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
// 最大值所在的下表右区间 构造右子树
// 最大值所在的下标右区间 构造右子树
if (maxValueIndex < (nums.size() - 1)) {
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
@ -141,7 +141,7 @@ public:
以上代码比较冗余，效率也不高，每次还要切割的时候每次都要定义新的vector（也就是数组），但逻辑比较清晰。
和文章[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中一样的优化思路，就是每次分隔不用定义新的数组，而是通过下表索引直接在原数组上操作。
和文章[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中一样的优化思路，就是每次分隔不用定义新的数组，而是通过下标索引直接在原数组上操作。
优化后代码如下：
@ -152,7 +152,7 @@ private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left >= right) return nullptr;
// 分割点下表：maxValueIndex
// 分割点下标：maxValueIndex
int maxValueIndex = left;
for (int i = left + 1; i < right; ++i) {
if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
@ -212,7 +212,7 @@ root->right = traversal(nums, maxValueIndex + 1, right);
这道题目其实和 [二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html) 是一个思路，比[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html) 还简单一些。
**注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下表索引直接在原数组上操作，这样可以节约时间和空间上的开销。**
**注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。**
一些同学也会疑惑，什么时候递归函数前面加if，什么时候不加if，这个问题我在最后也给出了解释。

2
problems/0674.最长连续递增序列.md
View File

@ -156,7 +156,7 @@ public:
Java：
```java
/**
* 1.dp[i] 代表当前下表最大连续值
* 1.dp[i] 代表当前下标最大连续值
* 2.递推公式 if（nums[i+1]>nums[i]） dp[i+1] = dp[i]+1
* 3.初始化 都为1
* 4.遍历方向，从其那往后

2
problems/0860.柠檬水找零.md
View File

@ -183,7 +183,7 @@ class Solution:
```golang
func lemonadeChange(bills []int) bool {
//left表示还剩多少 下表0位5元的个数 ，下表1为10元的个数
//left表示还剩多少 下标0位5元的个数 ，下标1为10元的个数
left:=[2]int{0,0}
//第一个元素不为5，直接退出
if bills[0]!=5{

4
problems/0922.按奇偶排序数组II.md
View File

@ -69,8 +69,8 @@ class Solution {
public:
vector<int> sortArrayByParityII(vector<int>& A) {
vector<int> result(A.size());
int evenIndex = 0; // 偶数下表
int oddIndex = 1; // 奇数下表
int evenIndex = 0; // 偶数下标
int oddIndex = 1; // 奇数下标
for (int i = 0; i < A.size(); i++) {
if (A[i] % 2 == 0) {
result[evenIndex] = A[i];

2
problems/0941.有效的山脉数组.md
View File

@ -43,7 +43,7 @@
**注意这里还是有一些细节，例如如下两点：**
* 因为left和right是数组下表，移动的过程中注意不要数组越界
* 因为left和right是数组下标，移动的过程中注意不要数组越界
* 如果left或者right没有移动，说明是一个单调递增或者递减的数组，依然不是山峰
C++代码如下：

2
problems/二叉树理论基础.md
View File

@ -93,7 +93,7 @@
用数组来存储二叉树如何遍历的呢？
**如果父节点的数组下表是i，那么它的左孩子就是i * 2 + 1，右孩子就是 i * 2 + 2。**
**如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。**
但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

2
problems/双指针总结.md
View File

@ -30,7 +30,7 @@ for (int i = 0; i < array.size(); i++) {
在[字符串：这道题目，使用库函数一行代码搞定](https://programmercarl.com/0344.反转字符串.html)中讲解了反转字符串，注意这里强调要原地反转，要不然就失去了题目的意义。
使用双指针法，**定义两个指针（也可以说是索引下表），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。**，时间复杂度是O(n)。
使用双指针法，**定义两个指针（也可以说是索引下标），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。**，时间复杂度是O(n)。
在[替换空格](https://programmercarl.com/剑指Offer05.替换空格.html) 中介绍使用双指针填充字符串的方法，如果想把这道题目做到极致，就不要只用额外的辅助空间了！

2
problems/周总结/20201010二叉树周末总结.md
View File

@ -67,7 +67,7 @@
知道了如何构造二叉树，那么使用一个套路就可以解决文章[二叉树：构造一棵最大的二叉树](https://programmercarl.com/0654.最大二叉树.html)中的问题。
**注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下表索引直接在原数组上操作，这样可以节约时间和空间上的开销。**
**注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。**
文章中我还给出了递归函数什么时候加if，什么时候不加if，其实就是控制空节点（空指针）是否进入递归，是不同的代码实现方式，都是可以的。

2
problems/哈希表总结.md
View File

@ -84,7 +84,7 @@ std::set和std::multiset底层实现都是红黑树，std::unordered_set的底
* 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
* set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。
map是一种`<key, value>`的结构，本题可以用key保存数值，用value在保存数值所在的下表。所以使用map最为合适。
map是一种`<key, value>`的结构，本题可以用key保存数值，用value在保存数值所在的下标。所以使用map最为合适。
C++提供如下三种map：：（详情请看[关于哈希表，你该了解这些！](https://programmercarl.com/哈希表理论基础.html)）

6
problems/哈希表理论基础.md
View File

@ -14,7 +14,7 @@
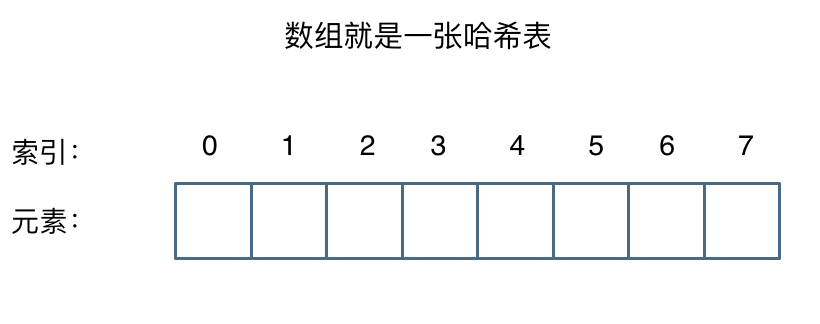
这么这官方的解释可能有点懵，其实直白来讲其实数组就是一张哈希表。
哈希表中关键码就是数组的索引下表，然后通过下表直接访问数组中的元素，如下图所示：
哈希表中关键码就是数组的索引下标，然后通过下标直接访问数组中的元素，如下图所示：
![哈希表1](https://img-blog.csdnimg.cn/20210104234805168.png)
@ -42,13 +42,13 @@
此时问题又来了，哈希表我们刚刚说过，就是一个数组。
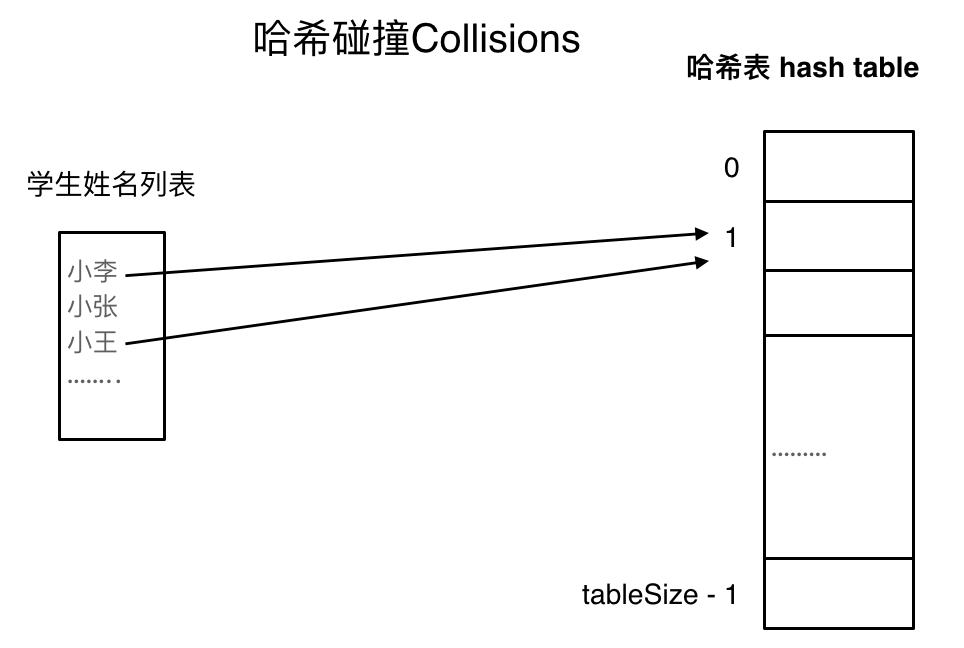
如果学生的数量大于哈希表的大小怎么办，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下表的位置。
如果学生的数量大于哈希表的大小怎么办，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。
接下来**哈希碰撞**登场
### 哈希碰撞
如图所示，小李和小王都映射到了索引下表 1的位置，**这一现象叫做哈希碰撞**。
如图所示，小李和小王都映射到了索引下标 1 的位置，**这一现象叫做哈希碰撞**。
![哈希表3](https://img-blog.csdnimg.cn/2021010423494884.png)

2
problems/字符串总结.md
View File

@ -93,7 +93,7 @@ KMP的主要思想是**当出现字符串不匹配时，可以知道一部分之
KMP的精髓所在就是前缀表，在[KMP精讲](https://programmercarl.com/0028.实现strStr.html)中提到了，什么是KMP，什么是前缀表，以及为什么要用前缀表。
前缀表：起始位置到下表i之前（包括i）的子串中，有多大长度的相同前缀后缀。
前缀表：起始位置到下标i之前（包括i）的子串中，有多大长度的相同前缀后缀。
那么使用KMP可以解决两类经典问题：