Merge branch 'youngyangyang04:master' into master

README.md

@@ -89,8 +89,7 @@
 
 ## 前序
 
-* [「代码随想录」后序安排](https://mp.weixin.qq.com/s/4eeGJREy6E-v6D7cR_5A4g)
-* [「代码随想录」学习社区](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+* [「代码随想录」学习社区](https://programmercarl.com/other/kstar.html)
 
 
 * 编程语言
@@ -124,7 +123,7 @@
     
 * 算法性能分析
     * [关于时间复杂度，你不知道的都在这里！](./problems/前序/关于时间复杂度，你不知道的都在这里！.md)
-    * [$O(n)$的算法居然超时了，此时的n究竟是多大？](./problems/前序/On的算法居然超时了，此时的n究竟是多大？.md)
+    * [O(n)的算法居然超时了，此时的n究竟是多大？](./problems/前序/On的算法居然超时了，此时的n究竟是多大？.md)
     * [通过一道面试题目，讲一讲递归算法的时间复杂度！](./problems/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.md)
     * [本周小结！（算法性能分析系列一）](./problems/周总结/20201210复杂度分析周末总结.md)
     * [关于空间复杂度，可能有几个疑问？](./problems/前序/关于空间复杂度，可能有几个疑问？.md)

problems/0015.三数之和.md

@@ -138,8 +138,12 @@ public:
                 */
                 if (nums[i] + nums[left] + nums[right] > 0) {
                     right--;
+                    // 当前元素不合适了，可以去重
+                    while (left < right && nums[right] == nums[right + 1]) right--;
                 } else if (nums[i] + nums[left] + nums[right] < 0) {
                     left++;
+                    // 不合适，去重
+                    while (left < right && nums[left] == nums[left - 1]) left++;
                 } else {
                     result.push_back(vector<int>{nums[i], nums[left], nums[right]});
                     // 去重逻辑应该放在找到一个三元组之后

problems/0018.四数之和.md

@@ -91,9 +91,13 @@ public:
                     // nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
                     if (nums[k] + nums[i] > target - (nums[left] + nums[right])) {
                         right--;
+                        // 当前元素不合适了，可以去重
+                        while (left < right && nums[right] == nums[right + 1]) right--;
                     // nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出
                     } else if (nums[k] + nums[i]  < target - (nums[left] + nums[right])) {
                         left++;
+                        // 不合适，去重
+                        while (left < right && nums[left] == nums[left - 1]) left++;
                     } else {
                         result.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});
                         // 去重逻辑应该放在找到一个四元组之后

problems/0020.有效的括号.md

@@ -159,7 +159,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 # 方法一，仅使用栈，更省空间
 class Solution:
     def isValid(self, s: str) -> bool:
@@ -180,7 +180,7 @@ class Solution:
         return True if not stack else False
 ```
 
-```python3
+```python
 # 方法二，使用字典
 class Solution:
     def isValid(self, s: str) -> bool:

problems/0027.移除元素.md

@@ -106,6 +106,37 @@ public:
 
 旧文链接：[数组：就移除个元素很难么？](https://programmercarl.com/0027.移除元素.html)
 
+```CPP
+/**
+* 相向双指针方法，基于元素顺序可以改变的题目描述改变了元素相对位置，确保了移动最少元素
+* 时间复杂度：$O(n)$
+* 空间复杂度：$O(1)$
+*/
+class Solution {
+public:
+    int removeElement(vector<int>& nums, int val) {
+        int leftIndex = 0;
+        int rightIndex = nums.size() - 1;
+        while (leftIndex <= rightIndex) {
+            // 找左边等于val的元素
+            while (leftIndex <= rightIndex && nums[leftIndex] != val){
+                ++leftIndex;
+            }
+            // 找右边不等于val的元素
+            while (leftIndex <= rightIndex && nums[rightIndex] == val) {
+                -- rightIndex;
+            }
+            // 将右边不等于val的元素覆盖左边等于val的元素
+            if (leftIndex < rightIndex) {
+                nums[leftIndex++] = nums[rightIndex--];
+            }
+        }
+        return leftIndex;   // leftIndex一定指向了最终数组末尾的下一个元素
+    }
+};
+```
+
+  
 ## 相关题目推荐
 
 * 26.删除排序数组中的重复项
@@ -142,7 +173,7 @@ class Solution {
 
 Python：
 
-```python3
+```python
 class Solution:
     """双指针法
     时间复杂度：O(n)

problems/0035.搜索插入位置.md

@@ -246,7 +246,7 @@ func searchInsert(nums []int, target int) int {
 ```
 
 ### Python 
-```python3
+```python
 class Solution:
     def searchInsert(self, nums: List[int], target: int) -> int:
         left, right = 0, len(nums) - 1

problems/0039.组合总和.md

@@ -264,7 +264,7 @@ class Solution {
 
 ## Python  
 **回溯**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.path = []
@@ -296,7 +296,7 @@ class Solution:
             self.path.pop()        # 回溯
 ```
 **剪枝回溯**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.path = []

problems/0040.组合总和II.md

@@ -334,7 +334,7 @@ class Solution {
 
 ## Python 
 **回溯+巧妙去重(省去使用used**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []
@@ -374,7 +374,7 @@ class Solution:
             sum_ -= candidates[i]       # 回溯，为了下一轮for loop
 ```
 **回溯+去重（使用used）**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []

problems/0042.接雨水.md

@@ -491,7 +491,7 @@ class Solution:
         return res
 ```
 动态规划
-```python3
+```python
 class Solution:
     def trap(self, height: List[int]) -> int:
         leftheight, rightheight = [0]*len(height), [0]*len(height)

problems/0046.全排列.md

@@ -243,7 +243,7 @@ class Solution:
             usage_list[i] = False
 ```
 **回溯+丢掉usage_list**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.path = []

problems/0059.螺旋矩阵II.md

@@ -10,7 +10,7 @@
 
 [力扣题目链接](https://leetcode-cn.com/problems/spiral-matrix-ii/)
 
-给定一个正整数 n，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
+给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
 
 示例:
 
@@ -188,51 +188,35 @@ class Solution {
 }
 ```
 
-python:
+python3:
 
-```python3
+```python
 class Solution:
-
     def generateMatrix(self, n: int) -> List[List[int]]:
-        # 初始化要填充的正方形
-        matrix = [[0] * n for _ in range(n)]
+        nums = [[0] * n for _ in range(n)]
+        startx, starty = 0, 0               # 起始点
+        loop, mid = n // 2, n // 2          # 迭代次数、n为奇数时，矩阵的中心点
+        count = 1                           # 计数
 
-        left, right, up, down = 0, n - 1, 0, n - 1
-        number = 1  # 要填充的数字
+        for offset in range(1, loop + 1) :      # 每循环一层偏移量加1，偏移量从1开始
+            for i in range(starty, n - offset) :    # 从左至右，左闭右开
+                nums[startx][i] = count
+                count += 1
+            for i in range(startx, n - offset) :    # 从上至下
+                nums[i][n - offset] = count
+                count += 1
+            for i in range(n - offset, starty, -1) : # 从右至左
+                nums[n - offset][i] = count
+                count += 1
+            for i in range(n - offset, startx, -1) : # 从下至上
+                nums[i][starty] = count
+                count += 1                
+            startx += 1         # 更新起始点
+            starty += 1
 
-        while left < right and up < down:
-
-            # 从左到右填充上边
-            for x in range(left, right):
-                matrix[up][x] = number
-                number += 1
-
-            # 从上到下填充右边
-            for y in range(up, down):
-                matrix[y][right] = number
-                number += 1
-
-            # 从右到左填充下边
-            for x in range(right, left, -1):
-                matrix[down][x] = number
-                number += 1
-
-            # 从下到上填充左边
-            for y in range(down, up, -1):
-                matrix[y][left] = number
-                number += 1
-
-            # 缩小要填充的范围
-            left += 1
-            right -= 1
-            up += 1
-            down -= 1
-
-        # 如果阶数为奇数，额外填充一次中心
-        if n % 2:
-            matrix[n // 2][n // 2] = number
-
-        return matrix
+        if n % 2 != 0 :			# n为奇数时，填充中心点
+            nums[mid][mid] = count 
+        return nums
 ```
 
 javaScript

problems/0070.爬楼梯.md

@@ -256,16 +256,28 @@ public int climbStairs(int n) {
 ### Python
 
 ```python
+# 空间复杂度为O(n)版本
 class Solution:
     def climbStairs(self, n: int) -> int:
-        # dp[i]表示爬到第i级楼梯的种数， (1, 2) (2, 1)是两种不同的类型
-        dp = [0] * (n + 1)
-        dp[0] = 1
-        for i in range(n+1):
-            for j in range(1, 3):
-                if i>=j:
-                    dp[i] += dp[i-j]
-        return dp[-1]
+        # dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
+        dp=[0]*(n+1)
+        dp[0]=1
+        dp[1]=1
+        for i in range(2,n+1):
+            dp[i]=dp[i-1]+dp[i-2]
+        return dp[n]
+        
+# 空间复杂度为O(1)版本
+class Solution:
+    def climbStairs(self, n: int) -> int:
+        dp=[0]*(n+1)
+        dp[0]=1
+        dp[1]=1
+        for i in range(2,n+1):
+            tmp=dp[0]+dp[1]
+            dp[0]=dp[1]
+            dp[1]=tmp
+        return dp[1]
 ```
 
 ### Go 

problems/0070.爬楼梯完全背包版本.md

@@ -143,10 +143,10 @@ class Solution {
 }
 ```
 
-Python：
+Python3：
 
 
-```python3
+```python
 class Solution:
     def climbStairs(self, n: int) -> int:
         dp = [0]*(n + 1)

problems/0077.组合优化.md

@@ -174,7 +174,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 class Solution:
     def combine(self, n: int, k: int) -> List[List[int]]:
         res=[]  #存放符合条件结果的集合

problems/0078.子集.md

@@ -203,7 +203,7 @@ class Solution {
 ```
 
 ## Python 
-```python3
+```python
 class Solution:
     def __init__(self):
         self.path: List[int] = []

problems/0084.柱状图中最大的矩形.md

@@ -277,9 +277,9 @@ class Solution {
 }
 ```
 
-Python:
+Python3:
 
-```python3
+```python
 
 # 双指针；暴力解法（leetcode超时）
 class Solution:

problems/0093.复原IP地址.md

@@ -304,6 +304,48 @@ class Solution {
         return true;
     }
 }
+
+//方法二：比上面的方法时间复杂度低，更好地剪枝，优化时间复杂度
+class Solution {
+    List<String> result = new ArrayList<String>();
+	StringBuilder stringBuilder = new StringBuilder();
+
+	public List<String> restoreIpAddresses(String s) {
+		restoreIpAddressesHandler(s, 0, 0);
+		return result;
+	}
+
+	// number表示stringbuilder中ip段的数量
+	public void restoreIpAddressesHandler(String s, int start, int number) {
+		// 如果start等于s的长度并且ip段的数量是4，则加入结果集，并返回
+		if (start == s.length() && number == 4) {
+			result.add(stringBuilder.toString());
+			return;
+		}
+		// 如果start等于s的长度但是ip段的数量不为4，或者ip段的数量为4但是start小于s的长度，则直接返回
+		if (start == s.length() || number == 4) {
+			return;
+		}
+		// 剪枝：ip段的长度最大是3，并且ip段处于[0,255]
+		for (int i = start; i < s.length() && i - start < 3 && Integer.parseInt(s.substring(start, i + 1)) >= 0
+				&& Integer.parseInt(s.substring(start, i + 1)) <= 255; i++) {
+			// 如果ip段的长度大于1，并且第一位为0的话，continue
+			if (i + 1 - start > 1 && s.charAt(start) - '0' == 0) {
+				continue;
+			}
+			stringBuilder.append(s.substring(start, i + 1));
+			// 当stringBuilder里的网段数量小于3时，才会加点；如果等于3，说明已经有3段了，最后一段不需要再加点
+			if (number < 3) {
+				stringBuilder.append(".");
+			}
+			number++;
+			restoreIpAddressesHandler(s, i + 1, number);
+			number--;
+			// 删除当前stringBuilder最后一个网段，注意考虑点的数量的问题
+			stringBuilder.delete(start + number, i + number + 2);
+		}
+	}
+}
 ```
 
 ## python
@@ -339,7 +381,7 @@ class Solution(object):
 ```
 
 python3:
-```python3
+```python
 class Solution:
     def __init__(self):
         self.result = []

problems/0098.验证二叉搜索树.md

@@ -526,6 +526,48 @@ var isValidBST = function (root) {
 };
 ```
 
+## TypeScript
+
+> 辅助数组解决：
+
+```typescript
+function isValidBST(root: TreeNode | null): boolean {
+    const traversalArr: number[] = [];
+    function inorderTraverse(root: TreeNode | null): void {
+        if (root === null) return;
+        inorderTraverse(root.left);
+        traversalArr.push(root.val);
+        inorderTraverse(root.right);
+    }
+    inorderTraverse(root);
+    for (let i = 0, length = traversalArr.length; i < length - 1; i++) {
+        if (traversalArr[i] >= traversalArr[i + 1]) return false;
+    }
+    return true;
+};
+```
+
+> 递归中解决：
+
+```typescript
+function isValidBST(root: TreeNode | null): boolean {
+    let maxVal = -Infinity;
+    function inorderTraverse(root: TreeNode | null): boolean {
+        if (root === null) return true;
+        let leftValid: boolean = inorderTraverse(root.left);
+        if (!leftValid) return false;
+        if (maxVal < root.val) {
+            maxVal = root.val
+        } else {
+            return false;
+        }
+        let rightValid: boolean = inorderTraverse(root.right);
+        return leftValid && rightValid;
+    }
+    return inorderTraverse(root);
+};
+```
+
 
 
 -----------------------

problems/0102.二叉树的层序遍历.md

@@ -83,10 +83,10 @@ public:
 };
 ```
 
-python代码：
+python3代码：
 
 
-```python3
+```python
 
 class Solution:
     """二叉树层序遍历迭代解法"""
@@ -273,32 +273,29 @@ function levelOrder(root: TreeNode | null): number[][] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func levelOrder(_ root: TreeNode?) -> [[Int]] {
-    var res = [[Int]]()
-    guard let root = root else {
-        return res
-    }
-    var queue = [TreeNode]()
-    queue.append(root)
+    var result = [[Int]]()
+    guard let root = root else { return result }
+    // 表示一层
+    var queue = [root]
     while !queue.isEmpty {
-        let size = queue.count
-        var sub = [Int]()
-        for _ in 0 ..< size {
+        let count = queue.count
+        var subarray = [Int]()
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            sub.append(node.val)
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+            subarray.append(node.val)
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
-        res.append(sub)
+        result.append(subarray)
     }
-    return res
+
+    return result
 }
 ```
 
@@ -505,30 +502,29 @@ function levelOrderBottom(root: TreeNode | null): number[][] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func levelOrderBottom(_ root: TreeNode?) -> [[Int]] {
-    var res =  [[Int]]()
-    guard let root = root else {
-        return res
-    }
-    var queue:  [TreeNode] = [root]
+    // 表示一层
+    var queue = [TreeNode]()
+    if let node = root { queue.append(node) }
+    var result = [[Int]]()
     while !queue.isEmpty {
-        var sub = [Int]()
-        for _ in 0 ..< queue.count {
+        let count = queue.count
+        var subarray = [Int]()
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            sub.append(node.val)
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+            subarray.append(node.val)
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node)}
         }
-        res.insert(sub, at: 0)
+        result.append(subarray)
     }
-    return res
+
+    return result.reversed()
 }
 ```
 
@@ -729,37 +725,31 @@ function rightSideView(root: TreeNode | null): number[] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func rightSideView(_ root: TreeNode?) -> [Int] {
-    var res = [Int]()
-    guard let root = root else {
-        return res
-    }
+    // 表示一层
     var queue = [TreeNode]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
+    var result = [Int]()
     while !queue.isEmpty {
-        let size = queue.count
-        for i in 0 ..< size {
+        let count = queue.count
+        for i in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            if i == size - 1 {
-                // 保存 每层最后一个元素
-                res.append(node.val)
-            }
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+            if i == count - 1 { result.append(node.val) }
+
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
     }
-    return res
+
+    return result
 }
 ```
 
-
 # 637.二叉树的层平均值
 
 [力扣题目链接](https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/)
@@ -965,32 +955,30 @@ function averageOfLevels(root: TreeNode | null): number[] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func averageOfLevels(_ root: TreeNode?) -> [Double] {
-    var res = [Double]()
-    guard let root = root else {
-        return res
-    }
+    // 表示一层
     var queue = [TreeNode]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
+    var result = [Double]()
     while !queue.isEmpty {
-        let size = queue.count
+        let count = queue.count
         var sum = 0
-        for _ in 0 ..< size {
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
             sum += node.val
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
-        res.append(Double(sum) / Double(size))
+        result.append(Double(sum) / Double(count))
     }
-    return res
+
+    return result
 }
 ```
 
@@ -1212,29 +1200,28 @@ function levelOrder(root: Node | null): number[][] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func levelOrder(_ root: Node?) -> [[Int]] {
-    var res = [[Int]]()
-    guard let root = root else {
-        return res
-    }
+    // 表示一层
     var queue = [Node]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
+    var result = [[Int]]()
     while !queue.isEmpty {
-        let size = queue.count
-        var sub = [Int]()
-        for _ in 0 ..< size {
+        let count = queue.count
+        var subarray = [Int]()
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            sub.append(node.val)
-            for childNode in node.children {
-                queue.append(childNode)
-            }
+            subarray.append(node.val)
+            // 下一层
+            for node in node.children { queue.append(node) }
         }
-        res.append(sub)
+        result.append(subarray)
     }
-    return res
+
+    return result
 }
 ```
 
@@ -1419,34 +1406,30 @@ function largestValues(root: TreeNode | null): number[] {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func largestValues(_ root: TreeNode?) -> [Int] {
-    var res = [Int]()
-    guard let root = root else {
-        return res
-    }
+    // 表示一层
     var queue = [TreeNode]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
+    var result = [Int]()
     while !queue.isEmpty {
-        let size = queue.count
-        var max: Int = Int.min
-        for _ in 0 ..< size {
+        let count = queue.count
+        var max = queue[0].val
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            if node.val > max {
-                max = node.val
-            }
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+            if node.val > max { max = node.val }
+
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
-        res.append(max)
+        result.append(max)
     }
-    return res
+
+    return result
 }
 ```
 
@@ -1456,7 +1439,7 @@ func largestValues(_ root: TreeNode?) -> [Int] {
 
 给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
 
-```
+```cpp
 struct Node {
   int val;
   Node *left;
@@ -1677,33 +1660,34 @@ func connect(root *Node) *Node {
 }
 ```
 
-Swift:
+Swift：
+
 ```swift
 func connect(_ root: Node?) -> Node? {
-    guard let root = root else {
-        return nil
-    }
+    // 表示一层
     var queue = [Node]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
     while !queue.isEmpty {
-        let size = queue.count
-        var preNode: Node?
-        for i in 0 ..< size {
-            let node = queue.removeFirst()
+        let count = queue.count
+        var current, previous: Node!
+        for i in 0 ..< count {
+            // 当前层
             if i == 0 {
-                preNode = node
+                previous = queue.removeFirst()
+                current = previous
             } else {
-                preNode?.next = node
-                preNode = node
-            }
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
+                current = queue.removeFirst()
+                previous.next = current
+                previous = current
             }
+
+            // 下一层
+            if let node = current.left { queue.append(node) }
+            if let node = current.right { queue.append(node) }
         }
+        previous.next = nil
     }
+
     return root
 }
 ```
@@ -1927,34 +1911,34 @@ func connect(root *Node) *Node {
     return root
 }
 ```
-
 Swift：
+
 ```swift
 func connect(_ root: Node?) -> Node? {
-    guard let root = root else {
-        return nil
-    }
+    // 表示一层
     var queue = [Node]()
-    queue.append(root)
+    if let node = root { queue.append(node) }
     while !queue.isEmpty {
-        let size = queue.count
-        var preNode: Node?
-        for i in 0 ..< size {
-            let node = queue.removeFirst()
+        let count = queue.count
+        var current, previous: Node!
+        for i in 0 ..< count {
+            // 当前层
             if i == 0 {
-                preNode = node
+                previous = queue.removeFirst()
+                current = previous
             } else {
-                preNode?.next = node
-                preNode = node
-            }
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
+                current = queue.removeFirst()
+                previous.next = current
+                previous = current
             }
+
+            // 下一层
+            if let node = current.left { queue.append(node) }
+            if let node = current.right { queue.append(node) }
         }
+        previous.next = nil
     }
+
     return root
 }
 ```
@@ -2151,29 +2135,28 @@ function maxDepth(root: TreeNode | null): number {
 };
 ```
 
-Swift:
+Swift：
 
 ```swift
 func maxDepth(_ root: TreeNode?) -> Int {
-    guard let root = root else {
-        return 0
-    }
+    guard root != nil else { return 0 }
+    var depth = 0
     var queue = [TreeNode]()
-    queue.append(root)
-    var res: Int = 0
+    queue.append(root!)
     while !queue.isEmpty {
-        for _ in 0 ..< queue.count {
+        let count = queue.count
+        depth += 1
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
-            }
+
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
-        res += 1
     }
-    return res
+
+    return depth
 }
 ```
 
@@ -2374,28 +2357,25 @@ Swift：
 
 ```swift
 func minDepth(_ root: TreeNode?) -> Int {
-    guard let root = root else {
-        return 0
-    }
-    var res = 0
-    var queue = [TreeNode]()
-    queue.append(root)
+    guard root != nil else { return 0 }
+    var depth = 0
+    var queue = [root!]
     while !queue.isEmpty {
-        res += 1
-        for _ in 0 ..< queue.count {
+        let count = queue.count
+        depth += 1
+        for _ in 0 ..< count {
+            // 当前层
             let node = queue.removeFirst()
-            if node.left == nil && node.right == nil {
-                return res
-            }
-            if let left = node.left {
-                queue.append(left)
-            }
-            if let right = node.right {
-                queue.append(right)
+            if node.left == nil, node.right == nil { // 遇到叶子结点则返回
+                return depth
             }
+
+            // 下一层
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
         }
     }
-    return res
+    return depth
 }
 ```
 

problems/0104.二叉树的最大深度.md

@@ -523,8 +523,8 @@ func maxdepth(root *treenode) int {
 
 ```javascript
 var maxdepth = function(root) {
-    if (!root) return root
-    return 1 + math.max(maxdepth(root.left), maxdepth(root.right))
+    if (root === null) return 0;
+    return 1 + Math.max(maxdepth(root.left), maxdepth(root.right))
 };
 ```
 
@@ -541,7 +541,7 @@ var maxdepth = function(root) {
     //3. 确定单层逻辑
         let leftdepth=getdepth(node.left);
         let rightdepth=getdepth(node.right);
-        let depth=1+math.max(leftdepth,rightdepth);
+        let depth=1+Math.max(leftdepth,rightdepth);
         return depth;
     }
     return getdepth(root);
@@ -591,7 +591,9 @@ var maxDepth = function(root) {
         count++
         while(size--) {
             let node = queue.shift()
-            node && (queue = [...queue, ...node.children])
+            for (let item of node.children) {
+                item && queue.push(item);
+            }
         }
     }
     return count

problems/0106.从中序与后序遍历序列构造二叉树.md

@@ -89,9 +89,9 @@ TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
 
 **难点大家应该发现了，就是如何切割，以及边界值找不好很容易乱套。**
 
-此时应该注意确定切割的标准，是左闭右开，还有左开又闭，还是左闭又闭，这个就是不变量，要在递归中保持这个不变量。
+此时应该注意确定切割的标准，是左闭右开，还有左开右闭，还是左闭右闭，这个就是不变量，要在递归中保持这个不变量。
 
-**在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭又闭，必然乱套！**
+**在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭右闭，必然乱套！**
 
 我在[数组：每次遇到二分法，都是一看就会，一写就废](https://programmercarl.com/0035.搜索插入位置.html)和[数组：这个循环可以转懵很多人！](https://programmercarl.com/0059.螺旋矩阵II.html)中都强调过循环不变量的重要性，在二分查找以及螺旋矩阵的求解中，坚持循环不变量非常重要，本题也是。
 
@@ -814,7 +814,114 @@ var buildTree = function(preorder, inorder) {
 };
 ```
 
+## TypeScript
+
+> 106.从中序与后序遍历序列构造二叉树
+
+**创建新数组:**
+
+```typescript
+function buildTree(inorder: number[], postorder: number[]): TreeNode | null {
+    if (postorder.length === 0) return null;
+    const rootVal: number = postorder.pop()!;
+    const rootValIndex: number = inorder.indexOf(rootVal);
+    const rootNode: TreeNode = new TreeNode(rootVal);
+    rootNode.left = buildTree(inorder.slice(0, rootValIndex), postorder.slice(0, rootValIndex));
+    rootNode.right = buildTree(inorder.slice(rootValIndex + 1), postorder.slice(rootValIndex));
+    return rootNode;
+};
+```
+
+**使用数组索引:**
+
+```typescript
+function buildTree(inorder: number[], postorder: number[]): TreeNode | null {
+    function recur(
+        inorder: number[], postorder: number[],
+        inBegin: number, inEnd: number,
+        postBegin: number, postEnd: number
+    ): TreeNode | null {
+        if (postBegin === postEnd) return null;
+        const rootVal: number = postorder[postEnd - 1]!;
+        const rootValIndex: number = inorder.indexOf(rootVal, inBegin);
+        const rootNode: TreeNode = new TreeNode(rootVal);
+
+        const leftInorderBegin: number = inBegin;
+        const leftInorderEnd: number = rootValIndex;
+        const rightInorderBegin: number = rootValIndex + 1;
+        const rightInorderEnd: number = inEnd;
+
+        const leftPostorderBegin: number = postBegin;
+        const leftPostorderEnd: number = postBegin + rootValIndex - inBegin;
+        const rightPostorderBegin: number = leftPostorderEnd;
+        const rightPostorderEnd: number = postEnd - 1;
+
+        rootNode.left = recur(
+            inorder, postorder,
+            leftInorderBegin, leftInorderEnd,
+            leftPostorderBegin, leftPostorderEnd
+        );
+        rootNode.right = recur(
+            inorder, postorder,
+            rightInorderBegin, rightInorderEnd,
+            rightPostorderBegin, rightPostorderEnd
+        );
+        return rootNode;
+    }
+    return recur(inorder, postorder, 0, inorder.length, 0, inorder.length);
+};
+```
+
+> 105.从前序与中序遍历序列构造二叉树
+
+**新建数组：**
+
+```typescript
+function buildTree(preorder: number[], inorder: number[]): TreeNode | null {
+    if (preorder.length === 0) return null;
+    const rootVal: number = preorder[0];
+    const rootNode: TreeNode = new TreeNode(rootVal);
+    const rootValIndex: number = inorder.indexOf(rootVal);
+    rootNode.left = buildTree(preorder.slice(1, rootValIndex + 1), inorder.slice(0, rootValIndex));
+    rootNode.right = buildTree(preorder.slice(rootValIndex + 1), inorder.slice(rootValIndex + 1));
+    return rootNode;
+};
+```
+
+**使用数组索引:**
+
+```typescript
+function buildTree(preorder: number[], inorder: number[]): TreeNode | null {
+    function recur(
+        preorder: number[], inorder: number[],
+        preBegin: number, preEnd: number,
+        inBegin: number, inEnd: number
+    ): TreeNode | null {
+        if (preBegin === preEnd) return null;
+        const rootVal: number = preorder[preBegin];
+        const rootNode: TreeNode = new TreeNode(rootVal);
+        const rootValIndex: number = inorder.indexOf(rootVal, inBegin);
+
+        const leftPreBegin: number = preBegin + 1;
+        const leftPreEnd: number = preBegin + rootValIndex - inBegin + 1;
+        const leftInBegin: number = inBegin;
+        const leftInEnd: number = rootValIndex;
+
+        const rightPreBegin: number = leftPreEnd;
+        const rightPreEnd: number = preEnd;
+        const rightInBegin: number = rootValIndex + 1;
+        const rightInEnd: number = inEnd;
+
+        rootNode.left = recur(preorder, inorder, leftPreBegin, leftPreEnd, leftInBegin, leftInEnd);
+        rootNode.right = recur(preorder, inorder, rightPreBegin, rightPreEnd, rightInBegin, rightInEnd);
+        return rootNode;
+    };
+    return recur(preorder, inorder, 0, preorder.length, 0, inorder.length);
+};
+```
+
 ## C
+
 106 从中序与后序遍历序列构造二叉树
 
 ```c

problems/0108.将有序数组转换为二叉搜索树.md

@@ -305,7 +305,7 @@ class Solution {
 ## Python  
 **递归**
 
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):

problems/0110.平衡二叉树.md

@@ -497,7 +497,7 @@ class Solution {
 ## Python 
 
 递归法：
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):

problems/0112.路径总和.md

@@ -747,11 +747,132 @@ let pathSum = function(root, targetSum) {
 };
 ```
 
+## TypeScript
+
+> 0112.路径总和
+
+**递归法：**
+
+```typescript
+function hasPathSum(root: TreeNode | null, targetSum: number): boolean {
+    function recur(node: TreeNode, sum: number): boolean {
+        console.log(sum);
+        if (
+            node.left === null &&
+            node.right === null &&
+            sum === 0
+        ) return true;
+        if (node.left !== null) {
+            sum -= node.left.val;
+            if (recur(node.left, sum) === true) return true;
+            sum += node.left.val;
+        }
+        if (node.right !== null) {
+            sum -= node.right.val;
+            if (recur(node.right, sum) === true) return true;
+            sum += node.right.val;
+        }
+        return false;
+    }
+    if (root === null) return false;
+    return recur(root, targetSum - root.val);
+};
+```
+
+**递归法（精简版）：**
+
+```typescript
+function hasPathSum(root: TreeNode | null, targetSum: number): boolean {
+    if (root === null) return false;
+    targetSum -= root.val;
+    if (
+        root.left === null &&
+        root.right === null &&
+        targetSum === 0
+    ) return true;
+    return hasPathSum(root.left, targetSum) ||
+        hasPathSum(root.right, targetSum);
+};
+```
+
+**迭代法：**
+
+```typescript
+function hasPathSum(root: TreeNode | null, targetSum: number): boolean {
+    type Pair = {
+        node: TreeNode, // 当前节点
+        sum: number // 根节点到当前节点的路径数值总和
+    }
+
+    const helperStack: Pair[] = [];
+    if (root !== null) helperStack.push({ node: root, sum: root.val });
+    let tempPair: Pair;
+    while (helperStack.length > 0) {
+        tempPair = helperStack.pop()!;
+        if (
+            tempPair.node.left === null &&
+            tempPair.node.right === null &&
+            tempPair.sum === targetSum
+        ) return true;
+        if (tempPair.node.right !== null) {
+            helperStack.push({
+                node: tempPair.node.right,
+                sum: tempPair.sum + tempPair.node.right.val
+            });
+        }
+        if (tempPair.node.left !== null) {
+            helperStack.push({
+                node: tempPair.node.left,
+                sum: tempPair.sum + tempPair.node.left.val
+            });
+        }
+    }
+    return false;
+};
+```
+
+> 0112.路径总和 ii
+
+**递归法：**
+
+```typescript
+function pathSum(root: TreeNode | null, targetSum: number): number[][] {
+    function recur(node: TreeNode, sumGap: number, routeArr: number[]): void {
+        if (
+            node.left === null &&
+            node.right === null &&
+            sumGap === 0
+        ) resArr.push([...routeArr]);
+        if (node.left !== null) {
+            sumGap -= node.left.val;
+            routeArr.push(node.left.val);
+            recur(node.left, sumGap, routeArr);
+            sumGap += node.left.val;
+            routeArr.pop();
+        }
+        if (node.right !== null) {
+            sumGap -= node.right.val;
+            routeArr.push(node.right.val);
+            recur(node.right, sumGap, routeArr);
+            sumGap += node.right.val;
+            routeArr.pop();
+        }
+    }
+    const resArr: number[][] = [];
+    if (root === null) return resArr;
+    const routeArr: number[] = [];
+    routeArr.push(root.val);
+    recur(root, targetSum - root.val, routeArr);
+    return resArr;
+};
+```
+
 ## Swift
 
 0112.路径总和
 
 **递归**
+
 ```swift
 func hasPathSum(_ root: TreeNode?, _ targetSum: Int) -> Bool {
     guard let root = root else {

problems/0127.单词接龙.md

@@ -9,7 +9,6 @@
 
 [力扣题目链接](https://leetcode-cn.com/problems/word-ladder/)
 
-
 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：
 * 序列中第一个单词是 beginWord 。
 * 序列中最后一个单词是 endWord 。

problems/0129.求根到叶子节点数字之和.md

@@ -217,7 +217,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 class Solution:
     def sumNumbers(self, root: TreeNode) -> int:
         res = 0

problems/0131.分割回文串.md

@@ -289,7 +289,7 @@ class Solution {
 
 ## Python 
 **回溯+正反序判断回文串**	
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []
@@ -326,7 +326,7 @@ class Solution:
                 continue    
 ```
 **回溯+函数判断回文串**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []

problems/0188.买卖股票的最佳时机IV.md

@@ -271,7 +271,7 @@ class Solution:
         return dp[-1][2*k]
 ```
 版本二
-```python3
+```python
 class Solution:
     def maxProfit(self, k: int, prices: List[int]) -> int:
         if len(prices) == 0: return 0

problems/0213.打家劫舍II.md

@@ -123,22 +123,24 @@ Python：
 ```Python
 class Solution:
     def rob(self, nums: List[int]) -> int:
-      if (n := len(nums)) == 0:
-        return 0
-      if n == 1:
-        return nums[0]
-      result1 = self.robRange(nums, 0, n - 2)
-      result2 = self.robRange(nums, 1, n - 1)
-      return max(result1 , result2)
+        #在198入门级的打家劫舍问题上分两种情况考虑
+        #一是不偷第一间房，二是不偷最后一间房
+        if len(nums)==1:#题目中提示nums.length>=1,所以不需要考虑len(nums)==0的情况
+            return nums[0]
+        val1=self.roblist(nums[1:])#不偷第一间房
+        val2=self.roblist(nums[:-1])#不偷最后一间房
+        return max(val1,val2)
 
-    def robRange(self, nums: List[int], start: int, end: int) -> int:
-      if end == start: return nums[start]
-      dp = [0] * len(nums)
-      dp[start] = nums[start]
-      dp[start + 1] = max(nums[start], nums[start + 1])
-      for i in range(start + 2, end + 1):
-        dp[i] = max(dp[i -2] + nums[i], dp[i - 1])
-      return dp[end]
+    def robRange(self,nums):
+        l=len(nums)
+        dp=[0]*l
+        dp[0]=nums[0]
+        for i in range(1,l):
+            if i==1:
+                dp[i]=max(dp[i-1],nums[i])
+            else:
+                dp[i]=max(dp[i-1],dp[i-2]+nums[i])
+        return dp[-1]
 ```
 
 javascipt:

problems/0226.翻转二叉树.md

@@ -47,8 +47,6 @@
 
 ## 递归法
 
-
-
 对于二叉树的递归法的前中后序遍历，已经在[二叉树：前中后序递归遍历](https://programmercarl.com/二叉树的递归遍历.html)详细讲解了。
 
 我们下文以前序遍历为例，通过动画来看一下翻转的过程:
@@ -63,7 +61,7 @@
 
 返回值的话其实也不需要，但是题目中给出的要返回root节点的指针，可以直接使用题目定义好的函数，所以就函数的返回类型为`TreeNode*`。
 
-```
+```cpp
 TreeNode* invertTree(TreeNode* root)
 ```
 
@@ -71,7 +69,7 @@ TreeNode* invertTree(TreeNode* root)
 
 当前节点为空的时候，就返回
 
-```
+```cpp
 if (root == NULL) return root;
 ```
 
@@ -79,7 +77,7 @@ if (root == NULL) return root;
 
 因为是先前序遍历，所以先进行交换左右孩子节点，然后反转左子树，反转右子树。
 
-```
+```cpp
 swap(root->left, root->right);
 invertTree(root->left);
 invertTree(root->right);
@@ -257,7 +255,7 @@ public:
 ## 其他语言版本
 
 
-### Java：
+### Java
 
 ```Java
 //DFS递归
@@ -469,8 +467,6 @@ func invertTree(root *TreeNode) *TreeNode {
 }
 ```
 
-
-
 ### JavaScript
 
 使用递归版本的前序遍历
@@ -690,7 +686,7 @@ function invertTree(root: TreeNode | null): TreeNode | null {
 };
 ```
 
-### C:
+### C
 
 递归法
 ```c
@@ -775,5 +771,54 @@ func invertTree1(_ root: TreeNode?) -> TreeNode? {
 }
 ```
 
+### Swift
+
+深度优先递归。
+
+```swift
+func invertTree(_ root: TreeNode?) -> TreeNode? {
+    guard let node = root else { return root }
+    swap(&node.left, &node.right)
+    _ = invertTree(node.left)
+    _ = invertTree(node.right)
+    return root
+}
+```
+
+深度优先迭代，子结点顺序不重要，从根结点出发深度遍历即可。
+
+```swift
+func invertTree(_ root: TreeNode?) -> TreeNode? {
+    guard let node = root else { return root }
+    var stack = [node]
+    while !stack.isEmpty {
+        guard let node = stack.popLast() else { break }
+        swap(&node.left, &node.right)
+        if let node = node.left { stack.append(node) }
+        if let node = node.right { stack.append(node) }
+    }
+    return root
+}
+```
+
+广度优先迭代。
+
+```swift
+func invertTree(_ root: TreeNode?) -> TreeNode? {
+    guard let node = root else { return root }
+    var queue = [node]
+    while !queue.isEmpty {
+        let count = queue.count
+        for _ in 0 ..< count {
+            let node = queue.removeFirst()
+            swap(&node.left, &node.right)
+            if let node = node.left { queue.append(node) }
+            if let node = node.right { queue.append(node) }
+        }
+    }
+    return root
+}
+```
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0257.二叉树的所有路径.md

@@ -581,7 +581,62 @@ var binaryTreePaths = function(root) {
 };  
 ```
 
+TypeScript：
+
+> 递归法
+
+```typescript
+function binaryTreePaths(root: TreeNode | null): string[] {
+    function recur(node: TreeNode, route: string, resArr: string[]): void {
+        route += String(node.val);
+        if (node.left === null && node.right === null) {
+            resArr.push(route);
+            return;
+        }
+        if (node.left !== null) recur(node.left, route + '->', resArr);
+        if (node.right !== null) recur(node.right, route + '->', resArr);
+    }
+    const resArr: string[] = [];
+    if (root === null) return resArr;
+    recur(root, '', resArr);
+    return resArr;
+};
+```
+
+> 迭代法
+
+```typescript
+// 迭代法2
+function binaryTreePaths(root: TreeNode | null): string[] {
+    let helperStack: TreeNode[] = [];
+    let tempNode: TreeNode;
+    let routeArr: string[] = [];
+    let resArr: string[] = [];
+    if (root !== null) {
+        helperStack.push(root);
+        routeArr.push(String(root.val));
+    };
+    while (helperStack.length > 0) {
+        tempNode = helperStack.pop()!;
+        let route: string = routeArr.pop()!; // tempNode 对应的路径
+        if (tempNode.left === null && tempNode.right === null) {
+            resArr.push(route);
+        }
+        if (tempNode.right !== null) {
+            helperStack.push(tempNode.right);
+            routeArr.push(route + '->' + tempNode.right.val);   // tempNode.right 对应的路径
+        }
+        if (tempNode.left !== null) {
+            helperStack.push(tempNode.left);
+            routeArr.push(route + '->' + tempNode.left.val);    // tempNode.left 对应的路径
+        }
+    }
+    return resArr;
+};
+```
+
 Swift:
+
 > 递归/回溯
 ```swift
 func binaryTreePaths(_ root: TreeNode?) -> [String] {

problems/0279.完全平方数.md

@@ -207,7 +207,7 @@ class Solution {
 
 Python：
 
-```python3
+```python
 class Solution:
     def numSquares(self, n: int) -> int:
         '''版本一，先遍历背包, 再遍历物品'''

problems/0322.零钱兑换.md

@@ -207,7 +207,7 @@ class Solution {
 
 Python：
 
-```python3
+```python
 class Solution:
     def coinChange(self, coins: List[int], amount: int) -> int:
         '''版本一'''

problems/0337.打家劫舍III.md

@@ -288,7 +288,7 @@ Python：
 
 > 暴力递归
 
-```python3
+```python
 
 # Definition for a binary tree node.
 # class TreeNode:
@@ -315,7 +315,7 @@ class Solution:
 
 > 记忆化递归
 
-```python3
+```python
 
 # Definition for a binary tree node.
 # class TreeNode:
@@ -345,7 +345,7 @@ class Solution:
 ```
 
 > 动态规划
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):

problems/0343.整数拆分.md

@@ -196,14 +196,17 @@ public:
 ```Java
 class Solution {
     public int integerBreak(int n) {
-        //dp[i]为正整数i拆分结果的最大乘积
-        int[] dp = new int[n+1]; 
-        dp[2] = 1;
-        for (int i = 3; i <= n; ++i) {
-            for (int j = 1; j < i - 1; ++j) {
-                //j*(i-j)代表把i拆分为j和i-j两个数相乘
-                //j*dp[i-j]代表把i拆分成j和继续把(i-j)这个数拆分，取(i-j)拆分结果中的最大乘积与j相乘
-                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
+        //dp[i] 为正整数 i 拆分后的结果的最大乘积
+        int[]dp=new int[n+1];
+        dp[2]=1;
+        for(int i=3;i<=n;i++){
+            for(int j=1;j<=i-j;j++){
+                // 这里的 j 其实最大值为 i-j,再大只不过是重复而已，
+                //并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，
+                //j 最大到 i-j,就不会用到 dp[0]与dp[1]
+                dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
+                // j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
+                //而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
             }
         }
         return dp[n];

problems/0376.摆动序列.md

@@ -228,7 +228,7 @@ class Solution {
 
 ### Python 
 
-```python3
+```python
 class Solution:
     def wiggleMaxLength(self, nums: List[int]) -> int:
         preC,curC,res = 0,0,1  #题目里nums长度大于等于1，当长度为1时，其实到不了for循环里去，所以不用考虑nums长度

problems/0383.赎金信.md

@@ -209,7 +209,7 @@ class Solution(object):
 
 Python写法四：
 
-```python3
+```python
 class Solution:
     def canConstruct(self, ransomNote: str, magazine: str) -> bool:
         c1 = collections.Counter(ransomNote)

problems/0392.判断子序列.md

@@ -77,7 +77,7 @@ if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前
 
 如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。
 
-这里dp[i][0]和dp[0][j]是没有含义的，仅仅是为了给递推公式做前期铺垫，所以初始化为0。
+dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。 
 
 **其实这里只初始化dp[i][0]就够了，但一起初始化也方便，所以就一起操作了**，代码如下：
 

problems/0404.左叶子之和.md

@@ -19,7 +19,7 @@
 
 **首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。**
 
-因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**如果左节点不为空，且左节点没有左右孩子，那么这个节点就是左叶子**
+因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**如果左节点不为空，且左节点没有左右孩子，那么这个节点的左节点就是左叶子**
 
 大家思考一下如下图中二叉树，左叶子之和究竟是多少？
 
@@ -229,7 +229,7 @@ class Solution {
 ## Python 
 
 **递归后序遍历**
-```python3
+```python
 class Solution:
     def sumOfLeftLeaves(self, root: TreeNode) -> int:
         if not root: 
@@ -246,7 +246,7 @@ class Solution:
 ```
 
 **迭代**
-```python3
+```python
 class Solution:
     def sumOfLeftLeaves(self, root: TreeNode) -> int:
         """
@@ -372,6 +372,50 @@ var sumOfLeftLeaves = function(root) {
 };
 ```
 
+## TypeScript
+
+> 递归法
+
+```typescript
+function sumOfLeftLeaves(root: TreeNode | null): number {
+    if (root === null) return 0;
+    let midVal: number = 0;
+    if (
+        root.left !== null &&
+        root.left.left === null &&
+        root.left.right === null
+    ) {
+        midVal = root.left.val;
+    }
+    let leftVal: number = sumOfLeftLeaves(root.left);
+    let rightVal: number = sumOfLeftLeaves(root.right);
+    return midVal + leftVal + rightVal;
+};
+```
+
+> 迭代法
+
+```typescript
+function sumOfLeftLeaves(root: TreeNode | null): number {
+    let helperStack: TreeNode[] = [];
+    let tempNode: TreeNode;
+    let sum: number = 0;
+    if (root !== null) helperStack.push(root);
+    while (helperStack.length > 0) {
+        tempNode = helperStack.pop()!;
+        if (
+            tempNode.left !== null &&
+            tempNode.left.left === null &&
+            tempNode.left.right === null
+        ) {
+            sum += tempNode.left.val;
+        }
+        if (tempNode.right !== null) helperStack.push(tempNode.right);
+        if (tempNode.left !== null) helperStack.push(tempNode.left);
+    }
+    return sum;
+};
+```
 
 ## Swift 
 

problems/0455.分发饼干.md

@@ -146,7 +146,7 @@ class Solution {
 ```
 
 ### Python 
-```python3
+```python
 class Solution:
     # 思路1：优先考虑胃饼干
     def findContentChildren(self, g: List[int], s: List[int]) -> int:

problems/0463.岛屿的周长.md

@@ -124,7 +124,7 @@ Python：
 ### 解法1:
 扫描每个cell,如果当前位置为岛屿 grid[i][j] == 1， 从当前位置判断四边方向，如果边界或者是水域，证明有边界存在，res矩阵的对应cell加一。
 
-```python3
+```python
 class Solution:
     def islandPerimeter(self, grid: List[List[int]]) -> int:
 

problems/0474.一和零.md

@@ -193,7 +193,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 class Solution:
     def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
         dp = [[0] * (n + 1) for _ in range(m + 1)]	# 默认初始化0

problems/0491.递增子序列.md

@@ -227,13 +227,45 @@ class Solution {
     }
 }
 ```
-
+```java
+//法二：使用map
+class Solution {
+    //结果集合
+    List<List<Integer>> res = new ArrayList<>();
+    //路径集合
+    LinkedList<Integer> path = new LinkedList<>();
+    public List<List<Integer>> findSubsequences(int[] nums) {
+        getSubsequences(nums,0);
+        return res;
+    }
+    private void getSubsequences( int[] nums, int start ) {
+        if(path.size()>1 ){
+            res.add( new ArrayList<>(path) );
+            // 注意这里不要加return，要取树上的节点
+        }
+        HashMap<Integer,Integer> map = new HashMap<>();
+        for(int i=start ;i < nums.length ;i++){
+            if(!path.isEmpty() && nums[i]< path.getLast()){
+                continue;
+            }
+            // 使用过了当前数字
+            if ( map.getOrDefault( nums[i],0 ) >=1 ){
+                continue;
+            }
+            map.put(nums[i],map.getOrDefault( nums[i],0 )+1);
+            path.add( nums[i] );
+            getSubsequences( nums,i+1 );
+            path.removeLast();
+        }
+    }
+}
+```
 
 ### Python 
 
 python3
 **回溯**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []
@@ -270,7 +302,7 @@ class Solution:
             self.path.pop() 
 ```
 **回溯+哈希表去重**
-```python3
+```python
 class Solution:
     def __init__(self):
         self.paths = []

problems/0494.目标和.md

@@ -160,11 +160,16 @@ dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法
 
 那么只要搞到nums[i]的话，凑成dp[j]就有dp[j - nums[i]] 种方法。
 
-举一个例子,nums[i] = 2： dp[3]，填满背包容量为3的话，有dp[3]种方法。
 
-那么只需要搞到一个2（nums[i]），有dp[3]方法可以凑齐容量为3的背包，相应的就有多少种方法可以凑齐容量为5的背包。
+例如：dp[j]，j 为5， 
 
-那么需要把 这些方法累加起来就可以了，dp[j] += dp[j - nums[i]]
+* 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
+* 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
+* 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]
+* 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]
+* 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 dp[5] 
+
+那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。
 
 所以求组合类问题的公式，都是类似这种：
 

problems/0496.下一个更大元素I.md

@@ -222,8 +222,8 @@ class Solution {
     }
 }
 ```
-Python：
-```python3
+Python3：
+```python
 class Solution:
     def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
         result = [-1]*len(nums1)

problems/0501.二叉搜索树中的众数.md

@@ -470,7 +470,7 @@ class Solution {
 
 > 递归法
 
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):
@@ -515,7 +515,7 @@ class Solution:
 
 
 > 迭代法-中序遍历-不使用额外空间，利用二叉搜索树特性 
-```python3
+```python
 class Solution:
     def findMode(self, root: TreeNode) -> List[int]:
         stack = []
@@ -699,6 +699,107 @@ var findMode = function(root) {
 };
 ```
 
+## TypeScript
+
+> 辅助Map法
+
+```typescript
+function findMode(root: TreeNode | null): number[] {
+    if (root === null) return [];
+    const countMap: Map<number, number> = new Map();
+    function traverse(root: TreeNode | null): void {
+        if (root === null) return;
+        countMap.set(root.val, (countMap.get(root.val) || 0) + 1);
+        traverse(root.left);
+        traverse(root.right);
+    }
+    traverse(root);
+    const countArr: number[][] = Array.from(countMap);
+    countArr.sort((a, b) => {
+        return b[1] - a[1];
+    })
+    const resArr: number[] = [];
+    const maxCount: number = countArr[0][1];
+    for (let i of countArr) {
+        if (i[1] === maxCount) resArr.push(i[0]);
+    }
+    return resArr;
+};
+```
+
+> 递归中直接解决
+
+```typescript
+function findMode(root: TreeNode | null): number[] {
+    let preNode: TreeNode | null = null;
+    let maxCount: number = 0;
+    let count: number = 0;
+    let resArr: number[] = [];
+    function traverse(root: TreeNode | null): void {
+        if (root === null) return;
+        traverse(root.left);
+        if (preNode === null) { // 第一个节点
+            count = 1;
+        } else if (preNode.val === root.val) {
+            count++;
+        } else {
+            count = 1;
+        }
+        if (count === maxCount) {
+            resArr.push(root.val);
+        } else if (count > maxCount) {
+            maxCount = count;
+            resArr.length = 0;
+            resArr.push(root.val);
+        }
+        preNode = root;
+        traverse(root.right);
+    }
+    traverse(root);
+    return resArr;
+};
+```
+
+> 迭代法
+
+```typescript
+function findMode(root: TreeNode | null): number[] {
+    const helperStack: TreeNode[] = [];
+    const resArr: number[] = [];
+    let maxCount: number = 0;
+    let count: number = 0;
+    let preNode: TreeNode | null = null;
+    let curNode: TreeNode | null = root;
+    while (curNode !== null || helperStack.length > 0) {
+        if (curNode !== null) {
+            helperStack.push(curNode);
+            curNode = curNode.left;
+        } else {
+            curNode = helperStack.pop()!;
+            if (preNode === null) { // 第一个节点
+                count = 1;
+            } else if (preNode.val === curNode.val) {
+                count++;
+            } else {
+                count = 1;
+            }
+            if (count === maxCount) {
+                resArr.push(curNode.val);
+            } else if (count > maxCount) {
+                maxCount = count;
+                resArr.length = 0;
+                resArr.push(curNode.val);
+            }
+            preNode = curNode;
+            curNode = curNode.right;
+        }
+    }
+    return resArr;
+};
+```
+
+
+
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0503.下一个更大元素II.md

@@ -124,7 +124,7 @@ class Solution {
 ```
 
 Python: 
-```python3
+```python
 class Solution:
     def nextGreaterElements(self, nums: List[int]) -> List[int]:
         dp = [-1] * len(nums)

problems/0513.找树左下角的值.md

@@ -433,6 +433,51 @@ var findBottomLeftValue = function(root) {
 };
 ```
 
+## TypeScript
+
+> 递归法：
+
+```typescript
+function findBottomLeftValue(root: TreeNode | null): number {
+    function recur(root: TreeNode, depth: number): void {
+        if (root.left === null && root.right === null) {
+            if (depth > maxDepth) {
+                maxDepth = depth;
+                resVal = root.val;
+            }
+            return;
+        }
+        if (root.left !== null) recur(root.left, depth + 1);
+        if (root.right !== null) recur(root.right, depth + 1);
+    }
+    let maxDepth: number = 0;
+    let resVal: number = 0;
+    if (root === null) return resVal;
+    recur(root, 1);
+    return resVal;
+};
+```
+
+> 迭代法：
+
+```typescript
+function findBottomLeftValue(root: TreeNode | null): number {
+    let helperQueue: TreeNode[] = [];
+    if (root !== null) helperQueue.push(root);
+    let resVal: number = 0;
+    let tempNode: TreeNode;
+    while (helperQueue.length > 0) {
+        resVal = helperQueue[0].val;
+        for (let i = 0, length = helperQueue.length; i < length; i++) {
+            tempNode = helperQueue.shift()!;
+            if (tempNode.left !== null) helperQueue.push(tempNode.left);
+            if (tempNode.right !== null) helperQueue.push(tempNode.right);
+        }
+    }
+    return resVal;
+};
+```
+
 ## Swift 
 
 递归版本：

problems/0518.零钱兑换II.md

@@ -207,7 +207,7 @@ class Solution {
 Python：
 
 
-```python3
+```python
 class Solution:
     def change(self, amount: int, coins: List[int]) -> int:
         dp = [0]*(amount + 1)

problems/0530.二叉搜索树的最小绝对差.md

@@ -364,5 +364,74 @@ var getMinimumDifference = function(root) {
 }
 ```
 
+## TypeScript
+
+> 辅助数组解决
+
+```typescript
+function getMinimumDifference(root: TreeNode | null): number {
+    let helperArr: number[] = [];
+    function recur(root: TreeNode | null): void {
+        if (root === null) return;
+        recur(root.left);
+        helperArr.push(root.val);
+        recur(root.right);
+    }
+    recur(root);
+    let resMin: number = Infinity;
+    for (let i = 0, length = helperArr.length; i < length - 1; i++) {
+        resMin = Math.min(resMin, helperArr[i + 1] - helperArr[i]);
+    }
+    return resMin;
+};
+```
+
+> 递归中解决
+
+```typescript
+function getMinimumDifference(root: TreeNode | null): number {
+    let preNode: TreeNode | null= null;
+    let resMin: number = Infinity;
+    function recur(root: TreeNode | null): void {
+        if (root === null) return;
+        recur(root.left);
+        if (preNode !== null) {
+            resMin = Math.min(resMin, root.val - preNode.val);
+        }
+        preNode = root;
+        recur(root.right);
+    }
+    recur(root);
+    return resMin;
+};
+```
+
+> 迭代法-中序遍历
+
+```typescript
+function getMinimumDifference(root: TreeNode | null): number {
+    const helperStack: TreeNode[] = [];
+    let curNode: TreeNode | null = root;
+    let resMin: number = Infinity;
+    let preNode: TreeNode | null = null;
+    while (curNode !== null || helperStack.length > 0) {
+        if (curNode !== null) {
+            helperStack.push(curNode);
+            curNode = curNode.left;
+        } else {
+            curNode = helperStack.pop()!;
+            if (preNode !== null) {
+                resMin = Math.min(resMin, curNode.val - preNode.val);
+            }
+            preNode = curNode;
+            curNode = curNode.right;
+        }
+    }
+    return resMin;
+};
+```
+
+
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0538.把二叉搜索树转换为累加树.md

@@ -196,7 +196,7 @@ class Solution {
 ## Python 
 **递归**
 
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):

problems/0541.反转字符串II.md

@@ -98,8 +98,31 @@ public:
 
 ## 其他语言版本
 
+C：
+
+```c
+char * reverseStr(char * s, int k){
+    int len = strlen(s);
+
+    for (int i = 0; i < len; i += (2 * k)) {
+        //判断剩余字符是否少于 k
+        k = i + k > len ? len - i : k;
+
+        int left = i;
+        int right = i + k - 1;
+        while (left < right) {
+            char temp = s[left];
+            s[left++] = s[right];
+            s[right--] = temp;
+        }
+    }
+
+    return s;
+}
+```
 
 Java：
+
 ```Java
 //解法一
 class Solution {

problems/0617.合并二叉树.md

@@ -583,6 +583,56 @@ var mergeTrees = function(root1, root2) {
 
 ```
 
+## TypeScript
+
+> 递归法：
+
+```type
+function mergeTrees(root1: TreeNode | null, root2: TreeNode | null): TreeNode | null {
+    if (root1 === null) return root2;
+    if (root2 === null) return root1;
+    const resNode: TreeNode = new TreeNode(root1.val + root2.val);
+    resNode.left = mergeTrees(root1.left, root2.left);
+    resNode.right = mergeTrees(root1.right, root2.right);
+    return resNode;
+};
+```
+
+> 迭代法：
+
+```typescript
+function mergeTrees(root1: TreeNode | null, root2: TreeNode | null): TreeNode | null {
+    if (root1 === null) return root2;
+    if (root2 === null) return root1;
+    const helperQueue1: TreeNode[] = [],
+        helperQueue2: TreeNode[] = [];
+    helperQueue1.push(root1);
+    helperQueue2.push(root2);
+    let tempNode1: TreeNode,
+        tempNode2: TreeNode;
+    while (helperQueue1.length > 0) {
+        tempNode1 = helperQueue1.shift()!;
+        tempNode2 = helperQueue2.shift()!;
+        tempNode1.val += tempNode2.val;
+        if (tempNode1.left !== null && tempNode2.left !== null) {
+            helperQueue1.push(tempNode1.left);
+            helperQueue2.push(tempNode2.left);
+        } else if (tempNode1.left === null) {
+            tempNode1.left = tempNode2.left;
+        }
+        if (tempNode1.right !== null && tempNode2.right !== null) {
+            helperQueue1.push(tempNode1.right);
+            helperQueue2.push(tempNode2.right);
+        } else if (tempNode1.right === null) {
+            tempNode1.right = tempNode2.right;
+        }
+    }
+    return root1;
+};
+```
+
+
+
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0654.最大二叉树.md

@@ -371,7 +371,56 @@ var constructMaximumBinaryTree = function (nums) {
 };
 ```
 
+## TypeScript
+
+> 新建数组法：
+
+```typescript
+function constructMaximumBinaryTree(nums: number[]): TreeNode | null {
+    if (nums.length === 0) return null;
+    let maxIndex: number = 0;
+    let maxVal: number = nums[0];
+    for (let i = 1, length = nums.length; i < length; i++) {
+        if (nums[i] > maxVal) {
+            maxIndex = i;
+            maxVal = nums[i];
+        }
+    }
+    const rootNode: TreeNode = new TreeNode(maxVal);
+    rootNode.left = constructMaximumBinaryTree(nums.slice(0, maxIndex));
+    rootNode.right = constructMaximumBinaryTree(nums.slice(maxIndex + 1));
+    return rootNode;
+};
+```
+
+> 使用数组索引法：
+
+```typescript
+function constructMaximumBinaryTree(nums: number[]): TreeNode | null {
+    // 左闭右开区间[begin, end)
+    function recur(nums: number[], begin: number, end: number): TreeNode | null {
+        if (begin === end) return null;
+        let maxIndex: number = begin;
+        let maxVal: number = nums[begin];
+        for (let i = begin + 1; i < end; i++) {
+            if (nums[i] > maxVal) {
+                maxIndex = i;
+                maxVal = nums[i];
+            }
+        }
+        const rootNode: TreeNode = new TreeNode(maxVal);
+        rootNode.left = recur(nums, begin, maxIndex);
+        rootNode.right = recur(nums, maxIndex + 1, end);
+        return rootNode;
+    }
+    return recur(nums, 0, nums.length);
+};
+```
+
+
+
 ## C
+
 ```c
 struct TreeNode* traversal(int* nums, int left, int right) {
     //若左边界大于右边界，返回NULL

problems/0669.修剪二叉搜索树.md

@@ -264,7 +264,7 @@ class Solution {
 
 ## Python  
 **递归**
-```python3
+```python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):

problems/0700.二叉搜索树中的搜索.md

@@ -334,6 +334,36 @@ var searchBST = function (root, val) {
 };
 ```
 
+## TypeScript
+
+> 递归法
+
+```typescript
+function searchBST(root: TreeNode | null, val: number): TreeNode | null {
+    if (root === null || root.val === val) return root;
+    if (root.val < val) return searchBST(root.right, val);
+    if (root.val > val) return searchBST(root.left, val);
+    return null;
+};
+```
+
+> 迭代法
+
+```typescript
+function searchBST(root: TreeNode | null, val: number): TreeNode | null {
+    let resNode: TreeNode | null = root;
+    while (resNode !== null) {
+        if (resNode.val === val) return resNode;
+        if (resNode.val < val) {
+            resNode = resNode.right;
+        } else {
+            resNode = resNode.left;
+        }
+    }
+    return null;
+};
+```
+
 
 
 -----------------------

problems/0701.二叉搜索树中的插入操作.md

@@ -310,6 +310,26 @@ class Solution:
         return root
 ``` 
 
+**递归法** - 无返回值 - another easier way
+```python
+class Solution:
+    def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
+        newNode = TreeNode(val)
+        if not root: return newNode
+        
+        if not root.left and val < root.val:
+            root.left = newNode
+        if not root.right and val > root.val:
+            root.right = newNode
+        
+        if val < root.val:
+            self.insertIntoBST(root.left, val)
+        if val > root.val:
+            self.insertIntoBST(root.right, val)
+        
+        return root
+```
+
 **迭代法**  
 与无返回值的递归函数的思路大体一致 
 ```python

problems/0841.钥匙和房间.md

@@ -152,7 +152,6 @@ class Solution {
 
 
 
-Python：
 
 python3
 

problems/0860.柠檬水找零.md

@@ -128,24 +128,24 @@ public:
 ```java
 class Solution {
     public boolean lemonadeChange(int[] bills) {
-        int cash_5 = 0;
-        int cash_10 = 0;
+        int five = 0;
+        int ten = 0;
 
         for (int i = 0; i < bills.length; i++) {
             if (bills[i] == 5) {
-                cash_5++;
+                five++;
             } else if (bills[i] == 10) {
-                cash_5--;
-                cash_10++;
+                five--;
+                ten++;
             } else if (bills[i] == 20) {
-                if (cash_10 > 0) {
-                    cash_10--;
-                    cash_5--;
+                if (ten > 0) {
+                    ten--;
+                    five--;
                 } else {
-                    cash_5 -= 3;
+                    five -= 3;
                 }
             }
-            if (cash_5 < 0 || cash_10 < 0) return false;
+            if (five < 0 || ten < 0) return false;
         }
         
         return true;

problems/1047.删除字符串中的所有相邻重复项.md

@@ -194,7 +194,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 # 方法一，使用栈，推荐！
 class Solution:
     def removeDuplicates(self, s: str) -> str:
@@ -207,7 +207,7 @@ class Solution:
         return "".join(res)  # 字符串拼接
 ```
 
-```python3
+```python
 # 方法二，使用双指针模拟栈，如果不让用栈可以作为备选方法。
 class Solution:
     def removeDuplicates(self, s: str) -> str:

problems/二叉树中递归带着回溯.md

@@ -171,7 +171,7 @@ if (cur->right) {
 ## 其他语言版本
 
 
-Java：
+### Java：
   100. 相同的树:递归代码
   ```java
   class Solution {
@@ -252,7 +252,7 @@ Java：
 }
   ```
 
-Python：
+### Python：
 
 100.相同的树
 > 递归法
@@ -332,7 +332,7 @@ class Solution:
             self.traversal(cur.right, path+"->", result) #右 回溯就隐藏在这里
 ```
 
-Go：
+### Go：
 
 100.相同的树
 ```go
@@ -436,7 +436,7 @@ func traversal(root *TreeNode,result *[]string,path *[]int){
 }
 ```
 
-JavaScript：
+### JavaScript：
 
 100.相同的树
 ```javascript
@@ -516,5 +516,107 @@ var binaryTreePaths = function(root) {
 ```
 
 
+### TypeScript：
+
+> 相同的树
+
+```typescript
+function isSameTree(p: TreeNode | null, q: TreeNode | null): boolean {
+    if (p === null && q === null) return true;
+    if (p === null || q === null) return false;
+    if (p.val !== q.val) return false;
+    let bool1: boolean, bool2: boolean;
+    bool1 = isSameTree(p.left, q.left);
+    bool2 = isSameTree(p.right, q.right);
+    return bool1 && bool2;
+};
+```
+
+> 二叉树的不同路径
+
+```typescript
+function binaryTreePaths(root: TreeNode | null): string[] {
+    function recur(node: TreeNode, nodeSeqArr: number[], resArr: string[]): void {
+        nodeSeqArr.push(node.val);
+        if (node.left === null && node.right === null) {
+            resArr.push(nodeSeqArr.join('->'));
+        }
+        if (node.left !== null) {
+            recur(node.left, nodeSeqArr, resArr);
+            nodeSeqArr.pop();
+        }
+        if (node.right !== null) {
+            recur(node.right, nodeSeqArr, resArr);
+            nodeSeqArr.pop();
+        }
+    }
+    let nodeSeqArr: number[] = [];
+    let resArr: string[] = [];
+    if (root === null) return resArr;
+    recur(root, nodeSeqArr, resArr);
+    return resArr;
+};
+```
+
+
+
+
+### Swift：
+> 100.相同的树
+```swift
+// 递归
+func isSameTree(_ p: TreeNode?, _ q: TreeNode?) -> Bool {
+    return _isSameTree3(p, q)
+}
+func _isSameTree3(_ p: TreeNode?, _ q: TreeNode?) -> Bool {
+    if p == nil && q == nil {
+        return true
+    } else if p == nil && q != nil {
+        return false
+    } else if p != nil && q == nil {
+        return false
+    } else if p!.val != q!.val {
+        return false
+    }
+    let leftSide = _isSameTree3(p!.left, q!.left)
+    let rightSide = _isSameTree3(p!.right, q!.right)
+    return leftSide && rightSide
+}
+```
+
+> 257.二叉树的不同路径
+```swift
+// 递归/回溯
+func binaryTreePaths(_ root: TreeNode?) -> [String] {
+    var res = [String]()
+    guard let root = root else {
+        return res
+    }
+    var paths = [Int]()
+    _binaryTreePaths3(root, res: &res, paths: &paths)
+    return res
+}
+func _binaryTreePaths3(_ root: TreeNode, res: inout [String], paths: inout [Int]) {
+    paths.append(root.val)
+    if root.left == nil && root.right == nil {
+        var str = ""
+        for i in 0 ..< (paths.count - 1) {
+            str.append("\(paths[i])->")
+        }
+        str.append("\(paths.last!)")
+        res.append(str)
+    }
+    if let left = root.left {
+        _binaryTreePaths3(left, res: &res, paths: &paths)
+        paths.removeLast()
+    }
+    if let right = root.right {
+        _binaryTreePaths3(right, res: &res, paths: &paths)
+        paths.removeLast()
+    }
+}
+```
+
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/二叉树总结篇.md

@@ -152,7 +152,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211030125421.png)
 
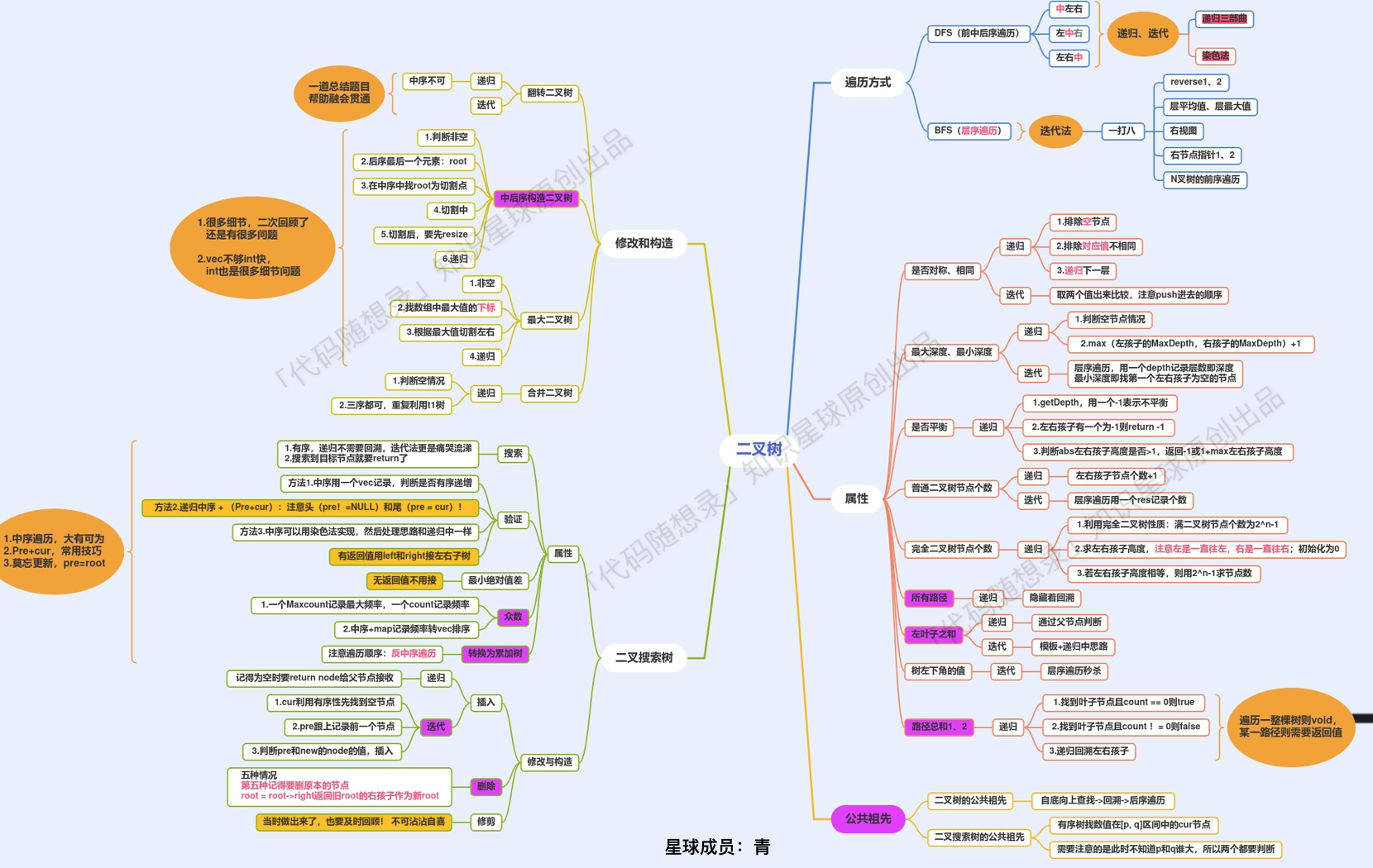
-这个图是 [代码随想录知识星球](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)，所画，总结的非常好，分享给大家。
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)，所画，总结的非常好，分享给大家。
 
 
 **最后，二叉树系列就这么完美结束了，估计这应该是最长的系列了，感谢大家33天的坚持与陪伴，接下来我们又要开始新的系列了「回溯算法」！**

problems/二叉树理论基础.md

@@ -33,7 +33,7 @@
 
 什么是完全二叉树？
 
-完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h -1  个节点。
+完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。
 
 **大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**
 

problems/二叉树的迭代遍历.md

@@ -390,7 +390,7 @@ func inorderTraversal(root *TreeNode) []int {
 }
 ```
 
-javaScript
+javaScript：
 
 ```js
 
@@ -454,7 +454,7 @@ var postorderTraversal = function(root, res = []) {
 };
 ```
 
-TypeScript:
+TypeScript：
 
 ```typescript
 // 前序遍历（迭代法）
@@ -509,77 +509,63 @@ function postorderTraversal(root: TreeNode | null): number[] {
 };
 ```
 
-Swift:
+Swift：
 
-> 迭代法前序遍历
 ```swift
+// 前序遍历迭代法
 func preorderTraversal(_ root: TreeNode?) -> [Int] {
-    var res = [Int]()
-    if root == nil {
-        return res
-    }
-    var stack = [TreeNode]()
-    stack.append(root!)
+    var result = [Int]()
+    guard let root = root else { return result }
+    var stack = [root]
     while !stack.isEmpty {
-        let node = stack.popLast()!
-        res.append(node.val)
-        if node.right != nil {
-            stack.append(node.right!)
+        let current = stack.removeLast()
+        // 先右后左，这样出栈的时候才是左右顺序
+        if let node = current.right { // 右
+            stack.append(node)
         }
-        if node.left != nil {
-            stack.append(node.left!)
+        if let node = current.left { // 左
+            stack.append(node)
         }
+        result.append(current.val) // 中
     }
-    return res
+    return result
 }
-```
 
-> 迭代法中序遍历
-```swift
-func inorderTraversal(_ root: TreeNode?) -> [Int] {
-    var res = [Int]()
-    if root == nil {
-        return res
-    }
-    var stack = [TreeNode]()
-    var cur: TreeNode? = root
-    while cur != nil || !stack.isEmpty {
-        if cur != nil {
-            stack.append(cur!)
-            cur = cur!.left
-        } else {
-            cur = stack.popLast()
-            res.append(cur!.val)
-            cur = cur!.right
-        }
-    }
-    return res
-}
-```
-
-> 迭代法后序遍历
-```swift
+// 后序遍历迭代法
 func postorderTraversal(_ root: TreeNode?) -> [Int] {
-    var res = [Int]()
-    if root == nil {
-        return res
-    }
-    var stack = [TreeNode]()
-    stack.append(root!)
-    // res 存储 中 -> 右 -> 左
+    var result = [Int]()
+    guard let root = root else { return result }
+    var stack = [root]
     while !stack.isEmpty {
-        let node = stack.popLast()!
-        res.append(node.val)
-        if node.left != nil  {
-            stack.append(node.left!)
+        let current = stack.removeLast()
+        // 与前序相反，即中右左，最后结果还需反转才是后序
+        if let node = current.left { // 左
+            stack.append(node)
         }
-        if node.right != nil  {
-            stack.append(node.right!)
+        if let node = current.right { // 右
+            stack.append(node)
+        }
+        result.append(current.val) // 中
+    }
+    return result.reversed()
+}
+
+// 中序遍历迭代法
+func inorderTraversal(_ root: TreeNode?) -> [Int] {
+    var result = [Int]()
+    var stack = [TreeNode]()
+    var current: TreeNode! = root
+    while current != nil || !stack.isEmpty {
+        if current != nil { // 先访问到最左叶子
+            stack.append(current)
+            current = current.left // 左
+        } else {
+            current = stack.removeLast()
+            result.append(current.val) // 中
+            current = current.right // 右
         }
     }
-    // res 翻转
-    res.reverse()
-    return res
+    return result
 }
 ```
 

problems/二叉树的递归遍历.md

@@ -34,19 +34,19 @@
 
 1. **确定递归函数的参数和返回值**：因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：
 
-```
+```cpp
 void traversal(TreeNode* cur, vector<int>& vec)
 ```
 
 2. **确定终止条件**：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：
 
-```
+```cpp
 if (cur == NULL) return;
 ```
 
 3. **确定单层递归的逻辑**：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：
 
-```
+```cpp
 vec.push_back(cur->val);    // 中
 traversal(cur->left, vec);  // 左
 traversal(cur->right, vec); // 右
@@ -168,7 +168,7 @@ class Solution {
 ```
 
 Python：
-```python3
+```python
 # 前序遍历-递归-LC144_二叉树的前序遍历
 class Solution:
     def preorderTraversal(self, root: TreeNode) -> List[int]:

problems/前序/ACM模式如何构建二叉树.md

@@ -45,21 +45,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20210914223147.png)
 
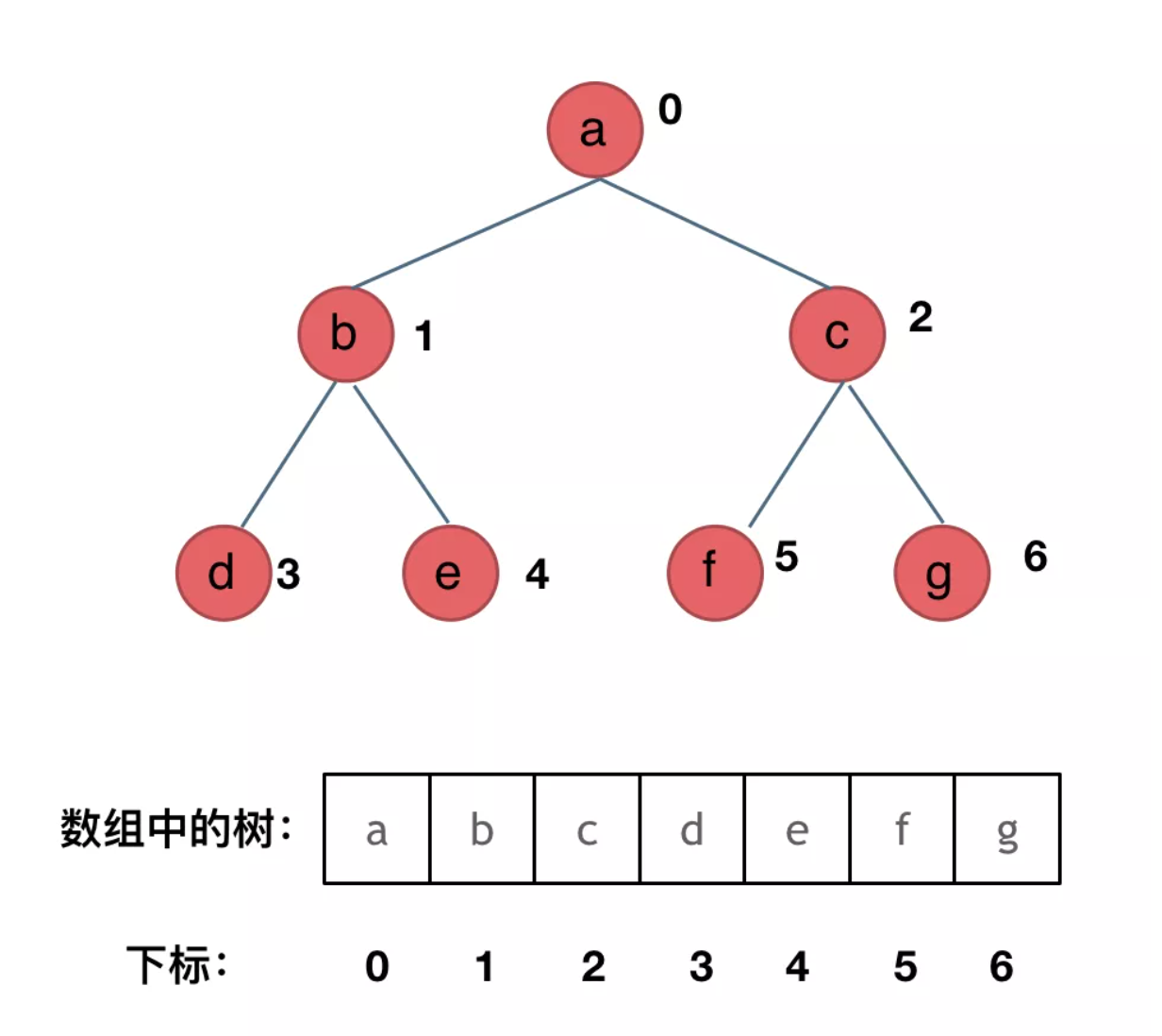
-那么此时大家是不是应该知道了，数组如何转化成 二叉树了。**如果父节点的数组下标是i，那么它的左孩子下标就是i * 2 + 1，右孩子下标就是 i * 2 + 2**。计算过程为：
-
-如果父节点在第$k$层，第$m,m \in [0,2^k]$个节点，则其左孩子所在的位置必然为$k+1$层，第$2*(m-1)+1$个节点。
-
-- 计算父节点在数组中的索引：
-  $$
-  index_{father}=(\sum_{i=0}^{i=k-1}2^i)+m-1=2^k-1+m-1
-  $$
-
-- 计算左子节点在数组的索引：
-  $$
-  index_{left}=(\sum_{i=0}^{i=k}2^i)+2*m-1-1=2^{k+1}+2m-3
-  $$
-
-- 故左孩子的下表为$index_{left}=index_{father}\times2+1$，同理可得到右子孩子的索引关系。也可以直接在左子孩子的基础上`+1`。
+那么此时大家是不是应该知道了，数组如何转化成 二叉树了。**如果父节点的数组下标是i，那么它的左孩子下标就是i * 2 + 1，右孩子下标就是 i * 2 + 2**。
 
 那么这里又有同学疑惑了，这些我都懂了，但我还是不知道 应该 怎么构造。
 

problems/前序/广州互联网公司总结.md

@@ -14,6 +14,7 @@
 ## 一线互联网
 
 * 微信（总部） 有点难进！
+* 字节跳动（广州）
 
 ## 二线
 * 网易（总部）主要是游戏

problems/剑指Offer05.替换空格.md

@@ -121,6 +121,37 @@ for (int i = 0; i < a.size(); i++) {
 
 ## 其他语言版本
 
+C：
+```C
+char* replaceSpace(char* s){
+    //统计空格数量
+    int count = 0;
+    int len = strlen(s);
+    for (int i = 0; i < len; i++) {
+        if (s[i] == ' ') {
+            count++;
+        }
+    }
+
+    //为新数组分配空间
+    int newLen = len + count * 2;
+    char* result = malloc(sizeof(char) * newLen + 1);
+    //填充新数组并替换空格
+    for (int i = len - 1, j = newLen - 1; i >= 0; i--, j--) {
+        if (s[i] != ' ') {
+            result[j] = s[i];
+        } else {
+            result[j--] = '0';
+            result[j--] = '2';
+            result[j] = '%';
+        }
+    }
+    result[newLen] = '\0';
+
+    return result;
+}
+```
+
 
 Java：
 ```Java

problems/动态规划总结篇.md

@@ -118,7 +118,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211121223754.png)
 
-这个图是 [代码随想录知识星球](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)，所画，总结的非常好，分享给大家。
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)，所画，总结的非常好，分享给大家。
 
 这已经是全网对动规最深刻的讲解系列了。
 

problems/周总结/20201003二叉树周末总结.md

@@ -34,8 +34,8 @@ public:
 
         // 此时就是：左右节点都不为空，且数值相同的情况
         // 此时才做递归，做下一层的判断
-        bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：左 （相对于求对称二叉树，只需改一下这里的顺序）
-        bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：右
+        bool outside = compare(left->left, right->left);   // 左子树：左、 右子树：左 （相对于求对称二叉树，只需改一下这里的顺序）
+        bool inside = compare(left->right, right->right);    // 左子树：右、 右子树：右
         bool isSame = outside && inside;                    // 左子树：中、 右子树：中 （逻辑处理）
         return isSame;
 

problems/回溯总结.md

@@ -432,7 +432,7 @@ N皇后问题分析：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211030124742.png)
 
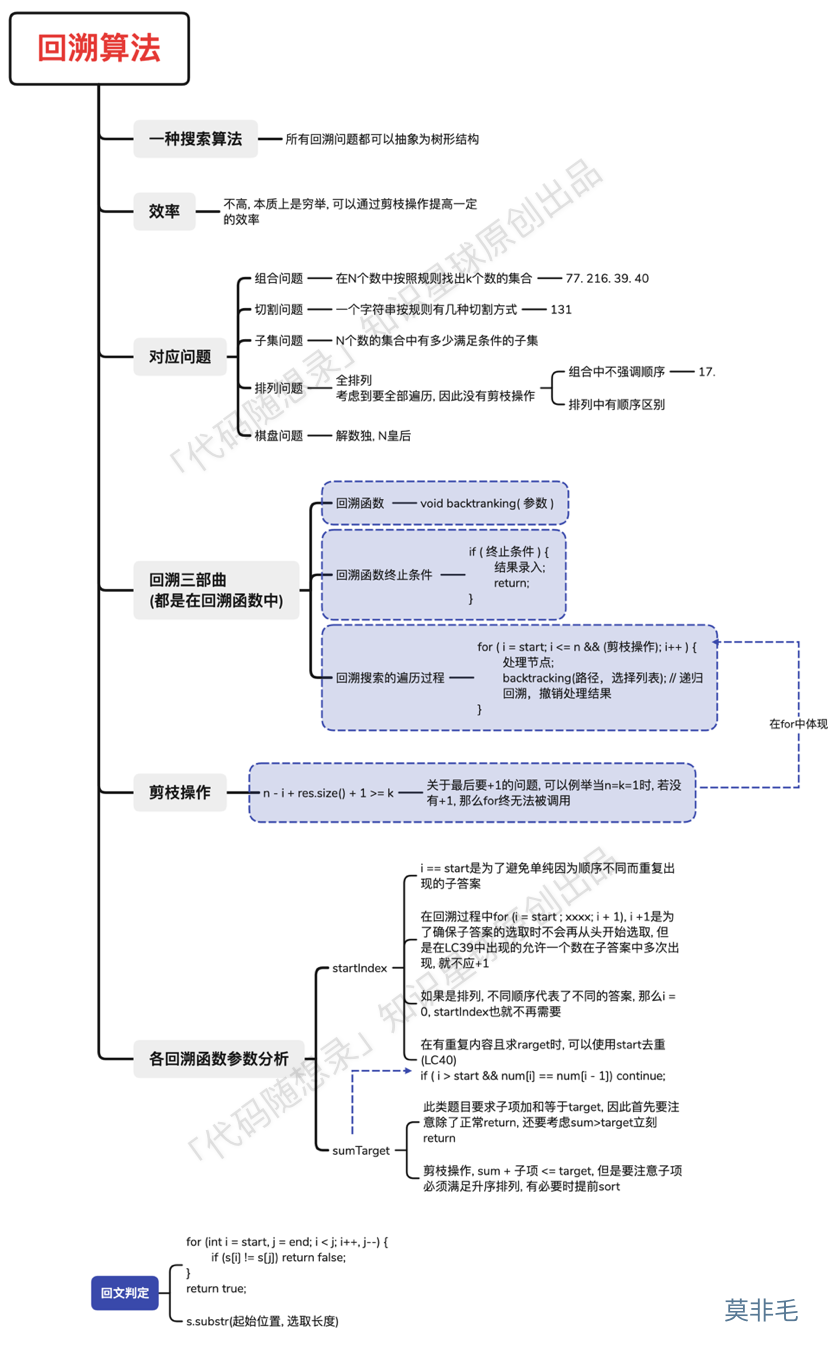
-这个图是 [代码随想录知识星球](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ) 成员：[莫非毛](https://wx.zsxq.com/dweb2/index/footprint/828844212542)，所画，总结的非常好，分享给大家。
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[莫非毛](https://wx.zsxq.com/dweb2/index/footprint/828844212542)，所画，总结的非常好，分享给大家。
 
 **回溯算法系列正式结束，新的系列终将开始，录友们准备开启新的征程！**
 

problems/算法模板.md

@@ -394,7 +394,7 @@ var postorder = function (root, list) {
 ```javascript
 var preorderTraversal = function (root) {
     let res = [];
-    if (root === null) return rs;
+    if (root === null) return res;
     let stack = [root],
         cur = null;
     while (stack.length) {
@@ -536,6 +536,269 @@ function backtracking(参数) {
     }
 ```
 
+TypeScript：
+
+## 二分查找法
+
+使用左闭右闭区间
+
+```typescript
+var search = function (nums: number[], target: number): number {
+    let left: number = 0, right: number = nums.length - 1;
+    // 使用左闭右闭区间
+    while (left <= right) {
+        let mid: number = left + Math.floor((right - left)/2);
+        if (nums[mid] > target) {
+            right = mid - 1;  // 去左面闭区间寻找
+        } else if (nums[mid] < target) {
+            left = mid + 1;   // 去右面闭区间寻找
+        } else {
+            return mid;
+        }
+    }
+    return -1;
+};
+```
+
+使用左闭右开区间
+
+```typescript
+var search = function (nums: number[], target: number): number {
+    let left: number = 0, right: number = nums.length;
+    // 使用左闭右开区间 [left, right)
+    while (left < right) {
+        let mid: number = left + Math.floor((right - left)/2);
+        if (nums[mid] > target) {
+            right = mid;  // 去左面闭区间寻找
+        } else if (nums[mid] < target) {
+            left = mid + 1;   // 去右面闭区间寻找
+        } else {
+            return mid;
+        }
+    }
+    return -1;
+};
+```
+
+## KMP
+
+```typescript
+var kmp = function (next: number[], s: number): void {
+    next[0] = -1;
+    let j: number = -1;
+    for(let i: number = 1; i < s.length; i++){
+        while (j >= 0 && s[i] !== s[j + 1]) {
+            j = next[j];
+        }
+        if (s[i] === s[j + 1]) {
+            j++;
+        }
+        next[i] = j;
+    }
+}
+```
+
+## 二叉树
+
+### 深度优先遍历（递归）
+
+二叉树节点定义：
+
+```typescript
+class TreeNode {
+    val: number
+    left: TreeNode | null
+    right: TreeNode | null
+    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
+        this.val = (val===undefined ? 0 : val)
+        this.left = (left===undefined ? null : left)
+        this.right = (right===undefined ? null : right)
+    }
+}
+```
+
+前序遍历（中左右）：
+
+```typescript
+var preorder = function (root: TreeNode | null, list: number[]): void {
+    if (root === null) return;
+    list.push(root.val);        // 中
+    preorder(root.left, list);  // 左
+    preorder(root.right, list); // 右
+}
+```
+
+中序遍历（左中右）：
+
+```typescript
+var inorder = function (root: TreeNode | null, list: number[]): void {
+    if (root === null) return;
+    inorder(root.left, list);  // 左
+    list.push(root.val);        // 中
+    inorder(root.right, list); // 右
+}
+```
+
+后序遍历（左右中）：
+
+```typescript
+var postorder = function (root: TreeNode | null, list: number[]): void {
+    if (root === null) return;
+    postorder(root.left, list);  // 左
+    postorder(root.right, list); // 右
+    list.push(root.val);        // 中
+}
+```
+
+### 深度优先遍历（迭代）
+
+前序遍历（中左右）：
+
+```typescript
+var preorderTraversal = function (root: TreeNode | null): number[] {
+    let res: number[] = [];
+    if (root === null) return res;
+    let stack: TreeNode[] = [root],
+        cur: TreeNode | null = null;
+    while (stack.length) {
+        cur = stack.pop();
+        res.push(cur.val);
+        cur.right && stack.push(cur.right);
+        cur.left && stack.push(cur.left);
+    }
+    return res;
+};
+```
+
+中序遍历（左中右）：
+
+```typescript
+var inorderTraversal = function (root: TreeNode | null): number[] {
+    let res: number[] = [];
+    if (root === null) return res;
+    let stack: TreeNode[] = [];
+    let cur: TreeNode | null = root;
+    while (stack.length ！== 0 || cur !== null) {
+        if (cur !== null) {
+            stack.push(cur);
+            cur = cur.left;
+        } else {
+            cur = stack.pop();
+            res.push(cur.val);
+            cur = cur.right;
+        }
+    }
+    return res;
+};
+```
+
+后序遍历（左右中）：
+
+```typescript
+var postorderTraversal = function (root: TreeNode | null): number[] {
+    let res: number[] = [];
+    if (root === null) return res;
+    let stack: TreeNode[] = [root];
+    let cur: TreeNode | null = null;
+    while (stack.length) {
+        cur = stack.pop();
+        res.push(cur.val);
+        cur.left && stack.push(cur.left);
+        cur.right && stack.push(cur.right);
+    }
+    return res.reverse()
+};
+```
+
+### 广度优先遍历（队列）
+
+```typescript
+var levelOrder = function (root: TreeNode | null): number[] {
+    let res: number[] = [];
+    if (root === null) return res;
+    let queue: TreeNode[] = [root];
+    while (queue.length) {
+        let n: number = queue.length;
+        let temp: number[] = [];
+        for (let i: number = 0; i < n; i++) {
+            let node: TreeNode = queue.shift();
+            temp.push(node.val);
+            node.left && queue.push(node.left);
+            node.right && queue.push(node.right);
+        }
+        res.push(temp);
+    }
+    return res;
+};
+```
+
+### 二叉树深度
+
+```typescript
+var getDepth = function (node: TreNode | null): number {
+    if (node === null) return 0;
+    return 1 + Math.max(getDepth(node.left), getDepth(node.right));
+}
+```
+
+### 二叉树节点数量
+
+```typescript
+var countNodes = function (root: TreeNode | null): number {
+    if (root === null) return 0;
+    return 1 + countNodes(root.left) + countNodes(root.right);
+}
+```
+
+## 回溯算法 
+
+```typescript
+function backtracking(参数) {
+    if (终止条件) {
+        存放结果;
+        return;
+    }
+
+    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
+        处理节点;
+        backtracking(路径，选择列表); // 递归
+        回溯，撤销处理结果
+    }
+}
+
+```
+
+## 并查集 
+
+```typescript
+    let n: number = 1005; // 根据题意而定 
+    let father: number[] = new Array(n).fill(0);
+
+    // 并查集初始化
+    function init () {
+        for (int i: number = 0; i < n; ++i) {
+            father[i] = i;
+        }
+    }
+    // 并查集里寻根的过程
+    function find (u: number): number {
+        return u === father[u] ? u : father[u] = find(father[u]);
+    }
+    // 将v->u 这条边加入并查集
+    function join(u: number, v: number) {
+        u = find(u);
+        v = find(v);
+        if (u === v) return ;
+        father[v] = u;
+    }
+    // 判断 u 和 v是否找到同一个根
+    function same(u: number, v: number): boolean {
+        u = find(u);
+        v = find(v);
+        return u === v;
+    }
+```
+
 Java：
 
 

problems/背包总结篇.md

@@ -82,6 +82,7 @@
 
 ## 总结
 
+
 **这篇背包问题总结篇是对背包问题的高度概括，讲最关键的两部：递推公式和遍历顺序，结合力扣上的题目全都抽象出来了**。
 
 **而且每一个点，我都给出了对应的力扣题目**。
@@ -90,7 +91,11 @@
 
 如果把我本篇总结出来的内容都掌握的话，可以说对背包问题理解的就很深刻了，用来对付面试中的背包问题绰绰有余！
 
+背包问题总结：
 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/背包问题1.jpeg)
+
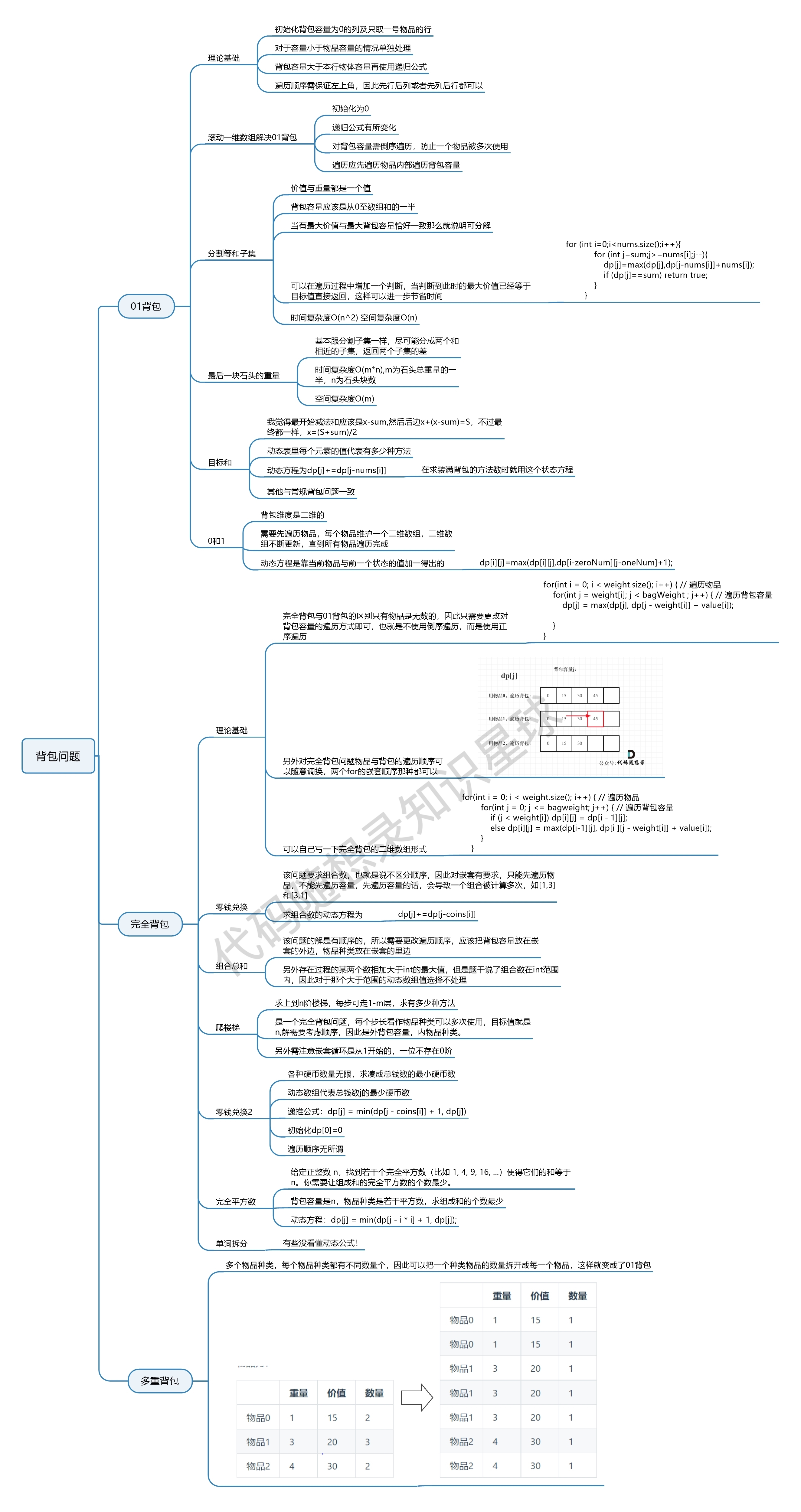
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)，所画结的非常好，分享给大家。
 
 
 

problems/背包理论基础01背包-1.md

@@ -271,7 +271,7 @@ int main() {
 ### java 
 
 ```java
-    public static void main(string[] args) {
+    public static void main(String[] args) {
         int[] weight = {1, 3, 4};
         int[] value = {15, 20, 30};
         int bagsize = 4;
@@ -292,16 +292,16 @@ int main() {
                 if (j < weight[i - 1]){
                     dp[i][j] = dp[i - 1][j];
                 }else{
-                    dp[i][j] = math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
+                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
                 }
             }
         }
         //打印dp数组
         for (int i = 0; i <= wlen; i++){
             for (int j = 0; j <= bagsize; j++){
-                system.out.print(dp[i][j] + " ");
+                System.out.print(dp[i][j] + " ");
             }
-            system.out.print("\n");
+            System.out.print("\n");
         }
     }
 ```

problems/背包问题理论基础完全背包.md

@@ -94,7 +94,7 @@ dp状态图如下：
 
 看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。
 
-先遍历被背包在遍历物品，代码如下：
+先遍历背包在遍历物品，代码如下：
 
 ```CPP
 // 先遍历背包，再遍历物品
@@ -216,7 +216,7 @@ private static void testCompletePackAnotherWay(){
 
 Python：
 
-```python3
+```python
 # 先遍历物品，再遍历背包
 def test_complete_pack1():
     weight = [1, 3, 4]

problems/贪心算法总结篇.md

@@ -129,7 +129,7 @@ Carl个人认为：如果找出局部最优并可以推出全局最优，就是
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211110121605.png) 
 
-这个图是 [代码随想录知识星球](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)所画，总结的非常好，分享给大家。
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)所画，总结的非常好，分享给大家。
 
 很多没有接触过贪心的同学都会感觉贪心有啥可学的，但只要跟着「代码随想录」坚持下来之后，就会发现，贪心是一种很重要的算法思维而且并不简单，贪心往往妙的出其不意，触不及防！