mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-12 05:20:59 +08:00
Update
This commit is contained in:
@ -9,18 +9,25 @@
|
||||
|
||||
> 数组就是简单的哈希表,但是数组的大小可不是无限开辟的
|
||||
|
||||
# 242.有效的字母异位词
|
||||
## 242.有效的字母异位词
|
||||
|
||||
https://leetcode-cn.com/problems/valid-anagram/
|
||||
|
||||
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
|
||||
|
||||

|
||||
示例 1:
|
||||
输入: s = "anagram", t = "nagaram"
|
||||
输出: true
|
||||
|
||||
示例 2:
|
||||
输入: s = "rat", t = "car"
|
||||
输出: false
|
||||
|
||||
|
||||
**说明:**
|
||||
你可以假设字符串只包含小写字母。
|
||||
|
||||
# 思路
|
||||
## 思路
|
||||
|
||||
先看暴力的解法,两层for循环,同时还要记录字符是否重复出现,很明显时间复杂度是 O(n^2)。
|
||||
|
||||
@ -52,7 +59,6 @@ https://leetcode-cn.com/problems/valid-anagram/
|
||||
|
||||
时间复杂度为O(n),空间上因为定义是的一个常量大小的辅助数组,所以空间复杂度为O(1)。
|
||||
|
||||
看完这篇哈希表总结:[哈希表:总结篇!(每逢总结必经典)](https://mp.weixin.qq.com/s/1s91yXtarL-PkX07BfnwLg),详细就可以哈希表的各种用法非常清晰了。
|
||||
|
||||
C++ 代码如下:
|
||||
```C++
|
||||
@ -134,9 +140,15 @@ func isAnagram(s string, t string) bool {
|
||||
}
|
||||
```
|
||||
|
||||
## 相关题目
|
||||
|
||||
* 383.赎金信
|
||||
* 49.字母异位词分组
|
||||
* 438.找到字符串中所有字母异位词
|
||||
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|
||||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|
||||
|
||||
@ -14,17 +14,17 @@
|
||||
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
|
||||
|
||||
|
||||
示例 1:
|
||||
输入: nums = [-1,0,3,5,9,12], target = 9
|
||||
输出: 4
|
||||
解释: 9 出现在 nums 中并且下标为 4
|
||||
示例 1:
|
||||
输入: nums = [-1,0,3,5,9,12], target = 9
|
||||
输出: 4
|
||||
解释: 9 出现在 nums 中并且下标为 4
|
||||
|
||||
示例 2:
|
||||
输入: nums = [-1,0,3,5,9,12], target = 2
|
||||
输出: -1
|
||||
解释: 2 不存在 nums 中因此返回 -1
|
||||
示例 2:
|
||||
输入: nums = [-1,0,3,5,9,12], target = 2
|
||||
输出: -1
|
||||
解释: 2 不存在 nums 中因此返回 -1
|
||||
|
||||
提示:
|
||||
提示:
|
||||
|
||||
* 你可以假设 nums 中的所有元素是不重复的。
|
||||
* n 将在 [1, 10000]之间。
|
||||
@ -217,4 +217,4 @@ Go:
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|
||||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|
||||
|
||||
@ -7,11 +7,12 @@
|
||||
<p align="center"><strong>欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 哈希表
|
||||
|
||||
## 哈希表
|
||||
|
||||
首先什么是 哈希表,哈希表(英文名字为Hash table,国内也有一些算法书籍翻译为散列表,大家看到这两个名称知道都是指hash table就可以了)。
|
||||
|
||||
> 哈希表是根据关键码的值而直接进行访问的数据结构。
|
||||
> 哈希表是根据关键码的值而直接进行访问的数据结构。
|
||||
|
||||
这么这官方的解释可能有点懵,其实直白来讲其实数组就是一张哈希表。
|
||||
|
||||
@ -19,17 +20,17 @@
|
||||
|
||||
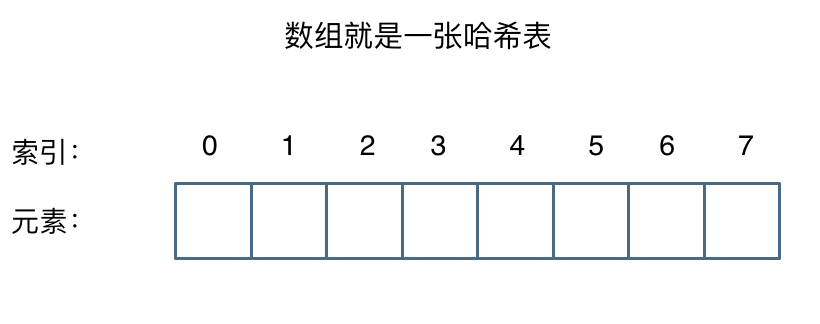
|
||||
|
||||
那么哈希表能解决什么问题呢,**一般哈希表都是用来快速判断一个元素是否出现集合里。**
|
||||
那么哈希表能解决什么问题呢,**一般哈希表都是用来快速判断一个元素是否出现集合里。**
|
||||
|
||||
例如要查询一个名字是否在这所学校里。
|
||||
例如要查询一个名字是否在这所学校里。
|
||||
|
||||
要枚举的话时间复杂度是O(n),但如果使用哈希表的话, 只需要O(1) 就可以做到。
|
||||
要枚举的话时间复杂度是O(n),但如果使用哈希表的话, 只需要O(1) 就可以做到。
|
||||
|
||||
我们只需要初始化把这所学校里学生的名字都存在哈希表里,在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
|
||||
|
||||
将学生姓名映射到哈希表上就涉及到了**hash function ,也就是哈希函数**。
|
||||
|
||||
# 哈希函数
|
||||
## 哈希函数
|
||||
|
||||
哈希函数,把学生的姓名直接映射为哈希表上的索引,然后就可以通过查询索引下表快速知道这位同学是否在这所学校里了。
|
||||
|
||||
@ -37,7 +38,7 @@
|
||||
|
||||
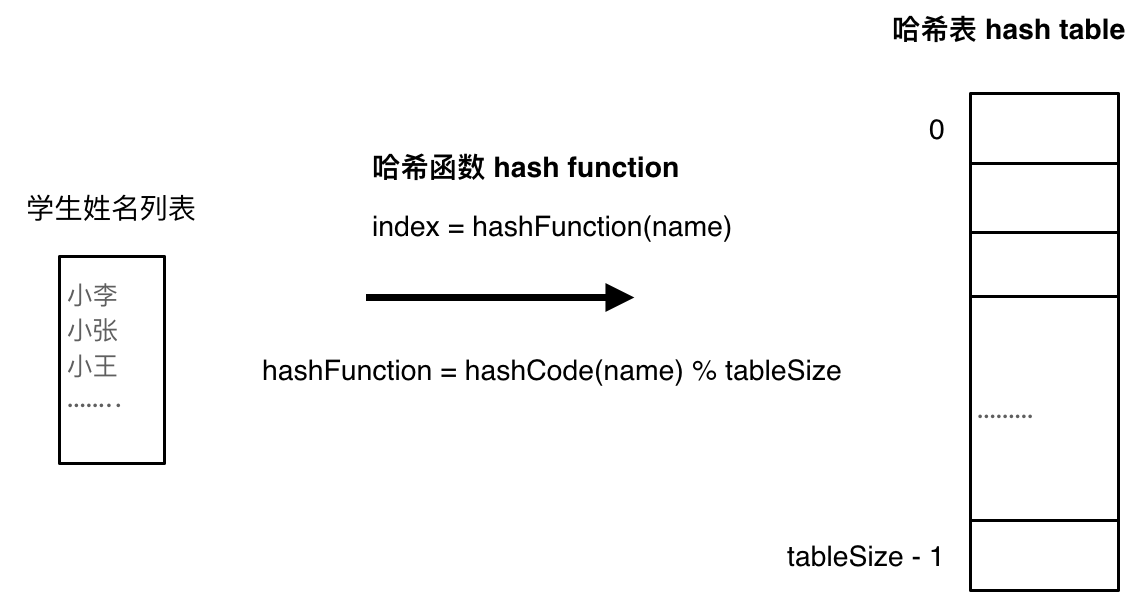
|
||||
|
||||
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
|
||||
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
|
||||
|
||||
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了。
|
||||
|
||||
@ -47,7 +48,7 @@
|
||||
|
||||
接下来**哈希碰撞**登场
|
||||
|
||||
# 哈希碰撞
|
||||
### 哈希碰撞
|
||||
|
||||
如图所示,小李和小王都映射到了索引下表 1的位置,**这一现象叫做哈希碰撞**。
|
||||
|
||||
@ -55,7 +56,7 @@
|
||||
|
||||
一般哈希碰撞有两种解决方法, 拉链法和线性探测法。
|
||||
|
||||
## 拉链法
|
||||
### 拉链法
|
||||
|
||||
刚刚小李和小王在索引1的位置发生了冲突,发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王了
|
||||
|
||||
@ -65,7 +66,7 @@
|
||||
|
||||
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
|
||||
|
||||
## 线性探测法
|
||||
### 线性探测法
|
||||
|
||||
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
|
||||
|
||||
@ -75,13 +76,13 @@
|
||||
|
||||
其实关于哈希碰撞还有非常多的细节,感兴趣的同学可以再好好研究一下,这里我就不再赘述了。
|
||||
|
||||
# 常见的三种哈希结构
|
||||
## 常见的三种哈希结构
|
||||
|
||||
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
|
||||
|
||||
* 数组
|
||||
* set (集合)
|
||||
* map(映射)
|
||||
* map(映射)
|
||||
|
||||
这里数组就没啥可说的了,我们来看一下set。
|
||||
|
||||
@ -117,7 +118,7 @@ std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底
|
||||
|
||||
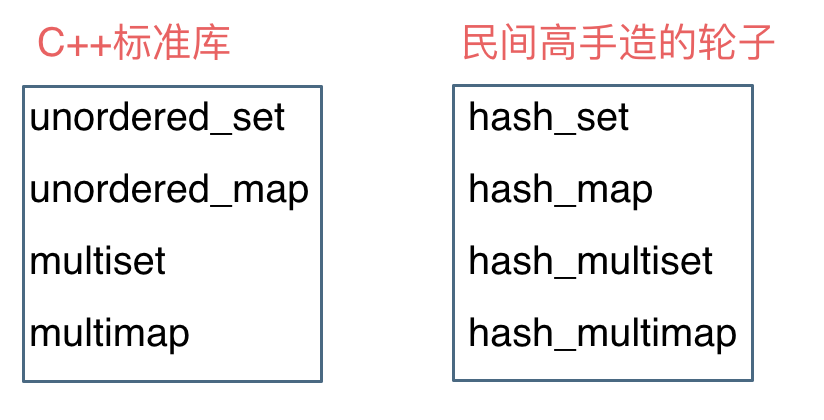
|
||||
|
||||
# 总结
|
||||
## 总结
|
||||
|
||||
总结一下,**当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法**。
|
||||
|
||||
@ -125,23 +126,6 @@ std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底
|
||||
|
||||
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法!
|
||||
|
||||
预告下篇讲解一波哈希表面试题的解题套路,我们下期见!
|
||||
|
||||
都看到这了,还有sei!sei没读懂单独找我!
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -262,26 +262,6 @@ int main() {
|
||||
```
|
||||
|
||||
|
||||
以上遍历的过程也可以这么写:
|
||||
|
||||
```
|
||||
// 遍历过程
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
|
||||
if (j - weight[i] >= 0) {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这么写打印出来的dp数据这就是这样:
|
||||
|
||||
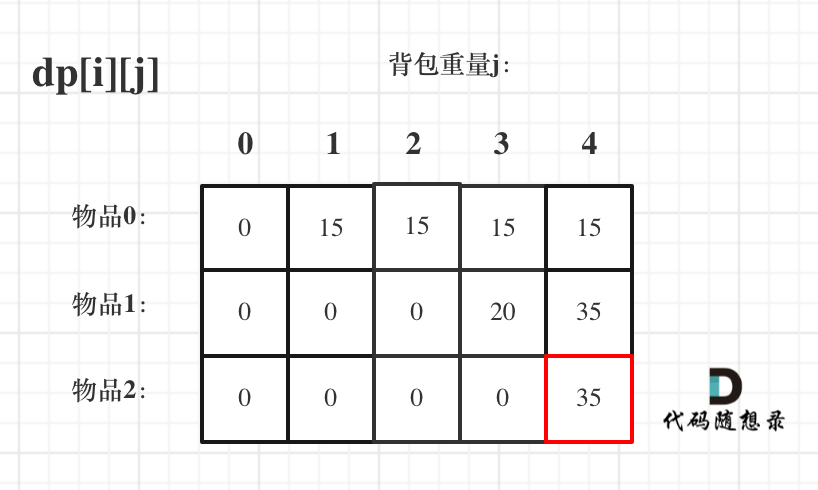
|
||||
|
||||
空出来的0其实是用不上的,版本一 能把完整的dp数组打印出来,出来我用版本一来讲解。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
讲了这么多才刚刚把二维dp的01背包讲完,**这里大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上**。
|
||||
|
||||
Reference in New Issue
Block a user