mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 16:54:50 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -131,6 +131,7 @@
|
||||
7. [英语到底重不重要!](https://mp.weixin.qq.com/s/1PRZiyF_-TVA-ipwDNjdKw)
|
||||
8. [计算机专业要不要读研!](https://mp.weixin.qq.com/s/c9v1L3IjqiXtkNH7sOMAdg)
|
||||
9. [秋招和提前批都越来越提前了....](https://mp.weixin.qq.com/s/SNFiRDx8CKyjhTPlys6ywQ)
|
||||
10. [你的简历里「专业技能」写的够专业么?](https://mp.weixin.qq.com/s/bp6y-e5FVN28H9qc8J9zrg)
|
||||
|
||||
|
||||
## 数组
|
||||
@ -395,7 +396,8 @@
|
||||
|
||||
## 单调栈
|
||||
|
||||
1. [每日温度](./problems/0739.每日温度.md)
|
||||
1. [单调栈:每日温度](./problems/0739.每日温度.md)
|
||||
2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
|
||||
|
||||
## 图论
|
||||
|
||||
|
||||
@ -41,6 +41,9 @@ candidates 中的每个数字在每个组合中只能使用一次。
|
||||
|
||||
## 思路
|
||||
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
这道题目和[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)如下区别:
|
||||
|
||||
1. 本题candidates 中的每个数字在每个组合中只能使用一次。
|
||||
|
||||
@ -30,7 +30,7 @@
|
||||
|
||||
## 思路
|
||||
|
||||
本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。
|
||||
本题相对于[55.跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。
|
||||
|
||||
但思路是相似的,还是要看最大覆盖范围。
|
||||
|
||||
@ -132,7 +132,7 @@ public:
|
||||
|
||||
## 总结
|
||||
|
||||
相信大家可以发现,这道题目相当于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。
|
||||
相信大家可以发现,这道题目相当于[55.跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。
|
||||
|
||||
但代码又十分简单,贪心就是这么巧妙。
|
||||
|
||||
@ -228,11 +228,6 @@ var jump = function(nums) {
|
||||
};
|
||||
```
|
||||
|
||||
/*
|
||||
dp[i]表示从起点到当前位置的最小跳跃次数
|
||||
dp[i]=min(dp[j]+1,dp[i]) 表示从j位置用一步跳跃到当前位置,这个j位置可能有很多个,却最小一个就可以
|
||||
*/
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -27,7 +27,10 @@
|
||||
|
||||
## 思路
|
||||
|
||||
此时我们已经学习了[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),接下来看一看排列问题。
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
此时我们已经学习了[77.组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、 [131.分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[78.子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),接下来看一看排列问题。
|
||||
|
||||
相信这个排列问题就算是让你用for循环暴力把结果搜索出来,这个暴力也不是很好写。
|
||||
|
||||
@ -81,7 +84,7 @@ if (path.size() == nums.size()) {
|
||||
|
||||
* 单层搜索的逻辑
|
||||
|
||||
这里和[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
|
||||
这里和[77.组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[131.切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[78.子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
|
||||
|
||||
因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
|
||||
|
||||
|
||||
@ -29,6 +29,8 @@
|
||||
* -10 <= nums[i] <= 10
|
||||
|
||||
## 思路
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
这道题目和[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
|
||||
|
||||
|
||||
@ -41,6 +41,9 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并
|
||||
|
||||
## 思路
|
||||
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二位矩阵还会有点不知所措。
|
||||
|
||||
首先来看一下皇后们的约束条件:
|
||||
|
||||
File diff suppressed because it is too large
Load Diff
@ -29,7 +29,7 @@
|
||||
|
||||
## 思路
|
||||
|
||||
看完了这篇[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),再来看看如何求最小深度。
|
||||
看完了这篇[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),再来看看如何求最小深度。
|
||||
|
||||
直觉上好像和求最大深度差不多,其实还是差不少的。
|
||||
|
||||
@ -154,7 +154,7 @@ public:
|
||||
|
||||
## 迭代法
|
||||
|
||||
相对于[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),本题还可以使用层序遍历的方式来解决,思路是一样的。
|
||||
相对于[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),本题还可以使用层序遍历的方式来解决,思路是一样的。
|
||||
|
||||
如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
|
||||
|
||||
|
||||
@ -291,6 +291,27 @@ func wordBreak(s string,wordDict []string) bool {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const wordBreak = (s, wordDict) => {
|
||||
|
||||
let dp = Array(s.length + 1).fill(false);
|
||||
dp[0] = true;
|
||||
|
||||
for(let i = 0; i <= s.length; i++){
|
||||
for(let j = 0; j < wordDict.length; j++) {
|
||||
if(i >= wordDict[j].length) {
|
||||
if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) {
|
||||
dp[i] = true
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[s.length];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -26,27 +26,26 @@ https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/
|
||||
|
||||
|
||||
示例 1:
|
||||
输入: ["2", "1", "+", "3", " * "]
|
||||
输出: 9
|
||||
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
|
||||
* 输入: ["2", "1", "+", "3", " * "]
|
||||
* 输出: 9
|
||||
* 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
|
||||
|
||||
示例 2:
|
||||
输入: ["4", "13", "5", "/", "+"]
|
||||
输出: 6
|
||||
解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
|
||||
* 输入: ["4", "13", "5", "/", "+"]
|
||||
* 输出: 6
|
||||
* 解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
|
||||
|
||||
示例 3:
|
||||
输入: ["10", "6", "9", "3", "+", "-11", " * ", "/", " * ", "17", "+", "5", "+"]
|
||||
输出: 22
|
||||
解释:
|
||||
该算式转化为常见的中缀算术表达式为:
|
||||
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
|
||||
= ((10 * (6 / (12 * -11))) + 17) + 5
|
||||
= ((10 * (6 / -132)) + 17) + 5
|
||||
= ((10 * 0) + 17) + 5
|
||||
= (0 + 17) + 5
|
||||
= 17 + 5
|
||||
= 22
|
||||
* 输入: ["10", "6", "9", "3", "+", "-11", " * ", "/", " * ", "17", "+", "5", "+"]
|
||||
* 输出: 22
|
||||
* 解释:该算式转化为常见的中缀算术表达式为:
|
||||
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
|
||||
= ((10 * (6 / (12 * -11))) + 17) + 5
|
||||
= ((10 * (6 / -132)) + 17) + 5
|
||||
= ((10 * 0) + 17) + 5
|
||||
= (0 + 17) + 5
|
||||
= 17 + 5
|
||||
= 22
|
||||
|
||||
|
||||
逆波兰表达式:是一种后缀表达式,所谓后缀就是指算符写在后面。
|
||||
@ -63,20 +62,20 @@ https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/
|
||||
|
||||
# 思路
|
||||
|
||||
在上一篇文章中[栈与队列:匹配问题都是栈的强项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)提到了 递归就是用栈来实现的。
|
||||
在上一篇文章中[1047.删除字符串中的所有相邻重复项](https://mp.weixin.qq.com/s/1-x6r1wGA9mqIHW5LrMvBg)提到了 递归就是用栈来实现的。
|
||||
|
||||
所以**栈与递归之间在某种程度上是可以转换的!**这一点我们在后续讲解二叉树的时候,会更详细的讲解到。
|
||||
所以**栈与递归之间在某种程度上是可以转换的!** 这一点我们在后续讲解二叉树的时候,会更详细的讲解到。
|
||||
|
||||
那么来看一下本题,**其实逆波兰表达式相当于是二叉树中的后序遍历**。 大家可以把运算符作为中间节点,按照后序遍历的规则画出一个二叉树。
|
||||
|
||||
但我们没有必要从二叉树的角度去解决这个问题,只要知道逆波兰表达式是用后续遍历的方式把二叉树序列化了,就可以了。
|
||||
|
||||
在进一步看,本题中每一个子表达式要得出一个结果,然后拿这个结果再进行运算,那么**这岂不就是一个相邻字符串消除的过程,和[栈与队列:匹配问题都是栈的强项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)中的对对碰游戏是不是就非常像了。**
|
||||
在进一步看,本题中每一个子表达式要得出一个结果,然后拿这个结果再进行运算,那么**这岂不就是一个相邻字符串消除的过程,和[1047.删除字符串中的所有相邻重复项](https://mp.weixin.qq.com/s/1-x6r1wGA9mqIHW5LrMvBg)中的对对碰游戏是不是就非常像了。**
|
||||
|
||||
如动画所示:
|
||||

|
||||

|
||||
|
||||
相信看完动画大家应该知道,这和[1047. 删除字符串中的所有相邻重复项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)是差不错的,只不过本题不要相邻元素做消除了,而是做运算!
|
||||
相信看完动画大家应该知道,这和[1047. 删除字符串中的所有相邻重复项](https://mp.weixin.qq.com/s/1-x6r1wGA9mqIHW5LrMvBg)是差不错的,只不过本题不要相邻元素做消除了,而是做运算!
|
||||
|
||||
C++代码如下:
|
||||
|
||||
@ -126,7 +125,7 @@ public:
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
java:
|
||||
|
||||
@ -153,23 +152,20 @@ public class EvalRPN {
|
||||
}
|
||||
return stack.pop();
|
||||
}
|
||||
|
||||
|
||||
private boolean isOpe(String s) {
|
||||
return s.length() == 1 && s.charAt(0) <'0' || s.charAt(0) >'9';
|
||||
}
|
||||
|
||||
private int stoi(String s) {
|
||||
return Integer.valueOf(s);
|
||||
}
|
||||
|
||||
|
||||
public static void main(String[] args) {
|
||||
new EvalRPN().evalRPN(new String[] {"10","6","9","3","+","-11","*","/","*","17","+","5","+"});
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
Go:
|
||||
```Go
|
||||
func evalRPN(tokens []string) int {
|
||||
|
||||
@ -34,7 +34,7 @@
|
||||
|
||||
本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。
|
||||
|
||||
相对于[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),无非就是多了一个限制,本题是要找到和为n的k个数的组合,而整个集合已经是固定的了[1,...,9]。
|
||||
相对于[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),无非就是多了一个限制,本题是要找到和为n的k个数的组合,而整个集合已经是固定的了[1,...,9]。
|
||||
|
||||
想到这一点了,做过[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)之后,本题是简单一些了。
|
||||
|
||||
@ -53,7 +53,7 @@
|
||||
|
||||
* **确定递归函数参数**
|
||||
|
||||
和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)一样,依然需要一维数组path来存放符合条件的结果,二维数组result来存放结果集。
|
||||
和[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)一样,依然需要一维数组path来存放符合条件的结果,二维数组result来存放结果集。
|
||||
|
||||
这里我依然定义path 和 result为全局变量。
|
||||
|
||||
@ -103,7 +103,7 @@ if (path.size() == k) {
|
||||
|
||||
* **单层搜索过程**
|
||||
|
||||
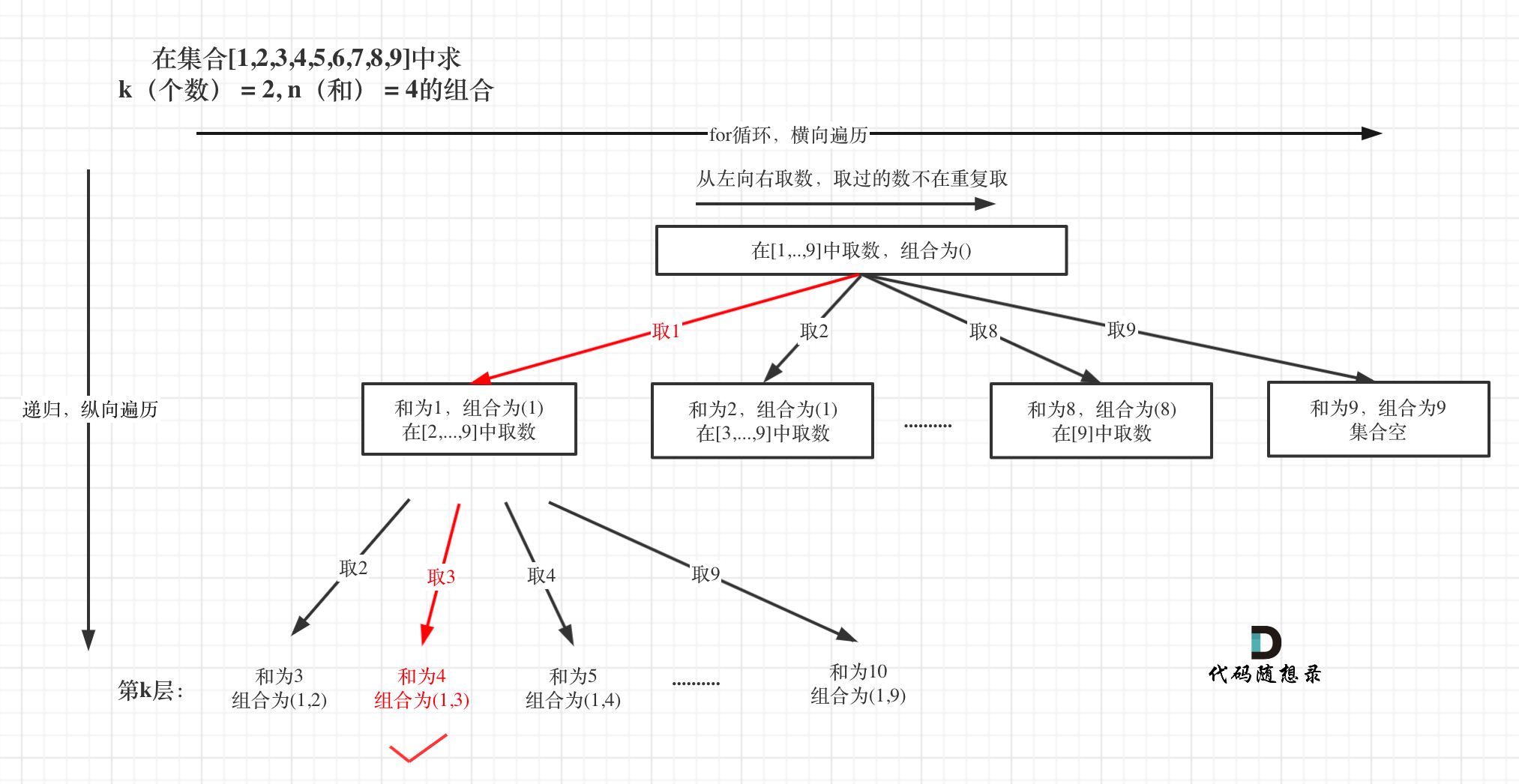
本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9
|
||||
本题和[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9
|
||||
|
||||
如图:
|
||||
|
||||
@ -227,6 +227,44 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
模板方法
|
||||
```java
|
||||
class Solution {
|
||||
List<List<Integer>> result = new ArrayList<>();
|
||||
LinkedList<Integer> path = new LinkedList<>();
|
||||
|
||||
public List<List<Integer>> combinationSum3(int k, int n) {
|
||||
backTracking(n, k, 1, 0);
|
||||
return result;
|
||||
}
|
||||
|
||||
private void backTracking(int targetSum, int k, int startIndex, int sum) {
|
||||
// 减枝
|
||||
if (sum > targetSum) {
|
||||
return;
|
||||
}
|
||||
|
||||
if (path.size() == k) {
|
||||
if (sum == targetSum) result.add(new ArrayList<>(path));
|
||||
return;
|
||||
}
|
||||
|
||||
// 减枝 9 - (k - path.size()) + 1
|
||||
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
|
||||
path.add(i);
|
||||
sum += i;
|
||||
backTracking(targetSum, k, i + 1, sum);
|
||||
//回溯
|
||||
path.removeLast();
|
||||
//回溯
|
||||
sum -= i;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
其他方法
|
||||
```java
|
||||
class Solution {
|
||||
List<List<Integer>> res = new ArrayList<>();
|
||||
|
||||
@ -22,13 +22,13 @@ https://leetcode-cn.com/problems/sliding-window-maximum/
|
||||
|
||||
你能在线性时间复杂度内解决此题吗?
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.png' width=600> </img></div>
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/239.滑动窗口最大值.png' width=600> </img></div>
|
||||
|
||||
提示:
|
||||
|
||||
1 <= nums.length <= 10^5
|
||||
-10^4 <= nums[i] <= 10^4
|
||||
1 <= k <= nums.length
|
||||
* 1 <= nums.length <= 10^5
|
||||
* -10^4 <= nums[i] <= 10^4
|
||||
* 1 <= k <= nums.length
|
||||
|
||||
|
||||
|
||||
@ -84,7 +84,7 @@ public:
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
|
||||
|
||||
@ -100,11 +100,11 @@ public:
|
||||
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
那么我们用什么数据结构来实现这个单调队列呢?
|
||||
|
||||
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://mp.weixin.qq.com/s/VZRjOccyE09aE-MgLbCMjQ)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
|
||||
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://mp.weixin.qq.com/s/HCXfQ_Bhpi63YaX0ZRSnAQ)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
|
||||
|
||||
基于刚刚说过的单调队列pop和push的规则,代码不难实现,如下:
|
||||
|
||||
@ -201,9 +201,7 @@ public:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
@ -337,36 +335,6 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
func maxSlidingWindow(nums []int, k int) []int {
|
||||
var queue []int
|
||||
var rtn []int
|
||||
|
||||
for f := 0; f < len(nums); f++ {
|
||||
//维持队列递减, 将 k 插入合适的位置, queue中 <=k 的 元素都不可能是窗口中的最大值, 直接弹出
|
||||
for len(queue) > 0 && nums[f] > nums[queue[len(queue)-1]] {
|
||||
queue = queue[:len(queue)-1]
|
||||
}
|
||||
// 等大的后来者也应入队
|
||||
if len(queue) == 0 || nums[f] <= nums[queue[len(queue)-1]] {
|
||||
queue = append(queue, f)
|
||||
}
|
||||
|
||||
if f >= k - 1 {
|
||||
rtn = append(rtn, nums[queue[0]])
|
||||
//弹出离开窗口的队首
|
||||
if f - k + 1 == queue[0] {
|
||||
queue = queue[1:]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return rtn
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```go
|
||||
// 封装单调队列的方式解题
|
||||
type MyQueue struct {
|
||||
|
||||
@ -304,6 +304,26 @@ func min(a, b int) int {
|
||||
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const coinChange = (coins, amount) => {
|
||||
if(!amount) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
let dp = Array(amount + 1).fill(Infinity);
|
||||
dp[0] = 0;
|
||||
|
||||
for(let i =0; i < coins.length; i++) {
|
||||
for(let j = coins[i]; j <= amount; j++) {
|
||||
dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);
|
||||
}
|
||||
}
|
||||
|
||||
return dp[amount] === Infinity ? -1 : dp[amount];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -33,6 +33,9 @@
|
||||
|
||||
## 思路
|
||||
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
这道题目还是很难的,之前我们用回溯法解决了如下问题:[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[分割问题](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA),[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),[排列问题](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)。
|
||||
|
||||
直觉上来看 这道题和回溯法没有什么关系,更像是图论中的深度优先搜索。
|
||||
|
||||
@ -201,6 +201,25 @@ func combinationSum4(nums []int, target int) int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const combinationSum4 = (nums, target) => {
|
||||
|
||||
let dp = Array(target + 1).fill(0);
|
||||
dp[0] = 1;
|
||||
|
||||
for(let i = 0; i <= target; i++) {
|
||||
for(let j = 0; j < nums.length; j++) {
|
||||
if (i >= nums[j]) {
|
||||
dp[i] += dp[i - nums[j]];
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[target];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -43,9 +43,9 @@
|
||||
|
||||
本题有两个维度,h和k,看到这种题目一定要想如何确定一个维度,然后在按照另一个维度重新排列。
|
||||
|
||||
其实如果大家认真做了[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ),就会发现和此题有点点的像。
|
||||
其实如果大家认真做了[135. 分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ),就会发现和此题有点点的像。
|
||||
|
||||
在[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)我就强调过一次,遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
|
||||
在[135. 分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)我就强调过一次,遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
|
||||
|
||||
**如果两个维度一起考虑一定会顾此失彼**。
|
||||
|
||||
@ -161,11 +161,11 @@ public:
|
||||
|
||||
## 总结
|
||||
|
||||
关于出现两个维度一起考虑的情况,我们已经做过两道题目了,另一道就是[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)。
|
||||
关于出现两个维度一起考虑的情况,我们已经做过两道题目了,另一道就是[135. 分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)。
|
||||
|
||||
**其技巧都是确定一边然后贪心另一边,两边一起考虑,就会顾此失彼**。
|
||||
|
||||
这道题目可以说比[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)难不少,其贪心的策略也是比较巧妙。
|
||||
这道题目可以说比[135. 分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)难不少,其贪心的策略也是比较巧妙。
|
||||
|
||||
最后我给出了两个版本的代码,可以明显看是使用C++中的list(底层链表实现)比vector(数组)效率高得多。
|
||||
|
||||
|
||||
@ -122,9 +122,9 @@ public:
|
||||
|
||||
## 补充
|
||||
|
||||
本题其实和[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)非常像,弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
|
||||
本题其实和[452.用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)非常像,弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
|
||||
|
||||
把[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)代码稍做修改,就可以AC本题。
|
||||
把[452.用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)代码稍做修改,就可以AC本题。
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
|
||||
@ -244,6 +244,35 @@ func max(a,b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const findMaxForm = (strs, m, n) => {
|
||||
const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
|
||||
let numOfZeros, numOfOnes;
|
||||
|
||||
for(let str of strs) {
|
||||
numOfZeros = 0;
|
||||
numOfOnes = 0;
|
||||
|
||||
for(let c of str) {
|
||||
if (c === '0') {
|
||||
numOfZeros++;
|
||||
} else {
|
||||
numOfOnes++;
|
||||
}
|
||||
}
|
||||
|
||||
for(let i = m; i >= numOfZeros; i--) {
|
||||
for(let j = n; j >= numOfOnes; j--) {
|
||||
dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[m][n];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -28,6 +28,9 @@
|
||||
|
||||
## 思路
|
||||
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
|
||||
|
||||
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)。
|
||||
@ -254,6 +257,34 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
```golang
|
||||
func findSubsequences(nums []int) [][]int {
|
||||
var subRes []int
|
||||
var res [][]int
|
||||
backTring(0,nums,subRes,&res)
|
||||
return res
|
||||
}
|
||||
func backTring(startIndex int,nums,subRes []int,res *[][]int){
|
||||
if len(subRes)>1{
|
||||
tmp:=make([]int,len(subRes))
|
||||
copy(tmp,subRes)
|
||||
*res=append(*res,tmp)
|
||||
}
|
||||
history:=[201]int{}//记录本层元素使用记录
|
||||
for i:=startIndex;i<len(nums);i++{
|
||||
//分两种情况判断:一,当前取的元素小于子集的最后一个元素,则继续寻找下一个适合的元素
|
||||
// 或者二,当前取的元素在本层已经出现过了,所以跳过该元素,继续寻找
|
||||
if len(subRes)>0&&nums[i]<subRes[len(subRes)-1]||history[nums[i] + 100]==1{
|
||||
continue
|
||||
}
|
||||
history[nums[i] + 100]=1//表示本层该元素使用过了
|
||||
subRes=append(subRes,nums[i])
|
||||
backTring(i+1,nums,subRes,res)
|
||||
subRes=subRes[:len(subRes)-1]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
|
||||
```Javascript
|
||||
|
||||
@ -306,6 +306,36 @@ func findTargetSumWays(nums []int, target int) int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const findTargetSumWays = (nums, target) => {
|
||||
|
||||
const sum = nums.reduce((a, b) => a+b);
|
||||
|
||||
if(target > sum) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
if((target + sum) % 2) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
const halfSum = (target + sum) / 2;
|
||||
nums.sort((a, b) => a - b);
|
||||
|
||||
let dp = new Array(halfSum+1).fill(0);
|
||||
dp[0] = 1;
|
||||
|
||||
for(let i = 0; i < nums.length; i++) {
|
||||
for(let j = halfSum; j >= nums[i]; j--) {
|
||||
dp[j] += dp[j - nums[i]];
|
||||
}
|
||||
}
|
||||
|
||||
return dp[halfSum];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
210
problems/0496.下一个更大元素I.md
Normal file
210
problems/0496.下一个更大元素I.md
Normal file
@ -0,0 +1,210 @@
|
||||
|
||||
# 496.下一个更大元素 I
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/next-greater-element-i/
|
||||
|
||||
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
|
||||
|
||||
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
|
||||
|
||||
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
|
||||
|
||||
示例 1:
|
||||
|
||||
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
|
||||
输出: [-1,3,-1]
|
||||
解释:
|
||||
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
|
||||
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
|
||||
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
|
||||
|
||||
示例 2:
|
||||
输入: nums1 = [2,4], nums2 = [1,2,3,4].
|
||||
输出: [3,-1]
|
||||
解释:
|
||||
对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。
|
||||
对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出-1 。
|
||||
|
||||
提示:
|
||||
|
||||
* 1 <= nums1.length <= nums2.length <= 1000
|
||||
* 0 <= nums1[i], nums2[i] <= 10^4
|
||||
* nums1和nums2中所有整数 互不相同
|
||||
* nums1 中的所有整数同样出现在 nums2 中
|
||||
|
||||
# 思路
|
||||
|
||||
做本题之前,建议先做一下[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)
|
||||
|
||||
在[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)中是求每个元素下一个比当前元素大的元素的位置。
|
||||
|
||||
本题则是说nums1 是 nums2的子集,找nums1中的元素在nums2中下一个比当前元素大的元素。
|
||||
|
||||
看上去和[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q) 就如出一辙了。
|
||||
|
||||
几乎是一样的,但是这么绕了一下,其实还上升了一点难度。
|
||||
|
||||
需要对单调栈使用的更熟练一些,才能顺利的把本题写出来。
|
||||
|
||||
从题目示例中我们可以看出最后是要求nums1的每个元素在nums2中下一个比当前元素大的元素,那么就要定义一个和nums1一样大小的数组result来存放结果。
|
||||
|
||||
一些同学可能看到两个数组都已经懵了,不知道要定一个一个多大的result数组来存放结果了。
|
||||
|
||||
**这么定义这个result数组初始化应该为多少呢?**
|
||||
|
||||
题目说如果不存在对应位置就输出 -1 ,所以result数组如果某位置没有被赋值,那么就应该是是-1,所以就初始化为-1。
|
||||
|
||||
在遍历nums2的过程中,我们要判断nums2[i]是否在nums1中出现过,因为最后是要根据nums1元素的下标来更新result数组。
|
||||
|
||||
**注意题目中说是两个没有重复元素 的数组 nums1 和 nums2**。
|
||||
|
||||
没有重复元素,我们就可以用map来做映射了。根据数值快速找到下标,还可以判断nums2[i]是否在nums1中出现过。
|
||||
|
||||
C++中,当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的。我在[关于哈希表,你该了解这些!](https://mp.weixin.qq.com/s/RSUANESA_tkhKhYe3ZR8Jg)中也做了详细的解释。
|
||||
|
||||
那么预处理代码如下:
|
||||
|
||||
```C++
|
||||
unordered_map<int, int> umap; // key:下表元素,value:下表
|
||||
for (int i = 0; i < nums1.size(); i++) {
|
||||
umap[nums1[i]] = i;
|
||||
}
|
||||
```
|
||||
|
||||
使用单调栈,首先要想单调栈是从大到小还是从小到大。
|
||||
|
||||
本题和739. 每日温度是一样的。
|
||||
|
||||
栈头到栈底的顺序,要从小到大,也就是保持栈里的元素为递增顺序。只要保持递增,才能找到右边第一个比自己大的元素。
|
||||
|
||||
可能这里有一些同学不理解,那么可以自己尝试一下用递减栈,能不能求出来。其实递减栈就是求右边第一个比自己小的元素了。
|
||||
|
||||
|
||||
接下来就要分析如下三种情况,一定要分析清楚。
|
||||
|
||||
1. 情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
|
||||
|
||||
此时满足递增栈(栈头到栈底的顺序),所以直接入栈。
|
||||
|
||||
2. 情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
|
||||
|
||||
如果相等的话,依然直接入栈,因为我们要求的是右边第一个比自己大的元素,而不是大于等于!
|
||||
|
||||
3. 情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
|
||||
|
||||
此时如果入栈就不满足递增栈了,这也是找到右边第一个比自己大的元素的时候。
|
||||
|
||||
判断栈顶元素是否在nums1里出现过,(注意栈里的元素是nums2的元素),如果出现过,开始记录结果。
|
||||
|
||||
记录结果这块逻辑有一点小绕,要清楚,此时栈顶元素在nums2中右面第一个大的元素是nums2[i]即当前遍历元素。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
while (!st.empty() && nums2[i] > nums2[st.top()]) {
|
||||
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
|
||||
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
|
||||
result[index] = nums2[i];
|
||||
}
|
||||
st.pop();
|
||||
}
|
||||
st.push(i);
|
||||
```
|
||||
|
||||
以上分析完毕,C++代码如下:
|
||||
|
||||
|
||||
```C++
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
|
||||
stack<int> st;
|
||||
vector<int> result(nums1.size(), -1);
|
||||
if (nums1.size() == 0) return result;
|
||||
|
||||
unordered_map<int, int> umap; // key:下表元素,value:下表
|
||||
for (int i = 0; i < nums1.size(); i++) {
|
||||
umap[nums1[i]] = i;
|
||||
}
|
||||
st.push(0);
|
||||
for (int i = 1; i < nums2.size(); i++) {
|
||||
if (nums2[i] < nums2[st.top()]) { // 情况一
|
||||
st.push(i);
|
||||
} else if (nums2[i] == nums2[st.top()]) { // 情况二
|
||||
st.push(i);
|
||||
} else { // 情况三
|
||||
while (!st.empty() && nums2[i] > nums2[st.top()]) {
|
||||
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
|
||||
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
|
||||
result[index] = nums2[i];
|
||||
}
|
||||
st.pop();
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
针对版本一,进行代码精简后,代码如下:
|
||||
|
||||
|
||||
```C++
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
|
||||
stack<int> st;
|
||||
vector<int> result(nums1.size(), -1);
|
||||
if (nums1.size() == 0) return result;
|
||||
|
||||
unordered_map<int, int> umap; // key:下表元素,value:下表
|
||||
for (int i = 0; i < nums1.size(); i++) {
|
||||
umap[nums1[i]] = i;
|
||||
}
|
||||
st.push(0);
|
||||
for (int i = 1; i < nums2.size(); i++) {
|
||||
while (!st.empty() && nums2[i] > nums2[st.top()]) {
|
||||
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
|
||||
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下表
|
||||
result[index] = nums2[i];
|
||||
}
|
||||
st.pop();
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
精简的代码是直接把情况一二三都合并到了一起,其实这种代码精简是精简,但思路不是很清晰。
|
||||
|
||||
建议大家把情况一二三想清楚了,先写出版本一的代码,然后在其基础上在做精简!
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
Python:
|
||||
```python3
|
||||
class Solution:
|
||||
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
|
||||
result = [-1]*len(nums1)
|
||||
stack = [0]
|
||||
for i in range(1,len(nums2)):
|
||||
# 情况一情况二
|
||||
if nums2[i]<=nums2[stack[-1]]:
|
||||
stack.append(i)
|
||||
# 情况三
|
||||
else:
|
||||
while len(stack)!=0 and nums2[i]>nums2[stack[-1]]:
|
||||
if nums2[stack[-1]] in nums1:
|
||||
index = nums1.index(nums2[stack[-1]])
|
||||
result[index]=nums2[i]
|
||||
stack.pop()
|
||||
stack.append(i)
|
||||
return result
|
||||
```
|
||||
|
||||
@ -243,6 +243,22 @@ func change(amount int, coins []int) int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const change = (amount, coins) => {
|
||||
let dp = Array(amount + 1).fill(0);
|
||||
dp[0] = 1;
|
||||
|
||||
for(let i =0; i < coins.length; i++) {
|
||||
for(let j = coins[i]; j <= amount; j++) {
|
||||
dp[j] += dp[j - coins[i]];
|
||||
}
|
||||
}
|
||||
|
||||
return dp[amount];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -319,7 +319,7 @@ Python:
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
//递归法*前序遍历
|
||||
# 递归法*前序遍历
|
||||
class Solution:
|
||||
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
|
||||
if not root1: return root2 // 如果t1为空,合并之后就应该是t2
|
||||
@ -328,6 +328,32 @@ class Solution:
|
||||
root1.left = self.mergeTrees(root1.left , root2.left) //左
|
||||
root1.right = self.mergeTrees(root1.right , root2.right) //右
|
||||
return root1 //root1修改了结构和数值
|
||||
|
||||
# 迭代法-覆盖原来的树
|
||||
class Solution:
|
||||
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
|
||||
if not root1: return root2
|
||||
if not root2: return root1
|
||||
# 迭代,将树2覆盖到树1
|
||||
queue1 = [root1]
|
||||
queue2 = [root2]
|
||||
root = root1
|
||||
while queue1 and queue2:
|
||||
root1 = queue1.pop(0)
|
||||
root2 = queue2.pop(0)
|
||||
root1.val += root2.val
|
||||
if not root1.left: # 如果树1左儿子不存在,则覆盖后树1的左儿子为树2的左儿子
|
||||
root1.left = root2.left
|
||||
elif root1.left and root2.left:
|
||||
queue1.append(root1.left)
|
||||
queue2.append(root2.left)
|
||||
|
||||
if not root1.right: # 同理,处理右儿子
|
||||
root1.right = root2.right
|
||||
elif root1.right and root2.right:
|
||||
queue1.append(root1.right)
|
||||
queue2.append(root2.right)
|
||||
return root
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
@ -211,7 +211,24 @@ Java:
|
||||
}
|
||||
```
|
||||
Python:
|
||||
|
||||
``` Python3
|
||||
class Solution:
|
||||
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
|
||||
answer = [0]*len(temperatures)
|
||||
stack = [0]
|
||||
for i in range(1,len(temperatures)):
|
||||
# 情况一和情况二
|
||||
if temperatures[i]<=temperatures[stack[-1]]:
|
||||
stack.append(i)
|
||||
# 情况三
|
||||
else:
|
||||
while len(stack) != 0 and temperatures[i]>temperatures[stack[-1]]:
|
||||
answer[stack[-1]]=i-stack[-1]
|
||||
stack.pop()
|
||||
stack.append(i)
|
||||
|
||||
return answer
|
||||
```
|
||||
Go:
|
||||
|
||||
> 暴力法
|
||||
|
||||
@ -99,10 +99,17 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
|
||||
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
代码如下:
|
||||
```
|
||||
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
|
||||
|
||||
当j >= weight[0]是,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
|
||||
|
||||
代码初始化如下:
|
||||
```
|
||||
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。
|
||||
dp[0][j] = 0;
|
||||
}
|
||||
// 正序遍历
|
||||
for (int j = weight[0]; j <= bagWeight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
@ -116,14 +123,11 @@ for (int j = weight[0]; j <= bagWeight; j++) {
|
||||
|
||||
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
|
||||
|
||||
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是又左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
|
||||
|
||||
dp[i][j]在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,因为0就是最小的了,不会影响取最大价值的结果。
|
||||
初始-1,初始-2,初始100,都可以!
|
||||
|
||||
如果题目给的价值有负数,那么非0下标就要初始化为负无穷了。例如:一个物品的价值是-2,但对应的位置依然初始化为0,那么取最大值的时候,就会取0而不是-2了,所以要初始化为负无穷。
|
||||
|
||||
而背包问题的物品价值都是正整数,所以初始化为0,就可以了。
|
||||
|
||||
**这样才能让dp数组在递归公式的过程中取最大的价值,而不是被初始值覆盖了**。
|
||||
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
|
||||
|
||||
如图:
|
||||
|
||||
@ -159,7 +163,7 @@ for (int j = weight[0]; j <= bagWeight; j++) {
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
|
||||
}
|
||||
|
||||
@ -176,9 +176,48 @@ int main() {
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
```java
|
||||
//先遍历物品,再遍历背包
|
||||
private static void testCompletePack(){
|
||||
int[] weight = {1, 3, 4};
|
||||
int[] value = {15, 20, 30};
|
||||
int bagWeight = 4;
|
||||
int[] dp = new int[bagWeight + 1];
|
||||
for (int i = 0; i < weight.length; i++){
|
||||
for (int j = 1; j <= bagWeight; j++){
|
||||
if (j - weight[i] >= 0){
|
||||
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
for (int maxValue : dp){
|
||||
System.out.println(maxValue + " ");
|
||||
}
|
||||
}
|
||||
|
||||
//先遍历背包,再遍历物品
|
||||
private static void testCompletePackAnotherWay(){
|
||||
int[] weight = {1, 3, 4};
|
||||
int[] value = {15, 20, 30};
|
||||
int bagWeight = 4;
|
||||
int[] dp = new int[bagWeight + 1];
|
||||
for (int i = 1; i <= bagWeight; i++){
|
||||
for (int j = 0; j < weight.length; j++){
|
||||
if (i - weight[j] >= 0){
|
||||
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
|
||||
}
|
||||
}
|
||||
}
|
||||
for (int maxValue : dp){
|
||||
System.out.println(maxValue + " ");
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
```python3
|
||||
|
||||
Reference in New Issue
Block a user