algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-09 03:34:02 +08:00
Code Issues Packages Projects Releases Wiki Activity

优化原题解，添加部分题目

Browse Source
This commit is contained in:
programmercarl
2022-07-20 09:45:11 +08:00
parent 1ca56dd472
commit d4f89d1b0e
27 changed files with 896 additions and 206 deletions
Download Patch File Download Diff File Expand all files Collapse all files

82
problems/0001.两数之和.md
View File

@ -24,7 +24,9 @@
## 思路
很明显暴力的解法是两层for循环查找，时间复杂度是$O(n^2)$。
建议看一下我录的这期视频：[梦开始的地方，Leetcode：1.两数之和](https://www.bilibili.com/video/BV1aT41177mK)，结合本题解来学习，事半功倍。
很明显暴力的解法是两层for循环查找，时间复杂度是O(n^2)。
建议大家做这道题目之前，先做一下这两道
* [242. 有效的字母异位词](https://www.programmercarl.com/0242.有效的字母异位词.html)
@ -32,7 +34,16 @@
[242. 有效的字母异位词](https://www.programmercarl.com/0242.有效的字母异位词.html) 这道题目是用数组作为哈希表来解决哈希问题，[349. 两个数组的交集](https://www.programmercarl.com/0349.两个数组的交集.html)这道题目是通过set作为哈希表来解决哈希问题。
本题呢，则要使用map，那么来看一下使用数组和set来做哈希法的局限。
首先我在强调一下 **什么时候使用哈希法**，当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。
本题呢，我就需要一个集合来存放我们遍历过的元素，然后在遍历数组的时候去询问这个集合，某元素是否遍历过，也就是 是否出现在这个集合。
那么我们就应该想到使用哈希法了。
因为本地，我们不仅要知道元素有没有遍历过，还有知道这个元素对应的下标，**需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适**。
再来看一下使用数组和set来做哈希法的局限。
* 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
* set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。
@ -43,20 +54,38 @@ C++中map，有三种类型：
|映射 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率|
|---|---| --- |---| --- | --- | ---|
|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | $O(\log n)$|$O(\log n)$ |
|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|$O(\log n)$ |$O(\log n)$ |
|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |$O(1)$ | $O(1)$|
|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | O(log n)|O(log n) |
|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|O(log n) |O(log n) |
|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |O(1) | O(1)|
std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。
同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。 更多哈希表的理论知识请看[关于哈希表，你该了解这些！](https://www.programmercarl.com/哈希表理论基础.html)。
**这道题目中并不需要key有序，选择std::unordered_map 效率更高！**
**这道题目中并不需要key有序，选择std::unordered_map 效率更高！** 使用其他语言的录友注意了解一下自己所用语言的数据结构就行。
解题思路动画如下：
接下来需要明确两点：
![](https://code-thinking.cdn.bcebos.com/gifs/1.两数之和.gif)
* **map用来做什么**
* **map中key和value分别表示什么**
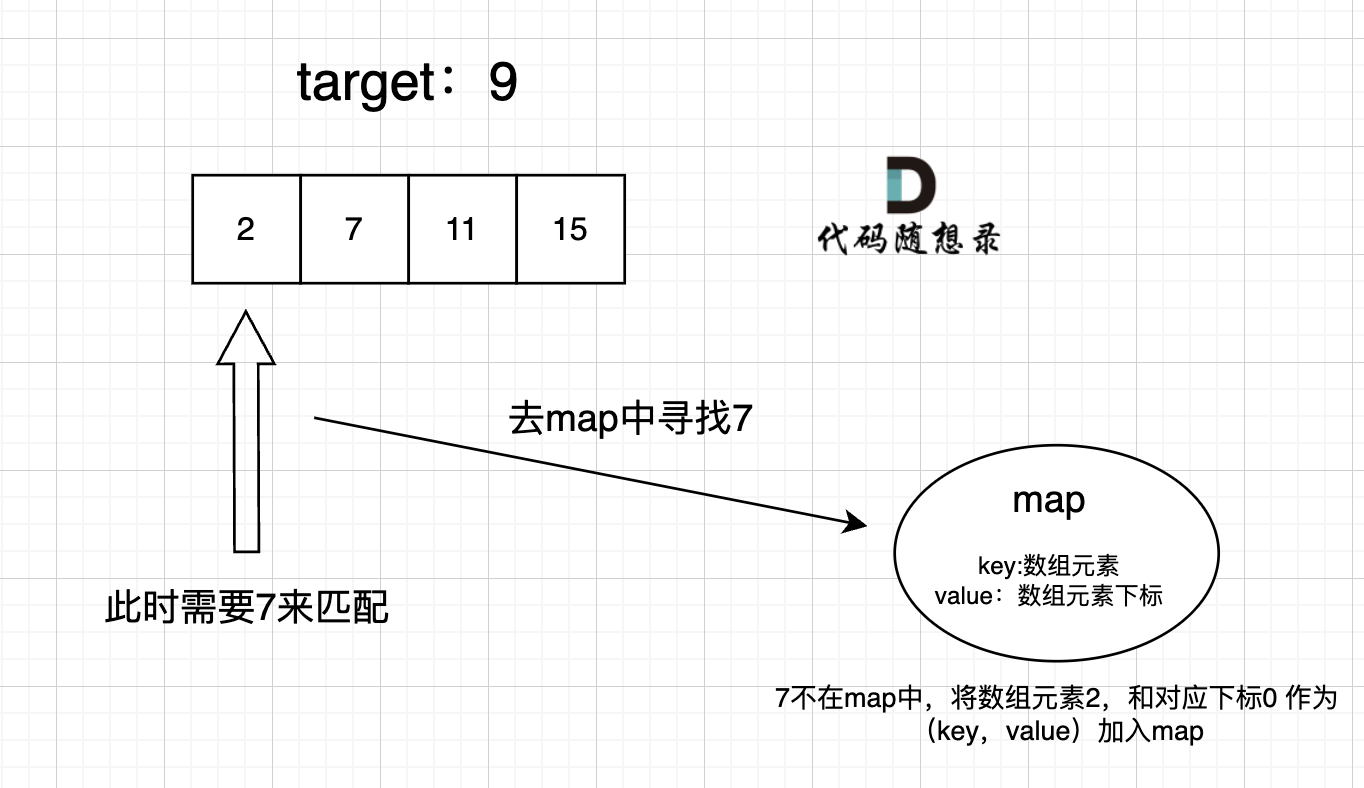
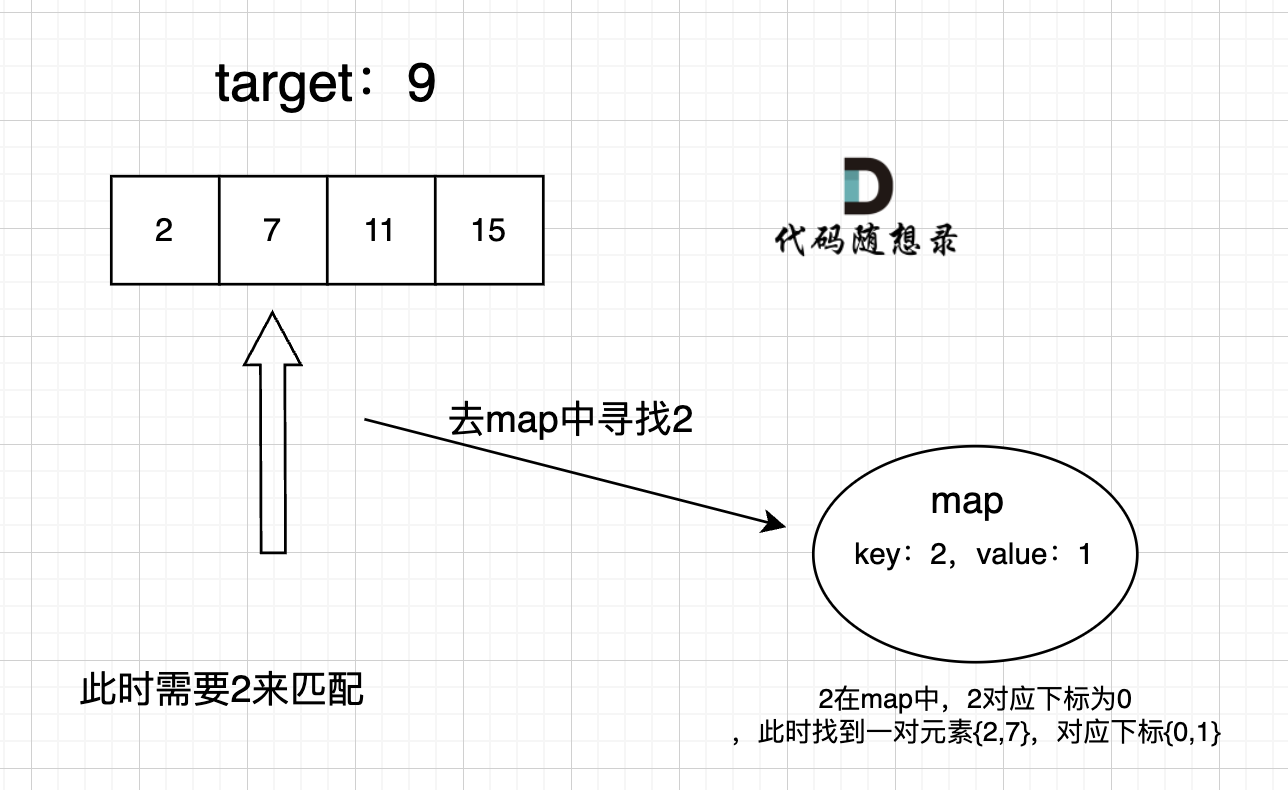
map目的用来存放我们访问过的元素，因为遍历数组的时候，需要记录我们之前遍历过哪些元素和对应的下表，这样才能找到与当前元素相匹配的（也就是相加等于target）
接下来是map中key和value分别表示什么。
这道题 我们需要 给出一个元素，判断这个元素是否出现过，如果出现过，返回这个元素的下标。
那么判断元素是否出现，这个元素就要作为key，所以数组中的元素作为key，有key对应的就是value，value用来存下标。
所以 map中的存储结构为 {key：数据元素，value：数组元素对应的下表}。
在遍历数组的时候，只需要向map去查询是否有和目前遍历元素比配的数值，如果有，就找到的匹配对，如果没有，就把目前遍历的元素放进map中，因为map存放的就是我们访问过的元素。
过程如下：
![过程一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220711202638.png)
![过程二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220711202708.png)
C++代码：
@ -66,10 +95,12 @@ public:
vector<int> twoSum(vector<int>& nums, int target) {
std::unordered_map <int,int> map;
for(int i = 0; i < nums.size(); i++) {
// 遍历当前元素，并在map中寻找是否有匹配的key
auto iter = map.find(target - nums[i]);
if(iter != map.end()) {
return {iter->second, i};
}
// 如果没找到匹配对，就把访问过的元素和下标加入到map中
map.insert(pair<int, int>(nums[i], i));
}
return {};
@ -77,7 +108,18 @@ public:
};
```
## 总结
本题其实有四个重点：
* 为什么会想到用哈希表
* 哈希表为什么用map
* 本题map是用来存什么的
* map中的key和value用来存什么的
把这四点想清楚了，本题才算是理解透彻了。
很多录友把这道题目 通过了，但都没想清楚map是用来做什么的，以至于对代码的理解其实是 一知半解的。
## 其他语言版本
@ -250,30 +292,6 @@ func twoSum(_ nums: [Int], _ target: Int) -> [Int] {
}
```
PHP:
```php
class Solution {
/**
* @param Integer[] $nums
* @param Integer $target
* @return Integer[]
*/
function twoSum($nums, $target) {
if (count($nums) == 0) {
return [];
}
$table = [];
for ($i = 0; $i < count($nums); $i++) {
$temp = $target - $nums[$i];
if (isset($table[$temp])) {
return [$table[$temp], $i];
}
$table[$nums[$i]] = $i;
}
return [];
}
}
```
Scala:
```scala

96
problems/0015.三数之和.md
View File

@ -39,7 +39,7 @@
去重的过程不好处理，有很多小细节，如果在面试中很难想到位。
时间复杂度可以做到$O(n^2)$，但还是比较费时的，因为不好做剪枝操作。
时间复杂度可以做到O(n^2)，但还是比较费时的，因为不好做剪枝操作。
大家可以尝试使用哈希法写一写，就知道其困难的程度了。
@ -85,7 +85,7 @@ public:
**其实这道题目使用哈希法并不十分合适**，因为在去重的操作中有很多细节需要注意，在面试中很难直接写出没有bug的代码。
而且使用哈希法 在使用两层for循环的时候，能做的剪枝操作很有限，虽然时间复杂度是$O(n^2)$，也是可以在leetcode上通过，但是程序的执行时间依然比较长 。
而且使用哈希法 在使用两层for循环的时候，能做的剪枝操作很有限，虽然时间复杂度是O(n^2)，也是可以在leetcode上通过，但是程序的执行时间依然比较长 。
接下来我来介绍另一个解法：双指针法，**这道题目使用双指针法 要比哈希法高效一些**，那么来讲解一下具体实现的思路。
@ -101,7 +101,7 @@ public:
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。
时间复杂度：$O(n^2)$。
时间复杂度：O(n^2)。
C++代码代码如下：
@ -118,13 +118,13 @@ public:
if (nums[i] > 0) {
return result;
}
// 错误去重方法，将会漏掉-1,-1,2 这种情况
// 错误去重a方法，将会漏掉-1,-1,2 这种情况
/*
if (nums[i] == nums[i + 1]) {
continue;
}
*/
// 正确去重方法
// 正确去重a方法
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
@ -136,17 +136,11 @@ public:
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
*/
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
// 当前元素不合适了，可以去重
while (left < right && nums[right] == nums[right + 1]) right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
// 不合适，去重
while (left < right && nums[left] == nums[left - 1]) left++;
} else {
if (nums[i] + nums[left] + nums[right] > 0) right--;
else if (nums[i] + nums[left] + nums[right] < 0) left++;
else {
result.push_back(vector<int>{nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个三元组之后
// 去重逻辑应该放在找到一个三元组之后，对b 和 c去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
@ -162,6 +156,78 @@ public:
};
```
## 去重逻辑的思考
### a的去重
说道去重，其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i]，nums[left]，nums[right]
a 如果重复了怎么办，a是nums里遍历的元素，那么应该直接跳过去。
但这里有一个问题，是判断 nums[i] 与 nums[i + 1]是否相同，还是判断 nums[i] 与 nums[i-1] 是否相同。
有同学可能想，这不都一样吗。
其实不一样！
都是和 nums[i]进行比较，是比较它的前一个，还是比较他的后一个。
如果我们的写法是 这样：
```C++
if (nums[i] == nums[i + 1]) { // 去重操作
continue;
}
```
那就我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据，当遍历到第一个-1 的时候，判断 下一个也是-1，那这组数据就pass了。
**我们要做的是 不能有重复的三元组，但三元组内的元素是可以重复的！**
所以这里是有两个重复的维度。
那么应该这么写：
```C++
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
```
这么写就是当前使用 nums[i]，我们判断前一位是不是一样的元素，在看 {-1, -1 ,2} 这组数据，当遍历到 第一个 -1 的时候，只要前一位没有-1，那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。
这是一个非常细节的思考过程。
### b与c的去重
很多同学写本题的时候，去重的逻辑多加了 对right 和left 的去重：（代码中注释部分）
```C++
while (right > left) {
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
// 去重 right
while (left < right && nums[right] == nums[right + 1]) right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
// 去重 left
while (left < right && nums[left] == nums[left - 1]) left++;
} else {
}
}
```
但细想一下，这种去重其实对提升程序运行效率是没有帮助的。
拿right去重为例，即使不加这个去重逻辑，依然根据 `while (right > left) ` 和 `if (nums[i] + nums[left] + nums[right] > 0)` 去完成right-- 的操作。
多加了 ` while (left < right && nums[right] == nums[right + 1]) right--;` 这一行代码，其实就是把 需要执行的逻辑提前执行了，但并没有减少 判断的逻辑。
最直白的思考过程，就是right还是一个数一个数的减下去的，所以在哪里减的都是一样的。
所以这种去重 是可以不加的。 仅仅是 把去重的逻辑提前了而已。
# 思考题

35
problems/0018.四数之和.md
View File

@ -35,11 +35,11 @@
[15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下标作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是$O(n^2)$，四数之和的时间复杂度是$O(n^3)$ 。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
那么一样的道理，五数之和、六数之和等等都采用这种解法。
对于[15.三数之和](https://programmercarl.com/0015.三数之和.html)双指针法就是将原本暴力$O(n^3)$的解法，降为$O(n^2)$的解法，四数之和的双指针解法就是将原本暴力$O(n^4)$的解法，降为$O(n^3)$的解法。
对于[15.三数之和](https://programmercarl.com/0015.三数之和.html)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。
之前我们讲过哈希表的经典题目：[454.四数相加II](https://programmercarl.com/0454.四数相加II.html)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
@ -47,14 +47,13 @@
我们来回顾一下，几道题目使用了双指针法。
双指针法将时间复杂度：$O(n^2)$的解法优化为 $O(n)$的解法。也就是降一个数量级，题目如下：
双指针法将时间复杂度：O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下：
* [27.移除元素](https://programmercarl.com/0027.移除元素.html)
* [15.三数之和](https://programmercarl.com/0015.三数之和.html)
* [18.四数之和](https://programmercarl.com/0018.四数之和.html)
操作链表：
链表相关双指针题目：
* [206.反转链表](https://programmercarl.com/0206.翻转链表.html)
* [19.删除链表的倒数第N个节点](https://programmercarl.com/0019.删除链表的倒数第N个节点.html)
@ -72,21 +71,21 @@ public:
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int k = 0; k < nums.size(); k++) {
// 剪枝处理
if (nums[k] > target && (nums[k] >= 0 || target >= 0)) {
// 剪枝处理
if (nums[k] > target && nums[k] >= 0 && target >= 0) {
break; // 这里使用break，统一通过最后的return返回
}
// 去重
// 对nums[k]去重
if (k > 0 && nums[k] == nums[k - 1]) {
continue;
}
for (int i = k + 1; i < nums.size(); i++) {
// 2级剪枝处理
if (nums[k] + nums[i] > target && (nums[k] + nums[i] >= 0 || target >= 0)) {
break;
}
// 2级剪枝处理
if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0 && target >= 0) {
break;
}
// 正确去重方法
// 对nums[i]去重
if (i > k + 1 && nums[i] == nums[i - 1]) {
continue;
}
@ -94,18 +93,14 @@ public:
int right = nums.size() - 1;
while (right > left) {
// nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
if (nums[k] + nums[i] > target - (nums[left] + nums[right])) {
if ((long) nums[k] + nums[i] + nums[left] + nums[right] > target) {
right--;
// 当前元素不合适了，可以去重
while (left < right && nums[right] == nums[right + 1]) right--;
// nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出
} else if (nums[k] + nums[i] < target - (nums[left] + nums[right])) {
} else if ((long) nums[k] + nums[i] + nums[left] + nums[right] < target) {
left++;
// 不合适，去重
while (left < right && nums[left] == nums[left - 1]) left++;
} else {
result.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个四元组之后
// 对nums[left]和nums[right]去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;

6
problems/0024.两两交换链表中的节点.md
View File

@ -18,6 +18,8 @@
## 思路
针对本题重点难点，我录制了B站讲解视频，[帮你把链表细节学清楚！ | LeetCode：24. 两两交换链表中的节点](https://www.bilibili.com/video/BV1YT411g7br)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
这道题目正常模拟就可以了。
建议使用虚拟头结点，这样会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。
@ -63,8 +65,8 @@ public:
};
```
* 时间复杂度：$O(n)$
* 空间复杂度：$O(1)$
* 时间复杂度：O(n)
* 空间复杂度：O(1)
## 拓展

2
problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
View File

@ -7,6 +7,8 @@
# 34. 在排序数组中查找元素的第一个和最后一个位置
[题目链接](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。

3
problems/0056.合并区间.md
View File

@ -22,9 +22,6 @@
* 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
* 注意：输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
提示：
* intervals[i][0] <= intervals[i][1]
## 思路

4
problems/0122.买卖股票的最佳时机II.md
View File

@ -91,8 +91,8 @@ public:
};
```
* 时间复杂度：$O(n)$
* 空间复杂度：$O(1)$
* 时间复杂度：O(n)
* 空间复杂度：O(1)
### 动态规划

2
problems/0142.环形链表II.md
View File

@ -24,6 +24,8 @@
## 思路
为了易于大家理解，我录制讲解视频：[B站：把环形链表讲清楚！ ](https://www.bilibili.com/video/BV1if4y1d7ob)。结合视频在看本篇题解，事半功倍。
这道题目，不仅考察对链表的操作，而且还需要一些数学运算。
主要考察两知识点：

47
problems/0202.快乐数.md
View File

@ -338,53 +338,6 @@ static inline int calcSquareSum(int num) {
return sum;
}
#define HASH_TABLE_SIZE (32)
bool isHappy(int n){
int sum = n;
int index = 0;
bool bHappy = false;
bool bExit = false;
/* allocate the memory for hash table with chaining method*/
HashNode ** hashTable = (HashNode **)calloc(HASH_TABLE_SIZE, sizeof(HashNode));
while(bExit == false) {
/* check if n has been calculated */
index = hash(n, HASH_TABLE_SIZE);
HashNode ** p = hashTable + index;
while((*p) && (bExit == false)) {
/* Check if this num was calculated, if yes, this will be endless loop */
if((*p)->key == n) {
bHappy = false;
bExit = true;
}
/* move to next node of the same index */
p = &((*p)->next);
}
/* put n intot hash table */
HashNode * newNode = (HashNode *)malloc(sizeof(HashNode));
newNode->key = n;
newNode->next = NULL;
*p = newNode;
sum = calcSquareSum(n);
if(sum == 1) {
bHappy = true;
bExit = true;
}
else {
n = sum;
}
}
return bHappy;
}
```
Scala:
```scala

2
problems/0206.翻转链表.md
View File

@ -19,6 +19,8 @@
# 思路
本题我录制了B站视频，[帮你拿下反转链表 | LeetCode：206.反转链表](https://www.bilibili.com/video/BV1nB4y1i7eL)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
如果再定义一个新的链表，实现链表元素的反转，其实这是对内存空间的浪费。
其实只需要改变链表的next指针的指向，直接将链表反转 ，而不用重新定义一个新的链表，如图所示:

2
problems/0209.长度最小的子数组.md
View File

@ -19,7 +19,7 @@
# 思路
为了易于大家理解，我特意录制了[拿下滑动窗口！ | LeetCode 209 长度最小的子数组](https://www.bilibili.com/video/BV1tZ4y1q7XE)
为了易于大家理解，我特意录制了B站视频[拿下滑动窗口！ | LeetCode 209 长度最小的子数组](https://www.bilibili.com/video/BV1tZ4y1q7XE)
## 暴力解法

2
problems/0216.组合总和III.md
View File

@ -212,7 +212,7 @@ public:
# 总结
开篇就介绍了本题与[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)的区别，相对来说加了元素总和的限制，如果做完[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)再做本题在合适不过。
开篇就介绍了本题与[77.组合](https://programmercarl.com/0077.组合.html)的区别，相对来说加了元素总和的限制，如果做完[77.组合](https://programmercarl.com/0077.组合.html)再做本题在合适不过。
分析完区别，依然把问题抽象为树形结构，按照回溯三部曲进行讲解，最后给出剪枝的优化。

2
problems/0242.有效的字母异位词.md
View File

@ -27,6 +27,8 @@
## 思路
本题B站视频讲解版：[学透哈希表，数组使用有技巧！Leetcode：242.有效的字母异位词](https://www.bilibili.com/video/BV1YG411p7BA)
先看暴力的解法，两层for循环，同时还要记录字符是否重复出现，很明显时间复杂度是 O(n^2)。
暴力的方法这里就不做介绍了，直接看一下有没有更优的方式。

37
problems/0349.两个数组的交集.md
View File

@ -24,6 +24,8 @@
## 思路
关于本题，我录制了讲解视频：[学透哈希表，set使用有技巧！Leetcode：349. 两个数组的交集](https://www.bilibili.com/video/BV1ba411S7wu)，看视频配合题解，事半功倍。
这道题目，主要要学会使用一种哈希数据结构：unordered_set，这个数据结构可以解决很多类似的问题。
注意题目特意说明：**输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的， 同时可以不考虑输出结果的顺序**
@ -48,7 +50,8 @@ std::set和std::multiset底层实现都是红黑树，std::unordered_set的底
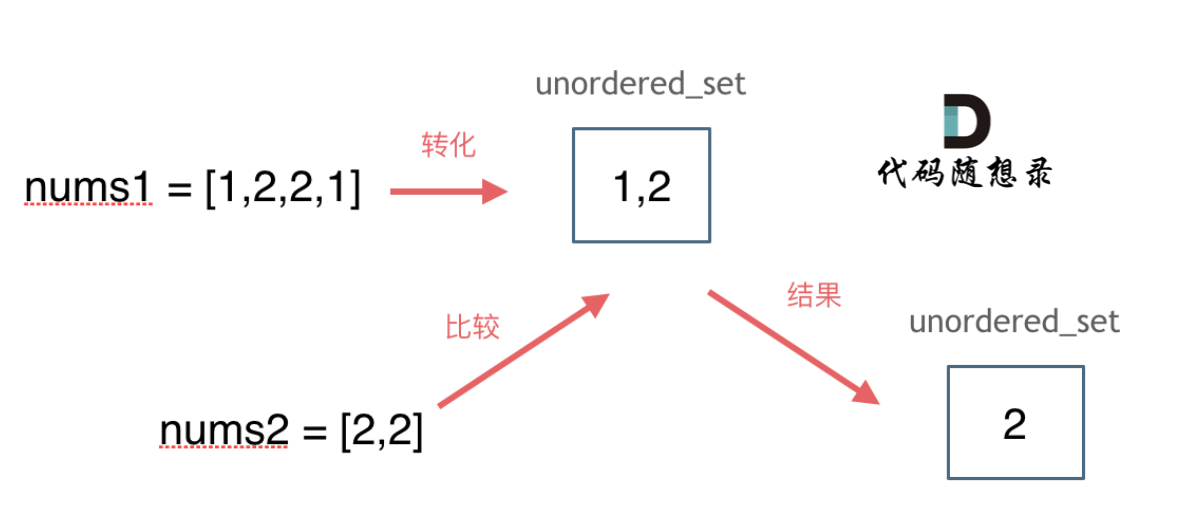
思路如图所示：
![set哈希法](https://img-blog.csdnimg.cn/2020080918570417.png)
![set哈希法](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707173513.png)
C++代码如下：
@ -56,7 +59,7 @@ C++代码如下：
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果
unordered_set<int> result_set; // 存放结果，之所以用set是为了给结果集去重
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 发现nums2的元素 在nums_set里又出现过
@ -77,6 +80,36 @@ public:
不要小瞧 这个耗时，在数据量大的情况，差距是很明显的。
## 后记
本题后面 力扣改了 题目描述 和 后台测试数据，增添了 数值范围：
* 1 <= nums1.length, nums2.length <= 1000
* 0 <= nums1[i], nums2[i] <= 1000
所以就可以 使用数组来做哈希表了， 因为数组都是 1000以内的。
对应C++代码如下：
```c++
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果，之所以用set是为了给结果集去重
int hash[1005] = {0}; // 默认数值为0
for (int num : nums1) { // nums1中出现的字母在hash数组中做记录
hash[num] = 1;
}
for (int num : nums2) { // nums2中出现话，result记录
if (hash[num] == 1) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};
```
## 其他语言版本

12
problems/0376.摆动序列.md
View File

@ -88,8 +88,8 @@ public:
};
```
* 时间复杂度：$O(n)$
* 空间复杂度：$O(1)$
* 时间复杂度：O(n)
* 空间复杂度：O(1)
## 思路2（动态规划）
@ -138,8 +138,8 @@ public:
};
```
* 时间复杂度：$O(n^2)$
* 空间复杂度：$O(n)$
* 时间复杂度：O(n^2)
* 空间复杂度：O(n)
**进阶**
@ -149,9 +149,9 @@ public:
* 每次更新`dp[i][1]`，则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
* 则dp转移方程中就没有必要j从0遍历到i-1，可以直接在线段树中查询指定区间的值即可。
时间复杂度：$O(n\log n)$
时间复杂度：O(nlog n)
空间复杂度：$O(n)$
空间复杂度：O(n)
## 总结

6
problems/0392.判断子序列.md
View File

@ -31,7 +31,7 @@
## 思路
（这道题可以用双指针的思路来实现，时间复杂度就是$O(n)$）
（这道题可以用双指针的思路来实现，时间复杂度就是O(n)）
这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。
@ -122,8 +122,8 @@ public:
};
```
* 时间复杂度：$O(n × m)$
* 空间复杂度：$O(n × m)$
* 时间复杂度：O(n × m)
* 空间复杂度：O(n × m)
## 总结

13
problems/0454.四数相加II.md
View File

@ -18,14 +18,19 @@
**例如:**
输入:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]
* A = [ 1, 2]
* B = [-2,-1]
* C = [-1, 2]
* D = [ 0, 2]
输出:
2
**解释:**
两个元组如下:
1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

10
problems/0647.回文子串.md
View File

@ -32,7 +32,7 @@
两层for循环，遍历区间起始位置和终止位置，然后判断这个区间是不是回文。
时间复杂度：$O(n^3)$
时间复杂度：O(n^3)
## 动态规划
@ -171,8 +171,8 @@ public:
};
```
* 时间复杂度：$O(n^2)$
* 空间复杂度：$O(n^2)$
* 时间复杂度：O(n^2)
* 空间复杂度：O(n^2)
## 双指针法
@ -213,8 +213,8 @@ public:
};
```
* 时间复杂度：$O(n^2)$
* 空间复杂度：$O(1)$
* 时间复杂度：O(n^2)
* 空间复杂度：O(1)
## 其他语言版本

2
problems/0704.二分查找.md
View File

@ -36,7 +36,7 @@
## 思路
为了易于大家理解，我还录制了视频，可以看这里：[手把手带你撕出正确的二分法](https://www.bilibili.com/video/BV1fA4y1o715)
为了易于大家理解，我还录制了视频，可以看这里：[B站：手把手带你撕出正确的二分法](https://www.bilibili.com/video/BV1fA4y1o715)
**这道题目的前提是数组为有序数组**，同时题目还强调**数组中无重复元素**，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

2
problems/0707.设计链表.md
View File

@ -26,6 +26,8 @@
# 思路
为了方便大家理解，我特意录制了视频：[帮你把链表操作学个通透！LeetCode：707.设计链表](https://www.bilibili.com/video/BV1FU4y1X7WD)，结合视频在看本题解，事半功倍。
如果对链表的基础知识还不太懂，可以看这篇文章：[关于链表，你该了解这些！](https://programmercarl.com/链表理论基础.html)
如果对链表的虚拟头结点不清楚，可以看这篇文章：[链表：听说用虚拟头节点会方便很多？](https://programmercarl.com/0203.移除链表元素.html)

2
problems/0718.最长重复子数组.md
View File

@ -31,7 +31,7 @@ B: [3,2,1,4,7]
1. 确定dp数组（dp table）以及下标的含义
dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。
dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （**特别注意**： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ）
此时细心的同学应该发现，那dp[0][0]是什么含义呢？总不能是以下标-1为结尾的A数组吧。

296
problems/0797.所有可能的路径.md Normal file
View File

@ -0,0 +1,296 @@
看一下 算法4，深搜是怎么讲的
# 797.所有可能的路径
本题是一道 原汁原味的 深度优先搜索（dfs）模板题，那么用这道题目 来讲解 深搜最合适不过了。
接下来给大家详细讲解dfs：
## dfs 与 bfs 区别
先来了解dfs的过程，很多录友可能对dfs（深度优先搜索），bfs（广度优先搜索）分不清。
先给大家说一下两者大概的区别：
* dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，在换方向（换方向的过程就涉及到了回溯）。
* bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。
当然以上讲的是，大体可以这么理解，接下来 我们详细讲解dfs，（bfs在用单独一篇文章详细讲解）
## dfs 搜索过程
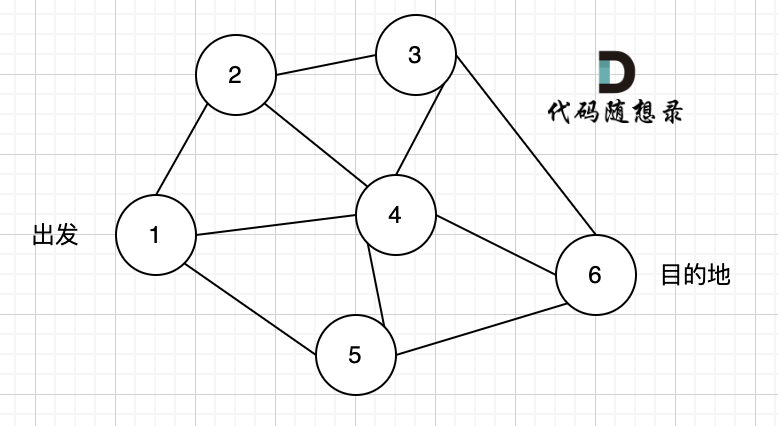
上面说道dfs是可一个方向搜，不到黄河不回头。 那么我们来举一个例子。
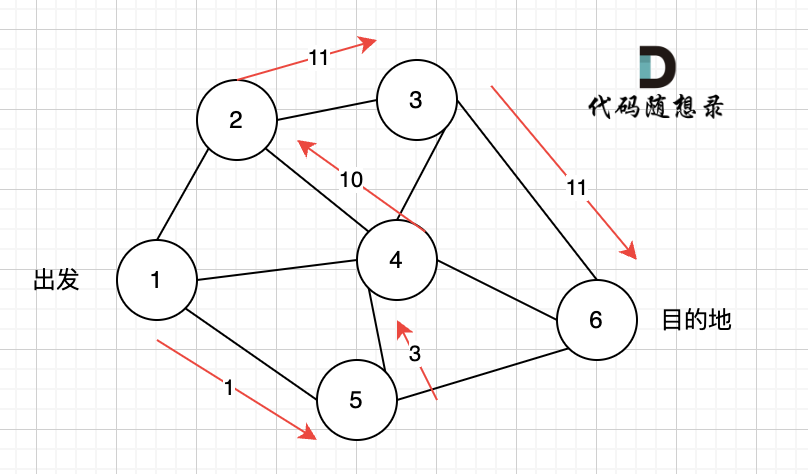
如图一，是一个无向图，我们要搜索从节点1到节点6的所有路径。
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707093643.png)
那么dfs搜索的第一条路径是这样的： （假设第一次延默认方向，就找到了节点6），图二
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707093807.png)
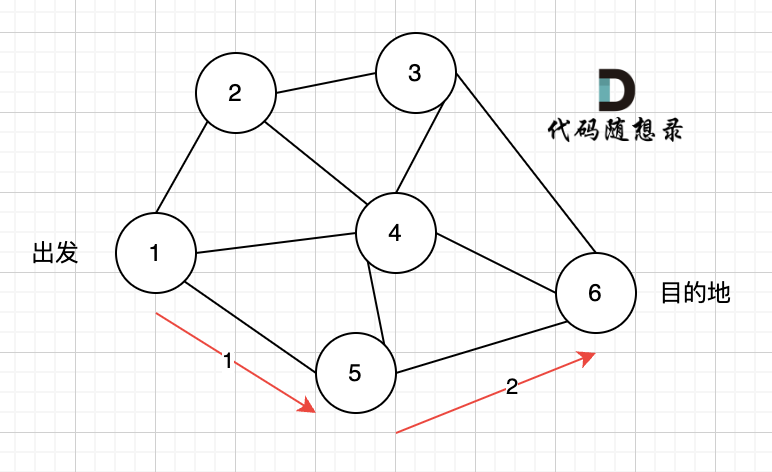
此时我们找到了节点6，（遇到黄河了，是不是应该回头了），那么应该再去搜索其他方向了。 如图三：
![图三](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094011.png)
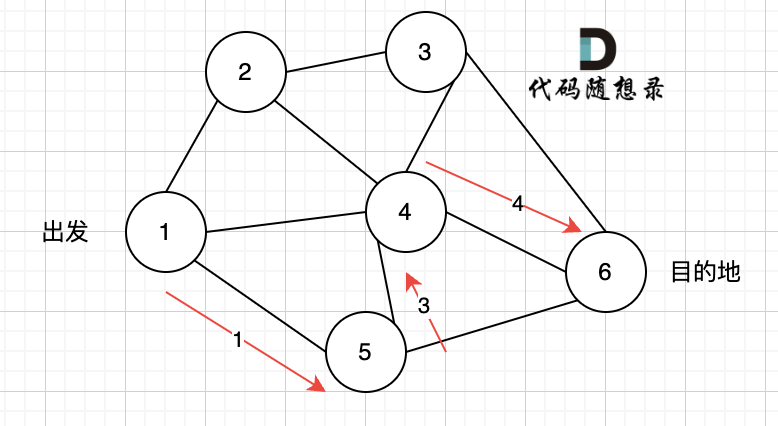
路径2撤销了，改变了方向，走路径3（红色线）， 接着也找到终点6。 那么撤销路径2，改为路径3，在dfs中其实就是回溯的过程（这一点很重要，很多录友，都不理解dfs代码中回溯是用来干什么的）
又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图四中，路径4撤销（回溯的过程），改为路径5。
![图四](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094322.png)
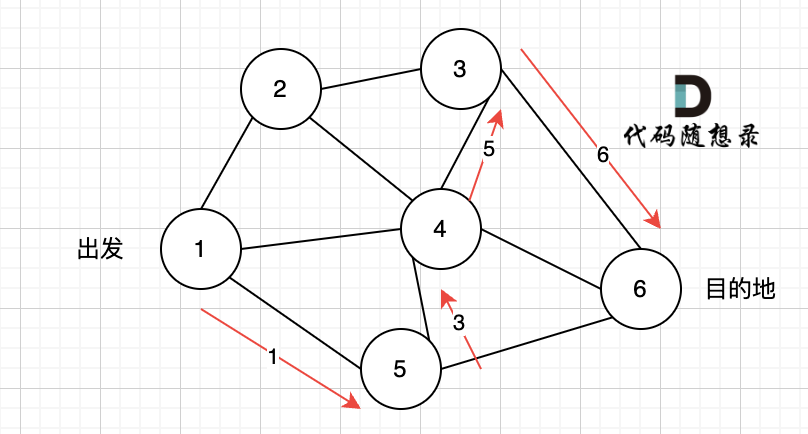
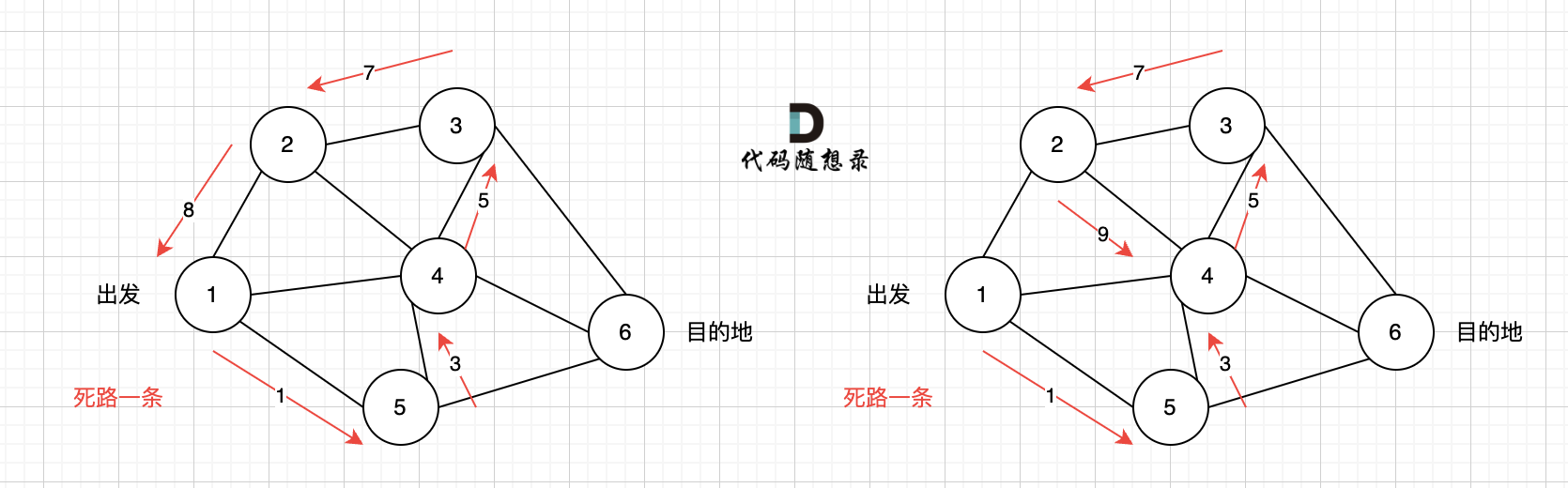
又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图五，路径6撤销（回溯的过程），改为路径7，路径8 和 路径7，路径9， 结果发现死路一条，都走到了自己走过的节点。
![图五](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094813.png)
那么节点2所连接路径和节点3所链接的路径 都走过了，撤销路径只能向上回退，去选择撤销当初节点4的选择，也就是撤销路径5，改为路径10 。 如图图六：
![图六](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707095232.png)
上图演示中，其实我并没有把 所有的 从节点1 到节点6的dfs（深度优先搜索）的过程都画出来，那样太冗余了，但 已经把dfs 关键的地方都涉及到了，关键就两点：
* 搜索方向，是认准一个方向搜，直到碰壁之后在换方向
* 换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程。
## 代码框架
正式因为dfs搜索可一个方向，并需要回溯，所以用递归的方式来实现是最方便的。
很多录友对回溯很陌生，建议先看看码随想录，[回溯算法章节](https://programmercarl.com/回溯算法理论基础.html)。
有递归的地方就有回溯，那么回溯在哪里呢？
就地递归函数的下面，例如如下代码：
```
void dfs(参数) {
处理节点
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
```
可以看到回溯操作就在递归函数的下面，递归和回溯是相辅相成的。
在讲解[二叉树章节](https://programmercarl.com/二叉树理论基础.html)的时候，二叉树的递归法其实就是dfs，而二叉树的迭代法，就是bfs（广度优先搜索）
所以**dfs，bfs其实是基础搜索算法，也广泛应用与其他数据结构与算法中**。
我们在回顾一下[回溯法](https://programmercarl.com/回溯算法理论基础.html)的代码框架：
```
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表); // 递归
回溯，撤销处理结果
}
}
```
回溯算法，其实就是dfs的过程，这里给出dfs的代码框架：
```
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本节点所连接的其他节点) {
处理节点;
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
}
```
可以发现dfs的代码框架和回溯算法的代码框架是差不多的。
下面我在用 深搜三部曲，来解读 dfs的代码框架。
## 深搜三部曲
在 [二叉树递归讲解](https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html)中，给出了递归三部曲。
[回溯算法](https://programmercarl.com/回溯算法理论基础.html)讲解中，给出了 回溯三部曲。
其实深搜也是一样的，深搜三部曲如下：
1. 确认递归函数，参数
```
void dfs(参数)
```
通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。
一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局遍历，避免让我们的函数参数过多。
例如这样：
```
vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)
```
但这种写法看个人习惯，不强求。
2. 确认终止条件
终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。
```
if (终止条件) {
存放结果;
return;
}
```
终止添加不仅是结束本层递归，同时也是我们收获结果的时候。
3. 处理目前搜索节点出发的路径
一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。
```
for (选择：本节点所连接的其他节点) {
处理节点;
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
```
不少录友疑惑的地方，都是 dfs代码框架中for循环里分明已经处理节点了，那么 dfs函数下面 为什么还要撤销的呢。
如图七所示， 路径2 已经走到了 目的地节点6，那么 路径2 是如何撤销，然后改为 路径3呢？ 其实这就是 回溯的过程，撤销路径2，走换下一个方向。
![图七](https://code-thinking-1253855093.file.myqcloud.com/pics/20220708093544.png)
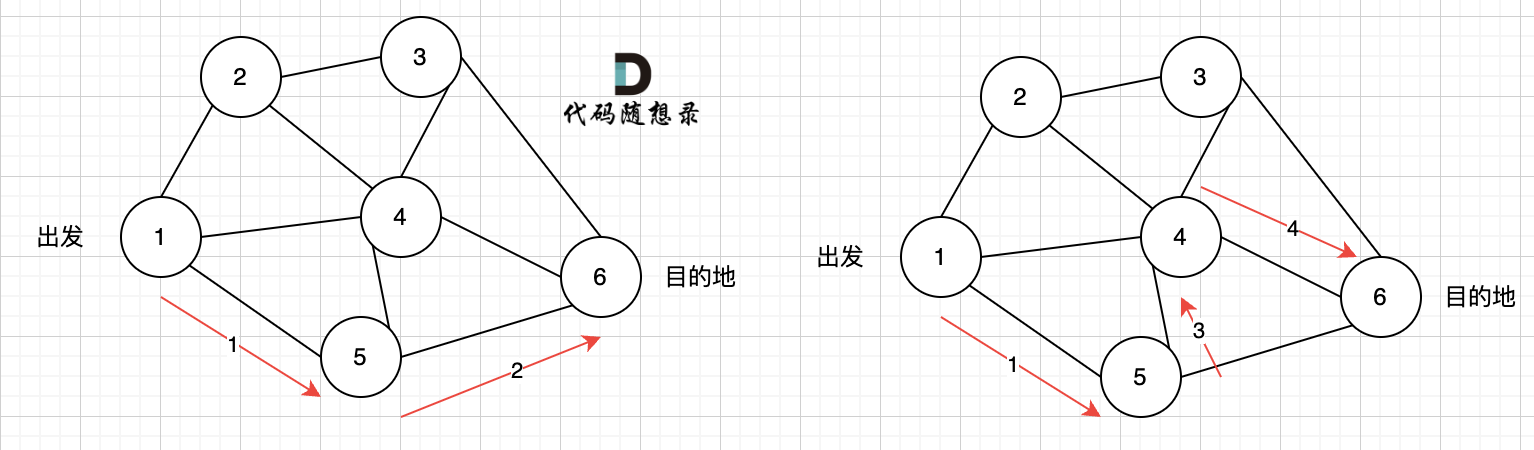
## 总结
我们讲解了，dfs 和 bfs的大体区别（bfs详细过程下篇来讲），dfs的搜索过程以及代码框架。
最后还有 深搜三部曲来解读这份代码框架。
以上如果大家都能理解了，其实搜索的代码就很好写，具体题目套用具体场景就可以了。
## 797. 所有可能的路径
### 思路
1. 确认递归函数，参数
首先我们dfs函数一定要存一个图，用来遍历的，还要存一个目前我们遍历的节点，定义为x
至于 单一路径，和路径集合可以放在全局变量，那么代码是这样的：
```c++
vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 0节点到终点的路径
// x：目前遍历的节点
// graph：存当前的图
void dfs (vector<vector<int>>& graph, int x)
```
2. 确认终止条件
什么时候我们就找到一条路径了？
当目前遍历的节点 为 最后一个节点的时候，就找到了一条，从 出发点到终止点的路径。
当前遍历的节点，我们定义为x，最后一点节点，就是 graph.size() - 1。
所以 但 x 等于 graph.size() - 1 的时候就找到一条有效路径。 代码如下：
```c++
// 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.size() - 1
if (x == graph.size() - 1) { // 找到符合条件的一条路径
result.push_back(path); // 收集有效路径
return;
}
```
3. 处理目前搜索节点出发的路径
接下来是走 当前遍历节点x的下一个节点。
首先是要找到 x节点链接了哪些节点呢？ 遍历方式是这样的：
```c++
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
```
接下来就是将 选中的x所连接的节点，加入到 单一路劲来。
```C++
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
```
当前遍历的节点就是 `graph[x][i]` 了，所以进入下一层递归
```C++
dfs(graph, graph[x][i]); // 进入下一层递归
```
最后就是回溯的过程，撤销本次添加节点的操作。 该过程整体代码：
```C++
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
dfs(graph, graph[x][i]); // 进入下一层递归
path.pop_back(); // 回溯，撤销本节点
}
```
### 本题代码
```c++
class Solution {
private:
vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 0节点到终点的路径
// x：目前遍历的节点
// graph：存当前的图
void dfs (vector<vector<int>>& graph, int x) {
// 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.size() - 1
if (x == graph.size() - 1) { // 找到符合条件的一条路径
result.push_back(path);
return;
}
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
dfs(graph, graph[x][i]); // 进入下一层递归
path.pop_back(); // 回溯，撤销本节点
}
}
public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
path.push_back(0); // 无论什么路径已经是从0节点出发
dfs(graph, 0); // 开始遍历
return result;
}
};
```
## 其他语言版本
### Java
### Python
### Go

229
problems/0841.钥匙和房间.md
View File

@ -31,21 +31,182 @@
* 解释：我们不能进入 2 号房间。
## 思
## 思路
其实这道题的本质就是判断各个房间所连成的有向图，说明不用访问所有的房间。
本题其实给我们是一个有向图， 意识到这是有向图很重要！
如图所示：
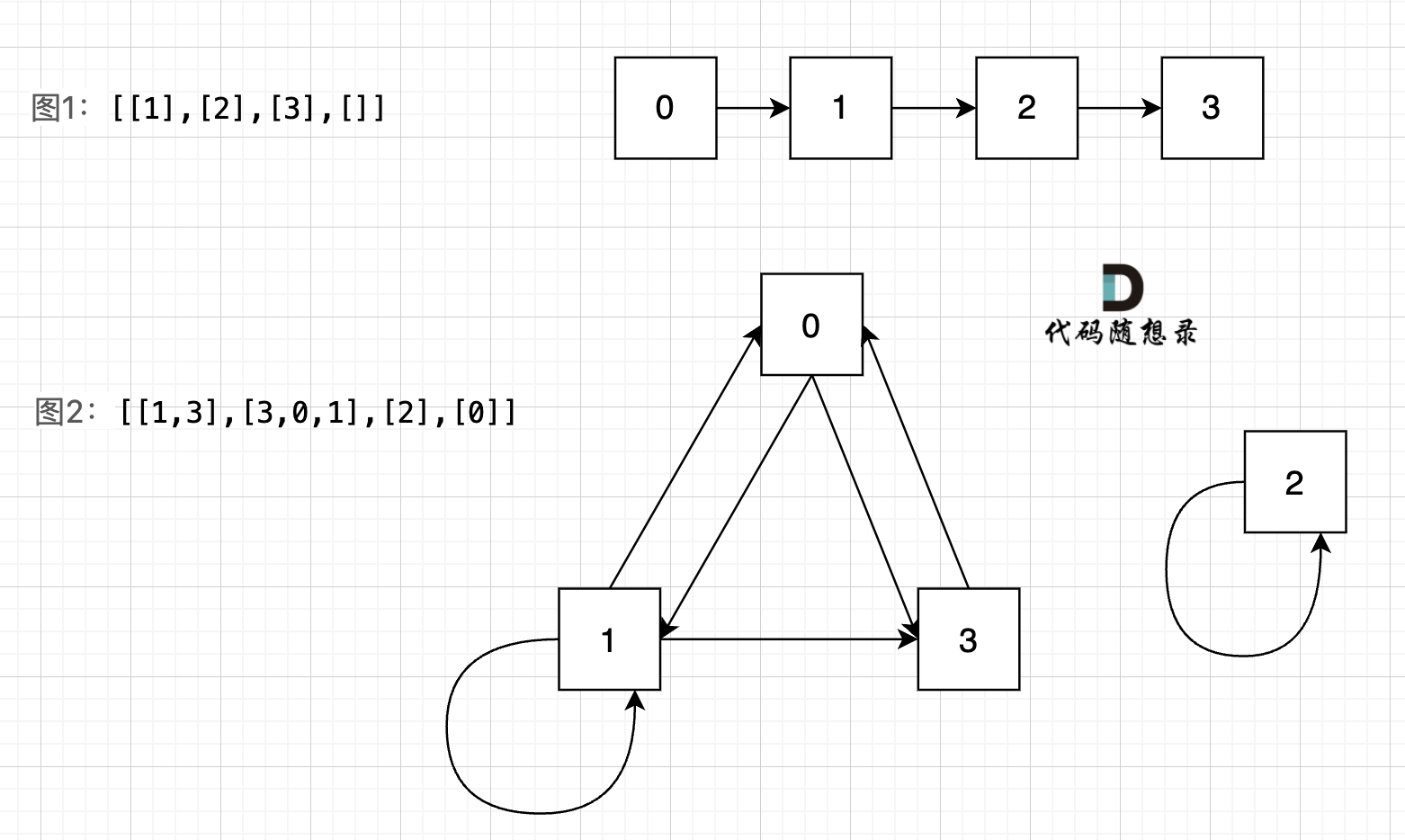
图中给我的两个示例： `[[1],[2],[3],[]]` `[[1,3],[3,0,1],[2],[0]]`，画成对应的图如下：
<img src='https://code-thinking.cdn.bcebos.com/pics/841.钥匙和房间.png' width=600> </img></div>
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220714101414.png)
示例1就可以访问所有的房间，因为通过房间里的key将房间连在了一起。
我们可以看出图1的所有节点都是链接的，而图二中，节点2 是孤立的。
示例2中，就不能访问所有房间，从图中就可以看出，房间2是一个孤岛，我们从0出发，无论怎么遍历，都访问不到房间2。
这就很容易让我们想起岛屿问题，只要发现独立的岛，就是不能进入所有房间。
认清本质问题之后，**使用 广度优先搜索(BFS) 还是 深度优先搜索(DFS) 都是可以的。**
此时也容易想到用并查集的方式去解决。
BFS C++代码代码如下：
**但本题是有向图**，在有向图中，即使所有节点都是链接的，但依然不可能从0出发遍历所有边。
给大家举一个例子：
图3：[[5], [], [1, 3], [5]] ，如图：
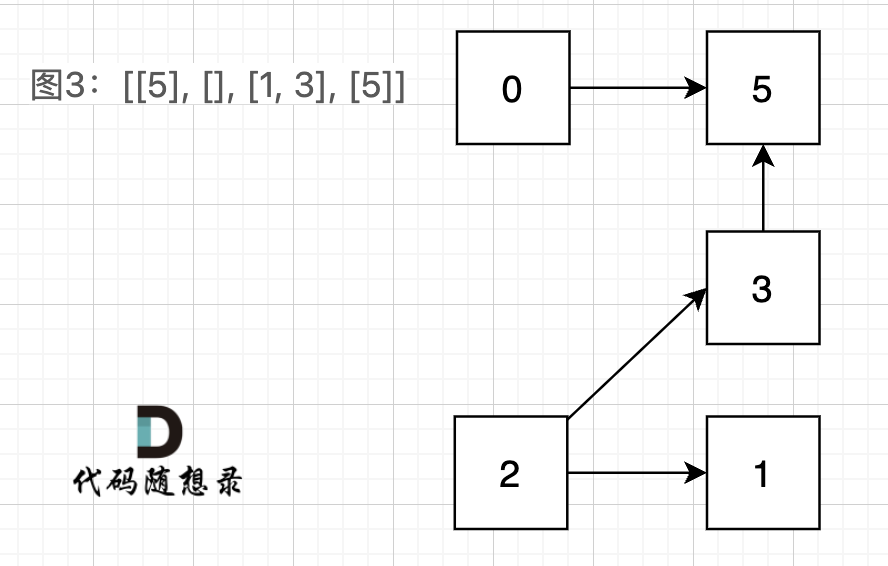
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220714102201.png)
在图3中，大家可以发现，节点0只能到节点5，然后就哪也去不了了。
所以本题是一个有向图搜索全路径的问题。 只能用深搜（BFS）或者广搜（DFS）来搜。
关于DFS的理论，如果大家有困惑，可以先看我这篇题解： [DFS理论基础](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf)
**以下dfs分析 大家一定要仔细看，本题有两种dfs的解法，很多题解没有讲清楚**。 看完之后 相信你对dfs会有更深的理解。
深搜三部曲：
1. 确认递归函数，参数
需要传入二维数组rooms来遍历地图，需要知道当前我们拿到的key，以至于去下一个房间。
同时还需要一个数组，用来记录我们都走过了哪些房间，这样好知道最后有没有把所有房间都遍历的，可以定义一个一维数组。
所以 递归函数参数如下：
```C++
// key 当前得到的可以
// visited 记录访问过的房间
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
```
2. 确认终止条件
遍历的时候，什么时候终止呢？
这里有一个很重要的逻辑，就是在递归中，**我们是处理当前访问的节点，还是处理下一个要访问的节点**。
这决定 终止条件怎么写。
首先明确，本题中什么叫做处理，就是 visited数组来记录访问过的节点，那么把该节点默认 数组里元素都是false，把元素标记为true就是处理 本节点了。
如果我们是处理当前访问的节点，当前访问的节点如果是 true ，说明是访问过的节点，那就终止本层递归，如果不是true，我们就把它赋值为true，因为我们处理本层递归的节点。
代码就是这样：
```C++
// 写法一：处理当前访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
if (visited[key]) { // 本层递归是true，说明访问过，立刻返回
return;
}
visited[key] = true; // 给当前遍历的节点赋值true
vector<int> keys = rooms[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(rooms, key, visited);
}
}
```
如果我们是处理下一层访问的节点，而不是当前层。那么就要在 深搜三部曲中第三步：处理目前搜索节点出发的路径 的时候对 节点进行处理。
这样的话，就不需要终止条件，而是在 搜索下一个节点的时候，直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的：
```C++
// 写法二：处理下一个要访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
// 这里 没有终止条件，而是在 处理下一层节点的时候来判断
vector<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) { // 处理下一层节点，判断是否要进行递归
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
```
可以看出，如果看待 我们要访问的节点，直接决定了两种不一样的写法，很多同学对这一块很模糊，其实做过这道题，也没有思考到这个维度上。
3. 处理目前搜索节点出发的路径
其实在上面，深搜三部曲 第二部，就已经讲了，因为终止条件的两种写法， 直接决定了两种不一样的递归写法。
这里还有细节：
看上面两个版本的写法中， 好像没有发现回溯的逻辑。
我们都知道，有递归就有回溯，回溯就在递归函数的下面， 那么之前我们做的dfs题目，都需要回溯操作，例如：[797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)， **为什么本题就没有回溯呢？**
代码中可以看到dfs函数下面并没有回溯的操作。
此时就要在思考本题的要求了，本题是需要判断 0节点是否能到所有节点，那么我们就没有必要回溯去撤销操作了，只要遍历过的节点一律都标记上。
**那什么时候需要回溯操作呢？**
当我们需要搜索一条可行路径的时候，就需要回溯操作了，因为没有回溯，就没法“调头”， 如果不理解的话，去看我写的 [797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/) 的题解。
以上分析完毕，DFS整体实现C++代码如下：
```CPP
// 写法一：处理当前访问的节点
class Solution {
private:
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
vector<int> keys = rooms[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(rooms, key, visited);
}
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<bool> visited(rooms.size(), false);
dfs(rooms, 0, visited);
//检查是否都访问到了
for (int i : visited) {
if (i == false) return false;
}
return true;
}
};
```
```c++
写法二：处理下一个要访问的节点
class Solution {
private:
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
vector<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) {
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<bool> visited(rooms.size(), false);
visited[0] = true; // 0 节点是出发节点，一定被访问过
dfs(rooms, 0, visited);
//检查是否都访问到了
for (int i : visited) {
if (i == false) return false;
}
return true;
}
};
```
本题我也给出 BFS C++代码，至于BFS，我后面会有单独文章来讲，代码如下：
```CPP
class Solution {
@ -80,39 +241,11 @@ public:
};
```
DFS C++代码如下：
```CPP
class Solution {
private:
void dfs(int key, const vector<vector<int>>& rooms, vector<int>& visited) {
if (visited[key]) {
return;
}
visited[key] = 1;
vector<int> keys = rooms[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(key, rooms, visited);
}
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<int> visited(rooms.size(), 0);
dfs(0, rooms, visited);
//检查是否都访问到了
for (int i : visited) {
if (i == 0) return false;
}
return true;
}
};
```
# 其他语言版本
## 其他语言版本
Java：
### Java
```java
class Solution {
@ -120,24 +253,19 @@ class Solution {
if (visited.get(key)) {
return;
}
visited.set(key, true);
for (int k : rooms.get(key)) {
// 深度优先搜索遍历
dfs(k, rooms, visited);
}
}
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
List<Boolean> visited = new ArrayList<Boolean>(){{
for(int i = 0 ; i < rooms.size(); i++){
add(false);
}
}};
dfs(0, rooms, visited);
//检查是否都访问到了
for (boolean flag : visited) {
if (!flag) {
@ -149,20 +277,14 @@ class Solution {
}
```
python3
### python3
```python
class Solution:
def dfs(self, key: int, rooms: List[List[int]] , visited : List[bool] ) :
if visited[key] :
return
visited[key] = True
keys = rooms[key]
for i in range(len(keys)) :
@ -183,7 +305,7 @@ class Solution:
```
Go：
### Go
```go
@ -201,11 +323,8 @@ func dfs(key int, rooms [][]int, visited []bool ) {
}
func canVisitAllRooms(rooms [][]int) bool {
visited := make([]bool, len(rooms));
dfs(0, rooms, visited);
//检查是否都访问到了
for i := 0; i < len(visited); i++ {
if !visited[i] {
@ -216,7 +335,7 @@ func canVisitAllRooms(rooms [][]int) bool {
}
```
JavaScript：
### JavaScript
```javascript
//DFS
var canVisitAllRooms = function(rooms) {

73
problems/1791.找出星型图的中心节点.md Normal file
View File

@ -0,0 +1,73 @@
# 1791.找出星型图的中心节点
[题目链接](https://leetcode.cn/problems/find-center-of-star-graph/)
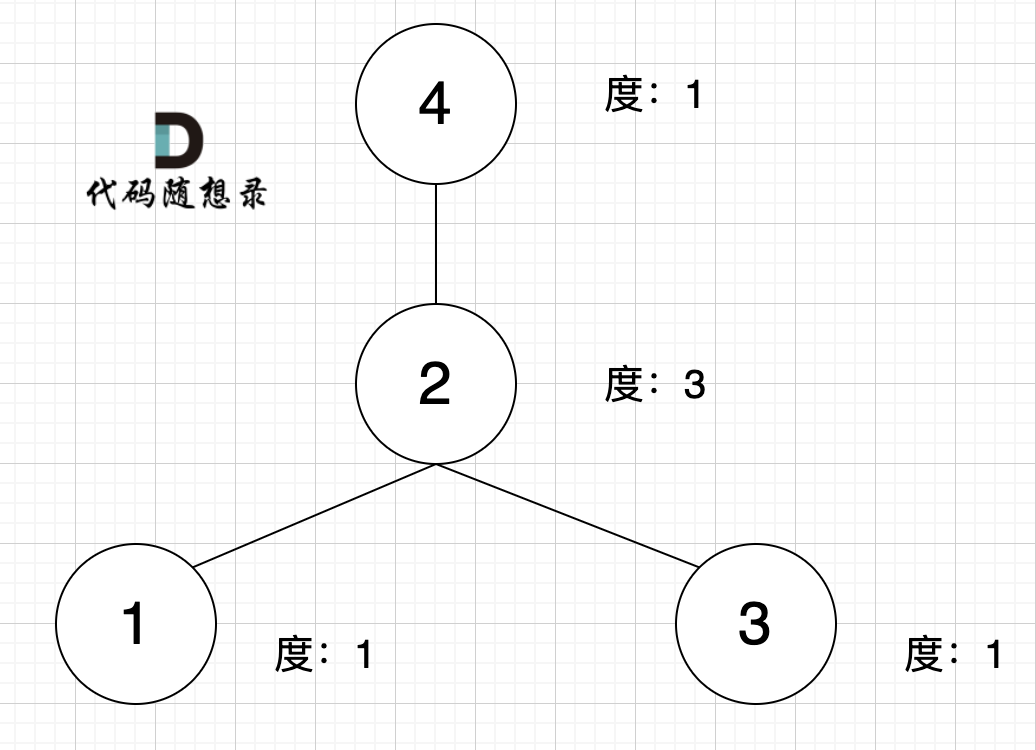
本题思路就是统计各个节点的度（这里没有区别入度和出度），如果某个节点的度等于这个图边的数量。 那么这个节点一定是中心节点。
什么是度，可以理解为，链接节点的边的数量。 题目中度如图所示：
![1791.找出星型图的中心节点](https://code-thinking-1253855093.file.myqcloud.com/pics/20220704113207.png)
至于出度和入度，那就是在有向图里的概念了，本题是无向图。
本题代码如下：
```c++
class Solution {
public:
int findCenter(vector<vector<int>>& edges) {
unordered_map<int ,int> du;
for (int i = 0; i < edges.size(); i++) { // 统计各个节点的度
du[edges[i][1]]++;
du[edges[i][0]]++;
}
unordered_map<int, int>::iterator iter; // 找出度等于边熟练的节点
for (iter = du.begin(); iter != du.end(); iter++) {
if (iter->second == edges.size()) return iter->first;
}
return -1;
}
};
```
其实可以只记录度不用最后统计，因为题目说了一定是星状图，所以 一旦有 节点的度 大于1，就返回该节点数值就行，只有中心节点的度会大于1。
代码如下：
```c++
class Solution {
public:
int findCenter(vector<vector<int>>& edges) {
vector<int> du(edges.size() + 2); // edges.size() + 1 为节点数量，下标表示节点数，所以+2
for (int i = 0; i < edges.size(); i++) {
du[edges[i][1]]++;
du[edges[i][0]]++;
if (du[edges[i][1]] > 1) return edges[i][1];
if (du[edges[i][0]] > 1) return edges[i][0];
}
return -1;
}
};
```
以上代码中没有使用 unordered_map，因为遍历的时候，开辟新空间会浪费时间，而采用 vector，这是 空间换时间的一种策略。
代码其实可以再精简：
```c++
class Solution {
public:
int findCenter(vector<vector<int>>& edges) {
vector<int> du(edges.size() + 2);
for (int i = 0; i < edges.size(); i++) {
if (++du[edges[i][1]] > 1) return edges[i][1];
if (++du[edges[i][0]] > 1) return edges[i][0];
}
return -1;
}
};
```

123
problems/1971.寻找图中是否存在路径.md Normal file
View File

@ -0,0 +1,123 @@
# 1971. 寻找图中是否存在路径
[题目链接](https://leetcode.cn/problems/find-if-path-exists-in-graph/)
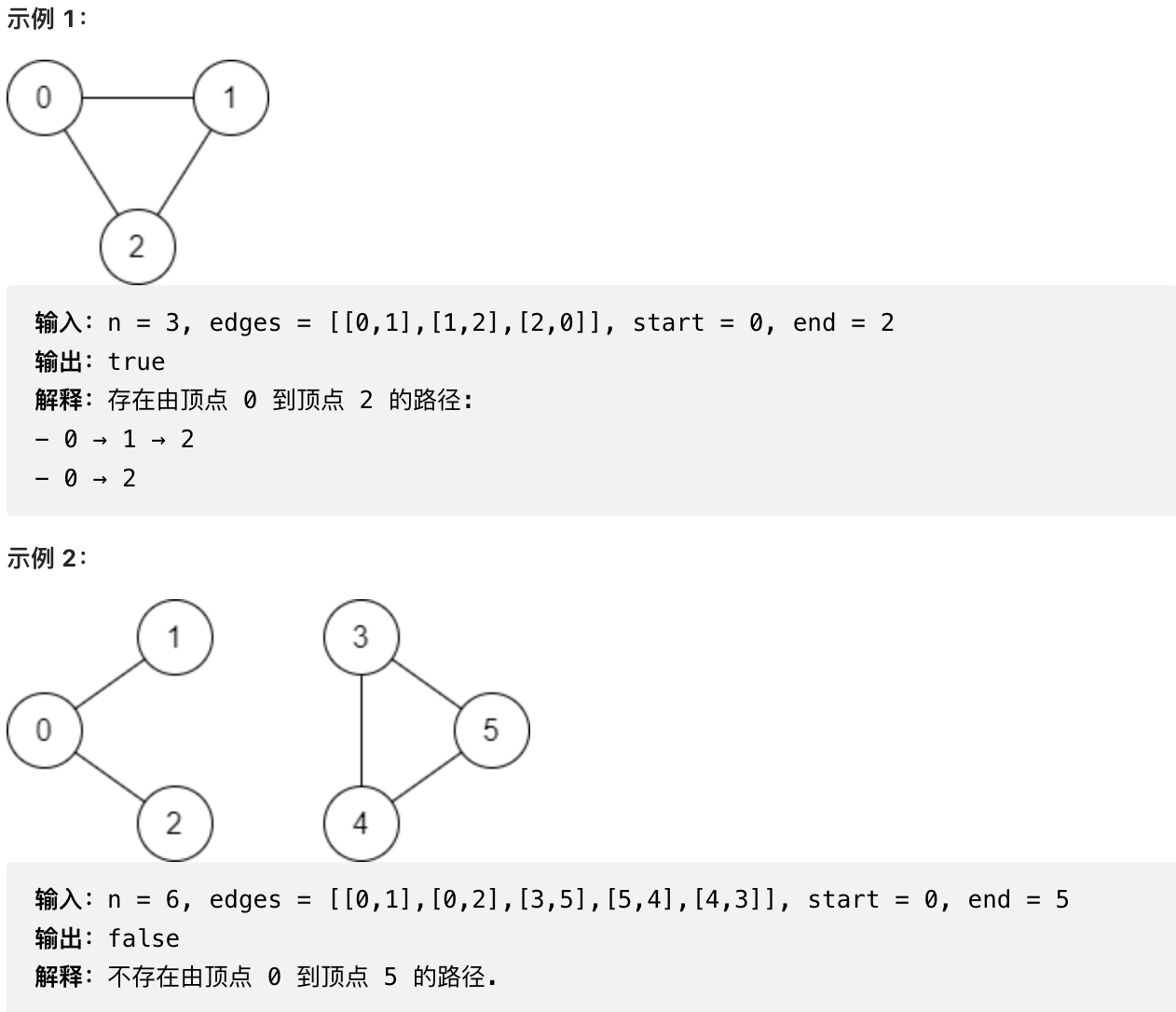
有一个具有 n个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。
给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220705101442.png)
提示:
* 1 <= n <= 2 * 10^5
* 0 <= edges.length <= 2 * 10^5
* edges[i].length == 2
* 0 <= ui, vi <= n - 1
* ui != vi
* 0 <= start, end <= n - 1
* 不存在双向边
* 不存在指向顶点自身的边
## 思路
这道题目也是并查集基础题目。
首先要知道并查集可以解决什么问题呢？
主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。
这里整理出我的并查集模板如下：
```CPP
int n = 1005; // 节点数量3 到 1000
int father[1005];
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
```
以上模板汇总，只要修改 n 和father数组的大小就可以了。
并查集主要有三个功能。
1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点
简单介绍并查集之后，我们再来看一下这道题目。
为什么说这道题目是并查集基础题目，因为 可以直接套用模板。
使用join(int u, int v)将每条边加入到并查集。
最后 same(int u, int v) 判断是否是同一个根 就可以里。
代码如下：
```c++
class Solution {
private:
int n = 200005; // 节点数量 20000
int father[200005];
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根，本题用不上
bool same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
public:
bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
init();
for (int i = 0; i < edges.size(); i++) {
join(edges[i][0], edges[i][1]);
}
return same(source, destination);
}
};
```

2
problems/动态规划总结篇.md
View File

@ -116,7 +116,7 @@
能把本篇中列举的题目都研究通透的话，你的动规水平就已经非常高了。 对付面试已经足够！
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211121223754.png)
![](https://kstar-1253855093.cos.ap-nanjing.myqcloud.com/baguwenpdf/_%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E6%80%9D%E7%BB%B4%E5%AF%BC%E5%9B%BE_%E9%9D%92.png)
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)，所画，总结的非常好，分享给大家。

4
problems/面试题02.07.链表相交.md
View File

@ -94,8 +94,8 @@ public:
};
```
* 时间复杂度：$O(n + m)$
* 空间复杂度：$O(1)$
* 时间复杂度：O(n + m)
* 空间复杂度：O(1)
## 其他语言版本