Merge branch 'youngyangyang04:master' into master

problems/0459.重复的子字符串.md

@@ -64,7 +64,7 @@
 
 如果有一个字符串s，在 s + s 拼接后， 不算首尾字符，如果能凑成s字符串，说明s 一定是重复子串组成。  
 
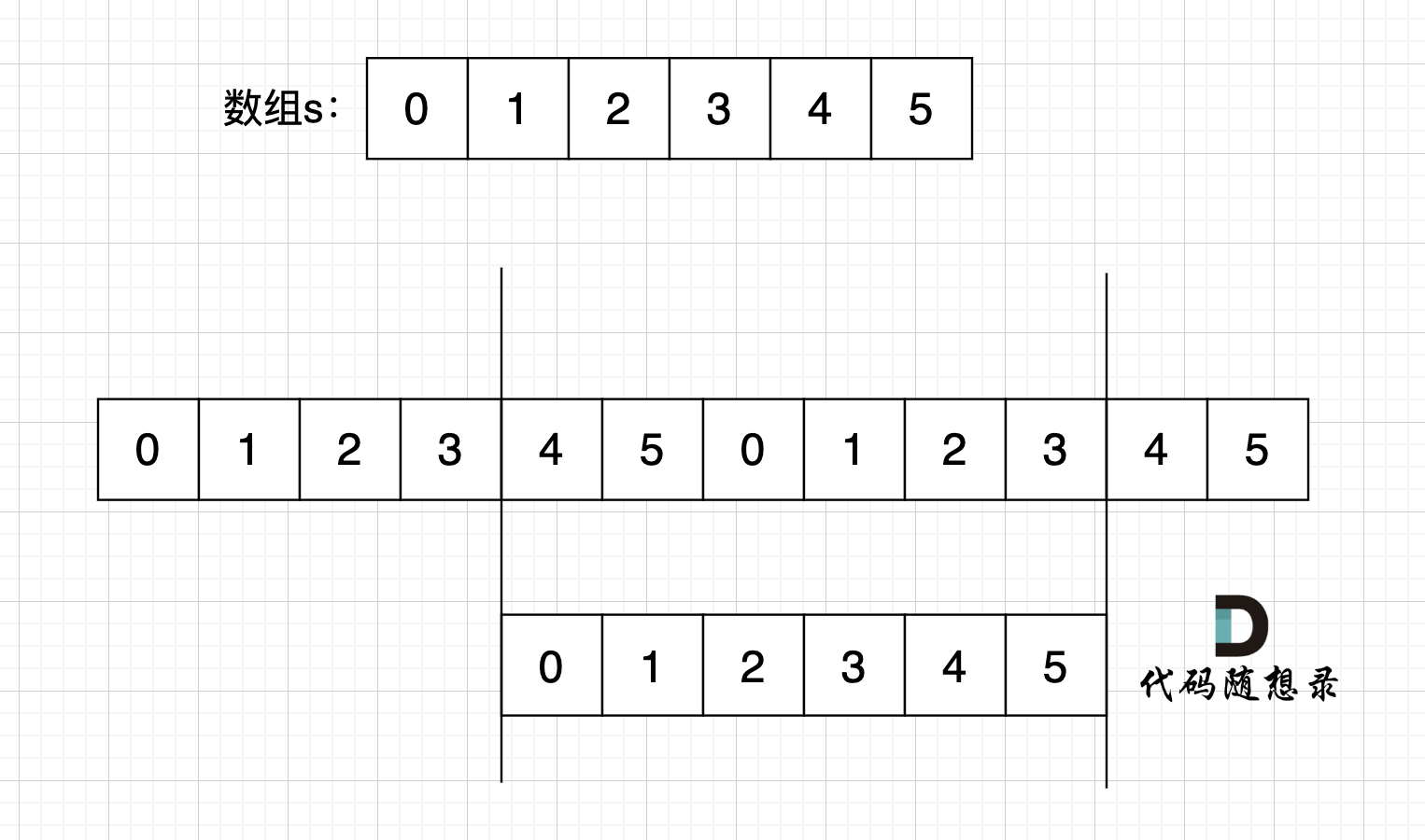
-如图，字符串s，图中数字为数组下标，在 s + s 拼接后， 不算首尾字符，中间凑成s字符串。 
+如图，字符串s，图中数字为数组下标，在 s + s 拼接后， 不算首尾字符，中间凑成s字符串。  （图中数字为数组下标）
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240910115555.png) 
 
@@ -163,9 +163,7 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
 
 如果一个字符串s是由重复子串组成，那么 最长相等前后缀不包含的子串一定是字符串s的最小重复子串。  
 
-证明： 如果s 是由最小重复子串p组成。 
-
-即 s = n * p 
+如果s 是由最小重复子串p组成，即 s = n * p 
 
 那么相同前后缀可以是这样： 
 
@@ -203,12 +201,14 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 最长相等前后缀不包含的子串已经是字符串s的最小重复子串，那么字符串s一定由重复子串组成，这个不需要证明了。 
 
-关键是要要证明：最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。 
+关键是要证明：最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。 
 
-情况一， 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大，那一定不是字符串s的重复子串
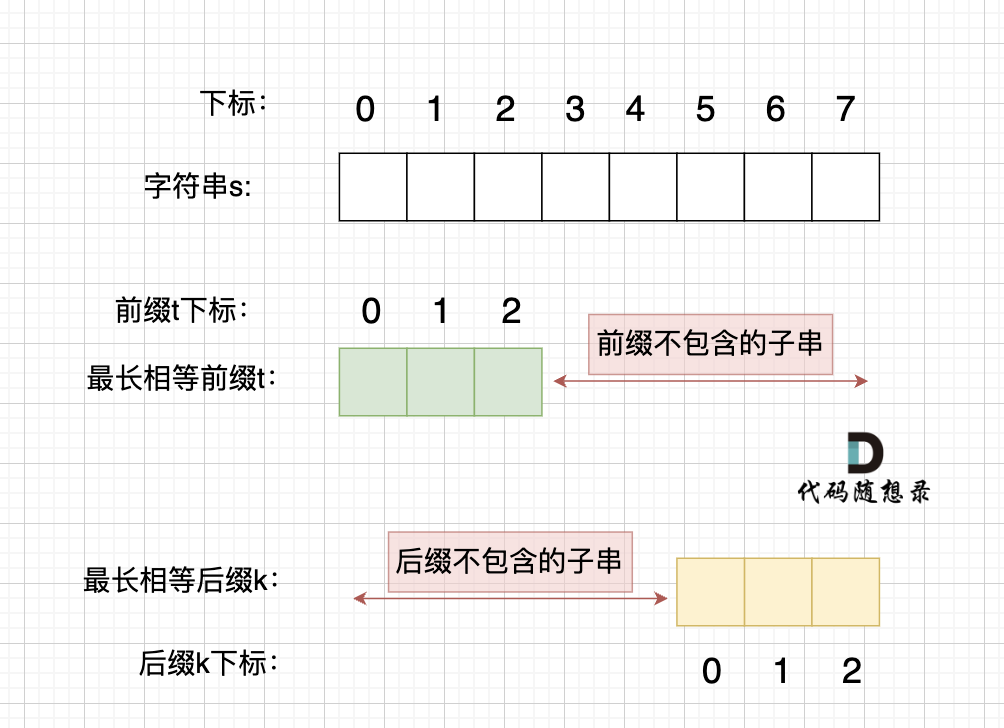
+情况一， 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大，那一定不是字符串s的重复子串，如图：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240911110236.png)
 
+图中：前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
+
 --------------
 
 情况二，最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，如图：
@@ -230,7 +230,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 即 s[0]s[1] 是最小重复子串
 
 
-以上推导中，录友可能想，你怎么知道 s[0] 和 s[1] 就不相同呢？ s[0] 为什么就不能使最小重复子串。
+以上推导中，录友可能想，你怎么知道 s[0] 和 s[1] 就不相同呢？ s[0] 为什么就不能是最小重复子串。
 
 如果 s[0] 和 s[1] 也相同，同时 s[0]s[1]与s[2]s[3]相同，s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同，那么这个字符串就是有一个字符构成的字符串。
 
@@ -246,7 +246,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 或者说，自己举个例子，`aaaaaa`，这个字符串，他的最长相等前后缀是什么？ 
 
-同上以上推导，最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除，就是一定是最小重复子串。
+同上以上推导，最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除，最长相等前后缀不包含的子串一定是最小重复子串。
 
 ----------------
 
@@ -267,7 +267,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 以上推导，可以得出 s[0],s[1],s[2] 与 s[3],s[4],s[5] 相同，s[3]s[4] 与 s[6]s[7]相同。
 
-那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ，就不是s的重复子串
+那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ，最长相等前后缀不包含的子串就不是s的重复子串
 
 -----------
 
@@ -277,7 +277,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 在必要条件，这个是 显而易见的，都已经假设 最长相等前后缀不包含的子串 是 s的最小重复子串了，那s必然是重复子串。 
 
-关键是需要证明， 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串。 
+**关键是需要证明， 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串**。 
 
 同上我们证明了，当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，那么不包含的子串 就是s的最小重复子串。 
 
@@ -312,7 +312,7 @@ next 数组记录的就是最长相同前后缀（ [字符串：KMP算法精讲]
 
 4可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。
 
-### 打码实现
+### 代码实现
 
 C++代码如下：（这里使用了前缀表统一减一的实现方式）
 

problems/0518.零钱兑换II.md

@@ -168,23 +168,43 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
 class Solution {
 public:
     int change(int amount, vector<int>& coins) {
-        vector<int> dp(amount + 1, 0);
-        dp[0] = 1;
+        vector<uint64_t> dp(amount + 1, 0); // 防止相加数据超int
+        dp[0] = 1; // 只有一种方式达到0
         for (int i = 0; i < coins.size(); i++) { // 遍历物品
             for (int j = coins[i]; j <= amount; j++) { // 遍历背包
                 dp[j] += dp[j - coins[i]];
             }
         }
-        return dp[amount];
+        return dp[amount]; // 返回组合数
     }
 };
 ```
 
+C++测试用例有两个数相加超过int的数据，所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
+
 * 时间复杂度: O(mn)，其中 m 是amount，n 是 coins 的长度
 * 空间复杂度: O(m)
 
+为了防止相加的数据 超int 也可以这么写：
+
+```CPP
+class Solution {
+public:
+    int change(int amount, vector<int>& coins) {
+        vector<int> dp(amount + 1, 0);
+        dp[0] = 1; // 只有一种方式达到0
+        for (int i = 0; i < coins.size(); i++) { // 遍历物品
+            for (int j = coins[i]; j <= amount; j++) { // 遍历背包
+                if (dp[j] < INT_MAX - dp[j - coins[i]]) { //防止相加数据超int
+                    dp[j] += dp[j - coins[i]];
+                }
+            }
+        }
+        return dp[amount]; // 返回组合数
+    }
+};
+```
 
-是不是发现代码如此精简
 
 ## 总结