algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-08 16:54:50 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
programmercarl
2022-09-03 10:17:03 +08:00
parent 07e00165b0
commit ca4f55ac2a
24 changed files with 1186 additions and 174 deletions
Download Patch File Download Diff File Expand all files Collapse all files

2
problems/0101.对称二叉树.md
View File

@ -15,6 +15,8 @@
# 思路 # 思路
《代码随想录》算法视频公开课：[同时操作两个二叉树 | LeetCode：101. 对称二叉树](https://www.bilibili.com/video/BV1ue4y1Y7Mf)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
**首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！** **首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！**
对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了**其实我们要比较的是两个树（这两个树是根节点的左右子树）**，所以在递归遍历的过程中，也是要同时遍历两棵树。 对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了**其实我们要比较的是两个树（这两个树是根节点的左右子树）**，所以在递归遍历的过程中，也是要同时遍历两棵树。

3
problems/0102.二叉树的层序遍历.md
View File

@ -6,6 +6,9 @@
# 二叉树层序遍历登场！ # 二叉树层序遍历登场！
《代码随想录》算法视频公开课：[讲透二叉树的层序遍历 | 广度优先搜索 | LeetCode：102.二叉树的层序遍历](https://www.bilibili.com/video/BV1GY4y1u7b2)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
学会二叉树的层序遍历，可以一口气打完以下十题： 学会二叉树的层序遍历，可以一口气打完以下十题：
* 102.二叉树的层序遍历 * 102.二叉树的层序遍历

3
problems/0104.二叉树的最大深度.md
View File

@ -31,6 +31,9 @@
本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。 本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
* 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
**而根节点的高度就是二叉树的最大深度**，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。 **而根节点的高度就是二叉树的最大深度**，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。 这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。

42
problems/0111.二叉树的最小深度.md
View File

@ -31,7 +31,16 @@
直觉上好像和求最大深度差不多，其实还是差不少的。 直觉上好像和求最大深度差不多，其实还是差不少的。
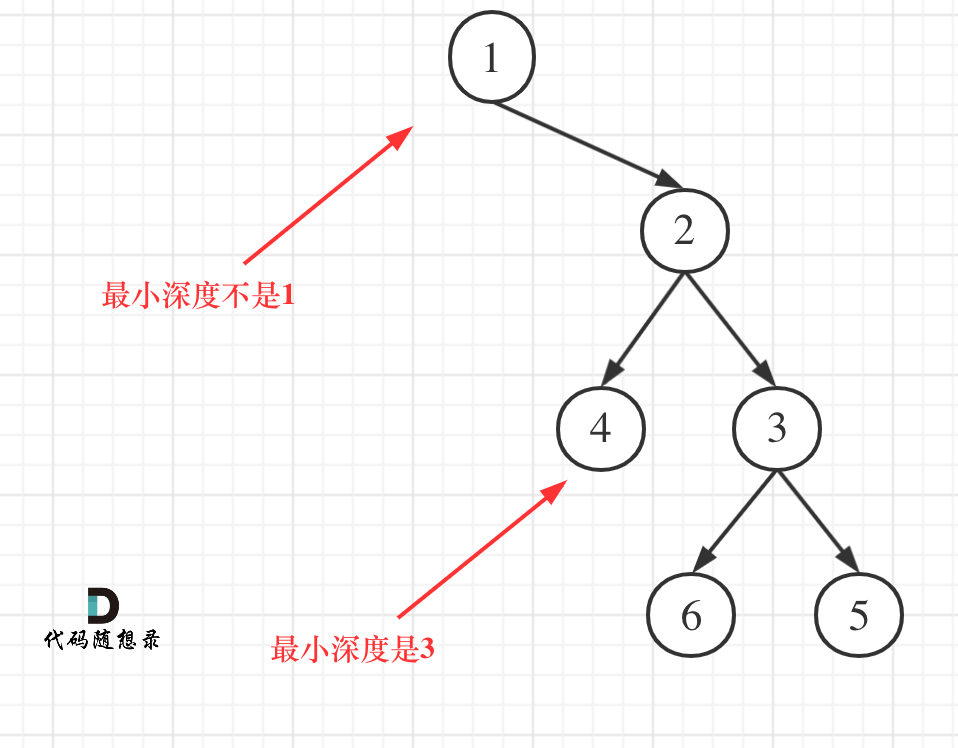
遍历顺序上依然是后序遍历（因为要比较递归返回之后的结果），但在处理中间节点的逻辑上，最大深度很容易理解，最小深度可有一个误区，如图： 本题依然是前序遍历和后序遍历都可以，前序求的是深度，后序求的是高度。
* 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，这不过这个最小距离 也同样是最小深度。
以下讲解中遍历顺序上依然采用后序遍历（因为要比较递归返回之后的结果，本文我也给出前序遍历的写法）。
本题还有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：
![111.二叉树的最小深度](https://img-blog.csdnimg.cn/20210203155800503.png) ![111.二叉树的最小深度](https://img-blog.csdnimg.cn/20210203155800503.png)
@ -150,6 +159,37 @@ public:
**精简之后的代码根本看不出是哪种遍历方式，所以依然还要强调一波：如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。** **精简之后的代码根本看不出是哪种遍历方式，所以依然还要强调一波：如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。**
前序遍历的方式：
```CPP
class Solution {
private:
int result;
void getdepth(TreeNode* node, int depth) {
if (node->left == NULL && node->right == NULL) {
result = min(depth, result);
return;
}
// 中 只不过中没有处理的逻辑
if (node->left) { // 左
getdepth(node->left, depth + 1);
}
if (node->right) { // 右
getdepth(node->right, depth + 1);
}
return ;
}
public:
int minDepth(TreeNode* root) {
if (root == NULL) return 0;
result = INT_MAX;
getdepth(root, 1);
return result;
}
};
```
## 迭代法 ## 迭代法
相对于[104.二叉树的最大深度](https://programmercarl.com/0104.二叉树的最大深度.html)，本题还可以使用层序遍历的方式来解决，思路是一样的。 相对于[104.二叉树的最大深度](https://programmercarl.com/0104.二叉树的最大深度.html)，本题还可以使用层序遍历的方式来解决，思路是一样的。

5
problems/0127.单词接龙.md
View File

@ -42,12 +42,11 @@
* 图中的线是如何连在一起的 * 图中的线是如何连在一起的
* 起点和终点的最短路径长度 * 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个，所以判断点与点之间的关系，要自己判断是不是差一个字符，如果差一个字符，那就是有链接。 首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个，所以判断点与点之间的关系，要自己判断是不是差一个字符，如果差一个字符，那就是有链接。
然后就是求起点和终点的最短路径长度，**这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径**。因为广搜就是以起点中心向四周扩散的搜索。 然后就是求起点和终点的最短路径长度，**这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径**。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜，会非常麻烦。 本题如果用深搜，会比较麻烦，要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点，一定是最短路。
另外需要有一个注意点： 另外需要有一个注意点：
@ -96,6 +95,8 @@ public:
}; };
``` ```
当然本题也可以用双向BFS，就是从头尾两端进行搜索，大家感兴趣，可以自己去实现，这里就不再做详细讲解了。
# 其他语言版本 # 其他语言版本
## Java ## Java

80
problems/0130.被围绕的区域.md Normal file
View File

@ -0,0 +1,80 @@
# 130. 被围绕的区域
[题目链接](https://leetcode.cn/problems/surrounded-regions/)
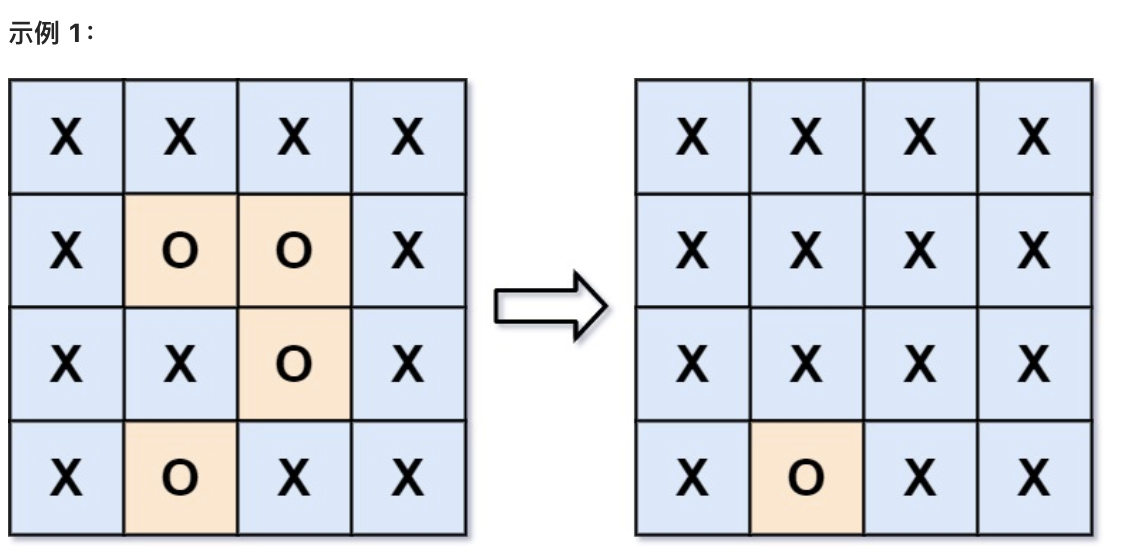
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220901104745.png)
* 输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
* 输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
* 解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。
## 思路
这道题目和1020. 飞地的数量正好反过来了，[1020. 飞地的数量](https://leetcode.cn/problems/number-of-enclaves/solution/by-carlsun-2-7lt9/)是求 地图中间的空格数，而本题是要把地图中间的'O'都改成'X'。
那么两题在思路上也是差不多的。
依然是从地图周边出发，将周边空格相邻的'O'都做上标记，然后在遍历一遍地图，遇到 'O' 且没做过标记的，那么都是地图中间的'O'，全部改成'X'就行。
有的录友可能想，我在定义一个 visited 二维数组，单独标记周边的'O'，然后遍历地图的时候同时对 数组board 和 数组visited 进行判断，是否'O'改成'X'。
这样做其实就有点麻烦了，不用额外定义空间了，标记周边的'O'，可以直接改board的数值为其他特殊值。
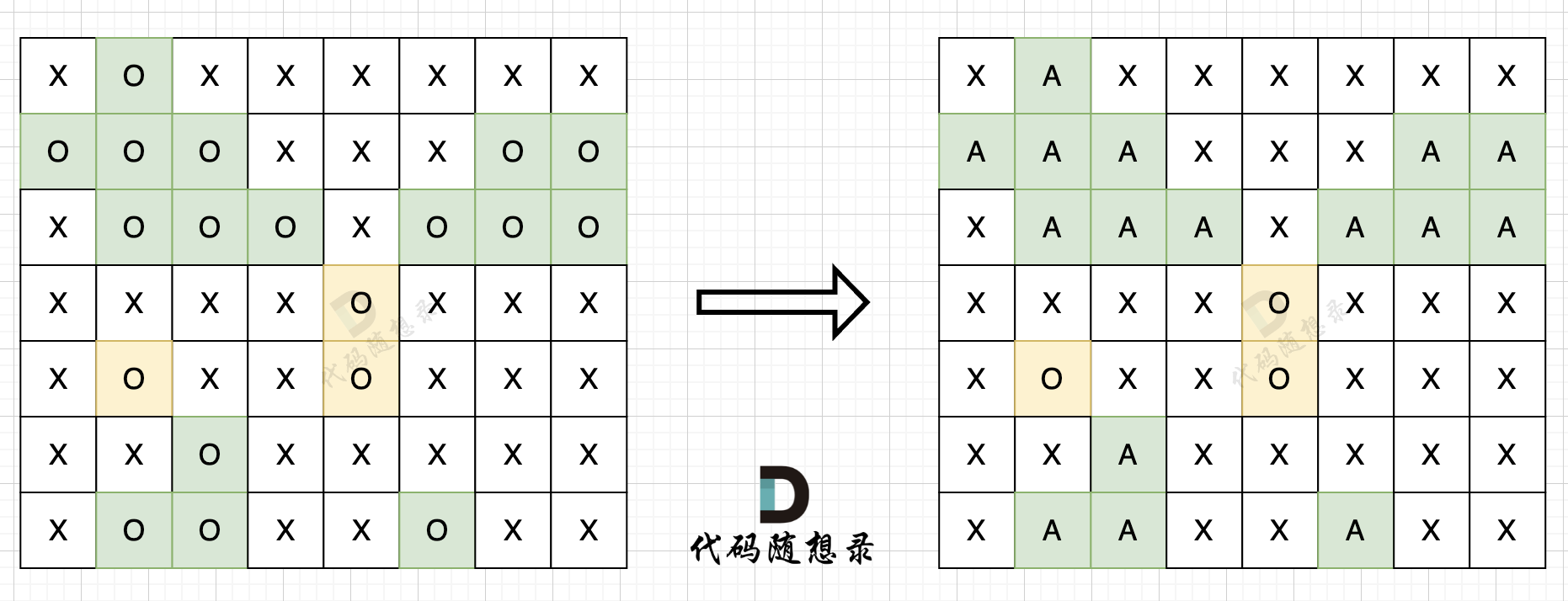
步骤一：深搜或者广搜将地图周边的'O'全部改成'A'，如图所示：
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902102337.png)
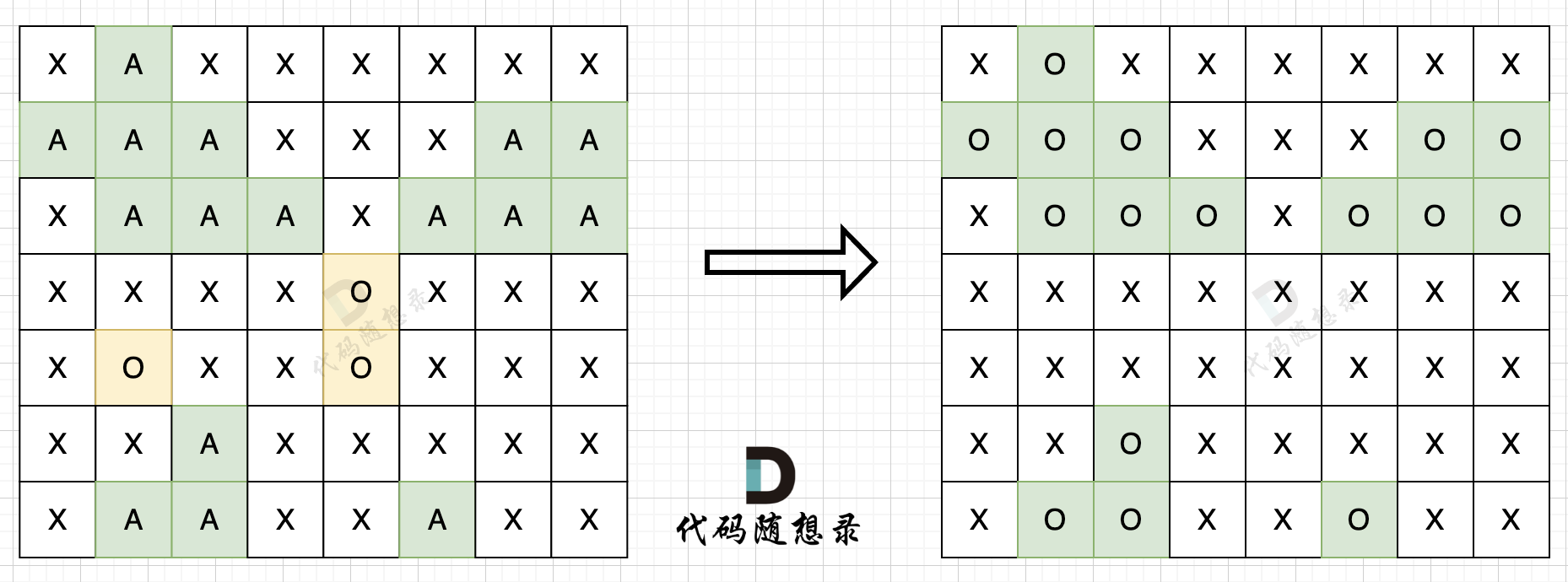
步骤二：在遍历地图，将'O'全部改成'X'（地图中间的'O'改成了'X'），将'A'改回'O'（保留的地图周边的'O'），如图所示：
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902102831.png)
整体C++代码如下，以下使用dfs实现，其实遍历方式dfs，bfs都是可以的。
```CPP
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
void dfs(vector<vector<char>>& board, int x, int y) {
board[x][y] = 'A';
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= board.size() || nexty < 0 || nexty >= board[0].size()) continue;
// 不符合条件，不继续遍历
if (board[nextx][nexty] == 'X' || board[nextx][nexty] == 'A') continue;
dfs (board, nextx, nexty);
}
return;
}
public:
void solve(vector<vector<char>>& board) {
int n = board.size(), m = board[0].size();
// 步骤一：
// 从左侧边，和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (board[i][0] == 'O') dfs(board, i, 0);
if (board[i][m - 1] == 'O') dfs(board, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (board[0][j] == 'O') dfs(board, 0, j);
if (board[n - 1][j] == 'O') dfs(board, n - 1, j);
}
// 步骤二：
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O') board[i][j] = 'X';
if (board[i][j] == 'A') board[i][j] = 'O';
}
}
}
};
```
## 其他语言版本

146
problems/0200.岛屿数量.广搜版.md Normal file
View File

@ -0,0 +1,146 @@
# 200. 岛屿数量
[题目链接](https://leetcode.cn/problems/number-of-islands/)
给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220726093256.png)
提示：
* m == grid.length
* n == grid[i].length
* 1 <= m, n <= 300
* grid[i][j] 的值为 '0' 或 '1'
## 思路
注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
也就是说斜角度链接是不算了， 例如示例二，是三个岛屿，如图：
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220726094200.png)
这道题题目是 DFS，BFS，并查集，基础题目。
本题思路，是用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么如果把节点陆地所能遍历到的陆地都标记上呢，就可以使用 DFS，BFS或者并查集。
### 广度优先搜索
不少同学用广搜做这道题目的时候，超时了。 这里有一个广搜中很重要的细节：
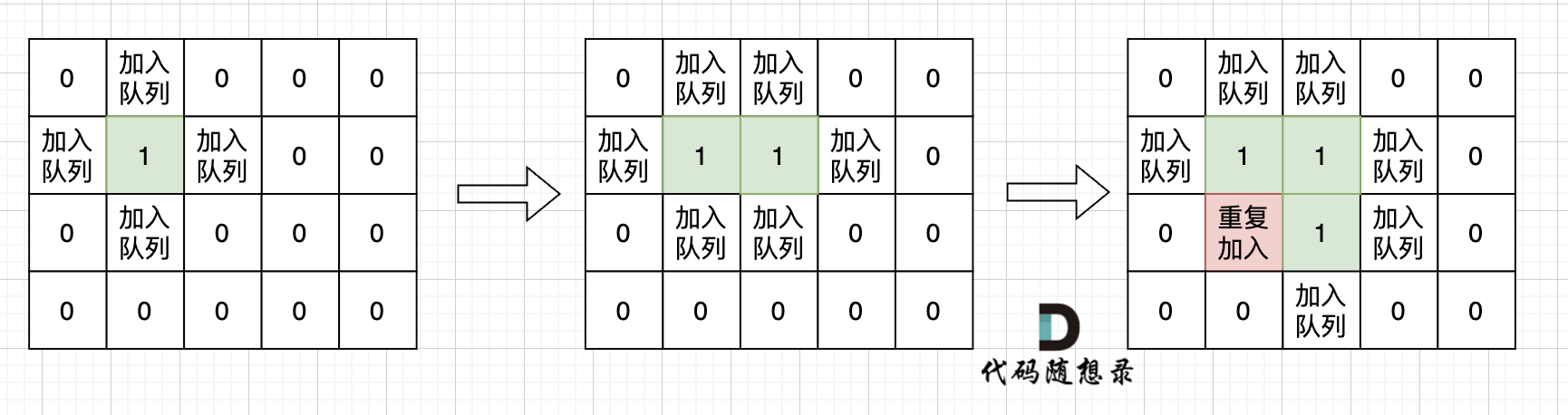
根本原因是**只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过**。
很多同学可能感觉这有区别吗？
如果从队列拿出节点，再去标记这个节点走过，就会发生下图所示的结果，会导致很多节点重复加入队列。
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220727100846.png)
超时写法 （从队列中取出节点再标记）
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
visited[curx][cury] = true; // 从队列中取出在标记走过
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
}
}
}
}
```
加入队列 就代表走过，立刻标记，正确写法：
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列，立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
```
以上两个版本其实，其实只有细微区别，就是 `visited[x][y] = true;` 放在的地方，着去取决于我们对 代码中队列的定义，队列中的节点就表示已经走过的节点。 **所以只要加入队列，理解标记该节点走过**。
本题完整广搜代码：
```CPP
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列，立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
result++; // 遇到没访问过的陆地，+1
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
return result;
}
};
```

110
problems/0200.岛屿数量.md → problems/0200.岛屿数量.深搜版.md
View File

@ -128,116 +128,6 @@ public:
很多同学看了同一道题目，都是dfs，写法却不一样，有时候有终止条件，有时候连终止条件都没有，其实这就是根本原因，两种写法而已。 很多同学看了同一道题目，都是dfs，写法却不一样，有时候有终止条件，有时候连终止条件都没有，其实这就是根本原因，两种写法而已。
### 广度优先搜索
不少同学用广搜做这道题目的时候，超时了。 这里有一个广搜中很重要的细节：
根本原因是**只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过**。
很多同学可能感觉这有区别吗？
如果从队列拿出节点，再去标记这个节点走过，就会发生下图所示的结果，会导致很多节点重复加入队列。
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220727100846.png)
超时写法 （从队列中取出节点再标记）
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
visited[curx][cury] = true; // 从队列中取出在标记走过
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
}
}
}
}
```
加入队列 就代表走过，立刻标记，正确写法：
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列，立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
```
以上两个版本其实，其实只有细微区别，就是 `visited[x][y] = true;` 放在的地方，着去取决于我们对 代码中队列的定义，队列中的节点就表示已经走过的节点。 **所以只要加入队列，理解标记该节点走过**。
本题完整广搜代码：
```CPP
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列，立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
result++; // 遇到没访问过的陆地，+1
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
return result;
}
};
```
## 总结 ## 总结
其实本题是 dfs，bfs 模板题，但正是因为是模板题，所以大家或者一些题解把重要的细节都很忽略了，我这里把大家没注意的但以后会踩的坑 都给列出来了。 其实本题是 dfs，bfs 模板题，但正是因为是模板题，所以大家或者一些题解把重要的细节都很忽略了，我这里把大家没注意的但以后会踩的坑 都给列出来了。

107
problems/0222.完全二叉树的节点个数.md
View File

@ -34,7 +34,6 @@
本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。 本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。
## 普通二叉树 ## 普通二叉树
首先按照普通二叉树的逻辑来求。 首先按照普通二叉树的逻辑来求。
@ -145,6 +144,14 @@ public:
以上方法都是按照普通二叉树来做的，对于完全二叉树特性不了解的同学可以看这篇 [关于二叉树，你该了解这些！](https://programmercarl.com/二叉树理论基础.html)，这篇详细介绍了各种二叉树的特性。 以上方法都是按照普通二叉树来做的，对于完全二叉树特性不了解的同学可以看这篇 [关于二叉树，你该了解这些！](https://programmercarl.com/二叉树理论基础.html)，这篇详细介绍了各种二叉树的特性。
在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。
**大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**
我来举一个典型的例子如题：
<img src='https://img-blog.csdnimg.cn/20200920221638903.png' width=600> </img></div>
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。 完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
@ -159,7 +166,59 @@ public:
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。 可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
C++代码如下： 这里关键在于如果去判断一个左子树或者右子树是不是满二叉树呢？
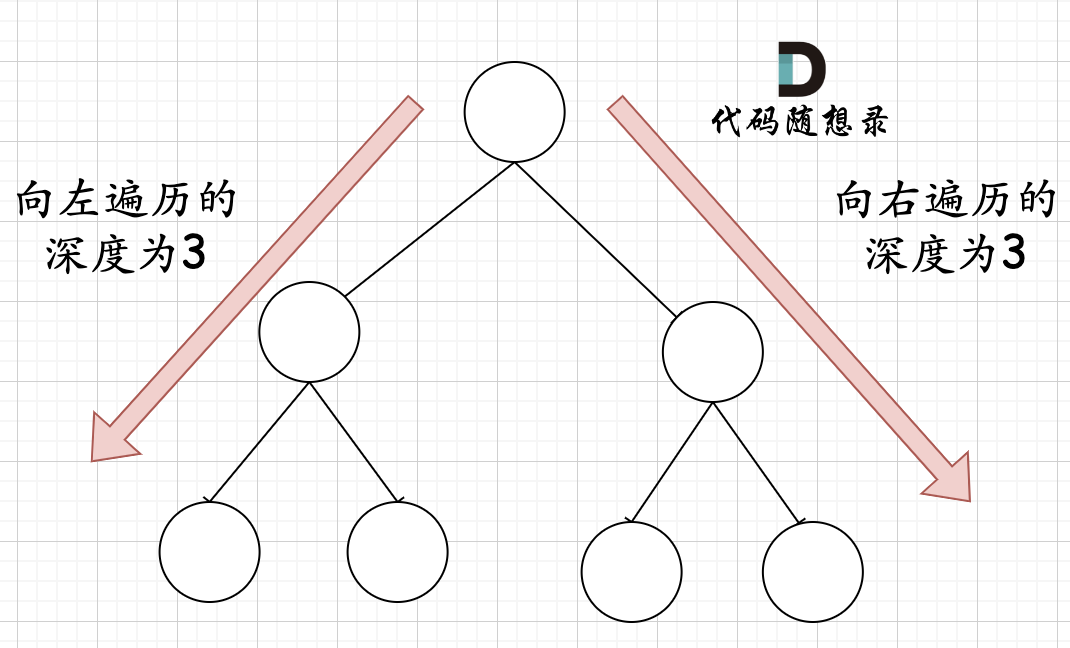
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：
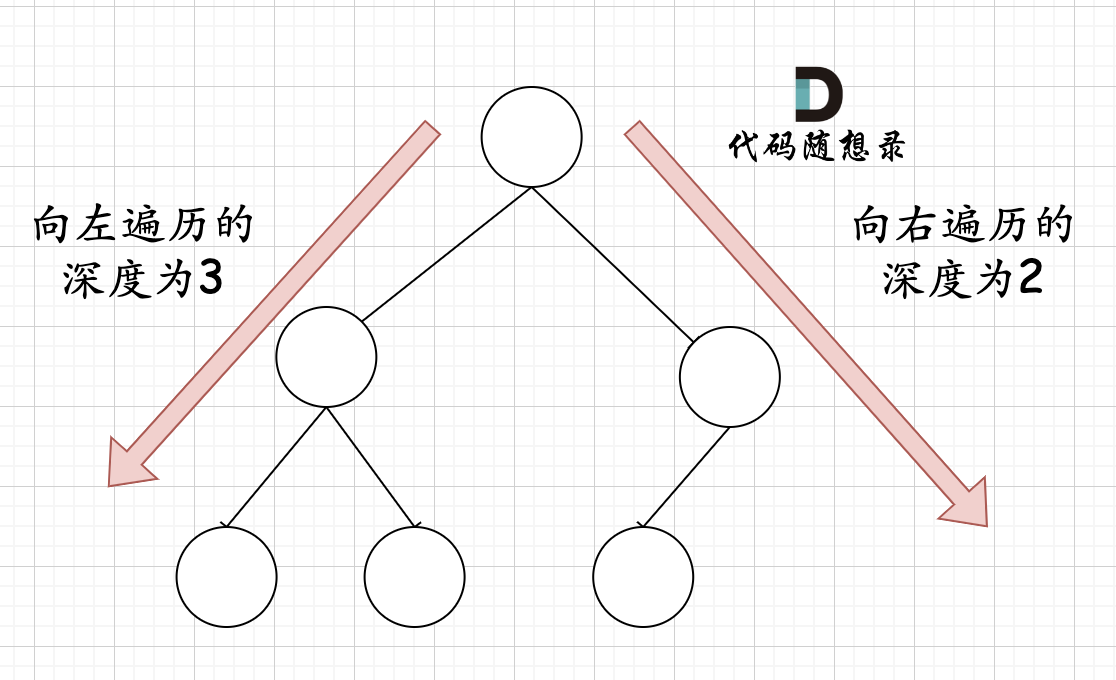
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163554.png)
在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：
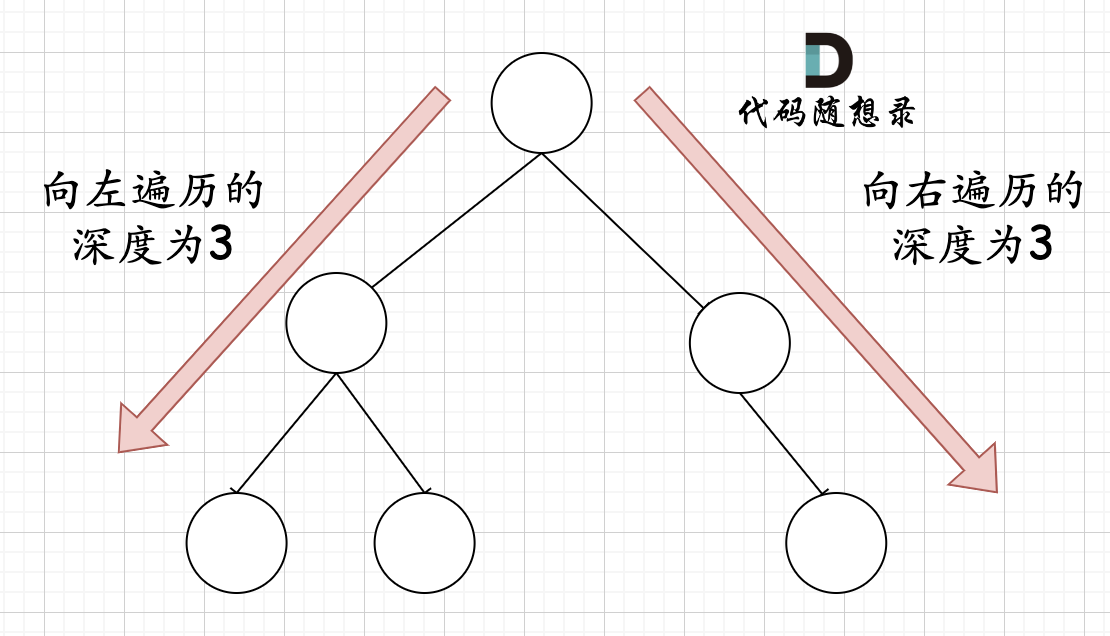
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163709.png)
哪有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163811.png)
如果这么想，大家就是对 完全二叉树理解有误区了，**以上这棵二叉树，它根本就不是一个完全二叉树**！
判断其子树岂不是满二叉树，如果是则利用用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的：
```CPP
if (root == nullptr) return 0;
// 开始根据做深度和有深度是否相同来判断该子树是不是满二叉树
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
}
```
递归三部曲，第三部，单层递归的逻辑：（可以看出使用后序遍历）
```CPP
int leftTreeNum = countNodes(root->left); // 左
int rightTreeNum = countNodes(root->right); // 右
int result = leftTreeNum + rightTreeNum + 1; // 中
return result;
```
该部分精简之后代码为：
```CPP
return countNodes(root->left) + countNodes(root->right) + 1;
```
最后整体C++代码如下：
```CPP ```CPP
class Solution { class Solution {
@ -168,17 +227,17 @@ public:
if (root == nullptr) return 0; if (root == nullptr) return 0;
TreeNode* left = root->left; TreeNode* left = root->left;
TreeNode* right = root->right; TreeNode* right = root->right;
int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的，为了下面求指数方便 int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left) { // 求左子树深度 while (left) { // 求左子树深度
left = left->left; left = left->left;
leftHeight++; leftDepth++;
} }
while (right) { // 求右子树深度 while (right) { // 求右子树深度
right = right->right; right = right->right;
rightHeight++; rightDepth++;
} }
if (leftHeight == rightHeight) { if (leftDepth == rightDepth) {
return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2，所以leftHeight初始为0 return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
} }
return countNodes(root->left) + countNodes(root->right) + 1; return countNodes(root->left) + countNodes(root->right) + 1;
} }
@ -310,16 +369,16 @@ class Solution:
return 0 return 0
left = root.left left = root.left
right = root.right right = root.right
leftHeight = 0 #这里初始为0是有目的的，为了下面求指数方便 leftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便
rightHeight = 0 rightDepth = 0
while left: #求左子树深度 while left: #求左子树深度
left = left.left left = left.left
leftHeight += 1 leftDepth += 1
while right: #求右子树深度 while right: #求右子树深度
right = right.right right = right.right
rightHeight += 1 rightDepth += 1
if leftHeight == rightHeight: if leftDepth == rightDepth:
return (2 << leftHeight) - 1 #注意(2<<1) 相当于2^2，所以leftHeight初始为0 return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0
return self.countNodes(root.left) + self.countNodes(root.right) + 1 return self.countNodes(root.left) + self.countNodes(root.right) + 1
``` ```
@ -431,17 +490,17 @@ var countNodes = function(root) {
} }
let left=root.left; let left=root.left;
let right=root.right; let right=root.right;
let leftHeight=0,rightHeight=0; let leftDepth=0,rightDepth=0;
while(left){ while(left){
left=left.left; left=left.left;
leftHeight++; leftDepth++;
} }
while(right){ while(right){
right=right.right; right=right.right;
rightHeight++; rightDepth++;
} }
if(leftHeight==rightHeight){ if(leftDepth==rightDepth){
return Math.pow(2,leftHeight+1)-1; return Math.pow(2,leftDepth+1)-1;
} }
return countNodes(root.left)+countNodes(root.right)+1; return countNodes(root.left)+countNodes(root.right)+1;
}; };
@ -554,24 +613,24 @@ int countNodes(struct TreeNode* root){
int countNodes(struct TreeNode* root){ int countNodes(struct TreeNode* root){
if(!root) if(!root)
return 0; return 0;
int leftHeight = 0; int leftDepth = 0;
int rightHeight = 0; int rightDepth = 0;
struct TreeNode* rightNode = root->right; struct TreeNode* rightNode = root->right;
struct TreeNode* leftNode = root->left; struct TreeNode* leftNode = root->left;
//求出左子树深度 //求出左子树深度
while(leftNode) { while(leftNode) {
leftNode = leftNode->left; leftNode = leftNode->left;
leftHeight++; leftDepth++;
} }
//求出右子树深度 //求出右子树深度
while(rightNode) { while(rightNode) {
rightNode = rightNode->right; rightNode = rightNode->right;
rightHeight++; rightDepth++;
} }
//若左右子树深度相同，为满二叉树。结点个数为2^height-1 //若左右子树深度相同，为满二叉树。结点个数为2^height-1
if(rightHeight == leftHeight) { if(rightDepth == leftDepth) {
return (2 << leftHeight) - 1; return (2 << leftDepth) - 1;
} }
//否则返回左右子树的结点个数+1 //否则返回左右子树的结点个数+1
return countNodes(root->right) + countNodes(root->left) + 1; return countNodes(root->right) + countNodes(root->left) + 1;

2
problems/0226.翻转二叉树.md
View File

@ -25,6 +25,8 @@
# 思路 # 思路
《代码随想录》算法视频公开课：[听说一位巨佬面Google被拒了，因为没写出翻转二叉树 | LeetCode：226.翻转二叉树](https://www.bilibili.com/video/BV1sP4y1f7q7)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
我们之前介绍的都是各种方式遍历二叉树，这次要翻转了，感觉还是有点懵逼。 我们之前介绍的都是各种方式遍历二叉树，这次要翻转了，感觉还是有点懵逼。
这得怎么翻转呢？ 这得怎么翻转呢？

77
problems/0257.二叉树的所有路径.md
View File

@ -141,11 +141,12 @@ if (cur->right) {
那么本题整体代码如下： 那么本题整体代码如下：
```CPP ```CPP
// 版本一
class Solution { class Solution {
private: private:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) { void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val); path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
// 这才到了叶子节点 // 这才到了叶子节点
if (cur->left == NULL && cur->right == NULL) { if (cur->left == NULL && cur->right == NULL) {
string sPath; string sPath;
@ -157,11 +158,11 @@ private:
result.push_back(sPath); result.push_back(sPath);
return; return;
} }
if (cur->left) { if (cur->left) { // 左
traversal(cur->left, path, result); traversal(cur->left, path, result);
path.pop_back(); // 回溯 path.pop_back(); // 回溯
} }
if (cur->right) { if (cur->right) { // 右
traversal(cur->right, path, result); traversal(cur->right, path, result);
path.pop_back(); // 回溯 path.pop_back(); // 回溯
} }
@ -209,7 +210,7 @@ public:
如上代码精简了不少，也隐藏了不少东西。 如上代码精简了不少，也隐藏了不少东西。
注意在函数定义的时候`void traversal(TreeNode* cur, string path, vector<string>& result)` ，定义的是`string path`，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。 注意在函数定义的时候`void traversal(TreeNode* cur, string path, vector<string>& result)` ，定义的是`string path`，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。（这里涉及到C++语法知识）
那么在如上代码中，**貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在`traversal(cur->left, path + "->", result);`中的 `path + "->"`。** 每次函数调用完，path依然是没有加上"->" 的，这就是回溯了。 那么在如上代码中，**貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在`traversal(cur->left, path + "->", result);`中的 `path + "->"`。** 每次函数调用完，path依然是没有加上"->" 的，这就是回溯了。
@ -247,22 +248,82 @@ if (cur->right) {
if (cur->left) { if (cur->left) {
path += "->"; path += "->";
traversal(cur->left, path, result); // 左 traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 path.pop_back(); // 回溯 '>'
path.pop_back(); path.pop_back(); // 回溯 '-'
} }
if (cur->right) { if (cur->right) {
path += "->"; path += "->";
traversal(cur->right, path, result); // 右 traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯 path.pop_back(); // 回溯 '>'
path.pop_back(); path.pop_back(); // 回溯 '-'
} }
``` ```
整体代码如下：
```CPP
//版本二
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯'>'
path.pop_back(); // 回溯 '-'
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
```
**大家应该可以感受出来，如果把 `path + "->"`作为函数参数就是可以的，因为并有没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）** **大家应该可以感受出来，如果把 `path + "->"`作为函数参数就是可以的，因为并有没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）**
**综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现了出来了。** **综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现了出来了。**
## 拓展
这里讲解本题解的写法逻辑以及一些更具体的细节，下面的讲解中，涉及到C++语法特性，如果不是C++的录友，就可以不看了，避免越看越晕。
如果是C++的录友，建议本题独立刷过两遍，在看下面的讲解，同样避免越看越晕，造成不必要的负担。
在第二版本的代码中，其实仅仅是回溯了 `->` 部分（调用两次pop_back，一个pop`>` 一次pop`-`），大家应该疑惑那么 `path += to_string(cur->val);` 这一步为什么没有回溯呢？ 一条路径能持续加节点 不做回溯吗？
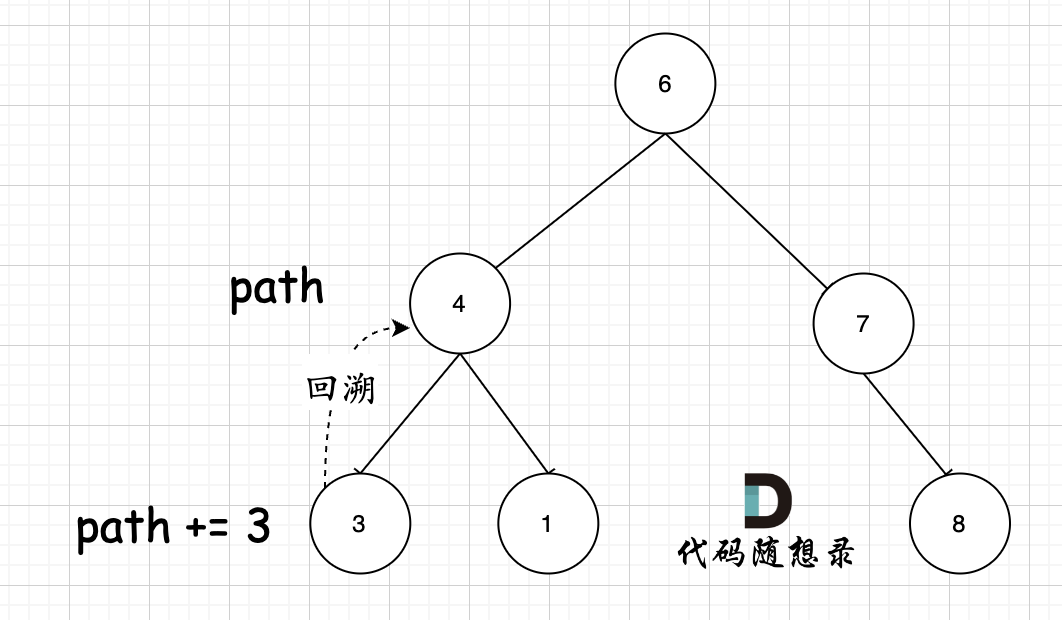
其实关键还在于 参数，使用的是 `string path`，这里并没有加上引用`&` ，即本层递归中，path + 该节点数值，但该层递归结束，上一层path的数值并不会受到任何影响。 如图所示：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220831173322.png)
节点4 的path，在遍历到节点3，path+3，遍历节点3的递归结束之后，返回节点4（回溯的过程），path并不会把3加上。
所以这是参数中，不带引用，不做地址拷贝，只做内容拷贝的效果。（这里涉及到C++引用方面的知识）
在第一个版本中，函数参数我就使用了引用，即 `vector<int>& path` ，这是会拷贝地址的，所以 本层递归逻辑如果有`path.push_back(cur->val);` 就一定要有对应的 `path.pop_back()`
那有同学可能想，为什么不去定义一个 `string& path` 这样的函数参数呢，然后也可能在递归函数中展现回溯的过程，但关键在于，`path += to_string(cur->val);` 每次是加上一个数字，这个数字如果是个位数，那好说，就调用一次`path.pop_back()`，但如果是 十位数，百位数，千位数呢？ 百位数就要调用三次`path.pop_back()`，才能实现对应的回溯操作，这样代码实现就太冗余了。
所以，第一个代码版本中，我才使用 vector 类型的path，这样方便给大家演示代码中回溯的操作。 vector类型的path，不管 每次 路径收集的数字是几位数，总之一定是int，所以就一次 pop_back就可以。
## 迭代法 ## 迭代法

6
problems/0347.前K个高频元素.md
View File

@ -33,12 +33,6 @@
《代码随想录》算法视频公开课：[优先级队列正式登场！大顶堆、小顶堆该怎么用？| LeetCode：347.前 K 个高频元素](https://www.bilibili.com/video/BV1Xg41167Lz)，相信结合视频在看本篇题解，更有助于大家对本题的理解。 《代码随想录》算法视频公开课：[优先级队列正式登场！大顶堆、小顶堆该怎么用？| LeetCode：347.前 K 个高频元素](https://www.bilibili.com/video/BV1Xg41167Lz)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
<p align="center">
<iframe src="//player.bilibili.com/player.html?aid=514643371&bvid=BV1Xg41167Lz&cid=808260290&page=1" scrolling="no" border="0" frameborder="no" framespacing="0" allowfullscreen="true" width=750 height=500> </iframe>
</p>
这道题目主要涉及到如下三块内容： 这道题目主要涉及到如下三块内容：
1. 要统计元素出现频率 1. 要统计元素出现频率
2. 对频率排序 2. 对频率排序

56
problems/0404.左叶子之和.md
View File

@ -19,7 +19,7 @@
**首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。** **首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。**
因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**如果左节点不为空，且左节点没有左右孩子，那么这个节点的左节点就是左叶子** 因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点**
大家思考一下如下图中二叉树，左叶子之和究竟是多少？ 大家思考一下如下图中二叉树，左叶子之和究竟是多少？
@ -27,12 +27,18 @@
**其实是0，因为这棵树根本没有左叶子！** **其实是0，因为这棵树根本没有左叶子！**
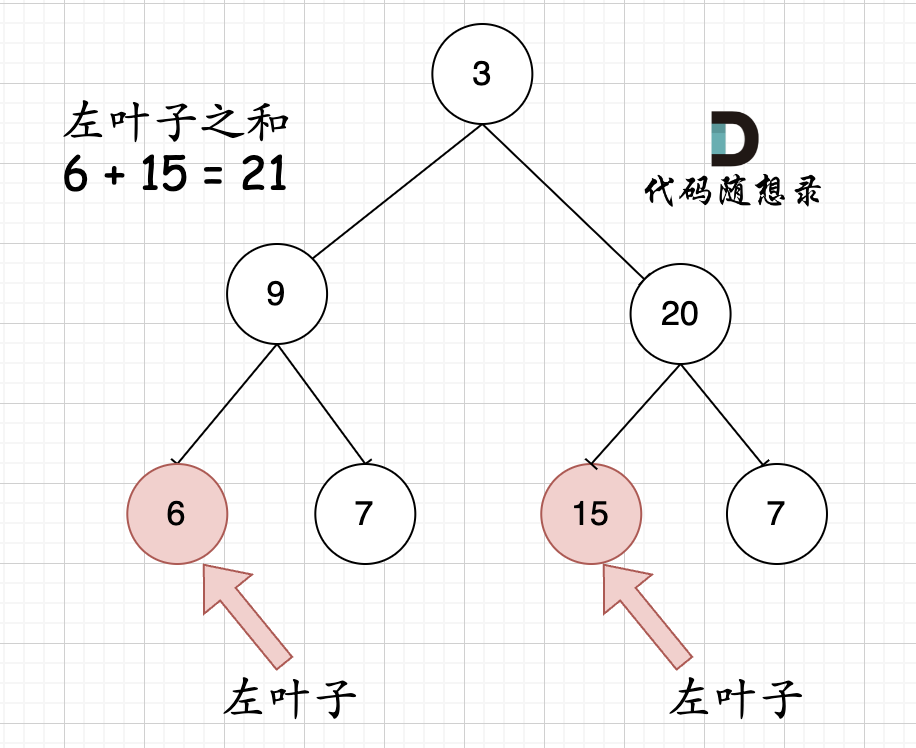
但看这个图的左叶子之和是多少？
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902165805.png)
相信通过这两个图，大家可以最左叶子的定义有明确理解了。
那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。** 那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。**
如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下： 如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下：
``` ```CPP
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) { if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
左叶子节点处理逻辑 左叶子节点处理逻辑
} }
@ -40,7 +46,7 @@ if (node->left != NULL && node->left->left == NULL && node->left->right == NULL)
## 递归法 ## 递归法
递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。。 递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲： 递归三部曲：
@ -52,11 +58,20 @@ if (node->left != NULL && node->left->left == NULL && node->left->right == NULL)
2. 确定终止条件 2. 确定终止条件
依然是 如果遍历到空节点，那么左叶子值一定是0
```
```CPP
if (root == NULL) return 0; if (root == NULL) return 0;
``` ```
注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：
```CPP
if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层。
```
3. 确定单层递归的逻辑 3. 确定单层递归的逻辑
当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。 当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。
@ -65,13 +80,12 @@ if (root == NULL) return 0;
```CPP ```CPP
int leftValue = sumOfLeftLeaves(root->left); // 左 int leftValue = sumOfLeftLeaves(root->left); // 左
int rightValue = sumOfLeftLeaves(root->right); // 右
// 中
int midValue = 0;
if (root->left && !root->left->left && !root->left->right) { if (root->left && !root->left->left && !root->left->right) {
midValue = root->left->val; leftValue = root->left->val;
} }
int sum = midValue + leftValue + rightValue; int rightValue = sumOfLeftLeaves(root->right); // 右
int sum = leftValue + rightValue; // 中
return sum; return sum;
``` ```
@ -84,18 +98,19 @@ class Solution {
public: public:
int sumOfLeftLeaves(TreeNode* root) { int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0; if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0;
int leftValue = sumOfLeftLeaves(root->left); // 左 int leftValue = sumOfLeftLeaves(root->left); // 左
int rightValue = sumOfLeftLeaves(root->right); // 右 if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况
// 中 leftValue = root->left->val;
int midValue = 0;
if (root->left && !root->left->left && !root->left->right) { // 中
midValue = root->left->val;
} }
int sum = midValue + leftValue + rightValue; int rightValue = sumOfLeftLeaves(root->right); // 右
int sum = leftValue + rightValue; // 中
return sum; return sum;
} }
}; };
``` ```
以上代码精简之后如下： 以上代码精简之后如下：
@ -105,17 +120,18 @@ class Solution {
public: public:
int sumOfLeftLeaves(TreeNode* root) { int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0; if (root == NULL) return 0;
int midValue = 0; int leftValue = 0;
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) { if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
midValue = root->left->val; leftValue = root->left->val;
} }
return midValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right); return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
} }
}; };
``` ```
## 迭代法 精简之后的代码其实看不出来用的是什么遍历方式了，对于算法初学者以上根据第一个版本来学习。
## 迭代法
本题迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了，那么参考文章 [二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)和[二叉树：迭代法统一写法](https://programmercarl.com/二叉树的统一迭代法.html)中的写法，可以写出一个前序遍历的迭代法。 本题迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了，那么参考文章 [二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)和[二叉树：迭代法统一写法](https://programmercarl.com/二叉树的统一迭代法.html)中的写法，可以写出一个前序遍历的迭代法。

12
problems/0695.岛屿的最大面积.md
View File

@ -16,8 +16,14 @@
# 思路 # 思路
这道题目也是 dfs bfs基础类题目。
注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
也就是说斜角度链接是不算了， 例如示例二，是三个岛屿，如图：
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220726094200.png)
这道题目也是 dfs bfs基础类题目。
## DFS ## DFS
@ -110,6 +116,10 @@ public:
## BFS ## BFS
关于广度优先搜索，如果大家还不了解的话，看这里：[广度优先搜索精讲](https://leetcode.cn/circle/discuss/V3FulB/)
本题BFS代码如下：
```CPP ```CPP
class Solution { class Solution {
private: private:

168
problems/0827.最大人工岛.md Normal file
View File

@ -0,0 +1,168 @@
# 827. 最大人工岛
给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
返回执行此操作后，grid 中最大的岛屿面积是多少？
岛屿 由一组上、下、左、右四个方向相连的 1 形成。
示例 1:
* 输入: grid = [[1, 0], [0, 1]]
* 输出: 3
* 解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。
示例 2:
* 输入: grid = [[1, 1], [1, 0]]
* 输出: 4
* 解释: 将一格0变成1，岛屿的面积扩大为 4。
示例 3:
* 输入: grid = [[1, 1], [1, 1]]
* 输出: 4
* 解释: 没有0可以让我们变成1，面积依然为 4。
# 思路
本题的一个暴力想法，应该是遍历地图尝试 将每一个 0 改成1，然后去搜索地图中的最大的岛屿面积。
计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n
每改变一个0的方格，都需要重新计算一个地图的最大面积，所以 整体时间复杂度为：n^4。
如果对深度优先搜索不了解的录友，可以看这里：[深度优先搜索精讲](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)
## 优化思路
其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。
只要把深搜就可以并每个岛屿的面积记录下来就好。
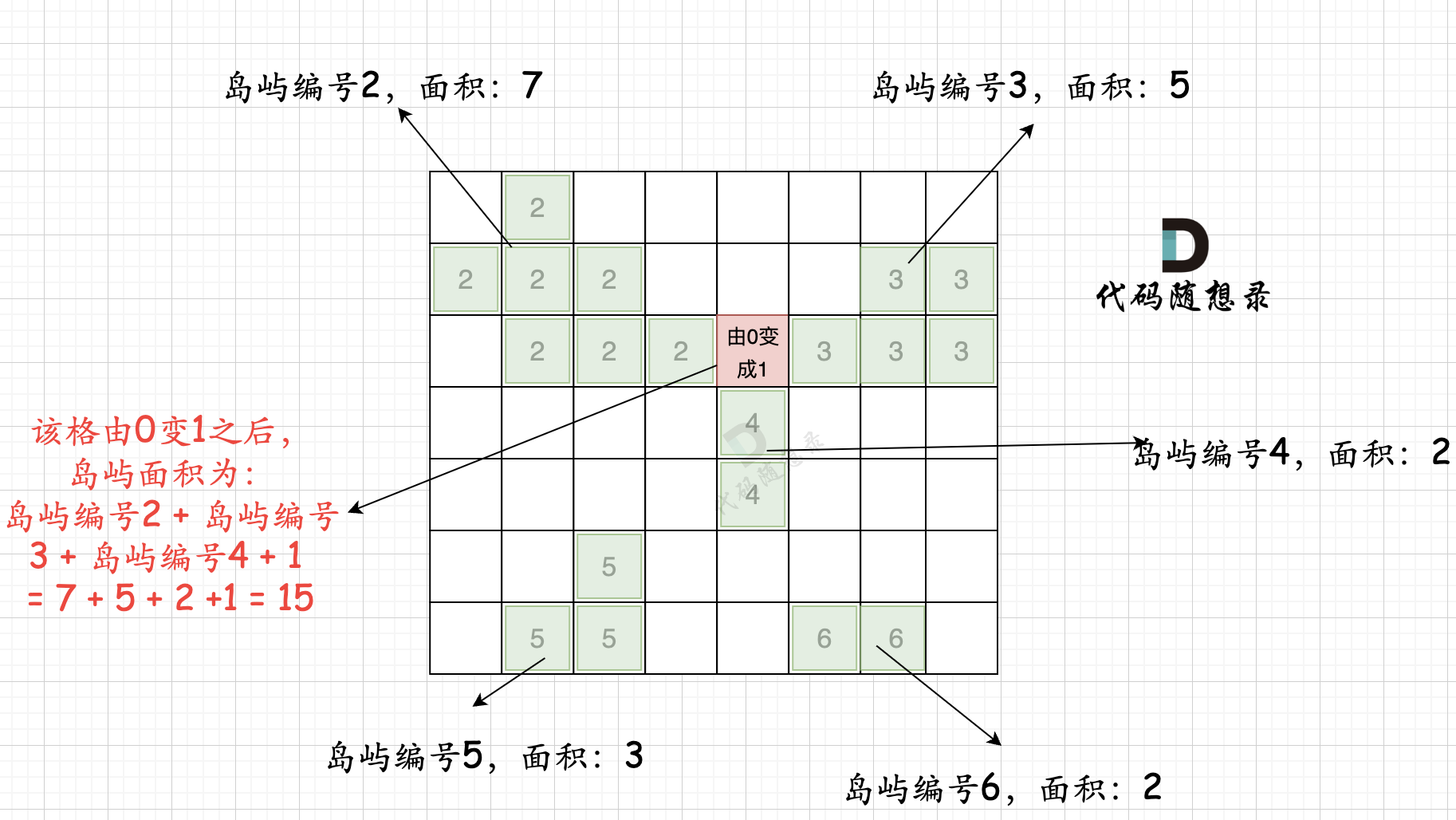
第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积
第二步：在遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。
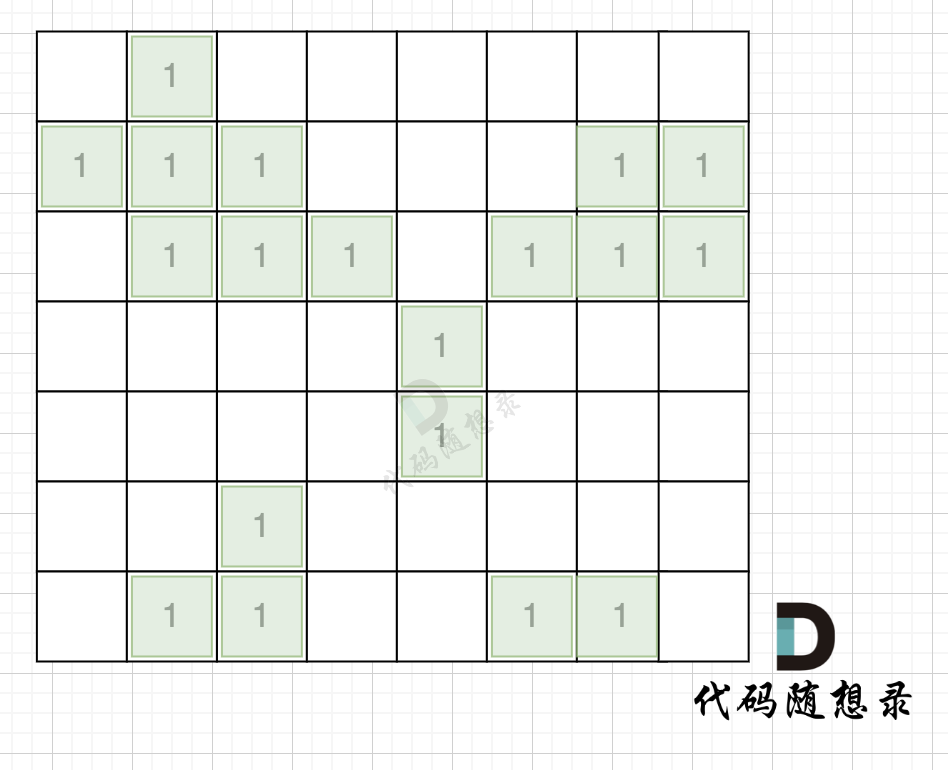
拿如下地图的岛屿情况来举例： （1为陆地）
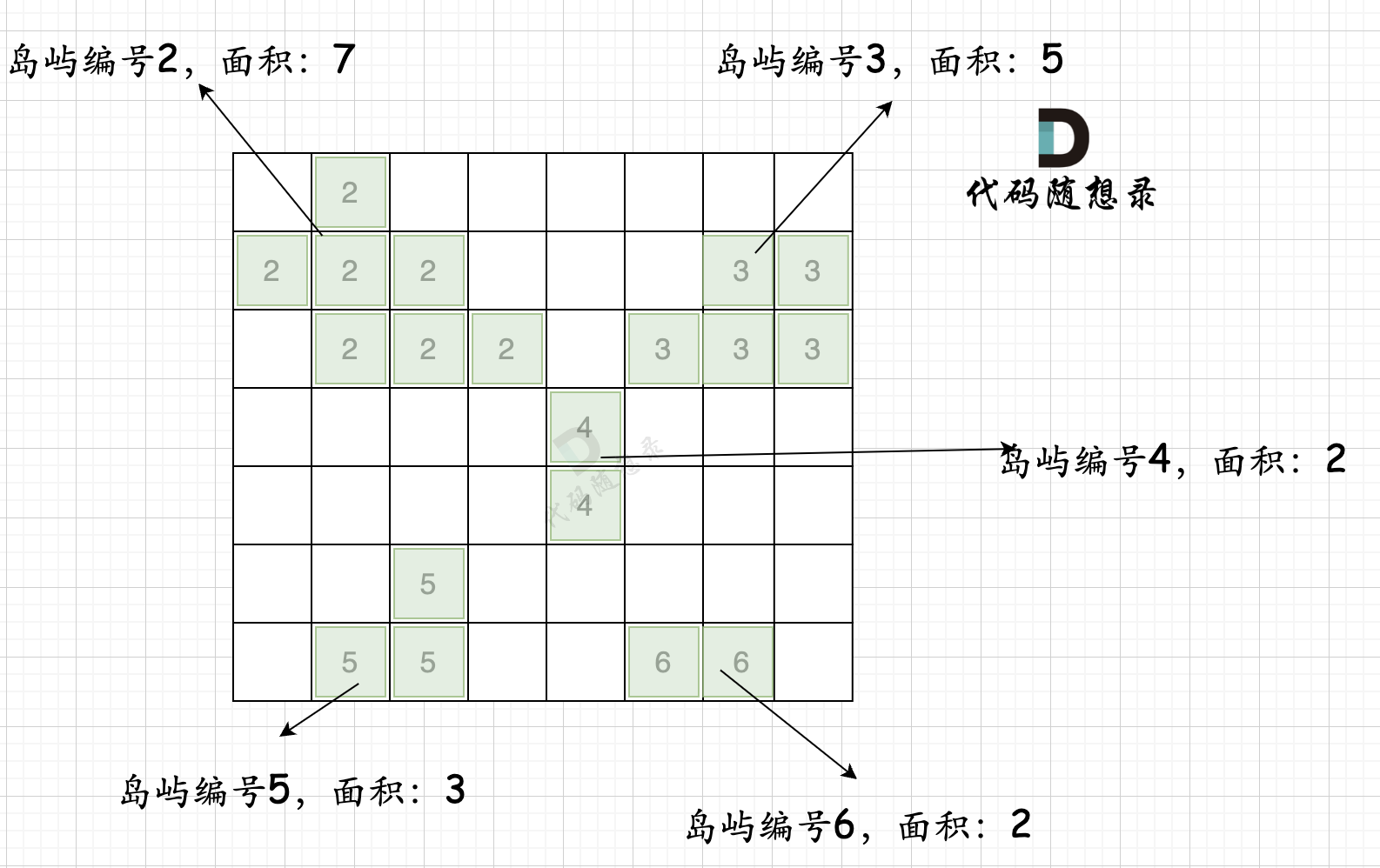
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829104834.png)
第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829105644.png)
本过程代码如下：
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
dfs(grid, visited, nextx, nexty, mark);
}
}
int largestIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
}
```
这个过程时间复杂度 n * n 。可能有录友想：分明是两个for循环下面套这一个dfs，时间复杂度怎么回事 n * n呢？
其实大家可以自己看代码的时候，**n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历**。
第二步过程如图所示：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829105249.png)
也就是遍历每一个0的方格，并统计其相邻岛屿面积，最后取一个最大值。
这个过程的时间复杂度也为 n * n。
所以整个解法的时间复杂度，为 n * n + n * n 也就是 n^2。
最后，整体代码如下：
```CPP
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
dfs(grid, visited, nextx, nexty, mark);
}
}
public:
int largestIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
if (isAllGrid) return n * m; // 如果都是陆地，返回全面积
// 以下逻辑是根据添加陆地的位置，计算周边岛屿面积之和
int result = 0; // 记录最后结果
unordered_set<int> visitedGrid; // 标记访问过的岛屿
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int count = 1; // 记录连接之后的岛屿数量
visitedGrid.clear(); // 每次使用时，清空
if (grid[i][j] == 0) {
for (int k = 0; k < 4; k++) {
int neari = i + dir[k][1]; // 计算相邻坐标
int nearj = j + dir[k][0];
if (neari < 0 || neari >= grid.size() || nearj < 0 || nearj >= grid[0].size()) continue;
if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
// 把相邻四面的岛屿数量加起来
count += gridNum[grid[neari][nearj]];
visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
}
}
result = max(result, count);
}
}
return result;
}
};
```

2
problems/0841.钥匙和房间.md
View File

@ -54,7 +54,7 @@
在图3中，大家可以发现，节点0只能到节点5，然后就哪也去不了了。 在图3中，大家可以发现，节点0只能到节点5，然后就哪也去不了了。
所以本题是一个有向图搜索全路径的问题。 只能用深搜（BFS）或者广搜（DFS）来搜。 所以本题是一个有向图搜索全路径的问题。 只能用深搜（DFS）或者广搜（BFS）来搜。
关于DFS的理论，如果大家有困惑，可以先看我这篇题解： [DFS理论基础](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf) 关于DFS的理论，如果大家有困惑，可以先看我这篇题解： [DFS理论基础](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf)

139
problems/1020.飞地的数量.md Normal file
View File

@ -0,0 +1,139 @@
# 1020. 飞地的数量
给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
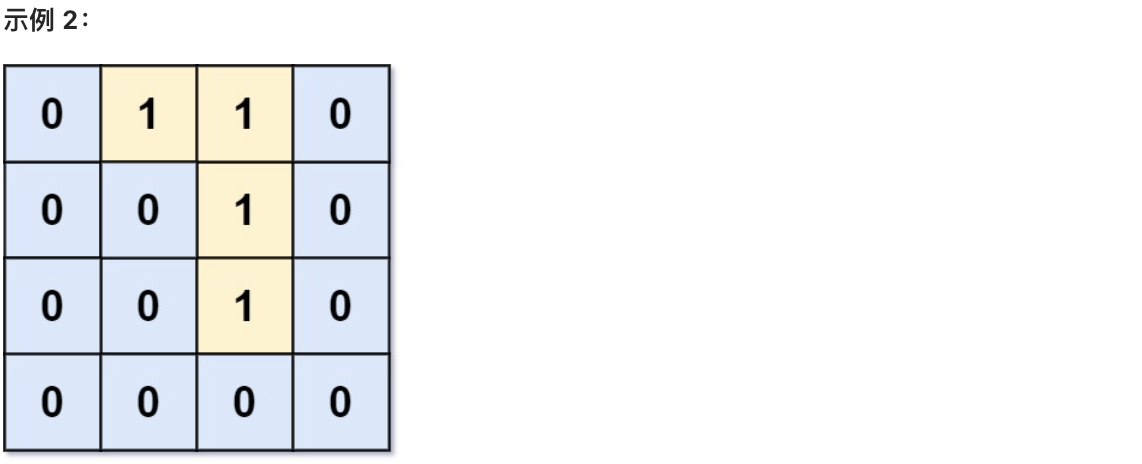
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830100710.png)
* 输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
* 输出：3
* 解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830100742.png)
* 输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
* 输出：0
* 解释：所有 1 都在边界上或可以到达边界。
## 思路
本题使用dfs，bfs，并查集都是可以的。 本题和 417. 太平洋大西洋水流问题 很像。
本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图的时候，统计此时还剩下的陆地就可以了。
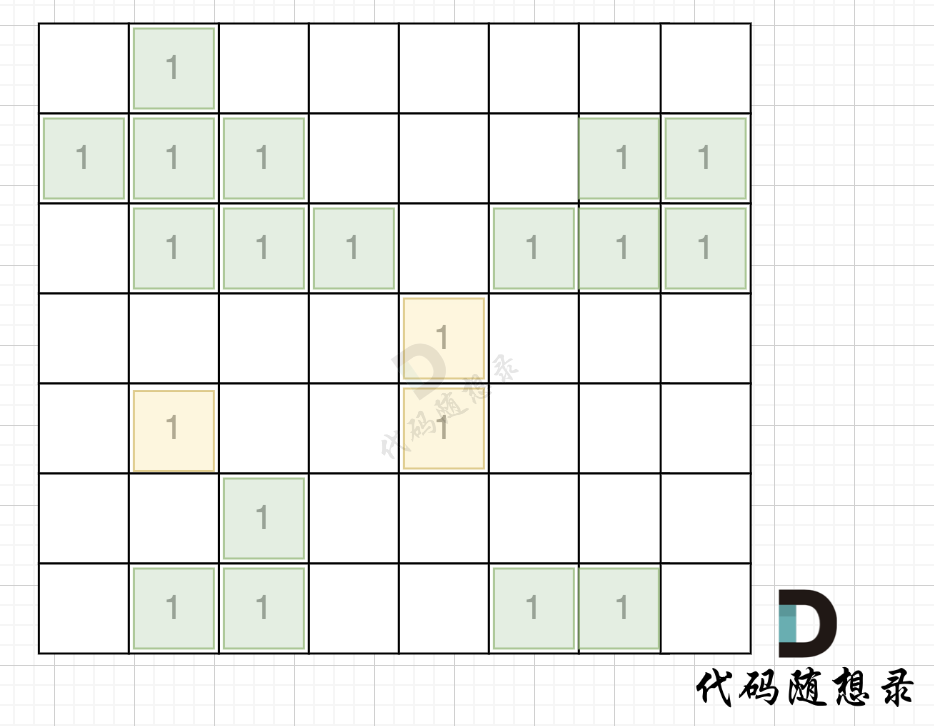
如图，在遍历地图周围四个边，靠地图四边的陆地，都为绿色，
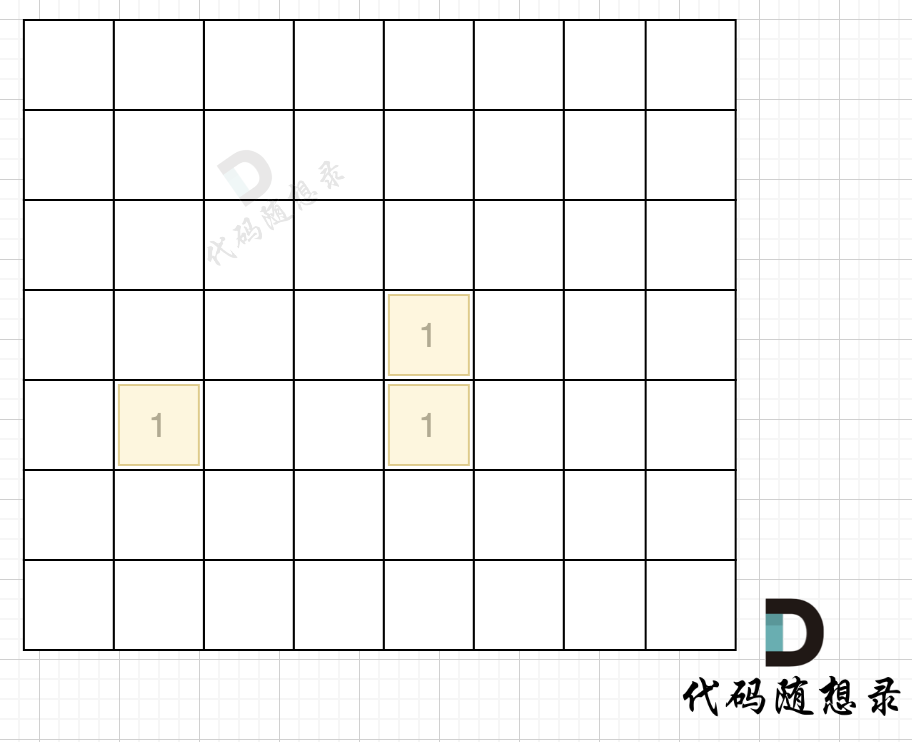
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830104632.png)
在遇到地图周边陆地的时候，将1都变为0，此时地图为这样：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830104651.png)
然后我们再去遍历这个地图，遇到有陆地的地方，去采用深搜或者广搜，边统计所有陆地。
如果对深搜或者广搜不够了解，建议先看这里：[深度优先搜索精讲](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)，[广度优先搜索精讲](https://leetcode.cn/circle/discuss/V3FulB/)
采用深度优先搜索的代码如下：
```CPP
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
int count; // 统计符合题目要求的陆地空格数量
void dfs(vector<vector<int>>& grid, int x, int y) {
grid[x][y] = 0;
count++;
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
// 不符合条件，不继续遍历
if (grid[nextx][nexty] == 0) continue;
dfs (grid, nextx, nexty);
}
return;
}
public:
int numEnclaves(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
// 从左侧边，和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) dfs(grid, i, 0);
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) dfs(grid, 0, j);
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) dfs(grid, i, j);
}
}
return count;
}
};
```
采用广度优先搜索的代码如下：
```CPP
class Solution {
private:
int count = 0;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<int>>& grid, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
grid[x][y] = 0; // 只要加入队列，立刻标记
count++;
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了，直接跳过
if (grid[nextx][nexty] == 1) {
que.push({nextx, nexty});
count++;
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
}
}
}
}
public:
int numEnclaves(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
// 从左侧边，和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) bfs(grid, i, 0);
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) bfs(grid, 0, j);
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) bfs(grid, i, j);
}
}
return count;
}
};
```

74
problems/1254.统计封闭岛屿的数目.md Normal file
View File

@ -0,0 +1,74 @@
# 1254. 统计封闭岛屿的数目
[力扣题目链接](https://leetcode.cn/problems/number-of-closed-islands/)
二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。
请返回 封闭岛屿 的数目。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830111533.png)
* 输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
* 输出：2
* 解释：灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220830111601.png)
* 输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
* 输出：1
提示：
* 1 <= grid.length, grid[0].length <= 100
* 0 <= grid[i][j] <=1
## 思路
和 [1020. 飞地的数量](https://leetcode.cn/problems/number-of-enclaves/solution/by-carlsun-2-7lt9/) 思路是一样的，代码也基本一样
```CPP
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
void dfs(vector<vector<int>>& grid, int x, int y) {
grid[x][y] = 1;
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
// 不符合条件，不继续遍历
if (grid[nextx][nexty] == 1) continue;
dfs (grid, nextx, nexty);
}
return;
}
public:
int closedIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
// 从左侧边，和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 0) dfs(grid, i, 0);
if (grid[i][m - 1] == 0) dfs(grid, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 0) dfs(grid, 0, j);
if (grid[n - 1][j] == 0) dfs(grid, n - 1, j);
}
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) {
count++;
dfs(grid, i, j);
}
}
}
return count;
}
};
```

4
problems/二叉树理论基础.md
View File

@ -6,6 +6,10 @@
# 二叉树理论基础篇 # 二叉树理论基础篇
《代码随想录》算法视频公开课：[关于二叉树，你该了解这些！](https://www.bilibili.com/video/BV1Hy4y1t7ij)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
题目分类大纲如下： 题目分类大纲如下：
<img src='https://img-blog.csdnimg.cn/20210219190809451.png' width=600 alt='二叉树大纲'> </img></div> <img src='https://img-blog.csdnimg.cn/20210219190809451.png' width=600 alt='二叉树大纲'> </img></div>

6
problems/二叉树的迭代遍历.md
View File

@ -7,6 +7,12 @@
# 二叉树的迭代遍历 # 二叉树的迭代遍历
《代码随想录》算法视频公开课：
* [写出二叉树的非递归遍历很难么？（前序和后序）](https://www.bilibili.com/video/BV15f4y1W7i2)
* [写出二叉树的非递归遍历很难么？（中序）)](https://www.bilibili.com/video/BV1Zf4y1a77g)
相信结合视频在看本篇题解，更有助于大家对本题的理解。
> 听说还可以用非递归的方式 > 听说还可以用非递归的方式
看完本篇大家可以使用迭代法，再重新解决如下三道leetcode上的题目： 看完本篇大家可以使用迭代法，再重新解决如下三道leetcode上的题目：

4
problems/二叉树的递归遍历.md
View File

@ -8,6 +8,10 @@
# 二叉树的递归遍历 # 二叉树的递归遍历
《代码随想录》算法视频公开课：[每次写递归都要靠直觉？ 这次带你学透二叉树的递归遍历！](https://www.bilibili.com/video/BV1Wh411S7xt)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
> 一看就会，一写就废！ > 一看就会，一写就废！
这次我们要好好谈一谈递归，为什么很多同学看递归算法都是“一看就会，一写就废”。 这次我们要好好谈一谈递归，为什么很多同学看递归算法都是“一看就会，一写就废”。

121
problems/图论广索理论基础.md Normal file
View File

@ -0,0 +1,121 @@
# 广度优先搜索理论基础
> 号外！！代码随想录图论内容已经计划开更了！
在[深度优先搜索](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)的讲解中，我们就讲过深度优先搜索和广度优先搜索的区别。
广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后在回溯。
## 广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题。
因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。
当然，也有一些问题是广搜 和 深搜都可以解决的，例如岛屿问题，**这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行**。 （我们会在具体题目讲解中详细来说）
## 广搜的过程
上面我们提过，BFS是一圈一圈的搜索过程，但具体是怎么一圈一圈来搜呢。
我们用一个方格地图，假如每次搜索的方向为 上下左右（不包含斜上方），那么给出一个start起始位置，那么BFS就是从四个方向走出第一步。
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220825104505.png)
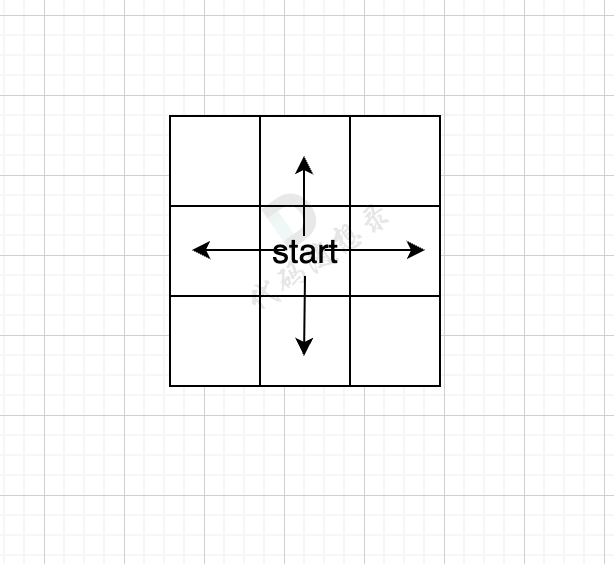
如果加上一个end终止位置，那么使用BFS的搜索过程如图所示：
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220825102653.png)
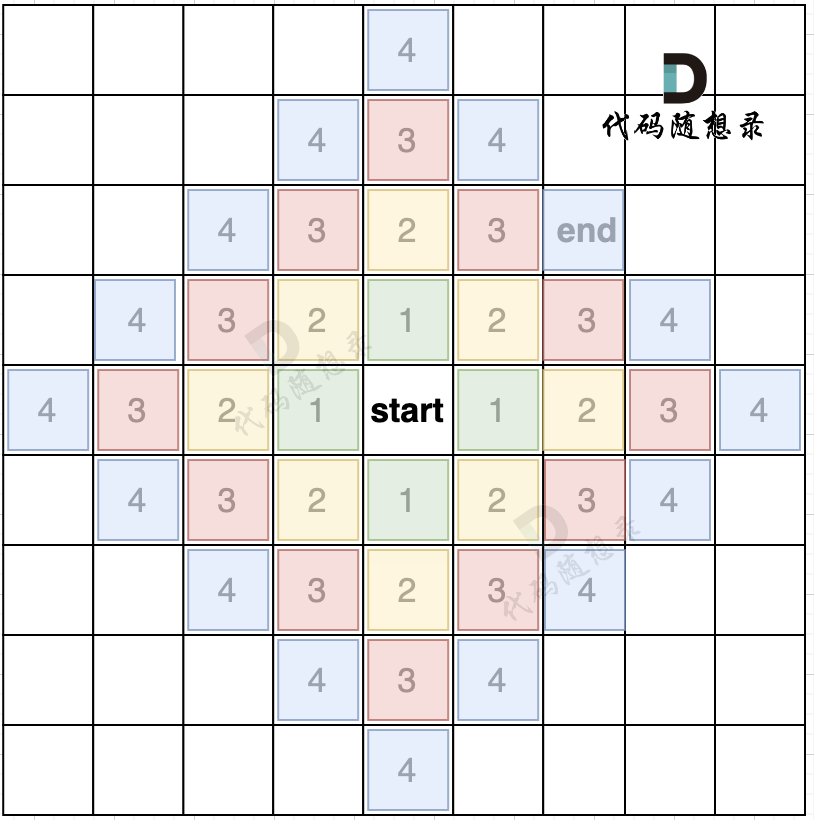
我们从图中可以看出，从start起点开始，是一圈一圈，向外搜索，方格编号1为第一步遍历的节点，方格编号2为第二步遍历的节点，第四步的时候我们找到终止点end。
正是因为BFS一圈一圈的遍历方式，所以一旦遇到终止点，那么一定是一条最短路径。
而且地图还可以有障碍，如图所示：
![图三](https://code-thinking-1253855093.file.myqcloud.com/pics/20220825103900.png)
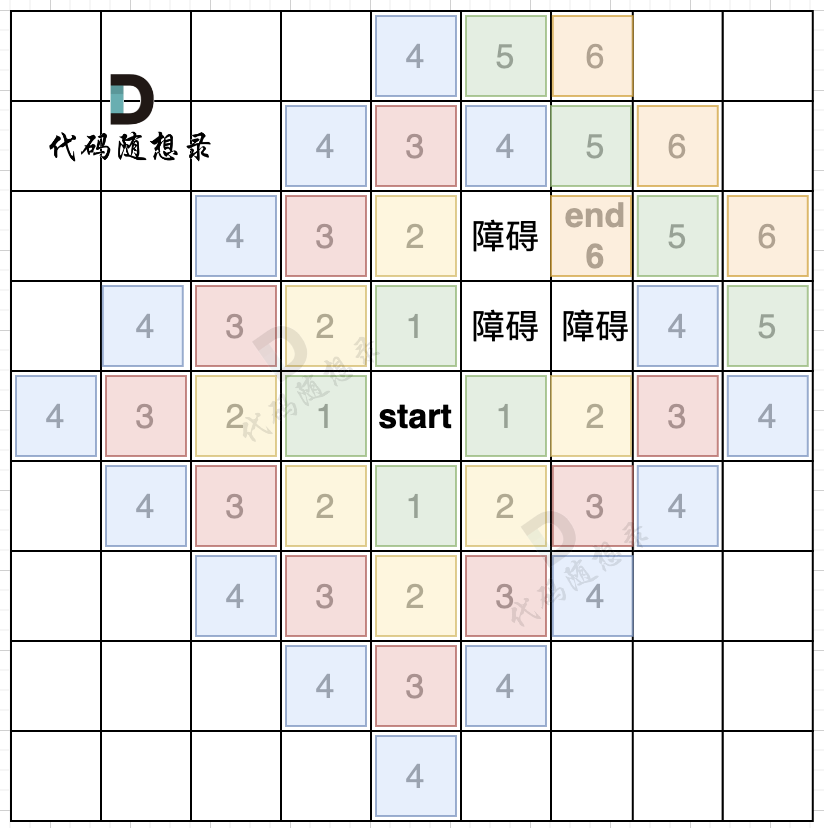
在第五步，第六步 我只把关键的节点染色了，其他方向周边没有去染色，大家只要关注关键地方染色的逻辑就可以。
从图中可以看出，如果添加了障碍，我们是第六步才能走到end终点。
只要BFS只要搜到终点一定是一条最短路径，大家可以参考上面的图，自己再去模拟一下。
## 代码框架
大家应该好奇，这一圈一圈的搜索过程是怎么做到的，是放在什么容器里，才能这样去遍历。
很多网上的资料都是直接说用队列来实现。
其实，我们仅仅需要一个容器，能保存我们要遍历过的元素就可以，**那么用队列，还是用栈，甚至用数组，都是可以的**。
用队列的话，就是保证每一圈都是一个方向去转，例如统一顺时针或者逆时针。
因为队列是先进先出，加入元素和弹出元素的顺序是没有改变的。
如果用栈的话，可能就是第一圈顺时针遍历，第二圈逆时针遍历，第三圈有顺时针遍历。
因为栈是先进后出，加入元素和弹出元素的顺序改变了。
那么广搜需要注意 转圈搜索的顺序吗？ 不需要！
所以用队列，还是用栈都是可以的，但大家都习惯用队列了，所以下面的讲解用我也用队列来讲，只不过要给大家说清楚，并不是非要用队列，用栈也可以。
下面给出广搜代码模板，该模板针对的就是，上面的四方格的地图： （详细注释）
```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que; // 定义队列
que.push({x, y}); // 起始节点加入队列
visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
while(!que.empty()) { // 开始遍历队列里的元素
pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
int curx = cur.first;
int cury = cur.second; // 当前节点坐标
for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了，直接跳过
if (!visited[nextx][nexty]) { // 如果节点没被访问过
que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
}
}
}
}
```
以上模板代码，就是可以直接拿来做 [200.岛屿数量](https://leetcode.cn/problems/number-of-islands/solution/by-carlsun-2-n72a/) 这道题目，唯一区别是 针对地图 grid 中有数字1的地方去做一个遍历。
即：
```
if (!visited[nextx][nexty]) { // 如果节点没被访问过
```
改为
```
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 如果节点没被访问过且节点是可遍历的
```
就可以通过 [200.岛屿数量](https://leetcode.cn/problems/number-of-islands/solution/by-carlsun-2-n72a/) 这道题目，大家可以去体验一下。
## 总结
当然广搜还有很多细节需要注意的地方，后面我会针对广搜的题目还做针对性的讲解，因为在理论篇讲太多细节，可能会让刚学广搜的录友们越看越懵，所以细节方面针对具体题目在做讲解。
本篇我们重点讲解了广搜的使用场景，广搜的过程以及广搜的代码框架。
其实在二叉树章节的[层序遍历](https://programmercarl.com/0102.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B1%82%E5%BA%8F%E9%81%8D%E5%8E%86.html)中，我们也讲过一次广搜，相当于是广搜在二叉树这种数据结构上的应用。
这次则从图论的角度上再详细讲解一次广度优先遍历。
相信看完本篇，大家会对广搜有一个基础性的认识，后面再来做对应的题目就会得心应手一些。

187
problems/图论深搜理论基础.md Normal file
View File

@ -0,0 +1,187 @@
# 深度优先搜索理论基础
提到深度优先搜索（dfs），就不得不说和广度优先有什么区别（bfs）
## dfs 与 bfs 区别
先来了解dfs的过程，很多录友可能对dfs（深度优先搜索），bfs（广度优先搜索）分不清。
先给大家说一下两者大概的区别：
* dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，在换方向（换方向的过程就涉及到了回溯）。
* bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。
当然以上讲的是，大体可以这么理解，接下来 我们详细讲解dfs，（bfs在用单独一篇文章详细讲解）
## dfs 搜索过程
上面说道dfs是可一个方向搜，不到黄河不回头。 那么我们来举一个例子。
如图一，是一个无向图，我们要搜索从节点1到节点6的所有路径。
![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707093643.png)
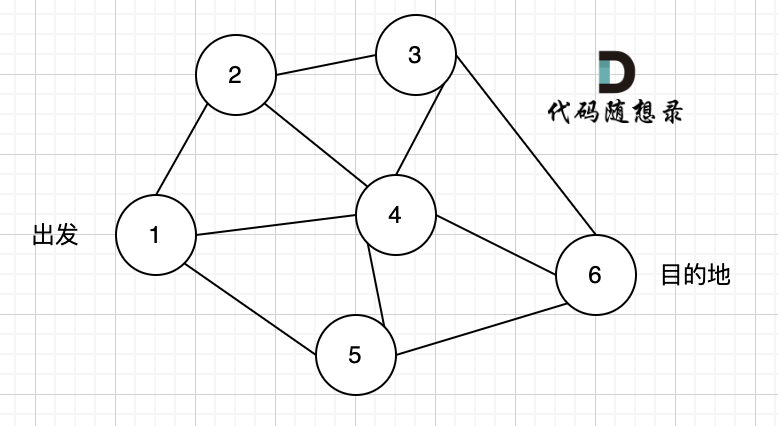
那么dfs搜索的第一条路径是这样的： （假设第一次延默认方向，就找到了节点6），图二
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707093807.png)
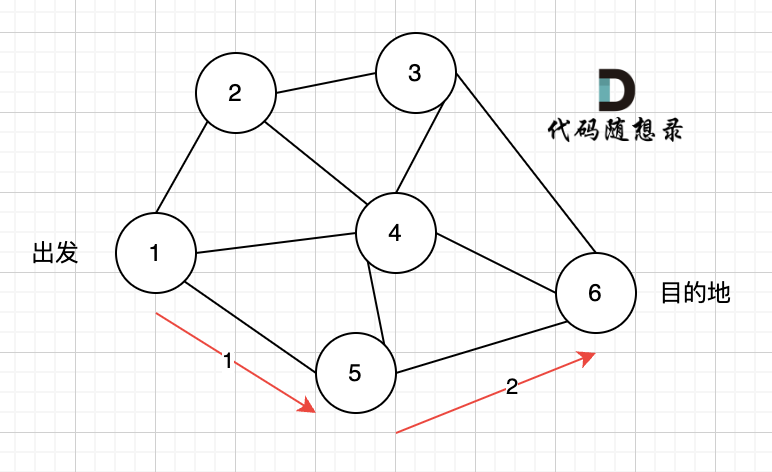
此时我们找到了节点6，（遇到黄河了，是不是应该回头了），那么应该再去搜索其他方向了。 如图三：
![图三](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094011.png)
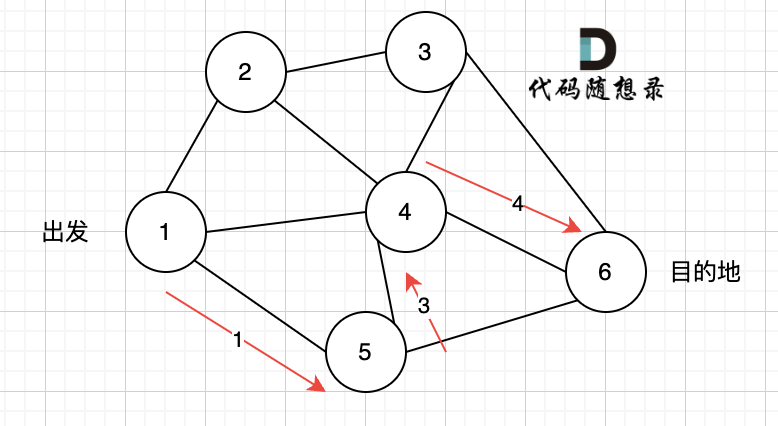
路径2撤销了，改变了方向，走路径3（红色线）， 接着也找到终点6。 那么撤销路径2，改为路径3，在dfs中其实就是回溯的过程（这一点很重要，很多录友，都不理解dfs代码中回溯是用来干什么的）
又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图四中，路径4撤销（回溯的过程），改为路径5。
![图四](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094322.png)
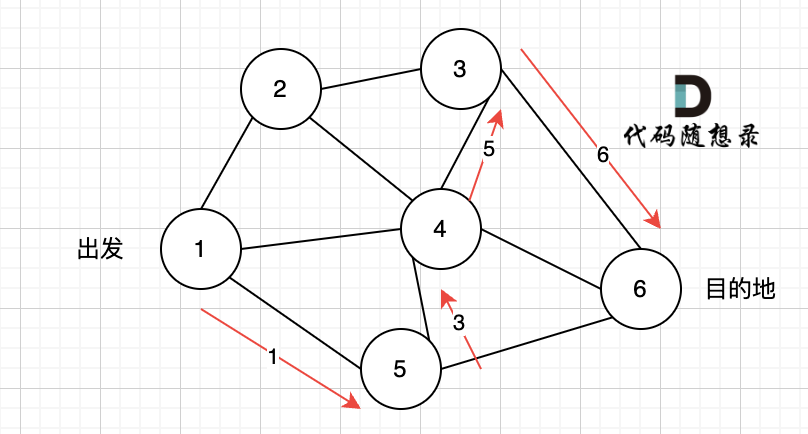
又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图五，路径6撤销（回溯的过程），改为路径7，路径8 和 路径7，路径9， 结果发现死路一条，都走到了自己走过的节点。
![图五](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707094813.png)
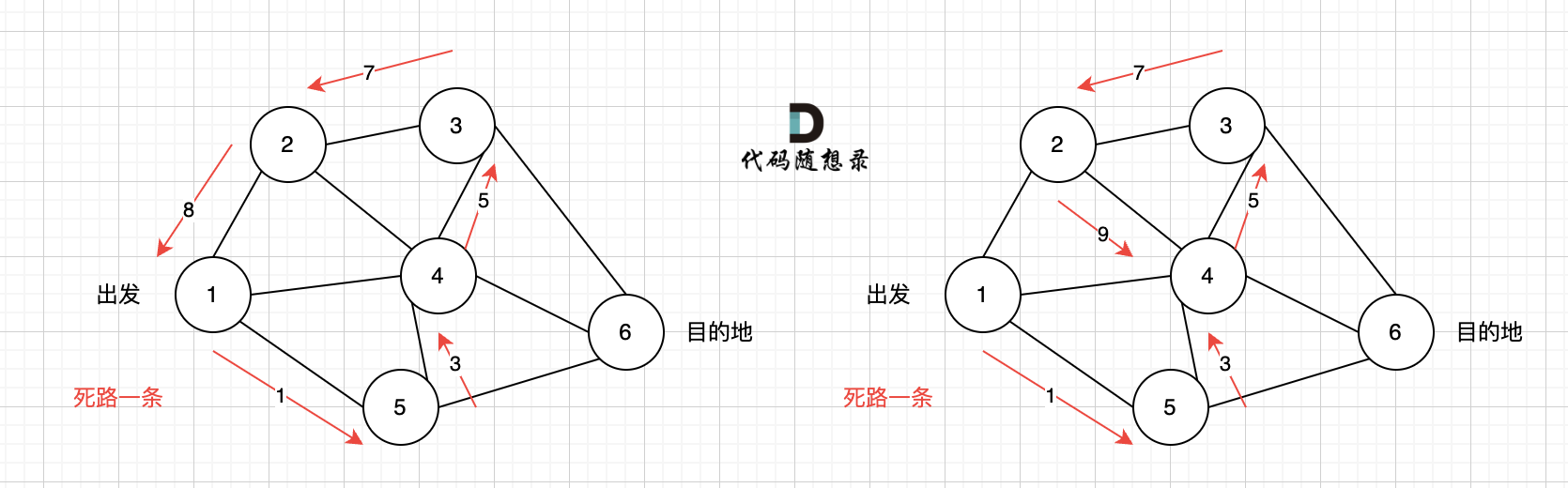
那么节点2所连接路径和节点3所链接的路径 都走过了，撤销路径只能向上回退，去选择撤销当初节点4的选择，也就是撤销路径5，改为路径10 。 如图图六：
![图六](https://code-thinking-1253855093.file.myqcloud.com/pics/20220707095232.png)
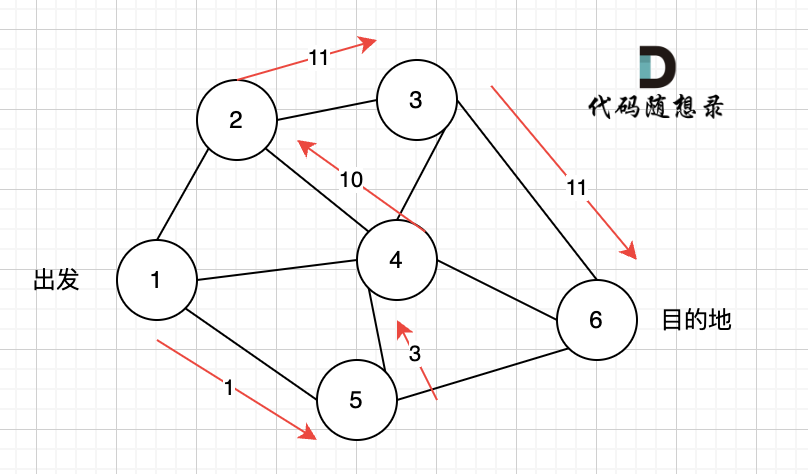
上图演示中，其实我并没有把 所有的 从节点1 到节点6的dfs（深度优先搜索）的过程都画出来，那样太冗余了，但 已经把dfs 关键的地方都涉及到了，关键就两点：
* 搜索方向，是认准一个方向搜，直到碰壁之后在换方向
* 换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程。
## 代码框架
正式因为dfs搜索可一个方向，并需要回溯，所以用递归的方式来实现是最方便的。
很多录友对回溯很陌生，建议先看看码随想录，[回溯算法章节](https://programmercarl.com/回溯算法理论基础.html)。
有递归的地方就有回溯，那么回溯在哪里呢？
就地递归函数的下面，例如如下代码：
```
void dfs(参数) {
处理节点
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
```
可以看到回溯操作就在递归函数的下面，递归和回溯是相辅相成的。
在讲解[二叉树章节](https://programmercarl.com/二叉树理论基础.html)的时候，二叉树的递归法其实就是dfs，而二叉树的迭代法，就是bfs（广度优先搜索）
所以**dfs，bfs其实是基础搜索算法，也广泛应用与其他数据结构与算法中**。
我们在回顾一下[回溯法](https://programmercarl.com/回溯算法理论基础.html)的代码框架：
```
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表); // 递归
回溯，撤销处理结果
}
}
```
回溯算法，其实就是dfs的过程，这里给出dfs的代码框架：
```
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本节点所连接的其他节点) {
处理节点;
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
}
```
可以发现dfs的代码框架和回溯算法的代码框架是差不多的。
下面我在用 深搜三部曲，来解读 dfs的代码框架。
## 深搜三部曲
在 [二叉树递归讲解](https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html)中，给出了递归三部曲。
[回溯算法](https://programmercarl.com/回溯算法理论基础.html)讲解中，给出了 回溯三部曲。
其实深搜也是一样的，深搜三部曲如下：
1. 确认递归函数，参数
```
void dfs(参数)
```
通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。
一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局遍历，避免让我们的函数参数过多。
例如这样：
```
vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)
```
但这种写法看个人习惯，不强求。
2. 确认终止条件
终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。
```
if (终止条件) {
存放结果;
return;
}
```
终止添加不仅是结束本层递归，同时也是我们收获结果的时候。
另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。
* 841.钥匙和房间
* 200. 岛屿数量
3. 处理目前搜索节点出发的路径
一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。
```
for (选择：本节点所连接的其他节点) {
处理节点;
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
```
不少录友疑惑的地方，都是 dfs代码框架中for循环里分明已经处理节点了，那么 dfs函数下面 为什么还要撤销的呢。
如图七所示， 路径2 已经走到了 目的地节点6，那么 路径2 是如何撤销，然后改为 路径3呢？ 其实这就是 回溯的过程，撤销路径2，走换下一个方向。
![图七](https://code-thinking-1253855093.file.myqcloud.com/pics/20220708093544.png)
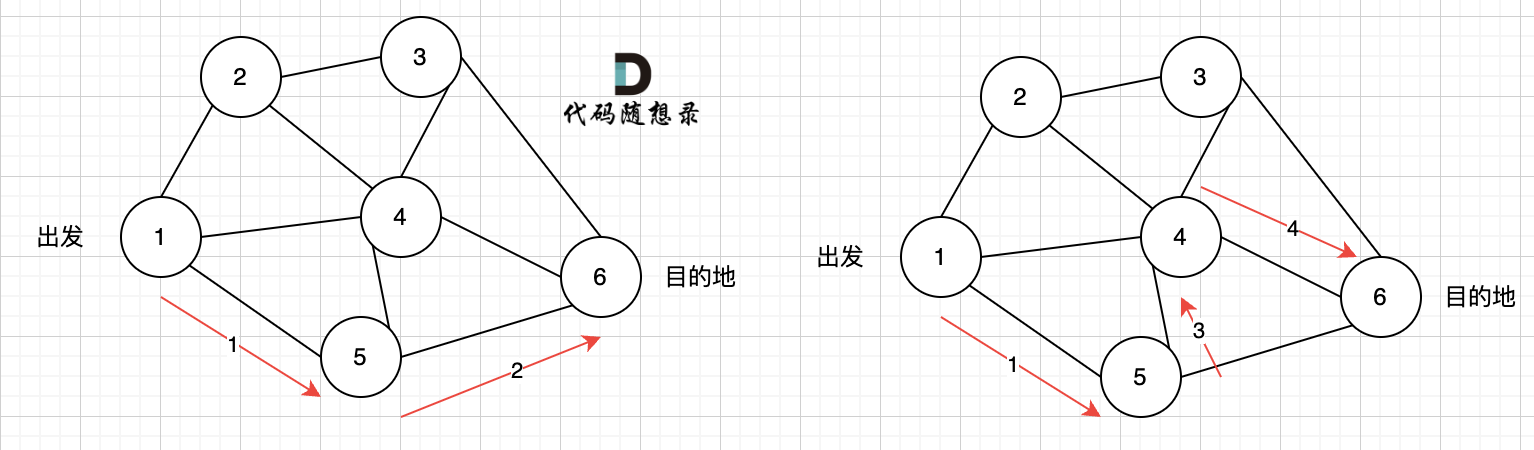
## 总结
我们讲解了，dfs 和 bfs的大体区别（bfs详细过程下篇来讲），dfs的搜索过程以及代码框架。
最后还有 深搜三部曲来解读这份代码框架。
以上如果大家都能理解了，其实搜索的代码就很好写，具体题目套用具体场景就可以了。

2
problems/背包总结篇.md
View File

@ -3,6 +3,8 @@
<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20210924105952.png" width="1000"/> <img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20210924105952.png" width="1000"/>
</a> </a>
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p> <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
# 听说背包问题很难？ 这篇总结篇来拯救你了 # 听说背包问题很难？ 这篇总结篇来拯救你了
年前我们已经把背包问题都讲完了，那么现在我们要对背包问题进行总结一番。 年前我们已经把背包问题都讲完了，那么现在我们要对背包问题进行总结一番。