mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
Update
This commit is contained in:
@ -282,12 +282,13 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
|
||||
```Python
|
||||
**回溯**
|
||||
```python3
|
||||
class Solution:
|
||||
ans = []
|
||||
s = ''
|
||||
letterMap = {
|
||||
def __init__(self):
|
||||
self.answers: List[str] = []
|
||||
self.answer: str = ''
|
||||
self.letter_map = {
|
||||
'2': 'abc',
|
||||
'3': 'def',
|
||||
'4': 'ghi',
|
||||
@ -298,45 +299,57 @@ class Solution:
|
||||
'9': 'wxyz'
|
||||
}
|
||||
|
||||
def letterCombinations(self, digits):
|
||||
self.ans.clear()
|
||||
if digits == '':
|
||||
return self.ans
|
||||
self.backtracking(digits, 0)
|
||||
return self.ans
|
||||
|
||||
def backtracking(self, digits, index):
|
||||
if index == len(digits):
|
||||
self.ans.append(self.s)
|
||||
return
|
||||
else:
|
||||
letters = self.letterMap[digits[index]] # 取出数字对应的字符集
|
||||
for letter in letters:
|
||||
self.s = self.s + letter # 处理
|
||||
self.backtracking(digits, index + 1)
|
||||
self.s = self.s[:-1] # 回溯
|
||||
```
|
||||
|
||||
python3:
|
||||
|
||||
```py
|
||||
class Solution:
|
||||
def letterCombinations(self, digits: str) -> List[str]:
|
||||
res = []
|
||||
s = ""
|
||||
letterMap = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"]
|
||||
if not len(digits): return res
|
||||
def backtrack(digits,index, s):
|
||||
if index == len(digits):
|
||||
return res.append(s)
|
||||
digit = int(digits[index]) #将index指向的数字转为int
|
||||
letters = letterMap[digit] #取数字对应的字符集
|
||||
for i in range(len(letters)):
|
||||
s += letters[i]
|
||||
backtrack(digits, index+1, s) #递归,注意index+1,一下层要处理下一个数字
|
||||
s = s[:-1] #回溯
|
||||
backtrack(digits, 0, s)
|
||||
return res
|
||||
self.answers.clear()
|
||||
if not digits: return []
|
||||
self.backtracking(digits, 0)
|
||||
return self.answers
|
||||
|
||||
def backtracking(self, digits: str, index: int) -> None:
|
||||
# 回溯函数没有返回值
|
||||
# Base Case
|
||||
if index == len(digits): # 当遍历穷尽后的下一层时
|
||||
self.answers.append(self.answer)
|
||||
return
|
||||
# 单层递归逻辑
|
||||
letters: str = self.letter_map[digits[index]]
|
||||
for letter in letters:
|
||||
self.answer += letter # 处理
|
||||
self.backtracking(digits, index + 1) # 递归至下一层
|
||||
self.answer = self.answer[:-1] # 回溯
|
||||
```
|
||||
**回溯简化**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.answers: List[str] = []
|
||||
self.letter_map = {
|
||||
'2': 'abc',
|
||||
'3': 'def',
|
||||
'4': 'ghi',
|
||||
'5': 'jkl',
|
||||
'6': 'mno',
|
||||
'7': 'pqrs',
|
||||
'8': 'tuv',
|
||||
'9': 'wxyz'
|
||||
}
|
||||
|
||||
def letterCombinations(self, digits: str) -> List[str]:
|
||||
self.answers.clear()
|
||||
if not digits: return []
|
||||
self.backtracking(digits, 0, '')
|
||||
return self.answers
|
||||
|
||||
def backtracking(self, digits: str, index: int, answer: str) -> None:
|
||||
# 回溯函数没有返回值
|
||||
# Base Case
|
||||
if index == len(digits): # 当遍历穷尽后的下一层时
|
||||
self.answers.append(answer)
|
||||
return
|
||||
# 单层递归逻辑
|
||||
letters: str = self.letter_map[digits[index]]
|
||||
for letter in letters:
|
||||
self.backtracking(digits, index + 1, answer + letter) # 递归至下一层 + 回溯
|
||||
```
|
||||
|
||||
|
||||
|
||||
@ -50,7 +50,7 @@
|
||||
* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B91.png' width=600> </img></div>
|
||||
|
||||
* fast和slow同时移动,之道fast指向末尾,如题:
|
||||
* fast和slow同时移动,直到fast指向末尾,如题:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B92.png' width=600> </img></div>
|
||||
|
||||
* 删除slow指向的下一个节点,如图:
|
||||
|
||||
@ -215,7 +215,7 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
|
||||
|
||||
其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
|
||||
|
||||
后面我会提供两种不同的实现代码,大家就明白了了。
|
||||
后面我会提供两种不同的实现代码,大家就明白了。
|
||||
|
||||
# 使用next数组来匹配
|
||||
|
||||
|
||||
@ -227,7 +227,24 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Golang:
|
||||
```golang
|
||||
// 第一种二分法
|
||||
func searchInsert(nums []int, target int) int {
|
||||
l, r := 0, len(nums) - 1
|
||||
for l <= r{
|
||||
m := l + (r - l)/2
|
||||
if nums[m] == target{
|
||||
return m
|
||||
}else if nums[m] > target{
|
||||
r = m - 1
|
||||
}else{
|
||||
l = m + 1
|
||||
}
|
||||
}
|
||||
return r + 1
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
```python3
|
||||
|
||||
@ -292,85 +292,40 @@ class Solution:
|
||||
"""
|
||||
Do not return anything, modify board in-place instead.
|
||||
"""
|
||||
def backtrack(board):
|
||||
for i in range(len(board)): #遍历行
|
||||
for j in range(len(board[0])): #遍历列
|
||||
if board[i][j] != ".": continue
|
||||
for k in range(1,10): #(i, j) 这个位置放k是否合适
|
||||
if isValid(i,j,k,board):
|
||||
board[i][j] = str(k) #放置k
|
||||
if backtrack(board): return True #如果找到合适一组立刻返回
|
||||
board[i][j] = "." #回溯,撤销k
|
||||
return False #9个数都试完了,都不行,那么就返回false
|
||||
return True #遍历完没有返回false,说明找到了合适棋盘位置了
|
||||
def isValid(row,col,val,board):
|
||||
for i in range(9): #判断行里是否重复
|
||||
self.backtracking(board)
|
||||
|
||||
def backtracking(self, board: List[List[str]]) -> bool:
|
||||
# 若有解,返回True;若无解,返回False
|
||||
for i in range(len(board)): # 遍历行
|
||||
for j in range(len(board[0])): # 遍历列
|
||||
# 若空格内已有数字,跳过
|
||||
if board[i][j] != '.': continue
|
||||
for k in range(1, 10):
|
||||
if self.is_valid(i, j, k, board):
|
||||
board[i][j] = str(k)
|
||||
if self.backtracking(board): return True
|
||||
board[i][j] = '.'
|
||||
# 若数字1-9都不能成功填入空格,返回False无解
|
||||
return False
|
||||
return True # 有解
|
||||
|
||||
def is_valid(self, row: int, col: int, val: int, board: List[List[str]]) -> bool:
|
||||
# 判断同一行是否冲突
|
||||
for i in range(9):
|
||||
if board[row][i] == str(val):
|
||||
return False
|
||||
for j in range(9): #判断列里是否重复
|
||||
# 判断同一列是否冲突
|
||||
for j in range(9):
|
||||
if board[j][col] == str(val):
|
||||
return False
|
||||
startRow = (row // 3) * 3
|
||||
startcol = (col // 3) * 3
|
||||
for i in range(startRow,startRow + 3): #判断9方格里是否重复
|
||||
for j in range(startcol,startcol + 3):
|
||||
# 判断同一九宫格是否有冲突
|
||||
start_row = (row // 3) * 3
|
||||
start_col = (col // 3) * 3
|
||||
for i in range(start_row, start_row + 3):
|
||||
for j in range(start_col, start_col + 3):
|
||||
if board[i][j] == str(val):
|
||||
return False
|
||||
return True
|
||||
backtrack(board)
|
||||
```
|
||||
|
||||
### Python3
|
||||
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self) -> None:
|
||||
self.board = []
|
||||
|
||||
def isValid(self, row: int, col: int, target: int) -> bool:
|
||||
for idx in range(len(self.board)):
|
||||
# 同列是否重复
|
||||
if self.board[idx][col] == str(target):
|
||||
return False
|
||||
# 同行是否重复
|
||||
if self.board[row][idx] == str(target):
|
||||
return False
|
||||
# 9宫格里是否重复
|
||||
box_row, box_col = (row // 3) * 3 + idx // 3, (col // 3) * 3 + idx % 3
|
||||
if self.board[box_row][box_col] == str(target):
|
||||
return False
|
||||
return True
|
||||
|
||||
def getPlace(self) -> List[int]:
|
||||
for row in range(len(self.board)):
|
||||
for col in range(len(self.board)):
|
||||
if self.board[row][col] == ".":
|
||||
return [row, col]
|
||||
return [-1, -1]
|
||||
|
||||
def isSolved(self) -> bool:
|
||||
row, col = self.getPlace() # 找个空位置
|
||||
|
||||
if row == -1 and col == -1: # 没有空位置,棋盘被填满的
|
||||
return True
|
||||
|
||||
for i in range(1, 10):
|
||||
if self.isValid(row, col, i): # 检查这个空位置放i,是否合适
|
||||
self.board[row][col] = str(i) # 放i
|
||||
if self.isSolved(): # 合适,立刻返回, 填下一个空位置。
|
||||
return True
|
||||
self.board[row][col] = "." # 不合适,回溯
|
||||
|
||||
return False # 空位置没法解决
|
||||
|
||||
def solveSudoku(self, board: List[List[str]]) -> None:
|
||||
"""
|
||||
Do not return anything, modify board in-place instead.
|
||||
"""
|
||||
if board is None or len(board) == 0:
|
||||
return
|
||||
self.board = board
|
||||
self.isSolved()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -265,24 +265,72 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
**回溯**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.path = []
|
||||
self.paths = []
|
||||
|
||||
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
|
||||
res = []
|
||||
path = []
|
||||
def backtrack(candidates,target,sum,startIndex):
|
||||
if sum > target: return
|
||||
if sum == target: return res.append(path[:])
|
||||
for i in range(startIndex,len(candidates)):
|
||||
if sum + candidates[i] >target: return #如果 sum + candidates[i] > target 就终止遍历
|
||||
sum += candidates[i]
|
||||
path.append(candidates[i])
|
||||
backtrack(candidates,target,sum,i) #startIndex = i:表示可以重复读取当前的数
|
||||
sum -= candidates[i] #回溯
|
||||
path.pop() #回溯
|
||||
candidates = sorted(candidates) #需要排序
|
||||
backtrack(candidates,target,0,0)
|
||||
return res
|
||||
'''
|
||||
因为本题没有组合数量限制,所以只要元素总和大于target就算结束
|
||||
'''
|
||||
self.path.clear()
|
||||
self.paths.clear()
|
||||
self.backtracking(candidates, target, 0, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
|
||||
# Base Case
|
||||
if sum_ == target:
|
||||
self.paths.append(self.path[:]) # 因为是shallow copy,所以不能直接传入self.path
|
||||
return
|
||||
if sum_ > target:
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(candidates)):
|
||||
sum_ += candidates[i]
|
||||
self.path.append(candidates[i])
|
||||
self.backtracking(candidates, target, sum_, i) # 因为无限制重复选取,所以不是i-1
|
||||
sum_ -= candidates[i] # 回溯
|
||||
self.path.pop() # 回溯
|
||||
```
|
||||
**剪枝回溯**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.path = []
|
||||
self.paths = []
|
||||
|
||||
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
|
||||
'''
|
||||
因为本题没有组合数量限制,所以只要元素总和大于target就算结束
|
||||
'''
|
||||
self.path.clear()
|
||||
self.paths.clear()
|
||||
|
||||
# 为了剪枝需要提前进行排序
|
||||
candidates.sort()
|
||||
self.backtracking(candidates, target, 0, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
|
||||
# Base Case
|
||||
if sum_ == target:
|
||||
self.paths.append(self.path[:]) # 因为是shallow copy,所以不能直接传入self.path
|
||||
return
|
||||
# 单层递归逻辑
|
||||
# 如果本层 sum + condidates[i] > target,就提前结束遍历,剪枝
|
||||
for i in range(start_index, len(candidates)):
|
||||
if sum_ + candidates[i] > target:
|
||||
return
|
||||
sum_ += candidates[i]
|
||||
self.path.append(candidates[i])
|
||||
self.backtracking(candidates, target, sum_, i) # 因为无限制重复选取,所以不是i-1
|
||||
sum_ -= candidates[i] # 回溯
|
||||
self.path.pop() # 回溯
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
@ -296,24 +296,91 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
```python
|
||||
**回溯+巧妙去重(省去使用used**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
|
||||
res = []
|
||||
path = []
|
||||
def backtrack(candidates,target,sum,startIndex):
|
||||
if sum == target: res.append(path[:])
|
||||
for i in range(startIndex,len(candidates)): #要对同一树层使用过的元素进行跳过
|
||||
if sum + candidates[i] > target: return
|
||||
if i > startIndex and candidates[i] == candidates[i-1]: continue #直接用startIndex来去重,要对同一树层使用过的元素进行跳过
|
||||
sum += candidates[i]
|
||||
path.append(candidates[i])
|
||||
backtrack(candidates,target,sum,i+1) #i+1:每个数字在每个组合中只能使用一次
|
||||
sum -= candidates[i] #回溯
|
||||
path.pop() #回溯
|
||||
candidates = sorted(candidates) #首先把给candidates排序,让其相同的元素都挨在一起。
|
||||
backtrack(candidates,target,0,0)
|
||||
return res
|
||||
'''
|
||||
类似于求三数之和,求四数之和,为了避免重复组合,需要提前进行数组排序
|
||||
'''
|
||||
self.paths.clear()
|
||||
self.path.clear()
|
||||
# 必须提前进行数组排序,避免重复
|
||||
candidates.sort()
|
||||
self.backtracking(candidates, target, 0, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
|
||||
# Base Case
|
||||
if sum_ == target:
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(candidates)):
|
||||
# 剪枝,同39.组合总和
|
||||
if sum_ + candidates[i] > target:
|
||||
return
|
||||
|
||||
# 跳过同一树层使用过的元素
|
||||
if i > start_index and candidates[i] == candidates[i-1]:
|
||||
continue
|
||||
|
||||
sum_ += candidates[i]
|
||||
self.path.append(candidates[i])
|
||||
self.backtracking(candidates, target, sum_, i+1)
|
||||
self.path.pop() # 回溯,为了下一轮for loop
|
||||
sum_ -= candidates[i] # 回溯,为了下一轮for loop
|
||||
```
|
||||
**回溯+去重(使用used)**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
self.used = []
|
||||
|
||||
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
|
||||
'''
|
||||
类似于求三数之和,求四数之和,为了避免重复组合,需要提前进行数组排序
|
||||
本题需要使用used,用来标记区别同一树层的元素使用重复情况:注意区分递归纵向遍历遇到的重复元素,和for循环遇到的重复元素,这两者的区别
|
||||
'''
|
||||
self.paths.clear()
|
||||
self.path.clear()
|
||||
self.usage_list = [False] * len(candidates)
|
||||
# 必须提前进行数组排序,避免重复
|
||||
candidates.sort()
|
||||
self.backtracking(candidates, target, 0, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
|
||||
# Base Case
|
||||
if sum_ == target:
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(candidates)):
|
||||
# 剪枝,同39.组合总和
|
||||
if sum_ + candidates[i] > target:
|
||||
return
|
||||
|
||||
# 检查同一树层是否出现曾经使用过的相同元素
|
||||
# 若数组中前后元素值相同,但前者却未被使用(used == False),说明是for loop中的同一树层的相同元素情况
|
||||
if i > 0 and candidates[i] == candidates[i-1] and self.usage_list[i-1] == False:
|
||||
continue
|
||||
|
||||
sum_ += candidates[i]
|
||||
self.path.append(candidates[i])
|
||||
self.usage_list[i] = True
|
||||
self.backtracking(candidates, target, sum_, i+1)
|
||||
self.usage_list[i] = False # 回溯,为了下一轮for loop
|
||||
self.path.pop() # 回溯,为了下一轮for loop
|
||||
sum_ -= candidates[i] # 回溯,为了下一轮for loop
|
||||
```
|
||||
|
||||
## Go:
|
||||
|
||||
@ -143,7 +143,7 @@ public:
|
||||
|
||||
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
|
||||
|
||||
为了的到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。这样就避免了重复计算,这就用到了动态规划。
|
||||
为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。这样就避免了重复计算,这就用到了动态规划。
|
||||
|
||||
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
|
||||
|
||||
@ -204,7 +204,7 @@ public:
|
||||
|
||||
2. 使用单调栈内元素的顺序
|
||||
|
||||
从大到小还是从小打到呢?
|
||||
从大到小还是从小到大呢?
|
||||
|
||||
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
|
||||
|
||||
@ -515,24 +515,95 @@ class Solution:
|
||||
```python3
|
||||
class Solution:
|
||||
def trap(self, height: List[int]) -> int:
|
||||
st =[0]
|
||||
# 单调栈
|
||||
'''
|
||||
单调栈是按照 行 的方向来计算雨水
|
||||
从栈顶到栈底的顺序:从小到大
|
||||
通过三个元素来接水:栈顶,栈顶的下一个元素,以及即将入栈的元素
|
||||
雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
|
||||
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度)
|
||||
'''
|
||||
# stack储存index,用于计算对应的柱子高度
|
||||
stack = [0]
|
||||
result = 0
|
||||
for i in range(1,len(height)):
|
||||
while st!=[] and height[i]>height[st[-1]]:
|
||||
midh = height[st[-1]]
|
||||
st.pop()
|
||||
if st!=[]:
|
||||
hright = height[i]
|
||||
hleft = height[st[-1]]
|
||||
h = min(hright,hleft)-midh
|
||||
w = i-st[-1]-1
|
||||
result+=h*w
|
||||
st.append(i)
|
||||
for i in range(1, len(height)):
|
||||
# 情况一
|
||||
if height[i] < height[stack[-1]]:
|
||||
stack.append(i)
|
||||
|
||||
# 情况二
|
||||
# 当当前柱子高度和栈顶一致时,左边的一个是不可能存放雨水的,所以保留右侧新柱子
|
||||
# 需要使用最右边的柱子来计算宽度
|
||||
elif height[i] == height[stack[-1]]:
|
||||
stack.pop()
|
||||
stack.append(i)
|
||||
|
||||
# 情况三
|
||||
else:
|
||||
# 抛出所有较低的柱子
|
||||
while stack and height[i] > height[stack[-1]]:
|
||||
# 栈顶就是中间的柱子:储水槽,就是凹槽的地步
|
||||
mid_height = height[stack[-1]]
|
||||
stack.pop()
|
||||
if stack:
|
||||
right_height = height[i]
|
||||
left_height = height[stack[-1]]
|
||||
# 两侧的较矮一方的高度 - 凹槽底部高度
|
||||
h = min(right_height, left_height) - mid_height
|
||||
# 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度
|
||||
w = i - stack[-1] - 1
|
||||
# 体积:高乘宽
|
||||
result += h * w
|
||||
stack.append(i)
|
||||
return result
|
||||
|
||||
# 单调栈压缩版
|
||||
class Solution:
|
||||
def trap(self, height: List[int]) -> int:
|
||||
stack = [0]
|
||||
result = 0
|
||||
for i in range(1, len(height)):
|
||||
while stack and height[i] > height[stack[-1]]:
|
||||
mid_height = stack.pop()
|
||||
if stack:
|
||||
# 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度
|
||||
h = min(height[stack[-1]], height[i]) - height[mid_height]
|
||||
# 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1
|
||||
w = i - stack[-1] - 1
|
||||
# 累计总雨水体积
|
||||
result += h * w
|
||||
stack.append(i)
|
||||
return result
|
||||
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
func trap(height []int) int {
|
||||
var left, right, leftMax, rightMax, res int
|
||||
right = len(height) - 1
|
||||
for left < right {
|
||||
if height[left] < height[right] {
|
||||
if height[left] >= leftMax {
|
||||
leftMax = height[left] // 设置左边最高柱子
|
||||
} else {
|
||||
res += leftMax - height[left] // //右边必定有柱子挡水,所以遇到所有值小于等于leftMax的,全部加入水池中
|
||||
}
|
||||
left++
|
||||
} else {
|
||||
if height[right] > rightMax {
|
||||
rightMax = height[right] // //设置右边最高柱子
|
||||
} else {
|
||||
res += rightMax - height[right] // //左边必定有柱子挡水,所以,遇到所有值小于等于rightMax的,全部加入水池
|
||||
}
|
||||
right--
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
//双指针
|
||||
|
||||
@ -211,44 +211,68 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
**回溯**
|
||||
```python
|
||||
class Solution:
|
||||
def permute(self, nums: List[int]) -> List[List[int]]:
|
||||
res = [] #存放符合条件结果的集合
|
||||
path = [] #用来存放符合条件的结果
|
||||
used = [] #用来存放已经用过的数字
|
||||
def backtrack(nums,used):
|
||||
if len(path) == len(nums):
|
||||
return res.append(path[:]) #此时说明找到了一组
|
||||
for i in range(0,len(nums)):
|
||||
if nums[i] in used:
|
||||
continue #used里已经收录的元素,直接跳过
|
||||
path.append(nums[i])
|
||||
used.append(nums[i])
|
||||
backtrack(nums,used)
|
||||
used.pop()
|
||||
path.pop()
|
||||
backtrack(nums,used)
|
||||
return res
|
||||
```
|
||||
def __init__(self):
|
||||
self.path = []
|
||||
self.paths = []
|
||||
|
||||
Python(优化,不用used数组):
|
||||
def permute(self, nums: List[int]) -> List[List[int]]:
|
||||
'''
|
||||
因为本题排列是有序的,这意味着同一层的元素可以重复使用,但同一树枝上不能重复使用(usage_list)
|
||||
所以处理排列问题每层都需要从头搜索,故不再使用start_index
|
||||
'''
|
||||
usage_list = [False] * len(nums)
|
||||
self.backtracking(nums, usage_list)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int], usage_list: List[bool]) -> None:
|
||||
# Base Case本题求叶子节点
|
||||
if len(self.path) == len(nums):
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(0, len(nums)): # 从头开始搜索
|
||||
# 若遇到self.path里已收录的元素,跳过
|
||||
if usage_list[i] == True:
|
||||
continue
|
||||
usage_list[i] = True
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums, usage_list) # 纵向传递使用信息,去重
|
||||
self.path.pop()
|
||||
usage_list[i] = False
|
||||
```
|
||||
**回溯+丢掉usage_list**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.path = []
|
||||
self.paths = []
|
||||
|
||||
def permute(self, nums: List[int]) -> List[List[int]]:
|
||||
res = [] #存放符合条件结果的集合
|
||||
path = [] #用来存放符合条件的结果
|
||||
def backtrack(nums):
|
||||
if len(path) == len(nums):
|
||||
return res.append(path[:]) #此时说明找到了一组
|
||||
for i in range(0,len(nums)):
|
||||
if nums[i] in path: #path里已经收录的元素,直接跳过
|
||||
'''
|
||||
因为本题排列是有序的,这意味着同一层的元素可以重复使用,但同一树枝上不能重复使用
|
||||
所以处理排列问题每层都需要从头搜索,故不再使用start_index
|
||||
'''
|
||||
self.backtracking(nums)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int]) -> None:
|
||||
# Base Case本题求叶子节点
|
||||
if len(self.path) == len(nums):
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(0, len(nums)): # 从头开始搜索
|
||||
# 若遇到self.path里已收录的元素,跳过
|
||||
if nums[i] in self.path:
|
||||
continue
|
||||
path.append(nums[i])
|
||||
backtrack(nums) #递归
|
||||
path.pop() #回溯
|
||||
backtrack(nums)
|
||||
return res
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums)
|
||||
self.path.pop()
|
||||
```
|
||||
|
||||
### Go
|
||||
@ -309,6 +333,72 @@ var permute = function(nums) {
|
||||
|
||||
```
|
||||
|
||||
C:
|
||||
```c
|
||||
int* path;
|
||||
int pathTop;
|
||||
int** ans;
|
||||
int ansTop;
|
||||
|
||||
//将used中元素都设置为0
|
||||
void initialize(int* used, int usedLength) {
|
||||
int i;
|
||||
for(i = 0; i < usedLength; i++) {
|
||||
used[i] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
//将path中元素拷贝到ans中
|
||||
void copy() {
|
||||
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
|
||||
int i;
|
||||
for(i = 0; i < pathTop; i++) {
|
||||
tempPath[i] = path[i];
|
||||
}
|
||||
ans[ansTop++] = tempPath;
|
||||
}
|
||||
|
||||
void backTracking(int* nums, int numsSize, int* used) {
|
||||
//若path中元素个数等于nums元素个数,将nums放入ans中
|
||||
if(pathTop == numsSize) {
|
||||
copy();
|
||||
return;
|
||||
}
|
||||
int i;
|
||||
for(i = 0; i < numsSize; i++) {
|
||||
//若当前下标中元素已使用过,则跳过当前元素
|
||||
if(used[i])
|
||||
continue;
|
||||
used[i] = 1;
|
||||
path[pathTop++] = nums[i];
|
||||
backTracking(nums, numsSize, used);
|
||||
//回溯
|
||||
pathTop--;
|
||||
used[i] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
|
||||
//初始化辅助变量
|
||||
path = (int*)malloc(sizeof(int) * numsSize);
|
||||
ans = (int**)malloc(sizeof(int*) * 1000);
|
||||
int* used = (int*)malloc(sizeof(int) * numsSize);
|
||||
//将used数组中元素都置0
|
||||
initialize(used, numsSize);
|
||||
ansTop = pathTop = 0;
|
||||
|
||||
backTracking(nums, numsSize, used);
|
||||
|
||||
//设置path和ans数组的长度
|
||||
*returnSize = ansTop;
|
||||
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
|
||||
int i;
|
||||
for(i = 0; i < ansTop; i++) {
|
||||
(*returnColumnSizes)[i] = numsSize;
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -241,6 +241,32 @@ var merge = function (intervals) {
|
||||
return result
|
||||
};
|
||||
```
|
||||
版本二:左右区间
|
||||
```javascript
|
||||
/**
|
||||
* @param {number[][]} intervals
|
||||
* @return {number[][]}
|
||||
*/
|
||||
var merge = function(intervals) {
|
||||
let n = intervals.length;
|
||||
if ( n < 2) return intervals;
|
||||
intervals.sort((a, b) => a[0]- b[0]);
|
||||
let res = [],
|
||||
left = intervals[0][0],
|
||||
right = intervals[0][1];
|
||||
for (let i = 1; i < n; i++) {
|
||||
if (intervals[i][0] > right) {
|
||||
res.push([left, right]);
|
||||
left = intervals[i][0];
|
||||
right = intervals[i][1];
|
||||
} else {
|
||||
right = Math.max(intervals[i][1], right);
|
||||
}
|
||||
}
|
||||
res.push([left, right]);
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -327,6 +327,25 @@ var uniquePaths = function(m, n) {
|
||||
return dp[m - 1][n - 1]
|
||||
};
|
||||
```
|
||||
>版本二:直接将dp数值值初始化为1
|
||||
```javascript
|
||||
/**
|
||||
* @param {number} m
|
||||
* @param {number} n
|
||||
* @return {number}
|
||||
*/
|
||||
var uniquePaths = function(m, n) {
|
||||
let dp = new Array(m).fill(1).map(() => new Array(n).fill(1));
|
||||
// dp[i][j] 表示到达(i,j) 点的路径数
|
||||
for (let i=1; i<m; i++) {
|
||||
for (let j=1; j< n;j++) {
|
||||
dp[i][j]=dp[i-1][j]+dp[i][j-1];
|
||||
}
|
||||
}
|
||||
return dp[m-1][n-1];
|
||||
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -88,7 +88,7 @@
|
||||
|
||||
|
||||
以上分析完毕,C++代码如下:
|
||||
```
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
int climbStairs(int n) {
|
||||
|
||||
@ -22,7 +22,7 @@
|
||||
|
||||
大家先回忆一下[77. 组合]给出的回溯法的代码:
|
||||
|
||||
```
|
||||
```c++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result; // 存放符合条件结果的集合
|
||||
@ -54,7 +54,7 @@ public:
|
||||
|
||||
在遍历的过程中有如下代码:
|
||||
|
||||
```
|
||||
```c++
|
||||
for (int i = startIndex; i <= n; i++) {
|
||||
path.push_back(i);
|
||||
backtracking(n, k, i + 1);
|
||||
@ -78,7 +78,7 @@ for (int i = startIndex; i <= n; i++) {
|
||||
**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
|
||||
|
||||
注意代码中i,就是for循环里选择的起始位置。
|
||||
```
|
||||
```c++
|
||||
for (int i = startIndex; i <= n; i++) {
|
||||
```
|
||||
|
||||
@ -100,13 +100,13 @@ for (int i = startIndex; i <= n; i++) {
|
||||
|
||||
所以优化之后的for循环是:
|
||||
|
||||
```
|
||||
```c++
|
||||
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
|
||||
```
|
||||
|
||||
优化后整体代码如下:
|
||||
|
||||
```
|
||||
```c++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
|
||||
@ -207,17 +207,28 @@ class Solution {
|
||||
## Python
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.path: List[int] = []
|
||||
self.paths: List[List[int]] = []
|
||||
|
||||
def subsets(self, nums: List[int]) -> List[List[int]]:
|
||||
res = []
|
||||
path = []
|
||||
def backtrack(nums,startIndex):
|
||||
res.append(path[:]) #收集子集,要放在终止添加的上面,否则会漏掉自己
|
||||
for i in range(startIndex,len(nums)): #当startIndex已经大于数组的长度了,就终止了,for循环本来也结束了,所以不需要终止条件
|
||||
path.append(nums[i])
|
||||
backtrack(nums,i+1) #递归
|
||||
path.pop() #回溯
|
||||
backtrack(nums,0)
|
||||
return res
|
||||
self.paths.clear()
|
||||
self.path.clear()
|
||||
self.backtracking(nums, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int], start_index: int) -> None:
|
||||
# 收集子集,要先于终止判断
|
||||
self.paths.append(self.path[:])
|
||||
# Base Case
|
||||
if start_index == len(nums):
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(nums)):
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums, i+1)
|
||||
self.path.pop() # 回溯
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
@ -281,52 +281,137 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
动态规划
|
||||
```python3
|
||||
|
||||
# 双指针;暴力解法(leetcode超时)
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
result = 0
|
||||
minleftindex, minrightindex = [0]*len(heights), [0]*len(heights)
|
||||
# 从左向右遍历:以每一根柱子为主心骨(当前轮最高的参照物),迭代直到找到左侧和右侧各第一个矮一级的柱子
|
||||
res = 0
|
||||
|
||||
minleftindex[0]=-1
|
||||
for i in range(1,len(heights)):
|
||||
t = i-1
|
||||
while t>=0 and heights[t]>=heights[i]: t=minleftindex[t]
|
||||
minleftindex[i]=t
|
||||
for i in range(len(heights)):
|
||||
left = i
|
||||
right = i
|
||||
# 向左侧遍历:寻找第一个矮一级的柱子
|
||||
for _ in range(left, -1, -1):
|
||||
if heights[left] < heights[i]:
|
||||
break
|
||||
left -= 1
|
||||
# 向右侧遍历:寻找第一个矮一级的柱子
|
||||
for _ in range(right, len(heights)):
|
||||
if heights[right] < heights[i]:
|
||||
break
|
||||
right += 1
|
||||
|
||||
minrightindex[-1]=len(heights)
|
||||
for i in range(len(heights)-2,-1,-1):
|
||||
t=i+1
|
||||
while t<len(heights) and heights[t]>=heights[i]: t=minrightindex[t]
|
||||
minrightindex[i]=t
|
||||
width = right - left - 1
|
||||
height = heights[i]
|
||||
res = max(res, width * height)
|
||||
|
||||
for i in range(0,len(heights)):
|
||||
left = minleftindex[i]
|
||||
right = minrightindex[i]
|
||||
summ = (right-left-1)*heights[i]
|
||||
result = max(result,summ)
|
||||
return result
|
||||
```
|
||||
单调栈 版本二
|
||||
```python3
|
||||
return res
|
||||
|
||||
# DP动态规划
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
heights.insert(0,0) # 数组头部加入元素0
|
||||
heights.append(0) # 数组尾部加入元素0
|
||||
st = [0]
|
||||
size = len(heights)
|
||||
# 两个DP数列储存的均是下标index
|
||||
min_left_index = [0] * size
|
||||
min_right_index = [0] * size
|
||||
result = 0
|
||||
for i in range(1,len(heights)):
|
||||
while st!=[] and heights[i]<heights[st[-1]]:
|
||||
midh = heights[st[-1]]
|
||||
st.pop()
|
||||
if st!=[]:
|
||||
minrightindex = i
|
||||
minleftindex = st[-1]
|
||||
summ = (minrightindex-minleftindex-1)*midh
|
||||
result = max(summ,result)
|
||||
st.append(i)
|
||||
|
||||
# 记录每个柱子的左侧第一个矮一级的柱子的下标
|
||||
min_left_index[0] = -1 # 初始化防止while死循环
|
||||
for i in range(1, size):
|
||||
# 以当前柱子为主心骨,向左迭代寻找次级柱子
|
||||
temp = i - 1
|
||||
while temp >= 0 and heights[temp] >= heights[i]:
|
||||
# 当左侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DP
|
||||
temp = min_left_index[temp]
|
||||
# 当找到左侧矮一级的目标柱子时
|
||||
min_left_index[i] = temp
|
||||
|
||||
# 记录每个柱子的右侧第一个矮一级的柱子的下标
|
||||
min_right_index[size-1] = size # 初始化防止while死循环
|
||||
for i in range(size-2, -1, -1):
|
||||
# 以当前柱子为主心骨,向右迭代寻找次级柱子
|
||||
temp = i + 1
|
||||
while temp < size and heights[temp] >= heights[i]:
|
||||
# 当右侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DP
|
||||
temp = min_right_index[temp]
|
||||
# 当找到右侧矮一级的目标柱子时
|
||||
min_right_index[i] = temp
|
||||
|
||||
for i in range(size):
|
||||
area = heights[i] * (min_right_index[i] - min_left_index[i] - 1)
|
||||
result = max(area, result)
|
||||
|
||||
return result
|
||||
|
||||
# 单调栈
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
# Monotonic Stack
|
||||
'''
|
||||
找每个柱子左右侧的第一个高度值小于该柱子的柱子
|
||||
单调栈:栈顶到栈底:从大到小(每插入一个新的小数值时,都要弹出先前的大数值)
|
||||
栈顶,栈顶的下一个元素,即将入栈的元素:这三个元素组成了最大面积的高度和宽度
|
||||
情况一:当前遍历的元素heights[i]大于栈顶元素的情况
|
||||
情况二:当前遍历的元素heights[i]等于栈顶元素的情况
|
||||
情况三:当前遍历的元素heights[i]小于栈顶元素的情况
|
||||
'''
|
||||
|
||||
# 输入数组首尾各补上一个0(与42.接雨水不同的是,本题原首尾的两个柱子可以作为核心柱进行最大面积尝试
|
||||
heights.insert(0, 0)
|
||||
heights.append(0)
|
||||
stack = [0]
|
||||
result = 0
|
||||
for i in range(1, len(heights)):
|
||||
# 情况一
|
||||
if heights[i] > heights[stack[-1]]:
|
||||
stack.append(i)
|
||||
# 情况二
|
||||
elif heights[i] == heights[stack[-1]]:
|
||||
stack.pop()
|
||||
stack.append(i)
|
||||
# 情况三
|
||||
else:
|
||||
# 抛出所有较高的柱子
|
||||
while stack and heights[i] < heights[stack[-1]]:
|
||||
# 栈顶就是中间的柱子,主心骨
|
||||
mid_index = stack[-1]
|
||||
stack.pop()
|
||||
if stack:
|
||||
left_index = stack[-1]
|
||||
right_index = i
|
||||
width = right_index - left_index - 1
|
||||
height = heights[mid_index]
|
||||
result = max(result, width * height)
|
||||
stack.append(i)
|
||||
return result
|
||||
|
||||
# 单调栈精简
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
heights.insert(0, 0)
|
||||
heights.append(0)
|
||||
stack = [0]
|
||||
result = 0
|
||||
for i in range(1, len(heights)):
|
||||
while stack and heights[i] < heights[stack[-1]]:
|
||||
mid_height = heights[stack[-1]]
|
||||
stack.pop()
|
||||
if stack:
|
||||
# area = width * height
|
||||
area = (i - stack[-1] - 1) * mid_height
|
||||
result = max(area, result)
|
||||
stack.append(i)
|
||||
return result
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
```
|
||||
*****
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
|
||||
@ -209,20 +209,30 @@ class Solution {
|
||||
### Python
|
||||
```python
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
|
||||
res = [] #存放符合条件结果的集合
|
||||
path = [] #用来存放符合条件结果
|
||||
def backtrack(nums,startIndex):
|
||||
res.append(path[:])
|
||||
for i in range(startIndex,len(nums)):
|
||||
if i > startIndex and nums[i] == nums[i - 1]: #我们要对同一树层使用过的元素进行跳过
|
||||
nums.sort()
|
||||
self.backtracking(nums, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int], start_index: int) -> None:
|
||||
# ps.空集合仍符合要求
|
||||
self.paths.append(self.path[:])
|
||||
# Base Case
|
||||
if start_index == len(nums):
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(nums)):
|
||||
if i > start_index and nums[i] == nums[i-1]:
|
||||
# 当前后元素值相同时,跳入下一个循环,去重
|
||||
continue
|
||||
path.append(nums[i])
|
||||
backtrack(nums,i+1) #递归
|
||||
path.pop() #回溯
|
||||
nums = sorted(nums) #去重需要排序
|
||||
backtrack(nums,0)
|
||||
return res
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums, i+1)
|
||||
self.path.pop()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -312,37 +312,6 @@ class Solution {
|
||||
|
||||
python2:
|
||||
```python
|
||||
class Solution:
|
||||
def restoreIpAddresses(self, s: str) -> List[str]:
|
||||
res = []
|
||||
path = [] # 存放分割后的字符
|
||||
# 判断数组中的数字是否合法
|
||||
def isValid(p):
|
||||
if p == '0': return True # 解决"0000"
|
||||
if p[0] == '0': return False
|
||||
if int(p) > 0 and int(p) <256: return True
|
||||
return False
|
||||
|
||||
def backtrack(s, startIndex):
|
||||
if len(s) > 12: return # 字符串长度最大为12
|
||||
if len(path) == 4 and startIndex == len(s): # 确保切割完,且切割后的长度为4
|
||||
res.append(".".join(path[:])) # 字符拼接
|
||||
return
|
||||
|
||||
for i in range(startIndex, len(s)):
|
||||
if len(s) - startIndex > 3*(4 - len(path)): continue # 剪枝,剩下的字符串大于允许的最大长度则跳过
|
||||
p = s[startIndex:i+1] # 分割字符
|
||||
if isValid(p): # 判断字符是否有效
|
||||
path.append(p)
|
||||
else: continue
|
||||
backtrack(s, i + 1) # 寻找i+1为起始位置的子串
|
||||
path.pop()
|
||||
backtrack(s, 0)
|
||||
return res
|
||||
```
|
||||
|
||||
python3:
|
||||
```python
|
||||
class Solution(object):
|
||||
def restoreIpAddresses(self, s):
|
||||
"""
|
||||
@ -371,6 +340,50 @@ class Solution(object):
|
||||
return ans
|
||||
```
|
||||
|
||||
python3:
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.result = []
|
||||
|
||||
def restoreIpAddresses(self, s: str) -> List[str]:
|
||||
'''
|
||||
本质切割问题使用回溯搜索法,本题只能切割三次,所以纵向递归总共四层
|
||||
因为不能重复分割,所以需要start_index来记录下一层递归分割的起始位置
|
||||
添加变量point_num来记录逗号的数量[0,3]
|
||||
'''
|
||||
self.result.clear()
|
||||
if len(s) > 12: return []
|
||||
self.backtracking(s, 0, 0)
|
||||
return self.result
|
||||
|
||||
def backtracking(self, s: str, start_index: int, point_num: int) -> None:
|
||||
# Base Case
|
||||
if point_num == 3:
|
||||
if self.is_valid(s, start_index, len(s)-1):
|
||||
self.result.append(s[:])
|
||||
return
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(s)):
|
||||
# [start_index, i]就是被截取的子串
|
||||
if self.is_valid(s, start_index, i):
|
||||
s = s[:i+1] + '.' + s[i+1:]
|
||||
self.backtracking(s, i+2, point_num+1) # 在填入.后,下一子串起始后移2位
|
||||
s = s[:i+1] + s[i+2:] # 回溯
|
||||
else:
|
||||
# 若当前被截取的子串大于255或者大于三位数,直接结束本层循环
|
||||
break
|
||||
|
||||
def is_valid(self, s: str, start: int, end: int) -> bool:
|
||||
if start > end: return False
|
||||
# 若数字是0开头,不合法
|
||||
if s[start] == '0' and start != end:
|
||||
return False
|
||||
if not 0 <= int(s[start:end+1]) <= 255:
|
||||
return False
|
||||
return True
|
||||
```
|
||||
|
||||
|
||||
## JavaScript
|
||||
|
||||
|
||||
@ -819,6 +819,81 @@ var buildTree = function(preorder, inorder) {
|
||||
};
|
||||
```
|
||||
|
||||
## C
|
||||
106 从中序与后序遍历序列构造二叉树
|
||||
```c
|
||||
int linearSearch(int* arr, int arrSize, int key) {
|
||||
int i;
|
||||
for(i = 0; i < arrSize; i++) {
|
||||
if(arr[i] == key)
|
||||
return i;
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
|
||||
struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize){
|
||||
//若中序遍历数组中没有元素,则返回NULL
|
||||
if(!inorderSize)
|
||||
return NULL;
|
||||
//创建一个新的结点,将node的val设置为后序遍历的最后一个元素
|
||||
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
|
||||
node->val = postorder[postorderSize - 1];
|
||||
|
||||
//通过线性查找找到中间结点在中序数组中的位置
|
||||
int index = linearSearch(inorder, inorderSize, postorder[postorderSize - 1]);
|
||||
|
||||
//左子树数组大小为index
|
||||
//右子树的数组大小为数组大小减index减1(减的1为中间结点)
|
||||
int rightSize = inorderSize - index - 1;
|
||||
node->left = buildTree(inorder, index, postorder, index);
|
||||
node->right = buildTree(inorder + index + 1, rightSize, postorder + index, rightSize);
|
||||
return node;
|
||||
}
|
||||
```
|
||||
|
||||
105 从前序与中序遍历序列构造二叉树
|
||||
```c
|
||||
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
|
||||
// 递归结束条件:传入的数组大小为0
|
||||
if(!preorderSize)
|
||||
return NULL;
|
||||
|
||||
// 1.找到前序遍历数组的第一个元素, 创建结点。左右孩子设置为NULL。
|
||||
int rootValue = preorder[0];
|
||||
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
|
||||
root->val = rootValue;
|
||||
root->left = NULL;
|
||||
root->right = NULL;
|
||||
|
||||
// 2.若前序遍历数组的大小为1,返回该结点
|
||||
if(preorderSize == 1)
|
||||
return root;
|
||||
|
||||
// 3.根据该结点切割中序遍历数组,将中序遍历数组分割成左右两个数组。算出他们的各自大小
|
||||
int index;
|
||||
for(index = 0; index < inorderSize; index++) {
|
||||
if(inorder[index] == rootValue)
|
||||
break;
|
||||
}
|
||||
int leftNum = index;
|
||||
int rightNum = inorderSize - index - 1;
|
||||
|
||||
int* leftInorder = inorder;
|
||||
int* rightInorder = inorder + leftNum + 1;
|
||||
|
||||
// 4.根据中序遍历数组左右数组的各子大小切割前序遍历数组。也分为左右数组
|
||||
int* leftPreorder = preorder+1;
|
||||
int* rightPreorder = preorder + 1 + leftNum;
|
||||
|
||||
// 5.递归进入左右数组,将返回的结果作为根结点的左右孩子
|
||||
root->left = buildTree(leftPreorder, leftNum, leftInorder, leftNum);
|
||||
root->right = buildTree(rightPreorder, rightNum, rightInorder, rightNum);
|
||||
|
||||
// 6.返回根节点
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
|
||||
@ -305,21 +305,41 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
**递归**
|
||||
|
||||
递归法:
|
||||
```python3
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
|
||||
def buildaTree(left,right):
|
||||
if left > right: return None #左闭右闭的区间,当区间 left > right的时候,就是空节点,当left = right的时候,不为空
|
||||
mid = left + (right - left) // 2 #保证数据不会越界
|
||||
val = nums[mid]
|
||||
root = TreeNode(val)
|
||||
root.left = buildaTree(left,mid - 1)
|
||||
root.right = buildaTree(mid + 1,right)
|
||||
return root
|
||||
root = buildaTree(0,len(nums) - 1) #左闭右闭区间
|
||||
'''
|
||||
构造二叉树:重点是选取数组最中间元素为分割点,左侧是递归左区间;右侧是递归右区间
|
||||
必然是平衡树
|
||||
左闭右闭区间
|
||||
'''
|
||||
# 返回根节点
|
||||
root = self.traversal(nums, 0, len(nums)-1)
|
||||
return root
|
||||
|
||||
def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:
|
||||
# Base Case
|
||||
if left > right:
|
||||
return None
|
||||
|
||||
# 确定左右界的中心,防越界
|
||||
mid = left + (right - left) // 2
|
||||
# 构建根节点
|
||||
mid_root = TreeNode(nums[mid])
|
||||
# 构建以左右界的中心为分割点的左右子树
|
||||
mid_root.left = self.traversal(nums, left, mid-1)
|
||||
mid_root.right = self.traversal(nums, mid+1, right)
|
||||
|
||||
# 返回由被传入的左右界定义的某子树的根节点
|
||||
return mid_root
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
@ -125,9 +125,10 @@ public:
|
||||
|
||||
1. 明确递归函数的参数和返回值
|
||||
|
||||
参数的话为传入的节点指针,就没有其他参数需要传递了,返回值要返回传入节点为根节点树的深度。
|
||||
参数:当前传入节点。
|
||||
返回值:以当前传入节点为根节点的树的高度。
|
||||
|
||||
那么如何标记左右子树是否差值大于1呢。
|
||||
那么如何标记左右子树是否差值大于1呢?
|
||||
|
||||
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
|
||||
|
||||
@ -136,9 +137,9 @@ public:
|
||||
代码如下:
|
||||
|
||||
|
||||
```
|
||||
```CPP
|
||||
// -1 表示已经不是平衡二叉树了,否则返回值是以该节点为根节点树的高度
|
||||
int getDepth(TreeNode* node)
|
||||
int getHeight(TreeNode* node)
|
||||
```
|
||||
|
||||
2. 明确终止条件
|
||||
@ -147,7 +148,7 @@ int getDepth(TreeNode* node)
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
if (node == NULL) {
|
||||
return 0;
|
||||
}
|
||||
@ -155,23 +156,23 @@ if (node == NULL) {
|
||||
|
||||
3. 明确单层递归的逻辑
|
||||
|
||||
如何判断当前传入节点为根节点的二叉树是否是平衡二叉树呢,当然是左子树高度和右子树高度相差。
|
||||
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
|
||||
|
||||
分别求出左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是二叉树了。
|
||||
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是二叉平衡树了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
int leftDepth = depth(node->left); // 左
|
||||
if (leftDepth == -1) return -1;
|
||||
int rightDepth = depth(node->right); // 右
|
||||
if (rightDepth == -1) return -1;
|
||||
int leftHeight = getHeight(node->left); // 左
|
||||
if (leftHeight == -1) return -1;
|
||||
int rightHeight = getHeight(node->right); // 右
|
||||
if (rightHeight == -1) return -1;
|
||||
|
||||
int result;
|
||||
if (abs(leftDepth - rightDepth) > 1) { // 中
|
||||
if (abs(leftHeight - rightHeight) > 1) { // 中
|
||||
result = -1;
|
||||
} else {
|
||||
result = 1 + max(leftDepth, rightDepth); // 以当前节点为根节点的最大高度
|
||||
result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
|
||||
}
|
||||
|
||||
return result;
|
||||
@ -180,27 +181,27 @@ return result;
|
||||
代码精简之后如下:
|
||||
|
||||
```CPP
|
||||
int leftDepth = getDepth(node->left);
|
||||
if (leftDepth == -1) return -1;
|
||||
int rightDepth = getDepth(node->right);
|
||||
if (rightDepth == -1) return -1;
|
||||
return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth);
|
||||
int leftHeight = getHeight(node->left);
|
||||
if (leftHeight == -1) return -1;
|
||||
int rightHeight = getHeight(node->right);
|
||||
if (rightHeight == -1) return -1;
|
||||
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
|
||||
```
|
||||
|
||||
此时递归的函数就已经写出来了,这个递归的函数传入节点指针,返回以该节点为根节点的二叉树的高度,如果不是二叉平衡树,则返回-1。
|
||||
|
||||
getDepth整体代码如下:
|
||||
getHeight整体代码如下:
|
||||
|
||||
```CPP
|
||||
int getDepth(TreeNode* node) {
|
||||
int getHeight(TreeNode* node) {
|
||||
if (node == NULL) {
|
||||
return 0;
|
||||
}
|
||||
int leftDepth = getDepth(node->left);
|
||||
if (leftDepth == -1) return -1;
|
||||
int rightDepth = getDepth(node->right);
|
||||
if (rightDepth == -1) return -1;
|
||||
return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth);
|
||||
int leftHeight = getHeight(node->left);
|
||||
if (leftHeight == -1) return -1;
|
||||
int rightHeight = getHeight(node->right);
|
||||
if (rightHeight == -1) return -1;
|
||||
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
|
||||
}
|
||||
```
|
||||
|
||||
@ -210,18 +211,18 @@ int getDepth(TreeNode* node) {
|
||||
class Solution {
|
||||
public:
|
||||
// 返回以该节点为根节点的二叉树的高度,如果不是二叉搜索树了则返回-1
|
||||
int getDepth(TreeNode* node) {
|
||||
int getHeight(TreeNode* node) {
|
||||
if (node == NULL) {
|
||||
return 0;
|
||||
}
|
||||
int leftDepth = getDepth(node->left);
|
||||
if (leftDepth == -1) return -1; // 说明左子树已经不是二叉平衡树
|
||||
int rightDepth = getDepth(node->right);
|
||||
if (rightDepth == -1) return -1; // 说明右子树已经不是二叉平衡树
|
||||
return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth);
|
||||
int leftHeight = getHeight(node->left);
|
||||
if (leftHeight == -1) return -1;
|
||||
int rightHeight = getHeight(node->right);
|
||||
if (rightHeight == -1) return -1;
|
||||
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
|
||||
}
|
||||
bool isBalanced(TreeNode* root) {
|
||||
return getDepth(root) == -1 ? false : true;
|
||||
return getHeight(root) == -1 ? false : true;
|
||||
}
|
||||
};
|
||||
```
|
||||
@ -498,20 +499,35 @@ class Solution {
|
||||
## Python
|
||||
|
||||
递归法:
|
||||
```python
|
||||
```python3
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def isBalanced(self, root: TreeNode) -> bool:
|
||||
return True if self.getDepth(root) != -1 else False
|
||||
if self.get_height(root) != -1:
|
||||
return True
|
||||
else:
|
||||
return False
|
||||
|
||||
#返回以该节点为根节点的二叉树的高度,如果不是二叉搜索树了则返回-1
|
||||
def getDepth(self, node):
|
||||
if not node:
|
||||
def get_height(self, root: TreeNode) -> int:
|
||||
# Base Case
|
||||
if not root:
|
||||
return 0
|
||||
leftDepth = self.getDepth(node.left)
|
||||
if leftDepth == -1: return -1 #说明左子树已经不是二叉平衡树
|
||||
rightDepth = self.getDepth(node.right)
|
||||
if rightDepth == -1: return -1 #说明右子树已经不是二叉平衡树
|
||||
return -1 if abs(leftDepth - rightDepth)>1 else 1 + max(leftDepth, rightDepth)
|
||||
# 左
|
||||
if (left_height := self.get_height(root.left)) == -1:
|
||||
return -1
|
||||
# 右
|
||||
if (right_height := self.get_height(root.right)) == -1:
|
||||
return -1
|
||||
# 中
|
||||
if abs(left_height - right_height) > 1:
|
||||
return -1
|
||||
else:
|
||||
return 1 + max(left_height, right_height)
|
||||
```
|
||||
|
||||
迭代法:
|
||||
|
||||
@ -335,6 +335,8 @@ func max(a,b int)int {
|
||||
|
||||
JavaScript:
|
||||
|
||||
> 动态规划
|
||||
|
||||
```javascript
|
||||
const maxProfit = prices => {
|
||||
const len = prices.length;
|
||||
@ -353,7 +355,19 @@ const maxProfit = prices => {
|
||||
};
|
||||
```
|
||||
|
||||
> 贪心法
|
||||
|
||||
```javascript
|
||||
var maxProfit = function(prices) {
|
||||
let lowerPrice = prices[0];// 重点是维护这个最小值(贪心的思想)
|
||||
let profit = 0;
|
||||
for(let i = 0; i < prices.length; i++){
|
||||
lowerPrice = Math.min(lowerPrice, prices[i]);// 贪心地选择左面的最小价格
|
||||
profit = Math.max(profit, prices[i] - lowerPrice);// 遍历一趟就可以获得最大利润
|
||||
}
|
||||
return profit;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -290,59 +290,92 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
```python
|
||||
# 版本一
|
||||
**回溯+正反序判断回文串**
|
||||
```python3
|
||||
class Solution:
|
||||
def partition(self, s: str) -> List[List[str]]:
|
||||
res = []
|
||||
path = [] #放已经回文的子串
|
||||
def backtrack(s,startIndex):
|
||||
if startIndex >= len(s): #如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
|
||||
return res.append(path[:])
|
||||
for i in range(startIndex,len(s)):
|
||||
p = s[startIndex:i+1] #获取[startIndex,i+1]在s中的子串
|
||||
if p == p[::-1]: path.append(p) #是回文子串
|
||||
else: continue #不是回文,跳过
|
||||
backtrack(s,i+1) #寻找i+1为起始位置的子串
|
||||
path.pop() #回溯过程,弹出本次已经填在path的子串
|
||||
backtrack(s,0)
|
||||
return res
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
```
|
||||
```python
|
||||
# 版本二
|
||||
class Solution:
|
||||
def partition(self, s: str) -> List[List[str]]:
|
||||
res = []
|
||||
path = [] #放已经回文的子串
|
||||
# 双指针法判断是否是回文串
|
||||
def isPalindrome(s):
|
||||
n = len(s)
|
||||
i, j = 0, n - 1
|
||||
'''
|
||||
递归用于纵向遍历
|
||||
for循环用于横向遍历
|
||||
当切割线迭代至字符串末尾,说明找到一种方法
|
||||
类似组合问题,为了不重复切割同一位置,需要start_index来做标记下一轮递归的起始位置(切割线)
|
||||
'''
|
||||
self.path.clear()
|
||||
self.paths.clear()
|
||||
self.backtracking(s, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, s: str, start_index: int) -> None:
|
||||
# Base Case
|
||||
if start_index >= len(s):
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(s)):
|
||||
# 此次比其他组合题目多了一步判断:
|
||||
# 判断被截取的这一段子串([start_index, i])是否为回文串
|
||||
temp = s[start_index:i+1]
|
||||
if temp == temp[::-1]: # 若反序和正序相同,意味着这是回文串
|
||||
self.path.append(temp)
|
||||
self.backtracking(s, i+1) # 递归纵向遍历:从下一处进行切割,判断其余是否仍为回文串
|
||||
self.path.pop()
|
||||
else:
|
||||
continue
|
||||
```
|
||||
**回溯+函数判断回文串**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
def partition(self, s: str) -> List[List[str]]:
|
||||
'''
|
||||
递归用于纵向遍历
|
||||
for循环用于横向遍历
|
||||
当切割线迭代至字符串末尾,说明找到一种方法
|
||||
类似组合问题,为了不重复切割同一位置,需要start_index来做标记下一轮递归的起始位置(切割线)
|
||||
'''
|
||||
self.path.clear()
|
||||
self.paths.clear()
|
||||
self.backtracking(s, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, s: str, start_index: int) -> None:
|
||||
# Base Case
|
||||
if start_index >= len(s):
|
||||
self.paths.append(self.path[:])
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
for i in range(start_index, len(s)):
|
||||
# 此次比其他组合题目多了一步判断:
|
||||
# 判断被截取的这一段子串([start_index, i])是否为回文串
|
||||
if self.is_palindrome(s, start_index, i):
|
||||
self.path.append(s[start_index:i+1])
|
||||
self.backtracking(s, i+1) # 递归纵向遍历:从下一处进行切割,判断其余是否仍为回文串
|
||||
self.path.pop() # 回溯
|
||||
else:
|
||||
continue
|
||||
|
||||
def is_palindrome(self, s: str, start: int, end: int) -> bool:
|
||||
i: int = start
|
||||
j: int = end
|
||||
while i < j:
|
||||
if s[i] != s[j]:return False
|
||||
if s[i] != s[j]:
|
||||
return False
|
||||
i += 1
|
||||
j -= 1
|
||||
return True
|
||||
|
||||
def backtrack(s, startIndex):
|
||||
if startIndex >= len(s): # 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
|
||||
res.append(path[:])
|
||||
return
|
||||
for i in range(startIndex, len(s)):
|
||||
p = s[startIndex:i+1] # 获取[startIndex,i+1]在s中的子串
|
||||
if isPalindrome(p): # 是回文子串
|
||||
path.append(p)
|
||||
else: continue #不是回文,跳过
|
||||
backtrack(s, i + 1)
|
||||
path.pop() #回溯过程,弹出本次已经填在path的子串
|
||||
backtrack(s, 0)
|
||||
return res
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
注意切片(go切片是披着值类型外衣的引用类型)
|
||||
|
||||
**注意切片(go切片是披着值类型外衣的引用类型)**
|
||||
```go
|
||||
func partition(s string) [][]string {
|
||||
var tmpString []string//切割字符串集合
|
||||
|
||||
@ -132,30 +132,33 @@ public:
|
||||
Java:
|
||||
```java
|
||||
class Solution {
|
||||
/**
|
||||
分两个阶段
|
||||
1、起点下标1 从左往右,只要 右边 比 左边 大,右边的糖果=左边 + 1
|
||||
2、起点下标 ratings.length - 2 从右往左, 只要左边 比 右边 大,此时 左边的糖果应该 取本身的糖果数(符合比它左边大) 和 右边糖果数 + 1 二者的最大值,这样才符合 它比它左边的大,也比它右边大
|
||||
*/
|
||||
public int candy(int[] ratings) {
|
||||
int[] candy = new int[ratings.length];
|
||||
for (int i = 0; i < candy.length; i++) {
|
||||
candy[i] = 1;
|
||||
}
|
||||
|
||||
int[] candyVec = new int[ratings.length];
|
||||
candyVec[0] = 1;
|
||||
for (int i = 1; i < ratings.length; i++) {
|
||||
if (ratings[i] > ratings[i - 1]) {
|
||||
candy[i] = candy[i - 1] + 1;
|
||||
candyVec[i] = candyVec[i - 1] + 1;
|
||||
} else {
|
||||
candyVec[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
for (int i = ratings.length - 2; i >= 0; i--) {
|
||||
if (ratings[i] > ratings[i + 1]) {
|
||||
candy[i] = Math.max(candy[i],candy[i + 1] + 1);
|
||||
candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
|
||||
}
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
for (int i = 0; i < candy.length; i++) {
|
||||
count += candy[i];
|
||||
int ans = 0;
|
||||
for (int s : candyVec) {
|
||||
ans += s;
|
||||
}
|
||||
|
||||
return count;
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -50,10 +50,6 @@ public:
|
||||
cur = cur->next;
|
||||
count++;
|
||||
}
|
||||
if (vec.size() % 2 == 0) { // 如果是偶数,还要多处理中间的一个
|
||||
cur->next = vec[i];
|
||||
cur = cur->next;
|
||||
}
|
||||
cur->next = nullptr; // 注意结尾
|
||||
}
|
||||
};
|
||||
@ -249,12 +245,6 @@ public class ReorderList {
|
||||
cur = cur.next;
|
||||
count++;
|
||||
}
|
||||
// 当是偶数的话,需要做额外处理
|
||||
if (list.size() % 2== 0){
|
||||
cur.next = list.get(l);
|
||||
cur = cur.next;
|
||||
}
|
||||
|
||||
// 注意结尾要结束一波
|
||||
cur.next = null;
|
||||
}
|
||||
@ -376,11 +366,6 @@ var reorderList = function(head, s = [], tmp) {
|
||||
cur = cur.next;
|
||||
count++;
|
||||
}
|
||||
// 当是偶数的话,需要做额外处理
|
||||
if(list.length % 2 == 0){
|
||||
cur.next = list[l];
|
||||
cur = cur.next;
|
||||
}
|
||||
// 注意结尾要结束一波
|
||||
cur.next = null;
|
||||
}
|
||||
|
||||
@ -40,7 +40,7 @@
|
||||
|
||||
**当然如果使用java ,python的话就不用手动管理内存了。**
|
||||
|
||||
还要说明一下,就算使用C++来做leetcode,如果移除一个节点之后,没有手动在内存中删除这个节点,leetcode依然也是可以通过的,只不过,内存使用的空间大一些而已,但建议依然要养生手动清理内存的习惯。
|
||||
还要说明一下,就算使用C++来做leetcode,如果移除一个节点之后,没有手动在内存中删除这个节点,leetcode依然也是可以通过的,只不过,内存使用的空间大一些而已,但建议依然要养成手动清理内存的习惯。
|
||||
|
||||
这种情况下的移除操作,就是让节点next指针直接指向下下一个节点就可以了,
|
||||
|
||||
|
||||
@ -27,9 +27,9 @@
|
||||
|
||||
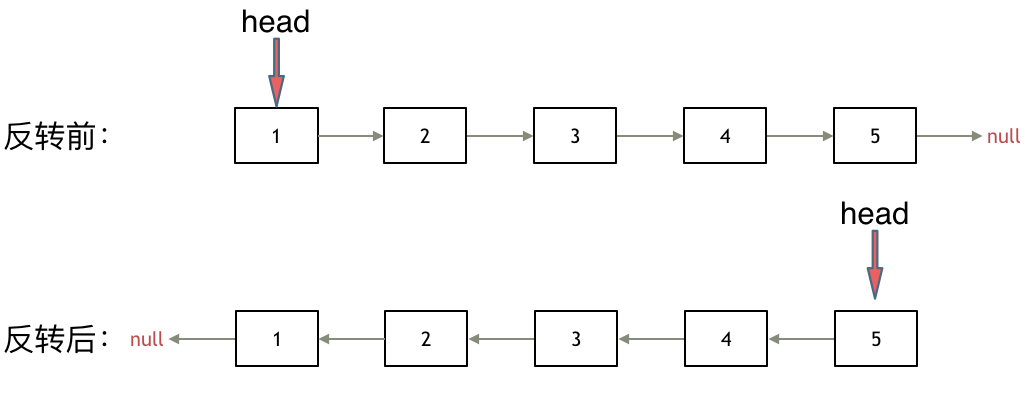
|
||||
|
||||
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改表next指针的方向。
|
||||
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
|
||||
|
||||
那么接下来看一看是如何反转呢?
|
||||
那么接下来看一看是如何反转的呢?
|
||||
|
||||
我们拿有示例中的链表来举例,如动画所示:
|
||||
|
||||
@ -96,6 +96,28 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
我们可以发现,上面的递归写法和双指针法实质上都是从前往后翻转指针指向,其实还有另外一种与双指针法不同思路的递归写法:从后往前翻转指针指向。
|
||||
|
||||
具体代码如下(带详细注释):
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
ListNode* reverseList(ListNode* head) {
|
||||
// 边缘条件判断
|
||||
if(head == NULL) return NULL;
|
||||
if (head->next == NULL) return head;
|
||||
|
||||
// 递归调用,翻转第二个节点开始往后的链表
|
||||
ListNode *last = reverseList(head->next);
|
||||
// 翻转头节点与第二个节点的指向
|
||||
head->next->next = head;
|
||||
// 此时的 head 节点为尾节点,next 需要指向 NULL
|
||||
head->next = NULL;
|
||||
return last;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
@ -135,9 +157,28 @@ class Solution {
|
||||
temp = cur.next;// 先保存下一个节点
|
||||
cur.next = prev;// 反转
|
||||
// 更新prev、cur位置
|
||||
prev = cur;
|
||||
cur = temp;
|
||||
return reverse(prev, cur);
|
||||
// prev = cur;
|
||||
// cur = temp;
|
||||
return reverse(cur, temp);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
// 从后向前递归
|
||||
class Solution {
|
||||
ListNode reverseList(ListNode head) {
|
||||
// 边缘条件判断
|
||||
if(head == null) return null;
|
||||
if (head.next == null) return head;
|
||||
|
||||
// 递归调用,翻转第二个节点开始往后的链表
|
||||
ListNode last = reverseList(head.next);
|
||||
// 翻转头节点与第二个节点的指向
|
||||
head.next.next = head;
|
||||
// 此时的 head 节点为尾节点,next 需要指向 NULL
|
||||
head.next = null;
|
||||
return last;
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -371,6 +412,45 @@ func reverse(pre: ListNode?, cur: ListNode?) -> ListNode? {
|
||||
}
|
||||
```
|
||||
|
||||
C:
|
||||
双指针法:
|
||||
```c
|
||||
struct ListNode* reverseList(struct ListNode* head){
|
||||
//保存cur的下一个结点
|
||||
struct ListNode* temp;
|
||||
//pre指针指向前一个当前结点的前一个结点
|
||||
struct ListNode* pre = NULL;
|
||||
//用head代替cur,也可以再定义一个cur结点指向head。
|
||||
while(head) {
|
||||
//保存下一个结点的位置
|
||||
temp = head->next;
|
||||
//翻转操作
|
||||
head->next = pre;
|
||||
//更新结点
|
||||
pre = head;
|
||||
head = temp;
|
||||
}
|
||||
return pre;
|
||||
}
|
||||
```
|
||||
|
||||
递归法:
|
||||
```c
|
||||
struct ListNode* reverse(struct ListNode* pre, struct ListNode* cur) {
|
||||
if(!cur)
|
||||
return pre;
|
||||
struct ListNode* temp = cur->next;
|
||||
cur->next = pre;
|
||||
//将cur作为pre传入下一层
|
||||
//将temp作为cur传入下一层,改变其指针指向当前cur
|
||||
return reverse(cur, temp);
|
||||
}
|
||||
|
||||
struct ListNode* reverseList(struct ListNode* head){
|
||||
return reverse(NULL, head);
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
|
||||
@ -112,7 +112,7 @@ public:
|
||||
|
||||
# 优化
|
||||
|
||||
其实这道题目就是用一个队里就够了。
|
||||
其实这道题目就是用一个队列就够了。
|
||||
|
||||
**一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时在去弹出元素就是栈的顺序了。**
|
||||
|
||||
|
||||
@ -565,6 +565,51 @@ var invertTree = function(root) {
|
||||
};
|
||||
```
|
||||
|
||||
C:
|
||||
递归法
|
||||
```c
|
||||
struct TreeNode* invertTree(struct TreeNode* root){
|
||||
if(!root)
|
||||
return NULL;
|
||||
//交换结点的左右孩子(中)
|
||||
struct TreeNode* temp = root->right;
|
||||
root->right = root->left;
|
||||
root->left = temp;
|
||||
左
|
||||
invertTree(root->left);
|
||||
//右
|
||||
invertTree(root->right);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
迭代法:深度优先遍历
|
||||
```c
|
||||
struct TreeNode* invertTree(struct TreeNode* root){
|
||||
if(!root)
|
||||
return NULL;
|
||||
//存储结点的栈
|
||||
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
|
||||
int stackTop = 0;
|
||||
//将根节点入栈
|
||||
stack[stackTop++] = root;
|
||||
//若栈中还有元素(进行循环)
|
||||
while(stackTop) {
|
||||
//取出栈顶元素
|
||||
struct TreeNode* temp = stack[--stackTop];
|
||||
//交换结点的左右孩子
|
||||
struct TreeNode* tempNode = temp->right;
|
||||
temp->right = temp->left;
|
||||
temp->left = tempNode;
|
||||
//若当前结点有左右孩子,将其入栈
|
||||
if(temp->right)
|
||||
stack[stackTop++] = temp->right;
|
||||
if(temp->left)
|
||||
stack[stackTop++] = temp->left;
|
||||
}
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
|
||||
@ -404,33 +404,41 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
```Python
|
||||
---
|
||||
Python:
|
||||
递归法+隐形回溯
|
||||
```Python3
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
"""二叉树的所有路径 递归法"""
|
||||
|
||||
def binaryTreePaths(self, root: TreeNode) -> List[str]:
|
||||
path, result = '', []
|
||||
path = ''
|
||||
result = []
|
||||
if not root: return result
|
||||
self.traversal(root, path, result)
|
||||
return result
|
||||
|
||||
def traversal(self, cur: TreeNode, path: List, result: List):
|
||||
def traversal(self, cur: TreeNode, path: str, result: List[str]) -> None:
|
||||
path += str(cur.val)
|
||||
# 如果当前节点为叶子节点,添加路径到结果中
|
||||
if not (cur.left or cur.right):
|
||||
# 若当前节点为leave,直接输出
|
||||
if not cur.left and not cur.right:
|
||||
result.append(path)
|
||||
return
|
||||
|
||||
if cur.left:
|
||||
# + '->' 是隐藏回溯
|
||||
self.traversal(cur.left, path + '->', result)
|
||||
|
||||
if cur.right:
|
||||
self.traversal(cur.right, path + '->', result)
|
||||
|
||||
```
|
||||
|
||||
```python
|
||||
迭代法:
|
||||
|
||||
```python3
|
||||
from collections import deque
|
||||
|
||||
|
||||
@ -458,6 +466,7 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
Go:
|
||||
```go
|
||||
@ -482,7 +491,7 @@ func binaryTreePaths(root *TreeNode) []string {
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
---
|
||||
JavaScript:
|
||||
|
||||
1.递归版本
|
||||
|
||||
@ -334,8 +334,8 @@ var numSquares1 = function(n) {
|
||||
let dp = new Array(n + 1).fill(Infinity)
|
||||
dp[0] = 0
|
||||
|
||||
for(let i = 0; i <= n; i++) {
|
||||
let val = i * i
|
||||
for(let i = 1; i**2 <= n; i++) {
|
||||
let val = i**2
|
||||
for(let j = val; j <= n; j++) {
|
||||
dp[j] = Math.min(dp[j], dp[j - val] + 1)
|
||||
}
|
||||
|
||||
@ -368,6 +368,41 @@ class Solution:
|
||||
return (val1, val2)
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
动态规划
|
||||
|
||||
```go
|
||||
func rob(root *TreeNode) int {
|
||||
res := robTree(root)
|
||||
return max(res[0], res[1])
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
func robTree(cur *TreeNode) []int {
|
||||
if cur == nil {
|
||||
return []int{0, 0}
|
||||
}
|
||||
// 后序遍历
|
||||
left := robTree(cur.Left)
|
||||
right := robTree(cur.Right)
|
||||
|
||||
// 考虑去偷当前的屋子
|
||||
robCur := cur.Val + left[0] + right[0]
|
||||
// 考虑不去偷当前的屋子
|
||||
notRobCur := max(left[0], left[1]) + max(right[0], right[1])
|
||||
|
||||
// 注意顺序:0:不偷,1:去偷
|
||||
return []int{notRobCur, robCur}
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
|
||||
> 动态规划
|
||||
|
||||
@ -218,12 +218,19 @@ func reverseString(_ s: inout [Character]) {
|
||||
}
|
||||
}
|
||||
|
||||
// 双指针法 - 库函数
|
||||
func reverseString(_ s: inout [Character]) {
|
||||
var j = s.count - 1
|
||||
for i in 0 ..< Int(Double(s.count) * 0.5) {
|
||||
s.swapAt(i, j)
|
||||
j -= 1
|
||||
```
|
||||
|
||||
C:
|
||||
```c
|
||||
void reverseString(char* s, int sSize){
|
||||
int left = 0;
|
||||
int right = sSize - 1;
|
||||
|
||||
while(left < right) {
|
||||
char temp = s[left];
|
||||
s[left++] = s[right];
|
||||
s[right--] = temp;
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -33,8 +33,7 @@
|
||||
输入: [1,2,3,4,5,6,7,8,9]
|
||||
输出: 2
|
||||
|
||||
|
||||
## 思路
|
||||
## 思路1(贪心解法)
|
||||
|
||||
本题要求通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
|
||||
|
||||
@ -93,6 +92,69 @@ public:
|
||||
时间复杂度O(n)
|
||||
空间复杂度O(1)
|
||||
|
||||
## 思路2(动态规划)
|
||||
|
||||
考虑用动态规划的思想来解决这个问题。
|
||||
|
||||
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即nums[i] > nums[i-1]),要么是作为山谷(即nums[i] < nums[i - 1])。
|
||||
|
||||
* 设dp状态`dp[i][0]`,表示考虑前i个数,第i个数作为山峰的摆动子序列的最长长度
|
||||
* 设dp状态`dp[i][1]`,表示考虑前i个数,第i个数作为山谷的摆动子序列的最长长度
|
||||
|
||||
则转移方程为:
|
||||
|
||||
* `dp[i][0] = max(dp[i][0], dp[j][1] + 1)`,其中`0 < j < i`且`nums[j] < nums[i]`,表示将nums[i]接到前面某个山谷后面,作为山峰。
|
||||
* `dp[i][1] = max(dp[i][1], dp[j][0] + 1)`,其中`0 < j < i`且`nums[j] > nums[i]`,表示将nums[i]接到前面某个山峰后面,作为山谷。
|
||||
|
||||
初始状态:
|
||||
|
||||
由于一个数可以接到前面的某个数后面,也可以以自身为子序列的起点,所以初始状态为:`dp[0][0] = dp[0][1] = 1`。
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
int dp[1005][2];
|
||||
int wiggleMaxLength(vector<int>& nums) {
|
||||
memset(dp, 0, sizeof dp);
|
||||
dp[0][0] = dp[0][1] = 1;
|
||||
|
||||
for (int i = 1; i < nums.size(); ++i)
|
||||
{
|
||||
dp[i][0] = dp[i][1] = 1;
|
||||
|
||||
for (int j = 0; j < i; ++j)
|
||||
{
|
||||
if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
|
||||
}
|
||||
|
||||
for (int j = 0; j < i; ++j)
|
||||
{
|
||||
if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
|
||||
}
|
||||
}
|
||||
return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
时间复杂度O(n^2)
|
||||
|
||||
空间复杂度O(n)
|
||||
|
||||
**进阶**
|
||||
|
||||
可以用两棵线段树来维护区间的最大值
|
||||
|
||||
* 每次更新`dp[i][0]`,则在`tree1`的`nums[i]`位置值更新为`dp[i][0]`
|
||||
* 每次更新`dp[i][1]`,则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
|
||||
* 则dp转移方程中就没有必要j从0遍历到i-1,可以直接在线段树中查询指定区间的值即可。
|
||||
|
||||
时间复杂度O(nlogn)
|
||||
|
||||
空间复杂度O(n)
|
||||
|
||||
## 总结
|
||||
|
||||
**贪心的题目说简单有的时候就是常识,说难就难在都不知道该怎么用贪心**。
|
||||
@ -177,7 +239,7 @@ var wiggleMaxLength = function(nums) {
|
||||
let result = 1
|
||||
let preDiff = 0
|
||||
let curDiff = 0
|
||||
for(let i = 0; i <= nums.length; i++) {
|
||||
for(let i = 0; i < nums.length - 1; i++) {
|
||||
curDiff = nums[i + 1] - nums[i]
|
||||
if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
|
||||
result++
|
||||
|
||||
@ -141,7 +141,7 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
```
|
||||
```java
|
||||
class Solution {
|
||||
public boolean isSubsequence(String s, String t) {
|
||||
int length1 = s.length(); int length2 = t.length();
|
||||
|
||||
@ -171,10 +171,10 @@ class Solution {
|
||||
int rightValue = sumOfLeftLeaves(root.right); // 右
|
||||
|
||||
int midValue = 0;
|
||||
if (root.left != null && root.left.left == null && root.left.right == null) { // 中
|
||||
if (root.left != null && root.left.left == null && root.left.right == null) {
|
||||
midValue = root.left.val;
|
||||
}
|
||||
int sum = midValue + leftValue + rightValue;
|
||||
int sum = midValue + leftValue + rightValue; // 中
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
@ -230,8 +230,8 @@ class Solution {
|
||||
|
||||
## Python
|
||||
|
||||
**递归**
|
||||
```python
|
||||
**递归后序遍历**
|
||||
```python3
|
||||
class Solution:
|
||||
def sumOfLeftLeaves(self, root: TreeNode) -> int:
|
||||
if not root:
|
||||
@ -242,13 +242,13 @@ class Solution:
|
||||
|
||||
cur_left_leaf_val = 0
|
||||
if root.left and not root.left.left and not root.left.right:
|
||||
cur_left_leaf_val = root.left.val # 中
|
||||
cur_left_leaf_val = root.left.val
|
||||
|
||||
return cur_left_leaf_val + left_left_leaves_sum + right_left_leaves_sum
|
||||
return cur_left_leaf_val + left_left_leaves_sum + right_left_leaves_sum # 中
|
||||
```
|
||||
|
||||
**迭代**
|
||||
```python
|
||||
```python3
|
||||
class Solution:
|
||||
def sumOfLeftLeaves(self, root: TreeNode) -> int:
|
||||
"""
|
||||
|
||||
@ -226,8 +226,34 @@ class Solution:
|
||||
return taraget == dp[taraget]
|
||||
```
|
||||
Go:
|
||||
```go
|
||||
// 分割等和子集 动态规划
|
||||
// 时间复杂度O(n^2) 空间复杂度O(n)
|
||||
func canPartition(nums []int) bool {
|
||||
sum := 0
|
||||
for _, num := range nums {
|
||||
sum += num
|
||||
}
|
||||
// 如果 nums 的总和为奇数则不可能平分成两个子集
|
||||
if sum % 2 == 1 {
|
||||
return false
|
||||
}
|
||||
|
||||
target := sum / 2
|
||||
dp := make([]int, target + 1)
|
||||
|
||||
for _, num := range nums {
|
||||
for j := target; j >= num; j-- {
|
||||
if dp[j] < dp[j - num] + num {
|
||||
dp[j] = dp[j - num] + num
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[target] == target
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
func canPartition(nums []int) bool {
|
||||
/**
|
||||
动态五部曲:
|
||||
|
||||
@ -72,7 +72,7 @@
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
// 按照区间右边界排序
|
||||
|
||||
@ -200,7 +200,7 @@ func findContentChildren(g []int, s []int) int {
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```
|
||||
```js
|
||||
var findContentChildren = function(g, s) {
|
||||
g = g.sort((a, b) => a - b)
|
||||
s = s.sort((a, b) => a - b)
|
||||
|
||||
@ -229,33 +229,86 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
<<<<<<< HEAD
|
||||
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
python3
|
||||
**回溯**
|
||||
```python3
|
||||
class Solution:
|
||||
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
|
||||
res = []
|
||||
path = []
|
||||
def backtrack(nums,startIndex):
|
||||
repeat = [] #这里使用数组来进行去重操作
|
||||
if len(path) >=2:
|
||||
res.append(path[:]) #注意这里不要加return,要取树上的节点
|
||||
for i in range(startIndex,len(nums)):
|
||||
if nums[i] in repeat:
|
||||
continue
|
||||
if len(path) >= 1:
|
||||
if nums[i] < path[-1]:
|
||||
continue
|
||||
repeat.append(nums[i]) #记录这个元素在本层用过了,本层后面不能再用了
|
||||
path.append(nums[i])
|
||||
backtrack(nums,i+1)
|
||||
path.pop()
|
||||
backtrack(nums,0)
|
||||
return res
|
||||
```
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
|
||||
'''
|
||||
本题求自增子序列,所以不能改变原数组顺序
|
||||
'''
|
||||
self.backtracking(nums, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int], start_index: int):
|
||||
# 收集结果,同78.子集,仍要置于终止条件之前
|
||||
if len(self.path) >= 2:
|
||||
# 本题要求所有的节点
|
||||
self.paths.append(self.path[:])
|
||||
|
||||
# Base Case(可忽略)
|
||||
if start_index == len(nums):
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
|
||||
usage_list = set()
|
||||
# 同层横向遍历
|
||||
for i in range(start_index, len(nums)):
|
||||
# 若当前元素值小于前一个时(非递增)或者曾用过,跳入下一循环
|
||||
if (self.path and nums[i] < self.path[-1]) or nums[i] in usage_list:
|
||||
continue
|
||||
usage_list.add(nums[i])
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums, i+1)
|
||||
self.path.pop()
|
||||
```
|
||||
**回溯+哈希表去重**
|
||||
```python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.paths = []
|
||||
self.path = []
|
||||
|
||||
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
|
||||
'''
|
||||
本题求自增子序列,所以不能改变原数组顺序
|
||||
'''
|
||||
self.backtracking(nums, 0)
|
||||
return self.paths
|
||||
|
||||
def backtracking(self, nums: List[int], start_index: int):
|
||||
# 收集结果,同78.子集,仍要置于终止条件之前
|
||||
if len(self.path) >= 2:
|
||||
# 本题要求所有的节点
|
||||
self.paths.append(self.path[:])
|
||||
|
||||
# Base Case(可忽略)
|
||||
if start_index == len(nums):
|
||||
return
|
||||
|
||||
# 单层递归逻辑
|
||||
# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
|
||||
usage_list = [False] * 201 # 使用列表去重,题中取值范围[-100, 100]
|
||||
# 同层横向遍历
|
||||
for i in range(start_index, len(nums)):
|
||||
# 若当前元素值小于前一个时(非递增)或者曾用过,跳入下一循环
|
||||
if (self.path and nums[i] < self.path[-1]) or usage_list[nums[i]+100] == True:
|
||||
continue
|
||||
usage_list[nums[i]+100] = True
|
||||
self.path.append(nums[i])
|
||||
self.backtracking(nums, i+1)
|
||||
self.path.pop()
|
||||
```
|
||||
### Go
|
||||
|
||||
```golang
|
||||
|
||||
@ -371,7 +371,6 @@ const findTargetSumWays = (nums, target) => {
|
||||
}
|
||||
|
||||
const halfSum = (target + sum) / 2;
|
||||
nums.sort((a, b) => a - b);
|
||||
|
||||
let dp = new Array(halfSum+1).fill(0);
|
||||
dp[0] = 1;
|
||||
|
||||
@ -470,38 +470,54 @@ class Solution {
|
||||
|
||||
## Python
|
||||
|
||||
递归法
|
||||
> 递归法
|
||||
|
||||
```python
|
||||
```python3
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.pre = TreeNode()
|
||||
self.count = 0
|
||||
self.max_count = 0
|
||||
self.result = []
|
||||
|
||||
def findMode(self, root: TreeNode) -> List[int]:
|
||||
if not root: return
|
||||
self.pre = root
|
||||
self.count = 0 //统计频率
|
||||
self.countMax = 0 //最大频率
|
||||
self.res = []
|
||||
def findNumber(root):
|
||||
if not root: return None // 第一个节点
|
||||
findNumber(root.left) //左
|
||||
if self.pre.val == root.val: //中: 与前一个节点数值相同
|
||||
self.count += 1
|
||||
else: // 与前一个节点数值不同
|
||||
self.pre = root
|
||||
if not root: return None
|
||||
self.search_BST(root)
|
||||
return self.result
|
||||
|
||||
def search_BST(self, cur: TreeNode) -> None:
|
||||
if not cur: return None
|
||||
self.search_BST(cur.left)
|
||||
# 第一个节点
|
||||
if not self.pre:
|
||||
self.count = 1
|
||||
if self.count > self.countMax: // 如果计数大于最大值频率
|
||||
self.countMax = self.count // 更新最大频率
|
||||
self.res = [root.val] //更新res
|
||||
elif self.count == self.countMax: // 如果和最大值相同,放进res中
|
||||
self.res.append(root.val)
|
||||
findNumber(root.right) //右
|
||||
return
|
||||
findNumber(root)
|
||||
return self.res
|
||||
# 与前一个节点数值相同
|
||||
elif self.pre.val == cur.val:
|
||||
self.count += 1
|
||||
# 与前一个节点数值不相同
|
||||
else:
|
||||
self.count = 1
|
||||
self.pre = cur
|
||||
|
||||
if self.count == self.max_count:
|
||||
self.result.append(cur.val)
|
||||
|
||||
if self.count > self.max_count:
|
||||
self.max_count = self.count
|
||||
self.result = [cur.val] # 清空self.result,确保result之前的的元素都失效
|
||||
|
||||
self.search_BST(cur.right)
|
||||
```
|
||||
|
||||
|
||||
迭代法-中序遍历-不使用额外空间,利用二叉搜索树特性
|
||||
```python
|
||||
> 迭代法-中序遍历-不使用额外空间,利用二叉搜索树特性
|
||||
```python3
|
||||
class Solution:
|
||||
def findMode(self, root: TreeNode) -> List[int]:
|
||||
stack = []
|
||||
|
||||
@ -196,20 +196,40 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
**递归**
|
||||
|
||||
递归法
|
||||
```python
|
||||
```python3
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def convertBST(self, root: TreeNode) -> TreeNode:
|
||||
def buildalist(root):
|
||||
if not root: return None
|
||||
buildalist(root.right) #右中左遍历
|
||||
root.val += self.pre
|
||||
self.pre = root.val
|
||||
buildalist(root.left)
|
||||
self.pre = 0 #记录前一个节点的数值
|
||||
buildalist(root)
|
||||
def __init__(self):
|
||||
self.pre = TreeNode()
|
||||
|
||||
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
|
||||
'''
|
||||
倒序累加替换:
|
||||
[2, 5, 13] -> [[2]+[1]+[0], [2]+[1], [2]] -> [20, 18, 13]
|
||||
'''
|
||||
self.traversal(root)
|
||||
return root
|
||||
|
||||
def traversal(self, root: TreeNode) -> None:
|
||||
# 因为要遍历整棵树,所以递归函数不需要返回值
|
||||
# Base Case
|
||||
if not root:
|
||||
return None
|
||||
# 单层递归逻辑:中序遍历的反译 - 右中左
|
||||
self.traversal(root.right) # 右
|
||||
|
||||
# 中节点:用当前root的值加上pre的值
|
||||
root.val += self.pre.val # 中
|
||||
self.pre = root
|
||||
|
||||
self.traversal(root.left) # 左
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
@ -265,18 +265,35 @@ class Solution {
|
||||
```
|
||||
|
||||
## Python
|
||||
|
||||
**递归**
|
||||
```python3
|
||||
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
|
||||
if not root: return root
|
||||
'''
|
||||
确认递归函数参数以及返回值:返回更新后剪枝后的当前root节点
|
||||
'''
|
||||
# Base Case
|
||||
if not root: return None
|
||||
|
||||
# 单层递归逻辑
|
||||
if root.val < low:
|
||||
return self.trimBST(root.right,low,high) // 寻找符合区间[low, high]的节点
|
||||
if root.val > high:
|
||||
return self.trimBST(root.left,low,high) // 寻找符合区间[low, high]的节点
|
||||
root.left = self.trimBST(root.left,low,high) // root->left接入符合条件的左孩子
|
||||
root.right = self.trimBST(root.right,low,high) // root->right接入符合条件的右孩子
|
||||
# 若当前root节点小于左界:只考虑其右子树,用于替代更新后的其本身,抛弃其左子树整体
|
||||
return self.trimBST(root.right, low, high)
|
||||
|
||||
if high < root.val:
|
||||
# 若当前root节点大于右界:只考虑其左子树,用于替代更新后的其本身,抛弃其右子树整体
|
||||
return self.trimBST(root.left, low, high)
|
||||
|
||||
if low <= root.val <= high:
|
||||
root.left = self.trimBST(root.left, low, high)
|
||||
root.right = self.trimBST(root.right, low, high)
|
||||
# 返回更新后的剪枝过的当前节点root
|
||||
return root
|
||||
```
|
||||
|
||||
|
||||
@ -253,21 +253,38 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
-----
|
||||
## Python
|
||||
|
||||
**递归法** - 有返回值
|
||||
|
||||
```python
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
|
||||
if root is None:
|
||||
return TreeNode(val) # 如果当前节点为空,也就意味着val找到了合适的位置,此时创建节点直接返回。
|
||||
# 返回更新后的以当前root为根节点的新树,方便用于更新上一层的父子节点关系链
|
||||
|
||||
# Base Case
|
||||
if not root: return TreeNode(val)
|
||||
|
||||
# 单层递归逻辑:
|
||||
if val < root.val:
|
||||
# 将val插入至当前root的左子树中合适的位置
|
||||
# 并更新当前root的左子树为包含目标val的新左子树
|
||||
root.left = self.insertIntoBST(root.left, val)
|
||||
|
||||
if root.val < val:
|
||||
root.right = self.insertIntoBST(root.right, val) # 递归创建右子树
|
||||
if root.val > val:
|
||||
root.left = self.insertIntoBST(root.left, val) # 递归创建左子树
|
||||
return root
|
||||
# 将val插入至当前root的右子树中合适的位置
|
||||
# 并更新当前root的右子树为包含目标val的新右子树
|
||||
root.right = self.insertIntoBST(root.right, val)
|
||||
|
||||
# 返回更新后的以当前root为根节点的新树
|
||||
return roo
|
||||
```
|
||||
|
||||
**递归法** - 无返回值
|
||||
@ -328,7 +345,7 @@ class Solution:
|
||||
return root
|
||||
|
||||
```
|
||||
|
||||
-----
|
||||
## Go
|
||||
|
||||
递归法
|
||||
@ -374,7 +391,7 @@ func insertIntoBST(root *TreeNode, val int) *TreeNode {
|
||||
return root
|
||||
}
|
||||
```
|
||||
|
||||
-----
|
||||
## JavaScript
|
||||
|
||||
有返回值的递归写法
|
||||
|
||||
@ -140,7 +140,7 @@ public:
|
||||
## 相关题目推荐
|
||||
|
||||
* [35.搜索插入位置](https://programmercarl.com/0035.搜索插入位置.html)
|
||||
* 34.在排序数组中查找元素的第一个和最后一个位置
|
||||
* [34.在排序数组中查找元素的第一个和最后一个位置](https://programmercarl.com/0034.%E5%9C%A8%E6%8E%92%E5%BA%8F%E6%95%B0%E7%BB%84%E4%B8%AD%E6%9F%A5%E6%89%BE%E5%85%83%E7%B4%A0%E7%9A%84%E7%AC%AC%E4%B8%80%E4%B8%AA%E5%92%8C%E6%9C%80%E5%90%8E%E4%B8%80%E4%B8%AA%E4%BD%8D%E7%BD%AE.html)
|
||||
* 69.x 的平方根
|
||||
* 367.有效的完全平方数
|
||||
|
||||
|
||||
@ -282,12 +282,12 @@ Java:
|
||||
```Java
|
||||
//单链表
|
||||
class ListNode {
|
||||
int val;
|
||||
ListNode next;
|
||||
ListNode(){}
|
||||
ListNode(int val) {
|
||||
this.val=val;
|
||||
}
|
||||
int val;
|
||||
ListNode next;
|
||||
ListNode(){}
|
||||
ListNode(int val) {
|
||||
this.val=val;
|
||||
}
|
||||
}
|
||||
class MyLinkedList {
|
||||
//size存储链表元素的个数
|
||||
|
||||
@ -262,6 +262,34 @@ var maxProfit = function(prices, fee) {
|
||||
}
|
||||
return result
|
||||
};
|
||||
|
||||
// 动态规划
|
||||
/**
|
||||
* @param {number[]} prices
|
||||
* @param {number} fee
|
||||
* @return {number}
|
||||
*/
|
||||
var maxProfit = function(prices, fee) {
|
||||
// 滚动数组
|
||||
// have表示当天持有股票的最大收益
|
||||
// notHave表示当天不持有股票的最大收益
|
||||
// 把手续费算在买入价格中
|
||||
let n = prices.length,
|
||||
have = -prices[0]-fee, // 第0天持有股票的最大收益
|
||||
notHave = 0; // 第0天不持有股票的最大收益
|
||||
for (let i = 1; i < n; i++) {
|
||||
// 第i天持有股票的最大收益由两种情况组成
|
||||
// 1、第i-1天就已经持有股票,第i天什么也没做
|
||||
// 2、第i-1天不持有股票,第i天刚买入
|
||||
have = Math.max(have, notHave - prices[i] - fee);
|
||||
// 第i天不持有股票的最大收益由两种情况组成
|
||||
// 1、第i-1天就已经不持有股票,第i天什么也没做
|
||||
// 2、第i-1天持有股票,第i天刚卖出
|
||||
notHave = Math.max(notHave, have + prices[i]);
|
||||
}
|
||||
// 最后手中不持有股票,收益才能最大化
|
||||
return notHave;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
@ -127,6 +127,7 @@ public:
|
||||
|
||||
Java:
|
||||
```java
|
||||
版本1
|
||||
class Solution {
|
||||
public int monotoneIncreasingDigits(int N) {
|
||||
String[] strings = (N + "").split("");
|
||||
@ -144,6 +145,31 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
java版本1中创建了String数组,多次使用Integer.parseInt了方法,这导致不管是耗时还是空间占用都非常高,用时12ms,下面提供一个版本在char数组上原地修改,用时1ms的版本
|
||||
```java
|
||||
版本2
|
||||
class Solution {
|
||||
public int monotoneIncreasingDigits(int n) {
|
||||
if (n==0)return 0;
|
||||
char[] chars= Integer.toString(n).toCharArray();
|
||||
int start=Integer.MAX_VALUE;//start初始值设为最大值,这是为了防止当数字本身是单调递增时,没有一位数字需要改成9的情况
|
||||
for (int i=chars.length-1;i>0;i--){
|
||||
if (chars[i]<chars[i-1]){
|
||||
chars[i-1]--;
|
||||
start=i;
|
||||
}
|
||||
}
|
||||
StringBuilder res=new StringBuilder();
|
||||
for (int i=0;i<chars.length;i++){
|
||||
if (chars[i]=='0'&&i==0)continue;//防止出现09这样的情况
|
||||
if (i>=start){
|
||||
res.append('9');
|
||||
}else res.append(chars[i]);
|
||||
}
|
||||
return Integer.parseInt(res.toString());
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
@ -88,15 +88,15 @@ Java:
|
||||
class Solution {
|
||||
public List<Integer> partitionLabels(String S) {
|
||||
List<Integer> list = new LinkedList<>();
|
||||
int[] edge = new int[123];
|
||||
int[] edge = new int[26];
|
||||
char[] chars = S.toCharArray();
|
||||
for (int i = 0; i < chars.length; i++) {
|
||||
edge[chars[i] - 0] = i;
|
||||
edge[chars[i] - 'a'] = i;
|
||||
}
|
||||
int idx = 0;
|
||||
int last = -1;
|
||||
for (int i = 0; i < chars.length; i++) {
|
||||
idx = Math.max(idx,edge[chars[i] - 0]);
|
||||
idx = Math.max(idx,edge[chars[i] - 'a']);
|
||||
if (i == idx) {
|
||||
list.add(i - last);
|
||||
last = i;
|
||||
|
||||
@ -27,7 +27,7 @@
|
||||
|
||||
## 暴力排序
|
||||
|
||||
最直观的相反,莫过于:每个数平方之后,排个序,美滋滋,代码如下:
|
||||
最直观的想法,莫过于:每个数平方之后,排个序,美滋滋,代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
|
||||
@ -224,10 +224,7 @@ javaScript
|
||||
var commonChars = function (words) {
|
||||
let res = []
|
||||
let size = 26
|
||||
let firstHash = new Array(size)
|
||||
for (let i = 0; i < size; i++) { // 初始化 hash 数组
|
||||
firstHash[i] = 0
|
||||
}
|
||||
let firstHash = new Array(size).fill(0) // 初始化 hash 数组
|
||||
|
||||
let a = "a".charCodeAt()
|
||||
let firstWord = words[0]
|
||||
@ -236,20 +233,19 @@ var commonChars = function (words) {
|
||||
firstHash[idx - a] += 1
|
||||
}
|
||||
|
||||
let otherHash = new Array(size).fill(0) // 初始化 hash 数组
|
||||
for (let i = 1; i < words.length; i++) { // 1-n 个单词统计
|
||||
let otherHash = new Array(size)
|
||||
for (let i = 0; i < size; i++) { // 初始化 hash 数组
|
||||
otherHash[i] = 0
|
||||
}
|
||||
|
||||
for (let j = 0; j < words[i].length; j++) {
|
||||
let idx = words[i][j].charCodeAt()
|
||||
otherHash[idx - a] += 1
|
||||
}
|
||||
|
||||
for (let i = 0; i < size; i++) {
|
||||
firstHash[i] = Math.min(firstHash[i], otherHash[i])
|
||||
}
|
||||
otherHash.fill(0)
|
||||
}
|
||||
|
||||
for (let i = 0; i < size; i++) {
|
||||
while (firstHash[i] > 0) {
|
||||
res.push(String.fromCharCode(i + a))
|
||||
|
||||
@ -119,6 +119,7 @@ Go:
|
||||
|
||||
JavaScript:
|
||||
``` javascript
|
||||
// 方法一:使用数组记录元素出现次数
|
||||
var uniqueOccurrences = function(arr) {
|
||||
const count = new Array(2002).fill(0);// -1000 <= arr[i] <= 1000
|
||||
for(let i = 0; i < arr.length; i++){
|
||||
@ -134,6 +135,21 @@ var uniqueOccurrences = function(arr) {
|
||||
}
|
||||
return true;
|
||||
};
|
||||
|
||||
// 方法二:使用Map 和 Set
|
||||
/**
|
||||
* @param {number[]} arr
|
||||
* @return {boolean}
|
||||
*/
|
||||
var uniqueOccurrences = function(arr) {
|
||||
// 记录每个元素出现次数
|
||||
let map = new Map();
|
||||
arr.forEach( x => {
|
||||
map.set(x, (map.get(x) || 0) + 1);
|
||||
})
|
||||
// Set() 里的元素是不重复的。如果有元素出现次数相同,则最后的set的长度不等于map的长度
|
||||
return map.size === new Set(map.values()).size
|
||||
};
|
||||
```
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -93,6 +93,18 @@ public:
|
||||
## Java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int balancedStringSplit(String s) {
|
||||
int result = 0;
|
||||
int count = 0;
|
||||
for (int i = 0; i < s.length(); i++) {
|
||||
if (s.charAt(i) == 'R') count++;
|
||||
else count--;
|
||||
if (count == 0) result++;
|
||||
}
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## Python
|
||||
|
||||
@ -156,6 +156,7 @@ Go:
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
// 方法一:使用哈希表记录位置
|
||||
var smallerNumbersThanCurrent = function(nums) {
|
||||
const map = new Map();// 记录数字 nums[i] 有多少个比它小的数字
|
||||
const res = nums.slice(0);//深拷贝nums
|
||||
@ -171,9 +172,27 @@ var smallerNumbersThanCurrent = function(nums) {
|
||||
}
|
||||
return res;
|
||||
};
|
||||
|
||||
// 方法二:不使用哈希表,只使用一个额外数组
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number[]}
|
||||
*/
|
||||
var smallerNumbersThanCurrent = function(nums) {
|
||||
let array = [...nums]; // 深拷贝
|
||||
// 升序排列,此时数组元素下标即是比他小的元素的个数
|
||||
array = array.sort((a, b) => a-b);
|
||||
let res = [];
|
||||
nums.forEach( x => {
|
||||
// 即使元素重复也不怕,indexOf 只返回找到的第一个元素的下标
|
||||
res.push(array.indexOf(x));
|
||||
})
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
|
||||
@ -145,21 +145,21 @@ if (cur->right) {
|
||||
}
|
||||
```
|
||||
|
||||
此时就没有回溯了,这个代码就是通过不了的了。
|
||||
因为在递归右子树之前需要还原path,所以在左子树递归后必须为了右子树而进行回溯操作。而只右子树自己不添加回溯也可以成功AC。
|
||||
|
||||
如果想把回溯加上,就要 在上面代码的基础上,加上回溯,就可以AC了。
|
||||
因此,在上面代码的基础上,再加上左右子树的回溯代码,就可以AC了。
|
||||
|
||||
```CPP
|
||||
if (cur->left) {
|
||||
path += "->";
|
||||
traversal(cur->left, path, result); // 左
|
||||
path.pop_back(); // 回溯
|
||||
path.pop_back();
|
||||
path.pop_back(); // 回溯,抛掉val
|
||||
path.pop_back(); // 回溯,抛掉->
|
||||
}
|
||||
if (cur->right) {
|
||||
path += "->";
|
||||
traversal(cur->right, path, result); // 右
|
||||
path.pop_back(); // 回溯
|
||||
path.pop_back(); // 回溯(非必要)
|
||||
path.pop_back();
|
||||
}
|
||||
```
|
||||
|
||||
@ -200,17 +200,14 @@ func reverse(b []byte, left, right int){
|
||||
JavaScript:
|
||||
|
||||
```javascript
|
||||
var reverseLeftWords = function (s, n) {
|
||||
const reverse = (str, left, right) => {
|
||||
let strArr = str.split("");
|
||||
for (; left < right; left++, right--) {
|
||||
[strArr[left], strArr[right]] = [strArr[right], strArr[left]];
|
||||
var reverseLeftWords = function(s, n) {
|
||||
const length = s.length;
|
||||
let i = 0;
|
||||
while (i < length - n) {
|
||||
s = s[length - 1] + s;
|
||||
i++;
|
||||
}
|
||||
return strArr.join("");
|
||||
}
|
||||
s = reverse(s, 0, n - 1);
|
||||
s = reverse(s, n, s.length - 1);
|
||||
return reverse(s, 0, s.length - 1);
|
||||
return s.slice(0, length);
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
@ -51,8 +51,8 @@ morris遍历是二叉树遍历算法的超强进阶算法,morris遍历可以
|
||||
在[二叉树:一入递归深似海,从此offer是路人](https://programmercarl.com/二叉树的递归遍历.html)中讲到了递归三要素,以及前中后序的递归写法。
|
||||
|
||||
文章中我给出了leetcode上三道二叉树的前中后序题目,但是看完[二叉树:一入递归深似海,从此offer是路人](https://programmercarl.com/二叉树的递归遍历.html),依然可以解决n叉树的前后序遍历,在leetcode上分别是
|
||||
* 589. N叉树的前序遍历
|
||||
* 590. N叉树的后序遍历
|
||||
* [589. N叉树的前序遍历](https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/)
|
||||
* [590. N叉树的后序遍历](https://leetcode-cn.com/problems/n-ary-tree-postorder-traversal/)
|
||||
|
||||
大家可以再去把这两道题目做了。
|
||||
|
||||
|
||||
@ -250,9 +250,84 @@ used数组可是全局变量,每层与每层之间公用一个used数组,所
|
||||
|
||||
Java:
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
**90.子集II**
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
|
||||
res = []
|
||||
nums.sort()
|
||||
def backtracking(start, path):
|
||||
res.append(path)
|
||||
uset = set()
|
||||
for i in range(start, len(nums)):
|
||||
if nums[i] not in uset:
|
||||
backtracking(i + 1, path + [nums[i]])
|
||||
uset.add(nums[i])
|
||||
|
||||
backtracking(0, [])
|
||||
return res
|
||||
```
|
||||
|
||||
**40. 组合总和 II**
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
|
||||
|
||||
res = []
|
||||
candidates.sort()
|
||||
|
||||
def backtracking(start, path):
|
||||
if sum(path) == target:
|
||||
res.append(path)
|
||||
elif sum(path) < target:
|
||||
used = set()
|
||||
for i in range(start, len(candidates)):
|
||||
if candidates[i] in used:
|
||||
continue
|
||||
else:
|
||||
used.add(candidates[i])
|
||||
backtracking(i + 1, path + [candidates[i]])
|
||||
|
||||
backtracking(0, [])
|
||||
|
||||
return res
|
||||
```
|
||||
|
||||
**47. 全排列 II**
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
|
||||
path = []
|
||||
res = []
|
||||
used = [False]*len(nums)
|
||||
|
||||
def backtracking():
|
||||
if len(path) == len(nums):
|
||||
res.append(path.copy())
|
||||
|
||||
deduplicate = set()
|
||||
for i, num in enumerate(nums):
|
||||
if used[i] == True:
|
||||
continue
|
||||
if num in deduplicate:
|
||||
continue
|
||||
used[i] = True
|
||||
path.append(nums[i])
|
||||
backtracking()
|
||||
used[i] = False
|
||||
path.pop()
|
||||
deduplicate.add(num)
|
||||
|
||||
backtracking()
|
||||
|
||||
return res
|
||||
```
|
||||
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
@ -65,9 +65,9 @@
|
||||
|
||||
[数组:每次遇到二分法,都是一看就会,一写就废](https://programmercarl.com/0704.二分查找.html)
|
||||
|
||||
这道题目呢,考察的数据的基本操作,思路很简单,但是在通过率在简单题里并不高,不要轻敌。
|
||||
这道题目呢,考察数组的基本操作,思路很简单,但是通过率在简单题里并不高,不要轻敌。
|
||||
|
||||
可以使用暴力解法,通过这道题目,如果准求更优的算法,建议试一试用二分法,来解决这道题目
|
||||
可以使用暴力解法,通过这道题目,如果追求更优的算法,建议试一试用二分法,来解决这道题目
|
||||
|
||||
暴力解法时间复杂度:O(n)
|
||||
二分法时间复杂度:O(logn)
|
||||
@ -86,10 +86,10 @@
|
||||
暴力解法时间复杂度:O(n^2)
|
||||
双指针时间复杂度:O(n)
|
||||
|
||||
这道题目迷惑了不少同学,纠结于数组中的元素为什么不能删除,主要是因为一下两点:
|
||||
这道题目迷惑了不少同学,纠结于数组中的元素为什么不能删除,主要是因为以下两点:
|
||||
|
||||
* 数组在内存中是连续的地址空间,不能释放单一元素,如果要释放,就是全释放(程序运行结束,回收内存栈空间)。
|
||||
* C++中vector和array的区别一定要弄清楚,vector的底层实现是array,所以vector展现出友好的一些都是因为经过包装了。
|
||||
* C++中vector和array的区别一定要弄清楚,vector的底层实现是array,封装后使用更友好。
|
||||
|
||||
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。
|
||||
|
||||
@ -124,7 +124,7 @@
|
||||
|
||||
从二分法到双指针,从滑动窗口到螺旋矩阵,相信如果大家真的认真做了「代码随想录」每日推荐的题目,定会有所收获。
|
||||
|
||||
推荐的题目即使大家之前做过了,再读一遍的文章,也会帮助你提炼出解题的精髓所在。
|
||||
推荐的题目即使大家之前做过了,再读一遍文章,也会帮助你提炼出解题的精髓所在。
|
||||
|
||||
如果感觉有所收获,希望大家多多支持,打卡转发,点赞在看 都是对我最大的鼓励!
|
||||
|
||||
|
||||
287
problems/算法模板.md
287
problems/算法模板.md
@ -8,7 +8,7 @@
|
||||
|
||||
## 二分查找法
|
||||
|
||||
```
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
int searchInsert(vector<int>& nums, int target) {
|
||||
@ -33,7 +33,7 @@ public:
|
||||
|
||||
## KMP
|
||||
|
||||
```
|
||||
```CPP
|
||||
void kmp(int* next, const string& s){
|
||||
next[0] = -1;
|
||||
int j = -1;
|
||||
@ -53,7 +53,7 @@ void kmp(int* next, const string& s){
|
||||
|
||||
二叉树的定义:
|
||||
|
||||
```
|
||||
```CPP
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode *left;
|
||||
@ -65,7 +65,7 @@ struct TreeNode {
|
||||
### 深度优先遍历(递归)
|
||||
|
||||
前序遍历(中左右)
|
||||
```
|
||||
```CPP
|
||||
void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
if (cur == NULL) return;
|
||||
vec.push_back(cur->val); // 中 ,同时也是处理节点逻辑的地方
|
||||
@ -74,7 +74,7 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
}
|
||||
```
|
||||
中序遍历(左中右)
|
||||
```
|
||||
```CPP
|
||||
void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
if (cur == NULL) return;
|
||||
traversal(cur->left, vec); // 左
|
||||
@ -83,7 +83,7 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
}
|
||||
```
|
||||
后序遍历(左右中)
|
||||
```
|
||||
```CPP
|
||||
void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
if (cur == NULL) return;
|
||||
traversal(cur->left, vec); // 左
|
||||
@ -97,7 +97,7 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
相关题解:[0094.二叉树的中序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0094.二叉树的中序遍历.md)
|
||||
|
||||
前序遍历(中左右)
|
||||
```
|
||||
```CPP
|
||||
vector<int> preorderTraversal(TreeNode* root) {
|
||||
vector<int> result;
|
||||
stack<TreeNode*> st;
|
||||
@ -123,7 +123,7 @@ vector<int> preorderTraversal(TreeNode* root) {
|
||||
```
|
||||
|
||||
中序遍历(左中右)
|
||||
```
|
||||
```CPP
|
||||
vector<int> inorderTraversal(TreeNode* root) {
|
||||
vector<int> result; // 存放中序遍历的元素
|
||||
stack<TreeNode*> st;
|
||||
@ -148,7 +148,7 @@ vector<int> inorderTraversal(TreeNode* root) {
|
||||
```
|
||||
|
||||
后序遍历(左右中)
|
||||
```
|
||||
```CPP
|
||||
vector<int> postorderTraversal(TreeNode* root) {
|
||||
vector<int> result;
|
||||
stack<TreeNode*> st;
|
||||
@ -176,7 +176,7 @@ vector<int> postorderTraversal(TreeNode* root) {
|
||||
|
||||
相关题解:[0102.二叉树的层序遍历](https://programmercarl.com/0102.二叉树的层序遍历.html)
|
||||
|
||||
```
|
||||
```CPP
|
||||
vector<vector<int>> levelOrder(TreeNode* root) {
|
||||
queue<TreeNode*> que;
|
||||
if (root != NULL) que.push(root);
|
||||
@ -212,7 +212,7 @@ vector<vector<int>> levelOrder(TreeNode* root) {
|
||||
|
||||
### 二叉树深度
|
||||
|
||||
```
|
||||
```CPP
|
||||
int getDepth(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
return 1 + max(getDepth(node->left), getDepth(node->right));
|
||||
@ -221,7 +221,7 @@ int getDepth(TreeNode* node) {
|
||||
|
||||
### 二叉树节点数量
|
||||
|
||||
```
|
||||
```CPP
|
||||
int countNodes(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
return 1 + countNodes(root->left) + countNodes(root->right);
|
||||
@ -229,7 +229,7 @@ int countNodes(TreeNode* root) {
|
||||
```
|
||||
|
||||
## 回溯算法
|
||||
```
|
||||
```CPP
|
||||
void backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
@ -247,8 +247,8 @@ void backtracking(参数) {
|
||||
|
||||
## 并查集
|
||||
|
||||
```
|
||||
int n = 1005; // 更具题意而定
|
||||
```CPP
|
||||
int n = 1005; // 根据题意而定
|
||||
int father[1005];
|
||||
|
||||
// 并查集初始化
|
||||
@ -280,6 +280,263 @@ void backtracking(参数) {
|
||||
(持续补充ing)
|
||||
## 其他语言版本
|
||||
|
||||
JavaScript:
|
||||
|
||||
## 二分查找法
|
||||
|
||||
使用左闭右闭区间
|
||||
|
||||
```javascript
|
||||
var search = function (nums, target) {
|
||||
let left = 0, right = nums.length - 1;
|
||||
// 使用左闭右闭区间
|
||||
while (left <= right) {
|
||||
let mid = left + Math.floor((right - left)/2);
|
||||
if (nums[mid] > target) {
|
||||
right = mid - 1; // 去左面闭区间寻找
|
||||
} else if (nums[mid] < target) {
|
||||
left = mid + 1; // 去右面闭区间寻找
|
||||
} else {
|
||||
return mid;
|
||||
}
|
||||
}
|
||||
return -1;
|
||||
};
|
||||
```
|
||||
|
||||
使用左闭右开区间
|
||||
|
||||
```javascript
|
||||
var search = function (nums, target) {
|
||||
let left = 0, right = nums.length;
|
||||
// 使用左闭右开区间 [left, right)
|
||||
while (left < right) {
|
||||
let mid = left + Math.floor((right - left)/2);
|
||||
if (nums[mid] > target) {
|
||||
right = mid; // 去左面闭区间寻找
|
||||
} else if (nums[mid] < target) {
|
||||
left = mid + 1; // 去右面闭区间寻找
|
||||
} else {
|
||||
return mid;
|
||||
}
|
||||
}
|
||||
return -1;
|
||||
};
|
||||
```
|
||||
|
||||
## KMP
|
||||
|
||||
```javascript
|
||||
var kmp = function (next, s) {
|
||||
next[0] = -1;
|
||||
let j = -1;
|
||||
for(let i = 1; i < s.length; i++){
|
||||
while (j >= 0 && s[i] !== s[j + 1]) {
|
||||
j = next[j];
|
||||
}
|
||||
if (s[i] === s[j + 1]) {
|
||||
j++;
|
||||
}
|
||||
next[i] = j;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## 二叉树
|
||||
|
||||
### 深度优先遍历(递归)
|
||||
|
||||
二叉树节点定义:
|
||||
|
||||
```javascript
|
||||
function TreeNode (val, left, right) {
|
||||
this.val = (val === undefined ? 0 : val);
|
||||
this.left = (left === undefined ? null : left);
|
||||
this.right = (right === undefined ? null : right);
|
||||
}
|
||||
```
|
||||
|
||||
前序遍历(中左右):
|
||||
|
||||
```javascript
|
||||
var preorder = function (root, list) {
|
||||
if (root === null) return;
|
||||
list.push(root.val); // 中
|
||||
preorder(root.left, list); // 左
|
||||
preorder(root.right, list); // 右
|
||||
}
|
||||
```
|
||||
|
||||
中序遍历(左中右):
|
||||
|
||||
```javascript
|
||||
var inorder = function (root, list) {
|
||||
if (root === null) return;
|
||||
inorder(root.left, list); // 左
|
||||
list.push(root.val); // 中
|
||||
inorder(root.right, list); // 右
|
||||
}
|
||||
```
|
||||
|
||||
后序遍历(左右中):
|
||||
|
||||
```javascript
|
||||
var postorder = function (root, list) {
|
||||
if (root === null) return;
|
||||
postorder(root.left, list); // 左
|
||||
postorder(root.right, list); // 右
|
||||
list.push(root.val); // 中
|
||||
}
|
||||
```
|
||||
|
||||
### 深度优先遍历(迭代)
|
||||
|
||||
前序遍历(中左右):
|
||||
|
||||
```javascript
|
||||
var preorderTraversal = function (root) {
|
||||
let res = [];
|
||||
if (root === null) return rs;
|
||||
let stack = [root],
|
||||
cur = null;
|
||||
while (stack.length) {
|
||||
cur = stack.pop();
|
||||
res.push(cur.val);
|
||||
cur.right && stack.push(cur.right);
|
||||
cur.left && stack.push(cur.left);
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
中序遍历(左中右):
|
||||
|
||||
```javascript
|
||||
var inorderTraversal = function (root) {
|
||||
let res = [];
|
||||
if (root === null) return res;
|
||||
let stack = [];
|
||||
let cur = root;
|
||||
while (stack.length !== 0 || cur !== null) {
|
||||
if (cur !== null) {
|
||||
stack.push(cur);
|
||||
cur = cur.left;
|
||||
} else {
|
||||
cur = stack.pop();
|
||||
res.push(cur.val);
|
||||
cur = cur.right;
|
||||
}
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
后序遍历(左右中):
|
||||
|
||||
```javascript
|
||||
var postorderTraversal = function (root) {
|
||||
let res = [];
|
||||
if (root === null) return res;
|
||||
let stack = [root];
|
||||
let cur = null;
|
||||
while (stack.length) {
|
||||
cur = stack.pop();
|
||||
res.push(cur.val);
|
||||
cur.left && stack.push(cur.left);
|
||||
cur.right && stack.push(cur.right);
|
||||
}
|
||||
return res.reverse()
|
||||
};
|
||||
```
|
||||
|
||||
### 广度优先遍历(队列)
|
||||
|
||||
```javascript
|
||||
var levelOrder = function (root) {
|
||||
let res = [];
|
||||
if (root === null) return res;
|
||||
let queue = [root];
|
||||
while (queue.length) {
|
||||
let n = queue.length;
|
||||
let temp = [];
|
||||
for (let i = 0; i < n; i++) {
|
||||
let node = queue.shift();
|
||||
temp.push(node.val);
|
||||
node.left &&queue.push(node.left);
|
||||
node.right && queue.push(node.right);
|
||||
}
|
||||
res.push(temp);
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
### 二叉树深度
|
||||
|
||||
```javascript
|
||||
var getDepth = function (node) {
|
||||
if (node === null) return 0;
|
||||
return 1 + Math.max(getDepth(node.left), getDepth(node.right));
|
||||
}
|
||||
```
|
||||
|
||||
### 二叉树节点数量
|
||||
|
||||
```javascript
|
||||
var countNodes = function (root) {
|
||||
if (root === null) return 0;
|
||||
return 1 + countNodes(root.left) + countNodes(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
## 回溯算法
|
||||
|
||||
```javascript
|
||||
function backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
return;
|
||||
}
|
||||
|
||||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||||
处理节点;
|
||||
backtracking(路径,选择列表); // 递归
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 并查集
|
||||
|
||||
```javascript
|
||||
let n = 1005; // 根据题意而定
|
||||
let father = new Array(n).fill(0);
|
||||
|
||||
// 并查集初始化
|
||||
function init () {
|
||||
for (int i = 0; i < n; ++i) {
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
// 并查集里寻根的过程
|
||||
function find (u) {
|
||||
return u === father[u] ? u : father[u] = find(father[u]);
|
||||
}
|
||||
// 将v->u 这条边加入并查集
|
||||
function join(u, v) {
|
||||
u = find(u);
|
||||
v = find(v);
|
||||
if (u === v) return ;
|
||||
father[v] = u;
|
||||
}
|
||||
// 判断 u 和 v是否找到同一个根
|
||||
function same(u, v) {
|
||||
u = find(u);
|
||||
v = find(v);
|
||||
return u === v;
|
||||
}
|
||||
```
|
||||
|
||||
Java:
|
||||
|
||||
|
||||
@ -9,9 +9,9 @@
|
||||
|
||||
# 关于链表,你该了解这些!
|
||||
|
||||
什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点是又两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
|
||||
什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
|
||||
|
||||
链接的入口点称为列表的头结点也就是head。
|
||||
链接的入口节点称为链表的头结点也就是head。
|
||||
|
||||
如图所示:
|
||||
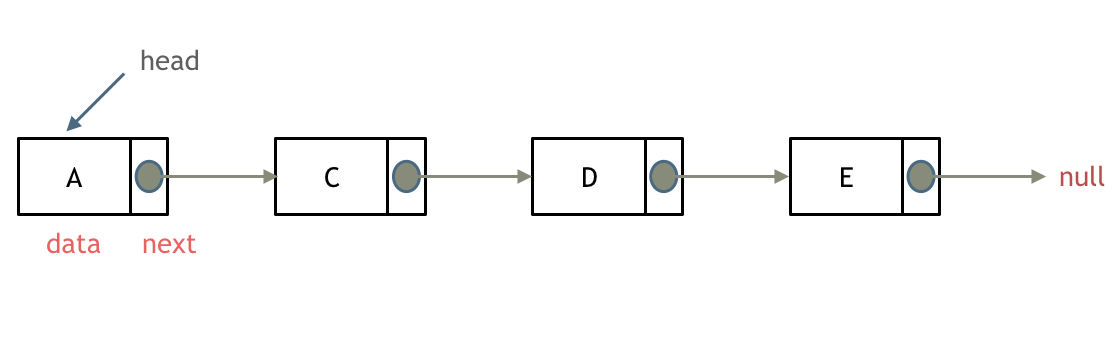
|
||||
|
||||
Reference in New Issue
Block a user