mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 08:50:15 +08:00
Update
This commit is contained in:
13
README.md
13
README.md
@ -44,19 +44,11 @@
|
|||||||
* [看了这么多代码,谈一谈代码风格!](https://mp.weixin.qq.com/s/UR9ztxz3AyL3qdHn_zMbqw)
|
* [看了这么多代码,谈一谈代码风格!](https://mp.weixin.qq.com/s/UR9ztxz3AyL3qdHn_zMbqw)
|
||||||
|
|
||||||
* 求职
|
* 求职
|
||||||
* [程序员应该如何写简历(附简历模板)](https://mp.weixin.qq.com/s/PkBpde0PV65dJjj9zZJYtg)
|
|
||||||
* [BAT级别技术面试流程和注意事项都在这里了](https://mp.weixin.qq.com/s/815qCyFGVIxwut9I_7PNFw)
|
* [BAT级别技术面试流程和注意事项都在这里了](https://mp.weixin.qq.com/s/815qCyFGVIxwut9I_7PNFw)
|
||||||
* [深圳原来有这么多互联网公司,你都知道么?](https://mp.weixin.qq.com/s/Yzrkim-5bY0Df66Ao-hoqA)
|
* [深圳原来有这么多互联网公司,你都知道么?](https://mp.weixin.qq.com/s/Yzrkim-5bY0Df66Ao-hoqA)
|
||||||
* [北京有这些互联网公司,你都知道么?](https://mp.weixin.qq.com/s/FQTzoZtqXQ2rlS1UthGrag)
|
* [北京有这些互联网公司,你都知道么?](https://mp.weixin.qq.com/s/FQTzoZtqXQ2rlS1UthGrag)
|
||||||
* [上海有这些互联网公司,你都知道么?](https://mp.weixin.qq.com/s/msqbX6eR2-JBQOYFfec4sg)
|
* [上海有这些互联网公司,你都知道么?](https://mp.weixin.qq.com/s/msqbX6eR2-JBQOYFfec4sg)
|
||||||
|
|
||||||
* 算法性能分析
|
|
||||||
* [究竟什么是时间复杂度,怎么求时间复杂度,看这一篇就够了](https://mp.weixin.qq.com/s/lYL9TSxLqCeFXIdjt4dcIw)
|
|
||||||
* [一文带你彻底理解程序为什么会超时](https://mp.weixin.qq.com/s/T-vcJSkq2-0s0bBB-itWbQ)
|
|
||||||
* [一场面试,带你彻底掌握递归算法的时间复杂度](https://mp.weixin.qq.com/s/Kt-Mvs8LeVqidLGUqySj1g)
|
|
||||||
* [算法分析中的空间复杂度,你真的会了么?](https://mp.weixin.qq.com/s/sXjjnOUEQ4Gf5F9QCRzy7g)
|
|
||||||
* [刷leetcode的时候,究竟什么时候可以使用库函数,什么时候不要使用库函数,过来人来说一说](https://leetcode-cn.com/circle/article/E1Kjzn/)
|
|
||||||
|
|
||||||
* 数组
|
* 数组
|
||||||
* [必须掌握的数组理论知识](https://mp.weixin.qq.com/s/X7R55wSENyY62le0Fiawsg)
|
* [必须掌握的数组理论知识](https://mp.weixin.qq.com/s/X7R55wSENyY62le0Fiawsg)
|
||||||
* [数组:每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)
|
* [数组:每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)
|
||||||
@ -177,6 +169,7 @@
|
|||||||
* [本周小结!(回溯算法系列三)续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)
|
* [本周小结!(回溯算法系列三)续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)
|
||||||
* [视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
|
* [视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
|
||||||
* [视频来了!!回溯算法:组合问题](https://mp.weixin.qq.com/s/a_r5JR93K_rBKSFplPGNAA)
|
* [视频来了!!回溯算法:组合问题](https://mp.weixin.qq.com/s/a_r5JR93K_rBKSFplPGNAA)
|
||||||
|
* [视频来了!!回溯算法:组合问题的剪枝操作](https://mp.weixin.qq.com/s/CK0kj9lq8-rFajxL4amyEg)
|
||||||
* [回溯算法:重新安排行程](https://mp.weixin.qq.com/s/3kmbS4qDsa6bkyxR92XCTA)
|
* [回溯算法:重新安排行程](https://mp.weixin.qq.com/s/3kmbS4qDsa6bkyxR92XCTA)
|
||||||
* [回溯算法:N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)
|
* [回溯算法:N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)
|
||||||
* [回溯算法:解数独](https://mp.weixin.qq.com/s/eWE9TapVwm77yW9Q81xSZQ)
|
* [回溯算法:解数独](https://mp.weixin.qq.com/s/eWE9TapVwm77yW9Q81xSZQ)
|
||||||
@ -188,6 +181,9 @@
|
|||||||
* [贪心算法:摆动序列](https://mp.weixin.qq.com/s/Xytl05kX8LZZ1iWWqjMoHA)
|
* [贪心算法:摆动序列](https://mp.weixin.qq.com/s/Xytl05kX8LZZ1iWWqjMoHA)
|
||||||
* [贪心算法:最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)
|
* [贪心算法:最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)
|
||||||
* [本周小结!(贪心算法系列一)](https://mp.weixin.qq.com/s/KQ2caT9GoVXgB1t2ExPncQ)
|
* [本周小结!(贪心算法系列一)](https://mp.weixin.qq.com/s/KQ2caT9GoVXgB1t2ExPncQ)
|
||||||
|
* [贪心算法:买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)
|
||||||
|
* [贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)
|
||||||
|
* [贪心算法:跳跃游戏II](https://mp.weixin.qq.com/s/kJBcsJ46DKCSjT19pxrNYg)
|
||||||
|
|
||||||
|
|
||||||
* 动态规划
|
* 动态规划
|
||||||
@ -227,6 +223,7 @@
|
|||||||
|[0027.移除元素](https://github.com/youngyangyang04/leetcode/blob/master/problems/0027.移除元素.md) |数组 |简单| **暴力** **双指针/快慢指针/双指针**|
|
|[0027.移除元素](https://github.com/youngyangyang04/leetcode/blob/master/problems/0027.移除元素.md) |数组 |简单| **暴力** **双指针/快慢指针/双指针**|
|
||||||
|[0028.实现strStr()](https://github.com/youngyangyang04/leetcode/blob/master/problems/0028.实现strStr().md) |字符串 |简单| **KMP** |
|
|[0028.实现strStr()](https://github.com/youngyangyang04/leetcode/blob/master/problems/0028.实现strStr().md) |字符串 |简单| **KMP** |
|
||||||
|[0031.下一个排列](https://github.com/youngyangyang04/leetcode/blob/master/problems/0031.下一个排列.md) |数组 |中等| **模拟** 这道题目还是有难度的|
|
|[0031.下一个排列](https://github.com/youngyangyang04/leetcode/blob/master/problems/0031.下一个排列.md) |数组 |中等| **模拟** 这道题目还是有难度的|
|
||||||
|
|[0034.在排序数组中查找元素的第一个和最后一个位置](https://github.com/youngyangyang04/leetcode/blob/master/problems/0031.下一个排列.md) |数组 |中等| **二分查找**比35.搜索插入位置难一些|
|
||||||
|[0035.搜索插入位置](https://github.com/youngyangyang04/leetcode/blob/master/problems/0035.搜索插入位置.md) |数组 |简单| **暴力** **二分**|
|
|[0035.搜索插入位置](https://github.com/youngyangyang04/leetcode/blob/master/problems/0035.搜索插入位置.md) |数组 |简单| **暴力** **二分**|
|
||||||
|[0037.解数独](https://github.com/youngyangyang04/leetcode/blob/master/problems/0037.解数独.md) |回溯 |困难| **回溯**|
|
|[0037.解数独](https://github.com/youngyangyang04/leetcode/blob/master/problems/0037.解数独.md) |回溯 |困难| **回溯**|
|
||||||
|[0039.组合总和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0039.组合总和.md) |数组/回溯 |中等| **回溯**|
|
|[0039.组合总和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0039.组合总和.md) |数组/回溯 |中等| **回溯**|
|
||||||
|
|||||||
Binary file not shown.
|
Before Width: | Height: | Size: 40 KiB After Width: | Height: | Size: 79 KiB |
BIN
pics/45.跳跃游戏II1.png
Normal file
BIN
pics/45.跳跃游戏II1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 57 KiB |
BIN
pics/45.跳跃游戏II2.png
Normal file
BIN
pics/45.跳跃游戏II2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 58 KiB |
134
problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
Normal file
134
problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
Normal file
@ -0,0 +1,134 @@
|
|||||||
|
> **如果对二分查找比较模糊,建议看这篇:[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q),这里详细介绍了二分的两种写法,以及循环不变量的重要性,顺便还可以把「leetcode:35.搜索插入位置」题目刷了**。
|
||||||
|
|
||||||
|
这道题目如果基础不是很好,不建议大家看简短的代码,简短的代码隐藏了太多逻辑,结果就是稀里糊涂把题AC了,但是没有想清楚具体细节!
|
||||||
|
|
||||||
|
下面我来把所有情况都讨论一下。
|
||||||
|
|
||||||
|
寻找target在数组里的左右边界,有如下三种情况:
|
||||||
|
|
||||||
|
* 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
|
||||||
|
* 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
|
||||||
|
* 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
|
||||||
|
|
||||||
|
这三种情况都考虑到,说明就想的很清楚了。
|
||||||
|
|
||||||
|
接下来,在去寻找左边界,和右边界了。
|
||||||
|
|
||||||
|
采用二分法来取寻找左右边界,为了让代码清晰,我分别写两个二分来寻找左边界和右边界。
|
||||||
|
|
||||||
|
**刚刚接触二分搜索的同学不建议上来就像如果用一个二分来查找左右边界,很容易把自己绕进去,建议扎扎实实的写两个二分分别找左边界和右边界**
|
||||||
|
|
||||||
|
## 寻找右边界
|
||||||
|
|
||||||
|
先来寻找右边界,至于二分查找,如果看过[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)就会知道,二分查找中什么时候用while (left <= right),有什么时候用while (left < right),其实只要清楚**循环不变量**,很容易区分两种写法。
|
||||||
|
|
||||||
|
那么这里我采用while (left <= right)的写法,区间定义为[left, right],即左闭又闭的区间(如果这里有点看不懂了,强烈建议把[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)这篇文章先看了,在把「leetcode:35.搜索插入位置」做了之后在做这道题目就好很多了)
|
||||||
|
|
||||||
|
确定好:计算出来的右边界是不包好target的右边界,左边界同理。
|
||||||
|
|
||||||
|
可以写出如下代码
|
||||||
|
|
||||||
|
```
|
||||||
|
// 二分查找,寻找target的右边界(不包括target)
|
||||||
|
// 如果rightBorder为没有被赋值(即target在数组范围的左边,例如数组[3,3],target为2),为了处理情况一
|
||||||
|
int getRightBorder(vector<int>& nums, int target) {
|
||||||
|
int left = 0;
|
||||||
|
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
|
||||||
|
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
|
||||||
|
while (left <= right) { // 当left==right,区间[left, right]依然有效
|
||||||
|
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
|
||||||
|
if (nums[middle] > target) {
|
||||||
|
right = middle - 1; // target 在左区间,所以[left, middle - 1]
|
||||||
|
} else { // 当nums[middle] == target的时候,更新left,这样才能得到target的右边界
|
||||||
|
left = middle + 1;
|
||||||
|
rightBorder = left;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return rightBorder;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
## 寻找左边界
|
||||||
|
|
||||||
|
```
|
||||||
|
// 二分查找,寻找target的左边界leftBorder(不包括target)
|
||||||
|
// 如果leftBorder没有被赋值(即target在数组范围的右边,例如数组[3,3],target为4),为了处理情况一
|
||||||
|
int getLeftBorder(vector<int>& nums, int target) {
|
||||||
|
int left = 0;
|
||||||
|
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
|
||||||
|
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
|
||||||
|
while (left <= right) {
|
||||||
|
int middle = left + ((right - left) / 2);
|
||||||
|
if (nums[middle] >= target) { // 寻找左边界,就要在nums[middle] == target的时候更新right
|
||||||
|
right = middle - 1;
|
||||||
|
leftBorder = right;
|
||||||
|
} else {
|
||||||
|
left = middle + 1;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return leftBorder;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
## 处理三种情况
|
||||||
|
|
||||||
|
左右边界计算完之后,看一下主体代码,这里把上面讨论的三种情况,都覆盖了
|
||||||
|
|
||||||
|
```
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<int> searchRange(vector<int>& nums, int target) {
|
||||||
|
int leftBorder = getLeftBorder(nums, target);
|
||||||
|
int rightBorder = getRightBorder(nums, target);
|
||||||
|
// 情况一
|
||||||
|
if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
|
||||||
|
// 情况三
|
||||||
|
if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
|
||||||
|
// 情况二
|
||||||
|
return {-1, -1};
|
||||||
|
}
|
||||||
|
private:
|
||||||
|
int getRightBorder(vector<int>& nums, int target) {
|
||||||
|
int left = 0;
|
||||||
|
int right = nums.size() - 1;
|
||||||
|
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
|
||||||
|
while (left <= right) {
|
||||||
|
int middle = left + ((right - left) / 2);
|
||||||
|
if (nums[middle] > target) {
|
||||||
|
right = middle - 1;
|
||||||
|
} else { // 寻找右边界,nums[middle] == target的时候更新left
|
||||||
|
left = middle + 1;
|
||||||
|
rightBorder = left;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return rightBorder;
|
||||||
|
}
|
||||||
|
int getLeftBorder(vector<int>& nums, int target) {
|
||||||
|
int left = 0;
|
||||||
|
int right = nums.size() - 1;
|
||||||
|
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
|
||||||
|
while (left <= right) {
|
||||||
|
int middle = left + ((right - left) / 2);
|
||||||
|
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
|
||||||
|
right = middle - 1;
|
||||||
|
leftBorder = right;
|
||||||
|
} else {
|
||||||
|
left = middle + 1;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return leftBorder;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
这份代码在简洁性很有大的优化空间,例如把寻找左右区间函数合并一起。
|
||||||
|
|
||||||
|
但拆开更清晰一些,而且把三种情况以及对应的处理逻辑完整的展现出来了。
|
||||||
|
|
||||||
|
# 总结
|
||||||
|
|
||||||
|
初学者建议大家一块一块的去分拆这道题目,正如本题解描述,想清楚三种情况之后,先专注于寻找右区间,然后专注于寻找左区间,左右根据左右区间做最后判断。
|
||||||
|
|
||||||
|
不要上来就想如果一起寻找左右区间,搞着搞着就会顾此失彼,绕进去拔不出来了。
|
||||||
|
|
||||||
|
|
||||||
@ -1,72 +1,114 @@
|
|||||||
## 题目链接
|
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
|
||||||
https://leetcode-cn.com/problems/jump-game-ii/
|
|
||||||
|
|
||||||
## 思路
|
# 45.跳跃游戏II
|
||||||
|
|
||||||
本题相对于[0055.跳跃游戏](https://github.com/youngyangyang04/leetcode/blob/master/problems/0053.最大子序和.md)还是难了不少。
|
题目地址:https://leetcode-cn.com/problems/jump-game-ii/
|
||||||
|
|
||||||
本题要计算最大步数,那么就要想清楚什么时候步数加一?
|
给定一个非负整数数组,你最初位于数组的第一个位置。
|
||||||
|
|
||||||
**这里需要统计两个距离,当前可移动距离和下一步最远距离**。
|
数组中的每个元素代表你在该位置可以跳跃的最大长度。
|
||||||
|
|
||||||
|
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
|
||||||
|
|
||||||
如果移动范围超过当前可移动距离,那么就必须再走一步来达到增加可移动距离的目的。
|
示例:
|
||||||
|
输入: [2,3,1,1,4]
|
||||||
|
输出: 2
|
||||||
|
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||||||
|
|
||||||
|
说明:
|
||||||
|
假设你总是可以到达数组的最后一个位置。
|
||||||
|
|
||||||
|
|
||||||
|
# 思路
|
||||||
|
|
||||||
|
本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。
|
||||||
|
|
||||||
|
但思路是相似的,还是要看最大覆盖范围。
|
||||||
|
|
||||||
|
本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
|
||||||
|
|
||||||
|
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
|
||||||
|
|
||||||
|
思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
|
||||||
|
|
||||||
|
**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
|
||||||
|
|
||||||
|
**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
|
||||||
|
|
||||||
|
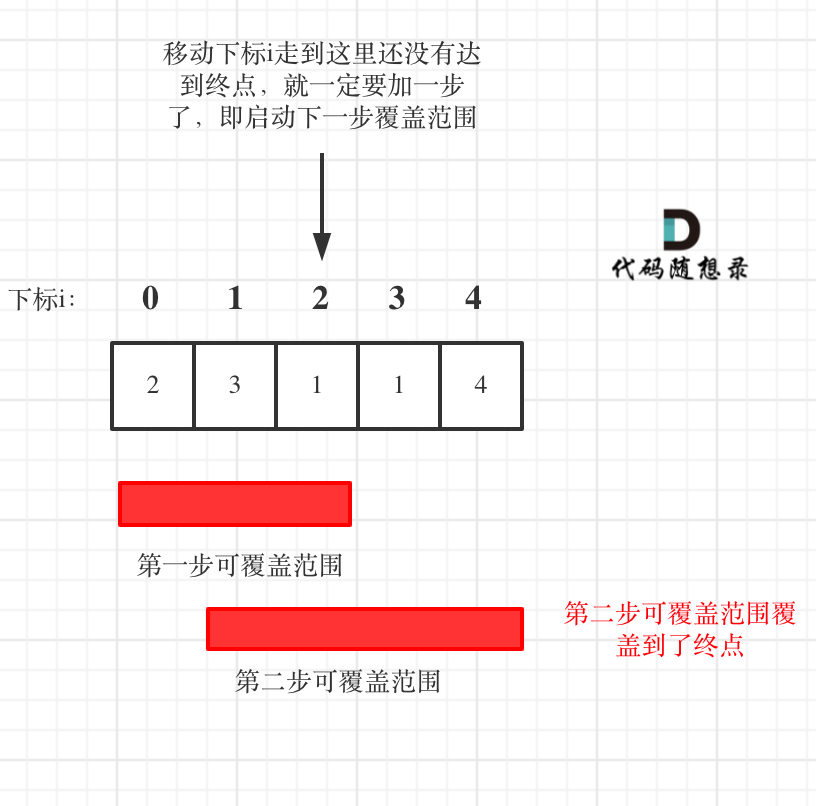
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
<img src='../pics/45.跳跃游戏II.png' width=600> </img></div>
|
|
||||||
|
|
||||||
### 方法一
|
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||||||
|
|
||||||
这里还是有个特殊情况需要考虑,如果当前可移动距离的终点就是是集合终点,那么就不用增加步数了,因为不能再往后走了。
|
## 方法一
|
||||||
|
|
||||||
详情可看代码(详细注释)
|
从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
|
||||||
|
|
||||||
```
|
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
|
||||||
|
|
||||||
|
* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||||||
|
* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||||||
|
|
||||||
|
C++代码如下:(详细注释)
|
||||||
|
|
||||||
|
```C++
|
||||||
// 版本一
|
// 版本一
|
||||||
class Solution {
|
class Solution {
|
||||||
public:
|
public:
|
||||||
int jump(vector<int>& nums) {
|
int jump(vector<int>& nums) {
|
||||||
if (nums.size() == 1) return 0;
|
if (nums.size() == 1) return 0;
|
||||||
int curDistance = 0; // 当前可移动距离
|
int curDistance = 0; // 当前覆盖最远距离下标
|
||||||
int ans = 0; // 记录走的最大步数
|
int ans = 0; // 记录走的最大步数
|
||||||
int nextDistance = 0; // 下一步最远距离
|
int nextDistance = 0; // 下一步覆盖最远距离下标
|
||||||
for (int i = 0; i < nums.size(); i++) {
|
for (int i = 0; i < nums.size(); i++) {
|
||||||
nextDistance = max(nums[i] + i, nextDistance);
|
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
|
||||||
if (i == curDistance) { // 遇到当前可移动距离的终点
|
if (i == curDistance) { // 遇到当前覆盖最远距离下标
|
||||||
if (curDistance != nums.size() - 1) { // 如果当前可移动距离的终点不是集合终点
|
if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
|
||||||
ans++; // 需要走下一步
|
ans++; // 需要走下一步
|
||||||
curDistance = nextDistance; // 更新下一步最远距离的范围
|
curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
|
||||||
if (nextDistance >= nums.size() - 1) break; // 下一步最远距离已经可以达到终点,结束循环
|
if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
|
||||||
} else break; // 当前可移动距离的终点是集合终点
|
} else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
|
||||||
}
|
}
|
||||||
}
|
}
|
||||||
return ans;
|
return ans;
|
||||||
}
|
}
|
||||||
};
|
};
|
||||||
```
|
```
|
||||||
|
|
||||||
### 方法二
|
## 方法二
|
||||||
|
|
||||||
依然是贪心,思路和方法一差不多,代码可以简洁一些。
|
依然是贪心,思路和方法一差不多,代码可以简洁一些。
|
||||||
|
|
||||||
在方法一种,处理 当前可移动距离的终点 是不是集合终点 来判断ans是否要做相应的加一操作。
|
**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
|
||||||
|
|
||||||
其实可以用 for循环遍历的时候i < nums.size() - 1,这样就是默认最后一步,一定是可以到终点的。
|
想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
|
||||||
|
|
||||||
|
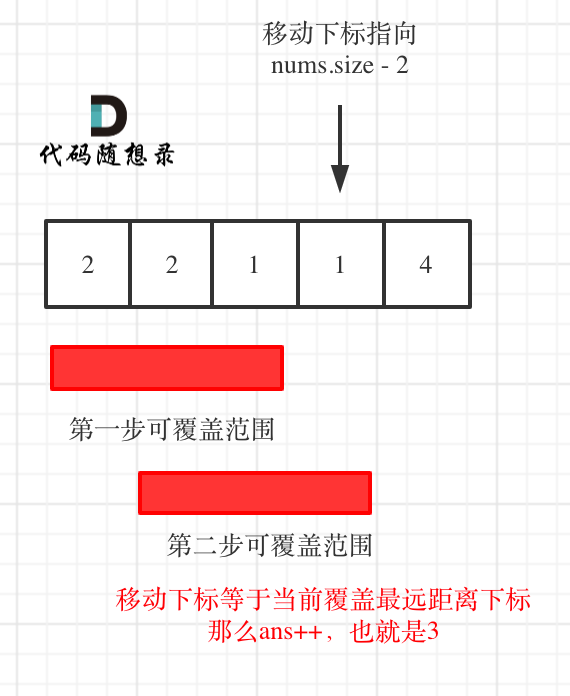
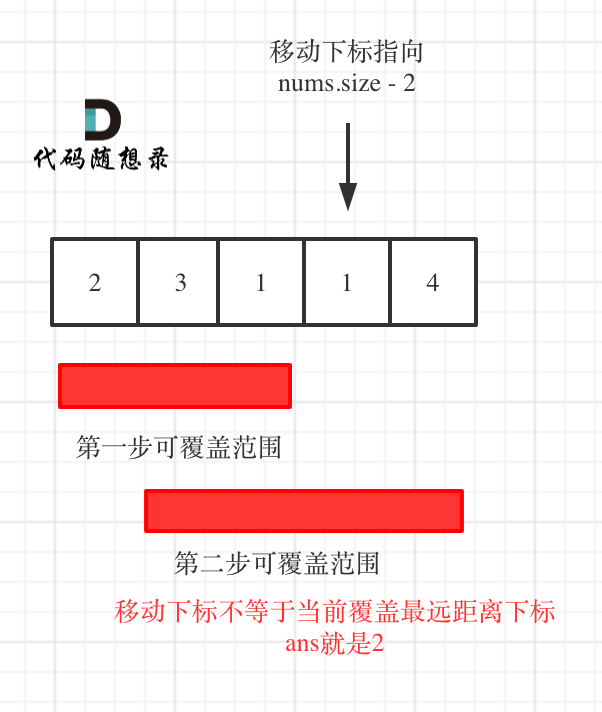
因为当移动下标指向nums.size - 2时:
|
||||||
|
|
||||||
|
* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||||
|
|
||||||
|
|
||||||
|
* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```C++
|
||||||
|
// 版本二
|
||||||
class Solution {
|
class Solution {
|
||||||
public:
|
public:
|
||||||
int jump(vector<int>& nums) {
|
int jump(vector<int>& nums) {
|
||||||
int curDistance = 0;
|
int curDistance = 0; // 当前覆盖的最远距离下标
|
||||||
int ans = 0; // 记录走的最大步数,初始为0
|
int ans = 0; // 记录走的最大步数
|
||||||
int nextDistance = 0; // 每走一步获得的跳跃范围
|
int nextDistance = 0; // 下一步覆盖的最远距离下标
|
||||||
for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1
|
for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
|
||||||
nextDistance = max(nums[i] + i, nextDistance);
|
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
|
||||||
if (i == curDistance) { // 遇到本次跳跃范围的终点
|
if (i == curDistance) { // 遇到当前覆盖的最远距离下标
|
||||||
curDistance = nextDistance;
|
curDistance = nextDistance; // 更新当前覆盖的最远距离下标
|
||||||
ans++;
|
ans++;
|
||||||
}
|
}
|
||||||
}
|
}
|
||||||
@ -74,3 +116,23 @@ public:
|
|||||||
}
|
}
|
||||||
};
|
};
|
||||||
```
|
```
|
||||||
|
|
||||||
|
可以看出版本二的代码相对于版本一简化了不少!
|
||||||
|
|
||||||
|
其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||||||
|
|
||||||
|
# 总结
|
||||||
|
|
||||||
|
相信大家可以发现,这道题目相当于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。
|
||||||
|
|
||||||
|
但代码又十分简单,贪心就是这么巧妙。
|
||||||
|
|
||||||
|
理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
|
||||||
|
|
||||||
|
就酱,如果感觉「代码随想录」很不错,就分享给身边的朋友同学吧!
|
||||||
|
|
||||||
|
|
||||||
|
> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
|
||||||
|
|
||||||
|
**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
|
||||||
|
|
||||||
|
|||||||
@ -68,7 +68,7 @@ public:
|
|||||||
```
|
```
|
||||||
# 总结
|
# 总结
|
||||||
|
|
||||||
这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内已经是可以跳过来的,不用管是怎么跳的。
|
这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
|
||||||
|
|
||||||
大家可以看出思路想出来了,代码还是非常简单的。
|
大家可以看出思路想出来了,代码还是非常简单的。
|
||||||
|
|
||||||
|
|||||||
@ -1,3 +1,5 @@
|
|||||||
|
(寻找更节点可以用unordered_map来优化一下,元素都是独一无二的)
|
||||||
|
|
||||||
## 题目地址
|
## 题目地址
|
||||||
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
|
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
|
||||||
|
|
||||||
@ -174,7 +176,6 @@ public:
|
|||||||
int depth = 0;
|
int depth = 0;
|
||||||
while (!que.empty()) {
|
while (!que.empty()) {
|
||||||
int size = que.size();
|
int size = que.size();
|
||||||
vector<int> vec;
|
|
||||||
depth++; // 记录深度
|
depth++; // 记录深度
|
||||||
for (int i = 0; i < size; i++) {
|
for (int i = 0; i < size; i++) {
|
||||||
Node* node = que.front();
|
Node* node = que.front();
|
||||||
|
|||||||
Reference in New Issue
Block a user