From b4fefffb0f07436b591b9c36df49e1259b5f39b4 Mon Sep 17 00:00:00 2001
From: youngyangyang04 <826123027@qq.com>
Date: Thu, 22 Apr 2021 11:06:18 +0800
Subject: [PATCH] Update
---
README.md | 20 +-
problems/0017.电话号码的字母组合.md | 243 ++++++++++++
problems/0027.移除元素.md | 124 +++++++
problems/0035.搜索插入位置.md | 20 +-
problems/0077.组合.md | 347 ++++++++++++++++++
problems/0077.组合优化.md | 147 ++++++++
problems/0216.组合总和III.md | 229 ++++++++++++
problems/0704.二分查找.md | 150 ++++++++
.../周总结/20201030回溯周末总结.md | 113 ++++++
9 files changed, 1381 insertions(+), 12 deletions(-)
create mode 100644 problems/0017.电话号码的字母组合.md
create mode 100644 problems/0027.移除元素.md
create mode 100644 problems/0077.组合.md
create mode 100644 problems/0077.组合优化.md
create mode 100644 problems/0216.组合总和III.md
create mode 100644 problems/0704.二分查找.md
create mode 100644 problems/周总结/20201030回溯周末总结.md
diff --git a/README.md b/README.md
index 1ee29bef..080865a5 100644
--- a/README.md
+++ b/README.md
@@ -17,12 +17,10 @@
- 
- 
+ 
+
- 
- 
@@ -130,8 +128,8 @@
## 数组
1. [数组过于简单，但你该了解这些！](./problems/数组理论基础.md)
-2. [数组：每次遇到二分法，都是一看就会，一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)
-3. [数组：就移除个元素很难么？](https://mp.weixin.qq.com/s/wj0T-Xs88_FHJFwayElQlA)
+2. [数组：每次遇到二分法，都是一看就会，一写就废](./problems/0704.二分查找.md)
+3. [数组：就移除个元素很难么？](./problems/0027.移除元素.md)
4. [数组：滑动窗口拯救了你](https://mp.weixin.qq.com/s/UrZynlqi4QpyLlLhBPglyg)
5. [数组：这个循环可以转懵很多人！](https://mp.weixin.qq.com/s/KTPhaeqxbMK9CxHUUgFDmg)
6. [数组：总结篇](https://mp.weixin.qq.com/s/LIfQFRJBH5ENTZpvixHEmg)
@@ -248,11 +246,11 @@
1. [关于回溯算法，你该了解这些！](./problems/回溯算法理论基础.md)
-2. [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
-3. [回溯算法：组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
-4. [回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
-5. [回溯算法：电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
-6. [本周小结！（回溯算法系列一）](https://mp.weixin.qq.com/s/m2GnTJdkYhAamustbb6lmw)
+2. [回溯算法：组合问题](./problems/0077.组合.md)
+3. [回溯算法：组合问题再剪剪枝](./problems/0077.组合优化.md)
+4. [回溯算法：求组合总和！](./problems/0216.组合总和III.md)
+5. [回溯算法：电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+6. [本周小结！（回溯算法系列一）](./problems/周总结/20201030回溯周末总结.md)
7. [回溯算法：求组合总和（二）](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)
8. [回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
9. [回溯算法：分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)
diff --git a/problems/0017.电话号码的字母组合.md b/problems/0017.电话号码的字母组合.md
new file mode 100644
index 00000000..0743ed9b
--- /dev/null
+++ b/problems/0017.电话号码的字母组合.md
@@ -0,0 +1,243 @@
+
+
+
+
+
+
+
+
+# 17.电话号码的字母组合
+
+题目链接：https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
+
+给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
+
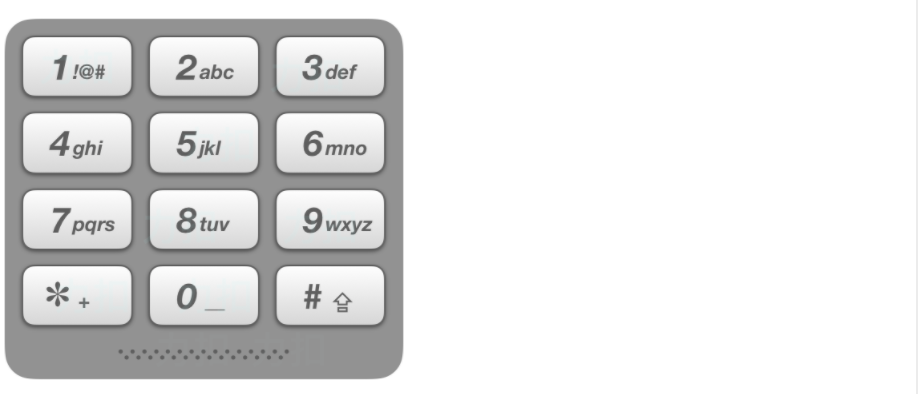
+给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
+
+
+
+示例:
+输入："23"
+输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
+
+说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。
+
+# 思路
+
+从示例上来说，输入"23"，最直接的想法就是两层for循环遍历了吧，正好把组合的情况都输出了。
+
+如果输入"233"呢，那么就三层for循环，如果"2333"呢，就四层for循环.......
+
+大家应该感觉出和[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)遇到的一样的问题，就是这for循环的层数如何写出来，此时又是回溯法登场的时候了。
+
+理解本题后，要解决如下三个问题：
+
+1. 数字和字母如何映射
+2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
+3. 输入1 * #按键等等异常情况
+
+## 数字和字母如何映射
+
+可以使用map或者定义一个二位数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：
+
+```
+const string letterMap[10] = {
+ "", // 0
+ "", // 1
+ "abc", // 2
+ "def", // 3
+ "ghi", // 4
+ "jkl", // 5
+ "mno", // 6
+ "pqrs", // 7
+ "tuv", // 8
+ "wxyz", // 9
+};
+```
+
+## 回溯法来解决n个for循环的问题
+
+对于回溯法还不了解的同学看这篇：[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)
+
+
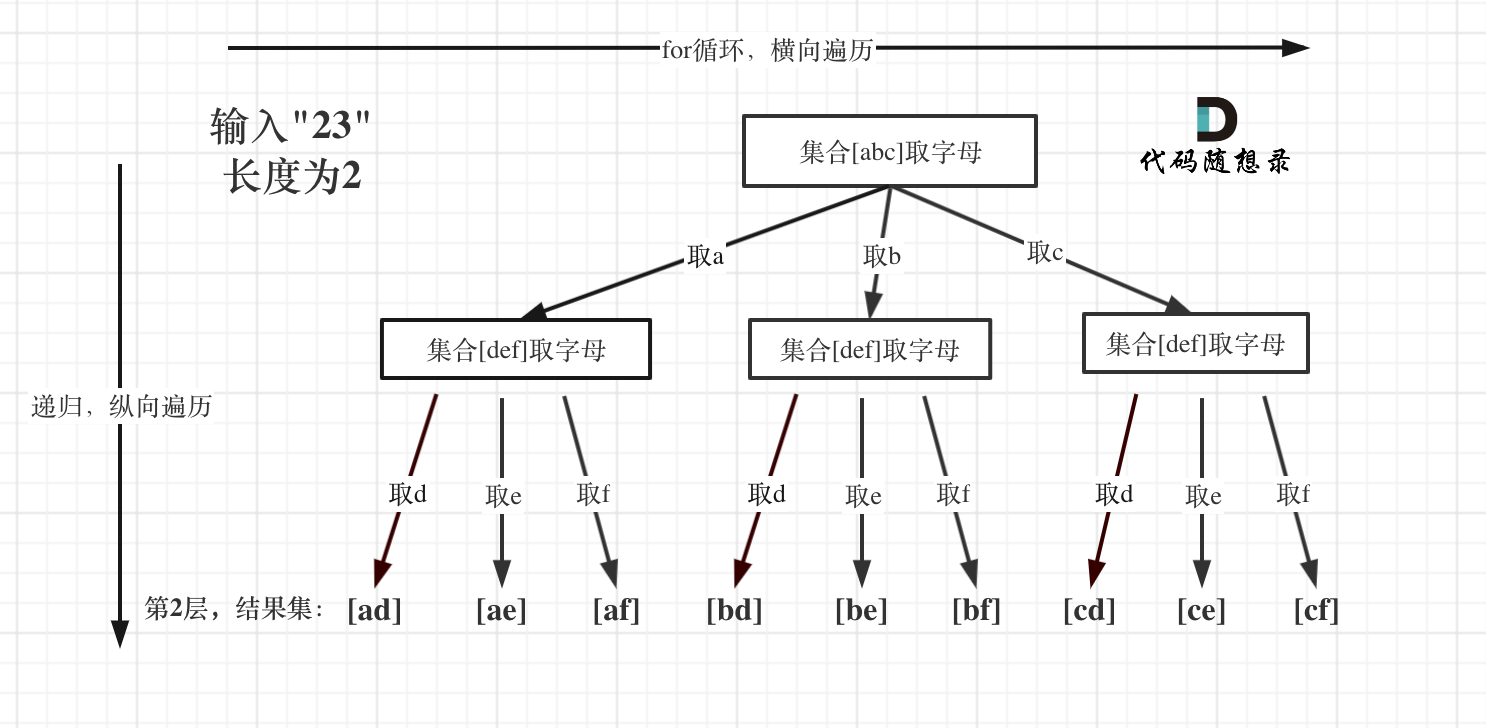
+例如：输入："23"，抽象为树形结构，如图所示：
+
+
+
+图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
+
+回溯三部曲：
+
+* 确定回溯函数参数
+
+首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。
+
+再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。
+
+注意这个index可不是 [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中的startIndex了。
+
+这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。
+
+代码如下：
+
+```
+vector result;
+string s;
+void backtracking(const string& digits, int index)
+```
+
+* 确定终止条件
+
+例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。
+
+那么终止条件就是如果index 等于 输入的数字个数（digits.size）了（本来index就是用来遍历digits的）。
+
+然后收集结果，结束本层递归。
+
+代码如下：
+
+```
+if (index == digits.size()) {
+ result.push_back(s);
+ return;
+}
+```
+
+* 确定单层遍历逻辑
+
+首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。
+
+然后for循环来处理这个字符集，代码如下：
+
+```
+int digit = digits[index] - '0'; // 将index指向的数字转为int
+string letters = letterMap[digit]; // 取数字对应的字符集
+for (int i = 0; i < letters.size(); i++) {
+ s.push_back(letters[i]); // 处理
+ backtracking(digits, index + 1); // 递归，注意index+1，一下层要处理下一个数字了
+ s.pop_back(); // 回溯
+}
+```
+
+**注意这里for循环，可不像是在[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中从startIndex开始遍历的**。
+
+**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)都是是求同一个集合中的组合！**
+
+
+注意：输入1 * #按键等等异常情况
+
+代码中最好考虑这些异常情况，但题目的测试数据中应该没有异常情况的数据，所以我就没有加了。
+
+**但是要知道会有这些异常，如果是现场面试中，一定要考虑到！**
+
+
+## C++代码
+
+关键地方都讲完了，按照[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中的回溯法模板，不难写出如下C++代码：
+
+
+```
+// 版本一
+class Solution {
+private:
+ const string letterMap[10] = {
+ "", // 0
+ "", // 1
+ "abc", // 2
+ "def", // 3
+ "ghi", // 4
+ "jkl", // 5
+ "mno", // 6
+ "pqrs", // 7
+ "tuv", // 8
+ "wxyz", // 9
+ };
+public:
+ vector result;
+ string s;
+ void backtracking(const string& digits, int index) {
+ if (index == digits.size()) {
+ result.push_back(s);
+ return;
+ }
+ int digit = digits[index] - '0'; // 将index指向的数字转为int
+ string letters = letterMap[digit]; // 取数字对应的字符集
+ for (int i = 0; i < letters.size(); i++) {
+ s.push_back(letters[i]); // 处理
+ backtracking(digits, index + 1); // 递归，注意index+1，一下层要处理下一个数字了
+ s.pop_back(); // 回溯
+ }
+ }
+ vector letterCombinations(string digits) {
+ s.clear();
+ result.clear();
+ if (digits.size() == 0) {
+ return result;
+ }
+ backtracking(digits, 0);
+ return result;
+ }
+};
+```
+
+一些写法，是把回溯的过程放在递归函数里了，例如如下代码，我可以写成这样：（注意注释中不一样的地方）
+
+```
+// 版本二
+class Solution {
+private:
+ const string letterMap[10] = {
+ "", // 0
+ "", // 1
+ "abc", // 2
+ "def", // 3
+ "ghi", // 4
+ "jkl", // 5
+ "mno", // 6
+ "pqrs", // 7
+ "tuv", // 8
+ "wxyz", // 9
+ };
+public:
+ vector result;
+ void getCombinations(const string& digits, int index, const string& s) { // 注意参数的不同
+ if (index == digits.size()) {
+ result.push_back(s);
+ return;
+ }
+ int digit = digits[index] - '0';
+ string letters = letterMap[digit];
+ for (int i = 0; i < letters.size(); i++) {
+ getCombinations(digits, index + 1, s + letters[i]); // 注意这里的不同
+ }
+ }
+ vector letterCombinations(string digits) {
+ result.clear();
+ if (digits.size() == 0) {
+ return result;
+ }
+ getCombinations(digits, 0, "");
+ return result;
+
+ }
+};
+```
+
+我不建议把回溯藏在递归的参数里这种写法，很不直观，我在[二叉树：以为使用了递归，其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)这篇文章中也深度分析了，回溯隐藏在了哪里。
+
+所以大家可以按照版本一来写就可以了。
+
+# 总结
+
+本篇将题目的三个要点一一列出，并重点强调了和前面讲解过的[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)的区别，本题是多个集合求组合，所以在回溯的搜索过程中，都有一些细节需要注意的。
+
+其实本题不算难，但也处处是细节，大家还要自己亲自动手写一写。
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
diff --git a/problems/0027.移除元素.md b/problems/0027.移除元素.md
new file mode 100644
index 00000000..3e4a68e0
--- /dev/null
+++ b/problems/0027.移除元素.md
@@ -0,0 +1,124 @@
+
+
+
+
+
+
+
+
+## 27. 移除元素
+
+题目地址：https://leetcode-cn.com/problems/remove-element/
+
+给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
+
+不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并**原地**修改输入数组。
+
+元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
+
+示例 1:
+给定 nums = [3,2,2,3], val = 3,
+函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
+你不需要考虑数组中超出新长度后面的元素。
+
+示例 2:
+给定 nums = [0,1,2,2,3,0,4,2], val = 2,
+函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
+
+**你不需要考虑数组中超出新长度后面的元素。**
+
+## 思路
+
+有的同学可能说了，多余的元素，删掉不就得了。
+
+**要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。**
+
+数组的基础知识可以看这里[程序员算法面试中，必须掌握的数组理论知识](https://mp.weixin.qq.com/s/c2KABb-Qgg66HrGf8z-8Og)。
+
+### 暴力解法
+
+这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。
+
+删除过程如下：
+
+
+
+很明显暴力解法的时间复杂度是O(n^2)，这道题目暴力解法在leetcode上是可以过的。
+
+代码如下：
+
+```C++
+// 时间复杂度：O(n^2)
+// 空间复杂度：O(1)
+class Solution {
+public:
+ int removeElement(vector& nums, int val) {
+ int size = nums.size();
+ for (int i = 0; i < size; i++) {
+ if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
+ for (int j = i + 1; j < size; j++) {
+ nums[j - 1] = nums[j];
+ }
+ i--; // 因为下表i以后的数值都向前移动了一位，所以i也向前移动一位
+ size--; // 此时数组的大小-1
+ }
+ }
+ return size;
+
+ }
+};
+```
+
+* 时间复杂度：$O(n^2)$
+* 空间复杂度：$O(1)$
+
+### 双指针法
+
+双指针法（快慢指针法）： **通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。**
+
+删除过程如下：
+
+
+
+**双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组、链表、字符串等操作的面试题，都使用双指针法。**
+
+后序都会一一介绍到，本题代码如下：
+
+```C++
+// 时间复杂度：O(n)
+// 空间复杂度：O(1)
+class Solution {
+public:
+ int removeElement(vector& nums, int val) {
+ int slowIndex = 0;
+ for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
+ if (val != nums[fastIndex]) {
+ nums[slowIndex++] = nums[fastIndex];
+ }
+ }
+ return slowIndex;
+ }
+};
+```
+注意这些实现方法并没有改变元素的相对位置！
+
+* 时间复杂度：$O(n)$
+* 空间复杂度：$O(1)$
+
+旧文链接：[数组：就移除个元素很难么？](https://mp.weixin.qq.com/s/wj0T-Xs88_FHJFwayElQlA)
+
+## 相关题目推荐
+
+* 26.删除排序数组中的重复项
+* 283.移动零
+* 844.比较含退格的字符串
+* 977.有序数组的平方
+
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
index 5e14b424..572b7a37 100644
--- a/problems/0035.搜索插入位置.md
+++ b/problems/0035.搜索插入位置.md
@@ -1,6 +1,14 @@
+
+
+
+
+
+
+
-# 编号35：搜索插入位置
+
+# 35.搜索插入位置
题目地址：https://leetcode-cn.com/problems/search-insert-position/
@@ -189,3 +197,13 @@ public:
**循序渐进学算法，认准「代码随想录」，Carl手把手带你过关斩将！**
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
+
diff --git a/problems/0077.组合.md b/problems/0077.组合.md
new file mode 100644
index 00000000..7cab9127
--- /dev/null
+++ b/problems/0077.组合.md
@@ -0,0 +1,347 @@
+
+
+
+
+
+
+
+
+
+
+# 第77题. 组合
+
+题目链接：https://leetcode-cn.com/problems/combinations/
+
+给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。
+
+示例:
+输入: n = 4, k = 2
+输出:
+[
+ [2,4],
+ [3,4],
+ [2,3],
+ [1,2],
+ [1,3],
+ [1,4],
+]
+
+也可以直接看我的B站视频：[带你学透回溯算法-组合问题（对应力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv#reply3733925949)
+
+## 思路
+
+> 可以直接看我的B栈视频讲解：
+> [带你学透回溯算法-组合问题](https://www.bilibili.com/video/BV1ti4y1L7cv)
+> [带你学透回溯算法-组合问题的剪枝操作](https://www.bilibili.com/video/BV1wi4y157er)
+
+
+本题这是回溯法的经典题目。
+
+直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。
+
+代码如下：
+```
+int n = 4;
+for (int i = 1; i <= n; i++) {
+ for (int j = i + 1; j <= n; j++) {
+ cout << i << " " << j << endl;
+ }
+}
+```
+
+输入：n = 100, k = 3
+那么就三层for循环，代码如下：
+
+```
+int n = 100;
+for (int i = 1; i <= n; i++) {
+ for (int j = i + 1; j <= n; j++) {
+ for (int u = j + 1; u <= n; n++) {
+ cout << i << " " << j << " " << u << endl;
+ }
+ }
+}
+```
+
+**如果n为100，k为50呢，那就50层for循环，是不是开始窒息**。
+
+**此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来！**
+
+咋整？
+
+回溯搜索法来了，虽然回溯法也是暴力，但至少能写出来，不像for循环嵌套k层让人绝望。
+
+那么回溯法怎么暴力搜呢？
+
+上面我们说了**要解决 n为100，k为50的情况，暴力写法需要嵌套50层for循环，那么回溯法就用递归来解决嵌套层数的问题**。
+
+递归来做层叠嵌套（可以理解是开k层for循环），**每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了**。
+
+此时递归的层数大家应该知道了，例如：n为100，k为50的情况下，就是递归50层。
+
+一些同学本来对递归就懵，回溯法中递归还要嵌套for循环，可能就直接晕倒了！
+
+如果脑洞模拟回溯搜索的过程，绝对可以让人窒息，所以需要抽象图形结构来进一步理解。
+
+**我们在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中说道回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了**。
+
+那么我把组合问题抽象为如下树形结构：
+
+
+
+可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
+
+第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
+
+**每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围**。
+
+**图中可以发现n相当于树的宽度，k相当于树的深度**。
+
+那么如何在这个树上遍历，然后收集到我们要的结果集呢？
+
+**图中每次搜索到了叶子节点，我们就找到了一个结果**。
+
+相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。
+
+在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中我们提到了回溯法三部曲，那么我们按照回溯法三部曲开始正式讲解代码了。
+
+
+## 回溯法三部曲
+
+* 递归函数的返回值以及参数
+
+在这里要定义两个全局变量，一个用来存放符合条件单一结果，一个用来存放符合条件结果的集合。
+
+代码如下：
+
+```
+vector> result; // 存放符合条件结果的集合
+vector path; // 用来存放符合条件结果
+```
+
+其实不定义这两个全局遍历也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。
+
+函数里一定有两个参数，既然是集合n里面取k的数，那么n和k是两个int型的参数。
+
+然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
+
+为什么要有这个startIndex呢？
+
+**每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex**。
+
+从下图中红线部分可以看出，在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。
+
+
+
+所以需要startIndex来记录下一层递归，搜索的起始位置。
+
+那么整体代码如下：
+
+```
+vector> result; // 存放符合条件结果的集合
+vector path; // 用来存放符合条件单一结果
+void backtracking(int n, int k, int startIndex)
+```
+
+* 回溯函数终止条件
+
+什么时候到达所谓的叶子节点了呢？
+
+path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。
+
+如图红色部分：
+
+
+
+此时用result二维数组，把path保存起来，并终止本层递归。
+
+所以终止条件代码如下：
+
+```
+if (path.size() == k) {
+ result.push_back(path);
+ return;
+}
+```
+
+* 单层搜索的过程
+
+回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。
+
+
+
+如此我们才遍历完图中的这棵树。
+
+for循环每次从startIndex开始遍历，然后用path保存取到的节点i。
+
+代码如下：
+
+```C++
+for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
+ path.push_back(i); // 处理节点
+ backtracking(n, k, i + 1); // 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
+ path.pop_back(); // 回溯，撤销处理的节点
+}
+```
+
+可以看出backtracking（递归函数）通过不断调用自己一直往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。
+
+backtracking的下面部分就是回溯的操作了，撤销本次处理的结果。
+
+关键地方都讲完了，组合问题C++完整代码如下：
+
+
+```C++
+class Solution {
+private:
+ vector> result; // 存放符合条件结果的集合
+ vector path; // 用来存放符合条件结果
+ void backtracking(int n, int k, int startIndex) {
+ if (path.size() == k) {
+ result.push_back(path);
+ return;
+ }
+ for (int i = startIndex; i <= n; i++) {
+ path.push_back(i); // 处理节点
+ backtracking(n, k, i + 1); // 递归
+ path.pop_back(); // 回溯，撤销处理的节点
+ }
+ }
+public:
+ vector> combine(int n, int k) {
+ result.clear(); // 可以不写
+ path.clear(); // 可以不写
+ backtracking(n, k, 1);
+ return result;
+ }
+};
+```
+
+还记得我们在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中给出的回溯法模板么？
+
+如下：
+```
+void backtracking(参数) {
+ if (终止条件) {
+ 存放结果;
+ return;
+ }
+
+ for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
+ 处理节点;
+ backtracking(路径，选择列表); // 递归
+ 回溯，撤销处理结果
+ }
+}
+```
+
+**对比一下本题的代码，是不是发现有点像！** 所以有了这个模板，就有解题的大体方向，不至于毫无头绪。
+
+# 总结
+
+组合问题是回溯法解决的经典问题，我们开始的时候给大家列举一个很形象的例子，就是n为100，k为50的话，直接想法就需要50层for循环。
+
+从而引出了回溯法就是解决这种k层for循环嵌套的问题。
+
+然后进一步把回溯法的搜索过程抽象为树形结构，可以直观的看出搜索的过程。
+
+接着用回溯法三部曲，逐步分析了函数参数、终止条件和单层搜索的过程。
+
+# 剪枝优化
+
+我们说过，回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。
+
+在遍历的过程中有如下代码：
+
+```
+for (int i = startIndex; i <= n; i++) {
+ path.push_back(i);
+ backtracking(n, k, i + 1);
+ path.pop_back();
+}
+```
+
+这个遍历的范围是可以剪枝优化的，怎么优化呢？
+
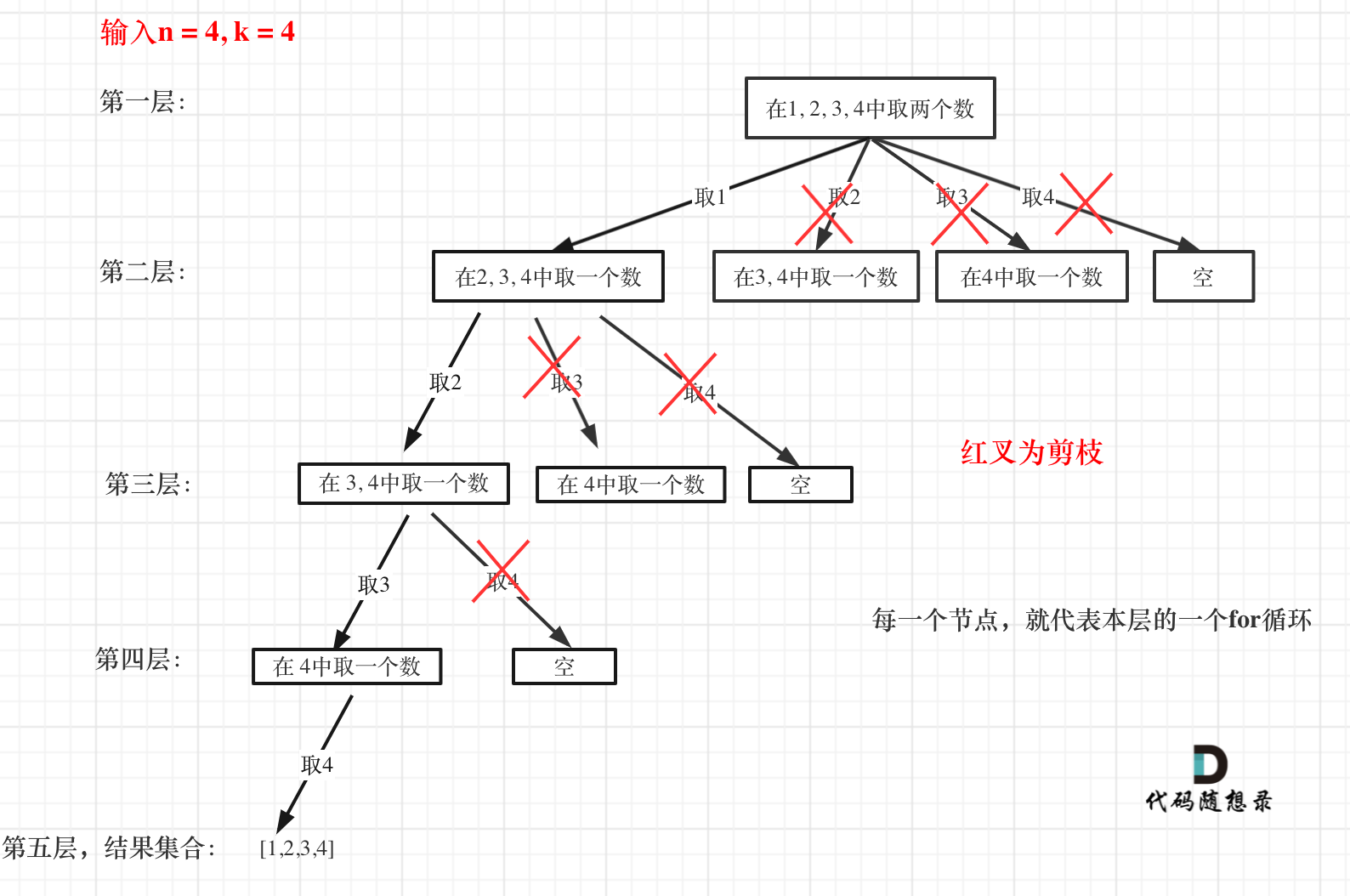
+来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。
+
+这么说有点抽象，如图所示：
+
+
+
+图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
+
+**所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
+
+**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了**。
+
+注意代码中i，就是for循环里选择的起始位置。
+```
+for (int i = startIndex; i <= n; i++) {
+```
+
+接下来看一下优化过程如下：
+
+1. 已经选择的元素个数：path.size();
+
+2. 还需要的元素个数为: k - path.size();
+
+3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历
+
+为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。
+
+举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
+
+从2开始搜索都是合理的，可以是组合[2, 3, 4]。
+
+这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。
+
+所以优化之后的for循环是：
+
+```
+for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
+```
+
+优化后整体代码如下：
+
+```
+class Solution {
+private:
+ vector> result;
+ vector path;
+ void backtracking(int n, int k, int startIndex) {
+ if (path.size() == k) {
+ result.push_back(path);
+ return;
+ }
+ for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
+ path.push_back(i); // 处理节点
+ backtracking(n, k, i + 1);
+ path.pop_back(); // 回溯，撤销处理的节点
+ }
+ }
+public:
+
+ vector> combine(int n, int k) {
+ backtracking(n, k, 1);
+ return result;
+ }
+};
+```
+
+# 剪枝总结
+
+本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
+
+所以我依然是把整个回溯过程抽象为一颗树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
+
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
+
diff --git a/problems/0077.组合优化.md b/problems/0077.组合优化.md
new file mode 100644
index 00000000..e4532c01
--- /dev/null
+++ b/problems/0077.组合优化.md
@@ -0,0 +1,147 @@
+
+
+
+
+
+
+
+
+
+
+
+在[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)中，我们通过回溯搜索法，解决了n个数中求k个数的组合问题。
+
+文中的回溯法是可以剪枝优化的，本篇我们继续来看一下题目77. 组合。
+
+链接：https://leetcode-cn.com/problems/combinations/
+
+**看本篇之前，需要先看[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)**。
+
+大家先回忆一下[77. 组合]给出的回溯法的代码：
+
+```
+class Solution {
+private:
+ vector> result; // 存放符合条件结果的集合
+ vector path; // 用来存放符合条件结果
+ void backtracking(int n, int k, int startIndex) {
+ if (path.size() == k) {
+ result.push_back(path);
+ return;
+ }
+ for (int i = startIndex; i <= n; i++) {
+ path.push_back(i); // 处理节点
+ backtracking(n, k, i + 1); // 递归
+ path.pop_back(); // 回溯，撤销处理的节点
+ }
+ }
+public:
+ vector> combine(int n, int k) {
+ result.clear(); // 可以不写
+ path.clear(); // 可以不写
+ backtracking(n, k, 1);
+ return result;
+ }
+};
+```
+
+# 剪枝优化
+
+我们说过，回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。
+
+在遍历的过程中有如下代码：
+
+```
+for (int i = startIndex; i <= n; i++) {
+ path.push_back(i);
+ backtracking(n, k, i + 1);
+ path.pop_back();
+}
+```
+
+这个遍历的范围是可以剪枝优化的，怎么优化呢？
+
+来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。
+
+这么说有点抽象，如图所示：
+
+
+
+
+图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
+
+**所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
+
+**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了**。
+
+注意代码中i，就是for循环里选择的起始位置。
+```
+for (int i = startIndex; i <= n; i++) {
+```
+
+接下来看一下优化过程如下：
+
+1. 已经选择的元素个数：path.size();
+
+2. 还需要的元素个数为: k - path.size();
+
+3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历
+
+为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。
+
+举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
+
+从2开始搜索都是合理的，可以是组合[2, 3, 4]。
+
+这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。
+
+所以优化之后的for循环是：
+
+```
+for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
+```
+
+优化后整体代码如下：
+
+```
+class Solution {
+private:
+ vector> result;
+ vector path;
+ void backtracking(int n, int k, int startIndex) {
+ if (path.size() == k) {
+ result.push_back(path);
+ return;
+ }
+ for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
+ path.push_back(i); // 处理节点
+ backtracking(n, k, i + 1);
+ path.pop_back(); // 回溯，撤销处理的节点
+ }
+ }
+public:
+
+ vector> combine(int n, int k) {
+ backtracking(n, k, 1);
+ return result;
+ }
+};
+```
+
+# 总结
+
+本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
+
+所以我依然是把整个回溯过程抽象为一颗树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
+
+**就酱，学到了就帮Carl转发一下吧，让更多的同学知道这里！**
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
+
diff --git a/problems/0216.组合总和III.md b/problems/0216.组合总和III.md
new file mode 100644
index 00000000..ca5b1bc1
--- /dev/null
+++ b/problems/0216.组合总和III.md
@@ -0,0 +1,229 @@
+
+
+
+
+
+
+
+
+
+
+> 别看本篇选的是组合总和III，而不是组合总和，本题和上一篇[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)相比难度刚刚好！
+
+# 216.组合总和III
+
+链接：https://leetcode-cn.com/problems/combination-sum-iii/
+
+找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。
+
+说明：
+* 所有数字都是正整数。
+* 解集不能包含重复的组合。
+
+示例 1:
+输入: k = 3, n = 7
+输出: [[1,2,4]]
+
+示例 2:
+输入: k = 3, n = 9
+输出: [[1,2,6], [1,3,5], [2,3,4]]
+
+
+## 思路
+
+本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。
+
+相对于[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,...,9]。
+
+想到这一点了，做过[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)之后，本题是简单一些了。
+
+本题k相当于了树的深度，9（因为整个集合就是9个数）就是树的宽度。
+
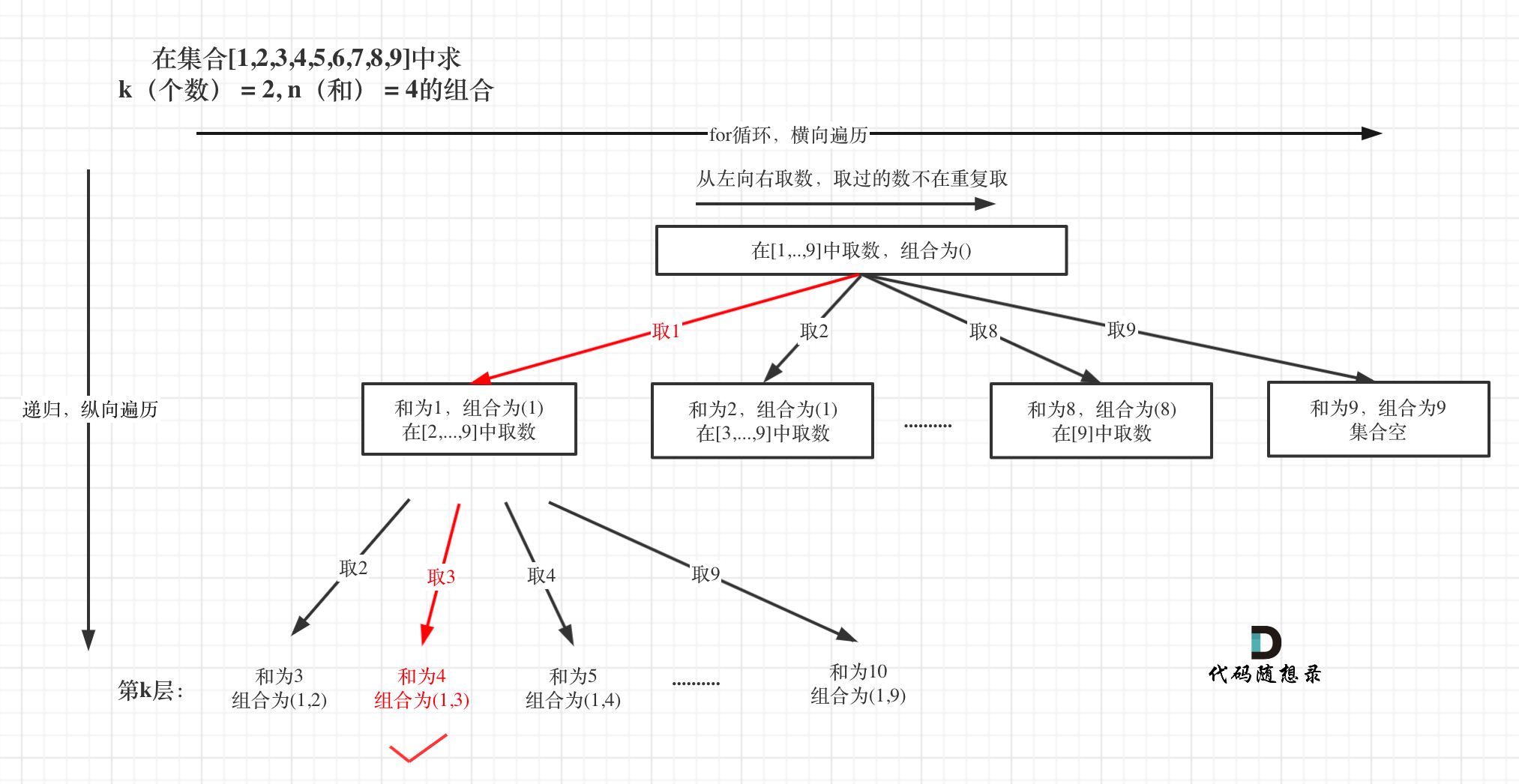
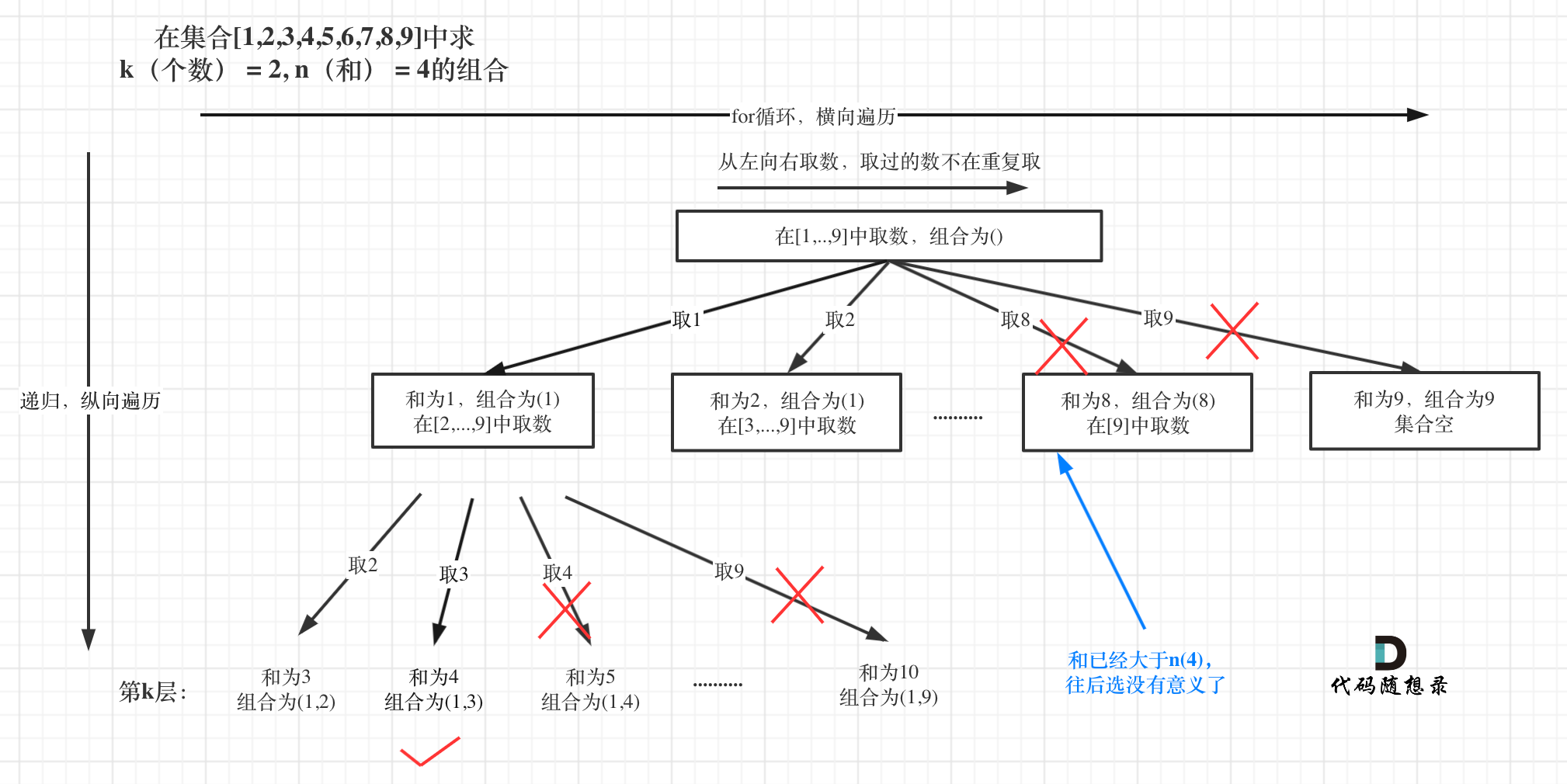
+例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。
+
+选取过程如图：
+
+
+
+图中，可以看出，只有最后取到集合（1，3）和为4 符合条件。
+
+
+## 回溯三部曲
+
+* **确定递归函数参数**
+
+和[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)一样，依然需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。
+
+这里我依然定义path 和 result为全局变量。
+
+至于为什么取名为path？从上面树形结构中，可以看出，结果其实就是一条根节点到叶子节点的路径。
+
+```
+vector> result; // 存放结果集
+vector path; // 符合条件的结果
+```
+
+接下来还需要如下参数：
+
+* targetSum（int）目标和，也就是题目中的n。
+* k（int）就是题目中要求k个数的集合。
+* sum（int）为已经收集的元素的总和，也就是path里元素的总和。
+* startIndex（int）为下一层for循环搜索的起始位置。
+
+所以代码如下：
+
+```
+vector> result;
+vector path;
+void backtracking(int targetSum, int k, int sum, int startIndex)
+```
+其实这里sum这个参数也可以省略，每次targetSum减去选取的元素数值，然后判断如果targetSum为0了，说明收集到符合条件的结果了，我这里为了直观便于理解，还是加一个sum参数。
+
+还要强调一下，回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要啥参数了，填什么参数。
+
+* 确定终止条件
+
+什么时候终止呢？
+
+在上面已经说了，k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。
+
+所以如果path.size() 和 k相等了，就终止。
+
+如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。
+
+所以 终止代码如下：
+
+```
+if (path.size() == k) {
+ if (sum == targetSum) result.push_back(path);
+ return; // 如果path.size() == k 但sum != targetSum 直接返回
+}
+```
+
+* **单层搜索过程**
+
+本题和[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)区别之一就是集合固定的就是9个数[1,...,9]，所以for循环固定i<=9
+
+如图：
+
+
+处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。
+
+代码如下：
+
+```
+for (int i = startIndex; i <= 9; i++) {
+ sum += i;
+ path.push_back(i);
+ backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
+ sum -= i; // 回溯
+ path.pop_back(); // 回溯
+}
+```
+
+**别忘了处理过程 和 回溯过程是一一对应的，处理有加，回溯就要有减！**
+
+参照[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中的模板，不难写出如下C++代码：
+
+```
+class Solution {
+private:
+ vector> result; // 存放结果集
+ vector path; // 符合条件的结果
+ // targetSum：目标和，也就是题目中的n。
+ // k：题目中要求k个数的集合。
+ // sum：已经收集的元素的总和，也就是path里元素的总和。
+ // startIndex：下一层for循环搜索的起始位置。
+ void backtracking(int targetSum, int k, int sum, int startIndex) {
+ if (path.size() == k) {
+ if (sum == targetSum) result.push_back(path);
+ return; // 如果path.size() == k 但sum != targetSum 直接返回
+ }
+ for (int i = startIndex; i <= 9; i++) {
+ sum += i; // 处理
+ path.push_back(i); // 处理
+ backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
+ sum -= i; // 回溯
+ path.pop_back(); // 回溯
+ }
+ }
+
+public:
+ vector> combinationSum3(int k, int n) {
+ result.clear(); // 可以不加
+ path.clear(); // 可以不加
+ backtracking(n, k, 0, 1);
+ return result;
+ }
+};
+```
+
+## 剪枝
+
+这道题目，剪枝操作其实是很容易想到了，想必大家看上面的树形图的时候已经想到了。
+
+如图：
+
+
+已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉。
+
+那么剪枝的地方一定是在递归终止的地方剪，剪枝代码如下：
+
+```
+if (sum > targetSum) { // 剪枝操作
+ return;
+}
+```
+
+和[回溯算法：组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA) 一样，for循环的范围也可以剪枝，i <= 9 - (k - path.size()) + 1就可以了。
+
+最后C++代码如下：
+
+```
+class Solution {
+private:
+ vector> result; // 存放结果集
+ vector path; // 符合条件的结果
+ void backtracking(int targetSum, int k, int sum, int startIndex) {
+ if (sum > targetSum) { // 剪枝操作
+ return; // 如果path.size() == k 但sum != targetSum 直接返回
+ }
+ if (path.size() == k) {
+ if (sum == targetSum) result.push_back(path);
+ return;
+ }
+ for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
+ sum += i; // 处理
+ path.push_back(i); // 处理
+ backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
+ sum -= i; // 回溯
+ path.pop_back(); // 回溯
+ }
+ }
+
+public:
+ vector> combinationSum3(int k, int n) {
+ result.clear(); // 可以不加
+ path.clear(); // 可以不加
+ backtracking(n, k, 0, 1);
+ return result;
+ }
+};
+```
+
+# 总结
+
+开篇就介绍了本题与[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)的区别，相对来说加了元素总和的限制，如果做完[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)再做本题在合适不过。
+
+分析完区别，依然把问题抽象为树形结构，按照回溯三部曲进行讲解，最后给出剪枝的优化。
+
+相信做完本题，大家对组合问题应该有初步了解了。
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
diff --git a/problems/0704.二分查找.md b/problems/0704.二分查找.md
new file mode 100644
index 00000000..2293e165
--- /dev/null
+++ b/problems/0704.二分查找.md
@@ -0,0 +1,150 @@
+
+
+
+
+
+
+
+
+## 704. 二分查找
+
+题目链接：https://leetcode-cn.com/problems/binary-search/
+
+给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
+
+
+示例 1:
+输入: nums = [-1,0,3,5,9,12], target = 9
+输出: 4
+解释: 9 出现在 nums 中并且下标为 4
+
+示例 2:
+输入: nums = [-1,0,3,5,9,12], target = 2
+输出: -1
+解释: 2 不存在 nums 中因此返回 -1
+
+提示：
+
+* 你可以假设 nums 中的所有元素是不重复的。
+* n 将在 [1, 10000]之间。
+* nums 的每个元素都将在 [-9999, 9999]之间。
+
+
+## 思路
+
+**这道题目的前提是数组为有序数组**，同时题目还强调**数组中无重复元素**，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。
+
+二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 `while(left < right)` 还是 `while(left <= right)`，到底是`right = middle`呢，还是要`right = middle - 1`呢？
+
+大家写二分法经常写乱，主要是因为**对区间的定义没有想清楚，区间的定义就是不变量**。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是**循环不变量**规则。
+
+写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。
+
+下面我用这两种区间的定义分别讲解两种不同的二分写法。
+
+### 二分法第一种写法
+
+第一种写法，我们定义 target 是在一个在左闭右闭的区间里，**也就是[left, right] （这个很重要非常重要）**。
+
+区间的定义这就决定了二分法的代码应该如何写，**因为定义target在[left, right]区间，所以有如下两点：**
+
+* while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
+* if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
+
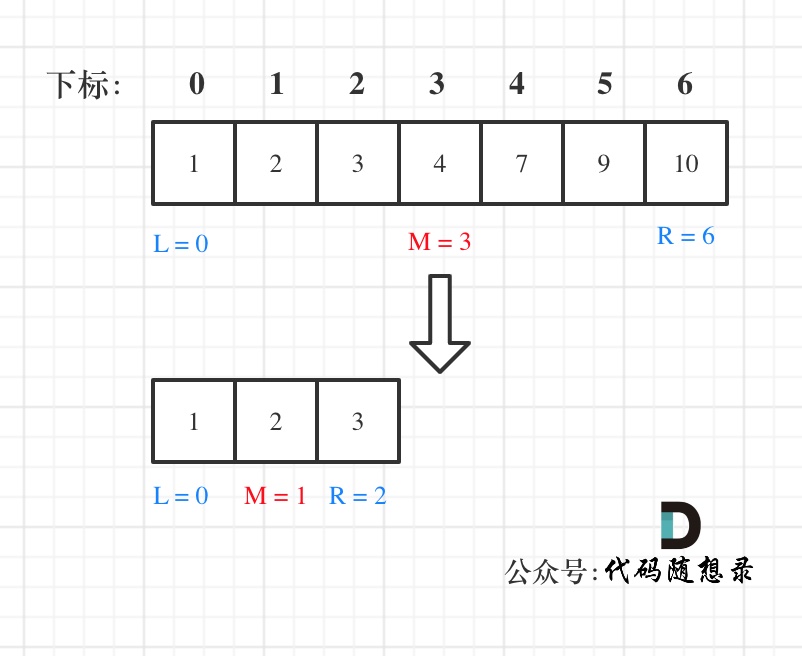
+例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：
+
+
+
+代码如下：（详细注释）
+
+```C++
+// 版本一
+class Solution {
+public:
+ int search(vector& nums, int target) {
+ int left = 0;
+ int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
+ while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
+ int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
+ if (nums[middle] > target) {
+ right = middle - 1; // target 在左区间，所以[left, middle - 1]
+ } else if (nums[middle] < target) {
+ left = middle + 1; // target 在右区间，所以[middle + 1, right]
+ } else { // nums[middle] == target
+ return middle; // 数组中找到目标值，直接返回下标
+ }
+ }
+ // 未找到目标值
+ return -1;
+ }
+};
+
+```
+
+### 二分法第二种写法
+
+如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。
+
+有如下两点：
+
+* while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
+* if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
+
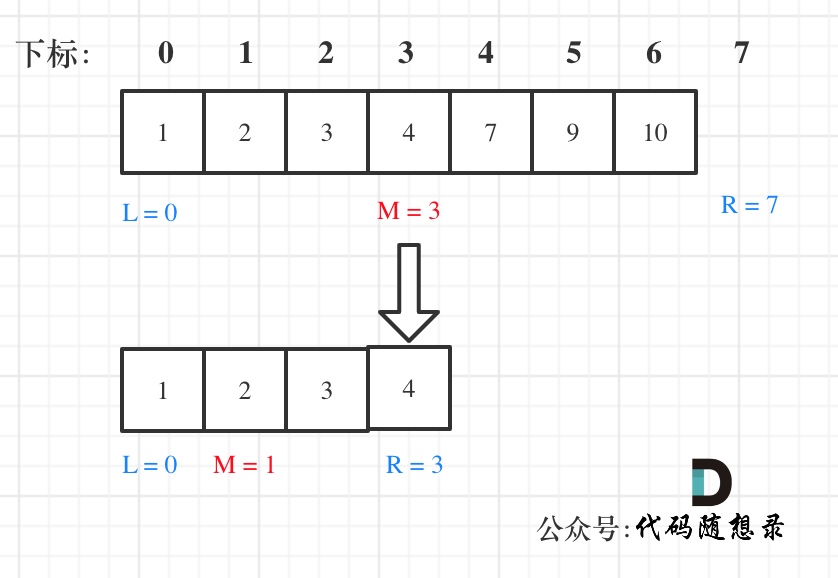
+在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（**注意和方法一的区别**）
+
+
+
+代码如下：（详细注释）
+
+```C++
+// 版本二
+class Solution {
+public:
+ int search(vector& nums, int target) {
+ int left = 0;
+ int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
+ while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
+ int middle = left + ((right - left) >> 1);
+ if (nums[middle] > target) {
+ right = middle; // target 在左区间，在[left, middle)中
+ } else if (nums[middle] < target) {
+ left = middle + 1; // target 在右区间，在[middle + 1, right)中
+ } else { // nums[middle] == target
+ return middle; // 数组中找到目标值，直接返回下标
+ }
+ }
+ // 未找到目标值
+ return -1;
+ }
+};
+```
+
+## 总结
+
+二分法是非常重要的基础算法，为什么很多同学对于二分法都是**一看就会，一写就废**？
+
+其实主要就是对区间的定义没有理解清楚，在循环中没有始终坚持根据查找区间的定义来做边界处理。
+
+区间的定义就是不变量，那么在循环中坚持根据查找区间的定义来做边界处理，就是循环不变量规则。
+
+本篇根据两种常见的区间定义，给出了两种二分法的写法，每一个边界为什么这么处理，都根据区间的定义做了详细介绍。
+
+相信看完本篇应该对二分法有更深刻的理解了。
+
+## 相关题目推荐
+
+* [35.搜索插入位置](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)
+* 34.在排序数组中查找元素的第一个和最后一个位置
+* 69.x 的平方根
+* 367.有效的完全平方数
+
+
+
+------------------------
+
+* 微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
+
diff --git a/problems/周总结/20201030回溯周末总结.md b/problems/周总结/20201030回溯周末总结.md
new file mode 100644
index 00000000..070b1abf
--- /dev/null
+++ b/problems/周总结/20201030回溯周末总结.md
@@ -0,0 +1,113 @@
+
+
+
+
+
+
+
+
+
+## 周一
+
+本周我们正式开始了回溯算法系列，那么首先当然是概述。
+
+在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中介绍了什么是回溯，回溯法的效率，回溯法解决的问题以及回溯法模板。
+
+**回溯是递归的副产品，只要有递归就会有回溯**。
+
+回溯法就是暴力搜索，并不是什么高效的算法，最多在剪枝一下。
+
+回溯算法能解决如下问题：
+
+* 组合问题：N个数里面按一定规则找出k个数的集合
+* 排列问题：N个数按一定规则全排列，有几种排列方式
+* 切割问题：一个字符串按一定规则有几种切割方式
+* 子集问题：一个N个数的集合里有多少符合条件的子集
+* 棋盘问题：N皇后，解数独等等
+
+是不是感觉回溯算法有点厉害了。
+
+回溯法确实不好理解，所以需要把回溯法抽象为一个图形来理解就容易多了，每一道回溯法的题目都可以抽象为树形结构。
+
+针对很多同学都写不好回溯，我在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)用回溯三部曲，分析了回溯算法，并给出了回溯法的模板。
+
+这个模板会伴随整个回溯法系列！
+
+## 周二
+
+
+在[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)中，我们开始用回溯法解决第一道题目，组合问题。
+
+我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴利解法，为什么要用回溯法。
+
+**此时大家应该深有体会回溯法的魅力，用递归控制for循环嵌套的数量！**
+
+本题我把回溯问题抽象为树形结构，可以直观的看出其搜索的过程：**for循环横向遍历，递归纵向遍历，回溯不断调整结果集**。
+
+## 周三
+
+针对[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)还可以做剪枝的操作。
+
+在[回溯算法：组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)中把回溯法代码做了剪枝优化，在文中我依然把问题抽象为一个树形结构，大家可以一目了然剪的究竟是哪里。
+
+**剪枝精髓是：for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够 题目要求的k个元素了，就没有必要搜索了**。
+
+## 周四
+
+在[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中，相当于 [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)加了一个元素总和的限制。
+
+整体思路还是一样的，本题的剪枝会好想一些，即：**已选元素总和如果已经大于n（题中要求的和）了，那么往后遍历就没有意义了，直接剪掉**。
+
+在本题中，依然还可以有一个剪枝，就是[回溯算法：组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)中提到的，对for循环选择的起始范围的剪枝。
+
+所以，剪枝的代码，可以把for循环，加上 `i <= 9 - (k - path.size()) + 1` 的限制！
+
+组合总和问题还有一些花样，下周还会介绍到。
+
+## 周五
+
+在[回溯算法：电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)中，开始用多个集合来求组合，还是熟悉的模板题目，但是有一些细节。
+
+例如这里for循环，可不像是在 [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中从startIndex开始遍历的。
+
+**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)都是是求同一个集合中的组合！**
+
+如果大家在现场面试的时候，一定要注意各种输入异常的情况，例如本题输入1 * #按键。
+
+其实本题不算难，但也处处是细节，还是要反复琢磨。
+
+## 周六
+
+因为之前链表系列没有写总结，虽然链表系列已经是两个月前的事情，但还是有必要补一下。
+
+所以给出[链表：总结篇！](https://mp.weixin.qq.com/s/vK0JjSTHfpAbs8evz5hH8A)，这里对之前链表理论基础和经典题目进行了总结。
+
+同时对[链表：环找到了，那入口呢？](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)中求环入口的问题又进行了补充证明，可以说把环形链表的方方面面都讲的很通透了，大家如果没有做过环形链表的题目一定要去做一做。
+
+## 总结
+
+相信通过这一周对回溯法的学习，大家已经掌握其题本套路了，也不会对回溯法那么畏惧了。
+
+回溯法抽象为树形结构后，其遍历过程就是：**for循环横向遍历，递归纵向遍历，回溯不断调整结果集**。
+
+这个是我做了很多回溯的题目，不断摸索其规律才总结出来的。
+
+对于回溯法的整体框架，网上搜的文章这块一般都说不清楚，按照天上掉下来的代码对着讲解，不知道究竟是怎么来的，也不知道为什么要这么写。
+
+所以，录友们刚开始学回溯法，起跑姿势就很标准了，哈哈。
+
+下周依然是回溯法，难度又要上升一个台阶了。
+
+最后祝录友们周末愉快！
+
+**如果感觉「代码随想录」不错，就分享给身边的同学朋友吧，一起来学习算法！**
+
+
+
+------------------------
+
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* 知乎：[代码随想录](https://www.zhihu.com/people/sun-xiu-yang-64)
+
+
+
+ 