update 0222.完全二叉树的节点个数: 替换 java 代码，调整 js 格式

problems/0222.完全二叉树的节点个数.md

@@ -63,7 +63,7 @@ int getNodesNum(TreeNode* cur) {
 if (cur == NULL) return 0;
 ```
 
-3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求的右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。
+3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。
 
 代码如下：
 
@@ -168,7 +168,7 @@ public:
 
 可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
 
-这里关键在于如果去判断一个左子树或者右子树是不是满二叉树呢？ 
+这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？ 
 
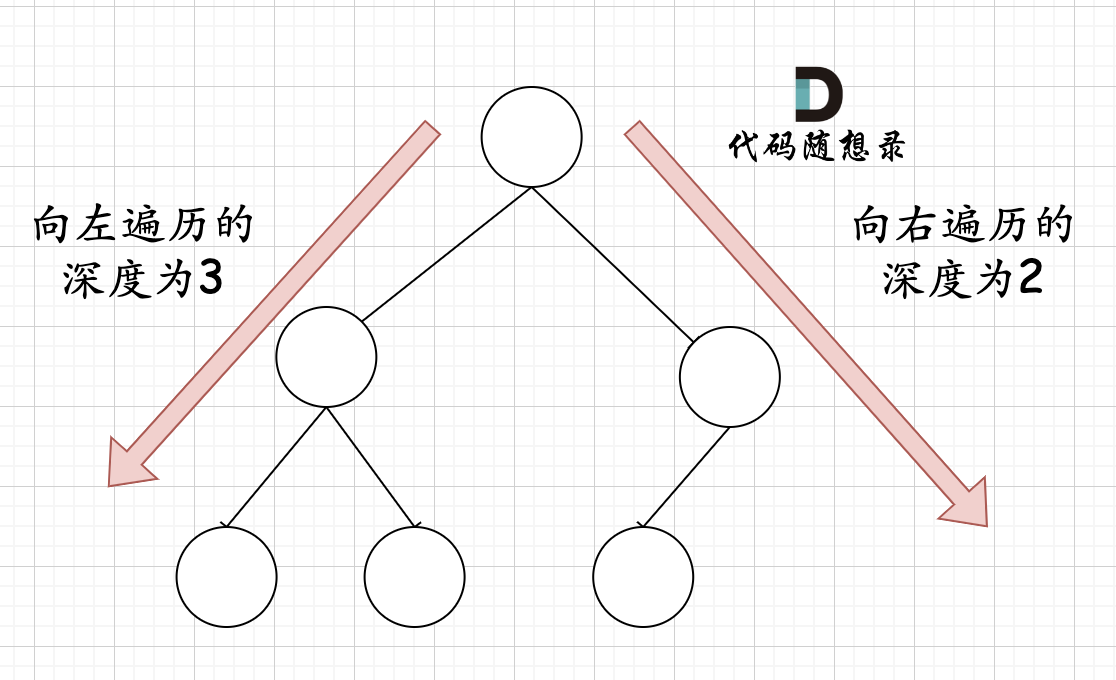
 在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图： 
 
@@ -178,13 +178,13 @@ public:
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163709.png) 
 
-哪有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题： 
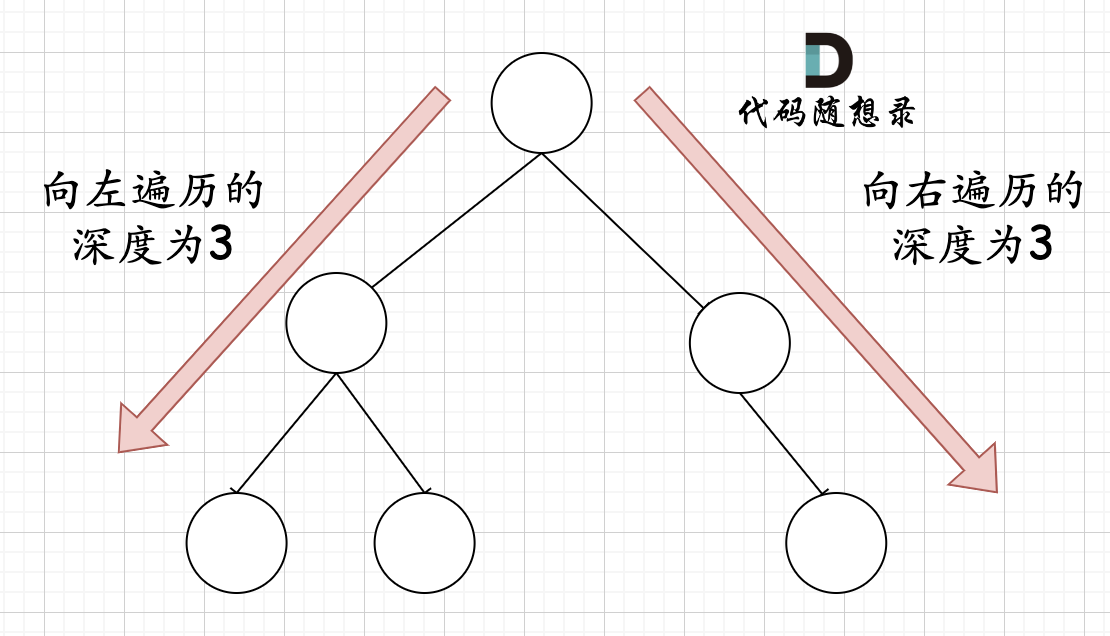
+那有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题： 
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163811.png) 
 
 如果这么想，大家就是对 完全二叉树理解有误区了，**以上这棵二叉树，它根本就不是一个完全二叉树**！ 
 
-判断其子树岂不是满二叉树，如果是则利用用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的： 
+判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的： 
 
 ```CPP
 if (root == nullptr) return 0; 
@@ -292,26 +292,22 @@ class Solution {
      * 满二叉树的结点数为：2^depth - 1
      */
     public int countNodes(TreeNode root) {
-        if(root == null) {
+        if (root == null) return 0;
-            return 0;
+        TreeNode left = root.left;
+        TreeNode right = root.right;
+        int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
+        while (left != null) {  // 求左子树深度
+            left = left.left;
+            leftDepth++;
         }
-        int leftDepth = getDepth(root.left);
+        while (right != null) { // 求右子树深度
-        int rightDepth = getDepth(root.right);
+            right = right.right;
-        if (leftDepth == rightDepth) {// 左子树是满二叉树
+            rightDepth++;
-            // 2^leftDepth其实是 （2^leftDepth - 1） + 1 ，左子树 + 根结点
-            return (1 << leftDepth) + countNodes(root.right);
-        } else {// 右子树是满二叉树
-            return (1 << rightDepth) + countNodes(root.left);
         }
+        if (leftDepth == rightDepth) {
+            return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
         }
-
+        return countNodes(root.left) + countNodes(root.right) + 1;
-    private int getDepth(TreeNode root) {
-        int depth = 0;
-        while (root != null) {
-            root = root.left;
-            depth++;
-        }
-        return depth;
     }
 }
 ```
@@ -397,7 +393,7 @@ class Solution:
  *     Right *TreeNode
  * }
  */
-//本题直接就是求有多少个节点，无脑存进数组算长度就行了。
+//本题直接就是求有多少个节点，无脑存进结果变量就行了。
 func countNodes(root *TreeNode) int {
     if root == nil {
         return 0