Merge pull request #1782 from juguagua/leetcode-modify-the-code-of-the-stack-and-queue

优化栈与队列部分代码与文本

problems/0020.有效的括号.md

@@ -76,7 +76,7 @@ cd a/b/c/../../
 
 **一些同学，在面试中看到这种题目上来就开始写代码，然后就越写越乱。**
 
-建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。
+建议在写代码之前要分析好有哪几种不匹配的情况，如果不在动手之前分析好，写出的代码也会有很多问题。
 
 先来分析一下 这里有三种不匹配的情况，
 

problems/0150.逆波兰表达式求值.md

@@ -51,7 +51,7 @@
   ```
 
 
-逆波兰表达式：是一种后缀表达式，所谓后缀就是指算符写在后面。
+逆波兰表达式：是一种后缀表达式，所谓后缀就是指运算符写在后面。
 
 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
 
@@ -61,11 +61,11 @@
 
 * 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
 
-* 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。
+* 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。
 
 # 思路
 
-《代码随想录》算法视频公开课：[栈的最后表演！ | LeetCode：150. 逆波兰表达式求值](https://www.bilibili.com/video/BV1kd4y1o7on)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
+《代码随想录》算法视频公开课：[栈的最后表演！ | LeetCode：150. 逆波兰表达式求值](https://www.bilibili.com/video/BV1kd4y1o7on)，相信结合视频再看本篇题解，更有助于大家对本题的理解。
 
 在上一篇文章中[1047.删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)提到了 递归就是用栈来实现的。
 
@@ -73,7 +73,7 @@
 
 那么来看一下本题，**其实逆波兰表达式相当于是二叉树中的后序遍历**。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。
 
-但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后续遍历的方式把二叉树序列化了，就可以了。
+但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。
 
 在进一步看，本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么**这岂不就是一个相邻字符串消除的过程，和[1047.删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)中的对对碰游戏是不是就非常像了。**
 
@@ -118,9 +118,9 @@ public:
 
 我们习惯看到的表达式都是中缀表达式，因为符合我们的习惯，但是中缀表达式对于计算机来说就不是很友好了。
 
-例如：4 + 13 / 5，这就是中缀表达式，计算机从左到右去扫描的话，扫到13，还要判断13后面是什么运算法，还要比较一下优先级，然后13还和后面的5做运算，做完运算之后，还要向前回退到 4 的位置，继续做加法，你说麻不麻烦！
+例如：4 + 13 / 5，这就是中缀表达式，计算机从左到右去扫描的话，扫到13，还要判断13后面是什么运算符，还要比较一下优先级，然后13还和后面的5做运算，做完运算之后，还要向前回退到 4 的位置，继续做加法，你说麻不麻烦！
 
-那么将中缀表达式，转化为后缀表达式之后：["4", "13", "5", "/", "+"] ，就不一样了，计算机可以利用栈里顺序处理，不需要考虑优先级了。也不用回退了， **所以后缀表达式对计算机来说是非常友好的。**
+那么将中缀表达式，转化为后缀表达式之后：["4", "13", "5", "/", "+"] ，就不一样了，计算机可以利用栈来顺序处理，不需要考虑优先级了。也不用回退了， **所以后缀表达式对计算机来说是非常友好的。**
 
 可以说本题不仅仅是一道好题，也展现出计算机的思考方式。
 
@@ -161,6 +161,24 @@ class Solution {
 }
 ```
 
+python3
+
+```python
+class Solution:
+    def evalRPN(self, tokens: List[str]) -> int:
+        stack = []
+        for item in tokens:
+            if item not in {"+", "-", "*", "/"}:
+                stack.append(item)
+            else:
+                first_num, second_num = stack.pop(), stack.pop()
+                stack.append(
+                    int(eval(f'{second_num} {item} {first_num}'))   # 第一个出来的在运算符后面
+                )
+        return int(stack.pop()) # 如果一开始只有一个数，那么会是字符串形式的
+
+```
+
 Go:
 ```Go
 func evalRPN(tokens []string) int {
@@ -169,7 +187,7 @@ func evalRPN(tokens []string) int {
 		val, err := strconv.Atoi(token)
 		if err == nil {
 			stack = append(stack, val)
-		} else {
+		} else {   // 如果err不为nil说明不是数字
 			num1, num2 := stack[len(stack)-2], stack[(len(stack))-1]
 			stack = stack[:len(stack)-2]
 			switch token {
@@ -191,27 +209,31 @@ func evalRPN(tokens []string) int {
 javaScript:
 
 ```js
-
-/**
- * @param {string[]} tokens
- * @return {number}
- */
-var evalRPN = function(tokens) {
-    const s = new Map([
-        ["+", (a, b) => a * 1  + b * 1],
-        ["-", (a, b) => b - a],
-        ["*", (a, b) => b * a],
-        ["/", (a, b) => (b / a) | 0]
-    ]);
+var evalRPN = function (tokens) {
     const stack = [];
-    for (const i of tokens) {
-        if(!s.has(i)) {
-            stack.push(i);
-            continue;
+    for (const token of tokens) {
+        if (isNaN(Number(token))) { // 非数字
+            const n2 = stack.pop(); // 出栈两个数字
+            const n1 = stack.pop();
+            switch (token) { // 判断运算符类型，算出新数入栈
+                case "+":
+                    stack.push(n1 + n2);
+                    break;
+                case "-":
+                    stack.push(n1 - n2);
+                    break;
+                case "*":
+                    stack.push(n1 * n2);
+                    break;
+                case "/":
+                    stack.push(n1 / n2 | 0);
+                    break;
             }
-        stack.push(s.get(i)(stack.pop(),stack.pop()))
+        } else { // 数字
+            stack.push(Number(token));
         }
-    return stack.pop();
+    }
+    return stack[0]; // 因没有遇到运算符而待在栈中的结果
 };
 ```
 
@@ -280,24 +302,6 @@ function evalRPN(tokens: string[]): number {
 };
 ```
 
-python3
-
-```python
-class Solution:
-    def evalRPN(self, tokens: List[str]) -> int:
-        stack = []
-        for item in tokens:
-            if item not in {"+", "-", "*", "/"}:
-                stack.append(item)
-            else:
-                first_num, second_num = stack.pop(), stack.pop()
-                stack.append(
-                    int(eval(f'{second_num} {item} {first_num}'))   # 第一个出来的在运算符后面
-                )
-        return int(stack.pop()) # 如果一开始只有一个数，那么会是字符串形式的
-
-```
-
 Swift：
 ```Swift
 func evalRPN(_ tokens: [String]) -> Int {

problems/0225.用队列实现栈.md

@@ -29,7 +29,7 @@
 # 思路
 
 
-《代码随想录》算法公开课：[队列的基本操作！ | LeetCode：225. 用队列实现栈](https://www.bilibili.com/video/BV1Fd4y1K7sm)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
+《代码随想录》算法公开课：[队列的基本操作！ | LeetCode：225. 用队列实现栈](https://www.bilibili.com/video/BV1Fd4y1K7sm)，相信结合视频再看本篇题解，更有助于大家对链表的理解。
 
 
 （这里要强调是单向队列）
@@ -44,7 +44,7 @@
 
 所以用栈实现队列， 和用队列实现栈的思路还是不一样的，这取决于这两个数据结构的性质。
 
-但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用又来备份的！
+但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用来备份的！
 
 如下面动画所示，**用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用**，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。
 
@@ -116,7 +116,7 @@ public:
 
 其实这道题目就是用一个队列就够了。
 
-**一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时在去弹出元素就是栈的顺序了。**
+**一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。**
 
 C++优化代码
 

problems/0232.用栈实现队列.md

@@ -38,14 +38,14 @@ queue.empty(); // 返回 false
 
 ## 思路
 
-《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
+《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频再看本篇题解，更有助于大家对链表的理解。
 
 
 这是一道模拟题，不涉及到具体算法，考察的就是对栈和队列的掌握程度。
 
 使用栈来模式队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈**一个输入栈，一个输出栈**，这里要注意输入栈和输出栈的关系。
 
-下面动画模拟以下队列的执行过程如下：
+下面动画模拟以下队列的执行过程：
 
 执行语句：     
 queue.push(1);     
@@ -120,7 +120,7 @@ public:
 
 这样的项目代码会越来越乱，**一定要懂得复用，功能相近的函数要抽象出来，不要大量的复制粘贴，很容易出问题！（踩过坑的人自然懂）**
 
-工作中如果发现某一个功能自己要经常用，同事们可能也会用到，自己就花点时间把这个功能抽象成一个好用的函数或者工具类，不仅自己方便，也方面了同事们。
+工作中如果发现某一个功能自己要经常用，同事们可能也会用到，自己就花点时间把这个功能抽象成一个好用的函数或者工具类，不仅自己方便，也方便了同事们。
 
 同事们就会逐渐认可你的工作态度和工作能力，自己的口碑都是这么一点一点积累起来的！在同事圈里口碑起来了之后，你就发现自己走上了一个正循环，以后的升职加薪才少不了你！哈哈哈
 
@@ -231,56 +231,51 @@ class MyQueue:
 Go：
 ```Go
 type MyQueue struct {
-    stack []int
-    back  []int
+    stackIn  []int //输入栈
+    stackOut []int //输出栈
 }
 
-/** Initialize your data structure here. */
 func Constructor() MyQueue {
     return MyQueue{
-        stack: make([]int, 0),
-        back:  make([]int, 0),
+        stackIn:  make([]int, 0),
+        stackOut: make([]int, 0),
     }
 }
 
-/** Push element x to the back of queue. */
+// 往输入栈做push
 func (this *MyQueue) Push(x int) {
-    for len(this.back) != 0 {
-        val := this.back[len(this.back)-1]
-        this.back = this.back[:len(this.back)-1]
-        this.stack = append(this.stack, val)
-    }
-    this.stack = append(this.stack, x)
+    this.stackIn = append(this.stackIn, x)
 }
 
-/** Removes the element from in front of queue and returns that element. */
+// 在输出栈做pop，pop时如果输出栈数据为空，需要将输入栈全部数据导入，如果非空，则可直接使用
 func (this *MyQueue) Pop() int {
-    for len(this.stack) != 0 {
-        val := this.stack[len(this.stack)-1]
-        this.stack = this.stack[:len(this.stack)-1]
-        this.back = append(this.back, val)
+    inLen, outLen := len(this.stackIn), len(this.stackOut)
+    if outLen == 0 {
+        if inLen == 0 {
+            return -1
         }
-    if len(this.back) == 0 {
-        return 0
+        for i := inLen - 1; i >= 0; i-- {
+            this.stackOut = append(this.stackOut, this.stackIn[i])
         }
-    val := this.back[len(this.back)-1]
-    this.back = this.back[:len(this.back)-1]
+        this.stackIn = []int{}      //导出后清空
+        outLen = len(this.stackOut) //更新长度值
+    }
+    val := this.stackOut[outLen-1]
+    this.stackOut = this.stackOut[:outLen-1]
     return val
 }
 
-/** Get the front element. */
 func (this *MyQueue) Peek() int {
     val := this.Pop()
-    if val == 0 {
-        return 0
+    if val == -1 {
+        return -1
     }
-    this.back = append(this.back, val)
+    this.stackOut = append(this.stackOut, val)
     return val
 }
 
-/** Returns whether the queue is empty. */
 func (this *MyQueue) Empty() bool {
-    return len(this.stack) == 0 && len(this.back) == 0
+    return len(this.stackIn) == 0 && len(this.stackOut) == 0
 }
 ```
 

problems/0239.滑动窗口最大值.md

@@ -38,7 +38,7 @@
 
 难点是如何求一个区间里的最大值呢？ （这好像是废话），暴力一下不就得了。
 
-暴力方法，遍历一遍的过程中每次从窗口中在找到最大的数值，这样很明显是O(n × k)的算法。
+暴力方法，遍历一遍的过程中每次从窗口中再找到最大的数值，这样很明显是O(n × k)的算法。
 
 有的同学可能会想用一个大顶堆（优先级队列）来存放这个窗口里的k个数字，这样就可以知道最大的最大值是多少了， **但是问题是这个窗口是移动的，而大顶堆每次只能弹出最大值，我们无法移除其他数值，这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
 
@@ -66,7 +66,7 @@ public:
 
 **可惜了，没有！ 我们需要自己实现这么个队列。**
 
-然后在分析一下，队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
+然后再分析一下，队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
 
 但如果把窗口里的元素都放进队列里，窗口移动的时候，队列需要弹出元素。
 
@@ -74,9 +74,9 @@ public:
 
 大家此时应该陷入深思.....
 
-**其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队里里的元素数值是由大到小的。**
+**其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队里的元素数值是由大到小的。**
 
-那么这个维护元素单调递减的队列就叫做**单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来一个单调队列**
+那么这个维护元素单调递减的队列就叫做**单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来实现一个单调队列**
 
 **不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。**
 
@@ -185,7 +185,7 @@ public:
 };
 ```
 
-在来看一下时间复杂度，使用单调队列的时间复杂度是 O(n)。
+再来看一下时间复杂度，使用单调队列的时间复杂度是 O(n)。
 
 有的同学可能想了，在队列中 push元素的过程中，还有pop操作呢，感觉不是纯粹的O(n)。
 

problems/0347.前K个高频元素.md

@@ -271,7 +271,7 @@ func (h *IHeap) Pop() interface{}{
 }
 
 
-//方法二:利用O(logn)排序
+//方法二:利用O(nlogn)排序
 func topKFrequent(nums []int, k int) []int {
     ans:=[]int{}
     map_num:=map[int]int{}

problems/1047.删除字符串中的所有相邻重复项.md

@@ -50,7 +50,7 @@
 
 ![1047.删除字符串中的所有相邻重复项](https://code-thinking.cdn.bcebos.com/gifs/1047.删除字符串中的所有相邻重复项.gif)
 
-从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以在对字符串进行反转一下，就得到了最终的结果。
+从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。
 
 C++代码 :
 
@@ -102,9 +102,9 @@ public:
 
 ## 题外话
 
-这道题目就像是我们玩过的游戏对对碰，如果相同的元素放在挨在一起就要消除。
+这道题目就像是我们玩过的游戏对对碰，如果相同的元素挨在一起就要消除。
 
-可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如果消除呢，特别是消除之后又有新的元素可能挨在一起。
+可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如何消除呢，特别是消除之后又有新的元素可能挨在一起。
 
 此时游戏的后端逻辑就可以用一个栈来实现（我没有实际考察对对碰或者爱消除游戏的代码实现，仅从原理上进行推断）。
 

problems/栈与队列理论基础.md

@@ -12,7 +12,7 @@
 
 ![栈与队列理论1](https://img-blog.csdnimg.cn/20210104235346563.png)
 
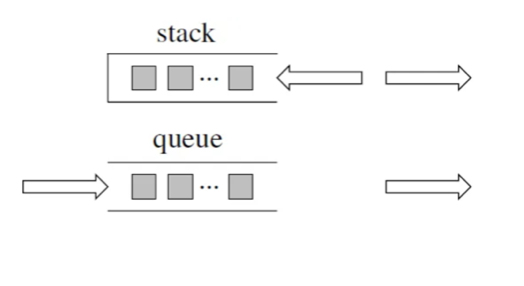
-那么我这里在列出四个关于栈的问题，大家可以思考一下。以下是以C++为例，相信使用其他编程语言的同学也对应思考一下，自己使用的编程语言里栈和队列是什么样的。
+那么我这里再列出四个关于栈的问题，大家可以思考一下。以下是以C++为例，使用其他编程语言的同学也对应思考一下，自己使用的编程语言里栈和队列是什么样的。
 
 1. C++中stack 是容器么？
 2. 我们使用的stack是属于哪个版本的STL？
@@ -23,7 +23,7 @@
 
 有的同学可能仅仅知道有栈和队列这么个数据结构，却不知道底层实现，也不清楚所使用栈和队列和STL是什么关系。
 
-所以这里我在给大家扫一遍基础知识，
+所以这里我再给大家扫一遍基础知识，
 
 首先大家要知道 栈和队列是STL（C++标准库）里面的两个数据结构。
 
@@ -83,7 +83,7 @@ std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列
 
 所以STL 队列也不被归类为容器，而被归类为container adapter（ 容器适配器）。
 
-我这里讲的都是C++ 语言中情况， 使用其他语言的同学也要思考栈与队列的底层实现问题， 不要对数据结构的使用浅尝辄止，而要深挖起内部原理，才能夯实基础。
+我这里讲的都是C++ 语言中的情况， 使用其他语言的同学也要思考栈与队列的底层实现问题， 不要对数据结构的使用浅尝辄止，而要深挖其内部原理，才能夯实基础。