diff --git a/README.md b/README.md
index 6f8dc435..53180718 100644
--- a/README.md
+++ b/README.md
@@ -272,7 +272,7 @@
## 动态规划
-动态规划专题已经开始啦,小伙伴快上车!
+动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
* [关于动态规划,你该了解这些!](https://leetcode-cn.com/circle/article/tNuNnM/)
diff --git a/pics/100.相同的树.png b/pics/100.相同的树.png
deleted file mode 100644
index 88da7600..00000000
Binary files a/pics/100.相同的树.png and /dev/null differ
diff --git a/pics/1002.查找常用字符.png b/pics/1002.查找常用字符.png
deleted file mode 100644
index 23d75057..00000000
Binary files a/pics/1002.查找常用字符.png and /dev/null differ
diff --git a/pics/101. 对称二叉树.png b/pics/101. 对称二叉树.png
deleted file mode 100644
index 6485026d..00000000
Binary files a/pics/101. 对称二叉树.png and /dev/null differ
diff --git a/pics/101. 对称二叉树1.png b/pics/101. 对称二叉树1.png
deleted file mode 100644
index 98286136..00000000
Binary files a/pics/101. 对称二叉树1.png and /dev/null differ
diff --git a/pics/102.二叉树的层序遍历.png b/pics/102.二叉树的层序遍历.png
deleted file mode 100644
index dcfcf972..00000000
Binary files a/pics/102.二叉树的层序遍历.png and /dev/null differ
diff --git a/pics/104. 二叉树的最大深度.png b/pics/104. 二叉树的最大深度.png
deleted file mode 100644
index 74873c76..00000000
Binary files a/pics/104. 二叉树的最大深度.png and /dev/null differ
diff --git a/pics/1047.删除字符串中的所有相邻重复项.png b/pics/1047.删除字符串中的所有相邻重复项.png
deleted file mode 100644
index 57587100..00000000
Binary files a/pics/1047.删除字符串中的所有相邻重复项.png and /dev/null differ
diff --git a/pics/105. 从前序与中序遍历序列构造二叉树.png b/pics/105. 从前序与中序遍历序列构造二叉树.png
deleted file mode 100644
index 7430be27..00000000
Binary files a/pics/105. 从前序与中序遍历序列构造二叉树.png and /dev/null differ
diff --git a/pics/106. 从中序与后序遍历序列构造二叉树1.png b/pics/106. 从中序与后序遍历序列构造二叉树1.png
deleted file mode 100644
index ab8fa4b9..00000000
Binary files a/pics/106. 从中序与后序遍历序列构造二叉树1.png and /dev/null differ
diff --git a/pics/106.从中序与后序遍历序列构造二叉树.png b/pics/106.从中序与后序遍历序列构造二叉树.png
deleted file mode 100644
index 081a7813..00000000
Binary files a/pics/106.从中序与后序遍历序列构造二叉树.png and /dev/null differ
diff --git a/pics/106.从中序与后序遍历序列构造二叉树2.png b/pics/106.从中序与后序遍历序列构造二叉树2.png
deleted file mode 100644
index 8726f4ce..00000000
Binary files a/pics/106.从中序与后序遍历序列构造二叉树2.png and /dev/null differ
diff --git a/pics/107.二叉树的层次遍历II.png b/pics/107.二叉树的层次遍历II.png
deleted file mode 100644
index b4021c44..00000000
Binary files a/pics/107.二叉树的层次遍历II.png and /dev/null differ
diff --git a/pics/108.将有序数组转换为二叉搜索树.png b/pics/108.将有序数组转换为二叉搜索树.png
deleted file mode 100644
index 7d25f99d..00000000
Binary files a/pics/108.将有序数组转换为二叉搜索树.png and /dev/null differ
diff --git a/pics/110.平衡二叉树.png b/pics/110.平衡二叉树.png
deleted file mode 100644
index f227f1ad..00000000
Binary files a/pics/110.平衡二叉树.png and /dev/null differ
diff --git a/pics/110.平衡二叉树1.png b/pics/110.平衡二叉树1.png
deleted file mode 100644
index 36e0a09c..00000000
Binary files a/pics/110.平衡二叉树1.png and /dev/null differ
diff --git a/pics/110.平衡二叉树2.png b/pics/110.平衡二叉树2.png
deleted file mode 100644
index 53d46be6..00000000
Binary files a/pics/110.平衡二叉树2.png and /dev/null differ
diff --git a/pics/111.二叉树的最小深度.png b/pics/111.二叉树的最小深度.png
deleted file mode 100644
index b1980df8..00000000
Binary files a/pics/111.二叉树的最小深度.png and /dev/null differ
diff --git a/pics/111.二叉树的最小深度1.png b/pics/111.二叉树的最小深度1.png
deleted file mode 100644
index a0ac70cb..00000000
Binary files a/pics/111.二叉树的最小深度1.png and /dev/null differ
diff --git a/pics/112.路径总和.png b/pics/112.路径总和.png
deleted file mode 100644
index 2a1b5100..00000000
Binary files a/pics/112.路径总和.png and /dev/null differ
diff --git a/pics/112.路径总和1.png b/pics/112.路径总和1.png
deleted file mode 100644
index 4c6c0f60..00000000
Binary files a/pics/112.路径总和1.png and /dev/null differ
diff --git a/pics/113.路径总和II.png b/pics/113.路径总和II.png
deleted file mode 100644
index 931c2a9a..00000000
Binary files a/pics/113.路径总和II.png and /dev/null differ
diff --git a/pics/113.路径总和II1.png b/pics/113.路径总和II1.png
deleted file mode 100644
index e1d5a2d1..00000000
Binary files a/pics/113.路径总和II1.png and /dev/null differ
diff --git a/pics/116.填充每个节点的下一个右侧节点指针.png b/pics/116.填充每个节点的下一个右侧节点指针.png
deleted file mode 100644
index bec25c0a..00000000
Binary files a/pics/116.填充每个节点的下一个右侧节点指针.png and /dev/null differ
diff --git a/pics/1207.独一无二的出现次数.png b/pics/1207.独一无二的出现次数.png
deleted file mode 100644
index bbb036e6..00000000
Binary files a/pics/1207.独一无二的出现次数.png and /dev/null differ
diff --git a/pics/122.买卖股票的最佳时机II.png b/pics/122.买卖股票的最佳时机II.png
deleted file mode 100644
index 9799abfd..00000000
Binary files a/pics/122.买卖股票的最佳时机II.png and /dev/null differ
diff --git a/pics/123.买卖股票的最佳时机III.png b/pics/123.买卖股票的最佳时机III.png
deleted file mode 100644
index 1037b690..00000000
Binary files a/pics/123.买卖股票的最佳时机III.png and /dev/null differ
diff --git a/pics/127.单词接龙.png b/pics/127.单词接龙.png
deleted file mode 100644
index 581bb558..00000000
Binary files a/pics/127.单词接龙.png and /dev/null differ
diff --git a/pics/129.求根到叶子节点数字之和.png b/pics/129.求根到叶子节点数字之和.png
deleted file mode 100644
index 58288a9d..00000000
Binary files a/pics/129.求根到叶子节点数字之和.png and /dev/null differ
diff --git a/pics/131.分割回文串.png b/pics/131.分割回文串.png
deleted file mode 100644
index 0b50823f..00000000
Binary files a/pics/131.分割回文串.png and /dev/null differ
diff --git a/pics/134.加油站.png b/pics/134.加油站.png
deleted file mode 100644
index 120f714d..00000000
Binary files a/pics/134.加油站.png and /dev/null differ
diff --git a/pics/135.分发糖果.png b/pics/135.分发糖果.png
deleted file mode 100644
index cacd2cbe..00000000
Binary files a/pics/135.分发糖果.png and /dev/null differ
diff --git a/pics/135.分发糖果1.png b/pics/135.分发糖果1.png
deleted file mode 100644
index 27209df9..00000000
Binary files a/pics/135.分发糖果1.png and /dev/null differ
diff --git a/pics/1356.根据数字二进制下1的数目排序.png b/pics/1356.根据数字二进制下1的数目排序.png
deleted file mode 100644
index 0fca9fed..00000000
Binary files a/pics/1356.根据数字二进制下1的数目排序.png and /dev/null differ
diff --git a/pics/1365.有多少小于当前数字的数字.png b/pics/1365.有多少小于当前数字的数字.png
deleted file mode 100644
index 9d67d07b..00000000
Binary files a/pics/1365.有多少小于当前数字的数字.png and /dev/null differ
diff --git a/pics/142环形链表1.png b/pics/142环形链表1.png
deleted file mode 100644
index 7814be45..00000000
Binary files a/pics/142环形链表1.png and /dev/null differ
diff --git a/pics/142环形链表2.png b/pics/142环形链表2.png
deleted file mode 100644
index 86294647..00000000
Binary files a/pics/142环形链表2.png and /dev/null differ
diff --git a/pics/142环形链表3.png b/pics/142环形链表3.png
deleted file mode 100644
index 9bd96f6b..00000000
Binary files a/pics/142环形链表3.png and /dev/null differ
diff --git a/pics/142环形链表4.png b/pics/142环形链表4.png
deleted file mode 100644
index e37690d8..00000000
Binary files a/pics/142环形链表4.png and /dev/null differ
diff --git a/pics/142环形链表5.png b/pics/142环形链表5.png
deleted file mode 100644
index b99a79f1..00000000
Binary files a/pics/142环形链表5.png and /dev/null differ
diff --git a/pics/143.重排链表.png b/pics/143.重排链表.png
deleted file mode 100644
index 2fc94408..00000000
Binary files a/pics/143.重排链表.png and /dev/null differ
diff --git a/pics/147.对链表进行插入排序.png b/pics/147.对链表进行插入排序.png
deleted file mode 100644
index 807f66f4..00000000
Binary files a/pics/147.对链表进行插入排序.png and /dev/null differ
diff --git a/pics/151_翻转字符串里的单词.png b/pics/151_翻转字符串里的单词.png
deleted file mode 100644
index dc844950..00000000
Binary files a/pics/151_翻转字符串里的单词.png and /dev/null differ
diff --git a/pics/17. 电话号码的字母组合.jpeg b/pics/17. 电话号码的字母组合.jpeg
deleted file mode 100644
index f80ec767..00000000
Binary files a/pics/17. 电话号码的字母组合.jpeg and /dev/null differ
diff --git a/pics/17. 电话号码的字母组合.png b/pics/17. 电话号码的字母组合.png
deleted file mode 100644
index b11f7114..00000000
Binary files a/pics/17. 电话号码的字母组合.png and /dev/null differ
diff --git a/pics/19.删除链表的倒数第N个节点.png b/pics/19.删除链表的倒数第N个节点.png
deleted file mode 100644
index 6f6aa9c5..00000000
Binary files a/pics/19.删除链表的倒数第N个节点.png and /dev/null differ
diff --git a/pics/19.删除链表的倒数第N个节点1.png b/pics/19.删除链表的倒数第N个节点1.png
deleted file mode 100644
index cca947b4..00000000
Binary files a/pics/19.删除链表的倒数第N个节点1.png and /dev/null differ
diff --git a/pics/19.删除链表的倒数第N个节点2.png b/pics/19.删除链表的倒数第N个节点2.png
deleted file mode 100644
index 0d8144cd..00000000
Binary files a/pics/19.删除链表的倒数第N个节点2.png and /dev/null differ
diff --git a/pics/19.删除链表的倒数第N个节点3.png b/pics/19.删除链表的倒数第N个节点3.png
deleted file mode 100644
index d15d05e7..00000000
Binary files a/pics/19.删除链表的倒数第N个节点3.png and /dev/null differ
diff --git a/pics/199.二叉树的右视图.png b/pics/199.二叉树的右视图.png
deleted file mode 100644
index e5244117..00000000
Binary files a/pics/199.二叉树的右视图.png and /dev/null differ
diff --git a/pics/203_链表删除元素1.png b/pics/203_链表删除元素1.png
deleted file mode 100644
index b32aa50e..00000000
Binary files a/pics/203_链表删除元素1.png and /dev/null differ
diff --git a/pics/203_链表删除元素2.png b/pics/203_链表删除元素2.png
deleted file mode 100644
index 5519a69d..00000000
Binary files a/pics/203_链表删除元素2.png and /dev/null differ
diff --git a/pics/203_链表删除元素3.png b/pics/203_链表删除元素3.png
deleted file mode 100644
index cd50ce13..00000000
Binary files a/pics/203_链表删除元素3.png and /dev/null differ
diff --git a/pics/203_链表删除元素4.png b/pics/203_链表删除元素4.png
deleted file mode 100644
index 02aaf115..00000000
Binary files a/pics/203_链表删除元素4.png and /dev/null differ
diff --git a/pics/203_链表删除元素5.png b/pics/203_链表删除元素5.png
deleted file mode 100644
index e24ad3d3..00000000
Binary files a/pics/203_链表删除元素5.png and /dev/null differ
diff --git a/pics/203_链表删除元素6.png b/pics/203_链表删除元素6.png
deleted file mode 100644
index 13f9b6d6..00000000
Binary files a/pics/203_链表删除元素6.png and /dev/null differ
diff --git a/pics/206_反转链表.png b/pics/206_反转链表.png
deleted file mode 100644
index f26ad08f..00000000
Binary files a/pics/206_反转链表.png and /dev/null differ
diff --git a/pics/216.组合总和III.png b/pics/216.组合总和III.png
deleted file mode 100644
index 1b71e67c..00000000
Binary files a/pics/216.组合总和III.png and /dev/null differ
diff --git a/pics/216.组合总和III1.png b/pics/216.组合总和III1.png
deleted file mode 100644
index e495191d..00000000
Binary files a/pics/216.组合总和III1.png and /dev/null differ
diff --git a/pics/222.完全二叉树的节点个数.png b/pics/222.完全二叉树的节点个数.png
deleted file mode 100644
index 2eb1eb94..00000000
Binary files a/pics/222.完全二叉树的节点个数.png and /dev/null differ
diff --git a/pics/222.完全二叉树的节点个数1.png b/pics/222.完全二叉树的节点个数1.png
deleted file mode 100644
index 49e1772c..00000000
Binary files a/pics/222.完全二叉树的节点个数1.png and /dev/null differ
diff --git a/pics/226.翻转二叉树.png b/pics/226.翻转二叉树.png
deleted file mode 100644
index 1e3aec91..00000000
Binary files a/pics/226.翻转二叉树.png and /dev/null differ
diff --git a/pics/226.翻转二叉树1.png b/pics/226.翻转二叉树1.png
deleted file mode 100644
index 9435a12d..00000000
Binary files a/pics/226.翻转二叉树1.png and /dev/null differ
diff --git a/pics/234.回文链表.png b/pics/234.回文链表.png
deleted file mode 100644
index 285c73bb..00000000
Binary files a/pics/234.回文链表.png and /dev/null differ
diff --git a/pics/235.二叉搜索树的最近公共祖先.png b/pics/235.二叉搜索树的最近公共祖先.png
deleted file mode 100644
index 277b8165..00000000
Binary files a/pics/235.二叉搜索树的最近公共祖先.png and /dev/null differ
diff --git a/pics/236.二叉树的最近公共祖先.png b/pics/236.二叉树的最近公共祖先.png
deleted file mode 100644
index 023dd955..00000000
Binary files a/pics/236.二叉树的最近公共祖先.png and /dev/null differ
diff --git a/pics/236.二叉树的最近公共祖先1.png b/pics/236.二叉树的最近公共祖先1.png
deleted file mode 100644
index 4542ad5c..00000000
Binary files a/pics/236.二叉树的最近公共祖先1.png and /dev/null differ
diff --git a/pics/236.二叉树的最近公共祖先2.png b/pics/236.二叉树的最近公共祖先2.png
deleted file mode 100644
index 1681fbcc..00000000
Binary files a/pics/236.二叉树的最近公共祖先2.png and /dev/null differ
diff --git a/pics/239.滑动窗口最大值.png b/pics/239.滑动窗口最大值.png
deleted file mode 100644
index 49734e5d..00000000
Binary files a/pics/239.滑动窗口最大值.png and /dev/null differ
diff --git a/pics/24.两两交换链表中的节点.png b/pics/24.两两交换链表中的节点.png
deleted file mode 100644
index 3051c5a1..00000000
Binary files a/pics/24.两两交换链表中的节点.png and /dev/null differ
diff --git a/pics/24.两两交换链表中的节点1.png b/pics/24.两两交换链表中的节点1.png
deleted file mode 100644
index e79642c3..00000000
Binary files a/pics/24.两两交换链表中的节点1.png and /dev/null differ
diff --git a/pics/24.两两交换链表中的节点2.png b/pics/24.两两交换链表中的节点2.png
deleted file mode 100644
index e6dba912..00000000
Binary files a/pics/24.两两交换链表中的节点2.png and /dev/null differ
diff --git a/pics/24.两两交换链表中的节点3.png b/pics/24.两两交换链表中的节点3.png
deleted file mode 100644
index 7d706cd2..00000000
Binary files a/pics/24.两两交换链表中的节点3.png and /dev/null differ
diff --git a/pics/257.二叉树的所有路径.png b/pics/257.二叉树的所有路径.png
deleted file mode 100644
index 0a0683e0..00000000
Binary files a/pics/257.二叉树的所有路径.png and /dev/null differ
diff --git a/pics/257.二叉树的所有路径1.png b/pics/257.二叉树的所有路径1.png
deleted file mode 100644
index 97452f51..00000000
Binary files a/pics/257.二叉树的所有路径1.png and /dev/null differ
diff --git a/pics/26_封面.png b/pics/26_封面.png
deleted file mode 100644
index b8a2f1a1..00000000
Binary files a/pics/26_封面.png and /dev/null differ
diff --git a/pics/27_封面.png b/pics/27_封面.png
deleted file mode 100644
index a4a2b009..00000000
Binary files a/pics/27_封面.png and /dev/null differ
diff --git a/pics/31.下一个排列.png b/pics/31.下一个排列.png
deleted file mode 100644
index f88ef392..00000000
Binary files a/pics/31.下一个排列.png and /dev/null differ
diff --git a/pics/332.重新安排行程.png b/pics/332.重新安排行程.png
deleted file mode 100644
index 56f3ab02..00000000
Binary files a/pics/332.重新安排行程.png and /dev/null differ
diff --git a/pics/332.重新安排行程1.png b/pics/332.重新安排行程1.png
deleted file mode 100644
index 69d51882..00000000
Binary files a/pics/332.重新安排行程1.png and /dev/null differ
diff --git a/pics/347.前K个高频元素.png b/pics/347.前K个高频元素.png
deleted file mode 100644
index 54b1417d..00000000
Binary files a/pics/347.前K个高频元素.png and /dev/null differ
diff --git a/pics/35_封面.png b/pics/35_封面.png
deleted file mode 100644
index dc2971b5..00000000
Binary files a/pics/35_封面.png and /dev/null differ
diff --git a/pics/35_搜索插入位置.png b/pics/35_搜索插入位置.png
deleted file mode 100644
index 5fa65490..00000000
Binary files a/pics/35_搜索插入位置.png and /dev/null differ
diff --git a/pics/35_搜索插入位置2.png b/pics/35_搜索插入位置2.png
deleted file mode 100644
index 71fca151..00000000
Binary files a/pics/35_搜索插入位置2.png and /dev/null differ
diff --git a/pics/35_搜索插入位置3.png b/pics/35_搜索插入位置3.png
deleted file mode 100644
index ec1ce1eb..00000000
Binary files a/pics/35_搜索插入位置3.png and /dev/null differ
diff --git a/pics/35_搜索插入位置4.png b/pics/35_搜索插入位置4.png
deleted file mode 100644
index efb88e22..00000000
Binary files a/pics/35_搜索插入位置4.png and /dev/null differ
diff --git a/pics/35_搜索插入位置5.png b/pics/35_搜索插入位置5.png
deleted file mode 100644
index ec021c9d..00000000
Binary files a/pics/35_搜索插入位置5.png and /dev/null differ
diff --git a/pics/37.解数独.png b/pics/37.解数独.png
deleted file mode 100644
index 46b0a15a..00000000
Binary files a/pics/37.解数独.png and /dev/null differ
diff --git a/pics/376.摆动序列.png b/pics/376.摆动序列.png
deleted file mode 100644
index c6a06dfe..00000000
Binary files a/pics/376.摆动序列.png and /dev/null differ
diff --git a/pics/376.摆动序列1.png b/pics/376.摆动序列1.png
deleted file mode 100644
index 212e7722..00000000
Binary files a/pics/376.摆动序列1.png and /dev/null differ
diff --git a/pics/39.组合总和.png b/pics/39.组合总和.png
deleted file mode 100644
index 95430a66..00000000
Binary files a/pics/39.组合总和.png and /dev/null differ
diff --git a/pics/39.组合总和1.png b/pics/39.组合总和1.png
deleted file mode 100644
index 88f7635b..00000000
Binary files a/pics/39.组合总和1.png and /dev/null differ
diff --git a/pics/40.组合总和II.png b/pics/40.组合总和II.png
deleted file mode 100644
index 104e5f4e..00000000
Binary files a/pics/40.组合总和II.png and /dev/null differ
diff --git a/pics/40.组合总和II1.png b/pics/40.组合总和II1.png
deleted file mode 100644
index 75fda6b3..00000000
Binary files a/pics/40.组合总和II1.png and /dev/null differ
diff --git a/pics/404.左叶子之和.png b/pics/404.左叶子之和.png
deleted file mode 100644
index 81b6d8c2..00000000
Binary files a/pics/404.左叶子之和.png and /dev/null differ
diff --git a/pics/404.左叶子之和1.png b/pics/404.左叶子之和1.png
deleted file mode 100644
index 8c050e04..00000000
Binary files a/pics/404.左叶子之和1.png and /dev/null differ
diff --git a/pics/406.根据身高重建队列.png b/pics/406.根据身高重建队列.png
deleted file mode 100644
index 9ea8f0b2..00000000
Binary files a/pics/406.根据身高重建队列.png and /dev/null differ
diff --git a/pics/416.分割等和子集.png b/pics/416.分割等和子集.png
deleted file mode 100644
index 8d1b9ef6..00000000
Binary files a/pics/416.分割等和子集.png and /dev/null differ
diff --git a/pics/416.分割等和子集1.png b/pics/416.分割等和子集1.png
deleted file mode 100644
index 6be70dc6..00000000
Binary files a/pics/416.分割等和子集1.png and /dev/null differ
diff --git a/pics/42.接雨水1.png b/pics/42.接雨水1.png
deleted file mode 100644
index 26624f4b..00000000
Binary files a/pics/42.接雨水1.png and /dev/null differ
diff --git a/pics/42.接雨水2.png b/pics/42.接雨水2.png
deleted file mode 100644
index 94eda97e..00000000
Binary files a/pics/42.接雨水2.png and /dev/null differ
diff --git a/pics/42.接雨水3.png b/pics/42.接雨水3.png
deleted file mode 100644
index 1e4b528a..00000000
Binary files a/pics/42.接雨水3.png and /dev/null differ
diff --git a/pics/42.接雨水4.png b/pics/42.接雨水4.png
deleted file mode 100644
index a18539ce..00000000
Binary files a/pics/42.接雨水4.png and /dev/null differ
diff --git a/pics/42.接雨水5.png b/pics/42.接雨水5.png
deleted file mode 100644
index 066792b0..00000000
Binary files a/pics/42.接雨水5.png and /dev/null differ
diff --git a/pics/429. N叉树的层序遍历.png b/pics/429. N叉树的层序遍历.png
deleted file mode 100644
index d28c543c..00000000
Binary files a/pics/429. N叉树的层序遍历.png and /dev/null differ
diff --git a/pics/435.无重叠区间.png b/pics/435.无重叠区间.png
deleted file mode 100644
index a45913c1..00000000
Binary files a/pics/435.无重叠区间.png and /dev/null differ
diff --git a/pics/45.跳跃游戏II.png b/pics/45.跳跃游戏II.png
deleted file mode 100644
index 77130cb2..00000000
Binary files a/pics/45.跳跃游戏II.png and /dev/null differ
diff --git a/pics/45.跳跃游戏II1.png b/pics/45.跳跃游戏II1.png
deleted file mode 100644
index 7850187f..00000000
Binary files a/pics/45.跳跃游戏II1.png and /dev/null differ
diff --git a/pics/45.跳跃游戏II2.png b/pics/45.跳跃游戏II2.png
deleted file mode 100644
index aa45f60a..00000000
Binary files a/pics/45.跳跃游戏II2.png and /dev/null differ
diff --git a/pics/452.用最少数量的箭引爆气球.png b/pics/452.用最少数量的箭引爆气球.png
deleted file mode 100644
index 64080914..00000000
Binary files a/pics/452.用最少数量的箭引爆气球.png and /dev/null differ
diff --git a/pics/455.分发饼干.png b/pics/455.分发饼干.png
deleted file mode 100644
index 17e15e09..00000000
Binary files a/pics/455.分发饼干.png and /dev/null differ
diff --git a/pics/459.重复的子字符串_1.png b/pics/459.重复的子字符串_1.png
deleted file mode 100644
index 2feddd6b..00000000
Binary files a/pics/459.重复的子字符串_1.png and /dev/null differ
diff --git a/pics/46.全排列.png b/pics/46.全排列.png
deleted file mode 100644
index d8c484ec..00000000
Binary files a/pics/46.全排列.png and /dev/null differ
diff --git a/pics/463.岛屿的周长.png b/pics/463.岛屿的周长.png
deleted file mode 100644
index 5b0fa013..00000000
Binary files a/pics/463.岛屿的周长.png and /dev/null differ
diff --git a/pics/463.岛屿的周长1.png b/pics/463.岛屿的周长1.png
deleted file mode 100644
index bb14dbd6..00000000
Binary files a/pics/463.岛屿的周长1.png and /dev/null differ
diff --git a/pics/47.全排列II1.png b/pics/47.全排列II1.png
deleted file mode 100644
index 8160dd86..00000000
Binary files a/pics/47.全排列II1.png and /dev/null differ
diff --git a/pics/47.全排列II2.png b/pics/47.全排列II2.png
deleted file mode 100644
index d2e096b1..00000000
Binary files a/pics/47.全排列II2.png and /dev/null differ
diff --git a/pics/47.全排列II3.png b/pics/47.全排列II3.png
deleted file mode 100644
index b6f5a862..00000000
Binary files a/pics/47.全排列II3.png and /dev/null differ
diff --git a/pics/486.预测赢家.png b/pics/486.预测赢家.png
deleted file mode 100644
index 03ddfaa8..00000000
Binary files a/pics/486.预测赢家.png and /dev/null differ
diff --git a/pics/486.预测赢家1.png b/pics/486.预测赢家1.png
deleted file mode 100644
index dbddef26..00000000
Binary files a/pics/486.预测赢家1.png and /dev/null differ
diff --git a/pics/486.预测赢家2.png b/pics/486.预测赢家2.png
deleted file mode 100644
index 7d26de9a..00000000
Binary files a/pics/486.预测赢家2.png and /dev/null differ
diff --git a/pics/486.预测赢家3.png b/pics/486.预测赢家3.png
deleted file mode 100644
index 506778c4..00000000
Binary files a/pics/486.预测赢家3.png and /dev/null differ
diff --git a/pics/486.预测赢家4.png b/pics/486.预测赢家4.png
deleted file mode 100644
index 8a679b74..00000000
Binary files a/pics/486.预测赢家4.png and /dev/null differ
diff --git a/pics/491. 递增子序列1.png b/pics/491. 递增子序列1.png
deleted file mode 100644
index 19da907e..00000000
Binary files a/pics/491. 递增子序列1.png and /dev/null differ
diff --git a/pics/491. 递增子序列2.png b/pics/491. 递增子序列2.png
deleted file mode 100644
index 24988010..00000000
Binary files a/pics/491. 递增子序列2.png and /dev/null differ
diff --git a/pics/491. 递增子序列3.png b/pics/491. 递增子序列3.png
deleted file mode 100644
index df293dd5..00000000
Binary files a/pics/491. 递增子序列3.png and /dev/null differ
diff --git a/pics/491. 递增子序列4.png b/pics/491. 递增子序列4.png
deleted file mode 100644
index 395fc515..00000000
Binary files a/pics/491. 递增子序列4.png and /dev/null differ
diff --git a/pics/501.二叉搜索树中的众数.png b/pics/501.二叉搜索树中的众数.png
deleted file mode 100644
index a7197b08..00000000
Binary files a/pics/501.二叉搜索树中的众数.png and /dev/null differ
diff --git a/pics/501.二叉搜索树中的众数1.png b/pics/501.二叉搜索树中的众数1.png
deleted file mode 100644
index 200bc2fa..00000000
Binary files a/pics/501.二叉搜索树中的众数1.png and /dev/null differ
diff --git a/pics/51.N皇后.png b/pics/51.N皇后.png
deleted file mode 100644
index 730b7cb8..00000000
Binary files a/pics/51.N皇后.png and /dev/null differ
diff --git a/pics/51.N皇后1.png b/pics/51.N皇后1.png
deleted file mode 100644
index e6c9c72d..00000000
Binary files a/pics/51.N皇后1.png and /dev/null differ
diff --git a/pics/513.找树左下角的值.png b/pics/513.找树左下角的值.png
deleted file mode 100644
index 67bda96f..00000000
Binary files a/pics/513.找树左下角的值.png and /dev/null differ
diff --git a/pics/513.找树左下角的值1.png b/pics/513.找树左下角的值1.png
deleted file mode 100644
index a5421ad6..00000000
Binary files a/pics/513.找树左下角的值1.png and /dev/null differ
diff --git a/pics/515.在每个树行中找最大值.png b/pics/515.在每个树行中找最大值.png
deleted file mode 100644
index e8f2f431..00000000
Binary files a/pics/515.在每个树行中找最大值.png and /dev/null differ
diff --git a/pics/530.二叉搜索树的最小绝对差.png b/pics/530.二叉搜索树的最小绝对差.png
deleted file mode 100644
index 04ca9a65..00000000
Binary files a/pics/530.二叉搜索树的最小绝对差.png and /dev/null differ
diff --git a/pics/538.把二叉搜索树转换为累加树.png b/pics/538.把二叉搜索树转换为累加树.png
deleted file mode 100644
index 27077f7b..00000000
Binary files a/pics/538.把二叉搜索树转换为累加树.png and /dev/null differ
diff --git a/pics/541_反转字符串II.png b/pics/541_反转字符串II.png
deleted file mode 100644
index 45f0ce6c..00000000
Binary files a/pics/541_反转字符串II.png and /dev/null differ
diff --git a/pics/55.跳跃游戏.png b/pics/55.跳跃游戏.png
deleted file mode 100644
index 012bb635..00000000
Binary files a/pics/55.跳跃游戏.png and /dev/null differ
diff --git a/pics/559.N叉树的最大深度.png b/pics/559.N叉树的最大深度.png
deleted file mode 100644
index d28c543c..00000000
Binary files a/pics/559.N叉树的最大深度.png and /dev/null differ
diff --git a/pics/56.合并区间.png b/pics/56.合并区间.png
deleted file mode 100644
index ff905c72..00000000
Binary files a/pics/56.合并区间.png and /dev/null differ
diff --git a/pics/57.插入区间.png b/pics/57.插入区间.png
deleted file mode 100644
index 67290167..00000000
Binary files a/pics/57.插入区间.png and /dev/null differ
diff --git a/pics/57.插入区间1.png b/pics/57.插入区间1.png
deleted file mode 100644
index 69835dee..00000000
Binary files a/pics/57.插入区间1.png and /dev/null differ
diff --git a/pics/59_封面.png b/pics/59_封面.png
deleted file mode 100644
index 795e8f04..00000000
Binary files a/pics/59_封面.png and /dev/null differ
diff --git a/pics/617.合并二叉树.png b/pics/617.合并二叉树.png
deleted file mode 100644
index 182f959c..00000000
Binary files a/pics/617.合并二叉树.png and /dev/null differ
diff --git a/pics/62.不同路径.png b/pics/62.不同路径.png
deleted file mode 100644
index d82c6ed0..00000000
Binary files a/pics/62.不同路径.png and /dev/null differ
diff --git a/pics/62.不同路径1.png b/pics/62.不同路径1.png
deleted file mode 100644
index 0d84838d..00000000
Binary files a/pics/62.不同路径1.png and /dev/null differ
diff --git a/pics/62.不同路径2.png b/pics/62.不同路径2.png
deleted file mode 100644
index 91984901..00000000
Binary files a/pics/62.不同路径2.png and /dev/null differ
diff --git a/pics/637.二叉树的层平均值.png b/pics/637.二叉树的层平均值.png
deleted file mode 100644
index 57018dab..00000000
Binary files a/pics/637.二叉树的层平均值.png and /dev/null differ
diff --git a/pics/654.最大二叉树.png b/pics/654.最大二叉树.png
deleted file mode 100644
index e8fc63aa..00000000
Binary files a/pics/654.最大二叉树.png and /dev/null differ
diff --git a/pics/657.机器人能否返回原点.png b/pics/657.机器人能否返回原点.png
deleted file mode 100644
index 6ea5b69b..00000000
Binary files a/pics/657.机器人能否返回原点.png and /dev/null differ
diff --git a/pics/669.修剪二叉搜索树.png b/pics/669.修剪二叉搜索树.png
deleted file mode 100644
index 89fe4104..00000000
Binary files a/pics/669.修剪二叉搜索树.png and /dev/null differ
diff --git a/pics/669.修剪二叉搜索树1.png b/pics/669.修剪二叉搜索树1.png
deleted file mode 100644
index 1b46e8d0..00000000
Binary files a/pics/669.修剪二叉搜索树1.png and /dev/null differ
diff --git a/pics/685.冗余连接II1.png b/pics/685.冗余连接II1.png
deleted file mode 100644
index ab833087..00000000
Binary files a/pics/685.冗余连接II1.png and /dev/null differ
diff --git a/pics/685.冗余连接II2.png b/pics/685.冗余连接II2.png
deleted file mode 100644
index 6dbb2ac7..00000000
Binary files a/pics/685.冗余连接II2.png and /dev/null differ
diff --git a/pics/700.二叉搜索树中的搜索.png b/pics/700.二叉搜索树中的搜索.png
deleted file mode 100644
index 1fd15466..00000000
Binary files a/pics/700.二叉搜索树中的搜索.png and /dev/null differ
diff --git a/pics/700.二叉搜索树中的搜索1.png b/pics/700.二叉搜索树中的搜索1.png
deleted file mode 100644
index 037627b1..00000000
Binary files a/pics/700.二叉搜索树中的搜索1.png and /dev/null differ
diff --git a/pics/763.划分字母区间.png b/pics/763.划分字母区间.png
deleted file mode 100644
index 45d1b93c..00000000
Binary files a/pics/763.划分字母区间.png and /dev/null differ
diff --git a/pics/77.组合.png b/pics/77.组合.png
deleted file mode 100644
index 17cde493..00000000
Binary files a/pics/77.组合.png and /dev/null differ
diff --git a/pics/77.组合1.png b/pics/77.组合1.png
deleted file mode 100644
index a6a4a272..00000000
Binary files a/pics/77.组合1.png and /dev/null differ
diff --git a/pics/77.组合2.png b/pics/77.组合2.png
deleted file mode 100644
index 94e305b6..00000000
Binary files a/pics/77.组合2.png and /dev/null differ
diff --git a/pics/77.组合3.png b/pics/77.组合3.png
deleted file mode 100644
index 4ba73549..00000000
Binary files a/pics/77.组合3.png and /dev/null differ
diff --git a/pics/77.组合4.png b/pics/77.组合4.png
deleted file mode 100644
index b2519ccd..00000000
Binary files a/pics/77.组合4.png and /dev/null differ
diff --git a/pics/78.子集.png b/pics/78.子集.png
deleted file mode 100644
index 1700030f..00000000
Binary files a/pics/78.子集.png and /dev/null differ
diff --git a/pics/841.钥匙和房间.png b/pics/841.钥匙和房间.png
deleted file mode 100644
index 3bfdeea4..00000000
Binary files a/pics/841.钥匙和房间.png and /dev/null differ
diff --git a/pics/90.子集II.png b/pics/90.子集II.png
deleted file mode 100644
index 972010f6..00000000
Binary files a/pics/90.子集II.png and /dev/null differ
diff --git a/pics/90.子集II1.png b/pics/90.子集II1.png
deleted file mode 100644
index 92a18238..00000000
Binary files a/pics/90.子集II1.png and /dev/null differ
diff --git a/pics/90.子集II2.png b/pics/90.子集II2.png
deleted file mode 100644
index e42a56f7..00000000
Binary files a/pics/90.子集II2.png and /dev/null differ
diff --git a/pics/925.长按键入.png b/pics/925.长按键入.png
deleted file mode 100644
index c6bee552..00000000
Binary files a/pics/925.长按键入.png and /dev/null differ
diff --git a/pics/93.复原IP地址.png b/pics/93.复原IP地址.png
deleted file mode 100644
index 63d11f2e..00000000
Binary files a/pics/93.复原IP地址.png and /dev/null differ
diff --git a/pics/941.有效的山脉数组.png b/pics/941.有效的山脉数组.png
deleted file mode 100644
index e261242c..00000000
Binary files a/pics/941.有效的山脉数组.png and /dev/null differ
diff --git a/pics/968.监控二叉树1.png b/pics/968.监控二叉树1.png
deleted file mode 100644
index 7e6a75df..00000000
Binary files a/pics/968.监控二叉树1.png and /dev/null differ
diff --git a/pics/968.监控二叉树2.png b/pics/968.监控二叉树2.png
deleted file mode 100644
index 664a656e..00000000
Binary files a/pics/968.监控二叉树2.png and /dev/null differ
diff --git a/pics/968.监控二叉树3.png b/pics/968.监控二叉树3.png
deleted file mode 100644
index 0a3a9ea6..00000000
Binary files a/pics/968.监控二叉树3.png and /dev/null differ
diff --git a/pics/977.有序数组的平方.png b/pics/977.有序数组的平方.png
deleted file mode 100644
index cb9ccf6c..00000000
Binary files a/pics/977.有序数组的平方.png and /dev/null differ
diff --git a/pics/98.验证二叉搜索树.png b/pics/98.验证二叉搜索树.png
deleted file mode 100644
index 8a164140..00000000
Binary files a/pics/98.验证二叉搜索树.png and /dev/null differ
diff --git a/pics/leetcode_209.png b/pics/leetcode_209.png
deleted file mode 100644
index 2278be41..00000000
Binary files a/pics/leetcode_209.png and /dev/null differ
diff --git a/pics/剑指Offer05.替换空格.png b/pics/剑指Offer05.替换空格.png
deleted file mode 100644
index e4a2dfbc..00000000
Binary files a/pics/剑指Offer05.替换空格.png and /dev/null differ
diff --git a/pics/剑指Offer58-II.左旋转字符串.png b/pics/剑指Offer58-II.左旋转字符串.png
deleted file mode 100644
index 9b41754e..00000000
Binary files a/pics/剑指Offer58-II.左旋转字符串.png and /dev/null differ
diff --git a/pics/动态规划-背包问题1.png b/pics/动态规划-背包问题1.png
deleted file mode 100644
index 0dada375..00000000
Binary files a/pics/动态规划-背包问题1.png and /dev/null differ
diff --git a/pics/动态规划-背包问题2.png b/pics/动态规划-背包问题2.png
deleted file mode 100644
index ca639197..00000000
Binary files a/pics/动态规划-背包问题2.png and /dev/null differ
diff --git a/pics/动态规划-背包问题3.png b/pics/动态规划-背包问题3.png
deleted file mode 100644
index f56f316d..00000000
Binary files a/pics/动态规划-背包问题3.png and /dev/null differ
diff --git a/pics/动态规划-背包问题4.png b/pics/动态规划-背包问题4.png
deleted file mode 100644
index 8b26e102..00000000
Binary files a/pics/动态规划-背包问题4.png and /dev/null differ
diff --git a/pics/动态规划-背包问题5.png b/pics/动态规划-背包问题5.png
deleted file mode 100644
index f35fa67d..00000000
Binary files a/pics/动态规划-背包问题5.png and /dev/null differ
diff --git a/pics/动态规划-背包问题6.png b/pics/动态规划-背包问题6.png
deleted file mode 100644
index f1017f19..00000000
Binary files a/pics/动态规划-背包问题6.png and /dev/null differ
diff --git a/pics/回溯算法理论基础.png b/pics/回溯算法理论基础.png
deleted file mode 100644
index f8f2eb2f..00000000
Binary files a/pics/回溯算法理论基础.png and /dev/null differ
diff --git a/pics/我要打十个.gif b/pics/我要打十个.gif
deleted file mode 100644
index c64eb70a..00000000
Binary files a/pics/我要打十个.gif and /dev/null differ
diff --git a/pics/螺旋矩阵.png b/pics/螺旋矩阵.png
deleted file mode 100644
index 5148db46..00000000
Binary files a/pics/螺旋矩阵.png and /dev/null differ
diff --git a/pics/面试题02.07.链表相交_1.png b/pics/面试题02.07.链表相交_1.png
deleted file mode 100644
index 678311d1..00000000
Binary files a/pics/面试题02.07.链表相交_1.png and /dev/null differ
diff --git a/pics/面试题02.07.链表相交_2.png b/pics/面试题02.07.链表相交_2.png
deleted file mode 100644
index 97881bec..00000000
Binary files a/pics/面试题02.07.链表相交_2.png and /dev/null differ
diff --git a/problems/0001.两数之和.md b/problems/0001.两数之和.md
deleted file mode 100644
index b7c9831b..00000000
--- a/problems/0001.两数之和.md
+++ /dev/null
@@ -1,137 +0,0 @@
-# 题目地址
-https://leetcode-cn.com/problems/two-sum/
-
-> 只用数组和set还是不够的!
-
-# 第1题. 两数之和
-
-给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
-
-你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
-
-**示例:**
-
-给定 nums = [2, 7, 11, 15], target = 9
-
-因为 nums[0] + nums[1] = 2 + 7 = 9
-
-所以返回 [0, 1]
-
-
-# 思路
-
-很明显暴力的解法是两层for循环查找,时间复杂度是O(n^2)。
-
-建议大家做这道题目之前,先做一下这两道
-* [242. 有效的字母异位词](https://mp.weixin.qq.com/s/vM6OszkM6L1Mx2Ralm9Dig)
-* [349. 两个数组的交集](https://mp.weixin.qq.com/s/N9iqAchXreSVW7zXUS4BVA)
-
-[242. 有效的字母异位词](https://mp.weixin.qq.com/s/vM6OszkM6L1Mx2Ralm9Dig) 这道题目是用数组作为哈希表来解决哈希问题,[349. 两个数组的交集](https://mp.weixin.qq.com/s/N9iqAchXreSVW7zXUS4BVA)这道题目是通过set作为哈希表来解决哈希问题。
-
-本题呢,则要使用map,那么来看一下使用数组和set来做哈希法的局限。
-
-* 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
-* set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下表位置,因为要返回x 和 y的下表。所以set 也不能用。
-
-此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value在保存数值所在的下表。
-
-C++中map,有三种类型:
-
-|映射 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率|
-|---|---| --- |---| --- | --- | ---|
-|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | O(logn)|O(logn) |
-|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|O(logn) |O(logn) |
-|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |O(1) | O(1)|
-
-std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。
-
-同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。 更多哈希表的理论知识请看[关于哈希表,你该了解这些!](https://mp.weixin.qq.com/s/g8N6WmoQmsCUw3_BaWxHZA)。
-
-**这道题目中并不需要key有序,选择std::unordered_map 效率更高!**
-
-解题思路动画如下:
-
-
-
-# C++代码
-
-```
-class Solution {
-public:
- vector twoSum(vector& nums, int target) {
- std::unordered_map map;
- for(int i = 0; i < nums.size(); i++) {
- auto iter = map.find(target - nums[i]);
- if(iter != map.end()) {
- return {iter->second, i};
- }
- map.insert(pair(nums[i], i));
- }
- return {};
- }
-};
-```
-
-## 一般解法
-
-代码:
-
-```C++
-```
-
-## 优化解法
-
-```C++
-class Solution {
-public:
- vector twoSum(vector& nums, int target) {
- for (int i = 0; i < nums.size(); i ++) {
- for (int j = i + 1; j < nums.size(); j++) {
- if (nums[i] + nums[j] == target) {
- return {i, j};
- }
- }
- }
- return {};
- }
-};
-
-```
-
-```
-class Solution {
-public:
- vector twoSum(vector& nums, int target) {
- std::map map;
- for(int i = 0; i < nums.size(); i++) {
- auto iter = map.find(target - nums[i]);
- if(iter != map.end()) {
- return {iter->second,i};
- }
- map.insert({nums, i});
- }
- return {};
- }
-};
-```
-
-```
-class Solution {
-public:
- vector twoSum(vector& nums, int target) {
- std::unordered_map map;
- for(int i = 0; i < nums.size(); i++) {
- auto iter = map.find(target - nums[i]);
- if(iter != map.end()) {
- return {iter->second, i};
- break;
- }
- map.emplace(nums[i], i);
- }
- return {};
- }
-};
-```
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0015.三数之和.md b/problems/0015.三数之和.md
deleted file mode 100644
index c437cadb..00000000
--- a/problems/0015.三数之和.md
+++ /dev/null
@@ -1,166 +0,0 @@
-# 题目地址
-https://leetcode-cn.com/problems/3sum/
-
-> 用哈希表解决了[两数之和](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ),那么三数之和呢?
-
-# 第15题. 三数之和
-
-给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
-
-**注意:** 答案中不可以包含重复的三元组。
-
-示例:
-
-给定数组 nums = [-1, 0, 1, 2, -1, -4],
-
-满足要求的三元组集合为:
-[
- [-1, 0, 1],
- [-1, -1, 2]
-]
-
-
-# 思路
-
-**注意[0, 0, 0, 0] 这组数据**
-
-## 哈希解法
-
-两层for循环就可以确定 a 和b 的数值了,可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
-
-把符合条件的三元组放进vector中,然后在去去重,这样是非常费时的,很容易超时,也是这道题目通过率如此之低的根源所在。
-
-去重的过程不好处理,有很多小细节,如果在面试中很难想到位。
-
-时间复杂度可以做到O(n^2),但还是比较费时的,因为不好做剪枝操作。
-
-大家可以尝试使用哈希法写一写,就知道其困难的程度了。
-
-## 哈希法C++代码
-```
-class Solution {
-public:
- vector> threeSum(vector& nums) {
- vector> result;
- sort(nums.begin(), nums.end());
- // 找出a + b + c = 0
- // a = nums[i], b = nums[j], c = -(a + b)
- for (int i = 0; i < nums.size(); i++) {
- // 排序之后如果第一个元素已经大于零,那么不可能凑成三元组
- if (nums[i] > 0) {
- continue;
- }
- if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重
- continue;
- }
- unordered_set set;
- for (int j = i + 1; j < nums.size(); j++) {
- if (j > i + 2
- && nums[j] == nums[j-1]
- && nums[j-1] == nums[j-2]) { // 三元组元素b去重
- continue;
- }
- int c = 0 - (nums[i] + nums[j]);
- if (set.find(c) != set.end()) {
- result.push_back({nums[i], nums[j], c});
- set.erase(c);// 三元组元素c去重
- } else {
- set.insert(nums[j]);
- }
- }
- }
- return result;
- }
-};
-```
-
-## 双指针
-
-**其实这道题目使用哈希法并不十分合适**,因为在去重的操作中有很多细节需要注意,在面试中很难直接写出没有bug的代码。
-
-而且使用哈希法 在使用两层for循环的时候,能做的剪枝操作很有限,虽然时间复杂度是O(n^2),也是可以在leetcode上通过,但是程序的执行时间依然比较长 。
-
-接下来我来介绍另一个解法:双指针法,**这道题目使用双指针法 要比哈希法高效一些**,那么来讲解一下具体实现的思路。
-
-动画效果如下:
-
-
-
-拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下表0的地方开始,同时定一个下表left 定义在i+1的位置上,定义下表right 在数组结尾的位置上。
-
-依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。
-
-接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下表就应该向左移动,这样才能让三数之和小一些。
-
-如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
-
-时间复杂度:O(n^2)。
-
-
-## 双指针法C++代码
-
-```
-class Solution {
-public:
- vector> threeSum(vector& nums) {
- vector> result;
- sort(nums.begin(), nums.end());
- // 找出a + b + c = 0
- // a = nums[i], b = nums[left], c = nums[right]
- for (int i = 0; i < nums.size(); i++) {
- // 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了
- if (nums[i] > 0) {
- return result;
- }
- // 错误去重方法,将会漏掉-1,-1,2 这种情况
- /*
- if (nums[i] == nums[i + 1]) {
- continue;
- }
- */
- // 正确去重方法
- if (i > 0 && nums[i] == nums[i - 1]) {
- continue;
- }
- int left = i + 1;
- int right = nums.size() - 1;
- while (right > left) {
- // 去重复逻辑如果放在这里,0,0,0 的情况,可能直接导致 right<=left 了,从而漏掉了 0,0,0 这种三元组
- /*
- while (right > left && nums[right] == nums[right - 1]) right--;
- while (right > left && nums[left] == nums[left + 1]) left++;
- */
- if (nums[i] + nums[left] + nums[right] > 0) {
- right--;
- } else if (nums[i] + nums[left] + nums[right] < 0) {
- left++;
- } else {
- result.push_back(vector{nums[i], nums[left], nums[right]});
- // 去重逻辑应该放在找到一个三元组之后
- while (right > left && nums[right] == nums[right - 1]) right--;
- while (right > left && nums[left] == nums[left + 1]) left++;
-
- // 找到答案时,双指针同时收缩
- right--;
- left++;
- }
- }
-
- }
- return result;
- }
-};
-```
-
-# 思考题
-
-既然三数之和可以使用双指针法,我们之前讲过的[两数之和](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ),可不可以使用双指针法呢?
-
-如果不能,题意如何更改就可以使用双指针法呢? **大家留言说出自己的想法吧!**
-
-两数之和 就不能使用双指针法,因为[两数之和](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ)要求返回的是索引下表, 而双指针法一定要排序,一旦排序之后原数组的索引就被改变了。
-
-如果[两数之和](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ)要求返回的是数值的话,就可以使用双指针法了。
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0017.电话号码的字母组合.md b/problems/0017.电话号码的字母组合.md
deleted file mode 100644
index e6d28496..00000000
--- a/problems/0017.电话号码的字母组合.md
+++ /dev/null
@@ -1,235 +0,0 @@
-
-> 多个集合求组合问题。
-
-# 17.电话号码的字母组合
-
-题目链接:https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
-
-给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
-
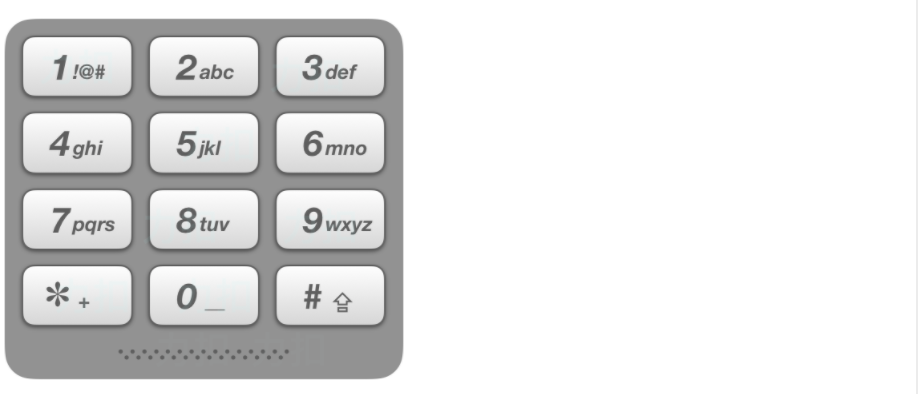
-给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
-
-
-
-示例:
-输入:"23"
-输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
-
-说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
-
-# 思路
-
-从示例上来说,输入"23",最直接的想法就是两层for循环遍历了吧,正好把组合的情况都输出了。
-
-如果输入"233"呢,那么就三层for循环,如果"2333"呢,就四层for循环.......
-
-大家应该感觉出和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)遇到的一样的问题,就是这for循环的层数如何写出来,此时又是回溯法登场的时候了。
-
-理解本题后,要解决如下三个问题:
-
-1. 数字和字母如何映射
-2. 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
-3. 输入1 * #按键等等异常情况
-
-## 数字和字母如何映射
-
-可以使用map或者定义一个二位数组,例如:string letterMap[10],来做映射,我这里定义一个二维数组,代码如下:
-
-```
-const string letterMap[10] = {
- "", // 0
- "", // 1
- "abc", // 2
- "def", // 3
- "ghi", // 4
- "jkl", // 5
- "mno", // 6
- "pqrs", // 7
- "tuv", // 8
- "wxyz", // 9
-};
-```
-
-## 回溯法来解决n个for循环的问题
-
-对于回溯法还不了解的同学看这篇:[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)
-
-
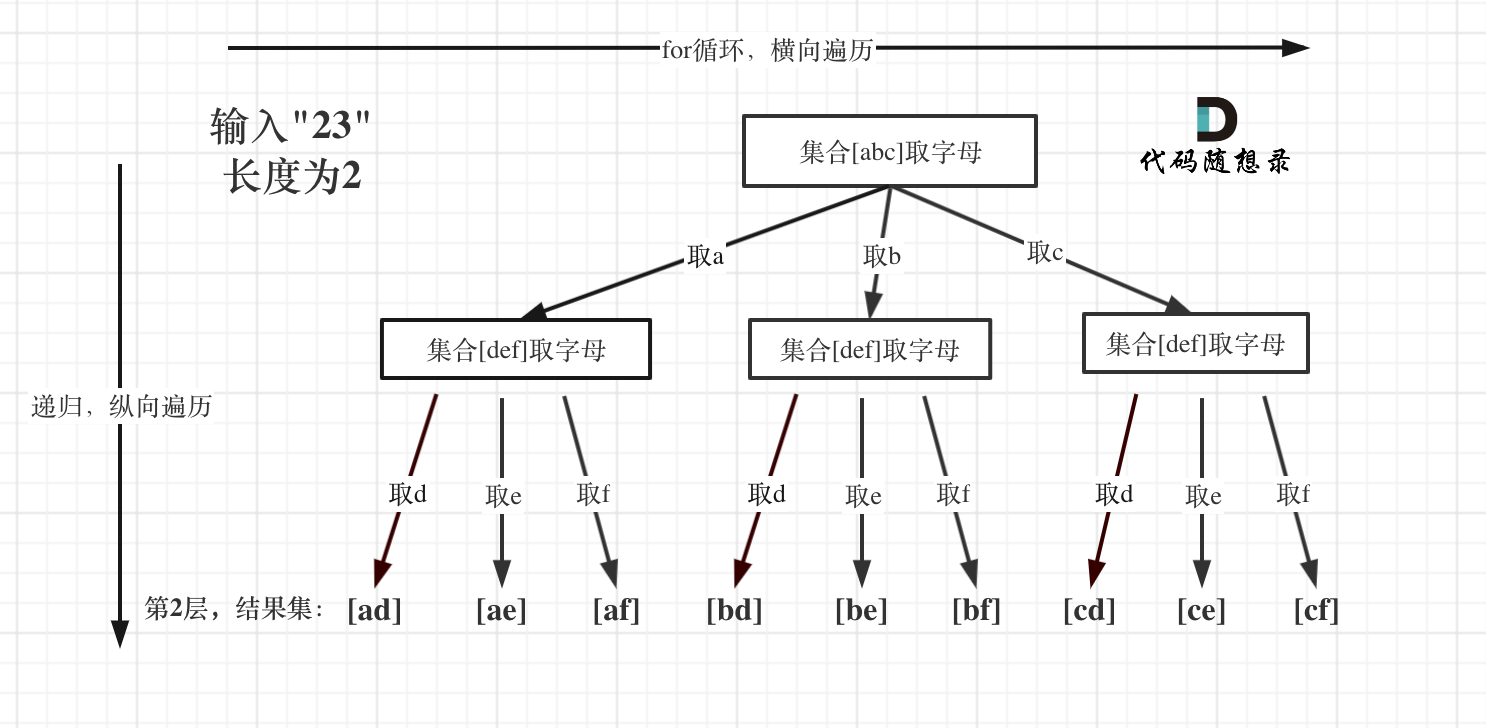
-例如:输入:"23",抽象为树形结构,如图所示:
-
-
-
-图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
-
-回溯三部曲:
-
-* 确定回溯函数参数
-
-首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
-
-再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
-
-注意这个index可不是 [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中的startIndex了。
-
-这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
-
-代码如下:
-
-```
-vector result;
-string s;
-void backtracking(const string& digits, int index)
-```
-
-* 确定终止条件
-
-例如输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
-
-那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
-
-然后收集结果,结束本层递归。
-
-代码如下:
-
-```
-if (index == digits.size()) {
- result.push_back(s);
- return;
-}
-```
-
-* 确定单层遍历逻辑
-
-首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
-
-然后for循环来处理这个字符集,代码如下:
-
-```
-int digit = digits[index] - '0'; // 将index指向的数字转为int
-string letters = letterMap[digit]; // 取数字对应的字符集
-for (int i = 0; i < letters.size(); i++) {
- s.push_back(letters[i]); // 处理
- backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
- s.pop_back(); // 回溯
-}
-```
-
-**注意这里for循环,可不像是在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中从startIndex开始遍历的**。
-
-**因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)都是是求同一个集合中的组合!**
-
-
-## 输入1 * #按键等等异常情况
-
-代码中最好考虑这些异常情况,但题目的测试数据中应该没有异常情况的数据,所以我就没有加了。
-
-**但是要知道会有这些异常,如果是现场面试中,一定要考虑到!**
-
-
-# C++代码
-关键地方都讲完了,按照[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中的回溯法模板,不难写出如下C++代码:
-
-
-```
-// 版本一
-class Solution {
-private:
- const string letterMap[10] = {
- "", // 0
- "", // 1
- "abc", // 2
- "def", // 3
- "ghi", // 4
- "jkl", // 5
- "mno", // 6
- "pqrs", // 7
- "tuv", // 8
- "wxyz", // 9
- };
-public:
- vector result;
- string s;
- void backtracking(const string& digits, int index) {
- if (index == digits.size()) {
- result.push_back(s);
- return;
- }
- int digit = digits[index] - '0'; // 将index指向的数字转为int
- string letters = letterMap[digit]; // 取数字对应的字符集
- for (int i = 0; i < letters.size(); i++) {
- s.push_back(letters[i]); // 处理
- backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
- s.pop_back(); // 回溯
- }
- }
- vector letterCombinations(string digits) {
- s.clear();
- result.clear();
- if (digits.size() == 0) {
- return result;
- }
- backtracking(digits, 0);
- return result;
- }
-};
-```
-
-一些写法,是把回溯的过程放在递归函数里了,例如如下代码,我可以写成这样:(注意注释中不一样的地方)
-
-```
-// 版本二
-class Solution {
-private:
- const string letterMap[10] = {
- "", // 0
- "", // 1
- "abc", // 2
- "def", // 3
- "ghi", // 4
- "jkl", // 5
- "mno", // 6
- "pqrs", // 7
- "tuv", // 8
- "wxyz", // 9
- };
-public:
- vector result;
- void getCombinations(const string& digits, int index, const string& s) { // 注意参数的不同
- if (index == digits.size()) {
- result.push_back(s);
- return;
- }
- int digit = digits[index] - '0';
- string letters = letterMap[digit];
- for (int i = 0; i < letters.size(); i++) {
- getCombinations(digits, index + 1, s + letters[i]); // 注意这里的不同
- }
- }
- vector letterCombinations(string digits) {
- result.clear();
- if (digits.size() == 0) {
- return result;
- }
- getCombinations(digits, 0, "");
- return result;
-
- }
-};
-```
-
-我不建议把回溯藏在递归的参数里这种写法,很不直观,我在[二叉树:以为使用了递归,其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)这篇文章中也深度分析了,回溯隐藏在了哪里。
-
-所以大家可以按照版本一来写就可以了。
-
-# 总结
-
-本篇将题目的三个要点一一列出,并重点强调了和前面讲解过的[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)的区别,本题是多个集合求组合,所以在回溯的搜索过程中,都有一些细节需要注意的。
-
-其实本题不算难,但也处处是细节,大家还要自己亲自动手写一写。
-
-**就酱,如果学到了,就帮Carl转发一波吧,让更多小伙伴知道这里!**
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
deleted file mode 100644
index 34430d1c..00000000
--- a/problems/0018.四数之和.md
+++ /dev/null
@@ -1,108 +0,0 @@
-# 题目地址
-https://leetcode-cn.com/problems/4sum/
-
-> 一样的道理,能解决四数之和
-
-> 那么五数之和、六数之和、N数之和呢?
-
-# 第18题. 四数之和
-
-题意:给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
-
-**注意:**
-
-答案中不可以包含重复的四元组。
-
-示例:
-给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
-满足要求的四元组集合为:
-[
- [-1, 0, 0, 1],
- [-2, -1, 1, 2],
- [-2, 0, 0, 2]
-]
-
-# 思路
-
-四数之和,和[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)是一个思路,都是使用双指针法, 基本解法就是在[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A) 的基础上再套一层for循环。
-
-但是有一些细节需要注意,例如: 不要判断`nums[k] > target` 就返回了,三数之和 可以通过 `nums[i] > 0` 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。(大家亲自写代码就能感受出来)
-
-[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下表作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
-
-四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下表作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2),四数之和的时间复杂度是O(n^3) 。
-
-那么一样的道理,五数之和、六数之和等等都采用这种解法。
-
-对于[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)双指针法就是将原本暴力O(n^3)的解法,降为O(n^2)的解法,四数之和的双指针解法就是将原本暴力O(n^4)的解法,降为O(n^3)的解法。
-
-之前我们讲过哈希表的经典题目:[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA),相对于本题简单很多,因为本题是要求在一个集合中找出四个数相加等于target,同时四元组不能重复。
-
-而[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况,所以相对于本题还是简单了不少!
-
-我们来回顾一下,几道题目使用了双指针法。
-
-双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
-* [0027.移除元素](https://mp.weixin.qq.com/s/wj0T-Xs88_FHJFwayElQlA)
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
-* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-
-双指针来记录前后指针实现链表反转:
-
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
-
-使用双指针来确定有环:
-
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用,后面还会介绍到。
-
-# C++代码
-```
-class Solution {
-public:
- vector> fourSum(vector& nums, int target) {
- vector> result;
- sort(nums.begin(), nums.end());
- for (int k = 0; k < nums.size(); k++) {
- // 这种剪枝是错误的,这道题目target 是任意值
- // if (nums[k] > target) {
- // return result;
- // }
- // 去重
- if (k > 0 && nums[k] == nums[k - 1]) {
- continue;
- }
- for (int i = k + 1; i < nums.size(); i++) {
- // 正确去重方法
- if (i > k + 1 && nums[i] == nums[i - 1]) {
- continue;
- }
- int left = i + 1;
- int right = nums.size() - 1;
- while (right > left) {
- if (nums[k] + nums[i] + nums[left] + nums[right] > target) {
- right--;
- } else if (nums[k] + nums[i] + nums[left] + nums[right] < target) {
- left++;
- } else {
- result.push_back(vector{nums[k], nums[i], nums[left], nums[right]});
- // 去重逻辑应该放在找到一个四元组之后
- while (right > left && nums[right] == nums[right - 1]) right--;
- while (right > left && nums[left] == nums[left + 1]) left++;
-
- // 找到答案时,双指针同时收缩
- right--;
- left++;
- }
- }
-
- }
- }
- return result;
- }
-
-};
-```
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0019.删除链表的倒数第N个节点.md b/problems/0019.删除链表的倒数第N个节点.md
deleted file mode 100644
index b332c9de..00000000
--- a/problems/0019.删除链表的倒数第N个节点.md
+++ /dev/null
@@ -1,49 +0,0 @@
-
-
-## 思路
-
-双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
-
-思路是这样的,但要注意一些细节。
-
-分为如下几步:
-
-* 首先这里我推荐大家使用虚拟头结点,这样方面处理删除实际头结点的逻辑,如果虚拟头结点不清楚,可以看这篇: [链表:听说用虚拟头节点会方便很多?](https://mp.weixin.qq.com/s/slM1CH5Ew9XzK93YOQYSjA)
-
-
-* 定义fast指针和slow指针,初始值为虚拟头结点,如图:
-
- -
-* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
-
-
-* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
- -
-* fast和slow同时移动,之道fast指向末尾,如题:
-
-
-* fast和slow同时移动,之道fast指向末尾,如题:
- -
-* 删除slow指向的下一个节点,如图:
-
-
-* 删除slow指向的下一个节点,如图:
- -
-此时不难写出如下C++代码:
-
-```
-class Solution {
-public:
- ListNode* removeNthFromEnd(ListNode* head, int n) {
- ListNode* dummyHead = new ListNode(0);
- dummyHead->next = head;
- ListNode* slow = dummyHead;
- ListNode* fast = dummyHead;
- while(n-- && fast != NULL) {
- fast = fast->next;
- }
- fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
- while (fast != NULL) {
- fast = fast->next;
- slow = slow->next;
- }
- slow->next = slow->next->next;
- return dummyHead->next;
- }
-};
-```
diff --git a/problems/0020.有效的括号.md b/problems/0020.有效的括号.md
deleted file mode 100644
index 293c53dd..00000000
--- a/problems/0020.有效的括号.md
+++ /dev/null
@@ -1,128 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/valid-parentheses/
-
-> 数据结构与算法应用往往隐藏在我们看不到的地方
-
-# 20. 有效的括号
-
-给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
-
-有效字符串需满足:
-* 左括号必须用相同类型的右括号闭合。
-* 左括号必须以正确的顺序闭合。
-* 注意空字符串可被认为是有效字符串。
-
-示例 1:
-输入: "()"
-输出: true
-
-示例 2:
-输入: "()[]{}"
-输出: true
-
-示例 3:
-输入: "(]"
-输出: false
-
-示例 4:
-输入: "([)]"
-输出: false
-
-示例 5:
-输入: "{[]}"
-输出: true
-
-# 思路
-
-## 题外话
-
-**括号匹配是使用栈解决的经典问题。**
-
-题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
-
-如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
-
-再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
-
-```
-cd a/b/c/../../
-```
-
-这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)
-
-所以栈在计算机领域中应用是非常广泛的。
-
-有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
-
-**所以数据结构与算法的应用往往隐藏在我们看不到的地方!**
-
-这里我就不过多展开了,先来看题。
-
-## 进入正题
-
-由于栈结构的特殊性,非常适合做对称匹配类的题目。
-
-首先要弄清楚,字符串里的括号不匹配有几种情况。
-
-**一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越远。**
-
-建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
-
-先来分析一下 这里有三种不匹配的情况,
-
-1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
-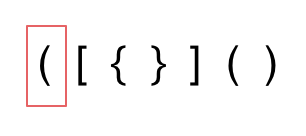
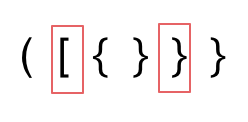
-2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
-
-3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
-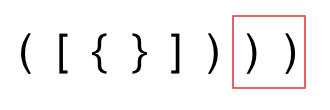
-
-我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
-
-动画如下:
-
-
-
-
-第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
-
-第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
-
-第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
-
-那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
-
-分析完之后,代码其实就比较好写了,
-
-但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
-
-实现代码如下:
-
-## C++代码
-
-
-```
-class Solution {
-public:
- bool isValid(string s) {
- stack st;
- for (int i = 0; i < s.size(); i++) {
- if (s[i] == '(') st.push(')');
- else if (s[i] == '{') st.push('}');
- else if (s[i] == '[') st.push(']');
- // 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
- // 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
- else if (st.empty() || st.top() != s[i]) return false;
- else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
- }
- // 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
- return st.empty();
- }
-};
-```
-技巧性的东西没有固定的学习方法,还是要多看多练,自己总灵活运用了。
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0021.合并两个有序链表.md b/problems/0021.合并两个有序链表.md
deleted file mode 100644
index 0272272a..00000000
--- a/problems/0021.合并两个有序链表.md
+++ /dev/null
@@ -1,60 +0,0 @@
-> 更多精彩文章持续更新,微信搜索「代码随想录」第一时间围观,本文[https://github.com/youngyangyang04/TechCPP](https://github.com/youngyangyang04/TechCPP) 已经收录,里面有更多干货等着你,欢迎Star!
-
-## 题目地址
-https://leetcode-cn.com/problems/merge-two-sorted-lists/
-
-## 思路
-
-链表的基本操作,一下代码中有详细注释
-
-
-## 代码
-
-```
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode() : val(0), next(nullptr) {}
- * ListNode(int x) : val(x), next(nullptr) {}
- * ListNode(int x, ListNode *next) : val(x), next(next) {}
- * };
- */
-// 内存消耗比较大,尝试一下 使用题目中的链表
-class Solution {
-public:
-// 题目中我们为什么定义了一个 新的head
- ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
- ListNode* head = new ListNode();
- ListNode* index = head;
- while(l1 != nullptr && l2 != nullptr) { // 注意null 和nullptr的区别
- if (l1->val < l2->val) {
- index->next = l1;
- l1 = l1->next;
- } else {
- index->next = l2;
- l2 = l2->next;
- }
- index = index->next;
- }
- if (l1 != nullptr) {
- index->next = l1;
- l1 = l1->next;
- }
- if (l2 != nullptr) {
- index->next = l2;
- l2 = l2->next;
- }
- ListNode* tmp = head; // 注意清理内存,不清理也没事
- head = head->next;
- delete tmp;
- return head;
- // return head->next
-
- }
-};
-```
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0024.两两交换链表中的节点.md b/problems/0024.两两交换链表中的节点.md
deleted file mode 100644
index 92f9b294..00000000
--- a/problems/0024.两两交换链表中的节点.md
+++ /dev/null
@@ -1,70 +0,0 @@
-
-
-## 题目地址
-
-## 思路
-
-这道题目正常模拟就可以了。
-
-建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
-
-对虚拟头结点的操作,还不熟悉的话,可以看这篇[链表:听说用虚拟头节点会方便很多?](https://mp.weixin.qq.com/s/slM1CH5Ew9XzK93YOQYSjA)。
-
-接下来就是交换相邻两个元素了,**此时一定要画图,不画图,操作多个指针很容易乱,而且要操作的先后顺序**
-
-初始时,cur指向虚拟头结点,然后进行如下三步:
-
-
-
-此时不难写出如下C++代码:
-
-```
-class Solution {
-public:
- ListNode* removeNthFromEnd(ListNode* head, int n) {
- ListNode* dummyHead = new ListNode(0);
- dummyHead->next = head;
- ListNode* slow = dummyHead;
- ListNode* fast = dummyHead;
- while(n-- && fast != NULL) {
- fast = fast->next;
- }
- fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
- while (fast != NULL) {
- fast = fast->next;
- slow = slow->next;
- }
- slow->next = slow->next->next;
- return dummyHead->next;
- }
-};
-```
diff --git a/problems/0020.有效的括号.md b/problems/0020.有效的括号.md
deleted file mode 100644
index 293c53dd..00000000
--- a/problems/0020.有效的括号.md
+++ /dev/null
@@ -1,128 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/valid-parentheses/
-
-> 数据结构与算法应用往往隐藏在我们看不到的地方
-
-# 20. 有效的括号
-
-给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
-
-有效字符串需满足:
-* 左括号必须用相同类型的右括号闭合。
-* 左括号必须以正确的顺序闭合。
-* 注意空字符串可被认为是有效字符串。
-
-示例 1:
-输入: "()"
-输出: true
-
-示例 2:
-输入: "()[]{}"
-输出: true
-
-示例 3:
-输入: "(]"
-输出: false
-
-示例 4:
-输入: "([)]"
-输出: false
-
-示例 5:
-输入: "{[]}"
-输出: true
-
-# 思路
-
-## 题外话
-
-**括号匹配是使用栈解决的经典问题。**
-
-题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
-
-如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
-
-再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
-
-```
-cd a/b/c/../../
-```
-
-这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)
-
-所以栈在计算机领域中应用是非常广泛的。
-
-有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
-
-**所以数据结构与算法的应用往往隐藏在我们看不到的地方!**
-
-这里我就不过多展开了,先来看题。
-
-## 进入正题
-
-由于栈结构的特殊性,非常适合做对称匹配类的题目。
-
-首先要弄清楚,字符串里的括号不匹配有几种情况。
-
-**一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越远。**
-
-建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
-
-先来分析一下 这里有三种不匹配的情况,
-
-1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
-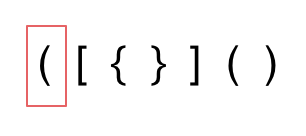
-2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
-
-3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
-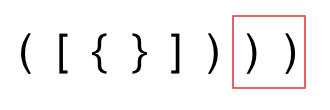
-
-我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
-
-动画如下:
-
-
-
-
-第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
-
-第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
-
-第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
-
-那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
-
-分析完之后,代码其实就比较好写了,
-
-但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
-
-实现代码如下:
-
-## C++代码
-
-
-```
-class Solution {
-public:
- bool isValid(string s) {
- stack st;
- for (int i = 0; i < s.size(); i++) {
- if (s[i] == '(') st.push(')');
- else if (s[i] == '{') st.push('}');
- else if (s[i] == '[') st.push(']');
- // 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
- // 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
- else if (st.empty() || st.top() != s[i]) return false;
- else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
- }
- // 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
- return st.empty();
- }
-};
-```
-技巧性的东西没有固定的学习方法,还是要多看多练,自己总灵活运用了。
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0021.合并两个有序链表.md b/problems/0021.合并两个有序链表.md
deleted file mode 100644
index 0272272a..00000000
--- a/problems/0021.合并两个有序链表.md
+++ /dev/null
@@ -1,60 +0,0 @@
-> 更多精彩文章持续更新,微信搜索「代码随想录」第一时间围观,本文[https://github.com/youngyangyang04/TechCPP](https://github.com/youngyangyang04/TechCPP) 已经收录,里面有更多干货等着你,欢迎Star!
-
-## 题目地址
-https://leetcode-cn.com/problems/merge-two-sorted-lists/
-
-## 思路
-
-链表的基本操作,一下代码中有详细注释
-
-
-## 代码
-
-```
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode() : val(0), next(nullptr) {}
- * ListNode(int x) : val(x), next(nullptr) {}
- * ListNode(int x, ListNode *next) : val(x), next(next) {}
- * };
- */
-// 内存消耗比较大,尝试一下 使用题目中的链表
-class Solution {
-public:
-// 题目中我们为什么定义了一个 新的head
- ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
- ListNode* head = new ListNode();
- ListNode* index = head;
- while(l1 != nullptr && l2 != nullptr) { // 注意null 和nullptr的区别
- if (l1->val < l2->val) {
- index->next = l1;
- l1 = l1->next;
- } else {
- index->next = l2;
- l2 = l2->next;
- }
- index = index->next;
- }
- if (l1 != nullptr) {
- index->next = l1;
- l1 = l1->next;
- }
- if (l2 != nullptr) {
- index->next = l2;
- l2 = l2->next;
- }
- ListNode* tmp = head; // 注意清理内存,不清理也没事
- head = head->next;
- delete tmp;
- return head;
- // return head->next
-
- }
-};
-```
-
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0024.两两交换链表中的节点.md b/problems/0024.两两交换链表中的节点.md
deleted file mode 100644
index 92f9b294..00000000
--- a/problems/0024.两两交换链表中的节点.md
+++ /dev/null
@@ -1,70 +0,0 @@
-
-
-## 题目地址
-
-## 思路
-
-这道题目正常模拟就可以了。
-
-建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
-
-对虚拟头结点的操作,还不熟悉的话,可以看这篇[链表:听说用虚拟头节点会方便很多?](https://mp.weixin.qq.com/s/slM1CH5Ew9XzK93YOQYSjA)。
-
-接下来就是交换相邻两个元素了,**此时一定要画图,不画图,操作多个指针很容易乱,而且要操作的先后顺序**
-
-初始时,cur指向虚拟头结点,然后进行如下三步:
-
- -
-操作之后,链表如下:
-
-
-
-
-操作之后,链表如下:
-
-
- -
-看这个可能就更直观一些了:
-
-
-
-
-看这个可能就更直观一些了:
-
-
- -
-对应的C++代码实现如下:
-
-```
-class Solution {
-public:
- ListNode* swapPairs(ListNode* head) {
- ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
- ListNode* cur = dummyHead;
- while(cur->next != nullptr && cur->next->next != nullptr) {
- ListNode* tmp = cur->next; // 记录临时节点
- ListNode* tmp1 = cur->next->next->next; // 记录临时节点
-
- cur->next = cur->next->next; // 步骤一
- cur->next->next = tmp; // 步骤二
- cur->next->next->next = tmp1; // 步骤三
-
- cur = cur->next->next; // cur移动两位,准备下一轮交换
- }
- return dummyHead->next;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-## 拓展
-
-**这里还是说一下,大家不必太在意leetcode上执行用时,打败多少多少用户,这个就是一个玩具,非常不准确。**
-
-做题的时候自己能分析出来时间复杂度就可以了,至于leetcode上执行用时,大概看一下就行。
-
-上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-
-心想应该没有更好的方法了吧,也就O(n)的时间复杂度,重复提交几次,这样了:
-
-
-
-对应的C++代码实现如下:
-
-```
-class Solution {
-public:
- ListNode* swapPairs(ListNode* head) {
- ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
- ListNode* cur = dummyHead;
- while(cur->next != nullptr && cur->next->next != nullptr) {
- ListNode* tmp = cur->next; // 记录临时节点
- ListNode* tmp1 = cur->next->next->next; // 记录临时节点
-
- cur->next = cur->next->next; // 步骤一
- cur->next->next = tmp; // 步骤二
- cur->next->next->next = tmp1; // 步骤三
-
- cur = cur->next->next; // cur移动两位,准备下一轮交换
- }
- return dummyHead->next;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-## 拓展
-
-**这里还是说一下,大家不必太在意leetcode上执行用时,打败多少多少用户,这个就是一个玩具,非常不准确。**
-
-做题的时候自己能分析出来时间复杂度就可以了,至于leetcode上执行用时,大概看一下就行。
-
-上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-
-心想应该没有更好的方法了吧,也就O(n)的时间复杂度,重复提交几次,这样了:
-
- -
-所以,不必过于在意leetcode上这个统计。
-
-
-
diff --git a/problems/0026.删除排序数组中的重复项.md b/problems/0026.删除排序数组中的重复项.md
deleted file mode 100644
index 114f2da2..00000000
--- a/problems/0026.删除排序数组中的重复项.md
+++ /dev/null
@@ -1,49 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
-
-# 思路
-
-此题使用双指针法,O(n)的时间复杂度,拼速度的话,可以剪剪枝。
-
-注意题目中:不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
-
-双指针法,动画如下:
-
-
-
-其实**双指针法在在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法,可以将时间复杂度O(n^2)的解法优化为 O(n)的解法,例如:**
-
-* [0015.三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md)
-* [0018.四数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0018.四数之和.md)
-* [0026.删除排序数组中的重复项](https://github.com/youngyangyang04/leetcode/blob/master/problems/0026.删除排序数组中的重复项.md)
-* [0206.翻转链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0206.翻转链表.md)
-* [0344.反转字符串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0344.反转字符串.md)
-* [剑指Offer05.替换空格](https://github.com/youngyangyang04/leetcode/blob/master/problems/剑指Offer05.替换空格.md)
-
-**还有链表找环,也用到双指针:**
-
-* [0142.环形链表II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0142.环形链表II.md)
-
-大家都可以去做一做,感受一下双指针法的内在逻辑!
-
-
-# C++ 代码
-
-
-```
-class Solution {
-public:
- int removeDuplicates(vector& nums) {
- if (nums.empty()) return 0; // 别忘记空数组的判断
- int slowIndex = 0;
- for (int fastIndex = 0; fastIndex < (nums.size() - 1); fastIndex++){
- if(nums[fastIndex] != nums[fastIndex + 1]) { // 发现和后一个不相同
- nums[++slowIndex] = nums[fastIndex + 1]; //slowIndex = 0 的数据一定是不重复的,所以直接 ++slowIndex
- }
- }
- return slowIndex + 1; //别忘了slowIndex是从0开始的,所以返回slowIndex + 1
- }
-};
-```
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0027.移除元素.md b/problems/0027.移除元素.md
deleted file mode 100644
index 637bd5ad..00000000
--- a/problems/0027.移除元素.md
+++ /dev/null
@@ -1,127 +0,0 @@
-
-
-所以,不必过于在意leetcode上这个统计。
-
-
-
diff --git a/problems/0026.删除排序数组中的重复项.md b/problems/0026.删除排序数组中的重复项.md
deleted file mode 100644
index 114f2da2..00000000
--- a/problems/0026.删除排序数组中的重复项.md
+++ /dev/null
@@ -1,49 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
-
-# 思路
-
-此题使用双指针法,O(n)的时间复杂度,拼速度的话,可以剪剪枝。
-
-注意题目中:不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
-
-双指针法,动画如下:
-
-
-
-其实**双指针法在在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法,可以将时间复杂度O(n^2)的解法优化为 O(n)的解法,例如:**
-
-* [0015.三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md)
-* [0018.四数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0018.四数之和.md)
-* [0026.删除排序数组中的重复项](https://github.com/youngyangyang04/leetcode/blob/master/problems/0026.删除排序数组中的重复项.md)
-* [0206.翻转链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0206.翻转链表.md)
-* [0344.反转字符串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0344.反转字符串.md)
-* [剑指Offer05.替换空格](https://github.com/youngyangyang04/leetcode/blob/master/problems/剑指Offer05.替换空格.md)
-
-**还有链表找环,也用到双指针:**
-
-* [0142.环形链表II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0142.环形链表II.md)
-
-大家都可以去做一做,感受一下双指针法的内在逻辑!
-
-
-# C++ 代码
-
-
-```
-class Solution {
-public:
- int removeDuplicates(vector& nums) {
- if (nums.empty()) return 0; // 别忘记空数组的判断
- int slowIndex = 0;
- for (int fastIndex = 0; fastIndex < (nums.size() - 1); fastIndex++){
- if(nums[fastIndex] != nums[fastIndex + 1]) { // 发现和后一个不相同
- nums[++slowIndex] = nums[fastIndex + 1]; //slowIndex = 0 的数据一定是不重复的,所以直接 ++slowIndex
- }
- }
- return slowIndex + 1; //别忘了slowIndex是从0开始的,所以返回slowIndex + 1
- }
-};
-```
-> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0027.移除元素.md b/problems/0027.移除元素.md
deleted file mode 100644
index 637bd5ad..00000000
--- a/problems/0027.移除元素.md
+++ /dev/null
@@ -1,127 +0,0 @@
-
- -
-
-
-  -
-  -
-  -
-  -
-  -
-  -
-
-
-> 移除元素想要高效的话,不是很简单!
-
-# 编号:27. 移除元素
-
-题目地址:https://leetcode-cn.com/problems/remove-element/
-
-给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
-
-不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并**原地**修改输入数组。
-
-元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
-
-示例 1:
-给定 nums = [3,2,2,3], val = 3,
-函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
-你不需要考虑数组中超出新长度后面的元素。
-
-示例 2:
-给定 nums = [0,1,2,2,3,0,4,2], val = 2,
-函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
-
-**你不需要考虑数组中超出新长度后面的元素。**
-
-# 思路
-
-有的同学可能说了,多余的元素,删掉不就得了。
-
-**要知道数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。**
-
-数组的基础知识可以看这里[程序员算法面试中,必须掌握的数组理论知识](https://mp.weixin.qq.com/s/X7R55wSENyY62le0Fiawsg)。
-
-# 暴力解法
-
-这个题目暴力的解法就是两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
-
-删除过程如下:
-
- -
-很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
-
-# 暴力解法C++代码
-
-```
-// 时间复杂度:O(n^2)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector& nums, int val) {
- int size = nums.size();
- for (int i = 0; i < size; i++) {
- if (nums[i] == val) { // 发现需要移除的元素,就将数组集体向前移动一位
- for (int j = i + 1; j < size; j++) {
- nums[j - 1] = nums[j];
- }
- i--; // 因为下表i以后的数值都向前移动了一位,所以i也向前移动一位
- size--; // 此时数组的大小-1
- }
- }
- return size;
-
- }
-};
-```
-
-# 双指针法
-
-双指针法(快慢指针法): **通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。**
-
-删除过程如下:
-
-
-
-很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
-
-# 暴力解法C++代码
-
-```
-// 时间复杂度:O(n^2)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector& nums, int val) {
- int size = nums.size();
- for (int i = 0; i < size; i++) {
- if (nums[i] == val) { // 发现需要移除的元素,就将数组集体向前移动一位
- for (int j = i + 1; j < size; j++) {
- nums[j - 1] = nums[j];
- }
- i--; // 因为下表i以后的数值都向前移动了一位,所以i也向前移动一位
- size--; // 此时数组的大小-1
- }
- }
- return size;
-
- }
-};
-```
-
-# 双指针法
-
-双指针法(快慢指针法): **通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。**
-
-删除过程如下:
-
- -
-**双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。**
-
-我们来回顾一下,之前已经讲过有四道题目使用了双指针法。
-
-双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
-
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
-* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-
-双指针来记录前后指针实现链表反转:
-
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
-
-使用双指针来确定有环:
-
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用,后面还会介绍到。
-
-# 双指针法C++代码:
-```
-// 时间复杂度:O(n)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector& nums, int val) {
- int slowIndex = 0;
- for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
- if (val != nums[fastIndex]) {
- nums[slowIndex++] = nums[fastIndex];
- }
- }
- return slowIndex;
- }
-};
-```
-
-**循序渐进学算法,认准「代码随想录」,Carl手把手带你过关斩将!**
-
-
-
-**双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。**
-
-我们来回顾一下,之前已经讲过有四道题目使用了双指针法。
-
-双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
-
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
-* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-
-双指针来记录前后指针实现链表反转:
-
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
-
-使用双指针来确定有环:
-
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用,后面还会介绍到。
-
-# 双指针法C++代码:
-```
-// 时间复杂度:O(n)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector& nums, int val) {
- int slowIndex = 0;
- for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
- if (val != nums[fastIndex]) {
- nums[slowIndex++] = nums[fastIndex];
- }
- }
- return slowIndex;
- }
-};
-```
-
-**循序渐进学算法,认准「代码随想录」,Carl手把手带你过关斩将!**
-
-
- -
-
diff --git a/problems/0028.实现strStr().md b/problems/0028.实现strStr().md
deleted file mode 100644
index f6e689d7..00000000
--- a/problems/0028.实现strStr().md
+++ /dev/null
@@ -1,538 +0,0 @@
-
-## 题目地址
-https://leetcode-cn.com/problems/implement-strstr/
-
-> 在一个串中查找是否出现过另一个串,这是KMP的看家本领。
-
-# 题目:28. 实现 strStr()
-
-实现 strStr() 函数。
-
-给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
-
-示例 1:
-输入: haystack = "hello", needle = "ll"
-输出: 2
-
-示例 2:
-输入: haystack = "aaaaa", needle = "bba"
-输出: -1
-
-说明:
-当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
-对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
-
-
-# 思路
-
-本题是KMP 经典题目。
-
-以下文字如果看不进去,可以看我的B站视频:
-
-* [帮你把KMP算法学个通透!B站(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd/)
-* [帮你把KMP算法学个通透!(求next数组代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
-
-KMP的经典思想就是:**当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。**
-
-本篇将以如下顺序来讲解KMP,
-
-
-* 什么是KMP
-* KMP有什么用
-* 什么是前缀表
-* 为什么一定要用前缀表
-* 如何计算前缀表
-* 前缀表与next数组
-* 使用next数组来匹配
-* 时间复杂度分析
-* 构造next数组
-* 使用next数组来做匹配
-* 前缀表统一减一 C++代码实现
-* 前缀表(不减一)C++实现
-* 总结
-
-
-读完本篇可以顺便,把leetcode上28.实现strStr()题目做了。
-
-如果文字实在看不下去,就看我在B站上的视频吧,如下:
-
-* [帮你把KMP算法学个通透!(理论篇)B站](https://www.bilibili.com/video/BV1PD4y1o7nd/)
-* [帮你把KMP算法学个通透!(求next数组代码篇)B站](https://www.bilibili.com/video/BV1M5411j7Xx/)
-
-
-# 什么是KMP
-
-说到KMP,先说一下KMP这个名字是怎么来的,为什么叫做KMP呢。
-
-因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP
-
-# KMP有什么用
-
-KMP主要应用在字符串匹配上。
-
-KMP的主要思想是**当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。**
-
-所以如何记录已经匹配的文本内容,是KMP的重点,也是next数组肩负的重任。
-
-其实KMP的代码不好理解,一些同学甚至直接把KMP代码的模板背下来。
-
-没有彻底搞懂,懵懵懂懂就把代码背下来太容易忘了。
-
-不仅面试的时候可能写不出来,如果面试官问:**next数组里的数字表示的是什么,为什么这么表示?**
-
-估计大多数候选人都是懵逼的。
-
-下面Carl就带大家把KMP的精髓,next数组弄清楚。
-
-# 什么是前缀表
-
-写过KMP的同学,一定都写过next数组,那么这个next数组究竟是个啥呢?
-
-next数组就是一个前缀表(prefix table)。
-
-前缀表有什么作用呢?
-
-**前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。**
-
-为了清楚的了解前缀表的来历,我们来举一个例子:
-
-要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
-
-请记住文本串和模式串的作用,对于理解下文很重要,要不然容易看懵。所以说三遍:
-
-要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
-
-要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
-
-要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
-
-如动画所示:
-
- -
-动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说道。
-
-可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
-
-但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
-
-此时就要问了**前缀表是如何记录的呢?**
-
-首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,在重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
-
-那么什么是前缀表:**记录下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-# 为什么一定要用前缀表
-
-这就是前缀表那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
-
-回顾一下,刚刚匹配的过程在下表5的地方遇到不匹配,模式串是指向f,如图:
-
-
-动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说道。
-
-可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
-
-但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
-
-此时就要问了**前缀表是如何记录的呢?**
-
-首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,在重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
-
-那么什么是前缀表:**记录下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-# 为什么一定要用前缀表
-
-这就是前缀表那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
-
-回顾一下,刚刚匹配的过程在下表5的地方遇到不匹配,模式串是指向f,如图:
- -
-
-然后就找到了下表2,指向b,继续匹配:如图:
-
-
-
-然后就找到了下表2,指向b,继续匹配:如图:
- -
-以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-
-**下表5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
-
-所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
-
-**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-
-# 如何计算前缀表
-
-接下来就要说一说怎么计算前缀表。
-
-如图:
-
-
-
-以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-
-**下表5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
-
-所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
-
-**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-
-# 如何计算前缀表
-
-接下来就要说一说怎么计算前缀表。
-
-如图:
-
- -
-长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
-
-
-长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
- -长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
-
-长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
- -长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
-
-以此类推:
-长度为前4个字符的子串`aaba`,最长相同前后缀的长度为1。
-长度为前5个字符的子串`aabaa`,最长相同前后缀的长度为2。
-长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
-
-那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
-
-长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
-
-以此类推:
-长度为前4个字符的子串`aaba`,最长相同前后缀的长度为1。
-长度为前5个字符的子串`aabaa`,最长相同前后缀的长度为2。
-长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
-
-那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
- -
-可以看出模式串与前缀表对应位置的数字表示的就是:**下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
-
-
-可以看出模式串与前缀表对应位置的数字表示的就是:**下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
- -
-找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
-
-为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
-
-所以要看前一位的 前缀表的数值。
-
-前一个字符的前缀表的数值是2, 所有把下表移动到下表2的位置继续比配。 可以再反复看一下上面的动画。
-
-最后就在文本串中找到了和模式串匹配的子串了。
-
-# 前缀表与next数组
-
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
-
-next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
-
-为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
-
-后面我会提供两种不同的实现代码,大家就明白了了。
-
-# 使用next数组来匹配
-
-以下我们以前缀表统一减一之后的next数组来做演示。
-
-有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
-
-注意next数组是新前缀表(旧前缀表统一减一了)。
-
-匹配过程动画如下:
-
-
-
-找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
-
-为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
-
-所以要看前一位的 前缀表的数值。
-
-前一个字符的前缀表的数值是2, 所有把下表移动到下表2的位置继续比配。 可以再反复看一下上面的动画。
-
-最后就在文本串中找到了和模式串匹配的子串了。
-
-# 前缀表与next数组
-
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
-
-next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
-
-为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
-
-后面我会提供两种不同的实现代码,大家就明白了了。
-
-# 使用next数组来匹配
-
-以下我们以前缀表统一减一之后的next数组来做演示。
-
-有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
-
-注意next数组是新前缀表(旧前缀表统一减一了)。
-
-匹配过程动画如下:
-
- -
-# 时间复杂度分析
-
-
-其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-
-暴力的解法显而易见是O(n * m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
-
-为了和[字符串:KMP是时候上场了(一文读懂系列)](https://mp.weixin.qq.com/s/70OXnZ4Ez29CKRrUpVJmug)字符串命名统一,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
-
-都知道使用KMP算法,一定要构造next数组。
-
-# 构造next数组
-
-我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
-
-```
-void getNext(int* next, const string& s)
-```
-
-**构造next数组其实就是计算模式串s,前缀表的过程。** 主要有如下三步:
-
-1. 初始化
-2. 处理前后缀不相同的情况
-3. 处理前后缀相同的情况
-
-接下来我们详解详解一下。
-
-1. 初始化:
-
-定义两个指针i和j,j指向前缀终止位置(严格来说是终止位置减一的位置),i指向后缀终止位置(与j同理)。
-
-然后还要对next数组进行初始化赋值,如下:
-
-```
-int j = -1;
-next[0] = j;
-```
-
-j 为什么要初始化为 -1呢,因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现,我们这里选择j初始化为-1,下文我还会给出j不初始化为-1的实现代码。
-
-next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
-
-所以初始化next[0] = j 。
-
-
-2. 处理前后缀不相同的情况
-
-
-因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
-
-所以遍历模式串s的循环下表i 要从 1开始,代码如下:
-
-```
-for(int i = 1; i < s.size(); i++) {
-```
-
-如果 s[i] 与 s[j+1]不相同,也就是遇到 前后缀末尾不相同的情况,就要向前回溯。
-
-怎么回溯呢?
-
-next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
-
-那么 s[i] 与 s[j+1] 不相同,就要找 j+1前一个元素在next数组里的值(就是next[j])。
-
-所以,处理前后缀不相同的情况代码如下:
-
-```
-while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
-}
-```
-
-3. 处理前后缀相同的情况
-
-如果s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
-
-代码如下:
-
-```
-if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
-}
-next[i] = j;
-```
-
-最后整体构建next数组的函数代码如下:
-
-```
-void getNext(int* next, const string& s){
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-```
-
-
-代码构造next数组的逻辑流程动画如下:
-
-
-
-# 时间复杂度分析
-
-
-其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-
-暴力的解法显而易见是O(n * m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
-
-为了和[字符串:KMP是时候上场了(一文读懂系列)](https://mp.weixin.qq.com/s/70OXnZ4Ez29CKRrUpVJmug)字符串命名统一,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
-
-都知道使用KMP算法,一定要构造next数组。
-
-# 构造next数组
-
-我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
-
-```
-void getNext(int* next, const string& s)
-```
-
-**构造next数组其实就是计算模式串s,前缀表的过程。** 主要有如下三步:
-
-1. 初始化
-2. 处理前后缀不相同的情况
-3. 处理前后缀相同的情况
-
-接下来我们详解详解一下。
-
-1. 初始化:
-
-定义两个指针i和j,j指向前缀终止位置(严格来说是终止位置减一的位置),i指向后缀终止位置(与j同理)。
-
-然后还要对next数组进行初始化赋值,如下:
-
-```
-int j = -1;
-next[0] = j;
-```
-
-j 为什么要初始化为 -1呢,因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现,我们这里选择j初始化为-1,下文我还会给出j不初始化为-1的实现代码。
-
-next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
-
-所以初始化next[0] = j 。
-
-
-2. 处理前后缀不相同的情况
-
-
-因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
-
-所以遍历模式串s的循环下表i 要从 1开始,代码如下:
-
-```
-for(int i = 1; i < s.size(); i++) {
-```
-
-如果 s[i] 与 s[j+1]不相同,也就是遇到 前后缀末尾不相同的情况,就要向前回溯。
-
-怎么回溯呢?
-
-next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
-
-那么 s[i] 与 s[j+1] 不相同,就要找 j+1前一个元素在next数组里的值(就是next[j])。
-
-所以,处理前后缀不相同的情况代码如下:
-
-```
-while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
-}
-```
-
-3. 处理前后缀相同的情况
-
-如果s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
-
-代码如下:
-
-```
-if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
-}
-next[i] = j;
-```
-
-最后整体构建next数组的函数代码如下:
-
-```
-void getNext(int* next, const string& s){
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-```
-
-
-代码构造next数组的逻辑流程动画如下:
-
- -
-
-得到了next数组之后,就要用这个来做匹配了。
-
-# 使用next数组来做匹配
-
-在文本串s里 找是否出现过模式串t。
-
-定义两个下表j 指向模式串起始位置,i指向文本串起始位置。
-
-那么j初始值依然为-1,为什么呢? **依然因为next数组里记录的起始位置为-1。**
-
-i就从0开始,遍历文本串,代码如下:
-
-```
-for (int i = 0; i < s.size(); i++)
-```
-
-接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 经行比较。
-
-如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
-
-代码如下:
-
-```
-while(j >= 0 && s[i] != t[j + 1]) {
- j = next[j];
-}
-```
-
-如果 s[i] 与 t[j + 1] 相同,那么i 和 j 同时向后移动, 代码如下:
-
-```
-if (s[i] == t[j + 1]) {
- j++; // i的增加在for循环里
-}
-```
-
-如何判断在文本串s里出现了模式串t呢,如果j指向了模式串t的末尾,那么就说明模式串t完全匹配文本串s里的某个子串了。
-
-本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
-
-代码如下:
-
-```
-if (j == (t.size() - 1) ) {
- return (i - t.size() + 1);
-}
-```
-
-那么使用next数组,用模式串匹配文本串的整体代码如下:
-
-```
-int j = -1; // 因为next数组里记录的起始位置为-1
-for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
- while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - t.size() + 1);
- }
-}
-```
-
-此时所有逻辑的代码都已经写出来了,本题整体代码如下:
-
-# 前缀表统一减一 C++代码实现
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = -1; // // 因为next数组里记录的起始位置为-1
- for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
- while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-
-```
-
-# 前缀表(不减一)C++实现
-
-那么前缀表就不减一了,也不右移的,到底行不行呢?行!
-
-我之前说过,这仅仅是KMP算法实现上的问题,如果就直接使用前缀表可以换一种回退方式,找j=next[j-1] 来进行回退。
-
-主要就是j=next[x]这一步最为关键!
-
-我给出的getNext的实现为:(前缀表统一减一)
-
-```
-void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-
-```
-此时如果输入的模式串为aabaaf,对应的next为-1 0 -1 0 1 -1。
-
-这里j和next[0]初始化为-1,整个next数组是以 前缀表减一之后的效果来构建的。
-
-那么前缀表不减一来构建next数组,代码如下:
-
-```
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) { // j要保证大于0,因为下面有取j-1作为数组下表的操作
- j = next[j - 1]; // 注意这里,是要找前一位的对应的回退位置了
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
-
-```
-
-此时如果输入的模式串为aabaaf,对应的next为 0 1 0 1 2 0,(其实这就是前缀表的数值了)。
-
-那么用这样的next数组也可以用来做匹配,代码要有所改动。
-
-实现代码如下:
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) {
- j = next[j - 1];
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = 0;
- for (int i = 0; i < haystack.size(); i++) {
- while(j > 0 && haystack[i] != needle[j]) {
- j = next[j - 1];
- }
- if (haystack[i] == needle[j]) {
- j++;
- }
- if (j == needle.size() ) {
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-```
-
-# 总结
-
-我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
-
-接着从给出的模式串中,我们一步一步的推导出了前缀表,得出前缀表无论是统一减一还是不同意减一得到的next数组仅仅是kmp的实现方式的不同。
-
-其中还分析了KMP算法的时间复杂度,并且和暴力方法做了对比。
-
-然后先用前缀表统一减一得到的next数组,求得文本串s里是否出现过模式串t,并给出了具体分析代码。
-
-又给出了直接用前缀表作为next数组,来做匹配的实现代码。
-
-可以说把KMP的每一个细微的细节都扣了出来,毫无遮掩的展示给大家了!
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0031.下一个排列.md b/problems/0031.下一个排列.md
deleted file mode 100644
index 68665d6b..00000000
--- a/problems/0031.下一个排列.md
+++ /dev/null
@@ -1,58 +0,0 @@
-
-## 思路
-
-一些同学可能手动写排列的顺序,都没有写对,那么写程序的话思路一定是有问题的了,我这里以1234为例子,把全排列都列出来。可以参考一下规律所在:
-
-```
-1 2 3 4
-1 2 4 3
-1 3 2 4
-1 3 4 2
-1 4 2 3
-1 4 3 2
-2 1 3 4
-2 1 4 3
-2 3 1 4
-2 3 4 1
-2 4 1 3
-2 4 3 1
-3 1 2 4
-3 1 4 2
-3 2 1 4
-3 2 4 1
-3 4 1 2
-3 4 2 1
-4 1 2 3
-4 1 3 2
-4 2 1 3
-4 2 3 1
-4 3 1 2
-4 3 2 1
-```
-
-如图:
-
-以求1243为例,流程如图:
-
-
-
-
-得到了next数组之后,就要用这个来做匹配了。
-
-# 使用next数组来做匹配
-
-在文本串s里 找是否出现过模式串t。
-
-定义两个下表j 指向模式串起始位置,i指向文本串起始位置。
-
-那么j初始值依然为-1,为什么呢? **依然因为next数组里记录的起始位置为-1。**
-
-i就从0开始,遍历文本串,代码如下:
-
-```
-for (int i = 0; i < s.size(); i++)
-```
-
-接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 经行比较。
-
-如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
-
-代码如下:
-
-```
-while(j >= 0 && s[i] != t[j + 1]) {
- j = next[j];
-}
-```
-
-如果 s[i] 与 t[j + 1] 相同,那么i 和 j 同时向后移动, 代码如下:
-
-```
-if (s[i] == t[j + 1]) {
- j++; // i的增加在for循环里
-}
-```
-
-如何判断在文本串s里出现了模式串t呢,如果j指向了模式串t的末尾,那么就说明模式串t完全匹配文本串s里的某个子串了。
-
-本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
-
-代码如下:
-
-```
-if (j == (t.size() - 1) ) {
- return (i - t.size() + 1);
-}
-```
-
-那么使用next数组,用模式串匹配文本串的整体代码如下:
-
-```
-int j = -1; // 因为next数组里记录的起始位置为-1
-for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
- while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - t.size() + 1);
- }
-}
-```
-
-此时所有逻辑的代码都已经写出来了,本题整体代码如下:
-
-# 前缀表统一减一 C++代码实现
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = -1; // // 因为next数组里记录的起始位置为-1
- for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
- while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-
-```
-
-# 前缀表(不减一)C++实现
-
-那么前缀表就不减一了,也不右移的,到底行不行呢?行!
-
-我之前说过,这仅仅是KMP算法实现上的问题,如果就直接使用前缀表可以换一种回退方式,找j=next[j-1] 来进行回退。
-
-主要就是j=next[x]这一步最为关键!
-
-我给出的getNext的实现为:(前缀表统一减一)
-
-```
-void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-
-```
-此时如果输入的模式串为aabaaf,对应的next为-1 0 -1 0 1 -1。
-
-这里j和next[0]初始化为-1,整个next数组是以 前缀表减一之后的效果来构建的。
-
-那么前缀表不减一来构建next数组,代码如下:
-
-```
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) { // j要保证大于0,因为下面有取j-1作为数组下表的操作
- j = next[j - 1]; // 注意这里,是要找前一位的对应的回退位置了
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
-
-```
-
-此时如果输入的模式串为aabaaf,对应的next为 0 1 0 1 2 0,(其实这就是前缀表的数值了)。
-
-那么用这样的next数组也可以用来做匹配,代码要有所改动。
-
-实现代码如下:
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) {
- j = next[j - 1];
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = 0;
- for (int i = 0; i < haystack.size(); i++) {
- while(j > 0 && haystack[i] != needle[j]) {
- j = next[j - 1];
- }
- if (haystack[i] == needle[j]) {
- j++;
- }
- if (j == needle.size() ) {
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-```
-
-# 总结
-
-我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
-
-接着从给出的模式串中,我们一步一步的推导出了前缀表,得出前缀表无论是统一减一还是不同意减一得到的next数组仅仅是kmp的实现方式的不同。
-
-其中还分析了KMP算法的时间复杂度,并且和暴力方法做了对比。
-
-然后先用前缀表统一减一得到的next数组,求得文本串s里是否出现过模式串t,并给出了具体分析代码。
-
-又给出了直接用前缀表作为next数组,来做匹配的实现代码。
-
-可以说把KMP的每一个细微的细节都扣了出来,毫无遮掩的展示给大家了!
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0031.下一个排列.md b/problems/0031.下一个排列.md
deleted file mode 100644
index 68665d6b..00000000
--- a/problems/0031.下一个排列.md
+++ /dev/null
@@ -1,58 +0,0 @@
-
-## 思路
-
-一些同学可能手动写排列的顺序,都没有写对,那么写程序的话思路一定是有问题的了,我这里以1234为例子,把全排列都列出来。可以参考一下规律所在:
-
-```
-1 2 3 4
-1 2 4 3
-1 3 2 4
-1 3 4 2
-1 4 2 3
-1 4 3 2
-2 1 3 4
-2 1 4 3
-2 3 1 4
-2 3 4 1
-2 4 1 3
-2 4 3 1
-3 1 2 4
-3 1 4 2
-3 2 1 4
-3 2 4 1
-3 4 1 2
-3 4 2 1
-4 1 2 3
-4 1 3 2
-4 2 1 3
-4 2 3 1
-4 3 1 2
-4 3 2 1
-```
-
-如图:
-
-以求1243为例,流程如图:
-
- -
-对应的C++代码如下:
-
-```
-class Solution {
-public:
- void nextPermutation(vector& nums) {
- for (int i = nums.size() - 1; i >= 0; i--) {
- for (int j = nums.size() - 1; j > i; j--) {
- if (nums[j] > nums[i]) {
- swap(nums[j], nums[i]);
- sort(nums.begin() + i + 1, nums.end());
- return;
- }
- }
- }
- // 到这里了说明整个数组都是倒叙了,反转一下便可
- reverse(nums.begin(), nums.end());
- }
-};
-```
diff --git a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
deleted file mode 100644
index a62261e9..00000000
--- a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
+++ /dev/null
@@ -1,134 +0,0 @@
-> **如果对二分查找比较模糊,建议看这篇:[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q),这里详细介绍了二分的两种写法,以及循环不变量的重要性,顺便还可以把「leetcode:35.搜索插入位置」题目刷了**。
-
-这道题目如果基础不是很好,不建议大家看简短的代码,简短的代码隐藏了太多逻辑,结果就是稀里糊涂把题AC了,但是没有想清楚具体细节!
-
-下面我来把所有情况都讨论一下。
-
-寻找target在数组里的左右边界,有如下三种情况:
-
-* 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
-* 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
-* 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
-
-这三种情况都考虑到,说明就想的很清楚了。
-
-接下来,在去寻找左边界,和右边界了。
-
-采用二分法来取寻找左右边界,为了让代码清晰,我分别写两个二分来寻找左边界和右边界。
-
-**刚刚接触二分搜索的同学不建议上来就像如果用一个二分来查找左右边界,很容易把自己绕进去,建议扎扎实实的写两个二分分别找左边界和右边界**
-
-## 寻找右边界
-
-先来寻找右边界,至于二分查找,如果看过[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)就会知道,二分查找中什么时候用while (left <= right),有什么时候用while (left < right),其实只要清楚**循环不变量**,很容易区分两种写法。
-
-那么这里我采用while (left <= right)的写法,区间定义为[left, right],即左闭又闭的区间(如果这里有点看不懂了,强烈建议把[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)这篇文章先看了,在把「leetcode:35.搜索插入位置」做了之后在做这道题目就好很多了)
-
-确定好:计算出来的右边界是不包好target的右边界,左边界同理。
-
-可以写出如下代码
-
-```
-// 二分查找,寻找target的右边界(不包括target)
-// 如果rightBorder为没有被赋值(即target在数组范围的左边,例如数组[3,3],target为2),为了处理情况一
-int getRightBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
- int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
- while (left <= right) { // 当left==right,区间[left, right]依然有效
- int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
- if (nums[middle] > target) {
- right = middle - 1; // target 在左区间,所以[left, middle - 1]
- } else { // 当nums[middle] == target的时候,更新left,这样才能得到target的右边界
- left = middle + 1;
- rightBorder = left;
- }
- }
- return rightBorder;
-}
-```
-
-## 寻找左边界
-
-```
-// 二分查找,寻找target的左边界leftBorder(不包括target)
-// 如果leftBorder没有被赋值(即target在数组范围的右边,例如数组[3,3],target为4),为了处理情况一
-int getLeftBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
- int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] >= target) { // 寻找左边界,就要在nums[middle] == target的时候更新right
- right = middle - 1;
- leftBorder = right;
- } else {
- left = middle + 1;
- }
- }
- return leftBorder;
-}
-```
-
-## 处理三种情况
-
-左右边界计算完之后,看一下主体代码,这里把上面讨论的三种情况,都覆盖了
-
-```
-class Solution {
-public:
- vector searchRange(vector& nums, int target) {
- int leftBorder = getLeftBorder(nums, target);
- int rightBorder = getRightBorder(nums, target);
- // 情况一
- if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
- // 情况三
- if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
- // 情况二
- return {-1, -1};
- }
-private:
- int getRightBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1;
- int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] > target) {
- right = middle - 1;
- } else { // 寻找右边界,nums[middle] == target的时候更新left
- left = middle + 1;
- rightBorder = left;
- }
- }
- return rightBorder;
- }
- int getLeftBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1;
- int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
- right = middle - 1;
- leftBorder = right;
- } else {
- left = middle + 1;
- }
- }
- return leftBorder;
- }
-};
-```
-
-这份代码在简洁性很有大的优化空间,例如把寻找左右区间函数合并一起。
-
-但拆开更清晰一些,而且把三种情况以及对应的处理逻辑完整的展现出来了。
-
-# 总结
-
-初学者建议大家一块一块的去分拆这道题目,正如本题解描述,想清楚三种情况之后,先专注于寻找右区间,然后专注于寻找左区间,左右根据左右区间做最后判断。
-
-不要上来就想如果一起寻找左右区间,搞着搞着就会顾此失彼,绕进去拔不出来了。
-
-
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
deleted file mode 100644
index 5c6a1545..00000000
--- a/problems/0035.搜索插入位置.md
+++ /dev/null
@@ -1,208 +0,0 @@
-
-
-
-对应的C++代码如下:
-
-```
-class Solution {
-public:
- void nextPermutation(vector& nums) {
- for (int i = nums.size() - 1; i >= 0; i--) {
- for (int j = nums.size() - 1; j > i; j--) {
- if (nums[j] > nums[i]) {
- swap(nums[j], nums[i]);
- sort(nums.begin() + i + 1, nums.end());
- return;
- }
- }
- }
- // 到这里了说明整个数组都是倒叙了,反转一下便可
- reverse(nums.begin(), nums.end());
- }
-};
-```
diff --git a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
deleted file mode 100644
index a62261e9..00000000
--- a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
+++ /dev/null
@@ -1,134 +0,0 @@
-> **如果对二分查找比较模糊,建议看这篇:[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q),这里详细介绍了二分的两种写法,以及循环不变量的重要性,顺便还可以把「leetcode:35.搜索插入位置」题目刷了**。
-
-这道题目如果基础不是很好,不建议大家看简短的代码,简短的代码隐藏了太多逻辑,结果就是稀里糊涂把题AC了,但是没有想清楚具体细节!
-
-下面我来把所有情况都讨论一下。
-
-寻找target在数组里的左右边界,有如下三种情况:
-
-* 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
-* 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
-* 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
-
-这三种情况都考虑到,说明就想的很清楚了。
-
-接下来,在去寻找左边界,和右边界了。
-
-采用二分法来取寻找左右边界,为了让代码清晰,我分别写两个二分来寻找左边界和右边界。
-
-**刚刚接触二分搜索的同学不建议上来就像如果用一个二分来查找左右边界,很容易把自己绕进去,建议扎扎实实的写两个二分分别找左边界和右边界**
-
-## 寻找右边界
-
-先来寻找右边界,至于二分查找,如果看过[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)就会知道,二分查找中什么时候用while (left <= right),有什么时候用while (left < right),其实只要清楚**循环不变量**,很容易区分两种写法。
-
-那么这里我采用while (left <= right)的写法,区间定义为[left, right],即左闭又闭的区间(如果这里有点看不懂了,强烈建议把[为什么每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)这篇文章先看了,在把「leetcode:35.搜索插入位置」做了之后在做这道题目就好很多了)
-
-确定好:计算出来的右边界是不包好target的右边界,左边界同理。
-
-可以写出如下代码
-
-```
-// 二分查找,寻找target的右边界(不包括target)
-// 如果rightBorder为没有被赋值(即target在数组范围的左边,例如数组[3,3],target为2),为了处理情况一
-int getRightBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
- int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
- while (left <= right) { // 当left==right,区间[left, right]依然有效
- int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
- if (nums[middle] > target) {
- right = middle - 1; // target 在左区间,所以[left, middle - 1]
- } else { // 当nums[middle] == target的时候,更新left,这样才能得到target的右边界
- left = middle + 1;
- rightBorder = left;
- }
- }
- return rightBorder;
-}
-```
-
-## 寻找左边界
-
-```
-// 二分查找,寻找target的左边界leftBorder(不包括target)
-// 如果leftBorder没有被赋值(即target在数组范围的右边,例如数组[3,3],target为4),为了处理情况一
-int getLeftBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
- int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] >= target) { // 寻找左边界,就要在nums[middle] == target的时候更新right
- right = middle - 1;
- leftBorder = right;
- } else {
- left = middle + 1;
- }
- }
- return leftBorder;
-}
-```
-
-## 处理三种情况
-
-左右边界计算完之后,看一下主体代码,这里把上面讨论的三种情况,都覆盖了
-
-```
-class Solution {
-public:
- vector searchRange(vector& nums, int target) {
- int leftBorder = getLeftBorder(nums, target);
- int rightBorder = getRightBorder(nums, target);
- // 情况一
- if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
- // 情况三
- if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
- // 情况二
- return {-1, -1};
- }
-private:
- int getRightBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1;
- int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] > target) {
- right = middle - 1;
- } else { // 寻找右边界,nums[middle] == target的时候更新left
- left = middle + 1;
- rightBorder = left;
- }
- }
- return rightBorder;
- }
- int getLeftBorder(vector& nums, int target) {
- int left = 0;
- int right = nums.size() - 1;
- int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
- while (left <= right) {
- int middle = left + ((right - left) / 2);
- if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
- right = middle - 1;
- leftBorder = right;
- } else {
- left = middle + 1;
- }
- }
- return leftBorder;
- }
-};
-```
-
-这份代码在简洁性很有大的优化空间,例如把寻找左右区间函数合并一起。
-
-但拆开更清晰一些,而且把三种情况以及对应的处理逻辑完整的展现出来了。
-
-# 总结
-
-初学者建议大家一块一块的去分拆这道题目,正如本题解描述,想清楚三种情况之后,先专注于寻找右区间,然后专注于寻找左区间,左右根据左右区间做最后判断。
-
-不要上来就想如果一起寻找左右区间,搞着搞着就会顾此失彼,绕进去拔不出来了。
-
-
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
deleted file mode 100644
index 5c6a1545..00000000
--- a/problems/0035.搜索插入位置.md
+++ /dev/null
@@ -1,208 +0,0 @@
-
-
- -
-
-
-  -
-  -
-  -
-  -
-  -
-  -
-
-
-
-> 二分查找法是数组里的常用方法,彻底掌握它是十分必要的。
-
-# 编号35:搜索插入位置
-
-题目地址:https://leetcode-cn.com/problems/search-insert-position/
-
-给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
-
-你可以假设数组中无重复元素。
-
-示例 1:
-输入: [1,3,5,6], 5
-输出: 2
-
-示例 2:
-输入: [1,3,5,6], 2
-输出: 1
-
-示例 3:
-输入: [1,3,5,6], 7
-输出: 4
-
-示例 4:
-输入: [1,3,5,6], 0
-输出: 0
-
-# 思路
-
-这道题目不难,但是为什么通过率相对来说并不高呢,我理解是大家对边界处理的判断有所失误导致的。
-
-这道题目,要在数组中插入目标值,无非是这四种情况。
-
-
-
-* 目标值在数组所有元素之前
-* 目标值等于数组中某一个元素
-* 目标值插入数组中的位置
-* 目标值在数组所有元素之后
-
-这四种情况确认清楚了,就可以尝试解题了。
-
-接下来我将从暴力的解法和二分法来讲解此题,也借此好好讲一讲二分查找法。
-
-## 暴力解法
-
-暴力解题 不一定时间消耗就非常高,关键看实现的方式,就像是二分查找时间消耗不一定就很低,是一样的。
-
-## 暴力解法C++代码
-
-```
-class Solution {
-public:
- int searchInsert(vector& nums, int target) {
- for (int i = 0; i < nums.size(); i++) {
- // 分别处理如下三种情况
- // 目标值在数组所有元素之前
- // 目标值等于数组中某一个元素
- // 目标值插入数组中的位置
- if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i],那么i就是我们要的结果
- return i;
- }
- }
- // 目标值在数组所有元素之后的情况
- return nums.size(); // 如果target是最大的,或者 nums为空,则返回nums的长度
- }
-};
-```
-
-时间复杂度:O(n)
-时间复杂度:O(1)
-
-效率如下:
-
-
-
-## 二分法
-
-既然暴力解法的时间复杂度是O(n),就要尝试一下使用二分查找法。
-
-
-
-大家注意这道题目的前提是数组是有序数组,这也是使用二分查找的基础条件。
-
-以后大家**只要看到面试题里给出的数组是有序数组,都可以想一想是否可以使用二分法。**
-
-同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下表可能不是唯一的。
-
-大体讲解一下二分法的思路,这里来举一个例子,例如在这个数组中,使用二分法寻找元素为5的位置,并返回其下标。
-
-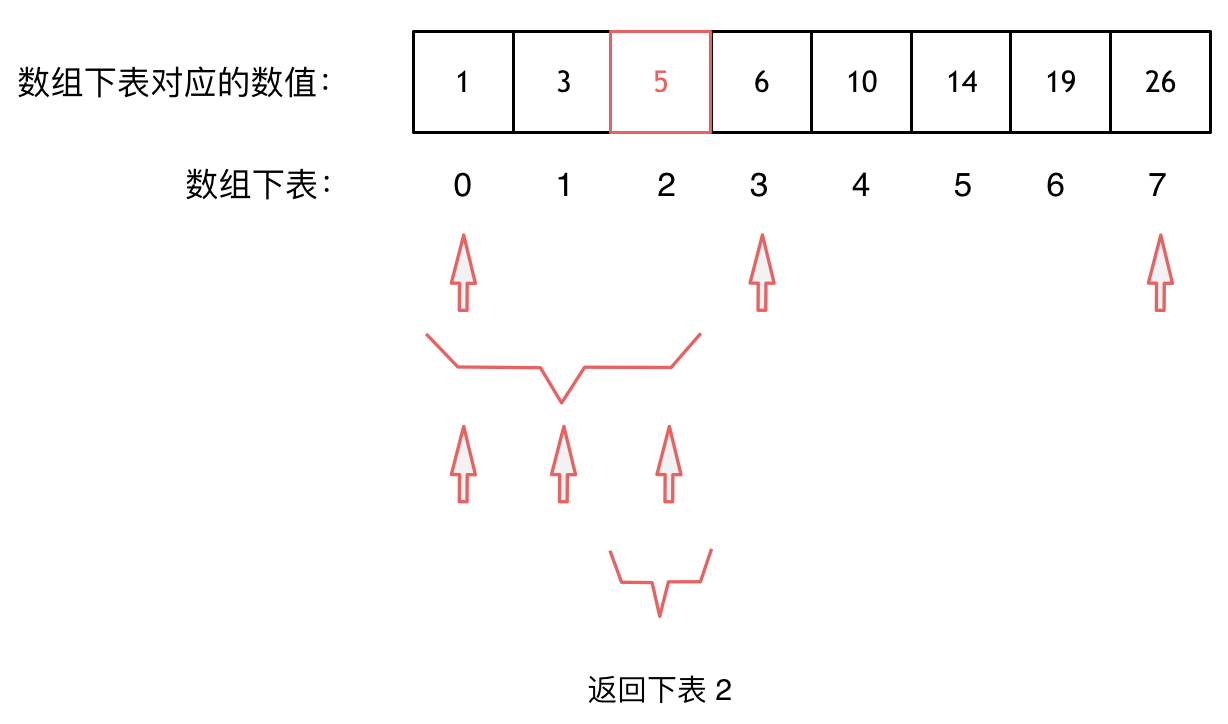
-
-二分查找涉及的很多的边界条件,逻辑比较简单,就是写不好。
-
-相信很多同学对二分查找法中边界条件处理不好。
-
-例如到底是 `while(left < right)` 还是 `while(left <= right)`,到底是`right = middle`呢,还是要`right = middle - 1`呢?
-
-这里弄不清楚主要是因为**对区间的定义没有想清楚,这就是不变量**。
-
-要在二分查找的过程中,保持不变量,这也就是**循环不变量** (感兴趣的同学可以查一查)。
-
-## 二分法第一种写法
-
-以这道题目来举例,以下的代码中定义 target 是在一个在左闭右闭的区间里,**也就是[left, right] (这个很重要)**。
-
-这就决定了这个二分法的代码如何去写,大家看如下代码:
-
-**大家要仔细看注释,思考为什么要写while(left <= right), 为什么要写right = middle - 1**。
-
-```
-class Solution {
-public:
- int searchInsert(vector& nums, int target) {
- int n = nums.size();
- int left = 0;
- int right = n - 1; // 定义target在左闭右闭的区间里,[left, right]
- while (left <= right) { // 当left==right,区间[left, right]依然有效
- int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
- if (nums[middle] > target) {
- right = middle - 1; // target 在左区间,所以[left, middle - 1]
- } else if (nums[middle] < target) {
- left = middle + 1; // target 在右区间,所以[middle + 1, right]
- } else { // nums[middle] == target
- return middle;
- }
- }
- // 分别处理如下四种情况
- // 目标值在数组所有元素之前 [0, -1]
- // 目标值等于数组中某一个元素 return middle;
- // 目标值插入数组中的位置 [left, right],return right + 1
- // 目标值在数组所有元素之后的情况 [left, right], return right + 1
- return right + 1;
- }
-};
-```
-时间复杂度:O(logn)
-时间复杂度:O(1)
-
-效率如下:
-
-
-## 二分法第二种写法
-
-如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) 。
-
-那么二分法的边界处理方式则截然不同。
-
-不变量是[left, right)的区间,如下代码可以看出是如何在循环中坚持不变量的。
-
-**大家要仔细看注释,思考为什么要写while (left < right), 为什么要写right = middle**。
-
-```
-class Solution {
-public:
- int searchInsert(vector& nums, int target) {
- int n = nums.size();
- int left = 0;
- int right = n; // 定义target在左闭右开的区间里,[left, right) target
- while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间
- int middle = left + ((right - left) >> 1);
- if (nums[middle] > target) {
- right = middle; // target 在左区间,在[left, middle)中
- } else if (nums[middle] < target) {
- left = middle + 1; // target 在右区间,在 [middle+1, right)中
- } else { // nums[middle] == target
- return middle; // 数组中找到目标值的情况,直接返回下标
- }
- }
- // 分别处理如下四种情况
- // 目标值在数组所有元素之前 [0,0)
- // 目标值等于数组中某一个元素 return middle
- // 目标值插入数组中的位置 [left, right) ,return right 即可
- // 目标值在数组所有元素之后的情况 [left, right),return right 即可
- return right;
- }
-};
-```
-
-时间复杂度:O(logn)
-时间复杂度:O(1)
-
-# 总结
-
-希望通过这道题目,大家会发现平时写二分法,为什么总写不好,就是因为对区间定义不清楚。
-
-确定要查找的区间到底是左闭右开[left, right),还是左闭又闭[left, right],这就是不变量。
-
-然后在**二分查找的循环中,坚持循环不变量的原则**,很多细节问题,自然会知道如何处理了。
-
-**循序渐进学算法,认准「代码随想录」,Carl手把手带你过关斩将!**
-
-
- -
-
diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
deleted file mode 100644
index 4e3a74e2..00000000
--- a/problems/0037.解数独.md
+++ /dev/null
@@ -1,215 +0,0 @@
-> 解数独,理解二维递归是关键
-
-如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
-
-# 37. 解数独
-
-题目地址:https://leetcode-cn.com/problems/sudoku-solver/
-
-编写一个程序,通过填充空格来解决数独问题。
-
-一个数独的解法需遵循如下规则:
-数字 1-9 在每一行只能出现一次。
-数字 1-9 在每一列只能出现一次。
-数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
-空白格用 '.' 表示。
-
-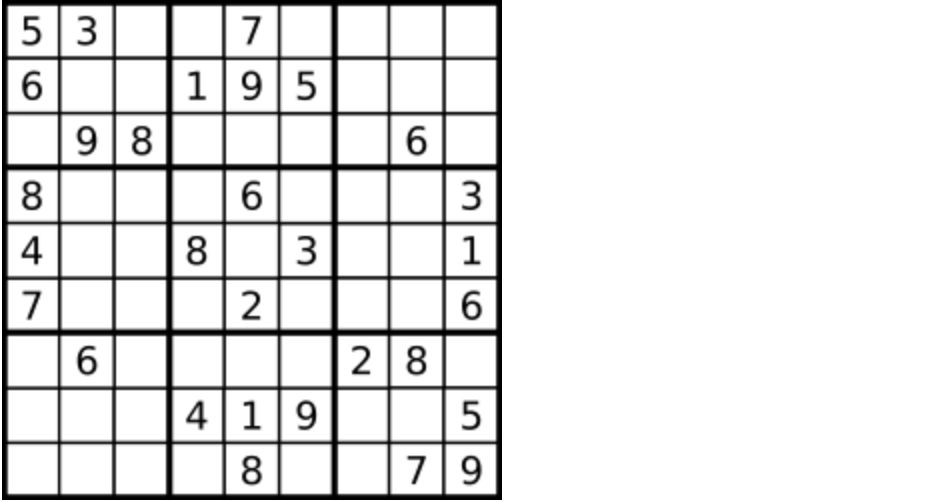
-
-一个数独。
-
-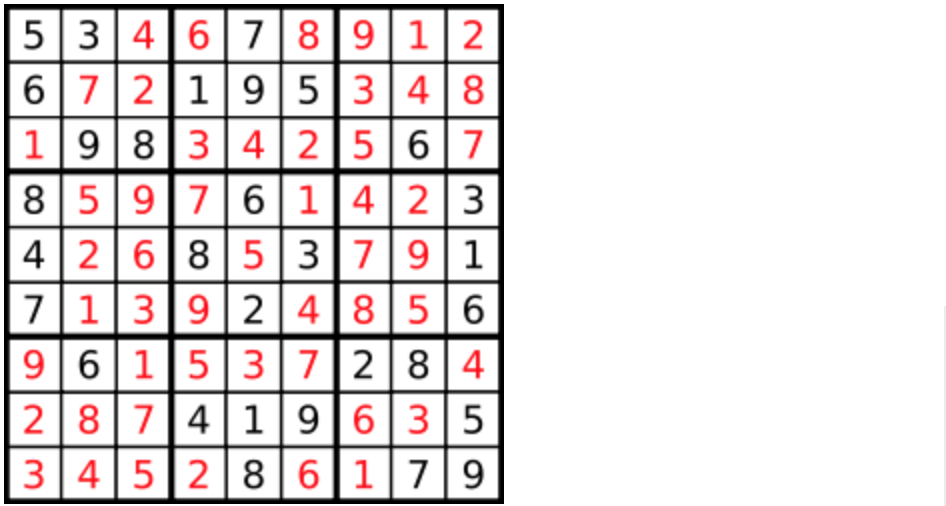
-
-答案被标成红色。
-
-提示:
-* 给定的数独序列只包含数字 1-9 和字符 '.' 。
-* 你可以假设给定的数独只有唯一解。
-* 给定数独永远是 9x9 形式的。
-
-# 思路
-
-棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是**二维递归**。
-
-怎么做二维递归呢?
-
-大家已经跟着「代码随想录」刷过了如下回溯法题目,例如:[77.组合(组合问题)](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[131.分割回文串(分割问题)](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q),[78.子集(子集问题)](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),[46.全排列(排列问题)](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw),以及[51.N皇后(N皇后问题)](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg),其实这些题目都是一维递归。
-
-**如果以上这几道题目没有做过的话,不建议上来就做这道题哈!**
-
-[N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
-
-本题就不一样了,**本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
-
-因为这个树形结构太大了,我抽取一部分,如图所示:
-
-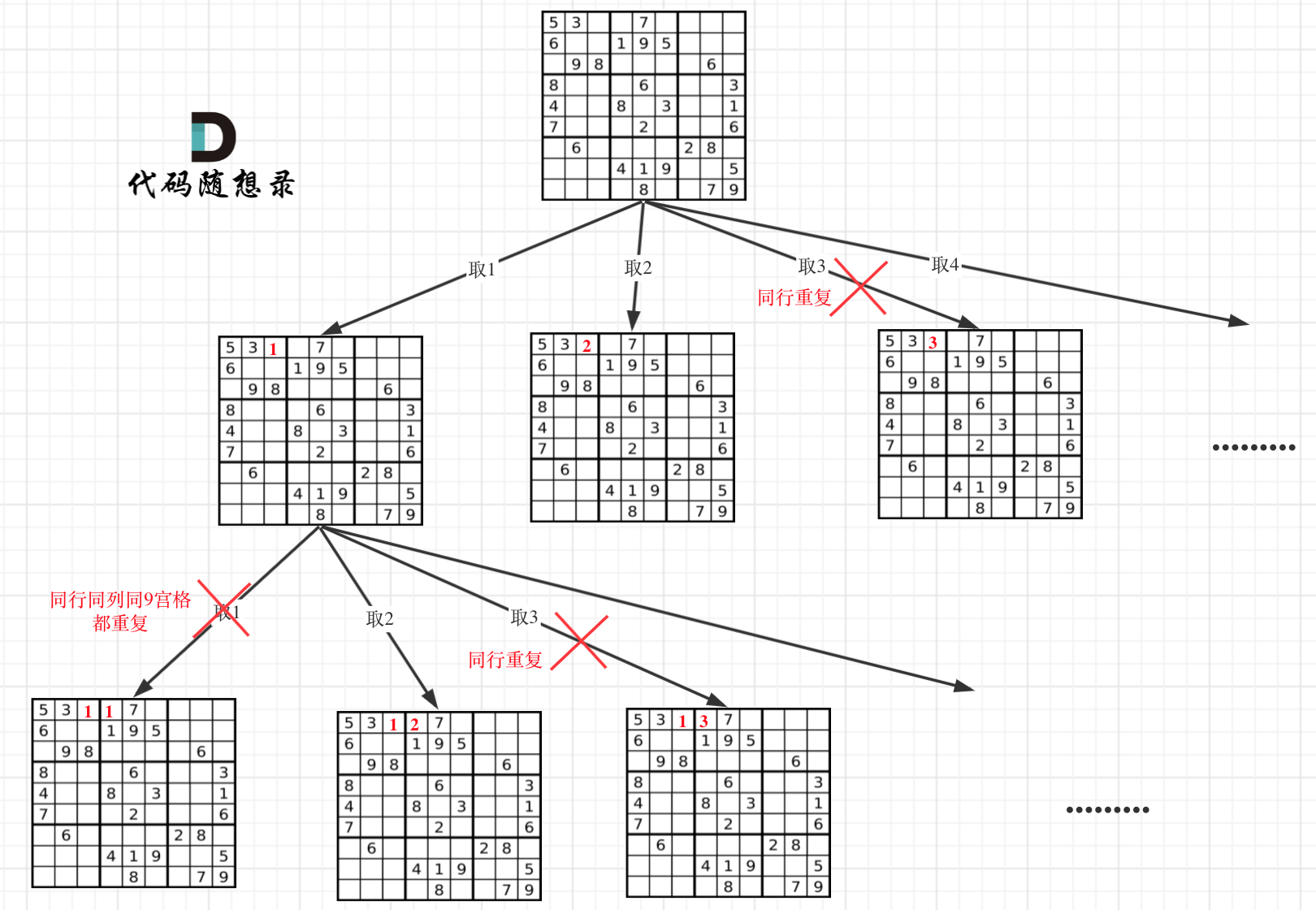
-
-
-## 回溯三部曲
-
-* 递归函数以及参数
-
-**递归函数的返回值需要是bool类型,为什么呢?**
-
-因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值,这一点在[回溯算法:N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)中已经介绍过了,一样的道理。
-
-代码如下:
-
-```
-bool backtracking(vector>& board)
-```
-
-* 递归终止条件
-
-本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
-
-**不用终止条件会不会死循环?**
-
-递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
-
-**那么有没有永远填不满的情况呢?**
-
-这个问题我在递归单层搜索逻辑里在来讲!
-
-* 递归单层搜索逻辑
-
-
-
-在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
-
-**一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!**
-
-
-代码如下:(**详细看注释**)
-
-```C++
-bool backtracking(vector>& board) {
- for (int i = 0; i < board.size(); i++) { // 遍历行
- for (int j = 0; j < board[0].size(); j++) { // 遍历列
- if (board[i][j] != '.') continue;
- for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
- if (isValid(i, j, k, board)) {
- board[i][j] = k; // 放置k
- if (backtracking(board)) return true; // 如果找到合适一组立刻返回
- board[i][j] = '.'; // 回溯,撤销k
- }
- }
- return false; // 9个数都试完了,都不行,那么就返回false
- }
- }
- return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
-}
-```
-
-**注意这里return false的地方,这里放return false 是有讲究的**。
-
-因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解!
-
-那么会直接返回, **这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!**
-
-## 判断棋盘是否合法
-
-判断棋盘是否合法有如下三个维度:
-
-* 同行是否重复
-* 同列是否重复
-* 9宫格里是否重复
-
-代码如下:
-
-```C++
-bool isValid(int row, int col, char val, vector>& board) {
- for (int i = 0; i < 9; i++) { // 判断行里是否重复
- if (board[row][i] == val) {
- return false;
- }
- }
- for (int j = 0; j < 9; j++) { // 判断列里是否重复
- if (board[j][col] == val) {
- return false;
- }
- }
- int startRow = (row / 3) * 3;
- int startCol = (col / 3) * 3;
- for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
- for (int j = startCol; j < startCol + 3; j++) {
- if (board[i][j] == val ) {
- return false;
- }
- }
- }
- return true;
-}
-```
-
-最后整体代码如下:
-
-# C++代码
-
-```C++
-class Solution {
-private:
-bool backtracking(vector>& board) {
- for (int i = 0; i < board.size(); i++) { // 遍历行
- for (int j = 0; j < board[0].size(); j++) { // 遍历列
- if (board[i][j] != '.') continue;
- for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
- if (isValid(i, j, k, board)) {
- board[i][j] = k; // 放置k
- if (backtracking(board)) return true; // 如果找到合适一组立刻返回
- board[i][j] = '.'; // 回溯,撤销k
- }
- }
- return false; // 9个数都试完了,都不行,那么就返回false
- }
- }
- return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
-}
-bool isValid(int row, int col, char val, vector>& board) {
- for (int i = 0; i < 9; i++) { // 判断行里是否重复
- if (board[row][i] == val) {
- return false;
- }
- }
- for (int j = 0; j < 9; j++) { // 判断列里是否重复
- if (board[j][col] == val) {
- return false;
- }
- }
- int startRow = (row / 3) * 3;
- int startCol = (col / 3) * 3;
- for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
- for (int j = startCol; j < startCol + 3; j++) {
- if (board[i][j] == val ) {
- return false;
- }
- }
- }
- return true;
-}
-public:
- void solveSudoku(vector>& board) {
- backtracking(board);
- }
-};
-```
-
-# 总结
-
-解数独可以说是非常难的题目了,如果还一直停留在单层递归的逻辑中,这道题目可以让大家瞬间崩溃。
-
-所以我在开篇就提到了**二维递归**,这也是我自创词汇,希望可以帮助大家理解解数独的搜索过程。
-
-一波分析之后,在看代码会发现其实也不难,唯一难点就是理解**二维递归**的思维逻辑。
-
-**这样,解数独这么难的问题,也被我们攻克了**。
-
-**恭喜一路上坚持打卡的录友们,回溯算法已经接近尾声了,接下来就是要一波总结了**。
-
-如果一直跟住「代码随想录」的节奏,你会发现自己进步飞快,从思维方式到刷题习惯,都会有质的飞跃,「代码随想录」绝对值得推荐给身边的同学朋友们!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0039.组合总和.md b/problems/0039.组合总和.md
deleted file mode 100644
index 9ec073e5..00000000
--- a/problems/0039.组合总和.md
+++ /dev/null
@@ -1,227 +0,0 @@
-
-> 看懂很容易,彻底掌握需要下功夫
-
-# 第39题. 组合总和
-
-题目链接:https://leetcode-cn.com/problems/combination-sum/
-
-给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
-
-candidates 中的数字可以无限制重复被选取。
-
-说明:
-
-* 所有数字(包括 target)都是正整数。
-* 解集不能包含重复的组合。
-
-示例 1:
-输入:candidates = [2,3,6,7], target = 7,
-所求解集为:
-[
- [7],
- [2,2,3]
-]
-
-示例 2:
-输入:candidates = [2,3,5], target = 8,
-所求解集为:
-[
- [2,2,2,2],
- [2,3,3],
- [3,5]
-]
-
-# 思路
-
-题目中的**无限制重复被选取,吓得我赶紧想想 出现0 可咋办**,然后看到下面提示:1 <= candidates[i] <= 200,我就放心了。
-
-本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
-
-本题搜索的过程抽象成树形结构如下:
-
-
-注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
-
-而在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w) 中都可以知道要递归K层,因为要取k个元素的组合。
-
-## 回溯三部曲
-
-* 递归函数参数
-
-这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
-
-首先是题目中给出的参数,集合candidates, 和目标值target。
-
-此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
-
-**本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?**
-
-我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)。
-
-如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:[回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
-
-**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我再讲解排列的时候就重点介绍**。
-
-代码如下:
-
-```
-vector> result;
-vector path;
-void backtracking(vector& candidates, int target, int sum, int startIndex)
-```
-
-* 递归终止条件
-
-在如下树形结构中:
-
-
-
-从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
-
-sum等于target的时候,需要收集结果,代码如下:
-
-```
-if (sum > target) {
- return;
-}
-if (sum == target) {
- result.push_back(path);
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-单层for循环依然是从startIndex开始,搜索candidates集合。
-
-**注意本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)的一个区别是:本题元素为可重复选取的**。
-
-如何重复选取呢,看代码,注释部分:
-
-```
-for (int i = startIndex; i < candidates.size(); i++) {
- sum += candidates[i];
- path.push_back(candidates[i]);
- backtracking(candidates, target, sum, i); // 关键点:不用i+1了,表示可以重复读取当前的数
- sum -= candidates[i]; // 回溯
- path.pop_back(); // 回溯
-}
-```
-
-按照[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中给出的模板,不难写出如下C++完整代码:
-
-```
-// 版本一
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& candidates, int target, int sum, int startIndex) {
- if (sum > target) {
- return;
- }
- if (sum == target) {
- result.push_back(path);
- return;
- }
-
- for (int i = startIndex; i < candidates.size(); i++) {
- sum += candidates[i];
- path.push_back(candidates[i]);
- backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数
- sum -= candidates[i];
- path.pop_back();
- }
- }
-public:
- vector> combinationSum(vector& candidates, int target) {
- result.clear();
- path.clear();
- backtracking(candidates, target, 0, 0);
- return result;
- }
-};
-```
-
-## 剪枝优化
-
-在这个树形结构中:
-
-
-
-以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
-
-其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
-
-那么可以在for循环的搜索范围上做做文章了。
-
-**对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历**。
-
-如图:
-
-
-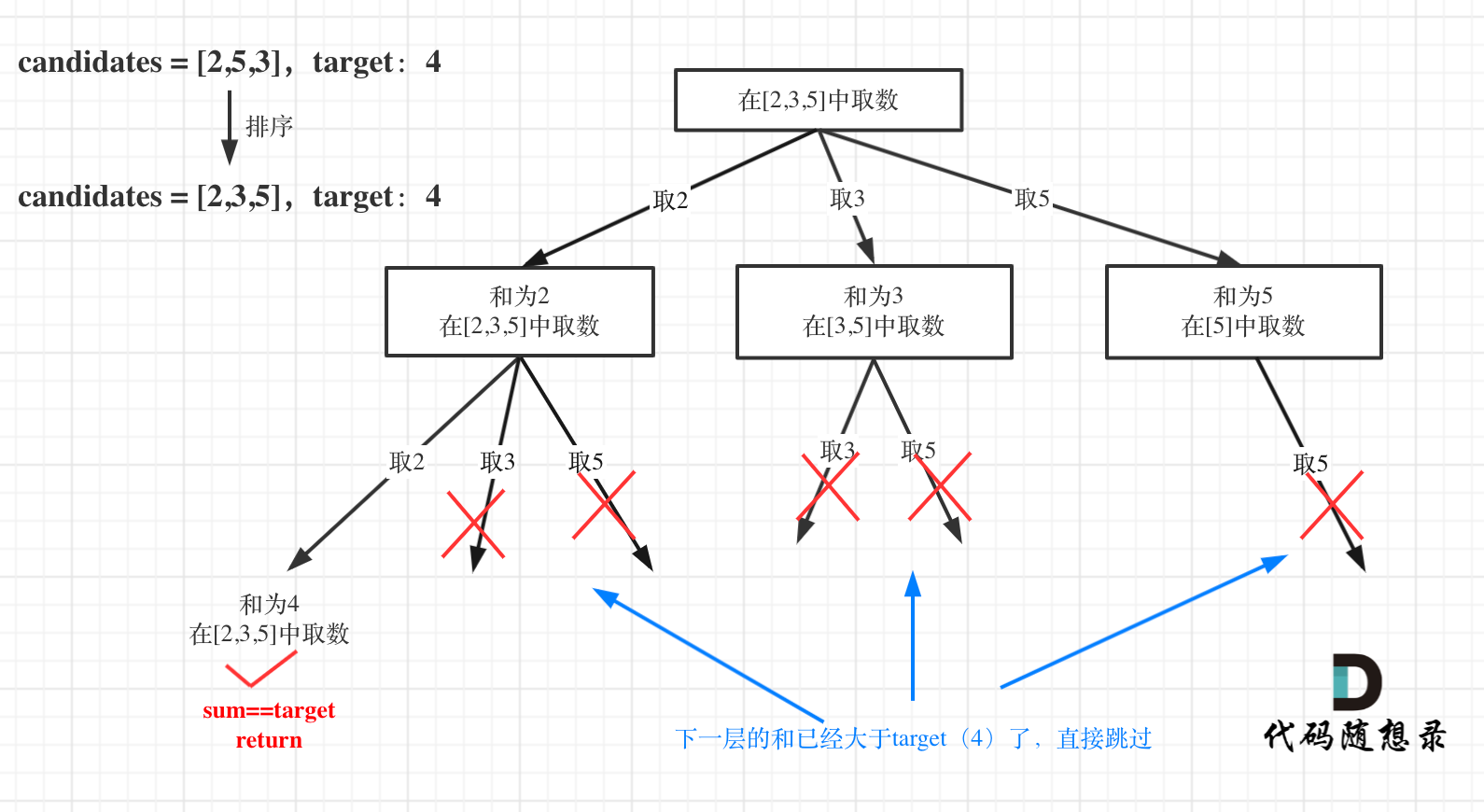
-
-for循环剪枝代码如下:
-
-```
-for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
-```
-
-整体代码如下:(注意注释的部分)
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& candidates, int target, int sum, int startIndex) {
- if (sum == target) {
- result.push_back(path);
- return;
- }
-
- // 如果 sum + candidates[i] > target 就终止遍历
- for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
- sum += candidates[i];
- path.push_back(candidates[i]);
- backtracking(candidates, target, sum, i);
- sum -= candidates[i];
- path.pop_back();
-
- }
- }
-public:
- vector> combinationSum(vector& candidates, int target) {
- result.clear();
- path.clear();
- sort(candidates.begin(), candidates.end()); // 需要排序
- backtracking(candidates, target, 0, 0);
- return result;
- }
-};
-```
-
-# 总结
-
-本题和我们之前讲过的[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)有两点不同:
-
-* 组合没有数量要求
-* 元素可无限重复选取
-
-针对这两个问题,我都做了详细的分析。
-
-并且给出了对于组合问题,什么时候用startIndex,什么时候不用,并用[回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)做了对比。
-
-最后还给出了本题的剪枝优化,这个优化如果是初学者的话并不容易想到。
-
-**在求和问题中,排序之后加剪枝是常见的套路!**
-
-可以看出我写的文章都会大量引用之前的文章,就是要不断作对比,分析其差异,然后给出代码解决的方法,这样才能彻底理解题目的本质与难点。
-
-**就酱,如果感觉很给力,就帮Carl宣传一波吧,哈哈**。
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0040.组合总和II.md b/problems/0040.组合总和II.md
deleted file mode 100644
index 40179710..00000000
--- a/problems/0040.组合总和II.md
+++ /dev/null
@@ -1,206 +0,0 @@
-> 这篇可以说是全网把组合问题如何去重,讲的最清晰的了!
-
-# 40.组合总和II
-
-题目链接:https://leetcode-cn.com/problems/combination-sum-ii/
-
-给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
-
-candidates 中的每个数字在每个组合中只能使用一次。
-
-说明:
-所有数字(包括目标数)都是正整数。
-解集不能包含重复的组合。
-
-示例 1:
-输入: candidates = [10,1,2,7,6,1,5], target = 8,
-所求解集为:
-[
- [1, 7],
- [1, 2, 5],
- [2, 6],
- [1, 1, 6]
-]
-
-示例 2:
-输入: candidates = [2,5,2,1,2], target = 5,
-所求解集为:
-[
- [1,2,2],
- [5]
-]
-
-# 思路
-
-这道题目和[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)如下区别:
-
-1. 本题candidates 中的每个数字在每个组合中只能使用一次。
-2. 本题数组candidates的元素是有重复的,而[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)是无重复元素的数组candidates
-
-最后本题和[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)要求一样,解集不能包含重复的组合。
-
-**本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合**。
-
-一些同学可能想了:我把所有组合求出来,再用set或者map去重,这么做很容易超时!
-
-所以要在搜索的过程中就去掉重复组合。
-
-很多同学在去重的问题上想不明白,其实很多题解也没有讲清楚,反正代码是能过的,感觉是那么回事,稀里糊涂的先把题目过了。
-
-这个去重为什么很难理解呢,**所谓去重,其实就是使用过的元素不能重复选取。** 这么一说好像很简单!
-
-都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。**没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。**
-
-那么问题来了,我们是要同一树层上使用过,还是统一树枝上使用过呢?
-
-回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
-
-
-**所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重**。
-
-为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)
-
-**强调一下,树层去重的话,需要对数组排序!**
-
-选择过程树形结构如图所示:
-
-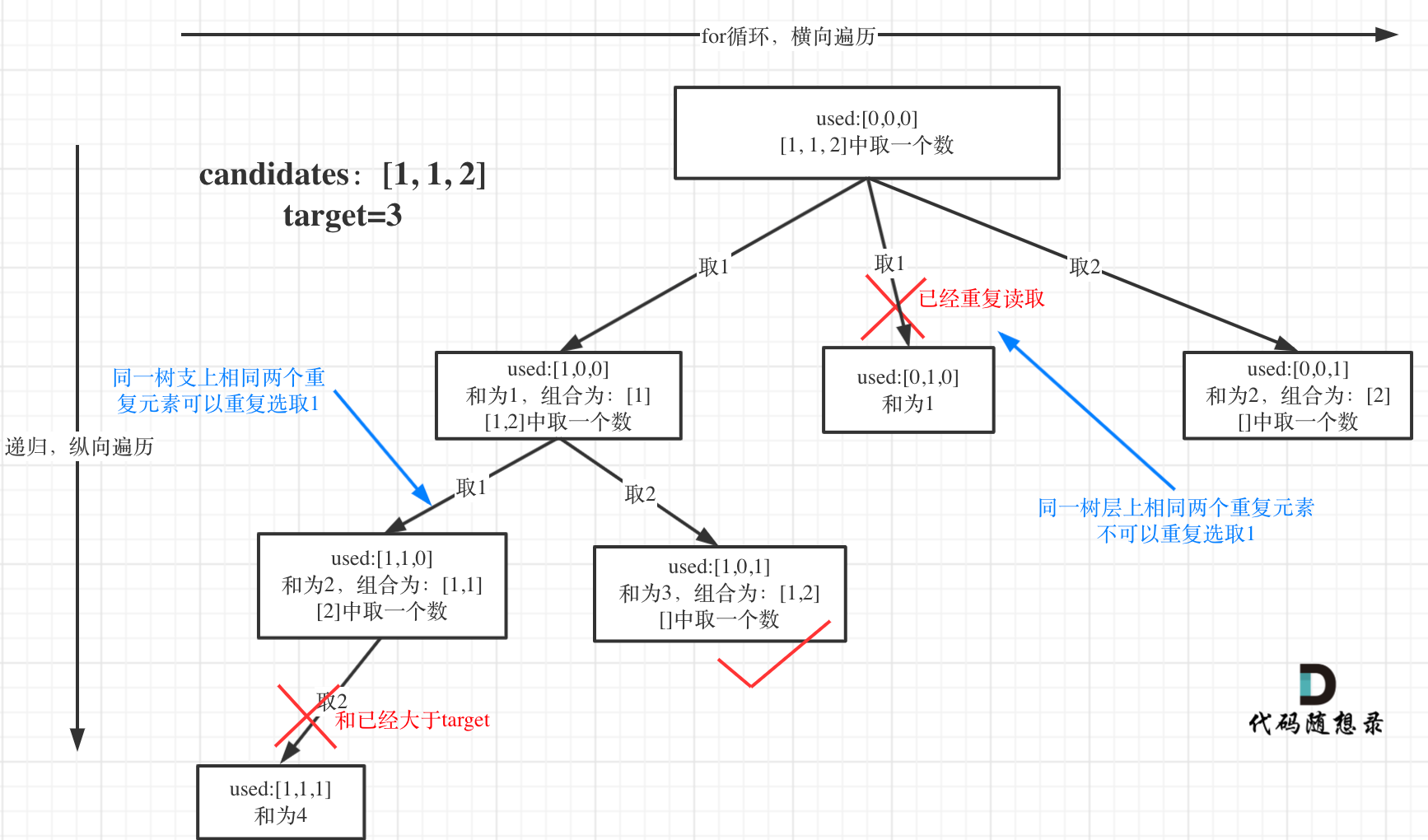
-
-可以看到图中,每个节点相对于 [39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)我多加了used数组,这个used数组下面会重点介绍。
-
-## 回溯三部曲
-
-* **递归函数参数**
-
-与[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
-
-这个集合去重的重任就是used来完成的。
-
-代码如下:
-
-```
-vector> result; // 存放组合集合
-vector path; // 符合条件的组合
-void backtracking(vector& candidates, int target, int sum, int startIndex, vector& used) {
-```
-
-* **递归终止条件**
-
-与[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)相同,终止条件为 `sum > target` 和 `sum == target`。
-
-代码如下:
-
-```
-if (sum > target) { // 这个条件其实可以省略
- return;
-}
-if (sum == target) {
- result.push_back(path);
- return;
-}
-```
-
-`sum > target` 这个条件其实可以省略,因为和在递归单层遍历的时候,会有剪枝的操作,下面会介绍到。
-
-* **单层搜索的逻辑**
-
-这里与[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)最大的不同就是要去重了。
-
-前面我们提到:要去重的是“同一树层上的使用过”,如果判断同一树层上元素(相同的元素)是否使用过了呢。
-
-**如果`candidates[i] == candidates[i - 1]` 并且 `used[i - 1] == false`,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]**。
-
-此时for循环里就应该做continue的操作。
-
-这块比较抽象,如图:
-
-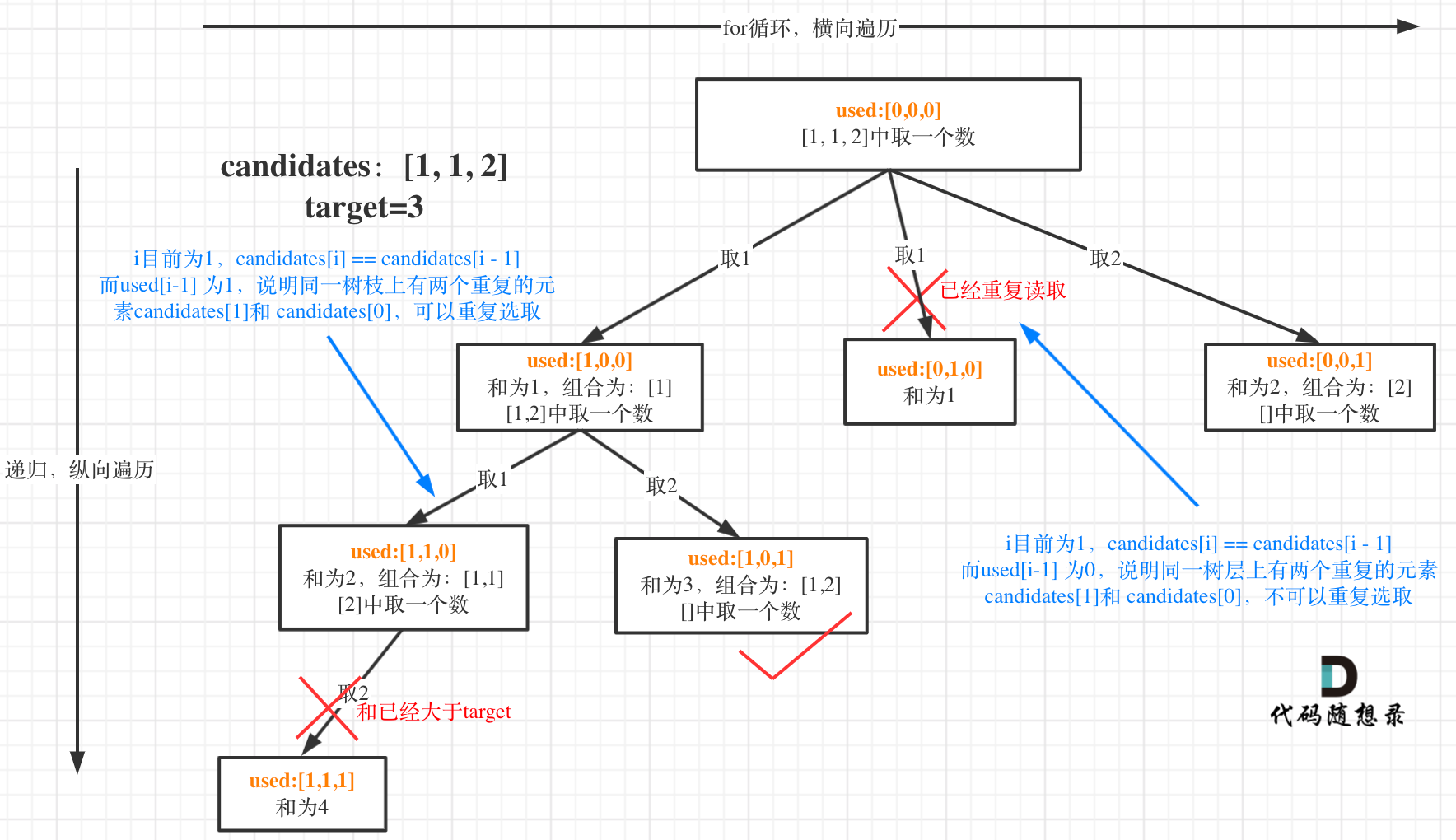
-
-我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
-
-* used[i - 1] == true,说明同一树支candidates[i - 1]使用过
-* used[i - 1] == false,说明同一树层candidates[i - 1]使用过
-
-**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
-
-那么单层搜索的逻辑代码如下:
-
-```
-for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
- // used[i - 1] == true,说明同一树支candidates[i - 1]使用过
- // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
- // 要对同一树层使用过的元素进行跳过
- if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
- continue;
- }
- sum += candidates[i];
- path.push_back(candidates[i]);
- used[i] = true;
- backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1:这里是i+1,每个数字在每个组合中只能使用一次
- used[i] = false;
- sum -= candidates[i];
- path.pop_back();
-}
-```
-
-**注意sum + candidates[i] <= target为剪枝操作,在[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)有讲解过!**
-
-## C++代码
-
-回溯三部曲分析完了,整体C++代码如下:
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& candidates, int target, int sum, int startIndex, vector& used) {
- if (sum == target) {
- result.push_back(path);
- return;
- }
- for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
- // used[i - 1] == true,说明同一树支candidates[i - 1]使用过
- // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
- // 要对同一树层使用过的元素进行跳过
- if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
- continue;
- }
- sum += candidates[i];
- path.push_back(candidates[i]);
- used[i] = true;
- backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
- used[i] = false;
- sum -= candidates[i];
- path.pop_back();
- }
- }
-
-public:
- vector> combinationSum2(vector& candidates, int target) {
- vector used(candidates.size(), false);
- path.clear();
- result.clear();
- // 首先把给candidates排序,让其相同的元素都挨在一起。
- sort(candidates.begin(), candidates.end());
- backtracking(candidates, target, 0, 0, used);
- return result;
- }
-};
-
-```
-
-# 总结
-
-本题同样是求组合总和,但就是因为其数组candidates有重复元素,而要求不能有重复的组合,所以相对于[39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)难度提升了不少。
-
-**关键是去重的逻辑,代码很简单,网上一搜一大把,但几乎没有能把这块代码含义讲明白的,基本都是给出代码,然后说这就是去重了,究竟怎么个去重法也是模棱两可**。
-
-所以Carl有必要把去重的这块彻彻底底的给大家讲清楚,**就连“树层去重”和“树枝去重”都是我自创的词汇,希望对大家理解有帮助!**
-
-**就酱,如果感觉「代码随想录」诚意满满,就帮Carl宣传一波吧,感谢啦!**
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
deleted file mode 100644
index 05cf9e08..00000000
--- a/problems/0042.接雨水.md
+++ /dev/null
@@ -1,340 +0,0 @@
-# 题目链接
-
-# 思路
-
-接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
-
-本文深度讲解如下三种方法:
-* 双指针法
-* 动态规划
-* 单调栈
-
-## 双指针解法
-
-这道题目暴力解法并不简单,我们来看一下思路。
-
-首先要明确,要按照行来计算,还是按照列来计算。如图所示:
-
- -
-
-
- -
-一些同学在实现暴力解法的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
-
-我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
-
-首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
-
-可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
-
-这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
-
-
-
-一些同学在实现暴力解法的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
-
-我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
-
-首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
-
-可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
-
-这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
-
- -
-列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
-
-列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
-
-列4 柱子的高度为1(以下用height表示)
-
-那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
-
-列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
-
-此时求出了列4的雨水体积。
-
-一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
-
-首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
-```
-for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-}
-```
-
-在for循环中求左右两边最高柱子,代码如下:
-
-```
-int rHeight = height[i]; // 记录右边柱子的最高高度
-int lHeight = height[i]; // 记录左边柱子的最高高度
-for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
-}
-for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
-}
-```
-
-最后,计算该列的雨水高度,代码如下:
-
-```
-int h = min(lHeight, rHeight) - height[i];
-if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
-```
-
-整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- int sum = 0;
- for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-
- int rHeight = height[i]; // 记录右边柱子的最高高度
- int lHeight = height[i]; // 记录左边柱子的最高高度
- for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
- }
- for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
- }
- int h = min(lHeight, rHeight) - height[i];
- if (h > 0) sum += h;
- }
- return sum;
- }
-};
-```
-
-因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2)。
-空间复杂度为O(1)。
-
-## 动态规划解法
-
-在上面的双指针解法,我们可以看到,只要知道左边柱子的最高高度 和 记录右边柱子的最高高度,就可以计算当前位置的雨水面积,这也是也列来计算的。
-
-即,当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度
-
-为了的到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一波。
-
-这其实是有重复计算的。
-
-我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。
-
-避免的重复计算,者就用到了动态规划。
-
-当前位置,左边的最高高度,是前一个位置的最高高度和本高度的最大值。
-
-即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
-
-从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
-
-这样就找到递推公式。
-
-是不是地推公式还挺简单的,其实动态规划就是这样,只要想到了递推公式,其实就比较简单了。
-
-代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- if (height.size() <= 2) return 0;
- vector maxLeft(height.size(), 0);
- vector maxRight(height.size(), 0);
- int size = maxRight.size();
-
- // 记录每个柱子左边柱子最大高度
- maxLeft[0] = height[0];
- for (int i = 1; i < size; i++) {
- maxLeft[i] = max(height[i], maxLeft[i - 1]);
- }
- // 记录每个柱子右边柱子最大高度
- maxRight[size - 1] = height[size - 1];
- for (int i = size - 2; i >= 0; i--) {
- maxRight[i] = max(height[i], maxRight[i + 1]);
- }
- // 求和
- int sum = 0;
- for (int i = 0; i < size; i++) {
- int count = min(maxLeft[i], maxRight[i]) - height[i];
- if (count > 0) sum += count;
- }
- return sum;
- }
-};
-```
-
-## 单调栈解法
-
-这个解法可以说是最不好理解的了,所以下面我花了大量的篇幅来介绍这种方法。
-
-单调栈就是保持栈内元素有序。和[栈与队列:单调队列](https://mp.weixin.qq.com/s/8c6l2bO74xyMjph09gQtpA)一样,需要我们自己维持顺序,没有现成的容器可以用。
-
-
-### 准备工作
-
-那么本题使用单调栈有如下几个问题:
-
-1. 首先单调栈是按照行方向来计算雨水,如图:
-
-
-
-列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
-
-列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
-
-列4 柱子的高度为1(以下用height表示)
-
-那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
-
-列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
-
-此时求出了列4的雨水体积。
-
-一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
-
-首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
-```
-for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-}
-```
-
-在for循环中求左右两边最高柱子,代码如下:
-
-```
-int rHeight = height[i]; // 记录右边柱子的最高高度
-int lHeight = height[i]; // 记录左边柱子的最高高度
-for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
-}
-for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
-}
-```
-
-最后,计算该列的雨水高度,代码如下:
-
-```
-int h = min(lHeight, rHeight) - height[i];
-if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
-```
-
-整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- int sum = 0;
- for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-
- int rHeight = height[i]; // 记录右边柱子的最高高度
- int lHeight = height[i]; // 记录左边柱子的最高高度
- for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
- }
- for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
- }
- int h = min(lHeight, rHeight) - height[i];
- if (h > 0) sum += h;
- }
- return sum;
- }
-};
-```
-
-因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2)。
-空间复杂度为O(1)。
-
-## 动态规划解法
-
-在上面的双指针解法,我们可以看到,只要知道左边柱子的最高高度 和 记录右边柱子的最高高度,就可以计算当前位置的雨水面积,这也是也列来计算的。
-
-即,当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度
-
-为了的到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一波。
-
-这其实是有重复计算的。
-
-我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。
-
-避免的重复计算,者就用到了动态规划。
-
-当前位置,左边的最高高度,是前一个位置的最高高度和本高度的最大值。
-
-即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
-
-从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
-
-这样就找到递推公式。
-
-是不是地推公式还挺简单的,其实动态规划就是这样,只要想到了递推公式,其实就比较简单了。
-
-代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- if (height.size() <= 2) return 0;
- vector maxLeft(height.size(), 0);
- vector maxRight(height.size(), 0);
- int size = maxRight.size();
-
- // 记录每个柱子左边柱子最大高度
- maxLeft[0] = height[0];
- for (int i = 1; i < size; i++) {
- maxLeft[i] = max(height[i], maxLeft[i - 1]);
- }
- // 记录每个柱子右边柱子最大高度
- maxRight[size - 1] = height[size - 1];
- for (int i = size - 2; i >= 0; i--) {
- maxRight[i] = max(height[i], maxRight[i + 1]);
- }
- // 求和
- int sum = 0;
- for (int i = 0; i < size; i++) {
- int count = min(maxLeft[i], maxRight[i]) - height[i];
- if (count > 0) sum += count;
- }
- return sum;
- }
-};
-```
-
-## 单调栈解法
-
-这个解法可以说是最不好理解的了,所以下面我花了大量的篇幅来介绍这种方法。
-
-单调栈就是保持栈内元素有序。和[栈与队列:单调队列](https://mp.weixin.qq.com/s/8c6l2bO74xyMjph09gQtpA)一样,需要我们自己维持顺序,没有现成的容器可以用。
-
-
-### 准备工作
-
-那么本题使用单调栈有如下几个问题:
-
-1. 首先单调栈是按照行方向来计算雨水,如图:
-
- -
-知道这一点,后面的就可以理解了。
-
-2. 使用单调栈内元素的顺序
-
-从大到小还是从小打到呢?
-
-要从栈底到栈头(元素从栈头弹出)是从大到小的顺序。
-
-因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
-
-如图:
-
-
-
-知道这一点,后面的就可以理解了。
-
-2. 使用单调栈内元素的顺序
-
-从大到小还是从小打到呢?
-
-要从栈底到栈头(元素从栈头弹出)是从大到小的顺序。
-
-因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
-
-如图:
-
- -
-
-3. 遇到相同高度的柱子怎么办。
-
-遇到相同的元素,更新栈内下表,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
-
-例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
-
-因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-如图所示:
-
-
-
-
-
-3. 遇到相同高度的柱子怎么办。
-
-遇到相同的元素,更新栈内下表,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
-
-例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
-
-因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-如图所示:
-
-
- -
-
-4. 栈里要保存什么数值
-
-是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
-
-长就是通过柱子的高度来计算,宽是通过柱子之间的下表来计算,
-
-那么栈里有没有必要存一个pair类型的元素,保存柱子的高度和下表呢。
-
-其实不用,栈里就存放int类型的元素就行了,表示下表,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下表对应的高度了。
-
-所以栈的定义如下:
-
-```
-stack st; // 存着下标,计算的时候用下标对应的柱子高度
-```
-
-明确了如上几点,我们再来看处理逻辑。
-
-### 单调栈处理逻辑
-
-先将下表0的柱子加入到栈中,`st.push(0);`。
-
-然后开始从下表1开始遍历所有的柱子,`for (int i = 1; i < height.size(); i++)`。
-
-如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从大到小的顺序(从栈底到栈头)。
-
-代码如下:
-
-```
-if (height[i] < height[st.top()]) st.push(i);
-```
-
-如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-代码如下:
-
-```
-if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
- st.pop();
- st.push(i);
-}
-```
-
-如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
-
-
-
-
-4. 栈里要保存什么数值
-
-是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
-
-长就是通过柱子的高度来计算,宽是通过柱子之间的下表来计算,
-
-那么栈里有没有必要存一个pair类型的元素,保存柱子的高度和下表呢。
-
-其实不用,栈里就存放int类型的元素就行了,表示下表,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下表对应的高度了。
-
-所以栈的定义如下:
-
-```
-stack st; // 存着下标,计算的时候用下标对应的柱子高度
-```
-
-明确了如上几点,我们再来看处理逻辑。
-
-### 单调栈处理逻辑
-
-先将下表0的柱子加入到栈中,`st.push(0);`。
-
-然后开始从下表1开始遍历所有的柱子,`for (int i = 1; i < height.size(); i++)`。
-
-如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从大到小的顺序(从栈底到栈头)。
-
-代码如下:
-
-```
-if (height[i] < height[st.top()]) st.push(i);
-```
-
-如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-代码如下:
-
-```
-if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
- st.pop();
- st.push(i);
-}
-```
-
-如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
-
- -
-取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下表记为mid,对应的高度为height[mid](就是图中的高度1)。
-
-栈顶元素st.top(),就是凹槽的左边位置,下表为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
-
-当前遍历的元素i,就是凹槽右边的位置,下表为i,对应的高度为height[i](就是图中的高度3)。
-
-那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
-
-雨水的宽度是 凹槽右边的下表 - 凹槽左边的下表 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
-
-当前凹槽雨水的体积就是:`h * w`。
-
-求当前凹槽雨水的体积代码如下:
-
-```
-while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
-}
-```
-
-关键部分讲完了,整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- if (height.size() <= 2) return 0; // 可以不加
- stack st; // 存着下标,计算的时候用下标对应的柱子高度
- st.push(0);
- int sum = 0;
- for (int i = 1; i < height.size(); i++) {
- if (height[i] < height[st.top()]) { // 情况一
- st.push(i);
- } if (height[i] == height[st.top()]) { // 情况二
- st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
- st.push(i);
- } else { // 情况三
- while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
- }
- st.push(i);
- }
- }
- return sum;
- }
-};
-```
-
-以上代码冗余了一些,但是思路是清晰的,下面我将代码精简一下,如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- stack st;
- st.push(0);
- int sum = 0;
- for (int i = 1; i < height.size(); i++) {
- while (!st.empty() && height[i] > height[st.top()]) {
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1;
- sum += h * w;
- }
- }
- st.push(i);
- }
- return sum;
- }
-};
-```
-
-精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
-
diff --git a/problems/0045.跳跃游戏II.md b/problems/0045.跳跃游戏II.md
deleted file mode 100644
index 2474b6d1..00000000
--- a/problems/0045.跳跃游戏II.md
+++ /dev/null
@@ -1,138 +0,0 @@
-> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
-
-# 45.跳跃游戏II
-
-题目地址:https://leetcode-cn.com/problems/jump-game-ii/
-
-给定一个非负整数数组,你最初位于数组的第一个位置。
-
-数组中的每个元素代表你在该位置可以跳跃的最大长度。
-
-你的目标是使用最少的跳跃次数到达数组的最后一个位置。
-
-示例:
-输入: [2,3,1,1,4]
-输出: 2
-解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
-
-说明:
-假设你总是可以到达数组的最后一个位置。
-
-
-# 思路
-
-本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。
-
-但思路是相似的,还是要看最大覆盖范围。
-
-本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
-
-贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
-
-思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
-
-**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
-
-**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
-
-如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
-
-如图:
-
-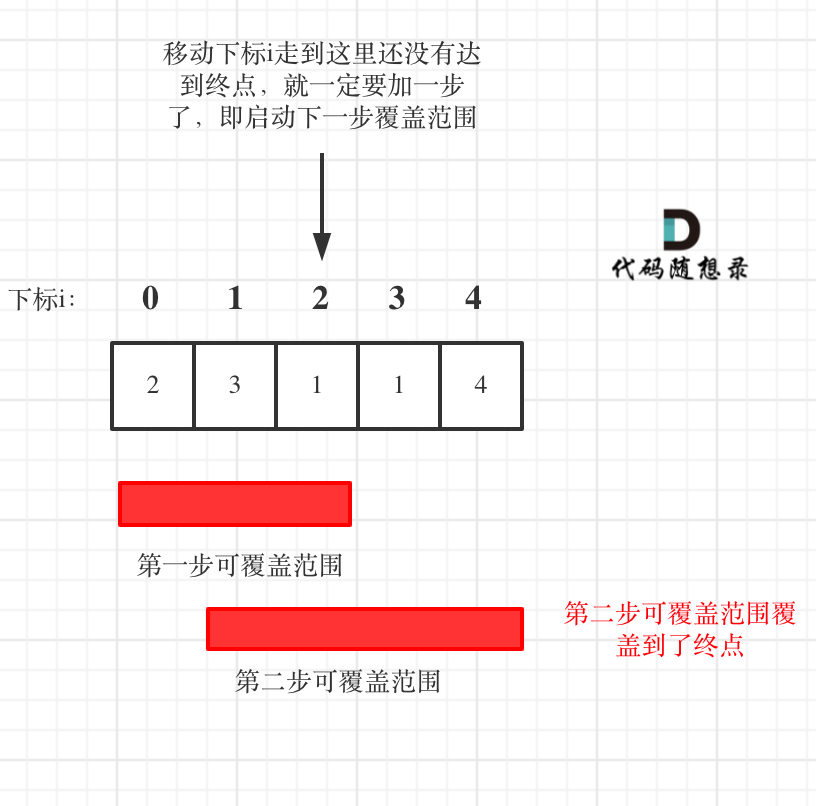
-
-**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
-
-## 方法一
-
-从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
-
-这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
-
-* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
-* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
-
-C++代码如下:(详细注释)
-
-```C++
-// 版本一
-class Solution {
-public:
- int jump(vector& nums) {
- if (nums.size() == 1) return 0;
- int curDistance = 0; // 当前覆盖最远距离下标
- int ans = 0; // 记录走的最大步数
- int nextDistance = 0; // 下一步覆盖最远距离下标
- for (int i = 0; i < nums.size(); i++) {
- nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
- if (i == curDistance) { // 遇到当前覆盖最远距离下标
- if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
- ans++; // 需要走下一步
- curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
- if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
- } else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
- }
- }
- return ans;
- }
-};
-```
-
-## 方法二
-
-依然是贪心,思路和方法一差不多,代码可以简洁一些。
-
-**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
-
-想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
-
-因为当移动下标指向nums.size - 2时:
-
-* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
-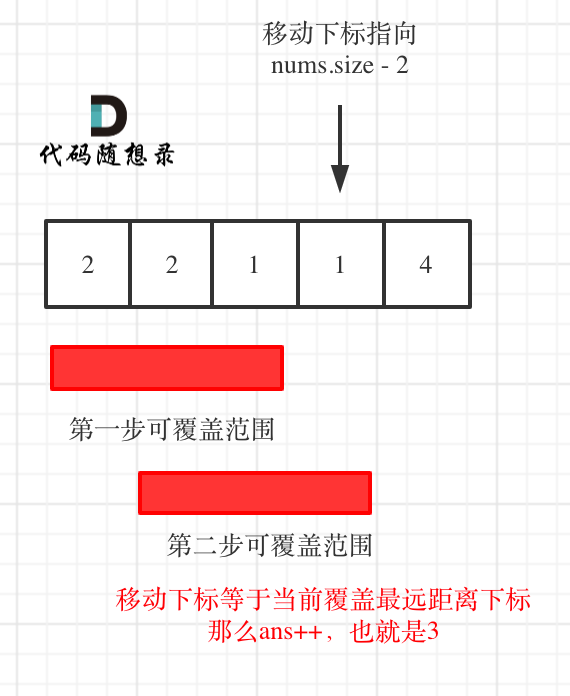
-
-* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
-
-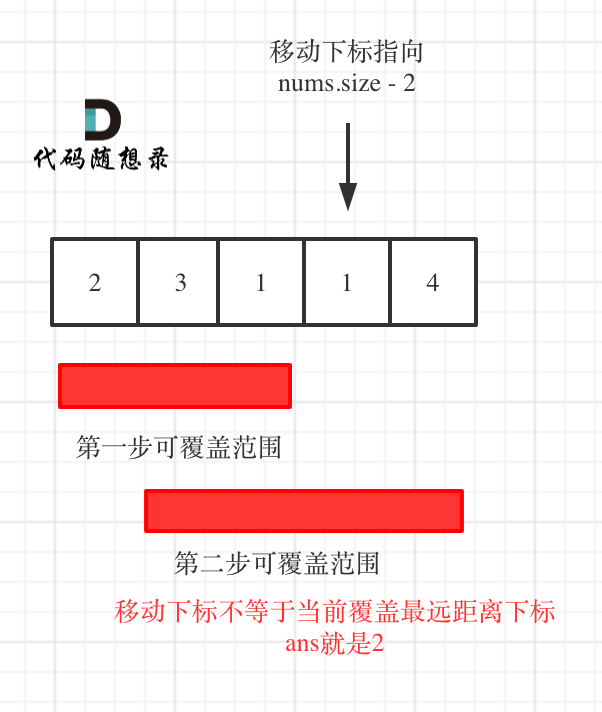
-
-代码如下:
-
-```C++
-// 版本二
-class Solution {
-public:
- int jump(vector& nums) {
- int curDistance = 0; // 当前覆盖的最远距离下标
- int ans = 0; // 记录走的最大步数
- int nextDistance = 0; // 下一步覆盖的最远距离下标
- for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
- nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
- if (i == curDistance) { // 遇到当前覆盖的最远距离下标
- curDistance = nextDistance; // 更新当前覆盖的最远距离下标
- ans++;
- }
- }
- return ans;
- }
-};
-```
-
-可以看出版本二的代码相对于版本一简化了不少!
-
-其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
-
-# 总结
-
-相信大家可以发现,这道题目相当于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。
-
-但代码又十分简单,贪心就是这么巧妙。
-
-理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
-
-就酱,如果感觉「代码随想录」很不错,就分享给身边的朋友同学吧!
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
deleted file mode 100644
index 7e1b87a2..00000000
--- a/problems/0046.全排列.md
+++ /dev/null
@@ -1,145 +0,0 @@
-
-> 开始排列问题
-
-# 46.全排列
-
-题目链接:https://leetcode-cn.com/problems/permutations/
-
-给定一个 没有重复 数字的序列,返回其所有可能的全排列。
-
-示例:
-输入: [1,2,3]
-输出:
-[
- [1,2,3],
- [1,3,2],
- [2,1,3],
- [2,3,1],
- [3,1,2],
- [3,2,1]
-]
-
-## 思路
-
-此时我们已经学习了[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),接下来看一看排列问题。
-
-相信这个排列问题就算是让你用for循环暴力把结果搜索出来,这个暴力也不是很好写。
-
-所以正如我们在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)所讲的为什么回溯法是暴力搜索,效率这么低,还要用它?
-
-**因为一些问题能暴力搜出来就已经很不错了!**
-
-我以[1,2,3]为例,抽象成树形结构如下:
-
-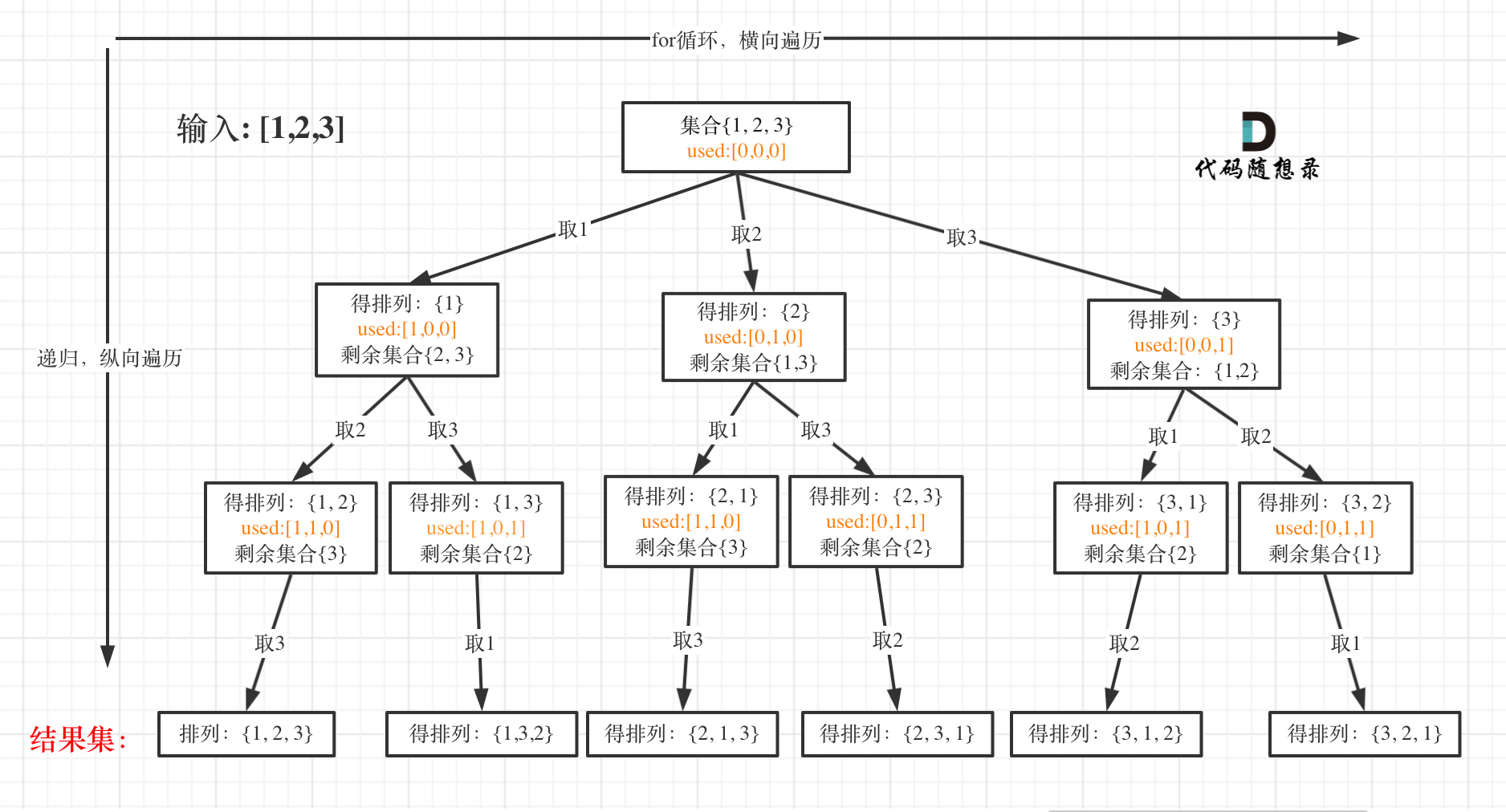
-
-## 回溯三部曲
-
-* 递归函数参数
-
-**首先排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方**。
-
-可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
-
-但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
-
-
-
-代码如下:
-
-```
-vector> result;
-vector path;
-void backtracking (vector& nums, vector& used)
-```
-
-* 递归终止条件
-
-
-
-可以看出叶子节点,就是收割结果的地方。
-
-那么什么时候,算是到达叶子节点呢?
-
-当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
-
-代码如下:
-
-```
-// 此时说明找到了一组
-if (path.size() == nums.size()) {
- result.push_back(path);
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-这里和[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
-
-因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
-
-**而used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次**。
-
-代码如下:
-
-```
-for (int i = 0; i < nums.size(); i++) {
- if (used[i] == true) continue; // path里已经收录的元素,直接跳过
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
-}
-```
-
-整体C++代码如下:
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> result;
- vector path;
- void backtracking (vector& nums, vector& used) {
- // 此时说明找到了一组
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- if (used[i] == true) continue; // path里已经收录的元素,直接跳过
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- vector> permute(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- backtracking(nums, used);
- return result;
- }
-};
-```
-
-# 总结
-
-大家此时可以感受出排列问题的不同:
-
-* 每层都是从0开始搜索而不是startIndex
-* 需要used数组记录path里都放了哪些元素了
-
-排列问题是回溯算法解决的经典题目,大家可以好好体会体会。
-
-就酱,如果感觉「代码随想录」诚意满满,就帮Carl宣传一波吧!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0047.全排列II.md b/problems/0047.全排列II.md
deleted file mode 100644
index dbe8a2e6..00000000
--- a/problems/0047.全排列II.md
+++ /dev/null
@@ -1,150 +0,0 @@
-
-> 排列也要去重了
-
-# 47.全排列 II
-
-题目链接:https://leetcode-cn.com/problems/permutations-ii/
-
-给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
-
-示例 1:
-输入:nums = [1,1,2]
-输出:
-[[1,1,2],
- [1,2,1],
- [2,1,1]]
-
-示例 2:
-输入:nums = [1,2,3]
-输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
-
-提示:
-* 1 <= nums.length <= 8
-* -10 <= nums[i] <= 10
-
-## 思路
-
-这道题目和[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
-
-这里又涉及到去重了。
-
-在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)我们分别详细讲解了组合问题和子集问题如何去重。
-
-那么排列问题其实也是一样的套路。
-
-**还要强调的是去重一定要对元素经行排序,这样我们才方便通过相邻的节点来判断是否重复使用了**。
-
-我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
-
-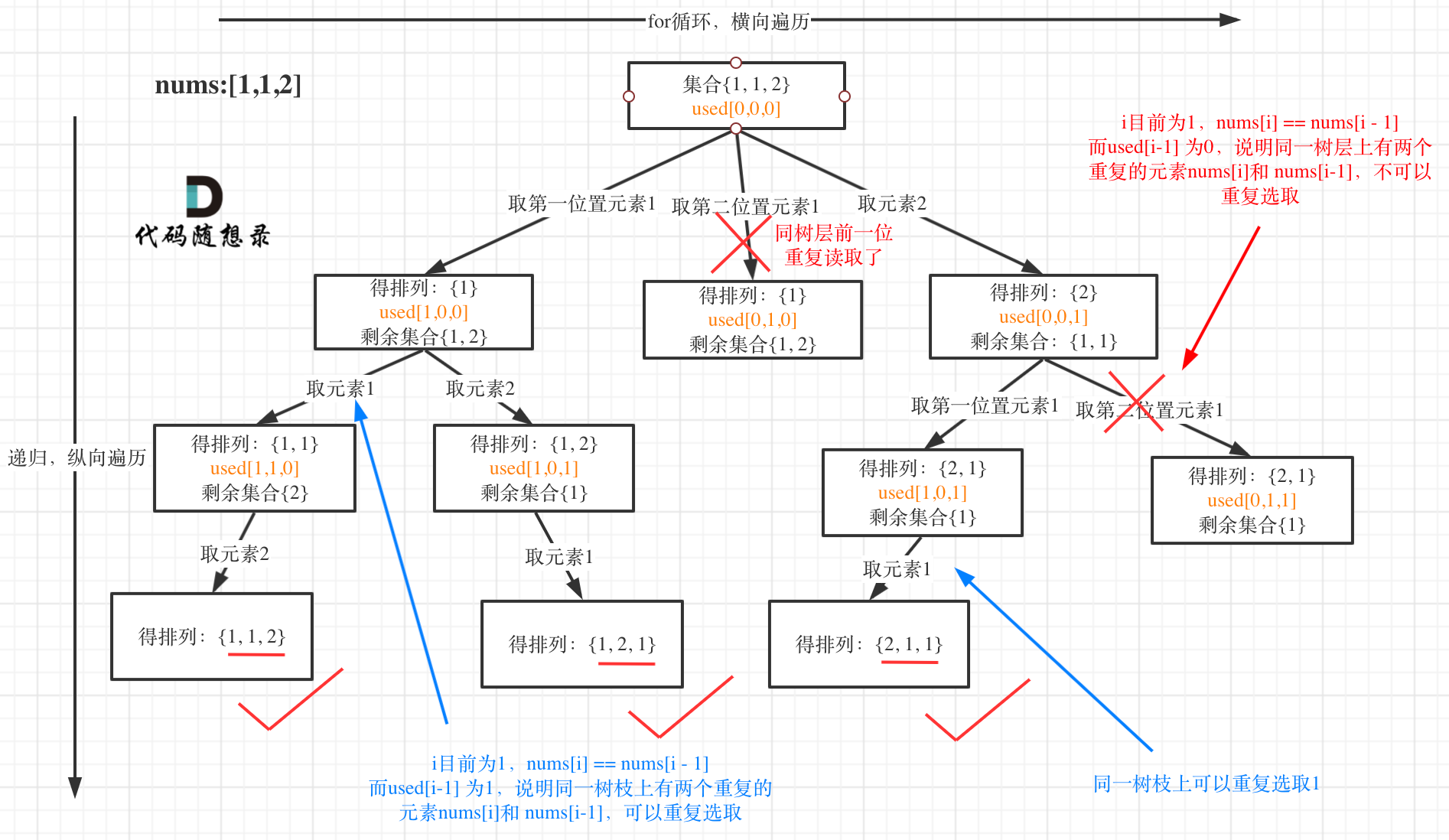
-
-图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
-
-**一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果**。
-
-在[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)中已经详解讲解了排列问题的写法,在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中详细讲解的去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
-
-## C++代码
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking (vector& nums, vector& used) {
- // 此时说明找到了一组
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- // used[i - 1] == true,说明同一树支nums[i - 1]使用过
- // used[i - 1] == false,说明同一树层nums[i - 1]使用过
- // 如果同一树层nums[i - 1]使用过则直接跳过
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- if (used[i] == false) {
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- }
-public:
- vector> permuteUnique(vector& nums) {
- result.clear();
- path.clear();
- sort(nums.begin(), nums.end()); // 排序
- vector used(nums.size(), false);
- backtracking(nums, vec, used);
- return result;
- }
-};
-
-```
-
-## 拓展
-
-大家发现,去重最为关键的代码为:
-
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
-}
-```
-
-**如果改成 `used[i - 1] == true`, 也是正确的!**,去重代码如下:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
-}
-```
-
-这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用`used[i - 1] == false`,如果要对树枝前一位去重用`used[i - 1] == true`。
-
-**对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!**
-
-这么说是不是有点抽象?
-
-来来来,我就用输入: [1,1,1] 来举一个例子。
-
-树层上去重(used[i - 1] == false),的树形结构如下:
-
-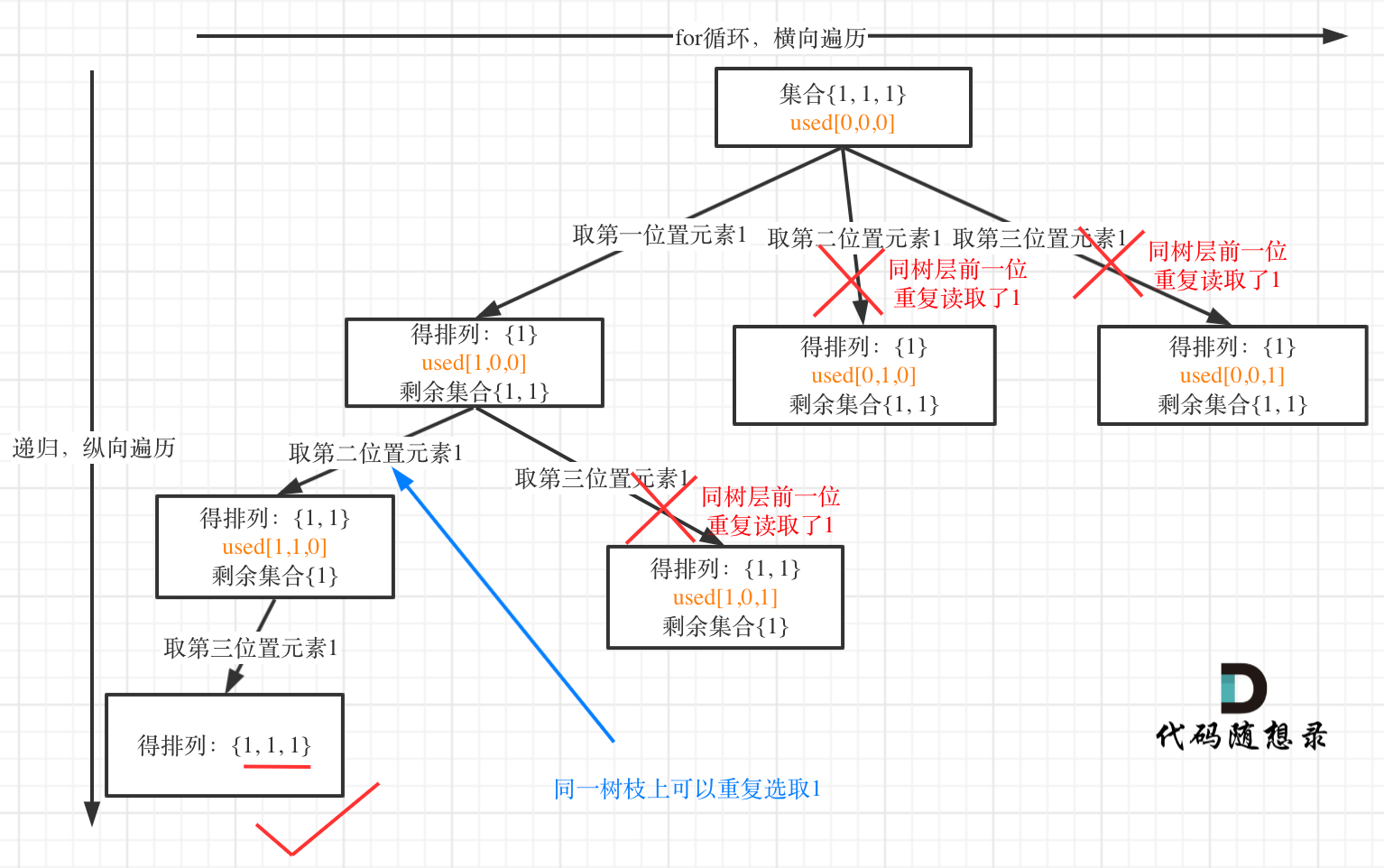
-
-树枝上去重(used[i - 1] == true)的树型结构如下:
-
-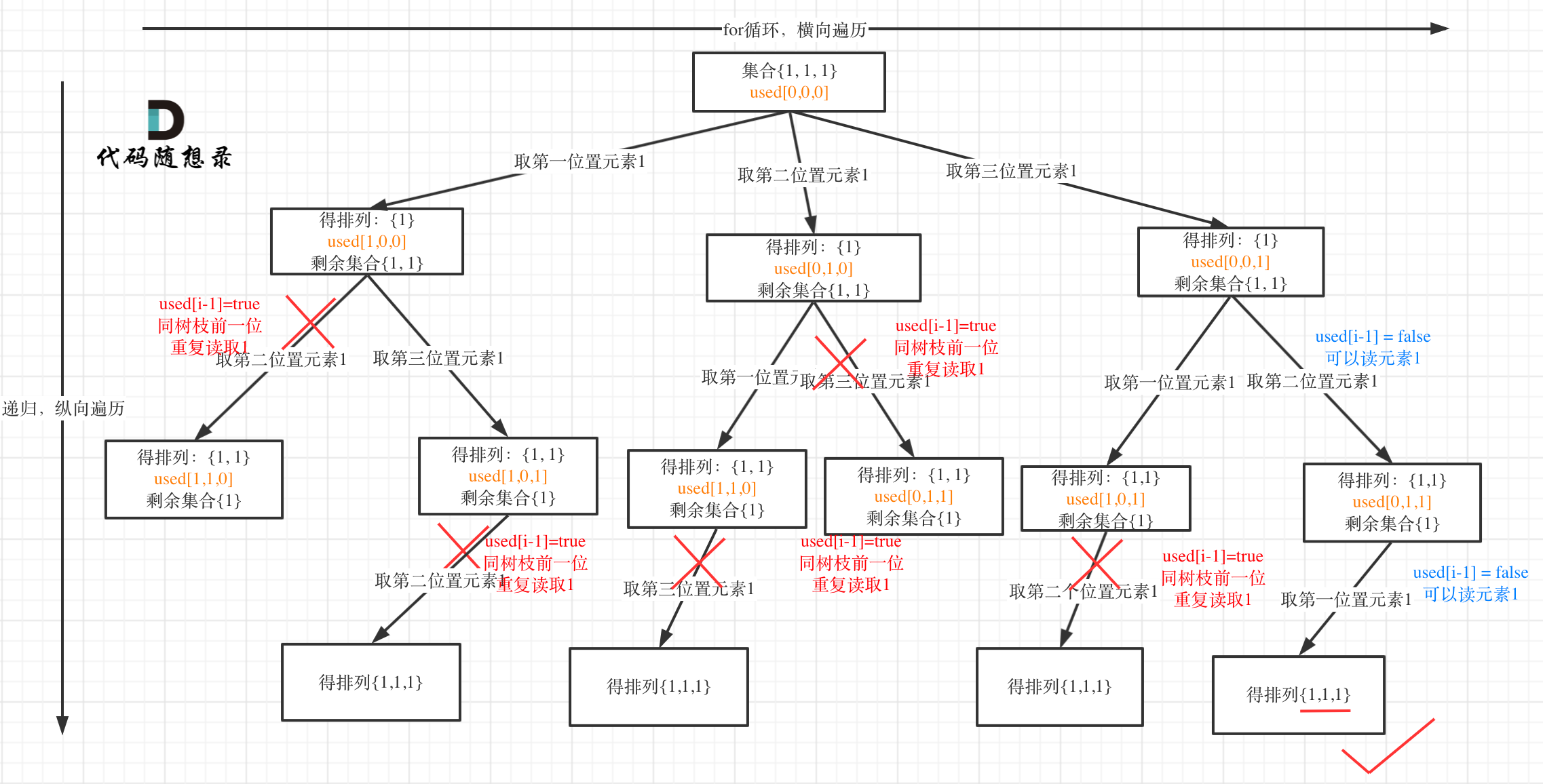
-
-大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
-
-# 总结
-
-这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
-}
-```
-和这么写:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
-}
-```
-
-都是可以的,这也是很多同学做这道题目困惑的地方,知道`used[i - 1] == false`也行而`used[i - 1] == true`也行,但是就想不明白为啥。
-
-所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
-
-是不是豁然开朗了!!
-
-就酱,很多录友表示和「代码随想录」相见恨晚,那么大家帮忙多多宣传,让更多的同学知道这里,感谢啦!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0051.N皇后.md b/problems/0051.N皇后.md
deleted file mode 100644
index 7475325e..00000000
--- a/problems/0051.N皇后.md
+++ /dev/null
@@ -1,234 +0,0 @@
-> 开始棋盘问题,如果对回溯法还不了解的同学可以看这个视频
-
-如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
-
-
-# 第51题. N皇后
-
-题目链接: https://leetcode-cn.com/problems/n-queens/
-
-n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
-
-上图为 8 皇后问题的一种解法。
-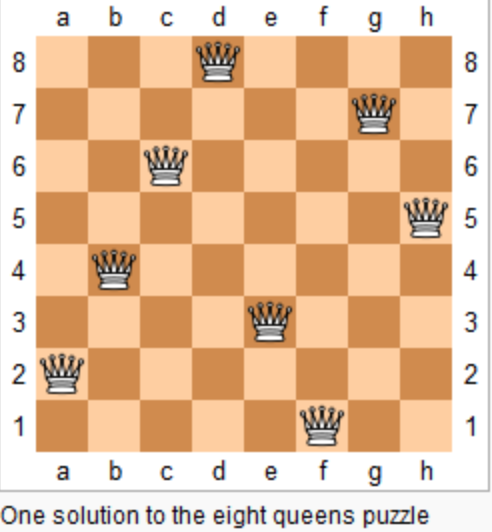
-
-给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
-
-每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
-
-示例:
-输入: 4
-输出: [
- [".Q..", // 解法 1
- "...Q",
- "Q...",
- "..Q."],
-
- ["..Q.", // 解法 2
- "Q...",
- "...Q",
- ".Q.."]
-]
-解释: 4 皇后问题存在两个不同的解法。
-
-提示:
-> 皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一到七步,可进可退。(引用自 百度百科 - 皇后 )
-
-
-# 思路
-
-都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二位矩阵还会有点不知所措。
-
-首先来看一下皇后们的约束条件:
-
-1. 不能同行
-2. 不能同列
-3. 不能同斜线
-
-确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
-
-下面我用一个3 * 3 的棋牌,将搜索过程抽象为一颗树,如图:
-
-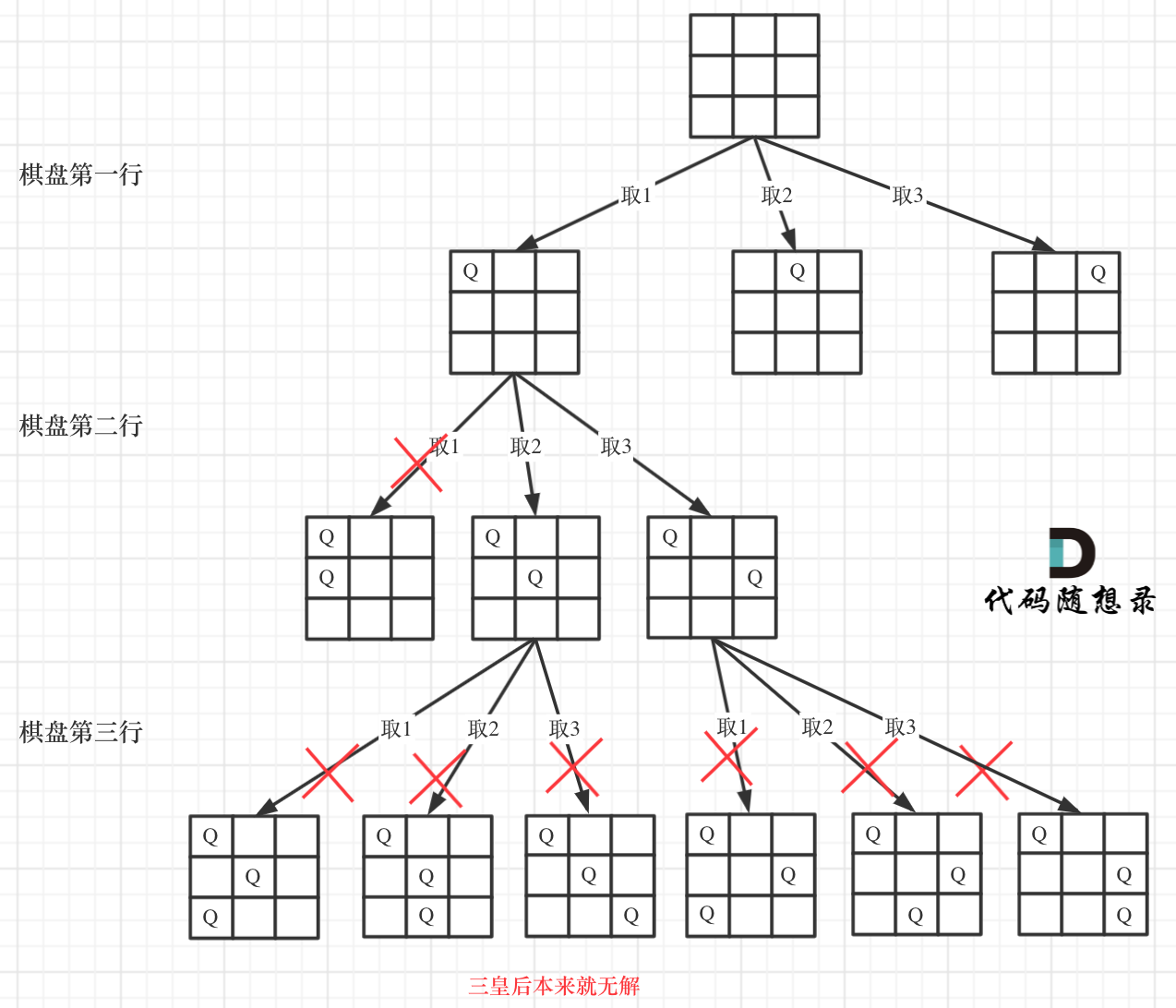
-
-从图中,可以看出,二维矩阵中矩阵的高就是这颗树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
-
-那么我们用皇后们的约束条件,来回溯搜索这颗树,**只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了**。
-
-## 回溯三部曲
-
-按照我总结的如下回溯模板,我们来依次分析:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-* 递归函数参数
-
-我依然是定义全局变量二维数组result来记录最终结果。
-
-参数n是棋牌的大小,然后用row来记录当前遍历到棋盘的第几层了。
-
-代码如下:
-
-```
-vector> result;
-void backtracking(int n, int row, vector& chessboard) {
-```
-
-* 递归终止条件
-
-在如下树形结构中:
-
-
-可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
-
-代码如下:
-
-```
-if (row == n) {
- result.push_back(chessboard);
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
-
-每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
-
-代码如下:
-
-```
-for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯,撤销皇后
- }
-}
-```
-
-* 验证棋牌是否合法
-
-按照如下标准去重:
-
-1. 不能同行
-2. 不能同列
-3. 不能同斜线 (45度和135度角)
-
-代码如下:
-
-```
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-```
-
-在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?
-
-因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
-
-那么按照这个模板不难写出如下代码:
-
-## C++代码
-
-```
-class Solution {
-private:
-vector> result;
-// n 为输入的棋盘大小
-// row 是当前递归到棋牌的第几行了
-void backtracking(int n, int row, vector& chessboard) {
- if (row == n) {
- result.push_back(chessboard);
- return;
- }
- for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯,撤销皇后
- }
- }
-}
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-public:
- vector> solveNQueens(int n) {
- result.clear();
- std::vector chessboard(n, std::string(n, '.'));
- backtracking(n, 0, chessboard);
- return result;
- }
-};
-```
-
-可以看出,除了验证棋盘合法性的代码,省下来部分就是按照回溯法模板来的。
-
-# 总结
-
-本题是我们解决棋盘问题的第一道题目。
-
-如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手,可能知道要用回溯法,但也不知道该怎么去搜。
-
-**这里我明确给出了棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了**。
-
-大家可以在仔细体会体会!
-
-就酱,如果感觉「代码随想录」干货满满,就分享给身边的朋友同学吧,他们可能也需要!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0052.N皇后II.md b/problems/0052.N皇后II.md
deleted file mode 100644
index 4cf103fb..00000000
--- a/problems/0052.N皇后II.md
+++ /dev/null
@@ -1,85 +0,0 @@
-# 题目链接
-https://leetcode-cn.com/problems/n-queens-ii/
-
-# 第51题. N皇后
-
-n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
-
-上图为 8 皇后问题的一种解法。
-
-
-给定一个整数 n,返回 n 皇后不同的解决方案的数量。
-
-示例:
-
-输入: 4
-输出: 2
-解释: 4 皇后问题存在如下两个不同的解法。
-[
- [".Q..", // 解法 1
- "...Q",
- "Q...",
- "..Q."],
-
- ["..Q.", // 解法 2
- "Q...",
- "...Q",
- ".Q.."]
-]
-# 思路
-
-这道题目和 51.N皇后 基本没有区别
-
-# C++代码
-
-```
-class Solution {
-private:
-int count = 0;
-void backtracking(int n, int row, vector& chessboard) {
- if (row == n) {
- count++;
- return;
- }
- for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) {
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯
- }
- }
-}
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-
-public:
- int totalNQueens(int n) {
- std::vector chessboard(n, std::string(n, '.'));
- backtracking(n, 0, chessboard);
- return count;
-
- }
-};
-```
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0053.最大子序和.md b/problems/0053.最大子序和.md
deleted file mode 100644
index ab83d861..00000000
--- a/problems/0053.最大子序和.md
+++ /dev/null
@@ -1,141 +0,0 @@
-
-> 从本题开始,贪心题目都比较难了!
-通知:一些录友表示经常看不到每天的文章,现在公众号已经不按照发送时间推荐了,而是根据一些规则乱序推送,所以可能关注了「代码随想录」也一直看不到文章,建议把「代码随想录」设置星标哈,设置星标之后,每天就按发文时间推送了,我每天都是定时8:35发送的,嗷嗷准时!
-
-# 53. 最大子序和
-
-题目地址:https://leetcode-cn.com/problems/maximum-subarray/
-
-给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
-
-示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
-
-# 思路
-
-## 暴力解法
-
-暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值
-
-时间复杂度:O(n^2)
-空间复杂度:O(1)
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- int result = INT32_MIN;
- int count = 0;
- for (int i = 0; i < nums.size(); i++) { // 设置起始位置
- count = 0;
- for (int j = i; j < nums.size(); j++) { // 每次从起始位置i开始遍历寻找最大值
- count += nums[j];
- result = count > result ? count : result;
- }
- }
- return result;
- }
-};
-```
-
-以上暴力的解法C++勉强可以过,其他语言就不确定了。
-
-## 贪心解法
-
-**贪心贪的是哪里呢?**
-
-如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
-
-局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
-
-全局最优:选取最大“连续和”
-
-**局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。
-
-
-从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
-
-**这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。
-
-
-**那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?**
-
-区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
-
-```
-if (count > result) result = count;
-```
-
-**这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。
-
-如动画所示:
-
-
-
-取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下表记为mid,对应的高度为height[mid](就是图中的高度1)。
-
-栈顶元素st.top(),就是凹槽的左边位置,下表为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
-
-当前遍历的元素i,就是凹槽右边的位置,下表为i,对应的高度为height[i](就是图中的高度3)。
-
-那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
-
-雨水的宽度是 凹槽右边的下表 - 凹槽左边的下表 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
-
-当前凹槽雨水的体积就是:`h * w`。
-
-求当前凹槽雨水的体积代码如下:
-
-```
-while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
-}
-```
-
-关键部分讲完了,整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- if (height.size() <= 2) return 0; // 可以不加
- stack st; // 存着下标,计算的时候用下标对应的柱子高度
- st.push(0);
- int sum = 0;
- for (int i = 1; i < height.size(); i++) {
- if (height[i] < height[st.top()]) { // 情况一
- st.push(i);
- } if (height[i] == height[st.top()]) { // 情况二
- st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
- st.push(i);
- } else { // 情况三
- while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
- }
- st.push(i);
- }
- }
- return sum;
- }
-};
-```
-
-以上代码冗余了一些,但是思路是清晰的,下面我将代码精简一下,如下:
-
-```
-class Solution {
-public:
- int trap(vector& height) {
- stack st;
- st.push(0);
- int sum = 0;
- for (int i = 1; i < height.size(); i++) {
- while (!st.empty() && height[i] > height[st.top()]) {
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1;
- sum += h * w;
- }
- }
- st.push(i);
- }
- return sum;
- }
-};
-```
-
-精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
-
diff --git a/problems/0045.跳跃游戏II.md b/problems/0045.跳跃游戏II.md
deleted file mode 100644
index 2474b6d1..00000000
--- a/problems/0045.跳跃游戏II.md
+++ /dev/null
@@ -1,138 +0,0 @@
-> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
-
-# 45.跳跃游戏II
-
-题目地址:https://leetcode-cn.com/problems/jump-game-ii/
-
-给定一个非负整数数组,你最初位于数组的第一个位置。
-
-数组中的每个元素代表你在该位置可以跳跃的最大长度。
-
-你的目标是使用最少的跳跃次数到达数组的最后一个位置。
-
-示例:
-输入: [2,3,1,1,4]
-输出: 2
-解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
-
-说明:
-假设你总是可以到达数组的最后一个位置。
-
-
-# 思路
-
-本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。
-
-但思路是相似的,还是要看最大覆盖范围。
-
-本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
-
-贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
-
-思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
-
-**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
-
-**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
-
-如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
-
-如图:
-
-
-
-**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
-
-## 方法一
-
-从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
-
-这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
-
-* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
-* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
-
-C++代码如下:(详细注释)
-
-```C++
-// 版本一
-class Solution {
-public:
- int jump(vector& nums) {
- if (nums.size() == 1) return 0;
- int curDistance = 0; // 当前覆盖最远距离下标
- int ans = 0; // 记录走的最大步数
- int nextDistance = 0; // 下一步覆盖最远距离下标
- for (int i = 0; i < nums.size(); i++) {
- nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
- if (i == curDistance) { // 遇到当前覆盖最远距离下标
- if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
- ans++; // 需要走下一步
- curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
- if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
- } else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
- }
- }
- return ans;
- }
-};
-```
-
-## 方法二
-
-依然是贪心,思路和方法一差不多,代码可以简洁一些。
-
-**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
-
-想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
-
-因为当移动下标指向nums.size - 2时:
-
-* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
-
-
-* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
-
-
-
-代码如下:
-
-```C++
-// 版本二
-class Solution {
-public:
- int jump(vector& nums) {
- int curDistance = 0; // 当前覆盖的最远距离下标
- int ans = 0; // 记录走的最大步数
- int nextDistance = 0; // 下一步覆盖的最远距离下标
- for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
- nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
- if (i == curDistance) { // 遇到当前覆盖的最远距离下标
- curDistance = nextDistance; // 更新当前覆盖的最远距离下标
- ans++;
- }
- }
- return ans;
- }
-};
-```
-
-可以看出版本二的代码相对于版本一简化了不少!
-
-其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
-
-# 总结
-
-相信大家可以发现,这道题目相当于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。
-
-但代码又十分简单,贪心就是这么巧妙。
-
-理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
-
-就酱,如果感觉「代码随想录」很不错,就分享给身边的朋友同学吧!
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
deleted file mode 100644
index 7e1b87a2..00000000
--- a/problems/0046.全排列.md
+++ /dev/null
@@ -1,145 +0,0 @@
-
-> 开始排列问题
-
-# 46.全排列
-
-题目链接:https://leetcode-cn.com/problems/permutations/
-
-给定一个 没有重复 数字的序列,返回其所有可能的全排列。
-
-示例:
-输入: [1,2,3]
-输出:
-[
- [1,2,3],
- [1,3,2],
- [2,1,3],
- [2,3,1],
- [3,1,2],
- [3,2,1]
-]
-
-## 思路
-
-此时我们已经学习了[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),接下来看一看排列问题。
-
-相信这个排列问题就算是让你用for循环暴力把结果搜索出来,这个暴力也不是很好写。
-
-所以正如我们在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)所讲的为什么回溯法是暴力搜索,效率这么低,还要用它?
-
-**因为一些问题能暴力搜出来就已经很不错了!**
-
-我以[1,2,3]为例,抽象成树形结构如下:
-
-
-
-## 回溯三部曲
-
-* 递归函数参数
-
-**首先排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方**。
-
-可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
-
-但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
-
-
-
-代码如下:
-
-```
-vector> result;
-vector path;
-void backtracking (vector& nums, vector& used)
-```
-
-* 递归终止条件
-
-
-
-可以看出叶子节点,就是收割结果的地方。
-
-那么什么时候,算是到达叶子节点呢?
-
-当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
-
-代码如下:
-
-```
-// 此时说明找到了一组
-if (path.size() == nums.size()) {
- result.push_back(path);
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-这里和[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
-
-因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
-
-**而used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次**。
-
-代码如下:
-
-```
-for (int i = 0; i < nums.size(); i++) {
- if (used[i] == true) continue; // path里已经收录的元素,直接跳过
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
-}
-```
-
-整体C++代码如下:
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> result;
- vector path;
- void backtracking (vector& nums, vector& used) {
- // 此时说明找到了一组
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- if (used[i] == true) continue; // path里已经收录的元素,直接跳过
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- vector> permute(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- backtracking(nums, used);
- return result;
- }
-};
-```
-
-# 总结
-
-大家此时可以感受出排列问题的不同:
-
-* 每层都是从0开始搜索而不是startIndex
-* 需要used数组记录path里都放了哪些元素了
-
-排列问题是回溯算法解决的经典题目,大家可以好好体会体会。
-
-就酱,如果感觉「代码随想录」诚意满满,就帮Carl宣传一波吧!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0047.全排列II.md b/problems/0047.全排列II.md
deleted file mode 100644
index dbe8a2e6..00000000
--- a/problems/0047.全排列II.md
+++ /dev/null
@@ -1,150 +0,0 @@
-
-> 排列也要去重了
-
-# 47.全排列 II
-
-题目链接:https://leetcode-cn.com/problems/permutations-ii/
-
-给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
-
-示例 1:
-输入:nums = [1,1,2]
-输出:
-[[1,1,2],
- [1,2,1],
- [2,1,1]]
-
-示例 2:
-输入:nums = [1,2,3]
-输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
-
-提示:
-* 1 <= nums.length <= 8
-* -10 <= nums[i] <= 10
-
-## 思路
-
-这道题目和[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
-
-这里又涉及到去重了。
-
-在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)我们分别详细讲解了组合问题和子集问题如何去重。
-
-那么排列问题其实也是一样的套路。
-
-**还要强调的是去重一定要对元素经行排序,这样我们才方便通过相邻的节点来判断是否重复使用了**。
-
-我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
-
-
-
-图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
-
-**一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果**。
-
-在[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)中已经详解讲解了排列问题的写法,在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中详细讲解的去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
-
-## C++代码
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking (vector& nums, vector& used) {
- // 此时说明找到了一组
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- // used[i - 1] == true,说明同一树支nums[i - 1]使用过
- // used[i - 1] == false,说明同一树层nums[i - 1]使用过
- // 如果同一树层nums[i - 1]使用过则直接跳过
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- if (used[i] == false) {
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- }
-public:
- vector> permuteUnique(vector& nums) {
- result.clear();
- path.clear();
- sort(nums.begin(), nums.end()); // 排序
- vector used(nums.size(), false);
- backtracking(nums, vec, used);
- return result;
- }
-};
-
-```
-
-## 拓展
-
-大家发现,去重最为关键的代码为:
-
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
-}
-```
-
-**如果改成 `used[i - 1] == true`, 也是正确的!**,去重代码如下:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
-}
-```
-
-这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用`used[i - 1] == false`,如果要对树枝前一位去重用`used[i - 1] == true`。
-
-**对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!**
-
-这么说是不是有点抽象?
-
-来来来,我就用输入: [1,1,1] 来举一个例子。
-
-树层上去重(used[i - 1] == false),的树形结构如下:
-
-
-
-树枝上去重(used[i - 1] == true)的树型结构如下:
-
-
-
-大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
-
-# 总结
-
-这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
-}
-```
-和这么写:
-```
-if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
-}
-```
-
-都是可以的,这也是很多同学做这道题目困惑的地方,知道`used[i - 1] == false`也行而`used[i - 1] == true`也行,但是就想不明白为啥。
-
-所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
-
-是不是豁然开朗了!!
-
-就酱,很多录友表示和「代码随想录」相见恨晚,那么大家帮忙多多宣传,让更多的同学知道这里,感谢啦!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0051.N皇后.md b/problems/0051.N皇后.md
deleted file mode 100644
index 7475325e..00000000
--- a/problems/0051.N皇后.md
+++ /dev/null
@@ -1,234 +0,0 @@
-> 开始棋盘问题,如果对回溯法还不了解的同学可以看这个视频
-
-如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
-
-
-# 第51题. N皇后
-
-题目链接: https://leetcode-cn.com/problems/n-queens/
-
-n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
-
-上图为 8 皇后问题的一种解法。
-
-
-给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
-
-每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
-
-示例:
-输入: 4
-输出: [
- [".Q..", // 解法 1
- "...Q",
- "Q...",
- "..Q."],
-
- ["..Q.", // 解法 2
- "Q...",
- "...Q",
- ".Q.."]
-]
-解释: 4 皇后问题存在两个不同的解法。
-
-提示:
-> 皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一到七步,可进可退。(引用自 百度百科 - 皇后 )
-
-
-# 思路
-
-都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二位矩阵还会有点不知所措。
-
-首先来看一下皇后们的约束条件:
-
-1. 不能同行
-2. 不能同列
-3. 不能同斜线
-
-确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
-
-下面我用一个3 * 3 的棋牌,将搜索过程抽象为一颗树,如图:
-
-
-
-从图中,可以看出,二维矩阵中矩阵的高就是这颗树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
-
-那么我们用皇后们的约束条件,来回溯搜索这颗树,**只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了**。
-
-## 回溯三部曲
-
-按照我总结的如下回溯模板,我们来依次分析:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-* 递归函数参数
-
-我依然是定义全局变量二维数组result来记录最终结果。
-
-参数n是棋牌的大小,然后用row来记录当前遍历到棋盘的第几层了。
-
-代码如下:
-
-```
-vector> result;
-void backtracking(int n, int row, vector& chessboard) {
-```
-
-* 递归终止条件
-
-在如下树形结构中:
-
-
-可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
-
-代码如下:
-
-```
-if (row == n) {
- result.push_back(chessboard);
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
-
-每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
-
-代码如下:
-
-```
-for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯,撤销皇后
- }
-}
-```
-
-* 验证棋牌是否合法
-
-按照如下标准去重:
-
-1. 不能同行
-2. 不能同列
-3. 不能同斜线 (45度和135度角)
-
-代码如下:
-
-```
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-```
-
-在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?
-
-因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
-
-那么按照这个模板不难写出如下代码:
-
-## C++代码
-
-```
-class Solution {
-private:
-vector> result;
-// n 为输入的棋盘大小
-// row 是当前递归到棋牌的第几行了
-void backtracking(int n, int row, vector& chessboard) {
- if (row == n) {
- result.push_back(chessboard);
- return;
- }
- for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯,撤销皇后
- }
- }
-}
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-public:
- vector> solveNQueens(int n) {
- result.clear();
- std::vector chessboard(n, std::string(n, '.'));
- backtracking(n, 0, chessboard);
- return result;
- }
-};
-```
-
-可以看出,除了验证棋盘合法性的代码,省下来部分就是按照回溯法模板来的。
-
-# 总结
-
-本题是我们解决棋盘问题的第一道题目。
-
-如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手,可能知道要用回溯法,但也不知道该怎么去搜。
-
-**这里我明确给出了棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了**。
-
-大家可以在仔细体会体会!
-
-就酱,如果感觉「代码随想录」干货满满,就分享给身边的朋友同学吧,他们可能也需要!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0052.N皇后II.md b/problems/0052.N皇后II.md
deleted file mode 100644
index 4cf103fb..00000000
--- a/problems/0052.N皇后II.md
+++ /dev/null
@@ -1,85 +0,0 @@
-# 题目链接
-https://leetcode-cn.com/problems/n-queens-ii/
-
-# 第51题. N皇后
-
-n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
-
-上图为 8 皇后问题的一种解法。
-
-
-给定一个整数 n,返回 n 皇后不同的解决方案的数量。
-
-示例:
-
-输入: 4
-输出: 2
-解释: 4 皇后问题存在如下两个不同的解法。
-[
- [".Q..", // 解法 1
- "...Q",
- "Q...",
- "..Q."],
-
- ["..Q.", // 解法 2
- "Q...",
- "...Q",
- ".Q.."]
-]
-# 思路
-
-这道题目和 51.N皇后 基本没有区别
-
-# C++代码
-
-```
-class Solution {
-private:
-int count = 0;
-void backtracking(int n, int row, vector& chessboard) {
- if (row == n) {
- count++;
- return;
- }
- for (int col = 0; col < n; col++) {
- if (isValid(row, col, chessboard, n)) {
- chessboard[row][col] = 'Q'; // 放置皇后
- backtracking(n, row + 1, chessboard);
- chessboard[row][col] = '.'; // 回溯
- }
- }
-}
-bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
- // 检查列
- for (int i = 0; i < row; i++) { // 这是一个剪枝
- if (chessboard[i][col] == 'Q') {
- return false;
- }
- }
- // 检查 45度角是否有皇后
- for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- // 检查 135度角是否有皇后
- for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if (chessboard[i][j] == 'Q') {
- return false;
- }
- }
- return true;
-}
-
-public:
- int totalNQueens(int n) {
- std::vector chessboard(n, std::string(n, '.'));
- backtracking(n, 0, chessboard);
- return count;
-
- }
-};
-```
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0053.最大子序和.md b/problems/0053.最大子序和.md
deleted file mode 100644
index ab83d861..00000000
--- a/problems/0053.最大子序和.md
+++ /dev/null
@@ -1,141 +0,0 @@
-
-> 从本题开始,贪心题目都比较难了!
-通知:一些录友表示经常看不到每天的文章,现在公众号已经不按照发送时间推荐了,而是根据一些规则乱序推送,所以可能关注了「代码随想录」也一直看不到文章,建议把「代码随想录」设置星标哈,设置星标之后,每天就按发文时间推送了,我每天都是定时8:35发送的,嗷嗷准时!
-
-# 53. 最大子序和
-
-题目地址:https://leetcode-cn.com/problems/maximum-subarray/
-
-给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
-
-示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
-
-# 思路
-
-## 暴力解法
-
-暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值
-
-时间复杂度:O(n^2)
-空间复杂度:O(1)
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- int result = INT32_MIN;
- int count = 0;
- for (int i = 0; i < nums.size(); i++) { // 设置起始位置
- count = 0;
- for (int j = i; j < nums.size(); j++) { // 每次从起始位置i开始遍历寻找最大值
- count += nums[j];
- result = count > result ? count : result;
- }
- }
- return result;
- }
-};
-```
-
-以上暴力的解法C++勉强可以过,其他语言就不确定了。
-
-## 贪心解法
-
-**贪心贪的是哪里呢?**
-
-如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
-
-局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
-
-全局最优:选取最大“连续和”
-
-**局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。
-
-
-从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
-
-**这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。
-
-
-**那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?**
-
-区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
-
-```
-if (count > result) result = count;
-```
-
-**这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。
-
-如动画所示:
-
- -
-红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
-
-那么不难写出如下C++代码(关键地方已经注释)
-
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- int result = INT32_MIN;
- int count = 0;
- for (int i = 0; i < nums.size(); i++) {
- count += nums[i];
- if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
- result = count;
- }
- if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
- }
- return result;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
-
-## 动态规划
-
-当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。
-
-那么先给出我的dp代码如下,有时间的录友可以提前做一做:
-
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- if (nums.size() == 0) return 0;
- vector dp(nums.size(), 0); // dp[i]表示包括i之前的最大连续子序列和
- dp[0] = nums[0];
- int result = dp[0];
- for (int i = 1; i < nums.size(); i++) {
- dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
- if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
- }
- return result;
- }
-};
-```
-
-时间复杂度:O(n)
-空间复杂度:O(n)
-
-# 总结
-
-本题的贪心思路其实并不好想,这也进一步验证了,别看贪心理论很直白,有时候看似是常识,但贪心的题目一点都不简单!
-
-后续将介绍的贪心题目都挺难的,哈哈,所以贪心很有意思,别小看贪心!
-
-就酱,如果感觉「代码随想录」干货满满,就帮忙转发一波吧,让更多的小伙伴知道这里!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
-
-
diff --git a/problems/0055.跳跃游戏.md b/problems/0055.跳跃游戏.md
deleted file mode 100644
index 2f0ab898..00000000
--- a/problems/0055.跳跃游戏.md
+++ /dev/null
@@ -1,79 +0,0 @@
-
-> 通知
-
-# 55. 跳跃游戏
-
-题目链接:https://leetcode-cn.com/problems/jump-game/
-
-给定一个非负整数数组,你最初位于数组的第一个位置。
-
-数组中的每个元素代表你在该位置可以跳跃的最大长度。
-
-判断你是否能够到达最后一个位置。
-
-示例 1:
-输入: [2,3,1,1,4]
-输出: true
-解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
-
-示例 2:
-输入: [3,2,1,0,4]
-输出: false
-解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
-
-
-## 思路
-
-刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
-
-其实跳几步无所谓,关键在于可跳的覆盖范围!
-
-不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。
-
-这个范围内,别管是怎么跳的,反正一定可以跳过来。
-
-**那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!**
-
-每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
-
-**贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点**。
-
-局部最优推出全局最优,找不出反例,试试贪心!
-
-如图:
-
-
-
-i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去。
-
-而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。
-
-如果cover大于等于了终点下标,直接return true就可以了。
-
-C++代码如下:
-
-```C++
-class Solution {
-public:
- bool canJump(vector& nums) {
- int cover = 0;
- if (nums.size() == 1) return true; // 只有一个元素,就是能达到
- for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
- cover = max(i + nums[i], cover);
- if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
- }
- return false;
- }
-};
-```
-# 总结
-
-这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
-
-大家可以看出思路想出来了,代码还是非常简单的。
-
-一些同学可能感觉,我在讲贪心系列的时候,题目和题目之间貌似没有什么联系?
-
-**是真的就是没什么联系,因为贪心无套路!**没有个整体的贪心框架解决一些列问题,只能是接触各种类型的题目锻炼自己的贪心思维!
-
-就酱,「代码随想录」值得推荐给身边的朋友同学们!
diff --git a/problems/0056.合并区间.md b/problems/0056.合并区间.md
deleted file mode 100644
index 1e0e1b9a..00000000
--- a/problems/0056.合并区间.md
+++ /dev/null
@@ -1,128 +0,0 @@
-> 「代码随想录」出品,毕竟精品!
-
-# 56. 合并区间
-
-题目链接:https://leetcode-cn.com/problems/merge-intervals/
-
-给出一个区间的集合,请合并所有重叠的区间。
-
-示例 1:
-输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
-输出: [[1,6],[8,10],[15,18]]
-解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
-
-示例 2:
-输入: intervals = [[1,4],[4,5]]
-输出: [[1,5]]
-解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
-注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
-
-提示:
-
-* intervals[i][0] <= intervals[i][1]
-
-# 思路
-
-大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
-
-都可以!
-
-那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
-
-局部最优可以推出全局最优,找不出反例,试试贪心。
-
-那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
-
-有时候贪心就是常识!哈哈
-
-按照左边界从小到大排序之后,如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
-
-即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
-
-这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
-
-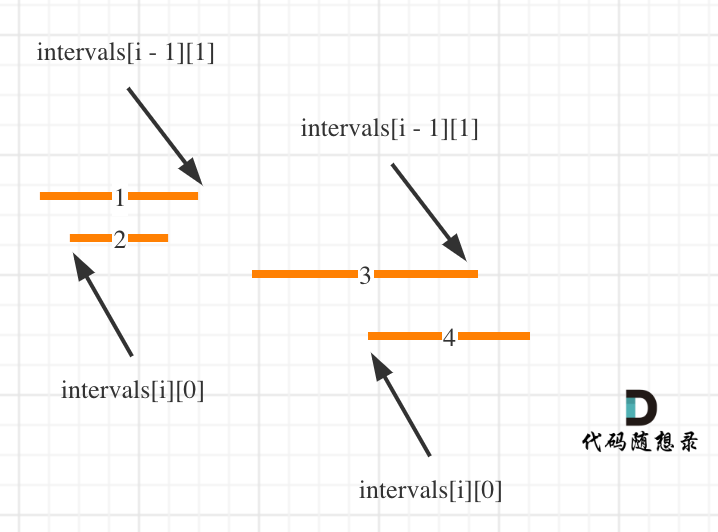
-
-知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
-
-其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
-
-C++代码如下:
-
-```C++
-class Solution {
-public:
- // 按照区间左边界从小到大排序
- static bool cmp (const vector& a, const vector& b) {
- return a[0] < b[0];
- }
- vector> merge(vector>& intervals) {
- vector> result;
- if (intervals.size() == 0) return result;
- sort(intervals.begin(), intervals.end(), cmp);
- bool flag = false; // 标记最后一个区间有没有合并
- int length = intervals.size();
-
- for (int i = 1; i < length; i++) {
- int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
- int end = intervals[i - 1][1]; // 初始i-1区间的右边界
- while (i < length && intervals[i][0] <= end) { // 合并区间
- end = max(end, intervals[i][1]); // 不断更新右区间
- if (i == length - 1) flag = true; // 最后一个区间也合并了
- i++; // 继续合并下一个区间
- }
- // start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
- result.push_back({start, end});
- }
- // 如果最后一个区间没有合并,将其加入result
- if (flag == false) {
- result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
- }
- return result;
- }
-};
-```
-
-当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
-
-```C++
-class Solution {
-public:
- vector> merge(vector>& intervals) {
- vector> result;
- if (intervals.size() == 0) return result;
- // 排序的参数使用了lamda表达式
- sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){return a[0] < b[0];});
-
- result.push_back(intervals[0]);
- for (int i = 1; i < intervals.size(); i++) {
- if (result.back()[1] >= intervals[i][0]) { // 合并区间
- result.back()[1] = max(result.back()[1], intervals[i][1]);
- } else {
- result.push_back(intervals[i]);
- }
- }
- return result;
- }
-};
-```
-
-* 时间复杂度:O(nlogn) ,有一个快排
-* 空间复杂度:O(1),我没有算result数组(返回值所需容器占的空间)
-
-
-# 总结
-
-对于贪心算法,很多同学都是:**如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
-
-跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
-
-那应该怎么办呢?
-
-正如我贪心系列开篇词[关于贪心算法,你该了解这些!](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
-
-「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
-
-就酱,学算法,就在「代码随想录」,值得介绍给身边的朋友同学们!
-
-
diff --git a/problems/0057.插入区间.md b/problems/0057.插入区间.md
deleted file mode 100644
index 79dba1c4..00000000
--- a/problems/0057.插入区间.md
+++ /dev/null
@@ -1,90 +0,0 @@
-
-# 链接
-https://leetcode-cn.com/problems/insert-interval/
-
-# 思路
-这道题目合并的情况有很多种,想想都让人头疼。
-
-我把这道题目化为三步:
-
-## 步骤一:找到需要合并的区间
-
-找到插入区间需要插入或者合并的位置。
-
-代码如下:
-
-```
-int index = 0; // intervals的索引
-while (index < intervals.size() && intervals[index][1] < newInterval[0]) {
- result.push_back(intervals[index++]);
-}
-```
-
-此时intervals[index]就需要合并的区间了
-
-## 步骤二:合并区间
-
-合并区间还有两种情况
-
-1. intervals[index]需要合并,如图:
-
-
-
-红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
-
-那么不难写出如下C++代码(关键地方已经注释)
-
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- int result = INT32_MIN;
- int count = 0;
- for (int i = 0; i < nums.size(); i++) {
- count += nums[i];
- if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
- result = count;
- }
- if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
- }
- return result;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
-
-## 动态规划
-
-当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。
-
-那么先给出我的dp代码如下,有时间的录友可以提前做一做:
-
-```
-class Solution {
-public:
- int maxSubArray(vector& nums) {
- if (nums.size() == 0) return 0;
- vector dp(nums.size(), 0); // dp[i]表示包括i之前的最大连续子序列和
- dp[0] = nums[0];
- int result = dp[0];
- for (int i = 1; i < nums.size(); i++) {
- dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
- if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
- }
- return result;
- }
-};
-```
-
-时间复杂度:O(n)
-空间复杂度:O(n)
-
-# 总结
-
-本题的贪心思路其实并不好想,这也进一步验证了,别看贪心理论很直白,有时候看似是常识,但贪心的题目一点都不简单!
-
-后续将介绍的贪心题目都挺难的,哈哈,所以贪心很有意思,别小看贪心!
-
-就酱,如果感觉「代码随想录」干货满满,就帮忙转发一波吧,让更多的小伙伴知道这里!
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
-
-
diff --git a/problems/0055.跳跃游戏.md b/problems/0055.跳跃游戏.md
deleted file mode 100644
index 2f0ab898..00000000
--- a/problems/0055.跳跃游戏.md
+++ /dev/null
@@ -1,79 +0,0 @@
-
-> 通知
-
-# 55. 跳跃游戏
-
-题目链接:https://leetcode-cn.com/problems/jump-game/
-
-给定一个非负整数数组,你最初位于数组的第一个位置。
-
-数组中的每个元素代表你在该位置可以跳跃的最大长度。
-
-判断你是否能够到达最后一个位置。
-
-示例 1:
-输入: [2,3,1,1,4]
-输出: true
-解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
-
-示例 2:
-输入: [3,2,1,0,4]
-输出: false
-解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
-
-
-## 思路
-
-刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
-
-其实跳几步无所谓,关键在于可跳的覆盖范围!
-
-不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。
-
-这个范围内,别管是怎么跳的,反正一定可以跳过来。
-
-**那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!**
-
-每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
-
-**贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点**。
-
-局部最优推出全局最优,找不出反例,试试贪心!
-
-如图:
-
-
-
-i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去。
-
-而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。
-
-如果cover大于等于了终点下标,直接return true就可以了。
-
-C++代码如下:
-
-```C++
-class Solution {
-public:
- bool canJump(vector& nums) {
- int cover = 0;
- if (nums.size() == 1) return true; // 只有一个元素,就是能达到
- for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
- cover = max(i + nums[i], cover);
- if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
- }
- return false;
- }
-};
-```
-# 总结
-
-这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
-
-大家可以看出思路想出来了,代码还是非常简单的。
-
-一些同学可能感觉,我在讲贪心系列的时候,题目和题目之间貌似没有什么联系?
-
-**是真的就是没什么联系,因为贪心无套路!**没有个整体的贪心框架解决一些列问题,只能是接触各种类型的题目锻炼自己的贪心思维!
-
-就酱,「代码随想录」值得推荐给身边的朋友同学们!
diff --git a/problems/0056.合并区间.md b/problems/0056.合并区间.md
deleted file mode 100644
index 1e0e1b9a..00000000
--- a/problems/0056.合并区间.md
+++ /dev/null
@@ -1,128 +0,0 @@
-> 「代码随想录」出品,毕竟精品!
-
-# 56. 合并区间
-
-题目链接:https://leetcode-cn.com/problems/merge-intervals/
-
-给出一个区间的集合,请合并所有重叠的区间。
-
-示例 1:
-输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
-输出: [[1,6],[8,10],[15,18]]
-解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
-
-示例 2:
-输入: intervals = [[1,4],[4,5]]
-输出: [[1,5]]
-解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
-注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
-
-提示:
-
-* intervals[i][0] <= intervals[i][1]
-
-# 思路
-
-大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
-
-都可以!
-
-那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
-
-局部最优可以推出全局最优,找不出反例,试试贪心。
-
-那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
-
-有时候贪心就是常识!哈哈
-
-按照左边界从小到大排序之后,如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
-
-即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
-
-这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
-
-
-
-知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
-
-其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
-
-C++代码如下:
-
-```C++
-class Solution {
-public:
- // 按照区间左边界从小到大排序
- static bool cmp (const vector& a, const vector& b) {
- return a[0] < b[0];
- }
- vector> merge(vector>& intervals) {
- vector> result;
- if (intervals.size() == 0) return result;
- sort(intervals.begin(), intervals.end(), cmp);
- bool flag = false; // 标记最后一个区间有没有合并
- int length = intervals.size();
-
- for (int i = 1; i < length; i++) {
- int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
- int end = intervals[i - 1][1]; // 初始i-1区间的右边界
- while (i < length && intervals[i][0] <= end) { // 合并区间
- end = max(end, intervals[i][1]); // 不断更新右区间
- if (i == length - 1) flag = true; // 最后一个区间也合并了
- i++; // 继续合并下一个区间
- }
- // start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
- result.push_back({start, end});
- }
- // 如果最后一个区间没有合并,将其加入result
- if (flag == false) {
- result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
- }
- return result;
- }
-};
-```
-
-当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
-
-```C++
-class Solution {
-public:
- vector> merge(vector>& intervals) {
- vector> result;
- if (intervals.size() == 0) return result;
- // 排序的参数使用了lamda表达式
- sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){return a[0] < b[0];});
-
- result.push_back(intervals[0]);
- for (int i = 1; i < intervals.size(); i++) {
- if (result.back()[1] >= intervals[i][0]) { // 合并区间
- result.back()[1] = max(result.back()[1], intervals[i][1]);
- } else {
- result.push_back(intervals[i]);
- }
- }
- return result;
- }
-};
-```
-
-* 时间复杂度:O(nlogn) ,有一个快排
-* 空间复杂度:O(1),我没有算result数组(返回值所需容器占的空间)
-
-
-# 总结
-
-对于贪心算法,很多同学都是:**如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
-
-跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
-
-那应该怎么办呢?
-
-正如我贪心系列开篇词[关于贪心算法,你该了解这些!](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
-
-「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
-
-就酱,学算法,就在「代码随想录」,值得介绍给身边的朋友同学们!
-
-
diff --git a/problems/0057.插入区间.md b/problems/0057.插入区间.md
deleted file mode 100644
index 79dba1c4..00000000
--- a/problems/0057.插入区间.md
+++ /dev/null
@@ -1,90 +0,0 @@
-
-# 链接
-https://leetcode-cn.com/problems/insert-interval/
-
-# 思路
-这道题目合并的情况有很多种,想想都让人头疼。
-
-我把这道题目化为三步:
-
-## 步骤一:找到需要合并的区间
-
-找到插入区间需要插入或者合并的位置。
-
-代码如下:
-
-```
-int index = 0; // intervals的索引
-while (index < intervals.size() && intervals[index][1] < newInterval[0]) {
- result.push_back(intervals[index++]);
-}
-```
-
-此时intervals[index]就需要合并的区间了
-
-## 步骤二:合并区间
-
-合并区间还有两种情况
-
-1. intervals[index]需要合并,如图:
-
- -
-对于这种情况,只要是intervals[index]起始位置 <= newInterval终止位置,就要一直合并下去。
-
-代码如下:
-
-```
-while (index < intervals.size() && intervals[index][0] <= newInterval[1]) { // 注意防止越界
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
-}
-```
-合并之后,将newInterval放入result就可以了
-
-2. intervals[index]不用合并,插入区间直接插入就行,如图:
-
-
-
-对于这种情况,只要是intervals[index]起始位置 <= newInterval终止位置,就要一直合并下去。
-
-代码如下:
-
-```
-while (index < intervals.size() && intervals[index][0] <= newInterval[1]) { // 注意防止越界
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
-}
-```
-合并之后,将newInterval放入result就可以了
-
-2. intervals[index]不用合并,插入区间直接插入就行,如图:
-
- -
-对于这种情况,就直接把newInterval放入result就可以了
-
-## 步骤三:处理合并区间之后的区间
-
-合并之后,就应该把合并之后的区间,以此加入result中。
-
-代码如下:
-
-```
-while (index < intervals.size()) {
- result.push_back(intervals[index++]);
-}
-```
-
-# 整体C++代码
-
-```
-class Solution {
-public:
- vector> insert(vector>& intervals, vector& newInterval) {
- vector> result;
- int index = 0; // intervals的索引
- // 步骤一:找到需要合并的区间
- while (index < intervals.size() && intervals[index][1] < newInterval[0]) {
- result.push_back(intervals[index++]);
- }
- // 步骤二:合并区间
- while (index < intervals.size() && intervals[index][0] <= newInterval[1]) {
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
- }
- result.push_back(newInterval);
- // 步骤三:处理合并区间之后的区间
- while (index < intervals.size()) {
- result.push_back(intervals[index++]);
- }
- return result;
- }
-};
-```
diff --git a/problems/0059.螺旋矩阵II.md b/problems/0059.螺旋矩阵II.md
deleted file mode 100644
index 111be4c4..00000000
--- a/problems/0059.螺旋矩阵II.md
+++ /dev/null
@@ -1,129 +0,0 @@
-
-
-
-对于这种情况,就直接把newInterval放入result就可以了
-
-## 步骤三:处理合并区间之后的区间
-
-合并之后,就应该把合并之后的区间,以此加入result中。
-
-代码如下:
-
-```
-while (index < intervals.size()) {
- result.push_back(intervals[index++]);
-}
-```
-
-# 整体C++代码
-
-```
-class Solution {
-public:
- vector> insert(vector>& intervals, vector& newInterval) {
- vector> result;
- int index = 0; // intervals的索引
- // 步骤一:找到需要合并的区间
- while (index < intervals.size() && intervals[index][1] < newInterval[0]) {
- result.push_back(intervals[index++]);
- }
- // 步骤二:合并区间
- while (index < intervals.size() && intervals[index][0] <= newInterval[1]) {
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
- }
- result.push_back(newInterval);
- // 步骤三:处理合并区间之后的区间
- while (index < intervals.size()) {
- result.push_back(intervals[index++]);
- }
- return result;
- }
-};
-```
diff --git a/problems/0059.螺旋矩阵II.md b/problems/0059.螺旋矩阵II.md
deleted file mode 100644
index 111be4c4..00000000
--- a/problems/0059.螺旋矩阵II.md
+++ /dev/null
@@ -1,129 +0,0 @@
-
-
- -
-
-
-  -
-  -
-  -
-  -
-  -
-  -
-
-
-
-> 一进循环深似海,从此offer是路人
-
-# 题目59.螺旋矩阵II
-
-题目地址:https://leetcode-cn.com/problems/spiral-matrix-ii/
-给定一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
-
-示例:
-
-输入: 3
-输出:
-[
- [ 1, 2, 3 ],
- [ 8, 9, 4 ],
- [ 7, 6, 5 ]
-]
-
-# 思路
-
-这道题目可以说在面试中出现频率较高的题目,**本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。**
-
-要如何画出这个螺旋排列的正方形矩阵呢?
-
-相信很多同学刚开始做这种题目的时候,上来就是一波判断猛如虎。
-
-结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里哪里有问题,改了那里这里又跑不起来了。
-
-大家还记得我们在这篇文章[数组:每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)中讲解了二分法,提到如果要写出正确的二分法一定要坚持**循环不变量原则**。
-
-而求解本题依然是要坚持循环不变量原则。
-
-模拟顺时针画矩阵的过程:
-
-* 填充上行从左到右
-* 填充右列从上到下
-* 填充下行从右到左
-* 填充左列从下到上
-
-由外向内一圈一圈这么画下去。
-
-可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是**一进循环深似海,从此offer是路人**。
-
-这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开又闭的原则,这样这一圈才能按照统一的规则画下来。
-
-那么我按照左闭右开的原则,来画一圈,大家看一下:
-
-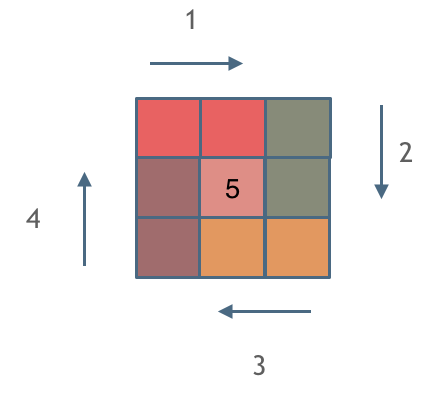
-
-这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
-
-这也是坚持了每条边左闭右开的原则。
-
-一些同学做这道题目之所以一直写不好,代码越写越乱。
-
-就是因为在画每一条边的时候,一会左开又闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
-
-代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
-
-# C++代码
-
-```C++
-class Solution {
-public:
- vector> generateMatrix(int n) {
- vector> res(n, vector(n, 0)); // 使用vector定义一个二维数组
- int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
- int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
- int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
- int count = 1; // 用来给矩阵中每一个空格赋值
- int offset = 1; // 每一圈循环,需要控制每一条边遍历的长度
- int i,j;
- while (loop --) {
- i = startx;
- j = starty;
-
- // 下面开始的四个for就是模拟转了一圈
- // 模拟填充上行从左到右(左闭右开)
- for (j = starty; j < starty + n - offset; j++) {
- res[startx][j] = count++;
- }
- // 模拟填充右列从上到下(左闭右开)
- for (i = startx; i < startx + n - offset; i++) {
- res[i][j] = count++;
- }
- // 模拟填充下行从右到左(左闭右开)
- for (; j > starty; j--) {
- res[i][j] = count++;
- }
- // 模拟填充左列从下到上(左闭右开)
- for (; i > startx; i--) {
- res[i][j] = count++;
- }
-
- // 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
- startx++;
- starty++;
-
- // offset 控制每一圈里每一条边遍历的长度
- offset += 2;
- }
-
- // 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
- if (n % 2) {
- res[mid][mid] = count;
- }
- return res;
- }
-};
-```
-
-**循序渐进学算法,认准「代码随想录」,Carl手把手带你过关斩将!**
-
-
- -
-
diff --git a/problems/0062.不同路径.md b/problems/0062.不同路径.md
deleted file mode 100644
index 7eee77b3..00000000
--- a/problems/0062.不同路径.md
+++ /dev/null
@@ -1,176 +0,0 @@
-
-# 思路
-
-## 深搜
-
-这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
-
-注意题目中说机器人每次只能向下或者向右移动一步,那么其实**机器人走过的路径可以抽象为一颗二叉树,而叶子节点就是终点!**
-
-如图举例:
-
-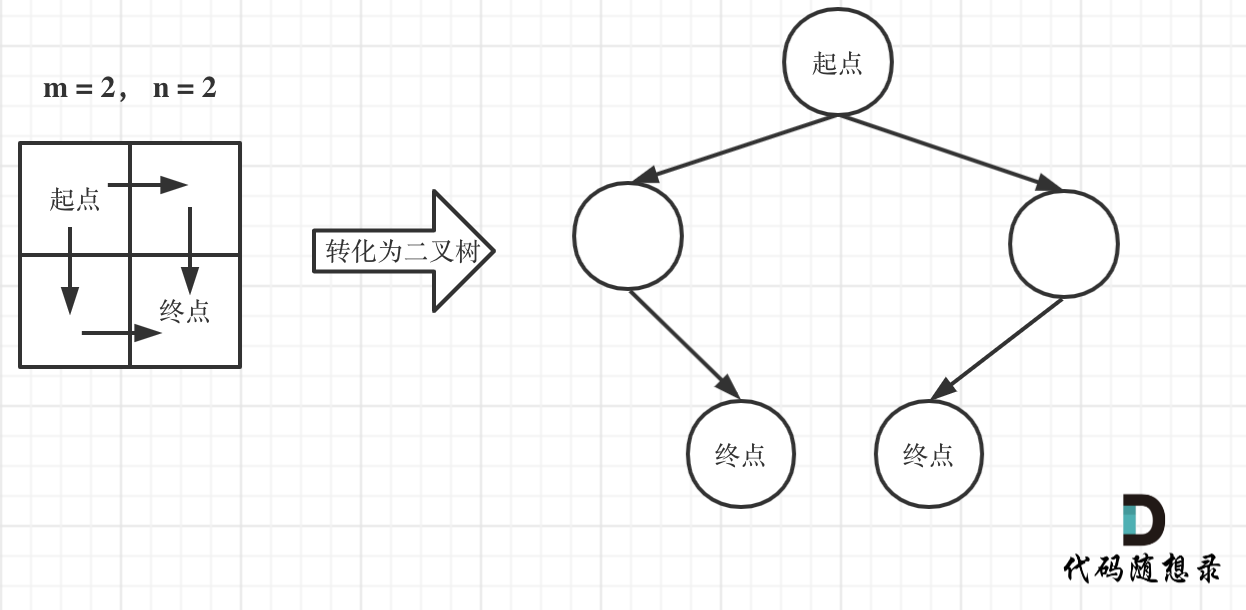
-
-此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
-
-```C++
-class Solution {
-private:
- int dfs(int i, int j, int m, int n) {
- if (i > m || j > n) return 0; // 越界了
- if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点
- return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
- }
-public:
- int uniquePaths(int m, int n) {
- return dfs(1, 1, m, n);
- }
-};
-```
-
-大家如果提交了代码就会发现超时了!
-
-来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
-
-这颗树的深度其实就是m+n-1(深度按从1开始计算)。
-
-那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有把搜索节点都遍历到,只是近似而已)
-
-所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
-
-## 动态规划
-
-机器人从(0 , 0) 位置触发,到(m - 1, n - 1)终点。
-
-按照动规三部曲来分析:
-
-* dp数组表述啥
-
-这里设计一个dp二维数组,dp[i][j] 表示从(0 ,0)出发,到(i, j) 有几条不同的路径。
-
-* dp数组的初始化
-
-如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
-
-所以初始化代码为:
-
-```
-for (int i = 0; i < m; i++) dp[i][0] = 1;
-for (int j = 0; j < n; j++) dp[0][j] = 1;
-```
-
-* 递推公式
-
-想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
-
-此时在回顾一下 dp[i-1][j] 表示啥,是从(0, 0)的位置到(i-1, j)有几条路径,dp[i][j - 1]同理。
-
-那么很自然,dp[i][j] = dp[i-1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
-
-如图所示:
-
-
-
-C++代码如下:
-
-```C++
-class Solution {
-public:
- int uniquePaths(int m, int n) {
- vector> dp(m, vector(n, 0));
- for (int i = 0; i < m; i++) dp[i][0] = 1;
- for (int j = 0; j < n; j++) dp[0][j] = 1;
- for (int i = 1; i < m; i++) {
- for (int j = 1; j < n; j++) {
- dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
- }
- }
- return dp[m - 1][n - 1];
- }
-};
-```
-* 时间复杂度:O(m * n)
-* 空间复杂度:O(m * n)
-
-其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下:
-
-```C++
-class Solution {
-public:
- int uniquePaths(int m, int n) {
- vector dp(n);
- for (int i = 0; i < n; i++) dp[i] = 1;
- for (int j = 1; j < m; j++) {
- for (int i = 1; i < n; i++) {
- dp[i] += dp[i - 1];
- }
- }
- return dp[n - 1];
- }
-};
-```
-* 时间复杂度:O(m * n)
-* 空间复杂度:O(n)
-
-# 数论方法
-
-在这个图中,可以看出一共 m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
-
-
-
-在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
-
-那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
-
-那么这就是一个组合问题了。
-
-那么答案,如图所示:
-
-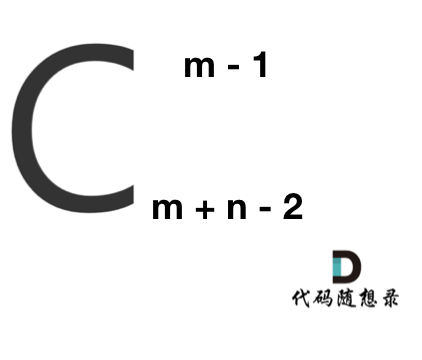
-
-**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。
-
-```
-class Solution {
-public:
- int uniquePaths(int m, int n) {
- int numerator = 1, denominator = 1;
- int count = m - 1;
- int t = m + n - 2;
- while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出
- for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
- return numerator / denominator;
- }
-};
-
-```
-
-需要在计算分子的时候,不算除以分母,代码如下:
-
-```
-class Solution {
-public:
- int uniquePaths(int m, int n) {
- long long numerator = 1; // 分子
- int denominator = m - 1; // 分母
- int count = m - 1;
- int t = m + n - 2;
- while (count--) {
- numerator *= (t--);
- while (denominator != 0 && numerator % denominator == 0) {
- numerator /= denominator;
- denominator--;
- }
- }
- return numerator;
- }
-};
-```
-
-计算组合问题的代码还是有难度的,特别是处理溢出的情况!
-
-最后这个代码还有点复杂了,还是可以优化,我就不继续优化了,有空在整理一下,哈哈,就酱!
-
-
-
-
diff --git a/problems/0070.爬楼梯.md b/problems/0070.爬楼梯.md
deleted file mode 100644
index bb98afca..00000000
--- a/problems/0070.爬楼梯.md
+++ /dev/null
@@ -1,86 +0,0 @@
-
-# 思路
-
-本题大家多举一个例子,就发现这其实就是斐波那契数列。
-
-题目509. 斐波那契数中的代码初始化部分稍加改动,就可以过了本题。
-
-C++代码如下:
-```
-class Solution {
-public:
- int climbStairs(int n) {
- if (n <= 1) return n;
- vector dp(n + 1);
- dp[0] = 1;
- dp[1] = 1;
- for (int i = 2; i <= n; i++) {
- dp[i] = dp[i - 1] + dp[i - 2];
- }
- return dp[n];
-
- }
-};
-```
-
-既然这么简单为什么还要讲呢,其实本题稍加改动就是一道面试好题,如果每次可以爬 1 或 2或3或者m 个台阶呢,走到楼顶有几种方法?
-
-* 确定dp数组以及下标的含义
-
-dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法
-
-* 确定递推公式
-
-dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
-
-那么递推公式为:dp[i] += dp[i - j]
-
-* dp数组如何初始化
-
-既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
-
-下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果
-
-* 确定遍历顺序
-
-这是背包里求排列问题,即:1 2 步 和 2 1 步都是上三个台阶,但是这两种方法不!
-
-所以需将target放在外循环,将nums放在内循环。
-
-每一步可以走多次,说明这是完全背包,内循环需要从前向后遍历。
-
-
-C++代码如下:
-```
-class Solution {
-public:
- int climbStairs(int n) {
- vector dp(n + 1, 0);
- dp[0] = 1;
- for (int i = 1; i <= n; i++) {
- for (int j = 1; j <= m; j++) {
- if (i - j >= 0) dp[i] += dp[i - j];
- }
- }
- return dp[n];
- }
-};
-```
-
-代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯的代码了。
-
-# 总结
-
-如果我来面试的话,我就会想给候选人出一个 本题原题,看其表现,如果顺利写出来,进而在要求每次可以爬[1 - m]个台阶应该怎么写。
-
-顺便再考察一下两个for循环的嵌套顺序,为什么target放外面,nums放里面。这就能反馈出对背包问题本质的掌握程度,是不是刷题背公式,一眼就看出来。
-
-这么一连套下来,如果候选人都能答出来,相信任何一位面试官都是非常满意的。
-
-**本题代码不长,题目也很普通,当稍稍一进阶就可以考察本质问题,而且题目进阶的内容在leetcode上并没有,一定程度上就可以排除掉刷题党了,简直是面试题目的绝佳选择!**
-
-相信通过这道简单的斐波那契数列题目,大家能感受到大厂面试官最喜欢什么样的面试题目了,并不是手撕红黑树!
-
-
-所以本题是一道非常好的题目。
-
diff --git a/problems/0077.组合.md b/problems/0077.组合.md
deleted file mode 100644
index 0a7187d1..00000000
--- a/problems/0077.组合.md
+++ /dev/null
@@ -1,248 +0,0 @@
-
-> 回溯法的第一道题目,就不简单呀!
-
-# 第77题. 组合
-
-题目链接:https://leetcode-cn.com/problems/combinations/
-
-给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
-
-示例:
-输入: n = 4, k = 2
-输出:
-[
- [2,4],
- [3,4],
- [2,3],
- [1,2],
- [1,3],
- [1,4],
-]
-
-也可以直接看我的B站视频:[带你学透回溯算法-组合问题(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv#reply3733925949)
-
-# 思路
-
-本题这是回溯法的经典题目。
-
-直接的解法当然是使用for循环,例如示例中k为2,很容易想到 用两个for循环,这样就可以输出 和示例中一样的结果。
-
-代码如下:
-```
-int n = 4;
-for (int i = 1; i <= n; i++) {
- for (int j = i + 1; j <= n; j++) {
- cout << i << " " << j << endl;
- }
-}
-```
-
-输入:n = 100, k = 3
-那么就三层for循环,代码如下:
-
-```
-int n = 100;
-for (int i = 1; i <= n; i++) {
- for (int j = i + 1; j <= n; j++) {
- for (int u = j + 1; u <= n; n++) {
- cout << i << " " << j << " " << u << endl;
- }
- }
-}
-```
-
-**如果n为100,k为50呢,那就50层for循环,是不是开始窒息**。
-
-**此时就会发现虽然想暴力搜索,但是用for循环嵌套连暴力都写不出来!**
-
-咋整?
-
-回溯搜索法来了,虽然回溯法也是暴力,但至少能写出来,不像for循环嵌套k层让人绝望。
-
-那么回溯法怎么暴力搜呢?
-
-上面我们说了**要解决 n为100,k为50的情况,暴力写法需要嵌套50层for循环,那么回溯法就用递归来解决嵌套层数的问题**。
-
-递归来做层叠嵌套(可以理解是开k层for循环),**每一次的递归中嵌套一个for循环,那么递归就可以用于解决多层嵌套循环的问题了**。
-
-此时递归的层数大家应该知道了,例如:n为100,k为50的情况下,就是递归50层。
-
-一些同学本来对递归就懵,回溯法中递归还要嵌套for循环,可能就直接晕倒了!
-
-如果脑洞模拟回溯搜索的过程,绝对可以让人窒息,所以需要抽象图形结构来进一步理解。
-
-**我们在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中说道回溯法解决的问题都可以抽象为树形结构(N叉树),用树形结构来理解回溯就容易多了**。
-
-那么我把组合问题抽象为如下树形结构:
-
-
-
-可以看出这个棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不在重复取。
-
-第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
-
-**每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围**。
-
-**图中可以发现n相当于树的宽度,k相当于树的深度**。
-
-那么如何在这个树上遍历,然后收集到我们要的结果集呢?
-
-**图中每次搜索到了叶子节点,我们就找到了一个结果**。
-
-相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
-
-在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中我们提到了回溯法三部曲,那么我们按照回溯法三部曲开始正式讲解代码了。
-
-
-## 回溯法三部曲
-
-* 递归函数的返回值以及参数
-
-在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
-
-代码如下:
-
-```
-vector> result; // 存放符合条件结果的集合
-vector path; // 用来存放符合条件结果
-```
-
-其实不定义这两个全局遍历也是可以的,把这两个变量放进递归函数的参数里,但函数里参数太多影响可读性,所以我定义全局变量了。
-
-函数里一定有两个参数,既然是集合n里面取k的数,那么n和k是两个int型的参数。
-
-然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
-
-为什么要有这个startIndex呢?
-
-**每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex**。
-
-从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
-
-
-
-所以需要startIndex来记录下一层递归,搜索的起始位置。
-
-那么整体代码如下:
-
-```
-vector> result; // 存放符合条件结果的集合
-vector path; // 用来存放符合条件单一结果
-void backtracking(int n, int k, int startIndex)
-```
-
-* 回溯函数终止条件
-
-什么时候到达所谓的叶子节点了呢?
-
-path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
-
-如图红色部分:
-
-
-
-此时用result二维数组,把path保存起来,并终止本层递归。
-
-所以终止条件代码如下:
-
-```
-if (path.size() == k) {
- result.push_back(path);
- return;
-}
-```
-
-* 单层搜索的过程
-
-回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
-
-
-
-如此我们才遍历完图中的这棵树。
-
-for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
-
-代码如下:
-
-```
-for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
- path.push_back(i); // 处理节点
- backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始
- path.pop_back(); // 回溯,撤销处理的节点
-}
-```
-
-可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
-
-backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
-
-关键地方都讲完了,组合问题C++完整代码如下:
-
-
-```
-class Solution {
-private:
- vector> result; // 存放符合条件结果的集合
- vector path; // 用来存放符合条件结果
- void backtracking(int n, int k, int startIndex) {
- if (path.size() == k) {
- result.push_back(path);
- return;
- }
- for (int i = startIndex; i <= n; i++) {
- path.push_back(i); // 处理节点
- backtracking(n, k, i + 1); // 递归
- path.pop_back(); // 回溯,撤销处理的节点
- }
- }
-public:
- vector> combine(int n, int k) {
- result.clear(); // 可以不写
- path.clear(); // 可以不写
- backtracking(n, k, 1);
- return result;
- }
-};
-```
-
-还记得我们在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中给出的回溯法模板么?
-
-如下:
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
-
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-**对比一下本题的代码,是不是发现有点像!** 所以有了这个模板,就有解题的大体方向,不至于毫无头绪。
-
-# 总结
-
-组合问题是回溯法解决的经典问题,我们开始的时候给大家列举一个很形象的例子,就是n为100,k为50的话,直接想法就需要50层for循环。
-
-从而引出了回溯法就是解决这种k层for循环嵌套的问题。
-
-然后进一步把回溯法的搜索过程抽象为树形结构,可以直观的看出搜索的过程。
-
-接着用回溯法三部曲,逐步分析了函数参数、终止条件和单层搜索的过程。
-
-**本题其实是可以剪枝优化的,大家可以思考一下,具体如何剪枝我会在下一篇详细讲解,敬请期待!**
-
-**就酱,如果对你有帮助,就帮Carl转发一下吧,让更多的同学发现这里!**
-
-
-**[本题剪枝操作文章链接](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)**
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0077.组合优化.md b/problems/0077.组合优化.md
deleted file mode 100644
index 6f12abd0..00000000
--- a/problems/0077.组合优化.md
+++ /dev/null
@@ -1,129 +0,0 @@
-
-> 如果想在电脑上看文章的话,可以看这里:https://github.com/youngyangyang04/leetcode-master,已经按照顺序整理了「代码随想录」的所有文章,可以fork到自己仓库里,随时复习。**那么重点来了,来都来了,顺便给一个star吧,哈哈**
-
-
-在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)中,我们通过回溯搜索法,解决了n个数中求k个数的组合问题。
-
-文中的回溯法是可以剪枝优化的,本篇我们继续来看一下题目77. 组合。
-
-链接:https://leetcode-cn.com/problems/combinations/
-
-**看本篇之前,需要先看[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)**。
-
-大家先回忆一下[77. 组合]给出的回溯法的代码:
-
-```
-class Solution {
-private:
- vector> result; // 存放符合条件结果的集合
- vector path; // 用来存放符合条件结果
- void backtracking(int n, int k, int startIndex) {
- if (path.size() == k) {
- result.push_back(path);
- return;
- }
- for (int i = startIndex; i <= n; i++) {
- path.push_back(i); // 处理节点
- backtracking(n, k, i + 1); // 递归
- path.pop_back(); // 回溯,撤销处理的节点
- }
- }
-public:
- vector> combine(int n, int k) {
- result.clear(); // 可以不写
- path.clear(); // 可以不写
- backtracking(n, k, 1);
- return result;
- }
-};
-```
-
-## 剪枝优化
-
-我们说过,回溯法虽然是暴力搜索,但也有时候可以有点剪枝优化一下的。
-
-在遍历的过程中有如下代码:
-
-```
-for (int i = startIndex; i <= n; i++) {
- path.push_back(i);
- backtracking(n, k, i + 1);
- path.pop_back();
-}
-```
-
-这个遍历的范围是可以剪枝优化的,怎么优化呢?
-
-来举一个例子,n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
-
-这么说有点抽象,如图所示:
-
- -
-图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
-
-**所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
-
-**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
-
-注意代码中i,就是for循环里选择的起始位置。
-```
-for (int i = startIndex; i <= n; i++) {
-```
-
-接下来看一下优化过程如下:
-
-1. 已经选择的元素个数:path.size();
-
-2. 还需要的元素个数为: k - path.size();
-
-3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
-
-为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
-
-举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
-
-从2开始搜索都是合理的,可以是组合[2, 3, 4]。
-
-这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
-
-所以优化之后的for循环是:
-
-```
-for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
-```
-
-优化后整体代码如下:
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(int n, int k, int startIndex) {
- if (path.size() == k) {
- result.push_back(path);
- return;
- }
- for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
- path.push_back(i); // 处理节点
- backtracking(n, k, i + 1);
- path.pop_back(); // 回溯,撤销处理的节点
- }
- }
-public:
-
- vector> combine(int n, int k) {
- backtracking(n, k, 1);
- return result;
- }
-};
-```
-
-# 总结
-
-本篇我们准对求组合问题的回溯法代码做了剪枝优化,这个优化如果不画图的话,其实不好理解,也不好讲清楚。
-
-所以我依然是把整个回溯过程抽象为一颗树形结构,然后可以直观的看出,剪枝究竟是剪的哪里。
-
-**就酱,学到了就帮Carl转发一下吧,让更多的同学知道这里!**
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
deleted file mode 100644
index 8a2ff8a3..00000000
--- a/problems/0078.子集.md
+++ /dev/null
@@ -1,175 +0,0 @@
-> 认识本质之后,这就是一道模板题
-
-# 第78题. 子集
-
-题目地址:https://leetcode-cn.com/problems/subsets/
-
-给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
-
-说明:解集不能包含重复的子集。
-
-示例:
-输入: nums = [1,2,3]
-输出:
-[
- [3],
- [1],
- [2],
- [1,2,3],
- [1,3],
- [2,3],
- [1,2],
- []
-]
-
-# 思路
-
-求子集问题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:分割问题!](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)又不一样了。
-
-如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,**那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!**
-
-其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
-
-**那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!**
-
-有同学问了,什么时候for可以从0开始呢?
-
-求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合,排列问题我们后续的文章就会讲到的。
-
-以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
-
-
-
-从图中红线部分,可以看出**遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合**。
-
-## 回溯三部曲
-
-* 递归函数参数
-
-全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
-
-递归函数参数在上面讲到了,需要startIndex。
-
-代码如下:
-
-```
-vector> result;
-vector path;
-void backtracking(vector& nums, int startIndex) {
-```
-
-* 递归终止条件
-
-从图中可以看出:
-
-
-
-剩余集合为空的时候,就是叶子节点。
-
-那么什么时候剩余集合为空呢?
-
-就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
-
-```
-if (startIndex >= nums.size()) {
- return;
-}
-```
-
-**其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了**。
-
-* 单层搜索逻辑
-
-**求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树**。
-
-那么单层递归逻辑代码如下:
-
-```
-for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]); // 子集收集元素
- backtracking(nums, i + 1); // 注意从i+1开始,元素不重复取
- path.pop_back(); // 回溯
-}
-```
-
-## C++代码
-
-根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
-
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-可以写出如下回溯算法C++代码:
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex) {
- result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
- if (startIndex >= nums.size()) { // 终止条件可以不加
- return;
- }
- for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
-public:
- vector> subsets(vector& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
-};
-
-```
-
-在注释中,可以发现可以不写终止条件,因为本来我们就要遍历整颗树。
-
-有的同学可能担心不写终止条件会不会无限递归?
-
-并不会,因为每次递归的下一层就是从i+1开始的。
-
-# 总结
-
-相信大家经过了
-* 组合问题:
- * [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
- * [回溯算法:组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
- * [回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
- * [回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
- * [回溯算法:求组合总和(二)](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)
- * [回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
-* 分割问题:
- * [回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)
- * [回溯算法:复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)
-
-洗礼之后,发现子集问题还真的有点简单了,其实这就是一道标准的模板题。
-
-但是要清楚子集问题和组合问题、分割问题的的区别,**子集是收集树形结构中树的所有节点的结果**。
-
-**而组合问题、分割问题是收集树形结构中叶子节点的结果**。
-
-**就酱,如果感觉收获满满,就帮Carl宣传一波「代码随想录」吧!**
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0083.删除排序链表中的重复元素.md b/problems/0083.删除排序链表中的重复元素.md
deleted file mode 100644
index b725f7f8..00000000
--- a/problems/0083.删除排序链表中的重复元素.md
+++ /dev/null
@@ -1,40 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list/
-
-## 思路
-
-这道题目没有必要设置虚拟节点,因为不会删除头结点
-
-## 代码
-
-```
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode(int x) : val(x), next(NULL) {}
- * };
- */
-class Solution {
-public:
- ListNode* deleteDuplicates(ListNode* head) {
- ListNode* p = head;
- while (p != NULL && p->next!= NULL) {
- if (p->val == p->next->val) {
- ListNode* tmp = p->next;
- p->next = p->next->next;
- delete tmp;
- } else {
- p = p->next;
- }
- }
- return head;
- }
-};
-```
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0084.柱状图中最大的矩形.md b/problems/0084.柱状图中最大的矩形.md
deleted file mode 100644
index e5057e55..00000000
--- a/problems/0084.柱状图中最大的矩形.md
+++ /dev/null
@@ -1,104 +0,0 @@
-
-# 链接
-
-https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
-
-## 思路
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- int sum = 0;
- for (int i = 0; i < heights.size(); i++) {
- int left = i;
- int right = i;
- for (; left >= 0; left--) {
- if (heights[left] < heights[i]) break;
- }
- for (; right < heights.size(); right++) {
- if (heights[right] < heights[i]) break;
- }
- int w = right - left - 1;
- int h = heights[i];
- sum = max(sum, w * h);
- }
- return sum;
- }
-};
-```
-
-如上代码并不能通过leetcode,超时了,因为时间复杂度是O(n^2)。
-
-## 思考一下动态规划
-
-## 单调栈
-
-单调栈的思路还是不容易理解的,
-
-想清楚从大到小,还是从小到大,
-
-本题是从栈底到栈头 从小到大,和 接雨水正好反过来。
-
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- stack st;
- heights.insert(heights.begin(), 0); // 数组头部加入元素0
- heights.push_back(0); // 数组尾部加入元素0
- st.push(0);
- int result = 0;
- // 第一个元素已经入栈,从下表1开始
- for (int i = 1; i < heights.size(); i++) {
- // 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下表
- if (heights[i] > heights[st.top()]) {
- st.push(i);
- } else if (heights[i] == heights[st.top()]) {
- st.pop(); // 这个可以加,可以不加,效果一样,思路不同
- st.push(i);
- } else {
- while (heights[i] < heights[st.top()]) { // 注意是while
- int mid = st.top();
- st.pop();
- int left = st.top();
- int right = i;
- int w = right - left - 1;
- int h = heights[mid];
- result = max(result, w * h);
- }
- st.push(i);
- }
- }
- return result;
- }
-};
-
-```
-
-代码精简之后:
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- stack st;
- heights.insert(heights.begin(), 0); // 数组头部加入元素0
- heights.push_back(0); // 数组尾部加入元素0
- st.push(0);
- int result = 0;
- for (int i = 1; i < heights.size(); i++) {
- while (heights[i] < heights[st.top()]) {
- int mid = st.top();
- st.pop();
- int w = i - st.top() - 1;
- int h = heights[mid];
- result = max(result, w * h);
- }
- st.push(i);
- }
- return result;
- }
-};
-```
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
deleted file mode 100644
index c8e29763..00000000
--- a/problems/0090.子集II.md
+++ /dev/null
@@ -1,132 +0,0 @@
-
-> 子集问题加去重!
-
-# 第90题.子集II
-
-题目链接:https://leetcode-cn.com/problems/subsets-ii/
-
-给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
-
-说明:解集不能包含重复的子集。
-
-示例:
-输入: [1,2,2]
-输出:
-[
- [2],
- [1],
- [1,2,2],
- [2,2],
- [1,2],
- []
-]
-
-
-# 思路
-
-做本题之前一定要先做[78.子集](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)。
-
-这道题目和[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)区别就是集合里有重复元素了,而且求取的子集要去重。
-
-那么关于回溯算法中的去重问题,**在[40.组合总和II](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)中已经详细讲解过了,和本题是一个套路**。
-
-**剧透一下,后期要讲解的排列问题里去重也是这个套路,所以理解“树层去重”和“树枝去重”非常重要**。
-
-用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
-
-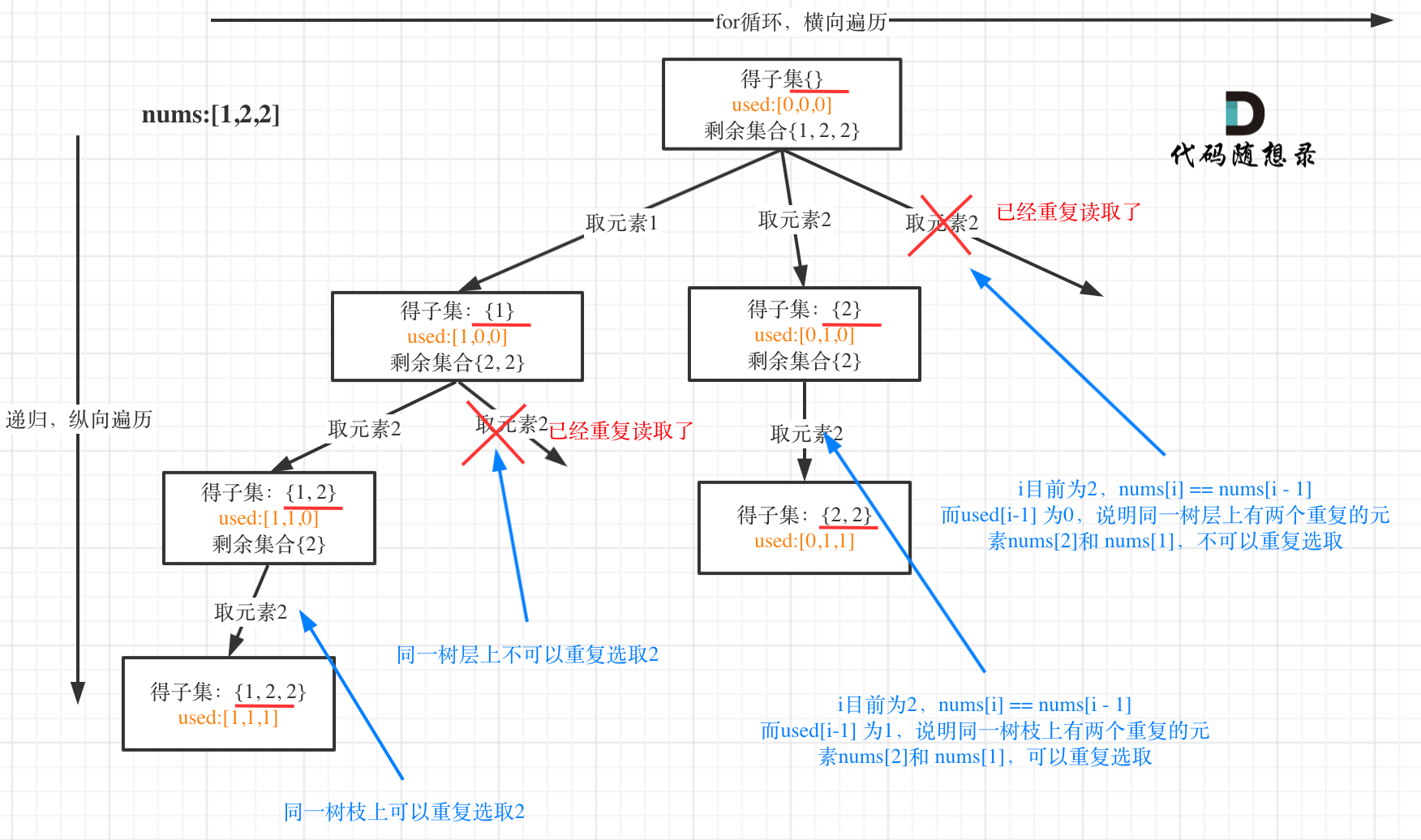
-
-从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
-
-本题就是其实就是[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重,去重我们在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了,所以我就直接给出代码了:
-
-# C++代码
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex, vector& used) {
- result.push_back(path);
- for (int i = startIndex; i < nums.size(); i++) {
- // used[i - 1] == true,说明同一树支candidates[i - 1]使用过
- // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
- // 而我们要对同一树层使用过的元素进行跳过
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- path.push_back(nums[i]);
- used[i] = true;
- backtracking(nums, i + 1, used);
- used[i] = false;
- path.pop_back();
- }
- }
-
-public:
- vector> subsetsWithDup(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- sort(nums.begin(), nums.end()); // 去重需要排序
- backtracking(nums, 0, used);
- return result;
- }
-};
-
-```
-
-使用set去重的版本。
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex, vector& used) {
- result.push_back(path);
- unordered_set uset;
- for (int i = startIndex; i < nums.size(); i++) {
- if (uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]);
- path.push_back(nums[i]);
- backtracking(nums, i + 1, used);
- path.pop_back();
- }
- }
-
-public:
- vector> subsetsWithDup(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- sort(nums.begin(), nums.end()); // 去重需要排序
- backtracking(nums, 0, used);
- return result;
- }
-};
-
-```
-
-# 总结
-
-其实这道题目的知识点,我们之前都讲过了,如果之前讲过的子集问题和去重问题都掌握的好,这道题目应该分分钟AC。
-
-当然本题去重的逻辑,也可以这么写
-
-```
-if (i > startIndex && nums[i] == nums[i - 1] ) {
- continue;
-}
-```
-
-**就酱,如果感觉融会贯通了,就把「代码随想录」介绍给自己的同学朋友吧,也许他们也需要!**
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
-
-
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
deleted file mode 100644
index e691852e..00000000
--- a/problems/0093.复原IP地址.md
+++ /dev/null
@@ -1,253 +0,0 @@
-> 一些录友表示跟不上现在的节奏,想从头开始打卡学习起来,可以在公众号左下方,「算法汇总」可以找到历史文章,都是按系列排好顺序的,挨个看就可以了,看文章下的留言你就会发现,有很多录友都在从头打卡,你并不孤单!
-
-# 93.复原IP地址
-
-题目地址:https://leetcode-cn.com/problems/restore-ip-addresses/
-
-给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
-
-有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
-
-例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
-
-示例 1:
-输入:s = "25525511135"
-输出:["255.255.11.135","255.255.111.35"]
-
-示例 2:
-输入:s = "0000"
-输出:["0.0.0.0"]
-
-示例 3:
-输入:s = "1111"
-输出:["1.1.1.1"]
-
-示例 4:
-输入:s = "010010"
-输出:["0.10.0.10","0.100.1.0"]
-
-示例 5:
-输入:s = "101023"
-输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
-
-提示:
-0 <= s.length <= 3000
-s 仅由数字组成
-
-
-# 思路
-
-做这道题目之前,最好先把[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)这个做了。
-
-这道题目相信大家刚看的时候,应该会一脸茫然。
-
-其实只要意识到这是切割问题,**切割问题就可以使用回溯搜索法把所有可能性搜出来**,和刚做过的[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)就十分类似了。
-
-切割问题可以抽象为树型结构,如图:
-
-
-
-
-## 回溯三部曲
-
-* 递归参数
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我们就提到切割问题类似组合问题。
-
-startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。
-
-本题我们还需要一个变量pointNum,记录添加逗点的数量。
-
-所以代码如下:
-
-```
- vector result;// 记录结果
- // startIndex: 搜索的起始位置,pointNum:添加逗点的数量
- void backtracking(string& s, int startIndex, int pointNum) {
-```
-
-* 递归终止条件
-
-终止条件和[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)情况就不同了,本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。
-
-pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。
-
-然后验证一下第四段是否合法,如果合法就加入到结果集里
-
-代码如下:
-
-```
-if (pointNum == 3) { // 逗点数量为3时,分隔结束
- // 判断第四段子字符串是否合法,如果合法就放进result中
- if (isValid(s, startIndex, s.size() - 1)) {
- result.push_back(s);
- }
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中已经讲过在循环遍历中如何截取子串。
-
-在`for (int i = startIndex; i < s.size(); i++)`循环中 [startIndex, i]这个区间就是截取的子串,需要判断这个子串是否合法。
-
-如果合法就在字符串后面加上符号`.`表示已经分割。
-
-如果不合法就结束本层循环,如图中剪掉的分支:
-
-
-
-然后就是递归和回溯的过程:
-
-递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符`.`),同时记录分割符的数量pointNum 要 +1。
-
-回溯的时候,就将刚刚加入的分隔符`.` 删掉就可以了,pointNum也要-1。
-
-代码如下:
-
-```
-for (int i = startIndex; i < s.size(); i++) {
- if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
- s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
- pointNum++;
- backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
- pointNum--; // 回溯
- s.erase(s.begin() + i + 1); // 回溯删掉逗点
- } else break; // 不合法,直接结束本层循环
-}
-```
-
-## 判断子串是否合法
-
-最后就是在写一个判断段位是否是有效段位了。
-
-主要考虑到如下三点:
-
-* 段位以0为开头的数字不合法
-* 段位里有非正整数字符不合法
-* 段位如果大于255了不合法
-
-代码如下:
-
-```
-// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
-bool isValid(const string& s, int start, int end) {
- if (start > end) {
- return false;
- }
- if (s[start] == '0' && start != end) { // 0开头的数字不合法
- return false;
- }
- int num = 0;
- for (int i = start; i <= end; i++) {
- if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
- return false;
- }
- num = num * 10 + (s[i] - '0');
- if (num > 255) { // 如果大于255了不合法
- return false;
- }
- }
- return true;
-}
-```
-
-## C++代码
-
-
-根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
-
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-可以写出如下回溯算法C++代码:
-
-```
-class Solution {
-private:
- vector result;// 记录结果
- // startIndex: 搜索的起始位置,pointNum:添加逗点的数量
- void backtracking(string& s, int startIndex, int pointNum) {
- if (pointNum == 3) { // 逗点数量为3时,分隔结束
- // 判断第四段子字符串是否合法,如果合法就放进result中
- if (isValid(s, startIndex, s.size() - 1)) {
- result.push_back(s);
- }
- return;
- }
- for (int i = startIndex; i < s.size(); i++) {
- if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
- s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
- pointNum++;
- backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
- pointNum--; // 回溯
- s.erase(s.begin() + i + 1); // 回溯删掉逗点
- } else break; // 不合法,直接结束本层循环
- }
- }
- // 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
- bool isValid(const string& s, int start, int end) {
- if (start > end) {
- return false;
- }
- if (s[start] == '0' && start != end) { // 0开头的数字不合法
- return false;
- }
- int num = 0;
- for (int i = start; i <= end; i++) {
- if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
- return false;
- }
- num = num * 10 + (s[i] - '0');
- if (num > 255) { // 如果大于255了不合法
- return false;
- }
- }
- return true;
- }
-public:
- vector restoreIpAddresses(string s) {
- result.clear();
- if (s.size() > 12) return result; // 算是剪枝了
- backtracking(s, 0, 0);
- return result;
- }
-};
-
-```
-
-# 总结
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我列举的分割字符串的难点,本题都覆盖了。
-
-而且本题还需要操作字符串添加逗号作为分隔符,并验证区间的合法性。
-
-可以说是[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)的加强版。
-
-在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
-
-**就酱,「代码随想录」值得推荐给你的朋友们!**
-
-
-一些录友表示跟不上现在的节奏,想从头开始打卡学习起来,可以在在公众号左下方,「算法汇总」可以找到历史文章,都是按系列排好顺序的,挨个看就可以了,别忘了打卡。
-
-**很多录友都在从头开始打卡学习,看看前面文章的留言区就知道了,你并不孤单!**
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0094.二叉树的中序遍历.md b/problems/0094.二叉树的中序遍历.md
deleted file mode 100644
index e63819c1..00000000
--- a/problems/0094.二叉树的中序遍历.md
+++ /dev/null
@@ -1,84 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
-
-## 思路
-
-详细题解请看这篇:[一文学通二叉树前中后序递归法与迭代法](https://github.com/youngyangyang04/leetcode/blob/master/problems/0144.二叉树的前序遍历.md)
-
-## C++代码
-
-### 递归
-```
-class Solution {
-public:
- void traversal(TreeNode* cur, vector& vec) {
- if (cur == NULL) return;
- traversal(cur->left, vec);
- vec.push_back(cur->val);
- traversal(cur->right, vec);
- }
- vector inorderTraversal(TreeNode* root) {
- vector result;
- traversal(root, result);
- return result;
- }
-};
-```
-
-### 栈
-```
-class Solution {
-public:
- vector inorderTraversal(TreeNode* root) {
- vector result;
- stack st;
- TreeNode* cur = root;
- while (cur != NULL || !st.empty()) {
- if (cur != NULL) {
- st.push(cur);
- cur = cur->left;
- } else {
- cur = st.top();
- st.pop();
- result.push_back(cur->val);
- cur = cur->right;
- }
- }
- return result;
- }
-};
-```
-
-### 栈 通用模板
-
-```
-class Solution {
-public:
- vector inorderTraversal(TreeNode* root) {
- vector result;
- stack st;
- if (root != NULL) st.push(root);
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- if (node->right) st.push(node->right); // 添加右节点
-
- st.push(node); // 添加中节点
- st.push(NULL); // 中节点访问过,但是还没有处理,需要做一下标记。
-
- if (node->left) st.push(node->left); // 添加左节点
- } else {
- st.pop(); // 将空节点弹出
- node = st.top(); // 重新取出栈中元素
- st.pop();
- result.push_back(node->val); // 加入到数组中
- }
- }
- return result;
- }
-};
-```
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0098.验证二叉搜索树.md b/problems/0098.验证二叉搜索树.md
deleted file mode 100644
index ac827324..00000000
--- a/problems/0098.验证二叉搜索树.md
+++ /dev/null
@@ -1,246 +0,0 @@
-## 题目地址
-
-> 学习完二叉搜索树的特性了,那么就验证一波
-
-# 98.验证二叉搜索树
-
-给定一个二叉树,判断其是否是一个有效的二叉搜索树。
-
-假设一个二叉搜索树具有如下特征:
-
-* 节点的左子树只包含小于当前节点的数。
-* 节点的右子树只包含大于当前节点的数。
-* 所有左子树和右子树自身必须也是二叉搜索树。
-
-
-
-图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
-
-**所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
-
-**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
-
-注意代码中i,就是for循环里选择的起始位置。
-```
-for (int i = startIndex; i <= n; i++) {
-```
-
-接下来看一下优化过程如下:
-
-1. 已经选择的元素个数:path.size();
-
-2. 还需要的元素个数为: k - path.size();
-
-3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
-
-为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
-
-举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
-
-从2开始搜索都是合理的,可以是组合[2, 3, 4]。
-
-这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
-
-所以优化之后的for循环是:
-
-```
-for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
-```
-
-优化后整体代码如下:
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(int n, int k, int startIndex) {
- if (path.size() == k) {
- result.push_back(path);
- return;
- }
- for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
- path.push_back(i); // 处理节点
- backtracking(n, k, i + 1);
- path.pop_back(); // 回溯,撤销处理的节点
- }
- }
-public:
-
- vector> combine(int n, int k) {
- backtracking(n, k, 1);
- return result;
- }
-};
-```
-
-# 总结
-
-本篇我们准对求组合问题的回溯法代码做了剪枝优化,这个优化如果不画图的话,其实不好理解,也不好讲清楚。
-
-所以我依然是把整个回溯过程抽象为一颗树形结构,然后可以直观的看出,剪枝究竟是剪的哪里。
-
-**就酱,学到了就帮Carl转发一下吧,让更多的同学知道这里!**
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
deleted file mode 100644
index 8a2ff8a3..00000000
--- a/problems/0078.子集.md
+++ /dev/null
@@ -1,175 +0,0 @@
-> 认识本质之后,这就是一道模板题
-
-# 第78题. 子集
-
-题目地址:https://leetcode-cn.com/problems/subsets/
-
-给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
-
-说明:解集不能包含重复的子集。
-
-示例:
-输入: nums = [1,2,3]
-输出:
-[
- [3],
- [1],
- [2],
- [1,2,3],
- [1,3],
- [2,3],
- [1,2],
- []
-]
-
-# 思路
-
-求子集问题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:分割问题!](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)又不一样了。
-
-如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,**那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!**
-
-其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
-
-**那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!**
-
-有同学问了,什么时候for可以从0开始呢?
-
-求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合,排列问题我们后续的文章就会讲到的。
-
-以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
-
-
-
-从图中红线部分,可以看出**遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合**。
-
-## 回溯三部曲
-
-* 递归函数参数
-
-全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
-
-递归函数参数在上面讲到了,需要startIndex。
-
-代码如下:
-
-```
-vector> result;
-vector path;
-void backtracking(vector& nums, int startIndex) {
-```
-
-* 递归终止条件
-
-从图中可以看出:
-
-
-
-剩余集合为空的时候,就是叶子节点。
-
-那么什么时候剩余集合为空呢?
-
-就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
-
-```
-if (startIndex >= nums.size()) {
- return;
-}
-```
-
-**其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了**。
-
-* 单层搜索逻辑
-
-**求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树**。
-
-那么单层递归逻辑代码如下:
-
-```
-for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]); // 子集收集元素
- backtracking(nums, i + 1); // 注意从i+1开始,元素不重复取
- path.pop_back(); // 回溯
-}
-```
-
-## C++代码
-
-根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
-
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-可以写出如下回溯算法C++代码:
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex) {
- result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
- if (startIndex >= nums.size()) { // 终止条件可以不加
- return;
- }
- for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
-public:
- vector> subsets(vector& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
-};
-
-```
-
-在注释中,可以发现可以不写终止条件,因为本来我们就要遍历整颗树。
-
-有的同学可能担心不写终止条件会不会无限递归?
-
-并不会,因为每次递归的下一层就是从i+1开始的。
-
-# 总结
-
-相信大家经过了
-* 组合问题:
- * [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
- * [回溯算法:组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
- * [回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
- * [回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
- * [回溯算法:求组合总和(二)](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)
- * [回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
-* 分割问题:
- * [回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)
- * [回溯算法:复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)
-
-洗礼之后,发现子集问题还真的有点简单了,其实这就是一道标准的模板题。
-
-但是要清楚子集问题和组合问题、分割问题的的区别,**子集是收集树形结构中树的所有节点的结果**。
-
-**而组合问题、分割问题是收集树形结构中叶子节点的结果**。
-
-**就酱,如果感觉收获满满,就帮Carl宣传一波「代码随想录」吧!**
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0083.删除排序链表中的重复元素.md b/problems/0083.删除排序链表中的重复元素.md
deleted file mode 100644
index b725f7f8..00000000
--- a/problems/0083.删除排序链表中的重复元素.md
+++ /dev/null
@@ -1,40 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list/
-
-## 思路
-
-这道题目没有必要设置虚拟节点,因为不会删除头结点
-
-## 代码
-
-```
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode(int x) : val(x), next(NULL) {}
- * };
- */
-class Solution {
-public:
- ListNode* deleteDuplicates(ListNode* head) {
- ListNode* p = head;
- while (p != NULL && p->next!= NULL) {
- if (p->val == p->next->val) {
- ListNode* tmp = p->next;
- p->next = p->next->next;
- delete tmp;
- } else {
- p = p->next;
- }
- }
- return head;
- }
-};
-```
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0084.柱状图中最大的矩形.md b/problems/0084.柱状图中最大的矩形.md
deleted file mode 100644
index e5057e55..00000000
--- a/problems/0084.柱状图中最大的矩形.md
+++ /dev/null
@@ -1,104 +0,0 @@
-
-# 链接
-
-https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
-
-## 思路
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- int sum = 0;
- for (int i = 0; i < heights.size(); i++) {
- int left = i;
- int right = i;
- for (; left >= 0; left--) {
- if (heights[left] < heights[i]) break;
- }
- for (; right < heights.size(); right++) {
- if (heights[right] < heights[i]) break;
- }
- int w = right - left - 1;
- int h = heights[i];
- sum = max(sum, w * h);
- }
- return sum;
- }
-};
-```
-
-如上代码并不能通过leetcode,超时了,因为时间复杂度是O(n^2)。
-
-## 思考一下动态规划
-
-## 单调栈
-
-单调栈的思路还是不容易理解的,
-
-想清楚从大到小,还是从小到大,
-
-本题是从栈底到栈头 从小到大,和 接雨水正好反过来。
-
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- stack st;
- heights.insert(heights.begin(), 0); // 数组头部加入元素0
- heights.push_back(0); // 数组尾部加入元素0
- st.push(0);
- int result = 0;
- // 第一个元素已经入栈,从下表1开始
- for (int i = 1; i < heights.size(); i++) {
- // 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下表
- if (heights[i] > heights[st.top()]) {
- st.push(i);
- } else if (heights[i] == heights[st.top()]) {
- st.pop(); // 这个可以加,可以不加,效果一样,思路不同
- st.push(i);
- } else {
- while (heights[i] < heights[st.top()]) { // 注意是while
- int mid = st.top();
- st.pop();
- int left = st.top();
- int right = i;
- int w = right - left - 1;
- int h = heights[mid];
- result = max(result, w * h);
- }
- st.push(i);
- }
- }
- return result;
- }
-};
-
-```
-
-代码精简之后:
-
-```
-class Solution {
-public:
- int largestRectangleArea(vector& heights) {
- stack st;
- heights.insert(heights.begin(), 0); // 数组头部加入元素0
- heights.push_back(0); // 数组尾部加入元素0
- st.push(0);
- int result = 0;
- for (int i = 1; i < heights.size(); i++) {
- while (heights[i] < heights[st.top()]) {
- int mid = st.top();
- st.pop();
- int w = i - st.top() - 1;
- int h = heights[mid];
- result = max(result, w * h);
- }
- st.push(i);
- }
- return result;
- }
-};
-```
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
deleted file mode 100644
index c8e29763..00000000
--- a/problems/0090.子集II.md
+++ /dev/null
@@ -1,132 +0,0 @@
-
-> 子集问题加去重!
-
-# 第90题.子集II
-
-题目链接:https://leetcode-cn.com/problems/subsets-ii/
-
-给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
-
-说明:解集不能包含重复的子集。
-
-示例:
-输入: [1,2,2]
-输出:
-[
- [2],
- [1],
- [1,2,2],
- [2,2],
- [1,2],
- []
-]
-
-
-# 思路
-
-做本题之前一定要先做[78.子集](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)。
-
-这道题目和[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)区别就是集合里有重复元素了,而且求取的子集要去重。
-
-那么关于回溯算法中的去重问题,**在[40.组合总和II](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)中已经详细讲解过了,和本题是一个套路**。
-
-**剧透一下,后期要讲解的排列问题里去重也是这个套路,所以理解“树层去重”和“树枝去重”非常重要**。
-
-用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
-
-
-
-从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
-
-本题就是其实就是[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重,去重我们在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了,所以我就直接给出代码了:
-
-# C++代码
-
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex, vector& used) {
- result.push_back(path);
- for (int i = startIndex; i < nums.size(); i++) {
- // used[i - 1] == true,说明同一树支candidates[i - 1]使用过
- // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
- // 而我们要对同一树层使用过的元素进行跳过
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- path.push_back(nums[i]);
- used[i] = true;
- backtracking(nums, i + 1, used);
- used[i] = false;
- path.pop_back();
- }
- }
-
-public:
- vector> subsetsWithDup(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- sort(nums.begin(), nums.end()); // 去重需要排序
- backtracking(nums, 0, used);
- return result;
- }
-};
-
-```
-
-使用set去重的版本。
-```
-class Solution {
-private:
- vector> result;
- vector path;
- void backtracking(vector& nums, int startIndex, vector& used) {
- result.push_back(path);
- unordered_set uset;
- for (int i = startIndex; i < nums.size(); i++) {
- if (uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]);
- path.push_back(nums[i]);
- backtracking(nums, i + 1, used);
- path.pop_back();
- }
- }
-
-public:
- vector> subsetsWithDup(vector& nums) {
- result.clear();
- path.clear();
- vector used(nums.size(), false);
- sort(nums.begin(), nums.end()); // 去重需要排序
- backtracking(nums, 0, used);
- return result;
- }
-};
-
-```
-
-# 总结
-
-其实这道题目的知识点,我们之前都讲过了,如果之前讲过的子集问题和去重问题都掌握的好,这道题目应该分分钟AC。
-
-当然本题去重的逻辑,也可以这么写
-
-```
-if (i > startIndex && nums[i] == nums[i - 1] ) {
- continue;
-}
-```
-
-**就酱,如果感觉融会贯通了,就把「代码随想录」介绍给自己的同学朋友吧,也许他们也需要!**
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
-
-
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
deleted file mode 100644
index e691852e..00000000
--- a/problems/0093.复原IP地址.md
+++ /dev/null
@@ -1,253 +0,0 @@
-> 一些录友表示跟不上现在的节奏,想从头开始打卡学习起来,可以在公众号左下方,「算法汇总」可以找到历史文章,都是按系列排好顺序的,挨个看就可以了,看文章下的留言你就会发现,有很多录友都在从头打卡,你并不孤单!
-
-# 93.复原IP地址
-
-题目地址:https://leetcode-cn.com/problems/restore-ip-addresses/
-
-给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
-
-有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
-
-例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
-
-示例 1:
-输入:s = "25525511135"
-输出:["255.255.11.135","255.255.111.35"]
-
-示例 2:
-输入:s = "0000"
-输出:["0.0.0.0"]
-
-示例 3:
-输入:s = "1111"
-输出:["1.1.1.1"]
-
-示例 4:
-输入:s = "010010"
-输出:["0.10.0.10","0.100.1.0"]
-
-示例 5:
-输入:s = "101023"
-输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
-
-提示:
-0 <= s.length <= 3000
-s 仅由数字组成
-
-
-# 思路
-
-做这道题目之前,最好先把[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)这个做了。
-
-这道题目相信大家刚看的时候,应该会一脸茫然。
-
-其实只要意识到这是切割问题,**切割问题就可以使用回溯搜索法把所有可能性搜出来**,和刚做过的[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)就十分类似了。
-
-切割问题可以抽象为树型结构,如图:
-
-
-
-
-## 回溯三部曲
-
-* 递归参数
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我们就提到切割问题类似组合问题。
-
-startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。
-
-本题我们还需要一个变量pointNum,记录添加逗点的数量。
-
-所以代码如下:
-
-```
- vector result;// 记录结果
- // startIndex: 搜索的起始位置,pointNum:添加逗点的数量
- void backtracking(string& s, int startIndex, int pointNum) {
-```
-
-* 递归终止条件
-
-终止条件和[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)情况就不同了,本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。
-
-pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。
-
-然后验证一下第四段是否合法,如果合法就加入到结果集里
-
-代码如下:
-
-```
-if (pointNum == 3) { // 逗点数量为3时,分隔结束
- // 判断第四段子字符串是否合法,如果合法就放进result中
- if (isValid(s, startIndex, s.size() - 1)) {
- result.push_back(s);
- }
- return;
-}
-```
-
-* 单层搜索的逻辑
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中已经讲过在循环遍历中如何截取子串。
-
-在`for (int i = startIndex; i < s.size(); i++)`循环中 [startIndex, i]这个区间就是截取的子串,需要判断这个子串是否合法。
-
-如果合法就在字符串后面加上符号`.`表示已经分割。
-
-如果不合法就结束本层循环,如图中剪掉的分支:
-
-
-
-然后就是递归和回溯的过程:
-
-递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符`.`),同时记录分割符的数量pointNum 要 +1。
-
-回溯的时候,就将刚刚加入的分隔符`.` 删掉就可以了,pointNum也要-1。
-
-代码如下:
-
-```
-for (int i = startIndex; i < s.size(); i++) {
- if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
- s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
- pointNum++;
- backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
- pointNum--; // 回溯
- s.erase(s.begin() + i + 1); // 回溯删掉逗点
- } else break; // 不合法,直接结束本层循环
-}
-```
-
-## 判断子串是否合法
-
-最后就是在写一个判断段位是否是有效段位了。
-
-主要考虑到如下三点:
-
-* 段位以0为开头的数字不合法
-* 段位里有非正整数字符不合法
-* 段位如果大于255了不合法
-
-代码如下:
-
-```
-// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
-bool isValid(const string& s, int start, int end) {
- if (start > end) {
- return false;
- }
- if (s[start] == '0' && start != end) { // 0开头的数字不合法
- return false;
- }
- int num = 0;
- for (int i = start; i <= end; i++) {
- if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
- return false;
- }
- num = num * 10 + (s[i] - '0');
- if (num > 255) { // 如果大于255了不合法
- return false;
- }
- }
- return true;
-}
-```
-
-## C++代码
-
-
-根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
-
-```
-void backtracking(参数) {
- if (终止条件) {
- 存放结果;
- return;
- }
-
- for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
- 处理节点;
- backtracking(路径,选择列表); // 递归
- 回溯,撤销处理结果
- }
-}
-```
-
-可以写出如下回溯算法C++代码:
-
-```
-class Solution {
-private:
- vector result;// 记录结果
- // startIndex: 搜索的起始位置,pointNum:添加逗点的数量
- void backtracking(string& s, int startIndex, int pointNum) {
- if (pointNum == 3) { // 逗点数量为3时,分隔结束
- // 判断第四段子字符串是否合法,如果合法就放进result中
- if (isValid(s, startIndex, s.size() - 1)) {
- result.push_back(s);
- }
- return;
- }
- for (int i = startIndex; i < s.size(); i++) {
- if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
- s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
- pointNum++;
- backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
- pointNum--; // 回溯
- s.erase(s.begin() + i + 1); // 回溯删掉逗点
- } else break; // 不合法,直接结束本层循环
- }
- }
- // 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
- bool isValid(const string& s, int start, int end) {
- if (start > end) {
- return false;
- }
- if (s[start] == '0' && start != end) { // 0开头的数字不合法
- return false;
- }
- int num = 0;
- for (int i = start; i <= end; i++) {
- if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
- return false;
- }
- num = num * 10 + (s[i] - '0');
- if (num > 255) { // 如果大于255了不合法
- return false;
- }
- }
- return true;
- }
-public:
- vector restoreIpAddresses(string s) {
- result.clear();
- if (s.size() > 12) return result; // 算是剪枝了
- backtracking(s, 0, 0);
- return result;
- }
-};
-
-```
-
-# 总结
-
-在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我列举的分割字符串的难点,本题都覆盖了。
-
-而且本题还需要操作字符串添加逗号作为分隔符,并验证区间的合法性。
-
-可以说是[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)的加强版。
-
-在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
-
-**就酱,「代码随想录」值得推荐给你的朋友们!**
-
-
-一些录友表示跟不上现在的节奏,想从头开始打卡学习起来,可以在在公众号左下方,「算法汇总」可以找到历史文章,都是按系列排好顺序的,挨个看就可以了,别忘了打卡。
-
-**很多录友都在从头开始打卡学习,看看前面文章的留言区就知道了,你并不孤单!**
-
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0094.二叉树的中序遍历.md b/problems/0094.二叉树的中序遍历.md
deleted file mode 100644
index e63819c1..00000000
--- a/problems/0094.二叉树的中序遍历.md
+++ /dev/null
@@ -1,84 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
-
-## 思路
-
-详细题解请看这篇:[一文学通二叉树前中后序递归法与迭代法](https://github.com/youngyangyang04/leetcode/blob/master/problems/0144.二叉树的前序遍历.md)
-
-## C++代码
-
-### 递归
-```
-class Solution {
-public:
- void traversal(TreeNode* cur, vector& vec) {
- if (cur == NULL) return;
- traversal(cur->left, vec);
- vec.push_back(cur->val);
- traversal(cur->right, vec);
- }
- vector inorderTraversal(TreeNode* root) {
- vector result;
- traversal(root, result);
- return result;
- }
-};
-```
-
-### 栈
-```
-class Solution {
-public:
- vector inorderTraversal(TreeNode* root) {
- vector result;
- stack st;
- TreeNode* cur = root;
- while (cur != NULL || !st.empty()) {
- if (cur != NULL) {
- st.push(cur);
- cur = cur->left;
- } else {
- cur = st.top();
- st.pop();
- result.push_back(cur->val);
- cur = cur->right;
- }
- }
- return result;
- }
-};
-```
-
-### 栈 通用模板
-
-```
-class Solution {
-public:
- vector inorderTraversal(TreeNode* root) {
- vector result;
- stack st;
- if (root != NULL) st.push(root);
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- if (node->right) st.push(node->right); // 添加右节点
-
- st.push(node); // 添加中节点
- st.push(NULL); // 中节点访问过,但是还没有处理,需要做一下标记。
-
- if (node->left) st.push(node->left); // 添加左节点
- } else {
- st.pop(); // 将空节点弹出
- node = st.top(); // 重新取出栈中元素
- st.pop();
- result.push_back(node->val); // 加入到数组中
- }
- }
- return result;
- }
-};
-```
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0098.验证二叉搜索树.md b/problems/0098.验证二叉搜索树.md
deleted file mode 100644
index ac827324..00000000
--- a/problems/0098.验证二叉搜索树.md
+++ /dev/null
@@ -1,246 +0,0 @@
-## 题目地址
-
-> 学习完二叉搜索树的特性了,那么就验证一波
-
-# 98.验证二叉搜索树
-
-给定一个二叉树,判断其是否是一个有效的二叉搜索树。
-
-假设一个二叉搜索树具有如下特征:
-
-* 节点的左子树只包含小于当前节点的数。
-* 节点的右子树只包含大于当前节点的数。
-* 所有左子树和右子树自身必须也是二叉搜索树。
-
- -
-# 思路
-
-要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
-
-有了这个特性,**验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。**
-
-## 递归法
-
-可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
-
-```
-vector vec;
-void traversal(TreeNode* root) {
- if (root == NULL) return;
- traversal(root->left);
- vec.push_back(root->val); // 将二叉搜索树转换为有序数组
- traversal(root->right);
-}
-```
-
-然后只要比较一下,这个数组是否是有序的,**注意二叉搜索树中不能有重复元素**。
-
-```
-traversal(root);
-for (int i = 1; i < vec.size(); i++) {
- // 注意要小于等于,搜索树里不能有相同元素
- if (vec[i] <= vec[i - 1]) return false;
-}
-return true;
-```
-
-整体代码如下:
-
-```
-class Solution {
-private:
- vector vec;
- void traversal(TreeNode* root) {
- if (root == NULL) return;
- traversal(root->left);
- vec.push_back(root->val); // 将二叉搜索树转换为有序数组
- traversal(root->right);
- }
-public:
- bool isValidBST(TreeNode* root) {
- vec.clear(); // 不加这句在leetcode上也可以过,但最好加上
- traversal(root);
- for (int i = 1; i < vec.size(); i++) {
- // 注意要小于等于,搜索树里不能有相同元素
- if (vec[i] <= vec[i - 1]) return false;
- }
- return true;
- }
-};
-```
-
-以上代码中,我们把二叉树转变为数组来判断,是最直观的,但其实不用转变成数组,可以在递归遍历的过程中直接判断是否有序。
-
-
-这道题目比较容易陷入两个陷阱:
-
-* 陷阱1
-
-**不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了**。
-
-写出了类似这样的代码:
-
-```
-if (root->val > root->left->val && root->val < root->right->val) {
- return true;
-} else {
- return false;
-}
-```
-
-**我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。**所以以上代码的判断逻辑是错误的。
-
-例如: [10,5,15,null,null,6,20] 这个case:
-
-
-
-节点10小于左节点5,大于右节点15,但右子树里出现了一个6 这就不符合了!
-
-* 陷阱2
-
-样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
-
-此时可以初始化比较元素为longlong的最小值。
-
-问题可以进一步演进:如果样例中根节点的val 可能是longlong的最小值 又要怎么办呢?文中会解答。
-
-了解这些陷阱之后我们来看一下代码应该怎么写:
-
-递归三部曲:
-
-* 确定递归函数,返回值以及参数
-
-要定义一个longlong的全局变量,用来比较遍历的节点是否有序,因为后台测试数据中有int最小值,所以定义为longlong的类型,初始化为longlong最小值。
-
-注意递归函数要有bool类型的返回值, 我们在[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg) 中讲了,只有寻找某一条边(或者一个节点)的时候,递归函数会有bool类型的返回值。
-
-其实本题是同样的道理,我们在寻找一个不符合条件的节点,如果没有找到这个节点就遍历了整个树,如果找到不符合的节点了,立刻返回。
-
-代码如下:
-
-```
-long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
-bool isValidBST(TreeNode* root)
-```
-
-* 确定终止条件
-
-如果是空节点 是不是二叉搜索树呢?
-
-是的,二叉搜索树也可以为空!
-
-代码如下:
-
-```
-if (root == NULL) return true;
-```
-
-* 确定单层递归的逻辑
-
-中序遍历,一直更新maxVal,一旦发现maxVal >= root->val,就返回false,注意元素相同时候也要返回false。
-
-代码如下:
-
-```
-bool left = isValidBST(root->left); // 左
-
-// 中序遍历,验证遍历的元素是不是从小到大
-if (maxVal < root->val) maxVal = root->val; // 中
-else return false;
-
-bool right = isValidBST(root->right); // 右
-return left && right;
-```
-
-整体代码如下:
-```
-class Solution {
-public:
- long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
- bool isValidBST(TreeNode* root) {
- if (root == NULL) return true;
-
- bool left = isValidBST(root->left);
- // 中序遍历,验证遍历的元素是不是从小到大
- if (maxVal < root->val) maxVal = root->val;
- else return false;
- bool right = isValidBST(root->right);
-
- return left && right;
- }
-};
-```
-
-以上代码是因为后台数据有int最小值测试用例,所以都把maxVal改成了longlong最小值。
-
-如果测试数据中有 longlong的最小值,怎么办?
-
-不可能在初始化一个更小的值了吧。 建议避免 初始化最小值,如下方法取到最左面节点的数值来比较。
-
-代码如下:
-
-```
-class Solution {
-public:
- TreeNode* pre = NULL; // 用来记录前一个节点
- bool isValidBST(TreeNode* root) {
- if (root == NULL) return true;
- bool left = isValidBST(root->left);
-
- if (pre != NULL && pre->val >= root->val) return false;
- pre = root; // 记录前一个节点
-
- bool right = isValidBST(root->right);
- return left && right;
- }
-};
-```
-
-最后这份代码看上去整洁一些,思路也清晰。
-
-## 迭代法
-
-可以用迭代法模拟二叉树中序遍历,对前中后序迭代法生疏的同学可以看这两篇[二叉树:听说递归能做的,栈也能做!](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg),[二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-迭代法中序遍历稍加改动就可以了,代码如下:
-
-```
-class Solution {
-public:
- bool isValidBST(TreeNode* root) {
- stack st;
- TreeNode* cur = root;
- TreeNode* pre = NULL; // 记录前一个节点
- while (cur != NULL || !st.empty()) {
- if (cur != NULL) {
- st.push(cur);
- cur = cur->left; // 左
- } else {
- cur = st.top(); // 中
- st.pop();
- if (pre != NULL && cur->val <= pre->val)
- return false;
- pre = cur; //保存前一个访问的结点
-
- cur = cur->right; // 右
- }
- }
- return true;
- }
-};
-```
-
-在[二叉树:二叉搜索树登场!](https://mp.weixin.qq.com/s/vsKrWRlETxCVsiRr8v_hHg)中我们分明写出了痛哭流涕的简洁迭代法,怎么在这里不行了呢,因为本题是要验证二叉搜索树啊。
-
-# 总结
-
-这道题目是一个简单题,但对于没接触过的同学还是有难度的。
-
-所以初学者刚开始学习算法的时候,看到简单题目没有思路很正常,千万别怀疑自己智商,学习过程都是这样的,大家智商都差不多,哈哈。
-
-只要把基本类型的题目都做过,总结过之后,思路自然就开阔了。
-
-**就酱,学到了的话,就转发给身边需要的同学吧!**
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0100.相同的树.md b/problems/0100.相同的树.md
deleted file mode 100644
index ac495f51..00000000
--- a/problems/0100.相同的树.md
+++ /dev/null
@@ -1,163 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/same-tree/
-
-
-# 100. 相同的树
-
-给定两个二叉树,编写一个函数来检验它们是否相同。
-
-如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
-
-
-
-# 思路
-
-要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
-
-有了这个特性,**验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。**
-
-## 递归法
-
-可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
-
-```
-vector vec;
-void traversal(TreeNode* root) {
- if (root == NULL) return;
- traversal(root->left);
- vec.push_back(root->val); // 将二叉搜索树转换为有序数组
- traversal(root->right);
-}
-```
-
-然后只要比较一下,这个数组是否是有序的,**注意二叉搜索树中不能有重复元素**。
-
-```
-traversal(root);
-for (int i = 1; i < vec.size(); i++) {
- // 注意要小于等于,搜索树里不能有相同元素
- if (vec[i] <= vec[i - 1]) return false;
-}
-return true;
-```
-
-整体代码如下:
-
-```
-class Solution {
-private:
- vector vec;
- void traversal(TreeNode* root) {
- if (root == NULL) return;
- traversal(root->left);
- vec.push_back(root->val); // 将二叉搜索树转换为有序数组
- traversal(root->right);
- }
-public:
- bool isValidBST(TreeNode* root) {
- vec.clear(); // 不加这句在leetcode上也可以过,但最好加上
- traversal(root);
- for (int i = 1; i < vec.size(); i++) {
- // 注意要小于等于,搜索树里不能有相同元素
- if (vec[i] <= vec[i - 1]) return false;
- }
- return true;
- }
-};
-```
-
-以上代码中,我们把二叉树转变为数组来判断,是最直观的,但其实不用转变成数组,可以在递归遍历的过程中直接判断是否有序。
-
-
-这道题目比较容易陷入两个陷阱:
-
-* 陷阱1
-
-**不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了**。
-
-写出了类似这样的代码:
-
-```
-if (root->val > root->left->val && root->val < root->right->val) {
- return true;
-} else {
- return false;
-}
-```
-
-**我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。**所以以上代码的判断逻辑是错误的。
-
-例如: [10,5,15,null,null,6,20] 这个case:
-
-
-
-节点10小于左节点5,大于右节点15,但右子树里出现了一个6 这就不符合了!
-
-* 陷阱2
-
-样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
-
-此时可以初始化比较元素为longlong的最小值。
-
-问题可以进一步演进:如果样例中根节点的val 可能是longlong的最小值 又要怎么办呢?文中会解答。
-
-了解这些陷阱之后我们来看一下代码应该怎么写:
-
-递归三部曲:
-
-* 确定递归函数,返回值以及参数
-
-要定义一个longlong的全局变量,用来比较遍历的节点是否有序,因为后台测试数据中有int最小值,所以定义为longlong的类型,初始化为longlong最小值。
-
-注意递归函数要有bool类型的返回值, 我们在[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg) 中讲了,只有寻找某一条边(或者一个节点)的时候,递归函数会有bool类型的返回值。
-
-其实本题是同样的道理,我们在寻找一个不符合条件的节点,如果没有找到这个节点就遍历了整个树,如果找到不符合的节点了,立刻返回。
-
-代码如下:
-
-```
-long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
-bool isValidBST(TreeNode* root)
-```
-
-* 确定终止条件
-
-如果是空节点 是不是二叉搜索树呢?
-
-是的,二叉搜索树也可以为空!
-
-代码如下:
-
-```
-if (root == NULL) return true;
-```
-
-* 确定单层递归的逻辑
-
-中序遍历,一直更新maxVal,一旦发现maxVal >= root->val,就返回false,注意元素相同时候也要返回false。
-
-代码如下:
-
-```
-bool left = isValidBST(root->left); // 左
-
-// 中序遍历,验证遍历的元素是不是从小到大
-if (maxVal < root->val) maxVal = root->val; // 中
-else return false;
-
-bool right = isValidBST(root->right); // 右
-return left && right;
-```
-
-整体代码如下:
-```
-class Solution {
-public:
- long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
- bool isValidBST(TreeNode* root) {
- if (root == NULL) return true;
-
- bool left = isValidBST(root->left);
- // 中序遍历,验证遍历的元素是不是从小到大
- if (maxVal < root->val) maxVal = root->val;
- else return false;
- bool right = isValidBST(root->right);
-
- return left && right;
- }
-};
-```
-
-以上代码是因为后台数据有int最小值测试用例,所以都把maxVal改成了longlong最小值。
-
-如果测试数据中有 longlong的最小值,怎么办?
-
-不可能在初始化一个更小的值了吧。 建议避免 初始化最小值,如下方法取到最左面节点的数值来比较。
-
-代码如下:
-
-```
-class Solution {
-public:
- TreeNode* pre = NULL; // 用来记录前一个节点
- bool isValidBST(TreeNode* root) {
- if (root == NULL) return true;
- bool left = isValidBST(root->left);
-
- if (pre != NULL && pre->val >= root->val) return false;
- pre = root; // 记录前一个节点
-
- bool right = isValidBST(root->right);
- return left && right;
- }
-};
-```
-
-最后这份代码看上去整洁一些,思路也清晰。
-
-## 迭代法
-
-可以用迭代法模拟二叉树中序遍历,对前中后序迭代法生疏的同学可以看这两篇[二叉树:听说递归能做的,栈也能做!](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg),[二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-迭代法中序遍历稍加改动就可以了,代码如下:
-
-```
-class Solution {
-public:
- bool isValidBST(TreeNode* root) {
- stack st;
- TreeNode* cur = root;
- TreeNode* pre = NULL; // 记录前一个节点
- while (cur != NULL || !st.empty()) {
- if (cur != NULL) {
- st.push(cur);
- cur = cur->left; // 左
- } else {
- cur = st.top(); // 中
- st.pop();
- if (pre != NULL && cur->val <= pre->val)
- return false;
- pre = cur; //保存前一个访问的结点
-
- cur = cur->right; // 右
- }
- }
- return true;
- }
-};
-```
-
-在[二叉树:二叉搜索树登场!](https://mp.weixin.qq.com/s/vsKrWRlETxCVsiRr8v_hHg)中我们分明写出了痛哭流涕的简洁迭代法,怎么在这里不行了呢,因为本题是要验证二叉搜索树啊。
-
-# 总结
-
-这道题目是一个简单题,但对于没接触过的同学还是有难度的。
-
-所以初学者刚开始学习算法的时候,看到简单题目没有思路很正常,千万别怀疑自己智商,学习过程都是这样的,大家智商都差不多,哈哈。
-
-只要把基本类型的题目都做过,总结过之后,思路自然就开阔了。
-
-**就酱,学到了的话,就转发给身边需要的同学吧!**
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0100.相同的树.md b/problems/0100.相同的树.md
deleted file mode 100644
index ac495f51..00000000
--- a/problems/0100.相同的树.md
+++ /dev/null
@@ -1,163 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/same-tree/
-
-
-# 100. 相同的树
-
-给定两个二叉树,编写一个函数来检验它们是否相同。
-
-如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
-
- -
-# 思路
-
-在[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)中,我们讲到对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-理解这一本质之后,就会发现,求二叉树是否对称,和求二叉树是否相同几乎是同一道题目。
-
-**如果没有读过[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)这一篇,请认真读完再做这道题,就会有感觉了。**
-
-递归三部曲中:
-
-1. 确定递归函数的参数和返回值
-
-我们要比较的是两个树是否是相互相同的,参数也就是两个树的根节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* tree1, TreeNode* tree2)
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)。
-
-2. 确定终止条件
-
-**要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。**
-
-节点为空的情况有:
-
-* tree1为空,tree2不为空,不对称,return false
-* tree1不为空,tree2为空,不对称 return false
-* tree1,tree2都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是tree1和tree2不为空的时候:
-
-* tree1、tree2都不为空,比较节点数值,不相同就return false
-
-此时tree1、tree2节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (tree1 == NULL && tree2 != NULL) return false;
-else if (tree1 != NULL && tree2 == NULL) return false;
-else if (tree1 == NULL && tree2 == NULL) return true;
-else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
-
-3. 确定单层递归的逻辑
-
-* 比较二叉树是否相同 :传入的是tree1的左孩子,tree2的右孩子。
-* 如果左右都相同就返回true ,有一侧不相同就返回false 。
-
-代码如下:
-
-```
-bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
-bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
-bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* tree1, TreeNode* tree2) {
- if (tree1 == NULL && tree2 != NULL) return false;
- else if (tree1 != NULL && tree2 == NULL) return false;
- else if (tree1 == NULL && tree2 == NULL) return true;
- else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
- bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
- bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
- return isSame;
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-
-## 递归
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->left) && compare(left->right, right->right);
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-## 迭代法
-
-```
-lass Solution {
-public:
-
- bool isSameTree(TreeNode* p, TreeNode* q) {
- if (p == NULL && q == NULL) return true;
- if (p == NULL || q == NULL) return false;
- queue que;
- que.push(p); //
- que.push(q); //
- while (!que.empty()) { //
- TreeNode* leftNode = que.front(); que.pop();
- TreeNode* rightNode = que.front(); que.pop();
- if (!leftNode && !rightNode) { //
- continue;
- }
- //
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- que.push(leftNode->left); //
- que.push(rightNode->left); //
- que.push(leftNode->right); //
- que.push(rightNode->right); //
- }
- return true;
- }
-};
-```
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0101.对称二叉树.md b/problems/0101.对称二叉树.md
deleted file mode 100644
index b454aa7d..00000000
--- a/problems/0101.对称二叉树.md
+++ /dev/null
@@ -1,246 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/symmetric-tree/
-
-> 又是一道“简单题”
-
-# 101. 对称二叉树
-
-给定一个二叉树,检查它是否是镜像对称的。
-
-
-
-# 思路
-
-在[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)中,我们讲到对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-理解这一本质之后,就会发现,求二叉树是否对称,和求二叉树是否相同几乎是同一道题目。
-
-**如果没有读过[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)这一篇,请认真读完再做这道题,就会有感觉了。**
-
-递归三部曲中:
-
-1. 确定递归函数的参数和返回值
-
-我们要比较的是两个树是否是相互相同的,参数也就是两个树的根节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* tree1, TreeNode* tree2)
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)。
-
-2. 确定终止条件
-
-**要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。**
-
-节点为空的情况有:
-
-* tree1为空,tree2不为空,不对称,return false
-* tree1不为空,tree2为空,不对称 return false
-* tree1,tree2都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是tree1和tree2不为空的时候:
-
-* tree1、tree2都不为空,比较节点数值,不相同就return false
-
-此时tree1、tree2节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (tree1 == NULL && tree2 != NULL) return false;
-else if (tree1 != NULL && tree2 == NULL) return false;
-else if (tree1 == NULL && tree2 == NULL) return true;
-else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
-
-3. 确定单层递归的逻辑
-
-* 比较二叉树是否相同 :传入的是tree1的左孩子,tree2的右孩子。
-* 如果左右都相同就返回true ,有一侧不相同就返回false 。
-
-代码如下:
-
-```
-bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
-bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
-bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* tree1, TreeNode* tree2) {
- if (tree1 == NULL && tree2 != NULL) return false;
- else if (tree1 != NULL && tree2 == NULL) return false;
- else if (tree1 == NULL && tree2 == NULL) return true;
- else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
- bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
- bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
- return isSame;
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-
-## 递归
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->left) && compare(left->right, right->right);
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-## 迭代法
-
-```
-lass Solution {
-public:
-
- bool isSameTree(TreeNode* p, TreeNode* q) {
- if (p == NULL && q == NULL) return true;
- if (p == NULL || q == NULL) return false;
- queue que;
- que.push(p); //
- que.push(q); //
- while (!que.empty()) { //
- TreeNode* leftNode = que.front(); que.pop();
- TreeNode* rightNode = que.front(); que.pop();
- if (!leftNode && !rightNode) { //
- continue;
- }
- //
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- que.push(leftNode->left); //
- que.push(rightNode->left); //
- que.push(leftNode->right); //
- que.push(rightNode->right); //
- }
- return true;
- }
-};
-```
-
-> **我是[程序员Carl](https://github.com/youngyangyang04),可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png),也可以在[B站上找到我](https://space.bilibili.com/525438321),本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号:[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png),关注后就会发现和「代码随想录」相见恨晚!**
-
-**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
-
diff --git a/problems/0101.对称二叉树.md b/problems/0101.对称二叉树.md
deleted file mode 100644
index b454aa7d..00000000
--- a/problems/0101.对称二叉树.md
+++ /dev/null
@@ -1,246 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/symmetric-tree/
-
-> 又是一道“简单题”
-
-# 101. 对称二叉树
-
-给定一个二叉树,检查它是否是镜像对称的。
-
- -
-# 思路
-
-**首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!**
-
-对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-那么如果比较呢?
-
-比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
-
-
-
-# 思路
-
-**首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!**
-
-对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-那么如果比较呢?
-
-比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
-
- -
-那么遍历的顺序应该是什么样的呢?
-
-本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
-
-**正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。**
-
-但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
-
-其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
-
-说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
-
-那么我们先来看看递归法的代码应该怎么写。
-
-## 递归法
-
-### 递归三部曲
-
-1. 确定递归函数的参数和返回值
-
-因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* left, TreeNode* right)
-```
-
-2. 确定终止条件
-
-要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
-
-节点为空的情况有:(**注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点**)
-
-* 左节点为空,右节点不为空,不对称,return false
-* 左不为空,右为空,不对称 return false
-* 左右都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
-
-* 左右都不为空,比较节点数值,不相同就return false
-
-此时左右节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (left == NULL && right != NULL) return false;
-else if (left != NULL && right == NULL) return false;
-else if (left == NULL && right == NULL) return true;
-else if (left->val != right->val) return false; // 注意这里我没有使用else
-```
-
-注意上面最后一种情况,我没有使用else,而是elseif, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
-
-3. 确定单层递归的逻辑
-
-此时才进入单层递归的逻辑,单层递归的逻辑就是处理 右节点都不为空,且数值相同的情况。
-
-
-* 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
-* 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
-* 如果左右都对称就返回true ,有一侧不对称就返回false 。
-
-代码如下:
-
-```
-bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
-bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
-bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-
-如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
-
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- // 首先排除空节点的情况
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- // 排除了空节点,再排除数值不相同的情况
- else if (left->val != right->val) return false;
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
- bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
- bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
- return isSame;
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->right) && compare(left->right, right->left);
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。**
-
-**所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把道题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。**
-
-## 迭代法
-
-这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
-
-这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(**注意这不是层序遍历**)
-
-### 使用队列
-
-通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
-
-
-
-那么遍历的顺序应该是什么样的呢?
-
-本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
-
-**正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。**
-
-但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
-
-其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
-
-说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
-
-那么我们先来看看递归法的代码应该怎么写。
-
-## 递归法
-
-### 递归三部曲
-
-1. 确定递归函数的参数和返回值
-
-因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* left, TreeNode* right)
-```
-
-2. 确定终止条件
-
-要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
-
-节点为空的情况有:(**注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点**)
-
-* 左节点为空,右节点不为空,不对称,return false
-* 左不为空,右为空,不对称 return false
-* 左右都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
-
-* 左右都不为空,比较节点数值,不相同就return false
-
-此时左右节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (left == NULL && right != NULL) return false;
-else if (left != NULL && right == NULL) return false;
-else if (left == NULL && right == NULL) return true;
-else if (left->val != right->val) return false; // 注意这里我没有使用else
-```
-
-注意上面最后一种情况,我没有使用else,而是elseif, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
-
-3. 确定单层递归的逻辑
-
-此时才进入单层递归的逻辑,单层递归的逻辑就是处理 右节点都不为空,且数值相同的情况。
-
-
-* 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
-* 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
-* 如果左右都对称就返回true ,有一侧不对称就返回false 。
-
-代码如下:
-
-```
-bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
-bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
-bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-
-如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
-
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- // 首先排除空节点的情况
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- // 排除了空节点,再排除数值不相同的情况
- else if (left->val != right->val) return false;
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
- bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
- bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
- return isSame;
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->right) && compare(left->right, right->left);
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。**
-
-**所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把道题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。**
-
-## 迭代法
-
-这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
-
-这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(**注意这不是层序遍历**)
-
-### 使用队列
-
-通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
-
- -
-
-如下的条件判断和递归的逻辑是一样的。
-
-代码如下:
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- queue que;
- que.push(root->left); // 将左子树头结点加入队列
- que.push(root->right); // 将右子树头结点加入队列
- while (!que.empty()) { // 接下来就要判断这这两个树是否相互翻转
- TreeNode* leftNode = que.front(); que.pop();
- TreeNode* rightNode = que.front(); que.pop();
- if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的
- continue;
- }
-
- // 左右一个节点不为空,或者都不为空但数值不相同,返回false
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- que.push(leftNode->left); // 加入左节点左孩子
- que.push(rightNode->right); // 加入右节点右孩子
- que.push(leftNode->right); // 加入左节点右孩子
- que.push(rightNode->left); // 加入右节点左孩子
- }
- return true;
- }
-};
-```
-
-### 使用栈
-
-细心的话,其实可以发现,这个迭代法,其实是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较,那么其实使用栈也是可以的。
-
-只要把队列原封不动的改成栈就可以了,我下面也给出了代码。
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- stack st; // 这里改成了栈
- st.push(root->left);
- st.push(root->right);
- while (!st.empty()) {
- TreeNode* leftNode = st.top(); st.pop();
- TreeNode* rightNode = st.top(); st.pop();
- if (!leftNode && !rightNode) {
- continue;
- }
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- st.push(leftNode->left);
- st.push(rightNode->right);
- st.push(leftNode->right);
- st.push(rightNode->left);
- }
- return true;
- }
-};
-```
-
-# 总结
-
-这次我们又深度剖析了一道二叉树的“简单题”,大家会发现,真正的把题目搞清楚其实并不简单,leetcode上accept了和真正掌握了还是有距离的。
-
-我们介绍了递归法和迭代法,递归依然通过递归三部曲来解决了这道题目,如果只看精简的代码根本看不出来递归三部曲是如果解题的。
-
-在迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,知道这一本质之后就发现,用队列,用栈,甚至用数组,都是可以的。
-
-如果已经做过这道题目的同学,读完文章可以再去看看这道题目,思考一下,会有不一样的发现!
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
deleted file mode 100644
index 7b404623..00000000
--- a/problems/0102.二叉树的层序遍历.md
+++ /dev/null
@@ -1,393 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
-
-> 我要打十个!
-
-看完这篇文章虽然不能打十个,但是可以迅速打八个!而且够快!
-
-学会二叉树的层序遍历,可以一口气撸完leetcode上八道题目:
-
-* 102.二叉树的层序遍历
-* 107.二叉树的层次遍历II
-* 199.二叉树的右视图
-* 637.二叉树的层平均值
-* 429.N叉树的前序遍历
-* 515.在每个树行中找最大值
-* 116. 填充每个节点的下一个右侧节点指针
-* 117.填充每个节点的下一个右侧节点指针II
-
-
-# 102.二叉树的层序遍历
-
-给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
-
-
-
-
-如下的条件判断和递归的逻辑是一样的。
-
-代码如下:
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- queue que;
- que.push(root->left); // 将左子树头结点加入队列
- que.push(root->right); // 将右子树头结点加入队列
- while (!que.empty()) { // 接下来就要判断这这两个树是否相互翻转
- TreeNode* leftNode = que.front(); que.pop();
- TreeNode* rightNode = que.front(); que.pop();
- if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的
- continue;
- }
-
- // 左右一个节点不为空,或者都不为空但数值不相同,返回false
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- que.push(leftNode->left); // 加入左节点左孩子
- que.push(rightNode->right); // 加入右节点右孩子
- que.push(leftNode->right); // 加入左节点右孩子
- que.push(rightNode->left); // 加入右节点左孩子
- }
- return true;
- }
-};
-```
-
-### 使用栈
-
-细心的话,其实可以发现,这个迭代法,其实是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较,那么其实使用栈也是可以的。
-
-只要把队列原封不动的改成栈就可以了,我下面也给出了代码。
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- stack st; // 这里改成了栈
- st.push(root->left);
- st.push(root->right);
- while (!st.empty()) {
- TreeNode* leftNode = st.top(); st.pop();
- TreeNode* rightNode = st.top(); st.pop();
- if (!leftNode && !rightNode) {
- continue;
- }
- if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
- return false;
- }
- st.push(leftNode->left);
- st.push(rightNode->right);
- st.push(leftNode->right);
- st.push(rightNode->left);
- }
- return true;
- }
-};
-```
-
-# 总结
-
-这次我们又深度剖析了一道二叉树的“简单题”,大家会发现,真正的把题目搞清楚其实并不简单,leetcode上accept了和真正掌握了还是有距离的。
-
-我们介绍了递归法和迭代法,递归依然通过递归三部曲来解决了这道题目,如果只看精简的代码根本看不出来递归三部曲是如果解题的。
-
-在迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,知道这一本质之后就发现,用队列,用栈,甚至用数组,都是可以的。
-
-如果已经做过这道题目的同学,读完文章可以再去看看这道题目,思考一下,会有不一样的发现!
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
deleted file mode 100644
index 7b404623..00000000
--- a/problems/0102.二叉树的层序遍历.md
+++ /dev/null
@@ -1,393 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
-
-> 我要打十个!
-
-看完这篇文章虽然不能打十个,但是可以迅速打八个!而且够快!
-
-学会二叉树的层序遍历,可以一口气撸完leetcode上八道题目:
-
-* 102.二叉树的层序遍历
-* 107.二叉树的层次遍历II
-* 199.二叉树的右视图
-* 637.二叉树的层平均值
-* 429.N叉树的前序遍历
-* 515.在每个树行中找最大值
-* 116. 填充每个节点的下一个右侧节点指针
-* 117.填充每个节点的下一个右侧节点指针II
-
-
-# 102.二叉树的层序遍历
-
-给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
-
- -
-## 思路
-
-我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
-
-* [二叉树:前中后序递归法](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)
-* [二叉树:前中后序迭代法](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)
-* [二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
-
-层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
-
-需要借用一个辅助数据结构即队列来实现,**队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
-
-**而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。**
-
-使用队列实现二叉树广度优先遍历,动画如下:
-
-
-
-
-这样就实现了层序从左到右遍历二叉树。
-
-代码如下:**这份代码也可以作为二叉树层序遍历的模板,以后再打七个就靠它了**。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrder(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- // 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- vec.push_back(node->val);
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(vec);
- }
- return result;
- }
-};
-```
-
-**此时我们就掌握了二叉树的层序遍历了,那么如下五道leetcode上的题目,只需要修改模板的一两行代码(不能再多了),便可打倒!**
-
-# 107.二叉树的层次遍历 II
-
-给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
-
-
-
-## 思路
-
-我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
-
-* [二叉树:前中后序递归法](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)
-* [二叉树:前中后序迭代法](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)
-* [二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
-
-层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
-
-需要借用一个辅助数据结构即队列来实现,**队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
-
-**而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。**
-
-使用队列实现二叉树广度优先遍历,动画如下:
-
-
-
-
-这样就实现了层序从左到右遍历二叉树。
-
-代码如下:**这份代码也可以作为二叉树层序遍历的模板,以后再打七个就靠它了**。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrder(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- // 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- vec.push_back(node->val);
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(vec);
- }
- return result;
- }
-};
-```
-
-**此时我们就掌握了二叉树的层序遍历了,那么如下五道leetcode上的题目,只需要修改模板的一两行代码(不能再多了),便可打倒!**
-
-# 107.二叉树的层次遍历 II
-
-给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
-
- -
-## 思路
-
-相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrderBottom(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- vec.push_back(node->val);
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(vec);
- }
- reverse(result.begin(), result.end()); // 在这里反转一下数组即可
- return result;
-
- }
-};
-```
-
-
-# 199.二叉树的右视图
-
-给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
-
-
-
-## 思路
-
-相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrderBottom(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- vec.push_back(node->val);
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(vec);
- }
- reverse(result.begin(), result.end()); // 在这里反转一下数组即可
- return result;
-
- }
-};
-```
-
-
-# 199.二叉树的右视图
-
-给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
-
- -
-## 思路
-
-层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector rightSideView(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- }
- return result;
- }
-};
-```
-
-# 637.二叉树的层平均值
-
-给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
-
-
-
-## 思路
-
-层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector rightSideView(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- }
- return result;
- }
-};
-```
-
-# 637.二叉树的层平均值
-
-给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
-
- -
-## 思路
-
-本题就是层序遍历的时候把一层求个总和在取一个均值。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector averageOfLevels(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- double sum = 0; // 统计每一层的和
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- sum += node->val;
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(sum / size); // 将每一层均值放进结果集
- }
- return result;
- }
-};
-
-```
-
-# 429.N叉树的层序遍历
-
-给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
-
-例如,给定一个 3叉树 :
-
-
-
-
-## 思路
-
-本题就是层序遍历的时候把一层求个总和在取一个均值。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector averageOfLevels(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- double sum = 0; // 统计每一层的和
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- sum += node->val;
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(sum / size); // 将每一层均值放进结果集
- }
- return result;
- }
-};
-
-```
-
-# 429.N叉树的层序遍历
-
-给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
-
-例如,给定一个 3叉树 :
-
-
- -
-返回其层序遍历:
-
-[
- [1],
- [3,2,4],
- [5,6]
-]
-
-
-## 思路
-
-这道题依旧是模板题,只不过一个节点有多个孩子了
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrder(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- for (int i = 0; i < size; i++) {
- Node* node = que.front();
- que.pop();
- vec.push_back(node->val);
- for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
- if (node->children[i]) que.push(node->children[i]);
- }
- }
- result.push_back(vec);
- }
- return result;
-
- }
-};
-```
-
-# 515.在每个树行中找最大值
-
-您需要在二叉树的每一行中找到最大的值。
-
-
-
-返回其层序遍历:
-
-[
- [1],
- [3,2,4],
- [5,6]
-]
-
-
-## 思路
-
-这道题依旧是模板题,只不过一个节点有多个孩子了
-
-## C++代码
-
-```
-class Solution {
-public:
- vector> levelOrder(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector> result;
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- for (int i = 0; i < size; i++) {
- Node* node = que.front();
- que.pop();
- vec.push_back(node->val);
- for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
- if (node->children[i]) que.push(node->children[i]);
- }
- }
- result.push_back(vec);
- }
- return result;
-
- }
-};
-```
-
-# 515.在每个树行中找最大值
-
-您需要在二叉树的每一行中找到最大的值。
-
- -
-## 思路
-
-层序遍历,取每一层的最大值
-
-## C++代码
-
-```
-class Solution {
-public:
- vector largestValues(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- int maxValue = INT_MIN; // 取每一层的最大值
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- maxValue = node->val > maxValue ? node->val : maxValue;
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(maxValue); // 把最大值放进数组
- }
- return result;
- }
-};
-```
-
-# 116.填充每个节点的下一个右侧节点指针
-
-给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
-
-struct Node {
- int val;
- Node *left;
- Node *right;
- Node *next;
-}
-填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
-
-初始状态下,所有 next 指针都被设置为 NULL。
-
-
-
-## 思路
-
-层序遍历,取每一层的最大值
-
-## C++代码
-
-```
-class Solution {
-public:
- vector largestValues(TreeNode* root) {
- queue que;
- if (root != NULL) que.push(root);
- vector result;
- while (!que.empty()) {
- int size = que.size();
- int maxValue = INT_MIN; // 取每一层的最大值
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- maxValue = node->val > maxValue ? node->val : maxValue;
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- result.push_back(maxValue); // 把最大值放进数组
- }
- return result;
- }
-};
-```
-
-# 116.填充每个节点的下一个右侧节点指针
-
-给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
-
-struct Node {
- int val;
- Node *left;
- Node *right;
- Node *next;
-}
-填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
-
-初始状态下,所有 next 指针都被设置为 NULL。
-
- -
-## 思路
-
-本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- Node* nodePre;
- Node* node;
- for (int i = 0; i < size; i++) {
- if (i == 0) {
- nodePre = que.front(); // 取出一层的头结点
- que.pop();
- node = nodePre;
- } else {
- node = que.front();
- que.pop();
- nodePre->next = node; // 本层前一个节点next指向本节点
- nodePre = nodePre->next;
- }
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- nodePre->next = NULL; // 本层最后一个节点指向NULL
- }
- return root;
-
- }
-};
-```
-
-# 117.填充每个节点的下一个右侧节点指针II
-
-## 思路
-
-这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- Node* nodePre;
- Node* node;
- for (int i = 0; i < size; i++) {
- if (i == 0) {
- nodePre = que.front(); // 取出一层的头结点
- que.pop();
- node = nodePre;
- } else {
- node = que.front();
- que.pop();
- nodePre->next = node; // 本层前一个节点next指向本节点
- nodePre = nodePre->next;
- }
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- nodePre->next = NULL; // 本层最后一个节点指向NULL
- }
- return root;
- }
-};
-```
-
-
-# 总结
-
-二叉树的层序遍历,就是图论中的广度优先搜索在二叉树中的应用,需要借助队列来实现(此时是不是又发现队列的应用了)。
-
-虽然不能一口气打十个,打八个也还行。
-
-* 102.二叉树的层序遍历
-* 107.二叉树的层次遍历II
-* 199.二叉树的右视图
-* 637.二叉树的层平均值
-* 429.N叉树的前序遍历
-* 515.在每个树行中找最大值
-* 116. 填充每个节点的下一个右侧节点指针
-* 117.填充每个节点的下一个右侧节点指针II
-
-如果非要打十个,还得找叶师傅!
-
-
-
-## 思路
-
-本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- Node* nodePre;
- Node* node;
- for (int i = 0; i < size; i++) {
- if (i == 0) {
- nodePre = que.front(); // 取出一层的头结点
- que.pop();
- node = nodePre;
- } else {
- node = que.front();
- que.pop();
- nodePre->next = node; // 本层前一个节点next指向本节点
- nodePre = nodePre->next;
- }
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- nodePre->next = NULL; // 本层最后一个节点指向NULL
- }
- return root;
-
- }
-};
-```
-
-# 117.填充每个节点的下一个右侧节点指针II
-
-## 思路
-
-这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- while (!que.empty()) {
- int size = que.size();
- vector vec;
- Node* nodePre;
- Node* node;
- for (int i = 0; i < size; i++) {
- if (i == 0) {
- nodePre = que.front(); // 取出一层的头结点
- que.pop();
- node = nodePre;
- } else {
- node = que.front();
- que.pop();
- nodePre->next = node; // 本层前一个节点next指向本节点
- nodePre = nodePre->next;
- }
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- nodePre->next = NULL; // 本层最后一个节点指向NULL
- }
- return root;
- }
-};
-```
-
-
-# 总结
-
-二叉树的层序遍历,就是图论中的广度优先搜索在二叉树中的应用,需要借助队列来实现(此时是不是又发现队列的应用了)。
-
-虽然不能一口气打十个,打八个也还行。
-
-* 102.二叉树的层序遍历
-* 107.二叉树的层次遍历II
-* 199.二叉树的右视图
-* 637.二叉树的层平均值
-* 429.N叉树的前序遍历
-* 515.在每个树行中找最大值
-* 116. 填充每个节点的下一个右侧节点指针
-* 117.填充每个节点的下一个右侧节点指针II
-
-如果非要打十个,还得找叶师傅!
-
- -
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
deleted file mode 100644
index 3aa5c4b6..00000000
--- a/problems/0104.二叉树的最大深度.md
+++ /dev/null
@@ -1,226 +0,0 @@
-(寻找更节点可以用unordered_map来优化一下,元素都是独一无二的)
-
-## 题目地址
-https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
-
-> “简单题”系列
-
-看完本篇可以一起做了如下两道题目:
-* 104.二叉树的最大深度
-* 559.N叉树的最大深度
-
-# 104.二叉树的最大深度
-
-给定一个二叉树,找出其最大深度。
-
-二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
-
-说明: 叶子节点是指没有子节点的节点。
-
-示例:
-给定二叉树 [3,9,20,null,null,15,7],
-
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
deleted file mode 100644
index 3aa5c4b6..00000000
--- a/problems/0104.二叉树的最大深度.md
+++ /dev/null
@@ -1,226 +0,0 @@
-(寻找更节点可以用unordered_map来优化一下,元素都是独一无二的)
-
-## 题目地址
-https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
-
-> “简单题”系列
-
-看完本篇可以一起做了如下两道题目:
-* 104.二叉树的最大深度
-* 559.N叉树的最大深度
-
-# 104.二叉树的最大深度
-
-给定一个二叉树,找出其最大深度。
-
-二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
-
-说明: 叶子节点是指没有子节点的节点。
-
-示例:
-给定二叉树 [3,9,20,null,null,15,7],
-
- -
-返回它的最大深度 3 。
-
-# 思路
-
-## 递归法
-
-本题其实也要后序遍历(左右中),依然是因为要通过递归函数的返回值做计算树的高度。
-
-按照递归三部曲,来看看如何来写。
-
-1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
-
-代码如下:
-```
-int getDepth(TreeNode* node)
-```
-
-2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
-
-代码如下:
-```
-if (node == NULL) return 0;
-```
-
-3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
-
-代码如下:
-
-```
-int leftDepth = getDepth(node->left); // 左
-int rightDepth = getDepth(node->right); // 右
-int depth = 1 + max(leftDepth, rightDepth); // 中
-return depth;
-```
-
-所以整体C++代码如下:
-
-```
-class Solution {
-public:
- int getDepth(TreeNode* node) {
- if (node == NULL) return 0;
- int leftDepth = getDepth(node->left); // 左
- int rightDepth = getDepth(node->right); // 右
- int depth = 1 + max(leftDepth, rightDepth); // 中
- return depth;
- }
- int maxDepth(TreeNode* root) {
- return getDepth(root);
- }
-};
-```
-
-代码精简之后C++代码如下:
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- return 1 + max(maxDepth(root->left), maxDepth(root->right));
- }
-};
-
-```
-
-**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
-
-
-## 迭代法
-
-使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
-
-在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
-
-
-
-所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
-
-如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
-
-C++代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- int depth = 0;
- queue que;
- que.push(root);
- while(!que.empty()) {
- int size = que.size();
- depth++; // 记录深度
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- }
- return depth;
- }
-};
-```
-
-那么我们可以顺便解决一下N叉树的最大深度问题
-
-# 559.N叉树的最大深度
-https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
-
-给定一个 N 叉树,找到其最大深度。
-
-最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
-
-例如,给定一个 3叉树 :
-
-
-
-返回它的最大深度 3 。
-
-# 思路
-
-## 递归法
-
-本题其实也要后序遍历(左右中),依然是因为要通过递归函数的返回值做计算树的高度。
-
-按照递归三部曲,来看看如何来写。
-
-1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
-
-代码如下:
-```
-int getDepth(TreeNode* node)
-```
-
-2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
-
-代码如下:
-```
-if (node == NULL) return 0;
-```
-
-3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
-
-代码如下:
-
-```
-int leftDepth = getDepth(node->left); // 左
-int rightDepth = getDepth(node->right); // 右
-int depth = 1 + max(leftDepth, rightDepth); // 中
-return depth;
-```
-
-所以整体C++代码如下:
-
-```
-class Solution {
-public:
- int getDepth(TreeNode* node) {
- if (node == NULL) return 0;
- int leftDepth = getDepth(node->left); // 左
- int rightDepth = getDepth(node->right); // 右
- int depth = 1 + max(leftDepth, rightDepth); // 中
- return depth;
- }
- int maxDepth(TreeNode* root) {
- return getDepth(root);
- }
-};
-```
-
-代码精简之后C++代码如下:
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- return 1 + max(maxDepth(root->left), maxDepth(root->right));
- }
-};
-
-```
-
-**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
-
-
-## 迭代法
-
-使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
-
-在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
-
-
-
-所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
-
-如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
-
-C++代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- int depth = 0;
- queue que;
- que.push(root);
- while(!que.empty()) {
- int size = que.size();
- depth++; // 记录深度
- for (int i = 0; i < size; i++) {
- TreeNode* node = que.front();
- que.pop();
- if (node->left) que.push(node->left);
- if (node->right) que.push(node->right);
- }
- }
- return depth;
- }
-};
-```
-
-那么我们可以顺便解决一下N叉树的最大深度问题
-
-# 559.N叉树的最大深度
-https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
-
-给定一个 N 叉树,找到其最大深度。
-
-最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
-
-例如,给定一个 3叉树 :
-
- -
-我们应返回其最大深度,3。
-
-# 思路
-
-依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
-
-## 递归法
-
-C++代码:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- if (root == 0) return 0;
- int depth = 0;
- for (int i = 0; i < root->children.size(); i++) {
- depth = max (depth, maxDepth(root->children[i]));
- }
- return depth + 1;
- }
-};
-```
-## 迭代法
-
-依然是层序遍历,代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- int depth = 0;
- while (!que.empty()) {
- int size = que.size();
- depth++; // 记录深度
- for (int i = 0; i < size; i++) {
- Node* node = que.front();
- que.pop();
- for (int j = 0; j < node->children.size(); j++) {
- if (node->children[j]) que.push(node->children[j]);
- }
- }
- }
- return depth;
- }
-};
-```
-
-使用栈来模拟后序遍历依然可以
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- stack st;
- if (root != NULL) st.push(root);
- int depth = 0;
- int result = 0;
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop();
- st.push(node); // 中
- st.push(NULL);
- depth++;
- if (node->right) st.push(node->right); // 右
- if (node->left) st.push(node->left); // 左
-
- } else {
- st.pop();
- node = st.top();
- st.pop();
- depth--;
- }
- result = result > depth ? result : depth;
- }
- return result;
-
- }
-};
-```
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0105.从前序与中序遍历序列构造二叉树.md b/problems/0105.从前序与中序遍历序列构造二叉树.md
deleted file mode 100644
index eb39b313..00000000
--- a/problems/0105.从前序与中序遍历序列构造二叉树.md
+++ /dev/null
@@ -1,8 +0,0 @@
-# 链接
-
-https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
-
-# 思路:
-
-详细见
-[0106.从中序与后序遍历序列构造二叉树](https://github.com/youngyangyang04/leetcode/blob/master/problems/0106.从中序与后序遍历序列构造二叉树.md)
diff --git a/problems/0106.从中序与后序遍历序列构造二叉树.md b/problems/0106.从中序与后序遍历序列构造二叉树.md
deleted file mode 100644
index 892f2167..00000000
--- a/problems/0106.从中序与后序遍历序列构造二叉树.md
+++ /dev/null
@@ -1,576 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
-
-> 给出两个序列 (可以加unorder_map优化一下)
-
-看完本文,可以一起解决如下两道题目
-
-* 106.从中序与后序遍历序列构造二叉树
-* 105.从前序与中序遍历序列构造二叉树
-
-
-# 106.从中序与后序遍历序列构造二叉树
-
-根据一棵树的中序遍历与后序遍历构造二叉树。
-
-注意:
-你可以假设树中没有重复的元素。
-
-例如,给出
-
-中序遍历 inorder = [9,3,15,20,7]
-后序遍历 postorder = [9,15,7,20,3]
-返回如下的二叉树:
-
-
-
-我们应返回其最大深度,3。
-
-# 思路
-
-依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
-
-## 递归法
-
-C++代码:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- if (root == 0) return 0;
- int depth = 0;
- for (int i = 0; i < root->children.size(); i++) {
- depth = max (depth, maxDepth(root->children[i]));
- }
- return depth + 1;
- }
-};
-```
-## 迭代法
-
-依然是层序遍历,代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- queue que;
- if (root != NULL) que.push(root);
- int depth = 0;
- while (!que.empty()) {
- int size = que.size();
- depth++; // 记录深度
- for (int i = 0; i < size; i++) {
- Node* node = que.front();
- que.pop();
- for (int j = 0; j < node->children.size(); j++) {
- if (node->children[j]) que.push(node->children[j]);
- }
- }
- }
- return depth;
- }
-};
-```
-
-使用栈来模拟后序遍历依然可以
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- stack st;
- if (root != NULL) st.push(root);
- int depth = 0;
- int result = 0;
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop();
- st.push(node); // 中
- st.push(NULL);
- depth++;
- if (node->right) st.push(node->right); // 右
- if (node->left) st.push(node->left); // 左
-
- } else {
- st.pop();
- node = st.top();
- st.pop();
- depth--;
- }
- result = result > depth ? result : depth;
- }
- return result;
-
- }
-};
-```
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0105.从前序与中序遍历序列构造二叉树.md b/problems/0105.从前序与中序遍历序列构造二叉树.md
deleted file mode 100644
index eb39b313..00000000
--- a/problems/0105.从前序与中序遍历序列构造二叉树.md
+++ /dev/null
@@ -1,8 +0,0 @@
-# 链接
-
-https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
-
-# 思路:
-
-详细见
-[0106.从中序与后序遍历序列构造二叉树](https://github.com/youngyangyang04/leetcode/blob/master/problems/0106.从中序与后序遍历序列构造二叉树.md)
diff --git a/problems/0106.从中序与后序遍历序列构造二叉树.md b/problems/0106.从中序与后序遍历序列构造二叉树.md
deleted file mode 100644
index 892f2167..00000000
--- a/problems/0106.从中序与后序遍历序列构造二叉树.md
+++ /dev/null
@@ -1,576 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
-
-> 给出两个序列 (可以加unorder_map优化一下)
-
-看完本文,可以一起解决如下两道题目
-
-* 106.从中序与后序遍历序列构造二叉树
-* 105.从前序与中序遍历序列构造二叉树
-
-
-# 106.从中序与后序遍历序列构造二叉树
-
-根据一棵树的中序遍历与后序遍历构造二叉树。
-
-注意:
-你可以假设树中没有重复的元素。
-
-例如,给出
-
-中序遍历 inorder = [9,3,15,20,7]
-后序遍历 postorder = [9,15,7,20,3]
-返回如下的二叉树:
-
- -
-## 思路
-
-首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
-
-如果让我们肉眼看两个序列,画一颗二叉树的话,应该分分钟都可以画出来。
-
-流程如图:
-
-
-
-## 思路
-
-首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
-
-如果让我们肉眼看两个序列,画一颗二叉树的话,应该分分钟都可以画出来。
-
-流程如图:
-
- -
-那么代码应该怎么写呢?
-
-说到一层一层切割,就应该想到了递归。
-
-来看一下一共分几步:
-
-* 第一步:如果数组大小为零的话,说明是空节点了。
-
-* 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
-* 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
-* 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
-* 第五步:切割后序数组,切成后序左数组和后序右数组
-
-* 第六步:递归处理左区间和右区间
-
-不难写出如下代码:(先把框架写出来)
-
-```
- TreeNode* traversal (vector& inorder, vector& postorder) {
-
- // 第一步
- if (postorder.size() == 0) return NULL;
-
- // 第二步:后序遍历数组最后一个元素,就是当前的中间节点
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- // 叶子节点
- if (postorder.size() == 1) return root;
-
- // 第三步:找切割点
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- // 第四步:切割中序数组,得到 中序左数组和中序右数组
- // 第五步:切割后序数组,得到 后序左数组和后序右数组
-
- // 第六步
- root->left = traversal(中序左数组, 后序左数组);
- root->right = traversal(中序右数组, 后序右数组);
-
- return root;
- }
-```
-
-**难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。**
-
-此时应该注意确定切割的标准,是左闭右开,还有左开又闭,还是左闭又闭,这个就是不变量,要在递归中保持这个不变量。
-
-**在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭又闭,必然乱套!**
-
-我在[数组:每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)和[数组:这个循环可以转懵很多人!](https://mp.weixin.qq.com/s/KTPhaeqxbMK9CxHUUgFDmg)中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
-
-
-首先要切割中序数组,为什么先切割中序数组呢?
-
-切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
-
-中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
-
-
-```
-// 找到中序遍历的切割点
-int delimiterIndex;
-for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
-}
-
-// 左闭右开区间:[0, delimiterIndex)
-vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
-// [delimiterIndex + 1, end)
-vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-```
-
-接下来就要切割后序数组了。
-
-首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
-
-后序数组的切割点怎么找?
-
-后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
-
-**此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。**
-
-中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
-
-代码如下:
-
-```
-// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了
-postorder.resize(postorder.size() - 1);
-
-// 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size)
-vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
-// [leftInorder.size(), end)
-vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-```
-
-此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
-
-接下来可以递归了,代码如下:
-
-```
-root->left = traversal(leftInorder, leftPostorder);
-root->right = traversal(rightInorder, rightPostorder);
-```
-
-完整代码如下:
-
-### C++完整代码
-
-```
-class Solution {
-private:
- TreeNode* traversal (vector& inorder, vector& postorder) {
- if (postorder.size() == 0) return NULL;
-
- // 后序遍历数组最后一个元素,就是当前的中间节点
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- // 叶子节点
- if (postorder.size() == 1) return root;
-
- // 找到中序遍历的切割点
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- // 切割中序数组
- // 左闭右开区间:[0, delimiterIndex)
- vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
- // [delimiterIndex + 1, end)
- vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-
- // postorder 舍弃末尾元素
- postorder.resize(postorder.size() - 1);
-
- // 切割后序数组
- // 依然左闭右开,注意这里使用了左中序数组大小作为切割点
- // [0, leftInorder.size)
- vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
- // [leftInorder.size(), end)
- vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-
- root->left = traversal(leftInorder, leftPostorder);
- root->right = traversal(rightInorder, rightPostorder);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector& postorder) {
- if (inorder.size() == 0 || postorder.size() == 0) return NULL;
- return traversal(inorder, postorder);
- }
-};
-
-```
-
-相信大家自己就算是思路清晰, 代码写出来一定是各种问题,所以一定要加日志来调试,看看是不是按照自己思路来切割的,不要大脑模拟,那样越想越糊涂。
-
-加了日志的代码如下:(加了日志的代码不要在leetcode上提交,容易超时)
-
-
-```
-class Solution {
-private:
- TreeNode* traversal (vector& inorder, vector& postorder) {
- if (postorder.size() == 0) return NULL;
-
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- if (postorder.size() == 1) return root;
-
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
- vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-
- postorder.resize(postorder.size() - 1);
-
- vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
- vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-
- // 一下为日志
- cout << "----------" << endl;
-
- cout << "leftInorder :";
- for (int i : leftInorder) {
- cout << i << " ";
- }
- cout << endl;
-
- cout << "rightInorder :";
- for (int i : rightInorder) {
- cout << i << " ";
- }
- cout << endl;
-
- cout << "leftPostorder :";
- for (int i : leftPostorder) {
- cout << i << " ";
- }
- cout << endl;
- cout << "rightPostorder :";
- for (int i : rightPostorder) {
- cout << i << " ";
- }
- cout << endl;
-
- root->left = traversal(leftInorder, leftPostorder);
- root->right = traversal(rightInorder, rightPostorder);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector& postorder) {
- if (inorder.size() == 0 || postorder.size() == 0) return NULL;
- return traversal(inorder, postorder);
- }
-};
-```
-
-**此时应该发现了,如上的代码性能并不好,应为每层递归定定义了新的vector(就是数组),既耗时又耗空间,但上面的代码是最好理解的,为了方便读者理解,所以用如上的代码来讲解。**
-
-下面给出用下表索引写出的代码版本:(思路是一样的,只不过不用重复定义vector了,每次用下表索引来分割)
-
-### C++优化版本
-```
-class Solution {
-private:
- // 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
- TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& postorder, int postorderBegin, int postorderEnd) {
- if (postorderBegin == postorderEnd) return NULL;
-
- int rootValue = postorder[postorderEnd - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- if (postorderEnd - postorderBegin == 1) return root;
-
- int delimiterIndex;
- for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
- // 切割中序数组
- // 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
- int leftInorderBegin = inorderBegin;
- int leftInorderEnd = delimiterIndex;
- // 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
- int rightInorderBegin = delimiterIndex + 1;
- int rightInorderEnd = inorderEnd;
-
- // 切割后序数组
- // 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
- int leftPostorderBegin = postorderBegin;
- int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
- // 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
- int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
- int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
-
- root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
- root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector
-
-那么代码应该怎么写呢?
-
-说到一层一层切割,就应该想到了递归。
-
-来看一下一共分几步:
-
-* 第一步:如果数组大小为零的话,说明是空节点了。
-
-* 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
-* 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
-* 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
-* 第五步:切割后序数组,切成后序左数组和后序右数组
-
-* 第六步:递归处理左区间和右区间
-
-不难写出如下代码:(先把框架写出来)
-
-```
- TreeNode* traversal (vector& inorder, vector& postorder) {
-
- // 第一步
- if (postorder.size() == 0) return NULL;
-
- // 第二步:后序遍历数组最后一个元素,就是当前的中间节点
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- // 叶子节点
- if (postorder.size() == 1) return root;
-
- // 第三步:找切割点
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- // 第四步:切割中序数组,得到 中序左数组和中序右数组
- // 第五步:切割后序数组,得到 后序左数组和后序右数组
-
- // 第六步
- root->left = traversal(中序左数组, 后序左数组);
- root->right = traversal(中序右数组, 后序右数组);
-
- return root;
- }
-```
-
-**难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。**
-
-此时应该注意确定切割的标准,是左闭右开,还有左开又闭,还是左闭又闭,这个就是不变量,要在递归中保持这个不变量。
-
-**在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭又闭,必然乱套!**
-
-我在[数组:每次遇到二分法,都是一看就会,一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)和[数组:这个循环可以转懵很多人!](https://mp.weixin.qq.com/s/KTPhaeqxbMK9CxHUUgFDmg)中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
-
-
-首先要切割中序数组,为什么先切割中序数组呢?
-
-切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
-
-中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
-
-
-```
-// 找到中序遍历的切割点
-int delimiterIndex;
-for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
-}
-
-// 左闭右开区间:[0, delimiterIndex)
-vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
-// [delimiterIndex + 1, end)
-vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-```
-
-接下来就要切割后序数组了。
-
-首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
-
-后序数组的切割点怎么找?
-
-后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
-
-**此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。**
-
-中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
-
-代码如下:
-
-```
-// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了
-postorder.resize(postorder.size() - 1);
-
-// 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size)
-vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
-// [leftInorder.size(), end)
-vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-```
-
-此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
-
-接下来可以递归了,代码如下:
-
-```
-root->left = traversal(leftInorder, leftPostorder);
-root->right = traversal(rightInorder, rightPostorder);
-```
-
-完整代码如下:
-
-### C++完整代码
-
-```
-class Solution {
-private:
- TreeNode* traversal (vector& inorder, vector& postorder) {
- if (postorder.size() == 0) return NULL;
-
- // 后序遍历数组最后一个元素,就是当前的中间节点
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- // 叶子节点
- if (postorder.size() == 1) return root;
-
- // 找到中序遍历的切割点
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- // 切割中序数组
- // 左闭右开区间:[0, delimiterIndex)
- vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
- // [delimiterIndex + 1, end)
- vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-
- // postorder 舍弃末尾元素
- postorder.resize(postorder.size() - 1);
-
- // 切割后序数组
- // 依然左闭右开,注意这里使用了左中序数组大小作为切割点
- // [0, leftInorder.size)
- vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
- // [leftInorder.size(), end)
- vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-
- root->left = traversal(leftInorder, leftPostorder);
- root->right = traversal(rightInorder, rightPostorder);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector& postorder) {
- if (inorder.size() == 0 || postorder.size() == 0) return NULL;
- return traversal(inorder, postorder);
- }
-};
-
-```
-
-相信大家自己就算是思路清晰, 代码写出来一定是各种问题,所以一定要加日志来调试,看看是不是按照自己思路来切割的,不要大脑模拟,那样越想越糊涂。
-
-加了日志的代码如下:(加了日志的代码不要在leetcode上提交,容易超时)
-
-
-```
-class Solution {
-private:
- TreeNode* traversal (vector& inorder, vector& postorder) {
- if (postorder.size() == 0) return NULL;
-
- int rootValue = postorder[postorder.size() - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- if (postorder.size() == 1) return root;
-
- int delimiterIndex;
- for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
-
- vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
- vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
-
- postorder.resize(postorder.size() - 1);
-
- vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
- vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
-
- // 一下为日志
- cout << "----------" << endl;
-
- cout << "leftInorder :";
- for (int i : leftInorder) {
- cout << i << " ";
- }
- cout << endl;
-
- cout << "rightInorder :";
- for (int i : rightInorder) {
- cout << i << " ";
- }
- cout << endl;
-
- cout << "leftPostorder :";
- for (int i : leftPostorder) {
- cout << i << " ";
- }
- cout << endl;
- cout << "rightPostorder :";
- for (int i : rightPostorder) {
- cout << i << " ";
- }
- cout << endl;
-
- root->left = traversal(leftInorder, leftPostorder);
- root->right = traversal(rightInorder, rightPostorder);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector& postorder) {
- if (inorder.size() == 0 || postorder.size() == 0) return NULL;
- return traversal(inorder, postorder);
- }
-};
-```
-
-**此时应该发现了,如上的代码性能并不好,应为每层递归定定义了新的vector(就是数组),既耗时又耗空间,但上面的代码是最好理解的,为了方便读者理解,所以用如上的代码来讲解。**
-
-下面给出用下表索引写出的代码版本:(思路是一样的,只不过不用重复定义vector了,每次用下表索引来分割)
-
-### C++优化版本
-```
-class Solution {
-private:
- // 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
- TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& postorder, int postorderBegin, int postorderEnd) {
- if (postorderBegin == postorderEnd) return NULL;
-
- int rootValue = postorder[postorderEnd - 1];
- TreeNode* root = new TreeNode(rootValue);
-
- if (postorderEnd - postorderBegin == 1) return root;
-
- int delimiterIndex;
- for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
- if (inorder[delimiterIndex] == rootValue) break;
- }
- // 切割中序数组
- // 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
- int leftInorderBegin = inorderBegin;
- int leftInorderEnd = delimiterIndex;
- // 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
- int rightInorderBegin = delimiterIndex + 1;
- int rightInorderEnd = inorderEnd;
-
- // 切割后序数组
- // 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
- int leftPostorderBegin = postorderBegin;
- int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
- // 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
- int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
- int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
-
- root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
- root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
-
- return root;
- }
-public:
- TreeNode* buildTree(vector& inorder, vector -
-* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
-
-
-* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
- -
-* fast和slow同时移动,之道fast指向末尾,如题:
-
-
-* fast和slow同时移动,之道fast指向末尾,如题:
- -
-* 删除slow指向的下一个节点,如图:
-
-
-* 删除slow指向的下一个节点,如图:
- -
-此时不难写出如下C++代码:
-
-```
-class Solution {
-public:
- ListNode* removeNthFromEnd(ListNode* head, int n) {
- ListNode* dummyHead = new ListNode(0);
- dummyHead->next = head;
- ListNode* slow = dummyHead;
- ListNode* fast = dummyHead;
- while(n-- && fast != NULL) {
- fast = fast->next;
- }
- fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
- while (fast != NULL) {
- fast = fast->next;
- slow = slow->next;
- }
- slow->next = slow->next->next;
- return dummyHead->next;
- }
-};
-```
diff --git a/problems/0020.有效的括号.md b/problems/0020.有效的括号.md
deleted file mode 100644
index 293c53dd..00000000
--- a/problems/0020.有效的括号.md
+++ /dev/null
@@ -1,128 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/valid-parentheses/
-
-> 数据结构与算法应用往往隐藏在我们看不到的地方
-
-# 20. 有效的括号
-
-给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
-
-有效字符串需满足:
-* 左括号必须用相同类型的右括号闭合。
-* 左括号必须以正确的顺序闭合。
-* 注意空字符串可被认为是有效字符串。
-
-示例 1:
-输入: "()"
-输出: true
-
-示例 2:
-输入: "()[]{}"
-输出: true
-
-示例 3:
-输入: "(]"
-输出: false
-
-示例 4:
-输入: "([)]"
-输出: false
-
-示例 5:
-输入: "{[]}"
-输出: true
-
-# 思路
-
-## 题外话
-
-**括号匹配是使用栈解决的经典问题。**
-
-题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
-
-如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
-
-再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
-
-```
-cd a/b/c/../../
-```
-
-这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)
-
-所以栈在计算机领域中应用是非常广泛的。
-
-有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
-
-**所以数据结构与算法的应用往往隐藏在我们看不到的地方!**
-
-这里我就不过多展开了,先来看题。
-
-## 进入正题
-
-由于栈结构的特殊性,非常适合做对称匹配类的题目。
-
-首先要弄清楚,字符串里的括号不匹配有几种情况。
-
-**一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越远。**
-
-建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
-
-先来分析一下 这里有三种不匹配的情况,
-
-1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
-
-2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
-
-3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
-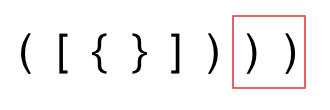
-
-我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
-
-动画如下:
-
-
-
-
-第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
-
-第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
-
-第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
-
-那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
-
-分析完之后,代码其实就比较好写了,
-
-但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
-
-实现代码如下:
-
-## C++代码
-
-
-```
-class Solution {
-public:
- bool isValid(string s) {
- stack
-
-此时不难写出如下C++代码:
-
-```
-class Solution {
-public:
- ListNode* removeNthFromEnd(ListNode* head, int n) {
- ListNode* dummyHead = new ListNode(0);
- dummyHead->next = head;
- ListNode* slow = dummyHead;
- ListNode* fast = dummyHead;
- while(n-- && fast != NULL) {
- fast = fast->next;
- }
- fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
- while (fast != NULL) {
- fast = fast->next;
- slow = slow->next;
- }
- slow->next = slow->next->next;
- return dummyHead->next;
- }
-};
-```
diff --git a/problems/0020.有效的括号.md b/problems/0020.有效的括号.md
deleted file mode 100644
index 293c53dd..00000000
--- a/problems/0020.有效的括号.md
+++ /dev/null
@@ -1,128 +0,0 @@
-
-## 题目地址
-
-https://leetcode-cn.com/problems/valid-parentheses/
-
-> 数据结构与算法应用往往隐藏在我们看不到的地方
-
-# 20. 有效的括号
-
-给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
-
-有效字符串需满足:
-* 左括号必须用相同类型的右括号闭合。
-* 左括号必须以正确的顺序闭合。
-* 注意空字符串可被认为是有效字符串。
-
-示例 1:
-输入: "()"
-输出: true
-
-示例 2:
-输入: "()[]{}"
-输出: true
-
-示例 3:
-输入: "(]"
-输出: false
-
-示例 4:
-输入: "([)]"
-输出: false
-
-示例 5:
-输入: "{[]}"
-输出: true
-
-# 思路
-
-## 题外话
-
-**括号匹配是使用栈解决的经典问题。**
-
-题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
-
-如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
-
-再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
-
-```
-cd a/b/c/../../
-```
-
-这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)
-
-所以栈在计算机领域中应用是非常广泛的。
-
-有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
-
-**所以数据结构与算法的应用往往隐藏在我们看不到的地方!**
-
-这里我就不过多展开了,先来看题。
-
-## 进入正题
-
-由于栈结构的特殊性,非常适合做对称匹配类的题目。
-
-首先要弄清楚,字符串里的括号不匹配有几种情况。
-
-**一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越远。**
-
-建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
-
-先来分析一下 这里有三种不匹配的情况,
-
-1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
-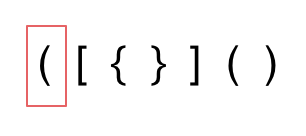
-2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
-
-3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
-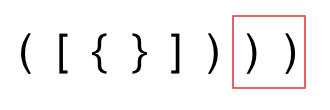
-
-我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
-
-动画如下:
-
-
-
-
-第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
-
-第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
-
-第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
-
-那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
-
-分析完之后,代码其实就比较好写了,
-
-但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
-
-实现代码如下:
-
-## C++代码
-
-
-```
-class Solution {
-public:
- bool isValid(string s) {
- stack -
-操作之后,链表如下:
-
-
-
-
-操作之后,链表如下:
-
-
- -
-看这个可能就更直观一些了:
-
-
-
-
-看这个可能就更直观一些了:
-
-
- -
-对应的C++代码实现如下:
-
-```
-class Solution {
-public:
- ListNode* swapPairs(ListNode* head) {
- ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
- ListNode* cur = dummyHead;
- while(cur->next != nullptr && cur->next->next != nullptr) {
- ListNode* tmp = cur->next; // 记录临时节点
- ListNode* tmp1 = cur->next->next->next; // 记录临时节点
-
- cur->next = cur->next->next; // 步骤一
- cur->next->next = tmp; // 步骤二
- cur->next->next->next = tmp1; // 步骤三
-
- cur = cur->next->next; // cur移动两位,准备下一轮交换
- }
- return dummyHead->next;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-## 拓展
-
-**这里还是说一下,大家不必太在意leetcode上执行用时,打败多少多少用户,这个就是一个玩具,非常不准确。**
-
-做题的时候自己能分析出来时间复杂度就可以了,至于leetcode上执行用时,大概看一下就行。
-
-上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-
-心想应该没有更好的方法了吧,也就O(n)的时间复杂度,重复提交几次,这样了:
-
-
-
-对应的C++代码实现如下:
-
-```
-class Solution {
-public:
- ListNode* swapPairs(ListNode* head) {
- ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
- ListNode* cur = dummyHead;
- while(cur->next != nullptr && cur->next->next != nullptr) {
- ListNode* tmp = cur->next; // 记录临时节点
- ListNode* tmp1 = cur->next->next->next; // 记录临时节点
-
- cur->next = cur->next->next; // 步骤一
- cur->next->next = tmp; // 步骤二
- cur->next->next->next = tmp1; // 步骤三
-
- cur = cur->next->next; // cur移动两位,准备下一轮交换
- }
- return dummyHead->next;
- }
-};
-```
-时间复杂度:O(n)
-空间复杂度:O(1)
-
-## 拓展
-
-**这里还是说一下,大家不必太在意leetcode上执行用时,打败多少多少用户,这个就是一个玩具,非常不准确。**
-
-做题的时候自己能分析出来时间复杂度就可以了,至于leetcode上执行用时,大概看一下就行。
-
-上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-
-心想应该没有更好的方法了吧,也就O(n)的时间复杂度,重复提交几次,这样了:
-
- -
-所以,不必过于在意leetcode上这个统计。
-
-
-
diff --git a/problems/0026.删除排序数组中的重复项.md b/problems/0026.删除排序数组中的重复项.md
deleted file mode 100644
index 114f2da2..00000000
--- a/problems/0026.删除排序数组中的重复项.md
+++ /dev/null
@@ -1,49 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
-
-# 思路
-
-此题使用双指针法,O(n)的时间复杂度,拼速度的话,可以剪剪枝。
-
-注意题目中:不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
-
-双指针法,动画如下:
-
-
-
-其实**双指针法在在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法,可以将时间复杂度O(n^2)的解法优化为 O(n)的解法,例如:**
-
-* [0015.三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md)
-* [0018.四数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0018.四数之和.md)
-* [0026.删除排序数组中的重复项](https://github.com/youngyangyang04/leetcode/blob/master/problems/0026.删除排序数组中的重复项.md)
-* [0206.翻转链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0206.翻转链表.md)
-* [0344.反转字符串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0344.反转字符串.md)
-* [剑指Offer05.替换空格](https://github.com/youngyangyang04/leetcode/blob/master/problems/剑指Offer05.替换空格.md)
-
-**还有链表找环,也用到双指针:**
-
-* [0142.环形链表II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0142.环形链表II.md)
-
-大家都可以去做一做,感受一下双指针法的内在逻辑!
-
-
-# C++ 代码
-
-
-```
-class Solution {
-public:
- int removeDuplicates(vector
-
-所以,不必过于在意leetcode上这个统计。
-
-
-
diff --git a/problems/0026.删除排序数组中的重复项.md b/problems/0026.删除排序数组中的重复项.md
deleted file mode 100644
index 114f2da2..00000000
--- a/problems/0026.删除排序数组中的重复项.md
+++ /dev/null
@@ -1,49 +0,0 @@
-## 题目地址
-https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
-
-# 思路
-
-此题使用双指针法,O(n)的时间复杂度,拼速度的话,可以剪剪枝。
-
-注意题目中:不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
-
-双指针法,动画如下:
-
-
-
-其实**双指针法在在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法,可以将时间复杂度O(n^2)的解法优化为 O(n)的解法,例如:**
-
-* [0015.三数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0015.三数之和.md)
-* [0018.四数之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0018.四数之和.md)
-* [0026.删除排序数组中的重复项](https://github.com/youngyangyang04/leetcode/blob/master/problems/0026.删除排序数组中的重复项.md)
-* [0206.翻转链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0206.翻转链表.md)
-* [0344.反转字符串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0344.反转字符串.md)
-* [剑指Offer05.替换空格](https://github.com/youngyangyang04/leetcode/blob/master/problems/剑指Offer05.替换空格.md)
-
-**还有链表找环,也用到双指针:**
-
-* [0142.环形链表II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0142.环形链表II.md)
-
-大家都可以去做一做,感受一下双指针法的内在逻辑!
-
-
-# C++ 代码
-
-
-```
-class Solution {
-public:
- int removeDuplicates(vector -
- -
-很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
-
-# 暴力解法C++代码
-
-```
-// 时间复杂度:O(n^2)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector
-
-很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
-
-# 暴力解法C++代码
-
-```
-// 时间复杂度:O(n^2)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector -
-**双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。**
-
-我们来回顾一下,之前已经讲过有四道题目使用了双指针法。
-
-双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
-
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
-* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-
-双指针来记录前后指针实现链表反转:
-
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
-
-使用双指针来确定有环:
-
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用,后面还会介绍到。
-
-# 双指针法C++代码:
-```
-// 时间复杂度:O(n)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector
-
-**双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。**
-
-我们来回顾一下,之前已经讲过有四道题目使用了双指针法。
-
-双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
-
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
-* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-
-双指针来记录前后指针实现链表反转:
-
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
-
-使用双指针来确定有环:
-
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用,后面还会介绍到。
-
-# 双指针法C++代码:
-```
-// 时间复杂度:O(n)
-// 空间复杂度:O(1)
-class Solution {
-public:
- int removeElement(vector -
- -
-动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说道。
-
-可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
-
-但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
-
-此时就要问了**前缀表是如何记录的呢?**
-
-首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,在重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
-
-那么什么是前缀表:**记录下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-# 为什么一定要用前缀表
-
-这就是前缀表那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
-
-回顾一下,刚刚匹配的过程在下表5的地方遇到不匹配,模式串是指向f,如图:
-
-
-动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说道。
-
-可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
-
-但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
-
-此时就要问了**前缀表是如何记录的呢?**
-
-首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,在重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
-
-那么什么是前缀表:**记录下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-# 为什么一定要用前缀表
-
-这就是前缀表那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
-
-回顾一下,刚刚匹配的过程在下表5的地方遇到不匹配,模式串是指向f,如图:
- -
-
-然后就找到了下表2,指向b,继续匹配:如图:
-
-
-
-然后就找到了下表2,指向b,继续匹配:如图:
- -
-以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-
-**下表5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
-
-所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
-
-**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-
-# 如何计算前缀表
-
-接下来就要说一说怎么计算前缀表。
-
-如图:
-
-
-
-以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-
-**下表5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
-
-所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
-
-**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-
-# 如何计算前缀表
-
-接下来就要说一说怎么计算前缀表。
-
-如图:
-
- -
-长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
-
-
-长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
- -长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
-
-长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
- -长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
-
-以此类推:
-长度为前4个字符的子串`aaba`,最长相同前后缀的长度为1。
-长度为前5个字符的子串`aabaa`,最长相同前后缀的长度为2。
-长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
-
-那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
-
-长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
-
-以此类推:
-长度为前4个字符的子串`aaba`,最长相同前后缀的长度为1。
-长度为前5个字符的子串`aabaa`,最长相同前后缀的长度为2。
-长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
-
-那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
- -
-可以看出模式串与前缀表对应位置的数字表示的就是:**下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
-
-
-可以看出模式串与前缀表对应位置的数字表示的就是:**下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-
-再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
- -
-找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
-
-为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
-
-所以要看前一位的 前缀表的数值。
-
-前一个字符的前缀表的数值是2, 所有把下表移动到下表2的位置继续比配。 可以再反复看一下上面的动画。
-
-最后就在文本串中找到了和模式串匹配的子串了。
-
-# 前缀表与next数组
-
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
-
-next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
-
-为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
-
-后面我会提供两种不同的实现代码,大家就明白了了。
-
-# 使用next数组来匹配
-
-以下我们以前缀表统一减一之后的next数组来做演示。
-
-有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
-
-注意next数组是新前缀表(旧前缀表统一减一了)。
-
-匹配过程动画如下:
-
-
-
-找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
-
-为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
-
-所以要看前一位的 前缀表的数值。
-
-前一个字符的前缀表的数值是2, 所有把下表移动到下表2的位置继续比配。 可以再反复看一下上面的动画。
-
-最后就在文本串中找到了和模式串匹配的子串了。
-
-# 前缀表与next数组
-
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
-
-next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
-
-为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
-
-后面我会提供两种不同的实现代码,大家就明白了了。
-
-# 使用next数组来匹配
-
-以下我们以前缀表统一减一之后的next数组来做演示。
-
-有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
-
-注意next数组是新前缀表(旧前缀表统一减一了)。
-
-匹配过程动画如下:
-
- -
-# 时间复杂度分析
-
-
-其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-
-暴力的解法显而易见是O(n * m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
-
-为了和[字符串:KMP是时候上场了(一文读懂系列)](https://mp.weixin.qq.com/s/70OXnZ4Ez29CKRrUpVJmug)字符串命名统一,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
-
-都知道使用KMP算法,一定要构造next数组。
-
-# 构造next数组
-
-我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
-
-```
-void getNext(int* next, const string& s)
-```
-
-**构造next数组其实就是计算模式串s,前缀表的过程。** 主要有如下三步:
-
-1. 初始化
-2. 处理前后缀不相同的情况
-3. 处理前后缀相同的情况
-
-接下来我们详解详解一下。
-
-1. 初始化:
-
-定义两个指针i和j,j指向前缀终止位置(严格来说是终止位置减一的位置),i指向后缀终止位置(与j同理)。
-
-然后还要对next数组进行初始化赋值,如下:
-
-```
-int j = -1;
-next[0] = j;
-```
-
-j 为什么要初始化为 -1呢,因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现,我们这里选择j初始化为-1,下文我还会给出j不初始化为-1的实现代码。
-
-next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
-
-所以初始化next[0] = j 。
-
-
-2. 处理前后缀不相同的情况
-
-
-因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
-
-所以遍历模式串s的循环下表i 要从 1开始,代码如下:
-
-```
-for(int i = 1; i < s.size(); i++) {
-```
-
-如果 s[i] 与 s[j+1]不相同,也就是遇到 前后缀末尾不相同的情况,就要向前回溯。
-
-怎么回溯呢?
-
-next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
-
-那么 s[i] 与 s[j+1] 不相同,就要找 j+1前一个元素在next数组里的值(就是next[j])。
-
-所以,处理前后缀不相同的情况代码如下:
-
-```
-while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
-}
-```
-
-3. 处理前后缀相同的情况
-
-如果s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
-
-代码如下:
-
-```
-if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
-}
-next[i] = j;
-```
-
-最后整体构建next数组的函数代码如下:
-
-```
-void getNext(int* next, const string& s){
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-```
-
-
-代码构造next数组的逻辑流程动画如下:
-
-
-
-# 时间复杂度分析
-
-
-其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-
-暴力的解法显而易见是O(n * m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
-
-为了和[字符串:KMP是时候上场了(一文读懂系列)](https://mp.weixin.qq.com/s/70OXnZ4Ez29CKRrUpVJmug)字符串命名统一,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
-
-都知道使用KMP算法,一定要构造next数组。
-
-# 构造next数组
-
-我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
-
-```
-void getNext(int* next, const string& s)
-```
-
-**构造next数组其实就是计算模式串s,前缀表的过程。** 主要有如下三步:
-
-1. 初始化
-2. 处理前后缀不相同的情况
-3. 处理前后缀相同的情况
-
-接下来我们详解详解一下。
-
-1. 初始化:
-
-定义两个指针i和j,j指向前缀终止位置(严格来说是终止位置减一的位置),i指向后缀终止位置(与j同理)。
-
-然后还要对next数组进行初始化赋值,如下:
-
-```
-int j = -1;
-next[0] = j;
-```
-
-j 为什么要初始化为 -1呢,因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现,我们这里选择j初始化为-1,下文我还会给出j不初始化为-1的实现代码。
-
-next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
-
-所以初始化next[0] = j 。
-
-
-2. 处理前后缀不相同的情况
-
-
-因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
-
-所以遍历模式串s的循环下表i 要从 1开始,代码如下:
-
-```
-for(int i = 1; i < s.size(); i++) {
-```
-
-如果 s[i] 与 s[j+1]不相同,也就是遇到 前后缀末尾不相同的情况,就要向前回溯。
-
-怎么回溯呢?
-
-next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
-
-那么 s[i] 与 s[j+1] 不相同,就要找 j+1前一个元素在next数组里的值(就是next[j])。
-
-所以,处理前后缀不相同的情况代码如下:
-
-```
-while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
-}
-```
-
-3. 处理前后缀相同的情况
-
-如果s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
-
-代码如下:
-
-```
-if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
-}
-next[i] = j;
-```
-
-最后整体构建next数组的函数代码如下:
-
-```
-void getNext(int* next, const string& s){
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-```
-
-
-代码构造next数组的逻辑流程动画如下:
-
- -
-
-得到了next数组之后,就要用这个来做匹配了。
-
-# 使用next数组来做匹配
-
-在文本串s里 找是否出现过模式串t。
-
-定义两个下表j 指向模式串起始位置,i指向文本串起始位置。
-
-那么j初始值依然为-1,为什么呢? **依然因为next数组里记录的起始位置为-1。**
-
-i就从0开始,遍历文本串,代码如下:
-
-```
-for (int i = 0; i < s.size(); i++)
-```
-
-接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 经行比较。
-
-如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
-
-代码如下:
-
-```
-while(j >= 0 && s[i] != t[j + 1]) {
- j = next[j];
-}
-```
-
-如果 s[i] 与 t[j + 1] 相同,那么i 和 j 同时向后移动, 代码如下:
-
-```
-if (s[i] == t[j + 1]) {
- j++; // i的增加在for循环里
-}
-```
-
-如何判断在文本串s里出现了模式串t呢,如果j指向了模式串t的末尾,那么就说明模式串t完全匹配文本串s里的某个子串了。
-
-本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
-
-代码如下:
-
-```
-if (j == (t.size() - 1) ) {
- return (i - t.size() + 1);
-}
-```
-
-那么使用next数组,用模式串匹配文本串的整体代码如下:
-
-```
-int j = -1; // 因为next数组里记录的起始位置为-1
-for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
- while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - t.size() + 1);
- }
-}
-```
-
-此时所有逻辑的代码都已经写出来了,本题整体代码如下:
-
-# 前缀表统一减一 C++代码实现
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = -1; // // 因为next数组里记录的起始位置为-1
- for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
- while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-
-```
-
-# 前缀表(不减一)C++实现
-
-那么前缀表就不减一了,也不右移的,到底行不行呢?行!
-
-我之前说过,这仅仅是KMP算法实现上的问题,如果就直接使用前缀表可以换一种回退方式,找j=next[j-1] 来进行回退。
-
-主要就是j=next[x]这一步最为关键!
-
-我给出的getNext的实现为:(前缀表统一减一)
-
-```
-void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-
-```
-此时如果输入的模式串为aabaaf,对应的next为-1 0 -1 0 1 -1。
-
-这里j和next[0]初始化为-1,整个next数组是以 前缀表减一之后的效果来构建的。
-
-那么前缀表不减一来构建next数组,代码如下:
-
-```
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) { // j要保证大于0,因为下面有取j-1作为数组下表的操作
- j = next[j - 1]; // 注意这里,是要找前一位的对应的回退位置了
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
-
-```
-
-此时如果输入的模式串为aabaaf,对应的next为 0 1 0 1 2 0,(其实这就是前缀表的数值了)。
-
-那么用这样的next数组也可以用来做匹配,代码要有所改动。
-
-实现代码如下:
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) {
- j = next[j - 1];
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = 0;
- for (int i = 0; i < haystack.size(); i++) {
- while(j > 0 && haystack[i] != needle[j]) {
- j = next[j - 1];
- }
- if (haystack[i] == needle[j]) {
- j++;
- }
- if (j == needle.size() ) {
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-```
-
-# 总结
-
-我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
-
-接着从给出的模式串中,我们一步一步的推导出了前缀表,得出前缀表无论是统一减一还是不同意减一得到的next数组仅仅是kmp的实现方式的不同。
-
-其中还分析了KMP算法的时间复杂度,并且和暴力方法做了对比。
-
-然后先用前缀表统一减一得到的next数组,求得文本串s里是否出现过模式串t,并给出了具体分析代码。
-
-又给出了直接用前缀表作为next数组,来做匹配的实现代码。
-
-可以说把KMP的每一个细微的细节都扣了出来,毫无遮掩的展示给大家了!
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0031.下一个排列.md b/problems/0031.下一个排列.md
deleted file mode 100644
index 68665d6b..00000000
--- a/problems/0031.下一个排列.md
+++ /dev/null
@@ -1,58 +0,0 @@
-
-## 思路
-
-一些同学可能手动写排列的顺序,都没有写对,那么写程序的话思路一定是有问题的了,我这里以1234为例子,把全排列都列出来。可以参考一下规律所在:
-
-```
-1 2 3 4
-1 2 4 3
-1 3 2 4
-1 3 4 2
-1 4 2 3
-1 4 3 2
-2 1 3 4
-2 1 4 3
-2 3 1 4
-2 3 4 1
-2 4 1 3
-2 4 3 1
-3 1 2 4
-3 1 4 2
-3 2 1 4
-3 2 4 1
-3 4 1 2
-3 4 2 1
-4 1 2 3
-4 1 3 2
-4 2 1 3
-4 2 3 1
-4 3 1 2
-4 3 2 1
-```
-
-如图:
-
-以求1243为例,流程如图:
-
-
-
-
-得到了next数组之后,就要用这个来做匹配了。
-
-# 使用next数组来做匹配
-
-在文本串s里 找是否出现过模式串t。
-
-定义两个下表j 指向模式串起始位置,i指向文本串起始位置。
-
-那么j初始值依然为-1,为什么呢? **依然因为next数组里记录的起始位置为-1。**
-
-i就从0开始,遍历文本串,代码如下:
-
-```
-for (int i = 0; i < s.size(); i++)
-```
-
-接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 经行比较。
-
-如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
-
-代码如下:
-
-```
-while(j >= 0 && s[i] != t[j + 1]) {
- j = next[j];
-}
-```
-
-如果 s[i] 与 t[j + 1] 相同,那么i 和 j 同时向后移动, 代码如下:
-
-```
-if (s[i] == t[j + 1]) {
- j++; // i的增加在for循环里
-}
-```
-
-如何判断在文本串s里出现了模式串t呢,如果j指向了模式串t的末尾,那么就说明模式串t完全匹配文本串s里的某个子串了。
-
-本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
-
-代码如下:
-
-```
-if (j == (t.size() - 1) ) {
- return (i - t.size() + 1);
-}
-```
-
-那么使用next数组,用模式串匹配文本串的整体代码如下:
-
-```
-int j = -1; // 因为next数组里记录的起始位置为-1
-for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
- while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - t.size() + 1);
- }
-}
-```
-
-此时所有逻辑的代码都已经写出来了,本题整体代码如下:
-
-# 前缀表统一减一 C++代码实现
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = -1; // // 因为next数组里记录的起始位置为-1
- for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
- while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
- j = next[j]; // j 寻找之前匹配的位置
- }
- if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
- j++; // i的增加在for循环里
- }
- if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-
-```
-
-# 前缀表(不减一)C++实现
-
-那么前缀表就不减一了,也不右移的,到底行不行呢?行!
-
-我之前说过,这仅仅是KMP算法实现上的问题,如果就直接使用前缀表可以换一种回退方式,找j=next[j-1] 来进行回退。
-
-主要就是j=next[x]这一步最为关键!
-
-我给出的getNext的实现为:(前缀表统一减一)
-
-```
-void getNext(int* next, const string& s) {
- int j = -1;
- next[0] = j;
- for(int i = 1; i < s.size(); i++) { // 注意i从1开始
- while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
- j = next[j]; // 向前回溯
- }
- if (s[i] == s[j + 1]) { // 找到相同的前后缀
- j++;
- }
- next[i] = j; // 将j(前缀的长度)赋给next[i]
- }
-}
-
-```
-此时如果输入的模式串为aabaaf,对应的next为-1 0 -1 0 1 -1。
-
-这里j和next[0]初始化为-1,整个next数组是以 前缀表减一之后的效果来构建的。
-
-那么前缀表不减一来构建next数组,代码如下:
-
-```
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) { // j要保证大于0,因为下面有取j-1作为数组下表的操作
- j = next[j - 1]; // 注意这里,是要找前一位的对应的回退位置了
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
-
-```
-
-此时如果输入的模式串为aabaaf,对应的next为 0 1 0 1 2 0,(其实这就是前缀表的数值了)。
-
-那么用这样的next数组也可以用来做匹配,代码要有所改动。
-
-实现代码如下:
-
-```
-class Solution {
-public:
- void getNext(int* next, const string& s) {
- int j = 0;
- next[0] = 0;
- for(int i = 1; i < s.size(); i++) {
- while (j > 0 && s[i] != s[j]) {
- j = next[j - 1];
- }
- if (s[i] == s[j]) {
- j++;
- }
- next[i] = j;
- }
- }
- int strStr(string haystack, string needle) {
- if (needle.size() == 0) {
- return 0;
- }
- int next[needle.size()];
- getNext(next, needle);
- int j = 0;
- for (int i = 0; i < haystack.size(); i++) {
- while(j > 0 && haystack[i] != needle[j]) {
- j = next[j - 1];
- }
- if (haystack[i] == needle[j]) {
- j++;
- }
- if (j == needle.size() ) {
- return (i - needle.size() + 1);
- }
- }
- return -1;
- }
-};
-```
-
-# 总结
-
-我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
-
-接着从给出的模式串中,我们一步一步的推导出了前缀表,得出前缀表无论是统一减一还是不同意减一得到的next数组仅仅是kmp的实现方式的不同。
-
-其中还分析了KMP算法的时间复杂度,并且和暴力方法做了对比。
-
-然后先用前缀表统一减一得到的next数组,求得文本串s里是否出现过模式串t,并给出了具体分析代码。
-
-又给出了直接用前缀表作为next数组,来做匹配的实现代码。
-
-可以说把KMP的每一个细微的细节都扣了出来,毫无遮掩的展示给大家了!
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
-
diff --git a/problems/0031.下一个排列.md b/problems/0031.下一个排列.md
deleted file mode 100644
index 68665d6b..00000000
--- a/problems/0031.下一个排列.md
+++ /dev/null
@@ -1,58 +0,0 @@
-
-## 思路
-
-一些同学可能手动写排列的顺序,都没有写对,那么写程序的话思路一定是有问题的了,我这里以1234为例子,把全排列都列出来。可以参考一下规律所在:
-
-```
-1 2 3 4
-1 2 4 3
-1 3 2 4
-1 3 4 2
-1 4 2 3
-1 4 3 2
-2 1 3 4
-2 1 4 3
-2 3 1 4
-2 3 4 1
-2 4 1 3
-2 4 3 1
-3 1 2 4
-3 1 4 2
-3 2 1 4
-3 2 4 1
-3 4 1 2
-3 4 2 1
-4 1 2 3
-4 1 3 2
-4 2 1 3
-4 2 3 1
-4 3 1 2
-4 3 2 1
-```
-
-如图:
-
-以求1243为例,流程如图:
-
- -
-对应的C++代码如下:
-
-```
-class Solution {
-public:
- void nextPermutation(vector
-
-对应的C++代码如下:
-
-```
-class Solution {
-public:
- void nextPermutation(vector -
- -
- -
-
-
- -
-一些同学在实现暴力解法的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
-
-我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
-
-首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
-
-可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
-
-这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
-
-
-
-一些同学在实现暴力解法的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
-
-我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
-
-首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
-
-可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
-
-这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
-
- -
-列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
-
-列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
-
-列4 柱子的高度为1(以下用height表示)
-
-那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
-
-列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
-
-此时求出了列4的雨水体积。
-
-一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
-
-首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
-```
-for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-}
-```
-
-在for循环中求左右两边最高柱子,代码如下:
-
-```
-int rHeight = height[i]; // 记录右边柱子的最高高度
-int lHeight = height[i]; // 记录左边柱子的最高高度
-for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
-}
-for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
-}
-```
-
-最后,计算该列的雨水高度,代码如下:
-
-```
-int h = min(lHeight, rHeight) - height[i];
-if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
-```
-
-整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector
-
-列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
-
-列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
-
-列4 柱子的高度为1(以下用height表示)
-
-那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
-
-列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
-
-此时求出了列4的雨水体积。
-
-一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
-
-首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
-```
-for (int i = 0; i < height.size(); i++) {
- // 第一个柱子和最后一个柱子不接雨水
- if (i == 0 || i == height.size() - 1) continue;
-}
-```
-
-在for循环中求左右两边最高柱子,代码如下:
-
-```
-int rHeight = height[i]; // 记录右边柱子的最高高度
-int lHeight = height[i]; // 记录左边柱子的最高高度
-for (int r = i + 1; r < height.size(); r++) {
- if (height[r] > rHeight) rHeight = height[r];
-}
-for (int l = i - 1; l >= 0; l--) {
- if (height[l] > lHeight) lHeight = height[l];
-}
-```
-
-最后,计算该列的雨水高度,代码如下:
-
-```
-int h = min(lHeight, rHeight) - height[i];
-if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
-```
-
-整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector -
-知道这一点,后面的就可以理解了。
-
-2. 使用单调栈内元素的顺序
-
-从大到小还是从小打到呢?
-
-要从栈底到栈头(元素从栈头弹出)是从大到小的顺序。
-
-因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
-
-如图:
-
-
-
-知道这一点,后面的就可以理解了。
-
-2. 使用单调栈内元素的顺序
-
-从大到小还是从小打到呢?
-
-要从栈底到栈头(元素从栈头弹出)是从大到小的顺序。
-
-因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
-
-如图:
-
- -
-
-3. 遇到相同高度的柱子怎么办。
-
-遇到相同的元素,更新栈内下表,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
-
-例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
-
-因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-如图所示:
-
-
-
-
-
-3. 遇到相同高度的柱子怎么办。
-
-遇到相同的元素,更新栈内下表,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
-
-例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
-
-因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
-
-如图所示:
-
-
- -
-
-4. 栈里要保存什么数值
-
-是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
-
-长就是通过柱子的高度来计算,宽是通过柱子之间的下表来计算,
-
-那么栈里有没有必要存一个pair
-
-
-4. 栈里要保存什么数值
-
-是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
-
-长就是通过柱子的高度来计算,宽是通过柱子之间的下表来计算,
-
-那么栈里有没有必要存一个pair -
-取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下表记为mid,对应的高度为height[mid](就是图中的高度1)。
-
-栈顶元素st.top(),就是凹槽的左边位置,下表为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
-
-当前遍历的元素i,就是凹槽右边的位置,下表为i,对应的高度为height[i](就是图中的高度3)。
-
-那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
-
-雨水的宽度是 凹槽右边的下表 - 凹槽左边的下表 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
-
-当前凹槽雨水的体积就是:`h * w`。
-
-求当前凹槽雨水的体积代码如下:
-
-```
-while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
-}
-```
-
-关键部分讲完了,整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector
-
-取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下表记为mid,对应的高度为height[mid](就是图中的高度1)。
-
-栈顶元素st.top(),就是凹槽的左边位置,下表为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
-
-当前遍历的元素i,就是凹槽右边的位置,下表为i,对应的高度为height[i](就是图中的高度3)。
-
-那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
-
-雨水的宽度是 凹槽右边的下表 - 凹槽左边的下表 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
-
-当前凹槽雨水的体积就是:`h * w`。
-
-求当前凹槽雨水的体积代码如下:
-
-```
-while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
- int mid = st.top();
- st.pop();
- if (!st.empty()) {
- int h = min(height[st.top()], height[i]) - height[mid];
- int w = i - st.top() - 1; // 注意减一,只求中间宽度
- sum += h * w;
- }
-}
-```
-
-关键部分讲完了,整体代码如下:
-
-```
-class Solution {
-public:
- int trap(vector -
-红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
-
-那么不难写出如下C++代码(关键地方已经注释)
-
-```
-class Solution {
-public:
- int maxSubArray(vector
-
-红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
-
-那么不难写出如下C++代码(关键地方已经注释)
-
-```
-class Solution {
-public:
- int maxSubArray(vector -
-对于这种情况,只要是intervals[index]起始位置 <= newInterval终止位置,就要一直合并下去。
-
-代码如下:
-
-```
-while (index < intervals.size() && intervals[index][0] <= newInterval[1]) { // 注意防止越界
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
-}
-```
-合并之后,将newInterval放入result就可以了
-
-2. intervals[index]不用合并,插入区间直接插入就行,如图:
-
-
-
-对于这种情况,只要是intervals[index]起始位置 <= newInterval终止位置,就要一直合并下去。
-
-代码如下:
-
-```
-while (index < intervals.size() && intervals[index][0] <= newInterval[1]) { // 注意防止越界
- newInterval[0] = min(intervals[index][0], newInterval[0]);
- newInterval[1] = max(intervals[index][1], newInterval[1]);
- index++;
-}
-```
-合并之后,将newInterval放入result就可以了
-
-2. intervals[index]不用合并,插入区间直接插入就行,如图:
-
- -
-对于这种情况,就直接把newInterval放入result就可以了
-
-## 步骤三:处理合并区间之后的区间
-
-合并之后,就应该把合并之后的区间,以此加入result中。
-
-代码如下:
-
-```
-while (index < intervals.size()) {
- result.push_back(intervals[index++]);
-}
-```
-
-# 整体C++代码
-
-```
-class Solution {
-public:
- vector
-
-对于这种情况,就直接把newInterval放入result就可以了
-
-## 步骤三:处理合并区间之后的区间
-
-合并之后,就应该把合并之后的区间,以此加入result中。
-
-代码如下:
-
-```
-while (index < intervals.size()) {
- result.push_back(intervals[index++]);
-}
-```
-
-# 整体C++代码
-
-```
-class Solution {
-public:
- vector -
- -
- -
-图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
-
-**所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
-
-**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
-
-注意代码中i,就是for循环里选择的起始位置。
-```
-for (int i = startIndex; i <= n; i++) {
-```
-
-接下来看一下优化过程如下:
-
-1. 已经选择的元素个数:path.size();
-
-2. 还需要的元素个数为: k - path.size();
-
-3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
-
-为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
-
-举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
-
-从2开始搜索都是合理的,可以是组合[2, 3, 4]。
-
-这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
-
-所以优化之后的for循环是:
-
-```
-for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
-```
-
-优化后整体代码如下:
-
-```
-class Solution {
-private:
- vector
-
-图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
-
-**所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
-
-**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
-
-注意代码中i,就是for循环里选择的起始位置。
-```
-for (int i = startIndex; i <= n; i++) {
-```
-
-接下来看一下优化过程如下:
-
-1. 已经选择的元素个数:path.size();
-
-2. 还需要的元素个数为: k - path.size();
-
-3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
-
-为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
-
-举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
-
-从2开始搜索都是合理的,可以是组合[2, 3, 4]。
-
-这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
-
-所以优化之后的for循环是:
-
-```
-for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
-```
-
-优化后整体代码如下:
-
-```
-class Solution {
-private:
- vector -
-# 思路
-
-要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
-
-有了这个特性,**验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。**
-
-## 递归法
-
-可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
-
-```
-vector
-
-# 思路
-
-要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
-
-有了这个特性,**验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。**
-
-## 递归法
-
-可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
-
-```
-vector -
-# 思路
-
-在[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)中,我们讲到对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-理解这一本质之后,就会发现,求二叉树是否对称,和求二叉树是否相同几乎是同一道题目。
-
-**如果没有读过[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)这一篇,请认真读完再做这道题,就会有感觉了。**
-
-递归三部曲中:
-
-1. 确定递归函数的参数和返回值
-
-我们要比较的是两个树是否是相互相同的,参数也就是两个树的根节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* tree1, TreeNode* tree2)
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)。
-
-2. 确定终止条件
-
-**要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。**
-
-节点为空的情况有:
-
-* tree1为空,tree2不为空,不对称,return false
-* tree1不为空,tree2为空,不对称 return false
-* tree1,tree2都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是tree1和tree2不为空的时候:
-
-* tree1、tree2都不为空,比较节点数值,不相同就return false
-
-此时tree1、tree2节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (tree1 == NULL && tree2 != NULL) return false;
-else if (tree1 != NULL && tree2 == NULL) return false;
-else if (tree1 == NULL && tree2 == NULL) return true;
-else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
-
-3. 确定单层递归的逻辑
-
-* 比较二叉树是否相同 :传入的是tree1的左孩子,tree2的右孩子。
-* 如果左右都相同就返回true ,有一侧不相同就返回false 。
-
-代码如下:
-
-```
-bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
-bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
-bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* tree1, TreeNode* tree2) {
- if (tree1 == NULL && tree2 != NULL) return false;
- else if (tree1 != NULL && tree2 == NULL) return false;
- else if (tree1 == NULL && tree2 == NULL) return true;
- else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
- bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
- bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
- return isSame;
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-
-## 递归
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->left) && compare(left->right, right->right);
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-## 迭代法
-
-```
-lass Solution {
-public:
-
- bool isSameTree(TreeNode* p, TreeNode* q) {
- if (p == NULL && q == NULL) return true;
- if (p == NULL || q == NULL) return false;
- queue
-
-# 思路
-
-在[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)中,我们讲到对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-理解这一本质之后,就会发现,求二叉树是否对称,和求二叉树是否相同几乎是同一道题目。
-
-**如果没有读过[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)这一篇,请认真读完再做这道题,就会有感觉了。**
-
-递归三部曲中:
-
-1. 确定递归函数的参数和返回值
-
-我们要比较的是两个树是否是相互相同的,参数也就是两个树的根节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* tree1, TreeNode* tree2)
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)。
-
-2. 确定终止条件
-
-**要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。**
-
-节点为空的情况有:
-
-* tree1为空,tree2不为空,不对称,return false
-* tree1不为空,tree2为空,不对称 return false
-* tree1,tree2都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是tree1和tree2不为空的时候:
-
-* tree1、tree2都不为空,比较节点数值,不相同就return false
-
-此时tree1、tree2节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (tree1 == NULL && tree2 != NULL) return false;
-else if (tree1 != NULL && tree2 == NULL) return false;
-else if (tree1 == NULL && tree2 == NULL) return true;
-else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-```
-
-分析过程同[二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
-
-3. 确定单层递归的逻辑
-
-* 比较二叉树是否相同 :传入的是tree1的左孩子,tree2的右孩子。
-* 如果左右都相同就返回true ,有一侧不相同就返回false 。
-
-代码如下:
-
-```
-bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
-bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
-bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* tree1, TreeNode* tree2) {
- if (tree1 == NULL && tree2 != NULL) return false;
- else if (tree1 != NULL && tree2 == NULL) return false;
- else if (tree1 == NULL && tree2 == NULL) return true;
- else if (tree1->val != tree2->val) return false; // 注意这里我没有使用else
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool left = compare(tree1->left, tree2->left); // 左子树:左、 右子树:左
- bool right = compare(tree1->right, tree2->right); // 左子树:右、 右子树:右
- bool isSame = left && right; // 左子树:中、 右子树:中(逻辑处理)
- return isSame;
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-
-## 递归
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->left) && compare(left->right, right->right);
-
- }
- bool isSameTree(TreeNode* p, TreeNode* q) {
- return compare(p, q);
- }
-};
-```
-
-## 迭代法
-
-```
-lass Solution {
-public:
-
- bool isSameTree(TreeNode* p, TreeNode* q) {
- if (p == NULL && q == NULL) return true;
- if (p == NULL || q == NULL) return false;
- queue -
-# 思路
-
-**首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!**
-
-对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-那么如果比较呢?
-
-比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
-
-
-
-# 思路
-
-**首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!**
-
-对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
-
-那么如果比较呢?
-
-比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
-
- -
-那么遍历的顺序应该是什么样的呢?
-
-本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
-
-**正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。**
-
-但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
-
-其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
-
-说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
-
-那么我们先来看看递归法的代码应该怎么写。
-
-## 递归法
-
-### 递归三部曲
-
-1. 确定递归函数的参数和返回值
-
-因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* left, TreeNode* right)
-```
-
-2. 确定终止条件
-
-要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
-
-节点为空的情况有:(**注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点**)
-
-* 左节点为空,右节点不为空,不对称,return false
-* 左不为空,右为空,不对称 return false
-* 左右都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
-
-* 左右都不为空,比较节点数值,不相同就return false
-
-此时左右节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (left == NULL && right != NULL) return false;
-else if (left != NULL && right == NULL) return false;
-else if (left == NULL && right == NULL) return true;
-else if (left->val != right->val) return false; // 注意这里我没有使用else
-```
-
-注意上面最后一种情况,我没有使用else,而是elseif, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
-
-3. 确定单层递归的逻辑
-
-此时才进入单层递归的逻辑,单层递归的逻辑就是处理 右节点都不为空,且数值相同的情况。
-
-
-* 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
-* 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
-* 如果左右都对称就返回true ,有一侧不对称就返回false 。
-
-代码如下:
-
-```
-bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
-bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
-bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-
-如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
-
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- // 首先排除空节点的情况
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- // 排除了空节点,再排除数值不相同的情况
- else if (left->val != right->val) return false;
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
- bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
- bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
- return isSame;
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->right) && compare(left->right, right->left);
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。**
-
-**所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把道题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。**
-
-## 迭代法
-
-这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
-
-这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(**注意这不是层序遍历**)
-
-### 使用队列
-
-通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
-
-
-
-那么遍历的顺序应该是什么样的呢?
-
-本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
-
-**正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。**
-
-但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
-
-其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
-
-说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
-
-那么我们先来看看递归法的代码应该怎么写。
-
-## 递归法
-
-### 递归三部曲
-
-1. 确定递归函数的参数和返回值
-
-因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
-
-返回值自然是bool类型。
-
-代码如下:
-```
-bool compare(TreeNode* left, TreeNode* right)
-```
-
-2. 确定终止条件
-
-要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
-
-节点为空的情况有:(**注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点**)
-
-* 左节点为空,右节点不为空,不对称,return false
-* 左不为空,右为空,不对称 return false
-* 左右都为空,对称,返回true
-
-此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
-
-* 左右都不为空,比较节点数值,不相同就return false
-
-此时左右节点不为空,且数值也不相同的情况我们也处理了。
-
-代码如下:
-```
-if (left == NULL && right != NULL) return false;
-else if (left != NULL && right == NULL) return false;
-else if (left == NULL && right == NULL) return true;
-else if (left->val != right->val) return false; // 注意这里我没有使用else
-```
-
-注意上面最后一种情况,我没有使用else,而是elseif, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
-
-3. 确定单层递归的逻辑
-
-此时才进入单层递归的逻辑,单层递归的逻辑就是处理 右节点都不为空,且数值相同的情况。
-
-
-* 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
-* 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
-* 如果左右都对称就返回true ,有一侧不对称就返回false 。
-
-代码如下:
-
-```
-bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
-bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
-bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
-return isSame;
-```
-
-如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
-
-最后递归的C++整体代码如下:
-
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- // 首先排除空节点的情况
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- // 排除了空节点,再排除数值不相同的情况
- else if (left->val != right->val) return false;
-
- // 此时就是:左右节点都不为空,且数值相同的情况
- // 此时才做递归,做下一层的判断
- bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
- bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
- bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
- return isSame;
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。**
-
-如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
-
-**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**
-
-当然我可以把如上代码整理如下:
-```
-class Solution {
-public:
- bool compare(TreeNode* left, TreeNode* right) {
- if (left == NULL && right != NULL) return false;
- else if (left != NULL && right == NULL) return false;
- else if (left == NULL && right == NULL) return true;
- else if (left->val != right->val) return false;
- else return compare(left->left, right->right) && compare(left->right, right->left);
-
- }
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- return compare(root->left, root->right);
- }
-};
-```
-
-**这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。**
-
-**所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把道题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。**
-
-## 迭代法
-
-这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
-
-这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(**注意这不是层序遍历**)
-
-### 使用队列
-
-通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
-
- -
-
-如下的条件判断和递归的逻辑是一样的。
-
-代码如下:
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- queue
-
-
-如下的条件判断和递归的逻辑是一样的。
-
-代码如下:
-
-```
-class Solution {
-public:
- bool isSymmetric(TreeNode* root) {
- if (root == NULL) return true;
- queue -
-## 思路
-
-我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
-
-* [二叉树:前中后序递归法](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)
-* [二叉树:前中后序迭代法](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)
-* [二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
-
-层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
-
-需要借用一个辅助数据结构即队列来实现,**队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
-
-**而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。**
-
-使用队列实现二叉树广度优先遍历,动画如下:
-
-
-
-
-这样就实现了层序从左到右遍历二叉树。
-
-代码如下:**这份代码也可以作为二叉树层序遍历的模板,以后再打七个就靠它了**。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-## 思路
-
-我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
-
-* [二叉树:前中后序递归法](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)
-* [二叉树:前中后序迭代法](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)
-* [二叉树:前中后序迭代方式统一写法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-
-接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
-
-层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
-
-需要借用一个辅助数据结构即队列来实现,**队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
-
-**而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。**
-
-使用队列实现二叉树广度优先遍历,动画如下:
-
-
-
-
-这样就实现了层序从左到右遍历二叉树。
-
-代码如下:**这份代码也可以作为二叉树层序遍历的模板,以后再打七个就靠它了**。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-## 思路
-
-相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-## 思路
-
-相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-## 思路
-
-层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-## 思路
-
-层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-## 思路
-
-本题就是层序遍历的时候把一层求个总和在取一个均值。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-## 思路
-
-本题就是层序遍历的时候把一层求个总和在取一个均值。
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-返回其层序遍历:
-
-[
- [1],
- [3,2,4],
- [5,6]
-]
-
-
-## 思路
-
-这道题依旧是模板题,只不过一个节点有多个孩子了
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-返回其层序遍历:
-
-[
- [1],
- [3,2,4],
- [5,6]
-]
-
-
-## 思路
-
-这道题依旧是模板题,只不过一个节点有多个孩子了
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-## 思路
-
-层序遍历,取每一层的最大值
-
-## C++代码
-
-```
-class Solution {
-public:
- vector
-
-## 思路
-
-层序遍历,取每一层的最大值
-
-## C++代码
-
-```
-class Solution {
-public:
- vector -
-## 思路
-
-本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue
-
-## 思路
-
-本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
-
-## C++代码
-
-```
-class Solution {
-public:
- Node* connect(Node* root) {
- queue -
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
deleted file mode 100644
index 3aa5c4b6..00000000
--- a/problems/0104.二叉树的最大深度.md
+++ /dev/null
@@ -1,226 +0,0 @@
-(寻找更节点可以用unordered_map来优化一下,元素都是独一无二的)
-
-## 题目地址
-https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
-
-> “简单题”系列
-
-看完本篇可以一起做了如下两道题目:
-* 104.二叉树的最大深度
-* 559.N叉树的最大深度
-
-# 104.二叉树的最大深度
-
-给定一个二叉树,找出其最大深度。
-
-二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
-
-说明: 叶子节点是指没有子节点的节点。
-
-示例:
-给定二叉树 [3,9,20,null,null,15,7],
-
-
-
-
-
-> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
deleted file mode 100644
index 3aa5c4b6..00000000
--- a/problems/0104.二叉树的最大深度.md
+++ /dev/null
@@ -1,226 +0,0 @@
-(寻找更节点可以用unordered_map来优化一下,元素都是独一无二的)
-
-## 题目地址
-https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
-
-> “简单题”系列
-
-看完本篇可以一起做了如下两道题目:
-* 104.二叉树的最大深度
-* 559.N叉树的最大深度
-
-# 104.二叉树的最大深度
-
-给定一个二叉树,找出其最大深度。
-
-二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
-
-说明: 叶子节点是指没有子节点的节点。
-
-示例:
-给定二叉树 [3,9,20,null,null,15,7],
-
- -
-返回它的最大深度 3 。
-
-# 思路
-
-## 递归法
-
-本题其实也要后序遍历(左右中),依然是因为要通过递归函数的返回值做计算树的高度。
-
-按照递归三部曲,来看看如何来写。
-
-1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
-
-代码如下:
-```
-int getDepth(TreeNode* node)
-```
-
-2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
-
-代码如下:
-```
-if (node == NULL) return 0;
-```
-
-3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
-
-代码如下:
-
-```
-int leftDepth = getDepth(node->left); // 左
-int rightDepth = getDepth(node->right); // 右
-int depth = 1 + max(leftDepth, rightDepth); // 中
-return depth;
-```
-
-所以整体C++代码如下:
-
-```
-class Solution {
-public:
- int getDepth(TreeNode* node) {
- if (node == NULL) return 0;
- int leftDepth = getDepth(node->left); // 左
- int rightDepth = getDepth(node->right); // 右
- int depth = 1 + max(leftDepth, rightDepth); // 中
- return depth;
- }
- int maxDepth(TreeNode* root) {
- return getDepth(root);
- }
-};
-```
-
-代码精简之后C++代码如下:
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- return 1 + max(maxDepth(root->left), maxDepth(root->right));
- }
-};
-
-```
-
-**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
-
-
-## 迭代法
-
-使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
-
-在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
-
-
-
-所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
-
-如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
-
-C++代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- int depth = 0;
- queue
-
-返回它的最大深度 3 。
-
-# 思路
-
-## 递归法
-
-本题其实也要后序遍历(左右中),依然是因为要通过递归函数的返回值做计算树的高度。
-
-按照递归三部曲,来看看如何来写。
-
-1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
-
-代码如下:
-```
-int getDepth(TreeNode* node)
-```
-
-2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
-
-代码如下:
-```
-if (node == NULL) return 0;
-```
-
-3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
-
-代码如下:
-
-```
-int leftDepth = getDepth(node->left); // 左
-int rightDepth = getDepth(node->right); // 右
-int depth = 1 + max(leftDepth, rightDepth); // 中
-return depth;
-```
-
-所以整体C++代码如下:
-
-```
-class Solution {
-public:
- int getDepth(TreeNode* node) {
- if (node == NULL) return 0;
- int leftDepth = getDepth(node->left); // 左
- int rightDepth = getDepth(node->right); // 右
- int depth = 1 + max(leftDepth, rightDepth); // 中
- return depth;
- }
- int maxDepth(TreeNode* root) {
- return getDepth(root);
- }
-};
-```
-
-代码精简之后C++代码如下:
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- return 1 + max(maxDepth(root->left), maxDepth(root->right));
- }
-};
-
-```
-
-**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
-
-
-## 迭代法
-
-使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
-
-在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
-
-
-
-所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
-
-如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
-
-C++代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(TreeNode* root) {
- if (root == NULL) return 0;
- int depth = 0;
- queue -
-我们应返回其最大深度,3。
-
-# 思路
-
-依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
-
-## 递归法
-
-C++代码:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- if (root == 0) return 0;
- int depth = 0;
- for (int i = 0; i < root->children.size(); i++) {
- depth = max (depth, maxDepth(root->children[i]));
- }
- return depth + 1;
- }
-};
-```
-## 迭代法
-
-依然是层序遍历,代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- queue
-
-我们应返回其最大深度,3。
-
-# 思路
-
-依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
-
-## 递归法
-
-C++代码:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- if (root == 0) return 0;
- int depth = 0;
- for (int i = 0; i < root->children.size(); i++) {
- depth = max (depth, maxDepth(root->children[i]));
- }
- return depth + 1;
- }
-};
-```
-## 迭代法
-
-依然是层序遍历,代码如下:
-
-```
-class Solution {
-public:
- int maxDepth(Node* root) {
- queue -
-## 思路
-
-首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
-
-如果让我们肉眼看两个序列,画一颗二叉树的话,应该分分钟都可以画出来。
-
-流程如图:
-
-
-
-## 思路
-
-首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
-
-如果让我们肉眼看两个序列,画一颗二叉树的话,应该分分钟都可以画出来。
-
-流程如图:
-
- -
-那么代码应该怎么写呢?
-
-说到一层一层切割,就应该想到了递归。
-
-来看一下一共分几步:
-
-* 第一步:如果数组大小为零的话,说明是空节点了。
-
-* 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
-* 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
-* 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
-* 第五步:切割后序数组,切成后序左数组和后序右数组
-
-* 第六步:递归处理左区间和右区间
-
-不难写出如下代码:(先把框架写出来)
-
-```
- TreeNode* traversal (vector
-
-那么代码应该怎么写呢?
-
-说到一层一层切割,就应该想到了递归。
-
-来看一下一共分几步:
-
-* 第一步:如果数组大小为零的话,说明是空节点了。
-
-* 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
-* 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
-* 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
-* 第五步:切割后序数组,切成后序左数组和后序右数组
-
-* 第六步:递归处理左区间和右区间
-
-不难写出如下代码:(先把框架写出来)
-
-```
- TreeNode* traversal (vector




