From a38ee5f525af998683a2d0fb38f6c6cac1312f5d Mon Sep 17 00:00:00 2001
From: Frankheartusf <104822497+Frankheartusf@users.noreply.github.com>
Date: Tue, 3 May 2022 17:31:37 +0800
Subject: [PATCH] Add files via upload
---
0045.跳跃游戏II.md | 287 +++++++++++++++++++++++++++++++++++++++++
1 file changed, 287 insertions(+)
create mode 100644 0045.跳跃游戏II.md
diff --git a/0045.跳跃游戏II.md b/0045.跳跃游戏II.md
new file mode 100644
index 00000000..c0d3c3e5
--- /dev/null
+++ b/0045.跳跃游戏II.md
@@ -0,0 +1,287 @@
+
+
+  +
+
+
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+
+
+> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
+
+# 45.跳跃游戏II
+
+[力扣题目链接](https://leetcode-cn.com/problems/jump-game-ii/)
+
+给定一个非负整数数组,你最初位于数组的第一个位置。
+
+数组中的每个元素代表你在该位置可以跳跃的最大长度。
+
+你的目标是使用最少的跳跃次数到达数组的最后一个位置。
+
+示例:
+* 输入: [2,3,1,1,4]
+* 输出: 2
+* 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
+
+说明:
+假设你总是可以到达数组的最后一个位置。
+
+
+## 思路
+
+本题相对于[55.跳跃游戏](https://programmercarl.com/0055.跳跃游戏.html)还是难了不少。
+
+但思路是相似的,还是要看最大覆盖范围。
+
+本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
+
+贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
+
+思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
+
+**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
+
+**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
+
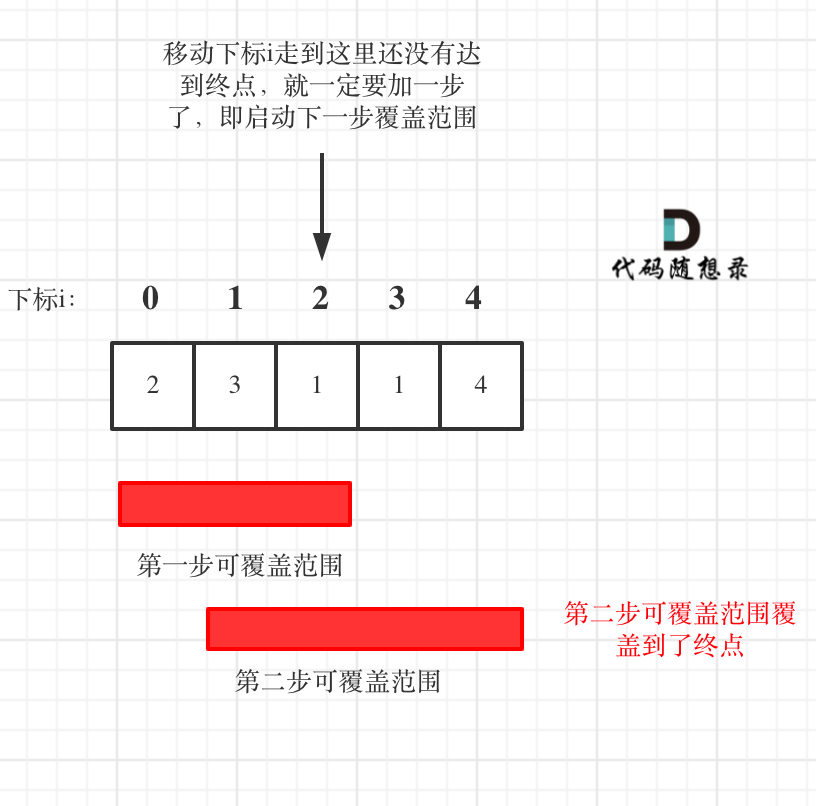
+如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
+
+如图:
+
+
+
+**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
+
+## 方法一
+
+从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
+
+这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
+
+* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
+* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
+
+C++代码如下:(详细注释)
+
+```CPP
+// 版本一
+class Solution {
+public:
+ int jump(vector& nums) {
+ if (nums.size() == 1) return 0;
+ int curDistance = 0; // 当前覆盖最远距离下标
+ int ans = 0; // 记录走的最大步数
+ int nextDistance = 0; // 下一步覆盖最远距离下标
+ for (int i = 0; i < nums.size(); i++) {
+ nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
+ if (i == curDistance) { // 遇到当前覆盖最远距离下标
+ if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
+ ans++; // 需要走下一步
+ curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
+ if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
+ } else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
+ }
+ }
+ return ans;
+ }
+};
+```
+
+## 方法二
+
+依然是贪心,思路和方法一差不多,代码可以简洁一些。
+
+**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
+
+想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
+
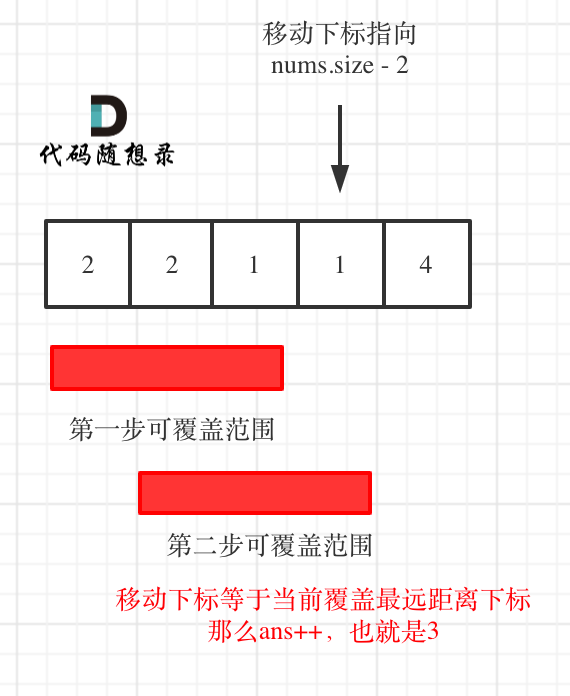
+因为当移动下标指向nums.size - 2时:
+
+* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
+
+
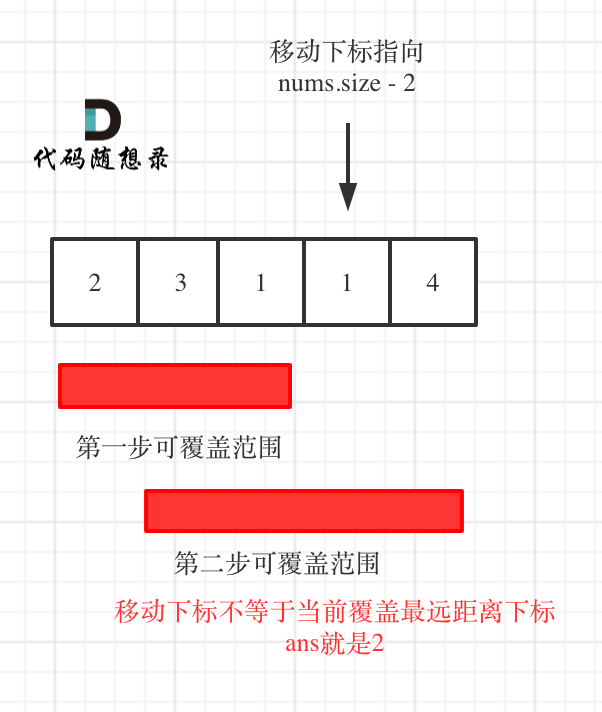
+* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
+
+
+
+代码如下:
+
+```CPP
+// 版本二
+class Solution {
+public:
+ int jump(vector& nums) {
+ int curDistance = 0; // 当前覆盖的最远距离下标
+ int ans = 0; // 记录走的最大步数
+ int nextDistance = 0; // 下一步覆盖的最远距离下标
+ for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
+ nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
+ if (i == curDistance) { // 遇到当前覆盖的最远距离下标
+ curDistance = nextDistance; // 更新当前覆盖的最远距离下标
+ ans++;
+ }
+ }
+ return ans;
+ }
+};
+```
+
+可以看出版本二的代码相对于版本一简化了不少!
+
+其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
+
+## 总结
+
+相信大家可以发现,这道题目相当于[55.跳跃游戏](https://programmercarl.com/0055.跳跃游戏.html)难了不止一点。
+
+但代码又十分简单,贪心就是这么巧妙。
+
+理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
+
+
+## 其他语言版本
+
+
+### Java
+```Java
+// 版本一
+class Solution {
+ public int jump(int[] nums) {
+ if (nums == null || nums.length == 0 || nums.length == 1) {
+ return 0;
+ }
+ //记录跳跃的次数
+ int count=0;
+ //当前的覆盖最大区域
+ int curDistance = 0;
+ //最大的覆盖区域
+ int maxDistance = 0;
+ for (int i = 0; i < nums.length; i++) {
+ //在可覆盖区域内更新最大的覆盖区域
+ maxDistance = Math.max(maxDistance,i+nums[i]);
+ //说明当前一步,再跳一步就到达了末尾
+ if (maxDistance>=nums.length-1){
+ count++;
+ break;
+ }
+ //走到当前覆盖的最大区域时,更新下一步可达的最大区域
+ if (i==curDistance){
+ curDistance = maxDistance;
+ count++;
+ }
+ }
+ return count;
+ }
+}
+```
+
+```java
+// 版本二
+class Solution {
+ public int jump(int[] nums) {
+ int result = 0;
+ // 当前覆盖的最远距离下标
+ int end = 0;
+ // 下一步覆盖的最远距离下标
+ int temp = 0;
+ for (int i = 0; i <= end && end < nums.length - 1; ++i) {
+ temp = Math.max(temp, i + nums[i]);
+ // 可达位置的改变次数就是跳跃次数
+ if (i == end) {
+ end = temp;
+ result++;
+ }
+ }
+ return result;
+ }
+}
+```
+
+### Python
+
+```python
+class Solution:
+ def jump(self, nums: List[int]) -> int:
+ if len(nums) == 1: return 0
+ ans = 0
+ curDistance = 0
+ nextDistance = 0
+ for i in range(len(nums)):
+ nextDistance = max(i + nums[i], nextDistance)
+ if i == curDistance:
+ if curDistance != len(nums) - 1:
+ ans += 1
+ curDistance = nextDistance
+ if nextDistance >= len(nums) - 1: break
+ return ans
+```
+
+### Go
+```Go
+func jump(nums []int) int {
+ dp := make([]int, len(nums))
+ dp[0] = 0//初始第一格跳跃数一定为0
+
+ for i := 1; i < len(nums); i++ {
+ dp[i] = i
+ for j := 0; j < i; j++ {
+ if nums[j] + j >= i {//nums[j]为起点,j为往右跳的覆盖范围,这行表示从j能跳到i
+ dp[i] = min(dp[j] + 1, dp[i])//更新最小能到i的跳跃次数
+ }
+ }
+ }
+ return dp[len(nums)-1]
+}
+
+func min(a, b int) int {
+ if a < b {
+ return a
+ } else {
+ return b
+ }
+}
+```
+
+### Javascript
+```Javascript
+var jump = function(nums) {
+ let curIndex = 0
+ let nextIndex = 0
+ let steps = 0
+ for(let i = 0; i < nums.length - 1; i++) {
+ nextIndex = Math.max(nums[i] + i, nextIndex)
+ if(i === curIndex) {
+ curIndex = nextIndex
+ steps++
+ }
+ }
+
+ return steps
+};
+```
+
+### TypeScript
+
+```typescript
+function jump(nums: number[]): number {
+ const length: number = nums.length;
+ let curFarthestIndex: number = 0,
+ nextFarthestIndex: number = 0;
+ let curIndex: number = 0;
+ let stepNum: number = 0;
+ while (curIndex < length - 1) {
+ nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
+ if (curIndex === curFarthestIndex) {
+ curFarthestIndex = nextFarthestIndex;
+ stepNum++;
+ }
+ curIndex++;
+ }
+ return stepNum;
+};
+```
+
+
+
+
+
+-----------------------
+
 +
+
+
+ +
+
+
+