mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
Merge pull request #1790 from juguagua/leetcode-modify-the-code-of-the-BinaryTree
更新完善二叉树部分:从二叉树最大深度至二叉树所有路径
This commit is contained in:
@ -59,7 +59,7 @@ int getdepth(treenode* node)
|
||||
if (node == NULL) return 0;
|
||||
```
|
||||
|
||||
3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
|
||||
3. 确定单层递归的逻辑:先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -591,15 +591,15 @@ var maxdepth = function(root) {
|
||||
var maxdepth = function(root) {
|
||||
//使用递归的方法 递归三部曲
|
||||
//1. 确定递归函数的参数和返回值
|
||||
const getdepth=function(node){
|
||||
const getdepth = function(node) {
|
||||
//2. 确定终止条件
|
||||
if(node===null){
|
||||
if(node === null) {
|
||||
return 0;
|
||||
}
|
||||
//3. 确定单层逻辑
|
||||
let leftdepth=getdepth(node.left);
|
||||
let rightdepth=getdepth(node.right);
|
||||
let depth=1+Math.max(leftdepth,rightdepth);
|
||||
let leftdepth = getdepth(node.left);
|
||||
let rightdepth = getdepth(node.right);
|
||||
let depth = 1 + Math.max(leftdepth, rightdepth);
|
||||
return depth;
|
||||
}
|
||||
return getdepth(root);
|
||||
|
||||
@ -158,7 +158,7 @@ if (node == NULL) {
|
||||
|
||||
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
|
||||
|
||||
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是二叉平衡树了。
|
||||
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -342,7 +342,7 @@ public:
|
||||
|
||||
**例如:都知道回溯法其实就是递归,但是很少人用迭代的方式去实现回溯算法!**
|
||||
|
||||
因为对于回溯算法已经是非常复杂的递归了,如果在用迭代的话,就是自己给自己找麻烦,效率也并不一定高。
|
||||
因为对于回溯算法已经是非常复杂的递归了,如果再用迭代的话,就是自己给自己找麻烦,效率也并不一定高。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -559,37 +559,32 @@ class Solution:
|
||||
### Go
|
||||
```Go
|
||||
func isBalanced(root *TreeNode) bool {
|
||||
if root==nil{
|
||||
return true
|
||||
}
|
||||
if !isBalanced(root.Left) || !isBalanced(root.Right){
|
||||
return false
|
||||
}
|
||||
LeftH:=maxdepth(root.Left)+1
|
||||
RightH:=maxdepth(root.Right)+1
|
||||
if abs(LeftH-RightH)>1{
|
||||
h := getHeight(root)
|
||||
if h == -1 {
|
||||
return false
|
||||
}
|
||||
return true
|
||||
}
|
||||
func maxdepth(root *TreeNode)int{
|
||||
if root==nil{
|
||||
// 返回以该节点为根节点的二叉树的高度,如果不是平衡二叉树了则返回-1
|
||||
func getHeight(root *TreeNode) int {
|
||||
if root == nil {
|
||||
return 0
|
||||
}
|
||||
return max(maxdepth(root.Left),maxdepth(root.Right))+1
|
||||
l, r := getHeight(root.Left), getHeight(root.Right)
|
||||
if l == -1 || r == -1 {
|
||||
return -1
|
||||
}
|
||||
if l - r > 1 || r - l > 1 {
|
||||
return -1
|
||||
}
|
||||
return max(l, r) + 1
|
||||
}
|
||||
func max(a,b int)int{
|
||||
if a>b{
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
func abs(a int)int{
|
||||
if a<0{
|
||||
return -a
|
||||
}
|
||||
return a
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
@ -39,7 +39,7 @@
|
||||
* 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
|
||||
* 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
|
||||
|
||||
那么使用后序遍历,其实求的是根节点到叶子节点的最小距离,就是求高度的过程,这不过这个最小距离 也同样是最小深度。
|
||||
那么使用后序遍历,其实求的是根节点到叶子节点的最小距离,就是求高度的过程,不过这个最小距离 也同样是最小深度。
|
||||
|
||||
以下讲解中遍历顺序上依然采用后序遍历(因为要比较递归返回之后的结果,本文我也给出前序遍历的写法)。
|
||||
|
||||
@ -199,7 +199,7 @@ public:
|
||||
|
||||
如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://programmercarl.com/0102.二叉树的层序遍历.html)
|
||||
|
||||
**需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点**
|
||||
**需要注意的是,只有当左右孩子都为空的时候,才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点**
|
||||
|
||||
代码如下:(详细注释)
|
||||
|
||||
|
||||
@ -63,7 +63,7 @@ int getNodesNum(TreeNode* cur) {
|
||||
if (cur == NULL) return 0;
|
||||
```
|
||||
|
||||
3. 确定单层递归的逻辑:先求它的左子树的节点数量,再求的右子树的节点数量,最后取总和再加一 (加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
|
||||
3. 确定单层递归的逻辑:先求它的左子树的节点数量,再求右子树的节点数量,最后取总和再加一 (加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -168,7 +168,7 @@ public:
|
||||
|
||||
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
|
||||
|
||||
这里关键在于如果去判断一个左子树或者右子树是不是满二叉树呢?
|
||||
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢?
|
||||
|
||||
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
|
||||
|
||||
@ -178,13 +178,13 @@ public:
|
||||
|
||||
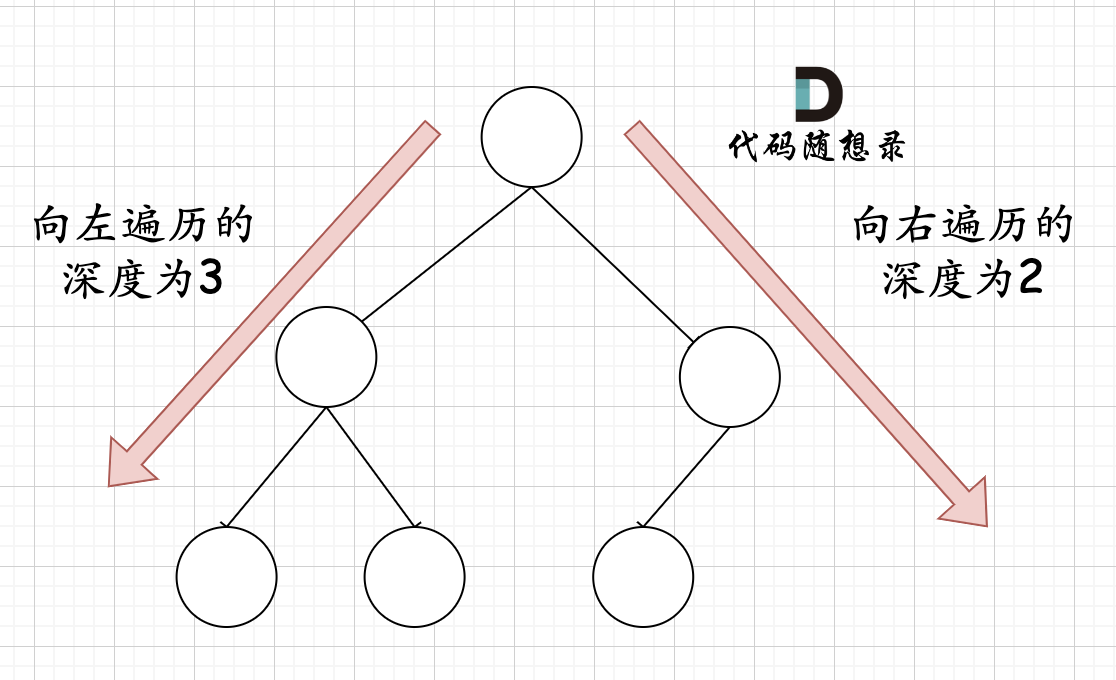
|
||||
|
||||
哪有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
|
||||
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
|
||||
|
||||
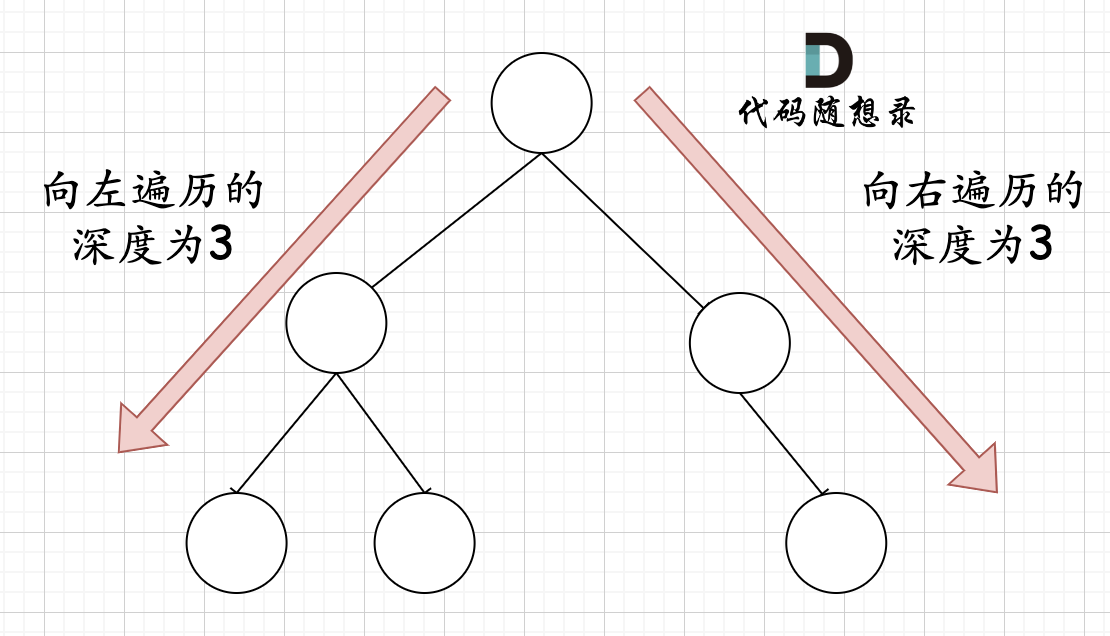
|
||||
|
||||
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
|
||||
|
||||
判断其子树岂不是满二叉树,如果是则利用用公式计算这个子树(满二叉树)的节点数量,如果不是则继续递归,那么 在递归三部曲中,第二部:终止条件的写法应该是这样的:
|
||||
判断其子树是不是满二叉树,如果是则利用公式计算这个子树(满二叉树)的节点数量,如果不是则继续递归,那么 在递归三部曲中,第二部:终止条件的写法应该是这样的:
|
||||
|
||||
```CPP
|
||||
if (root == nullptr) return 0;
|
||||
@ -292,26 +292,22 @@ class Solution {
|
||||
* 满二叉树的结点数为:2^depth - 1
|
||||
*/
|
||||
public int countNodes(TreeNode root) {
|
||||
if(root == null) {
|
||||
return 0;
|
||||
if (root == null) return 0;
|
||||
TreeNode left = root.left;
|
||||
TreeNode right = root.right;
|
||||
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
|
||||
while (left != null) { // 求左子树深度
|
||||
left = left.left;
|
||||
leftDepth++;
|
||||
}
|
||||
int leftDepth = getDepth(root.left);
|
||||
int rightDepth = getDepth(root.right);
|
||||
if (leftDepth == rightDepth) {// 左子树是满二叉树
|
||||
// 2^leftDepth其实是 (2^leftDepth - 1) + 1 ,左子树 + 根结点
|
||||
return (1 << leftDepth) + countNodes(root.right);
|
||||
} else {// 右子树是满二叉树
|
||||
return (1 << rightDepth) + countNodes(root.left);
|
||||
while (right != null) { // 求右子树深度
|
||||
right = right.right;
|
||||
rightDepth++;
|
||||
}
|
||||
}
|
||||
|
||||
private int getDepth(TreeNode root) {
|
||||
int depth = 0;
|
||||
while (root != null) {
|
||||
root = root.left;
|
||||
depth++;
|
||||
if (leftDepth == rightDepth) {
|
||||
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
|
||||
}
|
||||
return depth;
|
||||
return countNodes(root.left) + countNodes(root.right) + 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -397,7 +393,7 @@ class Solution:
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
//本题直接就是求有多少个节点,无脑存进数组算长度就行了。
|
||||
//本题直接就是求有多少个节点,无脑存进结果变量就行了。
|
||||
func countNodes(root *TreeNode) int {
|
||||
if root == nil {
|
||||
return 0
|
||||
@ -473,15 +469,15 @@ func countNodes(root *TreeNode) int {
|
||||
var countNodes = function(root) {
|
||||
//递归法计算二叉树节点数
|
||||
// 1. 确定递归函数参数
|
||||
const getNodeSum=function(node){
|
||||
const getNodeSum = function(node) {
|
||||
//2. 确定终止条件
|
||||
if(node===null){
|
||||
if(node === null) {
|
||||
return 0;
|
||||
}
|
||||
//3. 确定单层递归逻辑
|
||||
let leftNum=getNodeSum(node.left);
|
||||
let rightNum=getNodeSum(node.right);
|
||||
return leftNum+rightNum+1;
|
||||
let leftNum = getNodeSum(node.left);
|
||||
let rightNum = getNodeSum(node.right);
|
||||
return leftNum + rightNum + 1;
|
||||
}
|
||||
return getNodeSum(root);
|
||||
};
|
||||
@ -491,19 +487,19 @@ var countNodes = function(root) {
|
||||
```javascript
|
||||
var countNodes = function(root) {
|
||||
//层序遍历
|
||||
let queue=[];
|
||||
if(root===null){
|
||||
let queue = [];
|
||||
if(root === null) {
|
||||
return 0;
|
||||
}
|
||||
queue.push(root);
|
||||
let nodeNums=0;
|
||||
while(queue.length){
|
||||
let length=queue.length;
|
||||
while(length--){
|
||||
let node=queue.shift();
|
||||
let nodeNums = 0;
|
||||
while(queue.length) {
|
||||
let length = queue.length;
|
||||
while(length--) {
|
||||
let node = queue.shift();
|
||||
nodeNums++;
|
||||
node.left&&queue.push(node.left);
|
||||
node.right&&queue.push(node.right);
|
||||
node.left && queue.push(node.left);
|
||||
node.right && queue.push(node.right);
|
||||
}
|
||||
}
|
||||
return nodeNums;
|
||||
@ -514,24 +510,24 @@ var countNodes = function(root) {
|
||||
```javascript
|
||||
var countNodes = function(root) {
|
||||
//利用完全二叉树的特点
|
||||
if(root===null){
|
||||
if(root === null) {
|
||||
return 0;
|
||||
}
|
||||
let left=root.left;
|
||||
let right=root.right;
|
||||
let leftDepth=0,rightDepth=0;
|
||||
while(left){
|
||||
left=left.left;
|
||||
let left = root.left;
|
||||
let right = root.right;
|
||||
let leftDepth = 0, rightDepth = 0;
|
||||
while(left) {
|
||||
left = left.left;
|
||||
leftDepth++;
|
||||
}
|
||||
while(right){
|
||||
right=right.right;
|
||||
while(right) {
|
||||
right = right.right;
|
||||
rightDepth++;
|
||||
}
|
||||
if(leftDepth==rightDepth){
|
||||
return Math.pow(2,leftDepth+1)-1;
|
||||
if(leftDepth == rightDepth) {
|
||||
return Math.pow(2, leftDepth+1) - 1;
|
||||
}
|
||||
return countNodes(root.left)+countNodes(root.right)+1;
|
||||
return countNodes(root.left) + countNodes(root.right) + 1;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
@ -24,7 +24,7 @@
|
||||
|
||||
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
|
||||
|
||||
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一一个路径在进入另一个路径。
|
||||
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
|
||||
|
||||
前序遍历以及回溯的过程如图:
|
||||
|
||||
@ -44,7 +44,7 @@ void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
|
||||
|
||||
2. 确定递归终止条件
|
||||
|
||||
再写递归的时候都习惯了这么写:
|
||||
在写递归的时候都习惯了这么写:
|
||||
|
||||
```
|
||||
if (cur == NULL) {
|
||||
@ -67,7 +67,7 @@ if (cur->left == NULL && cur->right == NULL) {
|
||||
|
||||
再来看一下终止处理的逻辑。
|
||||
|
||||
这里使用vector<int> 结构path来记录路径,所以要把vector<int> 结构的path转为string格式,在把这个string 放进 result里。
|
||||
这里使用vector<int> 结构path来记录路径,所以要把vector<int> 结构的path转为string格式,再把这个string 放进 result里。
|
||||
|
||||
**那么为什么使用了vector<int> 结构来记录路径呢?** 因为在下面处理单层递归逻辑的时候,要做回溯,使用vector方便来做回溯。
|
||||
|
||||
@ -123,7 +123,7 @@ if (cur->right) {
|
||||
path.pop_back();
|
||||
```
|
||||
|
||||
这个回溯就要很大的问题,我们知道,**回溯和递归是一一对应的,有一个递归,就要有一个回溯**,这么写的话相当于把递归和回溯拆开了, 一个在花括号里,一个在花括号外。
|
||||
这个回溯就有很大的问题,我们知道,**回溯和递归是一一对应的,有一个递归,就要有一个回溯**,这么写的话相当于把递归和回溯拆开了, 一个在花括号里,一个在花括号外。
|
||||
|
||||
**所以回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!**
|
||||
|
||||
@ -300,16 +300,16 @@ public:
|
||||
|
||||
```
|
||||
|
||||
**大家应该可以感受出来,如果把 `path + "->"`作为函数参数就是可以的,因为并有没有改变path的数值,执行完递归函数之后,path依然是之前的数值(相当于回溯了)**
|
||||
**大家应该可以感受出来,如果把 `path + "->"`作为函数参数就是可以的,因为并没有改变path的数值,执行完递归函数之后,path依然是之前的数值(相当于回溯了)**
|
||||
|
||||
|
||||
**综合以上,第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里,第一种递归写法虽然代码多一些,但是把每一个逻辑处理都完整的展现了出来了。**
|
||||
**综合以上,第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里,第一种递归写法虽然代码多一些,但是把每一个逻辑处理都完整的展现出来了。**
|
||||
|
||||
## 拓展
|
||||
|
||||
这里讲解本题解的写法逻辑以及一些更具体的细节,下面的讲解中,涉及到C++语法特性,如果不是C++的录友,就可以不看了,避免越看越晕。
|
||||
|
||||
如果是C++的录友,建议本题独立刷过两遍,在看下面的讲解,同样避免越看越晕,造成不必要的负担。
|
||||
如果是C++的录友,建议本题独立刷过两遍,再看下面的讲解,同样避免越看越晕,造成不必要的负担。
|
||||
|
||||
在第二版本的代码中,其实仅仅是回溯了 `->` 部分(调用两次pop_back,一个pop`>` 一次pop`-`),大家应该疑惑那么 `path += to_string(cur->val);` 这一步为什么没有回溯呢? 一条路径能持续加节点 不做回溯吗?
|
||||
|
||||
@ -378,7 +378,7 @@ public:
|
||||
|
||||
最后我依然给出了迭代法。
|
||||
|
||||
对于本地充分了解递归与回溯的过程之后,有精力的同学可以在去实现迭代法。
|
||||
对于本题充分了解递归与回溯的过程之后,有精力的同学可以再去实现迭代法。
|
||||
|
||||
|
||||
|
||||
@ -386,7 +386,7 @@ public:
|
||||
|
||||
# 其他语言版本
|
||||
|
||||
Java:
|
||||
## Java:
|
||||
|
||||
```Java
|
||||
//解法一
|
||||
@ -466,7 +466,7 @@ class Solution {
|
||||
}
|
||||
```
|
||||
---
|
||||
Python:
|
||||
## Python:
|
||||
递归法+隐形回溯
|
||||
```Python3
|
||||
# Definition for a binary tree node.
|
||||
@ -529,7 +529,7 @@ class Solution:
|
||||
|
||||
---
|
||||
|
||||
Go:
|
||||
## Go:
|
||||
|
||||
递归法:
|
||||
|
||||
@ -591,28 +591,28 @@ func binaryTreePaths(root *TreeNode) []string {
|
||||
```
|
||||
|
||||
---
|
||||
JavaScript:
|
||||
## JavaScript:
|
||||
|
||||
递归法:
|
||||
|
||||
```javascript
|
||||
var binaryTreePaths = function(root) {
|
||||
//递归遍历+递归三部曲
|
||||
let res=[];
|
||||
let res = [];
|
||||
//1. 确定递归函数 函数参数
|
||||
const getPath=function(node,curPath){
|
||||
const getPath = function(node,curPath) {
|
||||
//2. 确定终止条件,到叶子节点就终止
|
||||
if(node.left===null&&node.right===null){
|
||||
curPath+=node.val;
|
||||
if(node.left === null && node.right === null) {
|
||||
curPath += node.val;
|
||||
res.push(curPath);
|
||||
return ;
|
||||
return;
|
||||
}
|
||||
//3. 确定单层递归逻辑
|
||||
curPath+=node.val+'->';
|
||||
node.left&&getPath(node.left,curPath);
|
||||
node.right&&getPath(node.right,curPath);
|
||||
curPath += node.val + '->';
|
||||
node.left && getPath(node.left, curPath);
|
||||
node.right && getPath(node.right, curPath);
|
||||
}
|
||||
getPath(root,'');
|
||||
getPath(root, '');
|
||||
return res;
|
||||
};
|
||||
```
|
||||
@ -644,7 +644,7 @@ var binaryTreePaths = function(root) {
|
||||
};
|
||||
```
|
||||
|
||||
TypeScript:
|
||||
## TypeScript:
|
||||
|
||||
> 递归法
|
||||
|
||||
@ -698,7 +698,7 @@ function binaryTreePaths(root: TreeNode | null): string[] {
|
||||
};
|
||||
```
|
||||
|
||||
Swift:
|
||||
## Swift:
|
||||
|
||||
> 递归/回溯
|
||||
```swift
|
||||
@ -765,7 +765,7 @@ func binaryTreePaths(_ root: TreeNode?) -> [String] {
|
||||
}
|
||||
```
|
||||
|
||||
Scala:
|
||||
## Scala:
|
||||
|
||||
递归:
|
||||
```scala
|
||||
|
||||
Reference in New Issue
Block a user