mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
图论更新
This commit is contained in:
@ -1,7 +1,7 @@
|
||||
|
||||
# dijkstra(堆优化版)精讲
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1047)
|
||||
[卡码网:47. 参加科学大会](https://kamacoder.com/problempage.php?pid=1047)
|
||||
|
||||
【题目描述】
|
||||
|
||||
@ -66,7 +66,7 @@
|
||||
|
||||
如果n很大的话,我们可以换一个角度来优先性能。
|
||||
|
||||
在 讲解 最小生成树的时候,我们 讲了两个算法,[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w)(从点的角度来求最小生成树)、[Kruskal算法](https://mp.weixin.qq.com/s/rUVaBjCES_4eSjngceT5bw)(从边的角度来求最小生成树)
|
||||
在 讲解 最小生成树的时候,我们 讲了两个算法,[prim算法](./0053.寻宝-prim.md)(从点的角度来求最小生成树)、[Kruskal算法](./0053.寻宝-Kruskal.md)(从边的角度来求最小生成树)
|
||||
|
||||
这么在n 很大的时候,也有另一个思考维度,即:从边的数量出发。
|
||||
|
||||
@ -649,3 +649,29 @@ int main() {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
|
||||
# dijkstra(朴素版)精讲
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1047)
|
||||
[卡码网:47. 参加科学大会](https://kamacoder.com/problempage.php?pid=1047)
|
||||
|
||||
【题目描述】
|
||||
|
||||
@ -80,7 +80,7 @@ dijkstra算法:在有权图(权值非负数)中求从起点到其他节点
|
||||
|
||||
最短路径的权值为12。
|
||||
|
||||
其实 dijkstra 算法 和 我们之前讲解的prim算法思路非常接近,如果大家认真学过[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w),那么理解 Dijkstra 算法会相对容易很多。(这也是我要先讲prim再讲dijkstra的原因)
|
||||
其实 dijkstra 算法 和 我们之前讲解的prim算法思路非常接近,如果大家认真学过[prim算法](./0053.寻宝-prim.md),那么理解 Dijkstra 算法会相对容易很多。(这也是我要先讲prim再讲dijkstra的原因)
|
||||
|
||||
dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
|
||||
|
||||
@ -92,7 +92,7 @@ dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没
|
||||
|
||||
大家此时已经会发现,这和prim算法 怎么这么像呢。
|
||||
|
||||
我在[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w)讲解中也给出了三部曲。 prim 和 dijkstra 确实很像,思路也是类似的,这一点我在后面还会详细来讲。
|
||||
我在[prim算法](./0053.寻宝-prim.md)讲解中也给出了三部曲。 prim 和 dijkstra 确实很像,思路也是类似的,这一点我在后面还会详细来讲。
|
||||
|
||||
在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
|
||||
|
||||
@ -462,7 +462,7 @@ select:7
|
||||
|
||||
如果题目要求把最短路的路径打印出来,应该怎么办呢?
|
||||
|
||||
这里还是有一些“坑”的,本题打印路径和 prim 打印路径是一样的,我在 [prim算法精讲](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w) 【拓展】中 已经详细讲解了。
|
||||
这里还是有一些“坑”的,本题打印路径和 prim 打印路径是一样的,我在 [prim算法精讲](./0053.寻宝-prim.md) 【拓展】中 已经详细讲解了。
|
||||
|
||||
在这里就不再赘述。
|
||||
|
||||
@ -660,7 +660,7 @@ int main() {
|
||||
|
||||
## dijkstra与prim算法的区别
|
||||
|
||||
> 这里再次提示,需要先看我的 [prim算法精讲](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w) ,否则可能不知道我下面讲的是什么。
|
||||
> 这里再次提示,需要先看我的 [prim算法精讲](./0053.寻宝-prim.md) ,否则可能不知道我下面讲的是什么。
|
||||
|
||||
大家可以发现 dijkstra的代码看上去 怎么和 prim算法这么像呢。
|
||||
|
||||
@ -731,3 +731,29 @@ for (int v = 1; v <= n; v++) {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -130,7 +130,7 @@ kruscal的思路:
|
||||
|
||||
**但在代码中,如果将两个节点加入同一个集合,又如何判断两个节点是否在同一个集合呢**?
|
||||
|
||||
这里就涉及到我们之前讲解的[并查集](https://www.programmercarl.com/%E5%9B%BE%E8%AE%BA%E5%B9%B6%E6%9F%A5%E9%9B%86%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html)。
|
||||
这里就涉及到我们之前讲解的[并查集](./图论并查集理论基础.md)。
|
||||
|
||||
我们在并查集开篇的时候就讲了,并查集主要就两个功能:
|
||||
|
||||
@ -139,7 +139,7 @@ kruscal的思路:
|
||||
|
||||
大家发现这正好符合 Kruskal算法的需求,这也是为什么 **我要先讲并查集,再讲 Kruskal**。
|
||||
|
||||
关于 并查集,我已经在[并查集精讲](https://www.programmercarl.com/%E5%9B%BE%E8%AE%BA%E5%B9%B6%E6%9F%A5%E9%9B%86%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html) 详细讲解过了,所以这里不再赘述,我们直接用。
|
||||
关于 并查集,我已经在[并查集精讲](./图论并查集理论基础.md) 详细讲解过了,所以这里不再赘述,我们直接用。
|
||||
|
||||
本题代码如下,已经详细注释:
|
||||
|
||||
@ -374,7 +374,7 @@ Kruskal 与 prim 的关键区别在于,prim维护的是节点的集合,而 K
|
||||
|
||||
在节点数量固定的情况下,图中的边越少,Kruskal 需要遍历的边也就越少。
|
||||
|
||||
而 prim 算法是对节点进行操作的,节点数量越少,prim算法效率就越少。
|
||||
而 prim 算法是对节点进行操作的,节点数量越少,prim算法效率就越优。
|
||||
|
||||
所以在 稀疏图中,用Kruskal更优。 在稠密图中,用prim算法更优。
|
||||
|
||||
@ -398,3 +398,29 @@ Kruskal算法 时间复杂度 为 nlogn,其中n 为边的数量,适用稀疏
|
||||
录友们可以细细体会。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -507,10 +507,36 @@ int main() {
|
||||
|
||||
最后我们拓展了如何求职 最小生成树 的每一条边,其实 添加的代码很简单,主要是理解 为什么使用 parent数组 来记录边 以及 在哪里 更新parent数组。
|
||||
|
||||
同时,因为使用一维数组,数组的下标和数组 如何赋值很重要,不要搞反,导师结果被覆盖。
|
||||
同时,因为使用一维数组,数组的下标和数组 如何赋值很重要,不要搞反,导致结果被覆盖。
|
||||
|
||||
好了,以上为总结,录友们学习愉快。
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -347,6 +347,32 @@ SPFA(队列优化版Bellman_ford) 在理论上 时间复杂度更胜一筹
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -387,3 +387,29 @@ Bellman_ford 是可以计算 负权值的单源最短路算法。
|
||||
|
||||
弄清楚 什么是 松弛? 为什么要 n-1 次? 对理解Bellman_ford 非常重要。
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -238,3 +238,30 @@ int main() {
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -630,3 +630,30 @@ dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非
|
||||
* 能否用dijkstra
|
||||
|
||||
学透了以上四个拓展,相信大家会对bellman_ford有更深入的理解。
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -418,6 +418,29 @@ floyd算法的时间复杂度相对较高,适合 稠密图且源点较多的
|
||||
如果 源点少,其实可以 多次dijsktra 求源点到终点。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -3,8 +3,6 @@
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1170)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0797.%E6%89%80%E6%9C%89%E5%8F%AF%E8%83%BD%E7%9A%84%E8%B7%AF%E5%BE%84.html#%E6%80%9D%E8%B7%AF)
|
||||
|
||||
【题目描述】
|
||||
|
||||
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
|
||||
@ -406,3 +404,36 @@ int main() {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -3,8 +3,6 @@
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1171)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0200.%E5%B2%9B%E5%B1%BF%E6%95%B0%E9%87%8F.%E5%B9%BF%E6%90%9C%E7%89%88.html)
|
||||
|
||||
题目描述:
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
|
||||
@ -185,3 +183,30 @@ int main() {
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -3,7 +3,6 @@
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1171)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0200.%E5%B2%9B%E5%B1%BF%E6%95%B0%E9%87%8F.%E6%B7%B1%E6%90%9C%E7%89%88.html)
|
||||
|
||||
题目描述:
|
||||
|
||||
@ -177,3 +176,30 @@ int main() {
|
||||
|
||||
本篇我只给出的dfs的写法,大家发现我写的还是比较细的,那么后面我再单独给出本题的bfs写法,虽然是模板题,但依然有很多注意的点,敬请期待!
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -3,8 +3,6 @@
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1172)
|
||||
|
||||
[力扣题目链接](https://programmercarl.com/0695.%E5%B2%9B%E5%B1%BF%E7%9A%84%E6%9C%80%E5%A4%A7%E9%9D%A2%E7%A7%AF.html#%E6%80%9D%E8%B7%AF)
|
||||
|
||||
题目描述
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
|
||||
@ -167,7 +165,7 @@ int main() {
|
||||
|
||||
### BFS
|
||||
|
||||
关于广度优先搜索,如果大家还不了解的话,看这里:[广度优先搜索精讲](https://programmercarl.com/kamacoder/图论广搜理论基础.html)
|
||||
关于广度优先搜索,如果大家还不了解的话,看这里:[广度优先搜索精讲](./图论广搜理论基础.md)
|
||||
|
||||
本题BFS代码如下:
|
||||
|
||||
@ -219,3 +217,30 @@ public:
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
|
||||
# 101. 孤岛的总面积
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1173)
|
||||
[卡码网:101. 孤岛的总面积](https://kamacoder.com/problempage.php?pid=1173)
|
||||
|
||||
题目描述
|
||||
|
||||
@ -60,7 +60,7 @@
|
||||
|
||||
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
|
||||
|
||||
如果对深搜或者广搜不够了解,建议先看这里:[深度优先搜索精讲](https://programmercarl.com/kamacoder/图论深搜理论基础.html),[广度优先搜索精讲](https://programmercarl.com/kamacoder/图论广搜理论基础.html)。
|
||||
如果对深搜或者广搜不够了解,建议先看这里:[深度优先搜索精讲](./图论深搜理论基础.md),[广度优先搜索精讲](./图论广搜理论基础.md)。
|
||||
|
||||
|
||||
采用深度优先搜索的代码如下:
|
||||
@ -178,3 +178,30 @@ int main() {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -131,3 +131,30 @@ int main() {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -276,4 +276,31 @@ for (int j = 0; j < m; j++) {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
|
||||
|
||||
@ -252,3 +252,30 @@ int main() {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -282,3 +282,30 @@ int main() {
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -152,3 +152,30 @@ int main() {
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -153,3 +153,30 @@ int main() {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -48,7 +48,7 @@
|
||||
|
||||
这里我依然降调一下,并查集可以解决什么问题:两个节点是否在一个集合,也可以将两个节点添加到一个集合中。
|
||||
|
||||
如果还不了解并查集,可以看这里:[并查集理论基础](https://programmercarl.com/图论并查集理论基础.html)
|
||||
如果还不了解并查集,可以看这里:[并查集理论基础](./图论并查集理论基础.md)
|
||||
|
||||
我们再来看一下这道题目。
|
||||
|
||||
@ -126,3 +126,30 @@ int main() {
|
||||
可以看出,主函数的代码很少,就判断一下边的两个节点在不在同一个集合就可以了。
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -238,3 +238,30 @@ int main() {
|
||||
getRemoveEdge(edges);
|
||||
}
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -147,3 +147,30 @@ int main() {
|
||||
|
||||
当然本题也可以用双向BFS,就是从头尾两端进行搜索,大家感兴趣,可以自己去实现,这里就不再做详细讲解了。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
|
||||
# 拓扑排序精讲
|
||||
|
||||
[卡码网:软件构建](https://kamacoder.com/problempage.php?pid=1191)
|
||||
[卡码网:117. 软件构建](https://kamacoder.com/problempage.php?pid=1191)
|
||||
|
||||
题目描述:
|
||||
|
||||
@ -128,7 +128,7 @@
|
||||
|
||||
## 模拟过程
|
||||
|
||||
用本题的示例来模拟一下这一过程:
|
||||
用本题的示例来模拟这一过程:
|
||||
|
||||
|
||||
1、找到入度为0 的节点,加入结果集
|
||||
@ -180,7 +180,9 @@
|
||||
这个图,我们只能将入度为0 的节点0 接入结果集。
|
||||
|
||||
之后,节点1、2、3、4 形成了环,找不到入度为0 的节点了,所以此时结果集里只有一个元素。
|
||||
|
||||
那么如果我们发现结果集元素个数 不等于 图中节点个数,我们就可以认定图中一定有 有向环!
|
||||
|
||||
这也是拓扑排序判断有向环的方法。
|
||||
|
||||
通过以上过程的模拟大家会发现这个拓扑排序好像不难,还有点简单。
|
||||
@ -296,42 +298,69 @@ using namespace std;
|
||||
int main() {
|
||||
int m, n, s, t;
|
||||
cin >> n >> m;
|
||||
vector<int> inDegree(n, 0); // 记录每个节点的入度
|
||||
vector<int> inDegree(n, 0); // 记录每个文件的入度
|
||||
|
||||
unordered_map<int, vector<int>> umap;// 记录节点依赖关系
|
||||
unordered_map<int, vector<int>> umap;// 记录文件依赖关系
|
||||
vector<int> result; // 记录结果
|
||||
|
||||
while (m--) {
|
||||
// s->t,先有s才能有t
|
||||
cin >> s >> t;
|
||||
inDegree[t]++; // t的入度加一
|
||||
umap[s].push_back(t); // 记录s指向哪些节点
|
||||
umap[s].push_back(t); // 记录s指向哪些文件
|
||||
}
|
||||
queue<int> que;
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 入度为0的节点,可以作为开头,先加入队列
|
||||
// 入度为0的文件,可以作为开头,先加入队列
|
||||
if (inDegree[i] == 0) que.push(i);
|
||||
//cout << inDegree[i] << endl;
|
||||
}
|
||||
// int count = 0;
|
||||
while (que.size()) {
|
||||
int cur = que.front(); // 当前选中的节点
|
||||
int cur = que.front(); // 当前选中的文件
|
||||
que.pop();
|
||||
//count++;
|
||||
result.push_back(cur);
|
||||
vector<int> files = umap[cur]; //获取该节点指向的节点
|
||||
if (files.size()) { // cur有后续节点
|
||||
vector<int> files = umap[cur]; //获取该文件指向的文件
|
||||
if (files.size()) { // cur有后续文件
|
||||
for (int i = 0; i < files.size(); i++) {
|
||||
inDegree[files[i]] --; // cur的指向的节点入度-1
|
||||
inDegree[files[i]] --; // cur的指向的文件入度-1
|
||||
if(inDegree[files[i]] == 0) que.push(files[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
// 判断是否有有向环
|
||||
if (result.size() == n) {
|
||||
// 注意输出格式,最后一个元素后面没有空格
|
||||
for (int i = 0; i < n - 2; i++) cout << result[i] << " ";
|
||||
for (int i = 0; i < n - 1; i++) cout << result[i] << " ";
|
||||
cout << result[n - 1];
|
||||
} else cout << -1 << endl;
|
||||
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
89
problems/kamacoder/0121.大数减法.md
Normal file
89
problems/kamacoder/0121.大数减法.md
Normal file
@ -0,0 +1,89 @@
|
||||
|
||||
# 大数减法
|
||||
|
||||
本题测试数据超过int 和 longlong了,所以考察的使用 string 来模拟 两个大数的 加减操作。
|
||||
|
||||
当然如果使用python或者Java 使用库函数都可以水过。
|
||||
|
||||
使用字符串来模拟过程,需要处理以下几个问题:
|
||||
|
||||
* 负号处理:要考虑正负数的处理,如果大数相减的结果是负数,需要在结果前加上负号。
|
||||
* 大数比较:在进行减法之前,需要确定哪个数大,以便知道结果是否需要添加负号。
|
||||
* 位数借位:处理大数相减时的借位问题,这类似于手动减法。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
#include <algorithm>
|
||||
using namespace std;
|
||||
|
||||
// 比较两个字符串表示的数字,返回1表示a > b,0表示a == b,-1表示a < b
|
||||
int compareStrings(const string& a, const string& b) {
|
||||
if (a.length() > b.length()) return 1;
|
||||
if (a.length() < b.length()) return -1;
|
||||
return a.compare(b);
|
||||
}
|
||||
|
||||
// 去除字符串左侧的前导零
|
||||
string removeLeadingZeros(const string& num) {
|
||||
size_t start = 0;
|
||||
while (start < num.size() && num[start] == '0') {
|
||||
start++;
|
||||
}
|
||||
return start == num.size() ? "0" : num.substr(start);
|
||||
}
|
||||
|
||||
// 大数相减,假设a >= b
|
||||
string subtractStrings(const string& a, const string& b) {
|
||||
string result;
|
||||
int len1 = a.length(), len2 = b.length();
|
||||
int carry = 0;
|
||||
|
||||
for (int i = 0; i < len1; i++) {
|
||||
int digitA = a[len1 - 1 - i] - '0';
|
||||
int digitB = i < len2 ? b[len2 - 1 - i] - '0' : 0;
|
||||
|
||||
int digit = digitA - digitB - carry;
|
||||
if (digit < 0) {
|
||||
digit += 10;
|
||||
carry = 1;
|
||||
} else {
|
||||
carry = 0;
|
||||
}
|
||||
|
||||
result.push_back(digit + '0');
|
||||
}
|
||||
|
||||
// 去除结果中的前导零
|
||||
reverse(result.begin(), result.end());
|
||||
return removeLeadingZeros(result);
|
||||
}
|
||||
|
||||
string subtractLargeNumbers(const string& num1, const string& num2) {
|
||||
string a = num1, b = num2;
|
||||
|
||||
// 比较两个数的大小
|
||||
int cmp = compareStrings(a, b);
|
||||
|
||||
if (cmp == 0) {
|
||||
return "0"; // 如果两个数相等,结果为0
|
||||
} else if (cmp < 0) {
|
||||
// 如果a < b,交换它们并在结果前加上负号
|
||||
swap(a, b);
|
||||
return "-" + subtractStrings(a, b);
|
||||
} else {
|
||||
return subtractStrings(a, b);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
string num1, num2;
|
||||
cin >> num1 >> num2;
|
||||
|
||||
string result = subtractLargeNumbers(num1, num2);
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
127
problems/kamacoder/0122.滑动窗口最大值.md
Normal file
127
problems/kamacoder/0122.滑动窗口最大值.md
Normal file
@ -0,0 +1,127 @@
|
||||
|
||||
# 滑动窗口最大值
|
||||
|
||||
本题是 [代码随想录:滑动窗口最大值](https://www.programmercarl.com/0239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.html) 的升级版。
|
||||
|
||||
在[代码随想录:滑动窗口最大值](https://www.programmercarl.com/0239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.html) 中详细讲解了如何求解 滑动窗口的最大值。
|
||||
|
||||
那么求滑动窗口的最小值原理也是一样的, 大家稍加思考,把优先级队列里的 大于 改成小于 就行了。
|
||||
|
||||
求最大值的优先级队列(从大到小)
|
||||
```
|
||||
while (!que.empty() && value > que.back()) {
|
||||
```
|
||||
|
||||
求最小值的优先级队列(从小到大)
|
||||
```
|
||||
while (!que.empty() && value > que.back()) {
|
||||
```
|
||||
|
||||
这样在滑动窗口里 最大值最小值都求出来了,遍历一遍找出 差值最大的就好。
|
||||
|
||||
至于输入,需要一波字符串处理,比较考察基本功。
|
||||
|
||||
CPP代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <sstream>
|
||||
#include <vector>
|
||||
#include <string>
|
||||
#include <deque>
|
||||
using namespace std;
|
||||
class MyBigQueue { //单调队列(从大到小)
|
||||
public:
|
||||
deque<int> que; // 使用deque来实现单调队列
|
||||
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
|
||||
// 同时pop之前判断队列当前是否为空。
|
||||
void pop(int value) {
|
||||
if (!que.empty() && value == que.front()) {
|
||||
que.pop_front();
|
||||
}
|
||||
}
|
||||
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
|
||||
// 这样就保持了队列里的数值是单调从大到小的了。
|
||||
void push(int value) {
|
||||
while (!que.empty() && value > que.back()) {
|
||||
que.pop_back();
|
||||
}
|
||||
que.push_back(value);
|
||||
|
||||
}
|
||||
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
|
||||
int front() {
|
||||
return que.front();
|
||||
}
|
||||
};
|
||||
|
||||
class MySmallQueue { //单调队列(从小到大)
|
||||
public:
|
||||
deque<int> que;
|
||||
|
||||
void pop(int value) {
|
||||
if (!que.empty() && value == que.front()) {
|
||||
que.pop_front();
|
||||
}
|
||||
}
|
||||
|
||||
// 和上面队列的区别是这里换成了小于,
|
||||
void push(int value) {
|
||||
while (!que.empty() && value < que.back()) {
|
||||
que.pop_back();
|
||||
}
|
||||
que.push_back(value);
|
||||
|
||||
}
|
||||
|
||||
int front() {
|
||||
return que.front();
|
||||
}
|
||||
};
|
||||
|
||||
int main() {
|
||||
string input;
|
||||
|
||||
getline(cin, input);
|
||||
|
||||
vector<int> nums;
|
||||
int k;
|
||||
|
||||
// 找到并截取nums的部分
|
||||
int numsStart = input.find('[');
|
||||
int numsEnd = input.find(']');
|
||||
string numsStr = input.substr(numsStart + 1, numsEnd - numsStart - 1);
|
||||
// cout << numsStr << endl;
|
||||
|
||||
// 用字符串流处理nums字符串,提取数字
|
||||
stringstream ss(numsStr);
|
||||
string temp;
|
||||
while (getline(ss, temp, ',')) {
|
||||
nums.push_back(stoi(temp));
|
||||
}
|
||||
|
||||
// 找到并提取k的值
|
||||
int kStart = input.find("k = ") + 4;
|
||||
k = stoi(input.substr(kStart));
|
||||
|
||||
MyBigQueue queB; // 获取区间最大值
|
||||
MySmallQueue queS; // 获取区间最小值
|
||||
// vector<int> result;
|
||||
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
|
||||
queB.push(nums[i]);
|
||||
queS.push(nums[i]);
|
||||
}
|
||||
|
||||
int result = queB.front() - queS.front();
|
||||
for (int i = k; i < nums.size(); i++) {
|
||||
queB.pop(nums[i - k]); // 滑动窗口移除最前面元素
|
||||
queB.push(nums[i]); // 滑动窗口前加入最后面的元素
|
||||
|
||||
queS.pop(nums[i - k]);
|
||||
queS.push(nums[i]);
|
||||
|
||||
result = max (result, queB.front() - queS.front());
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
52
problems/kamacoder/0123.小红的数组构造.md
Normal file
52
problems/kamacoder/0123.小红的数组构造.md
Normal file
@ -0,0 +1,52 @@
|
||||
|
||||
121. 小红的数组构造
|
||||
|
||||
本题大家不要想着真去模拟数组的情况,那样就想复杂了。
|
||||
|
||||
数组只能是:1k、2k、3k ... (n-1)k、nk,这样 总和就是最小的。
|
||||
|
||||
注意最后的和可能超过int,所以用 long long。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
int main () {
|
||||
long long result = 0;
|
||||
int n, k;
|
||||
cin >> n >> k;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
result += i * k;
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
优化思路:
|
||||
|
||||
|
||||
由于要计算1到n的整数之和,可以利用等差数列求和公式来优化计算。
|
||||
|
||||
和公式:1 + 2 + 3 + ... + n = n * (n + 1) / 2
|
||||
|
||||
因此,总和 result = k * (n * (n + 1) / 2)
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
long long result = 0;
|
||||
int n, k;
|
||||
cin >> n >> k;
|
||||
|
||||
// 使用等差数列求和公式进行计算
|
||||
result = k * (n * (n + 1LL) / 2);
|
||||
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
38
problems/kamacoder/0124.精华帖子.md
Normal file
38
problems/kamacoder/0124.精华帖子.md
Normal file
@ -0,0 +1,38 @@
|
||||
|
||||
|
||||
# 122.精华帖子
|
||||
|
||||
|
||||
开辟一个数组,默认都是0,把精华帖标记为1.
|
||||
|
||||
使用前缀和,快速计算出,k 范围内 有多少个精华帖。
|
||||
|
||||
前缀和要特别注意区间问题,即 vec[i+k] - vec[i] 求得区间和是 (i, i + k] 这个区间,注意这是一个左开右闭的区间。
|
||||
|
||||
所以前缀和 很容易漏掉 vec[0] 这个数值的计算
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m, k, l, r;
|
||||
cin >> n >> m >> k;
|
||||
vector<int> vec(n);
|
||||
while (m--) {
|
||||
cin >> l >> r;
|
||||
for (int i = l; i < r; i++) vec[i] = 1;
|
||||
}
|
||||
int result = 0;
|
||||
for (int i = 0; i < k; i++) result += vec[i]; // 提前预处理result,包含vec[0]的区间,否则前缀和容易漏掉这个区间
|
||||
|
||||
for (int i = 1; i < n; i++) {
|
||||
vec[i] += vec[i - 1];
|
||||
}
|
||||
|
||||
for (int i = 0; i < n - k; i++) {
|
||||
result = max (result, vec[i + k] - vec[i]);
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
66
problems/kamacoder/0125.连续子数组最大和.md
Normal file
66
problems/kamacoder/0125.连续子数组最大和.md
Normal file
@ -0,0 +1,66 @@
|
||||
|
||||
# 123.连续子数组最大和
|
||||
|
||||
这道题目可以说是 [代码随想录,动态规划:最大子序和](https://www.programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html) 的升级版。
|
||||
|
||||
题目求的是 可以替换一个数字 之后 的 连续子数组最大和。
|
||||
|
||||
如果替换的是数组下标 i 的元素。
|
||||
|
||||
那么可以用 [代码随想录,动态规划:最大子序和](https://www.programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html) 的方法,先求出 [0 - i) 区间的 最大子序和 dp1 和 (i, n)的最大子序和dp2 。
|
||||
|
||||
然后在遍历一遍i, 计算 dp1 + dp2 + vec[i] 的最大值就可以。
|
||||
|
||||
正序遍历,求出 [0 - i) 区间的 最大子序,dp[ i - 1] 表示 是 包括下标i - 1(以vec[i - 1]为结尾)的最大连续子序列和为dp[i - 1]。
|
||||
|
||||
所以 在计算区间 (i, n)即 dp2 的时候,我们要倒叙。 因为我们求的是以 包括下标i + 1 为起始位置的最大连续子序列和为dp[i + 1]。
|
||||
|
||||
这样 dp1 + dp2 + vec[i] 才是一个完整区间。
|
||||
|
||||
这里就体现出对 dp数组定义的把控,本题如果对 dp数组含义理解不清,其实是不容易做出来的。
|
||||
|
||||
代码:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int t, n, x;
|
||||
cin >> t;
|
||||
while (t--) {
|
||||
cin >> n >> x;
|
||||
vector<int> vec(n);
|
||||
for (int i = 0; i < n; i++) cin >> vec[i];
|
||||
vector<int> dp1(n);
|
||||
dp1[0] = vec[0];
|
||||
int res = vec[0];
|
||||
// 从前向后统计最大子序和
|
||||
for (int i = 1; i < n; i++) {
|
||||
dp1[i] = max(dp1[i - 1] + vec[i], vec[i]); // 状态转移公式
|
||||
res = max(res, dp1[i]);
|
||||
}
|
||||
|
||||
res = max(res, vec[n - 1]);
|
||||
// 从后向前统计最大子序和
|
||||
vector<int> dp2(n);
|
||||
dp2[n - 1] = vec[n - 1];
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
dp2[i] = max(dp2[i + 1] + vec[i], vec[i]);
|
||||
|
||||
}
|
||||
|
||||
for (int i = 0 ; i < n ; i++) {
|
||||
int dp1res = 0;
|
||||
if (i > 0) dp1res = max(dp1[i-1], 0);
|
||||
int dp2res = 0;
|
||||
if (i < n - 1 ) dp2res = max(dp2[i+1], 0);
|
||||
|
||||
res = max(res, dp1res + dp2res + x);
|
||||
}
|
||||
cout << res << endl;
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
361
problems/kamacoder/0126.骑士的攻击astar.md
Normal file
361
problems/kamacoder/0126.骑士的攻击astar.md
Normal file
@ -0,0 +1,361 @@
|
||||
|
||||
# A * 算法精讲 (A star算法)
|
||||
|
||||
[卡码网:126. 骑士的攻击](https://kamacoder.com/problempage.php?pid=1203)
|
||||
|
||||
题目描述
|
||||
|
||||
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
|
||||
|
||||
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含一个整数 n,表示测试用例的数量。
|
||||
|
||||
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
|
||||
|
||||
输出描述
|
||||
|
||||
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
6
|
||||
5 2 5 4
|
||||
1 1 2 2
|
||||
1 1 8 8
|
||||
1 1 8 7
|
||||
2 1 3 3
|
||||
4 6 4 6
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
```
|
||||
2
|
||||
4
|
||||
6
|
||||
5
|
||||
1
|
||||
0
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
我们看到这道题目的第一个想法就是广搜,这也是最经典的广搜类型题目。
|
||||
|
||||
这里我直接给出广搜的C++代码:
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
#include<queue>
|
||||
#include<string.h>
|
||||
using namespace std;
|
||||
int moves[1001][1001];
|
||||
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
|
||||
void bfs(int a1,int a2, int b1, int b2)
|
||||
{
|
||||
queue<int> q;
|
||||
q.push(a1);
|
||||
q.push(a2);
|
||||
while(!q.empty())
|
||||
{
|
||||
int m=q.front(); q.pop();
|
||||
int n=q.front(); q.pop();
|
||||
if(m == b1 && n == b2)
|
||||
break;
|
||||
for(int i=0;i<8;i++)
|
||||
{
|
||||
int mm=m + dir[i][0];
|
||||
int nn=n + dir[i][1];
|
||||
if(mm < 1 || mm > 1000 || nn < 1 || nn > 1000)
|
||||
continue;
|
||||
if(!moves[mm][nn])
|
||||
{
|
||||
moves[mm][nn]=moves[m][n]+1;
|
||||
q.push(mm);
|
||||
q.push(nn);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main()
|
||||
{
|
||||
int n, a1, a2, b1, b2;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
cin >> a1 >> a2 >> b1 >> b2;
|
||||
memset(moves,0,sizeof(moves));
|
||||
bfs(a1, a2, b1, b2);
|
||||
cout << moves[b1][b2] << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
提交后,大家会发现,超时了。
|
||||
|
||||
因为本题地图足够大,且 n 也有可能很大,导致有非常多的查询。
|
||||
|
||||
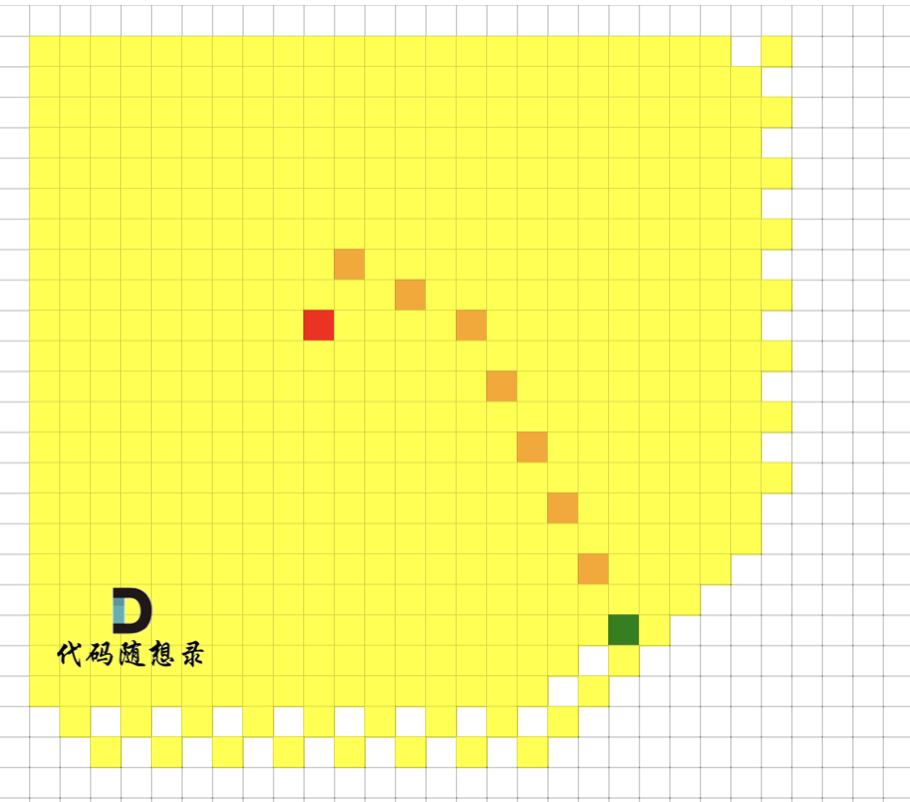
我们来看一下广搜的搜索过程,如图,红色是起点,绿色是终点,黄色是要遍历的点,最后从 起点 找到 达到终点的最短路径是棕色。
|
||||
|
||||
|
||||
|
||||
可以看出 广搜中,做了很多无用的遍历, 黄色的格子是广搜遍历到的点。
|
||||
|
||||
这里我们能不能让便利方向,向这终点的方向去遍历呢?
|
||||
|
||||
这样我们就可以避免很多无用遍历。
|
||||
|
||||
|
||||
## Astar
|
||||
|
||||
Astar 是一种 广搜的改良版。 有的是 Astar是 dijkstra 的改良版。
|
||||
|
||||
其实只是场景不同而已 我们在搜索最短路的时候, 如果是无权图(边的权值都是1) 那就用广搜,代码简洁,时间效率和 dijkstra 差不多 (具体要取决于图的稠密)
|
||||
|
||||
如果是有权图(边有不同的权值),优先考虑 dijkstra。
|
||||
|
||||
而 Astar 关键在于 启发式函数, 也就是 影响 广搜或者 dijkstra 从 容器(队列)里取元素的优先顺序。
|
||||
|
||||
以下,我用BFS版本的A * 来进行讲解。
|
||||
|
||||
在BFS中,我们想搜索,从起点到终点的最短路径,要一层一层去遍历。
|
||||
|
||||

|
||||
|
||||
如果 使用A * 的话,其搜索过程是这样的,如图,图中着色的都是我们要遍历的点。
|
||||
|
||||

|
||||
|
||||
|
||||
(上面两图中 最短路长度都是8,只是走的方式不同而已)
|
||||
|
||||
大家可以发现 **BFS 是没有目的性的 一圈一圈去搜索, 而 A * 是有方向性的去搜索**。
|
||||
|
||||
看出 A * 可以节省很多没有必要的遍历步骤。
|
||||
|
||||
为了让大家可以明显看到区别,我将 BFS 和 A * 制作成可视化动图,大家可以自己看看动图,效果更好。
|
||||
|
||||
地址:https://kamacoder.com/tools/knight.html
|
||||
|
||||
那么 A * 为什么可以有方向性的去搜索,它的如何知道方向呢?
|
||||
|
||||
**其关键在于 启发式函数**。
|
||||
|
||||
那么启发式函数落实到代码处,如果指引搜索的方向?
|
||||
|
||||
在本篇开篇中给出了BFS代码,指引 搜索的方向的关键代码在这里:
|
||||
|
||||
```CPP
|
||||
int m=q.front();q.pop();
|
||||
int n=q.front();q.pop();
|
||||
```
|
||||
|
||||
从队列里取出什么元素,接下来就是从哪里开始搜索。
|
||||
|
||||
**所以 启发式函数 要影响的就是队列里元素的排序**!
|
||||
|
||||
这是影响BFS搜索方向的关键。
|
||||
|
||||
对队列里节点进行排序,就需要给每一个节点权值,如何计算权值呢?
|
||||
|
||||
每个节点的权值为F,给出公式为:F = G + H
|
||||
|
||||
G:起点达到目前遍历节点的距离
|
||||
|
||||
F:目前遍历的节点到达终点的距离
|
||||
|
||||
起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。
|
||||
|
||||
本题的图是无权网格状,在计算两点距离通常有如下三种计算方式:
|
||||
|
||||
1. 曼哈顿距离,计算方式: d = abs(x1-x2)+abs(y1-y2)
|
||||
2. 欧氏距离(欧拉距离) ,计算方式:d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
|
||||
3. 切比雪夫距离,计算方式:d = max(abs(x1 - x2), abs(y1 - y2))
|
||||
|
||||
x1, x2 为起点坐标,y1, y2 为终点坐标 ,abs 为求绝对值,sqrt 为求开根号,
|
||||
|
||||
选择哪一种距离计算方式 也会导致 A * 算法的结果不同。
|
||||
|
||||
本题,采用欧拉距离才能最大程度体现 点与点之间的距离。
|
||||
|
||||
所以 使用欧拉距离计算 和 广搜搜出来的最短路的节点数是一样的。 (路径可能不同,但路径上的节点数是相同的)
|
||||
|
||||
我在制作动画演示的过程中,分别给出了曼哈顿、欧拉以及契比雪夫 三种计算方式下,A * 算法的寻路过程,大家可以自己看看看其区别。
|
||||
|
||||
动画地址:https://kamacoder.com/tools/knight.html
|
||||
|
||||
计算出来 F 之后,按照 F 的 大小,来选去出队列的节点。
|
||||
|
||||
可以使用 优先级队列 帮我们排好序,每次出队列,就是F最大的节点。
|
||||
|
||||
实现代码如下:(启发式函数 采用 欧拉距离计算方式)
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
#include<queue>
|
||||
#include<string.h>
|
||||
using namespace std;
|
||||
int moves[1001][1001];
|
||||
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
|
||||
int b1, b2;
|
||||
// F = G + H
|
||||
// G = 从起点到该节点路径消耗
|
||||
// H = 该节点到终点的预估消耗
|
||||
|
||||
struct Knight{
|
||||
int x,y;
|
||||
int g,h,f;
|
||||
bool operator < (const Knight & k) const{ // 重载运算符, 从小到大排序
|
||||
return k.f < f;
|
||||
}
|
||||
};
|
||||
|
||||
priority_queue<Knight> que;
|
||||
|
||||
int Heuristic(const Knight& k) { // 欧拉距离
|
||||
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号,这样可以提高精度
|
||||
}
|
||||
void astar(const Knight& k)
|
||||
{
|
||||
Knight cur, next;
|
||||
que.push(k);
|
||||
while(!que.empty())
|
||||
{
|
||||
cur=que.top(); que.pop();
|
||||
if(cur.x == b1 && cur.y == b2)
|
||||
break;
|
||||
for(int i = 0; i < 8; i++)
|
||||
{
|
||||
next.x = cur.x + dir[i][0];
|
||||
next.y = cur.y + dir[i][1];
|
||||
if(next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000)
|
||||
continue;
|
||||
if(!moves[next.x][next.y])
|
||||
{
|
||||
moves[next.x][next.y] = moves[cur.x][cur.y] + 1;
|
||||
|
||||
// 开始计算F
|
||||
next.g = cur.g + 5; // 统一不开根号,这样可以提高精度,马走日,1 * 1 + 2 * 2 = 5
|
||||
next.h = Heuristic(next);
|
||||
next.f = next.g + next.h;
|
||||
que.push(next);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main()
|
||||
{
|
||||
int n, a1, a2;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
cin >> a1 >> a2 >> b1 >> b2;
|
||||
memset(moves,0,sizeof(moves));
|
||||
Knight start;
|
||||
start.x = a1;
|
||||
start.y = a2;
|
||||
start.g = 0;
|
||||
start.h = Heuristic(start);
|
||||
start.f = start.g + start.h;
|
||||
astar(start);
|
||||
while(!que.empty()) que.pop(); // 队列清空
|
||||
cout << moves[b1][b2] << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 复杂度分析
|
||||
|
||||
A * 算法的时间复杂度 其实是不好去量化的,因为他取决于 启发式函数怎么写。
|
||||
|
||||
最坏情况下,A * 退化成广搜,算法的时间复杂度 是 O(n * 2),n 为节点数量。
|
||||
|
||||
最佳情况,是从起点直接到终点,时间复杂度为 O(dlogd),d 为起点到终点的深度。
|
||||
|
||||
因为在搜索的过程中也需要堆排序,所以是 O(dlogd)。
|
||||
|
||||
实际上 A * 的时间复杂度是介于 最优 和最坏 情况之间, 可以 非常粗略的认为 A * 算法的时间复杂度是 O(nlogn) ,n 为节点数量。
|
||||
|
||||
A * 算法的空间复杂度 O(b ^ d) ,d 为起点到终点的深度,b 是 图中节点间的连接数量,本题因为是无权网格图,所以 节点间连接数量为 4。
|
||||
|
||||
|
||||
## 拓展
|
||||
|
||||
如果本题大家使用 曼哈顿距离 或者 切比雪夫距离 计算的话,可以提交试一试,有的最短路结果是并不是最短的。
|
||||
|
||||
原因也是 曼哈顿 和 切比雪夫这两种计算方式在 本题的网格地图中,都没有体现出点到点的真正距离!
|
||||
|
||||
可能有些录友找到类似的题目,例如 [poj 2243](http://poj.org/problem?id=2243),使用 曼哈顿距离 提交也过了, 那是因为题目中的地图太小了,仅仅是一张 8 * 8的地图,根本看不出来 不同启发式函数写法的区别。
|
||||
|
||||
A * 算法 并不是一个明确的最短路算法,**A * 算法搜的路径如何,完全取决于 启发式函数怎么写**。
|
||||
|
||||
**A * 算法并不能保证一定是最短路**,因为在设计 启发式函数的时候,要考虑 时间效率与准确度之间的一个权衡。
|
||||
|
||||
虽然本题中,A * 算法得到是最短路,也是因为本题 启发式函数 和 地图结构都是最简单的。
|
||||
|
||||
例如在游戏中,在地图很大、不同路径权值不同、有障碍 且多个游戏单位在地图中寻路的情况,如果要计算准确最短路,耗时很大,会给玩家一种卡顿的感觉。
|
||||
|
||||
而真实玩家在玩游戏的时候,并不要求一定是最短路,次短路也是可以的 (玩家不一定能感受出来,及时感受出来也不是很在意),只要奔着目标走过去 大体就可以接受。
|
||||
|
||||
所以 在游戏开发设计中,**保证运行效率的情况下,A * 算法中的启发式函数 设计往往不是最短路,而是接近最短路的 次短路设计**。
|
||||
|
||||
大家如果玩 LOL,或者 王者荣耀 可以回忆一下:如果 从很远的地方点击 让英雄直接跑过去 是 跑的路径是不靠谱的,所以玩家们才会在 距离英雄尽可能近的位置去点击 让英雄跑过去。
|
||||
|
||||
## A * 的缺点
|
||||
|
||||
大家看上述 A * 代码的时候,可以看到 我们想 队列里添加了很多节点,但真正从队列里取出来的 仅仅是 靠启发式函数判断 距离终点最近的节点。
|
||||
|
||||
相对了 普通BFS,A * 算法只从 队列里取出 距离终点最近的节点。
|
||||
|
||||
那么问题来了,A * 在一次路径搜索中,大量不需要访问的节点都在队列里,会造成空间的过度消耗。
|
||||
|
||||
IDA * 算法 对这一空间增长问题进行了优化,关于 IDA * 算法,本篇不再做讲解,感兴趣的录友可以自行找资料学习。
|
||||
|
||||
另外还有一种场景 是 A * 解决不了的。
|
||||
|
||||
如果题目中,给出 多个可能的目标,然后在这多个目标中 选择最近的目标,这种 A * 就不擅长了, A * 只擅长给出明确的目标 然后找到最短路径。
|
||||
|
||||
如果是多个目标找最近目标(特别是潜在目标数量很多的时候),可以考虑 Dijkstra ,BFS 或者 Floyd。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
### C#
|
||||
|
||||
### Dart
|
||||
|
||||
### C
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -29,7 +29,7 @@
|
||||
|
||||
但如果我们要判断两个元素是否在同一个集合里的时候 我们又能怎么办? 只能把而二维数组都遍历一遍。
|
||||
|
||||
而且每当想添加一个元素到某集合的时候,依然需要把把二维数组组都遍历一遍,才知道要放在哪个集合里。
|
||||
而且每当想添加一个元素到某集合的时候,依然需要把把二维数组都遍历一遍,才知道要放在哪个集合里。
|
||||
|
||||
这仅仅是一个粗略的思路,如果沿着这个思路去实现代码,非常复杂,因为管理集合还需要很多逻辑。
|
||||
|
||||
@ -208,7 +208,7 @@ bool isSame(int u, int v) {
|
||||
|
||||
// 将v->u 这条边加入并查集
|
||||
void join(int u, int v) {
|
||||
if (isSame) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||||
if (isSame(u, v)) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||||
father[v] = u;
|
||||
}
|
||||
```
|
||||
@ -219,7 +219,7 @@ void join(int u, int v) {
|
||||
|
||||
举一个例子:
|
||||
|
||||
```
|
||||
```CPP
|
||||
join(1, 2);
|
||||
join(3, 2);
|
||||
```
|
||||
@ -271,7 +271,7 @@ join(3, 2);
|
||||
|
||||
不少录友在接触并查集模板之后,用起来很娴熟,因为模板确实相对固定,但是对并查集内部数据组织方式以及如何判断是否是同一个集合的原理很模糊。
|
||||
|
||||
通过以上讲解之后,我在带大家一步一步去画一下,并查集内部数据连接方式。
|
||||
通过以上讲解之后,我再带大家一步一步去画一下,并查集内部数据连接方式。
|
||||
|
||||
1、`join(1, 8);`
|
||||
|
||||
@ -301,7 +301,7 @@ join(3, 2);
|
||||
|
||||
即如下代码在寻找根的过程中,会有路径压缩,减少 下次查询的路径长度。
|
||||
|
||||
```
|
||||
```CPP
|
||||
// 并查集里寻根的过程
|
||||
int find(int u) {
|
||||
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
|
||||
|
||||
@ -1,7 +1,6 @@
|
||||
# 广度优先搜索理论基础
|
||||
|
||||
|
||||
在[深度优先搜索](https://programmercarl.com/图论深搜理论基础.html)的讲解中,我们就讲过深度优先搜索和广度优先搜索的区别。
|
||||
在[深度优先搜索](./图论深搜理论基础.md)的讲解中,我们就讲过深度优先搜索和广度优先搜索的区别。
|
||||
|
||||
广搜(bfs)是一圈一圈的搜索过程,和深搜(dfs)是一条路跑到黑然后再回溯。
|
||||
|
||||
@ -88,28 +87,12 @@ void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y
|
||||
}
|
||||
```
|
||||
|
||||
以上模板代码,就是可以直接拿来做 [200.岛屿数量](https://leetcode.cn/problems/number-of-islands/solution/by-carlsun-2-n72a/) 这道题目,唯一区别是 针对地图 grid 中有数字1的地方去做一个遍历。
|
||||
|
||||
即:
|
||||
|
||||
```
|
||||
if (!visited[nextx][nexty]) { // 如果节点没被访问过
|
||||
```
|
||||
|
||||
改为
|
||||
|
||||
```
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 如果节点没被访问过且节点是可遍历的
|
||||
|
||||
```
|
||||
就可以通过 [200.岛屿数量](https://leetcode.cn/problems/number-of-islands/solution/by-carlsun-2-n72a/) 这道题目,大家可以去体验一下。
|
||||
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
当然广搜还有很多细节需要注意的地方,后面我会针对广搜的题目还做针对性的讲解,因为在理论篇讲太多细节,可能会让刚学广搜的录友们越看越懵,所以细节方面针对具体题目在做讲解。
|
||||
当然广搜还有很多细节需要注意的地方,后面我会针对广搜的题目还做针对性的讲解。
|
||||
|
||||
**因为在理论篇讲太多细节,可能会让刚学广搜的录友们越看越懵**,所以细节方面针对具体题目在做讲解。
|
||||
|
||||
本篇我们重点讲解了广搜的使用场景,广搜的过程以及广搜的代码框架。
|
||||
|
||||
@ -119,34 +102,3 @@ if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 如果节点没被
|
||||
|
||||
相信看完本篇,大家会对广搜有一个基础性的认识,后面再来做对应的题目就会得心应手一些。
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Python
|
||||
```python
|
||||
from collections import deque
|
||||
|
||||
dir = [(0, 1), (1, 0), (-1, 0), (0, -1)] # 创建方向元素
|
||||
|
||||
def bfs(grid, visited, x, y):
|
||||
|
||||
queue = deque() # 初始化队列
|
||||
queue.append((x, y)) # 放入第一个元素/起点
|
||||
visited[x][y] = True # 标记为访问过的节点
|
||||
|
||||
while queue: # 遍历队列里的元素
|
||||
|
||||
curx, cury = queue.popleft() # 取出第一个元素
|
||||
|
||||
for dx, dy in dir: # 遍历四个方向
|
||||
|
||||
nextx, nexty = curx + dx, cury + dy
|
||||
|
||||
if nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]): # 越界了,直接跳过
|
||||
continue
|
||||
|
||||
if not visited[nextx][nexty]: # 如果节点没被访问过
|
||||
queue.append((nextx, nexty)) # 加入队列
|
||||
visited[nextx][nexty] = True # 标记为访问过的节点
|
||||
|
||||
```
|
||||
|
||||
|
||||
@ -3,7 +3,7 @@
|
||||
|
||||
从深搜广搜 到并查集,从最小生成树到拓扑排序, 最后是最短路算法系列。
|
||||
|
||||
至此算上本篇,一共32篇文章,图论之旅就在此收官了。
|
||||
至此算上本篇,一共30篇文章,图论之旅就在此收官了。
|
||||
|
||||
在[0098.所有可达路径](./0098.所有可达路径.md) ,我们接触了两种图的存储方式,邻接表和邻接矩阵,掌握两种图的存储方式很重要。
|
||||
|
||||
@ -67,20 +67,79 @@
|
||||
|
||||
其实理论基础篇就算是给大家出了一道裸的并查集题目了,所以在后面的题目安排中,会稍稍的拔高一些,重点在于并查集的应用上。
|
||||
|
||||
例如 并查集可以判断这个图是否是树,因为树的话,只有一个根,符合并查集判断集合的逻辑,题目:[0108.冗余连接](./0108.冗余连接.md)。
|
||||
|
||||
|
||||
[0108.冗余连接](./0108.冗余连接.md), [0109.冗余连接II](./0109.冗余连接II.md)
|
||||
|
||||
后面的两道题目,[0108.冗余连接](./0108.冗余连接.md) 和
|
||||
|
||||
在[0109.冗余连接II](./0109.冗余连接II.md) 中 对有向树的判断难度更大一些,需要考虑的情况比较多。
|
||||
|
||||
|
||||
## 最小生成树
|
||||
|
||||
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起。
|
||||
|
||||
最小生成树算法,有prim 和 kruskal。
|
||||
|
||||
**prim 算法是维护节点的集合,而 Kruskal 是维护边的集合**。
|
||||
|
||||
在 稀疏图中,用Kruskal更优。 在稠密图中,用prim算法更优。
|
||||
|
||||
> 边数量较少为稀疏图,接近或等于完全图(所有节点皆相连)为稠密图
|
||||
|
||||
Prim 算法 时间复杂度为 O(n^2),其中 n 为节点数量,它的运行效率和图中边树无关,适用稠密图。
|
||||
|
||||
Kruskal算法 时间复杂度 为 O(nlogn),其中n 为边的数量,适用稀疏图。
|
||||
|
||||
关于 prim算法,我自创了三部曲,来帮助大家理解:
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
大家只要理解这三部曲, prim算法 至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于 自己在写prim的时候 两眼一抹黑 完全凭感觉去写。
|
||||
|
||||
**minDist数组 是prim算法的灵魂,它帮助 prim算法完成最重要的一步,就是如何找到 距离最小生成树最近的点**。
|
||||
|
||||
kruscal的主要思路:
|
||||
|
||||
* 边的权值排序,因为要优先选最小的边加入到生成树里
|
||||
* 遍历排序后的边
|
||||
* 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
|
||||
* 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
|
||||
|
||||
而判断节点是否在一个集合 以及将两个节点放入同一个集合,正是并查集的擅长所在。
|
||||
|
||||
所以 Kruskal 是需要用到并查集的。
|
||||
|
||||
这也是我在代码随想录图论编排上 为什么要先 讲解 并查集 在讲解 最小生成树。
|
||||
|
||||
|
||||
## 拓扑排序
|
||||
|
||||
拓扑排序 是在图上的一种排序。
|
||||
|
||||
概括来说,**给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序**。
|
||||
|
||||
同样,拓扑排序也可以检测这个有向图 是否有环,即存在循环依赖的情况。
|
||||
|
||||
拓扑排序的一些应用场景,例如:大学排课,文件下载依赖 等等。
|
||||
|
||||
只要记住如下两步拓扑排序的过程,代码就容易写了:
|
||||
|
||||
1. 找到入度为0 的节点,加入结果集
|
||||
2. 将该节点从图中移除
|
||||
|
||||
## 最短路算法
|
||||
|
||||
最短路算法是图论中,比较复杂的算法,而且不同的最短路算法都有不同的应用场景。
|
||||
|
||||
我在 [最短路算法总结篇](./最短路问题总结篇.md) 里已经做了一个高度的概括。
|
||||
|
||||
大家要时常温故而知新,才能透彻理解各个最短路算法。
|
||||
|
||||
|
||||
算法4,只讲解了 Dijkstra,SPFA (Bellman-Ford算法基于队列) 和 拓扑排序,
|
||||
## 总结
|
||||
|
||||
到最后,图论终于剧终了,相信这是市面上大家能看到最全最细致的图论讲解教程。
|
||||
|
||||
图论也是我 《代码随想录》所有章节里 所费精力最大的一个章节。
|
||||
|
||||
只为了不负录友们的期待。 大家加油💪🏻
|
||||
|
||||
@ -62,7 +62,7 @@
|
||||
|
||||
正是因为dfs搜索可一个方向,并需要回溯,所以用递归的方式来实现是最方便的。
|
||||
|
||||
很多录友对回溯很陌生,建议先看看代码随想录,[回溯算法章节](https://programmercarl.com/回溯算法理论基础.html)。
|
||||
很多录友对回溯很陌生,建议先看看代码随想录,[回溯算法章节](../回溯算法理论基础.md)。
|
||||
|
||||
有递归的地方就有回溯,那么回溯在哪里呢?
|
||||
|
||||
@ -78,11 +78,11 @@ void dfs(参数) {
|
||||
|
||||
可以看到回溯操作就在递归函数的下面,递归和回溯是相辅相成的。
|
||||
|
||||
在讲解[二叉树章节](https://programmercarl.com/二叉树理论基础.html)的时候,二叉树的递归法其实就是dfs,而二叉树的迭代法,就是bfs(广度优先搜索)
|
||||
在讲解[二叉树章节](../二叉树理论基础.md)的时候,二叉树的递归法其实就是dfs,而二叉树的迭代法,就是bfs(广度优先搜索)
|
||||
|
||||
所以**dfs,bfs其实是基础搜索算法,也广泛应用与其他数据结构与算法中**。
|
||||
|
||||
我们在回顾一下[回溯法](https://programmercarl.com/回溯算法理论基础.html)的代码框架:
|
||||
我们在回顾一下[回溯法](../回溯算法理论基础.md)的代码框架:
|
||||
|
||||
```cpp
|
||||
void backtracking(参数) {
|
||||
@ -123,9 +123,9 @@ void dfs(参数) {
|
||||
|
||||
## 深搜三部曲
|
||||
|
||||
在 [二叉树递归讲解](https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html)中,给出了递归三部曲。
|
||||
在 [二叉树递归讲解](../二叉树的递归遍历.md)中,给出了递归三部曲。
|
||||
|
||||
[回溯算法](https://programmercarl.com/回溯算法理论基础.html)讲解中,给出了 回溯三部曲。
|
||||
[回溯算法](../回溯算法理论基础.md)讲解中,给出了 回溯三部曲。
|
||||
|
||||
其实深搜也是一样的,深搜三部曲如下:
|
||||
|
||||
|
||||
@ -12,12 +12,15 @@
|
||||
* bellman_ford 算法判断负权回路
|
||||
* bellman_ford之单源有限最短路
|
||||
* Floyd 算法精讲
|
||||
* 启发式搜索:A * 算法
|
||||
|
||||
|
||||
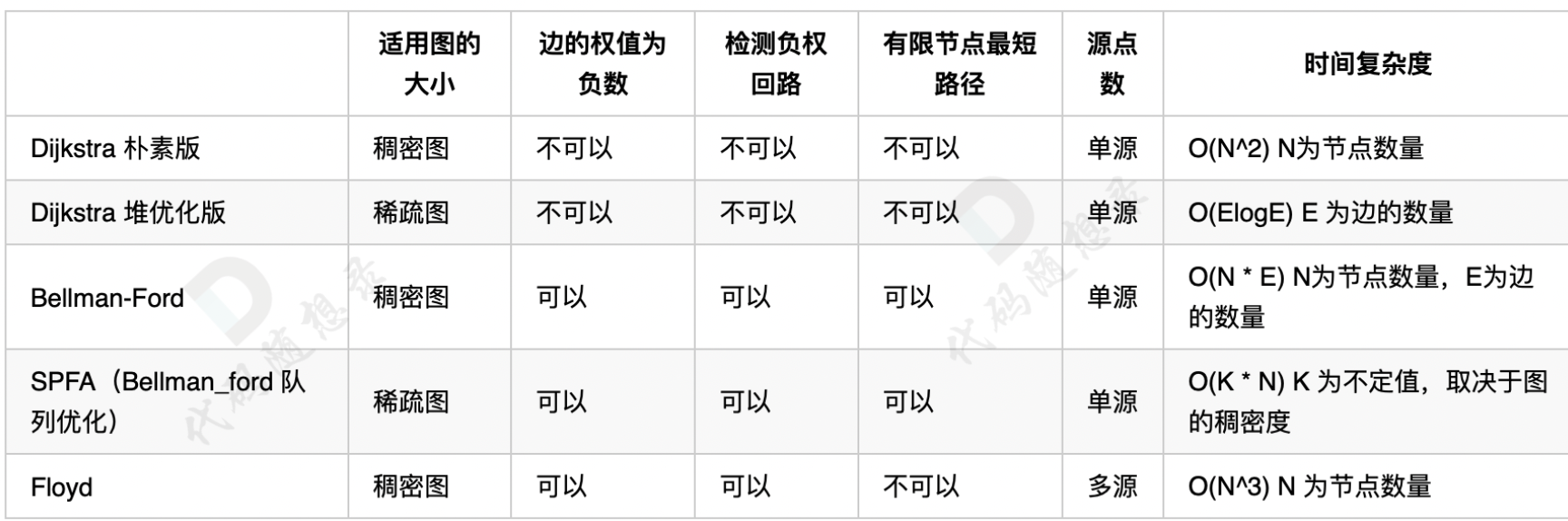
最短路算法比较复杂,而且各自有各自的应用场景,我来用一张表把讲过的最短路算法的使用场景都展现出来:
|
||||
|
||||
|
||||
|
||||
(因为A * 属于启发式搜索,和上面最短路算法并不是一类,不适合一起对比,所以没有放在一起)
|
||||
|
||||
|
||||
可能有同学感觉:这个表太复杂了,我记也记不住。
|
||||
|
||||
@ -25,23 +28,25 @@
|
||||
|
||||
这里我给大家一个大体使用场景的分析:
|
||||
|
||||
如果遇到单源且边为正数,直接Dijkstra。
|
||||
**如果遇到单源且边为正数,直接Dijkstra**。
|
||||
|
||||
至于 使用朴素版还是 堆优化版 还是取决于图的稠密度, 多少节点多少边算是稠密图,多少算是稀疏图,这个没有量化,如果想量化只能写出两个版本然后做实验去测试,不同的判题机得出的结果还不太一样。
|
||||
至于 **使用朴素版还是 堆优化版 还是取决于图的稠密度**, 多少节点多少边算是稠密图,多少算是稀疏图,这个没有量化,如果想量化只能写出两个版本然后做实验去测试,不同的判题机得出的结果还不太一样。
|
||||
|
||||
一般情况下,可以直接用堆优化版本。
|
||||
|
||||
如果遇到单源边可为负数,直接 Bellman-Ford,同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。
|
||||
**如果遇到单源边可为负数,直接 Bellman-Ford**,同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。
|
||||
|
||||
一般情况下,直接用 SPFA。
|
||||
|
||||
如果有负权回路,优先 Bellman-Ford, 如果是有限节点最短路 也优先 Bellman-Ford,理由是写代码比较方便。
|
||||
**如果有负权回路,优先 Bellman-Ford**, 如果是有限节点最短路 也优先 Bellman-Ford,理由是写代码比较方便。
|
||||
|
||||
如果是遇到多源点求最短路,直接 Floyd。
|
||||
**如果是遇到多源点求最短路,直接 Floyd**。
|
||||
|
||||
除非 源点特别少,且边都是正数,那可以 多次 Dijkstra 求出最短路径,但这种情况很少,一般出现多个源点了,就是想让你用 Floyd 了。
|
||||
|
||||
|
||||
对于A * ,由于其高效性,所以在实际工程应用中使用最为广泛 ,由于其 结果的不唯一性,也就是可能是次短路的特性,一般不适合作为算法题。
|
||||
|
||||
游戏开发、地图导航、数据包路由等都广泛使用 A * 算法。
|
||||
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user