Merge branch 'master' of https://github.com/Chenxue3/leetcode-master

problems/0028.实现strStr.md

@@ -425,8 +425,8 @@ public:
         if (needle.size() == 0) {
             return 0;
         }
-        int next[needle.size()];
+		vector<int> next(needle.size());
-        getNext(next, needle);
+		getNext(&next[0], needle);
         int j = -1; // // 因为next数组里记录的起始位置为-1
         for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
             while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
@@ -524,8 +524,8 @@ public:
         if (needle.size() == 0) {
             return 0;
         }
-        int next[needle.size()];
+        vector<int> next(needle.size());
-        getNext(next, needle);
+        getNext(&next[0], needle);
         int j = 0;
         for (int i = 0; i < haystack.size(); i++) {
             while(j > 0 && haystack[i] != needle[j]) {
@@ -1428,4 +1428,3 @@ public int[] GetNext(string needle)
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
-

problems/0045.跳跃游戏II.md

@@ -285,6 +285,34 @@ class Solution:
 
 ### Go
 
+
+```go
+/**
+ * @date: 2024 Jan 06
+ * @time: 13:44
+ * @author: Chris
+**/
+// 贪心算法优化版
+
+// 记录步骤规则：每超过上一次可达最大范围，需要跳跃一次，次数+1
+// 记录位置：i == lastDistance + 1
+func jump(nums []int) int {
+	// 根据题目规则，初始位置为nums[0]
+	lastDistance := 0 // 上一次覆盖范围
+	curDistance := 0  // 当前覆盖范围（可达最大范围）
+	minStep := 0      // 记录最少跳跃次数
+
+	for i := 0; i < len(nums); i++ {
+		if i == lastDistance+1 { // 在上一次可达范围+1的位置，记录步骤
+			minStep++                  // 跳跃次数+1
+			lastDistance = curDistance // 记录时才可以更新
+		}
+		curDistance = max(nums[i]+i, curDistance) // 更新当前可达的最大范围
+	}
+	return minStep
+}
+```
+
 ```go
 // 贪心版本一
 func jump(nums []int) int {

problems/0200.岛屿数量.深搜版.md

@@ -389,50 +389,41 @@ function numIslands(grid: string[][]): number {
 ### Go
 
 ```go
+
+var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
+
 func numIslands(grid [][]byte) int {
-    // 用1标记已访问
+	res := 0
-    visited := make([][]int, len(grid))
-    for i := 0; i < len(visited); i++{
-        visited[i] = make([]int, len(grid[0]))
-    }
 
-    var bfs func(x, y int)
+	visited := make([][]bool, len(grid))
-    bfs = func(x, y int){
+	for i := 0; i < len(grid); i++ {
-        stack := make([][]int, 0)
+		visited[i] = make([]bool, len(grid[0]))
-        stack = append(stack, []int{x, y})
+	}
-        moveX := []int{1, -1, 0, 0}
-        moveY := []int{0, 0, 1, -1} 
 
-        for len(stack) != 0{
+	for i, rows := range grid {
-            node := stack[len(stack) - 1]
+		for j, v := range rows {
-            stack = stack[:len(stack) - 1]
+			if v == '1' && !visited[i][j] {
+				res++
+				dfs(grid, visited, i, j)
+			}
+		}
+	}
 
-            for i := 0; i < 4; i++{
+	return res
-                dx := moveX[i] + node[0]
+}
-                dy := moveY[i] + node[1]
-                if dx < 0 || dx >= len(grid) || dy < 0 || dy >= len(grid[0]) || visited[dx][dy] == 1{
-                    continue
-                }
-                visited[dx][dy] = 1
-                if grid[dx][dy] == '1'{
-                    stack = append(stack, []int{dx,dy})
-                }
-            }
-        }
-    }
 
-    result := 0
+func dfs(grid [][]byte, visited [][]bool, i, j int) {
-    for i := 0; i < len(grid); i++{
+        visited[x][y] = true
-        for j := 0; j < len(grid[0]); j++{
+	for _, d := range DIRECTIONS {
-            if visited[i][j] == 0 && grid[i][j] == '1'{
+		x, y := i+d[0], j+d[1]
-                bfs(i, j)
+		if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
-                visited[i][j] = 1
+			continue
-                result++
+		}
-            }
+		if grid[x][y] == '1' && !visited[x][y] {
-        }
+			dfs(grid, visited, x, y)
-    }
+		}
+	}
 
-    return result
 }
 ```
 

problems/1971.寻找图中是否存在路径.md

@@ -8,26 +8,24 @@
 
 [题目链接](https://leetcode.cn/problems/find-if-path-exists-in-graph/)
 
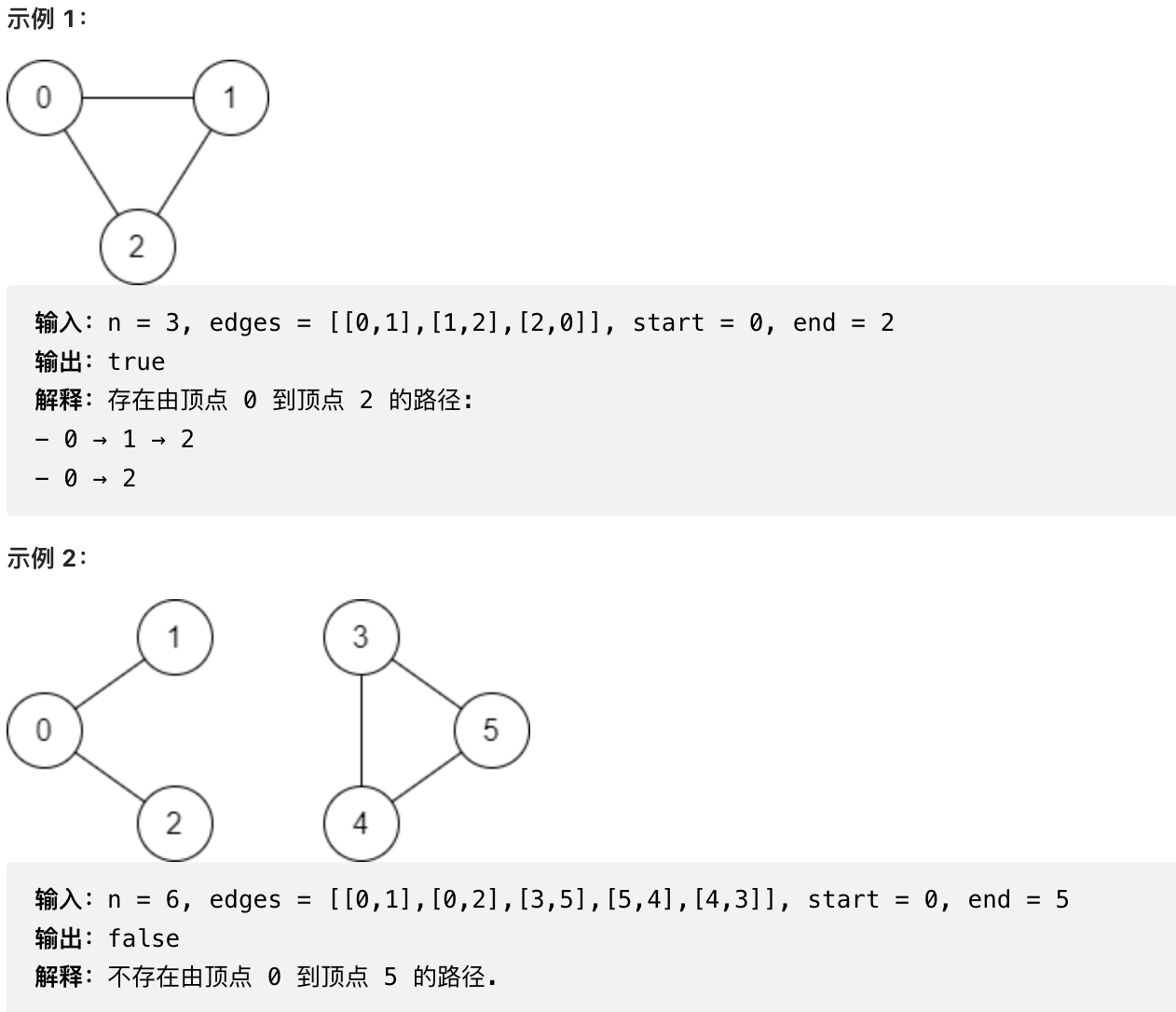
-有一个具有 n个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。
+有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。
 
 请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。
 
-给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。
+给你数组 edges 和整数 n、start 和 end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。
-
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220705101442.png)
 
-
 提示:
 
-* 1 <= n <= 2 * 10^5
+- 1 <= n <= 2 \* 10^5
-* 0 <= edges.length <= 2 * 10^5
+- 0 <= edges.length <= 2 \* 10^5
-* edges[i].length == 2
+- edges[i].length == 2
-* 0 <= ui, vi <= n - 1
+- 0 <= ui, vi <= n - 1
-* ui != vi
+- ui != vi
-* 0 <= start, end <= n - 1
+- 0 <= start, end <= n - 1
-* 不存在双向边
+- 不存在双向边
-* 不存在指向顶点自身的边
+- 不存在指向顶点自身的边
 
 ## 思路
 
@@ -70,7 +68,7 @@ void join(int u, int v) {
 }
 ```
 
-以上模板中，只要修改 n 大小就可以，本题n不会超过2 * 10^5。
+以上模板中，只要修改 n 大小就可以，本题 n 不会超过 2 \* 10^5。
 
 并查集主要有三个功能。
 
@@ -86,7 +84,7 @@ void join(int u, int v) {
 
 此时我们就可以直接套用并查集模板。
 
-使用join(int u, int v)将每条边加入到并查集。 
+使用 join(int u, int v)将每条边加入到并查集。
 
 最后 isSame(int u, int v) 判断是否是同一个根 就可以了。
 
@@ -191,7 +189,7 @@ class Solution {
 
 ### Python：
 
-PYTHON并查集解法如下：
+PYTHON 并查集解法如下：
 
 ```PYTHON
 class Solution:
@@ -206,6 +204,85 @@ class Solution:
         return find(source) == find(destination)
 ```
 
+### Javascript：
+
+Javascript 并查集解法如下：
+
+```Javascript
+class unionF{
+    constructor(n){
+        this.count = n
+        this.roots = new Array(n).fill(0).map((item,index)=>index)
+    }
+
+    findRoot(x){
+        if(this.roots[x]!==x){
+            this.roots[x] = this.findRoot(this.roots[x])
+        }
+        return this.roots[x]
+    }
+
+    union(x,y){
+        const rx = this.findRoot(x)
+        const ry = this.findRoot(y)
+        this.roots[rx] = ry
+        this.count--
+    }
+
+    isConnected(x,y){
+        return this.findRoot(x)===this.findRoot(y)
+    }
+}
+
+var validPath = function(n, edges, source, destination) {
+    const UF = new unionF(n)
+    for(const [s,t] of edges){
+        UF.union(s,t)
+    }
+    return UF.isConnected(source,destination)
+};
+```
+
+Javascript 双向 bfs 解法如下：
+
+```Javascript
+var validPath = function(n, edges, source, destination) {
+    const graph = new Array(n).fill(0).map(()=>[])
+    for(const [s,t] of edges){
+        graph[s].push(t)
+        graph[t].push(s)
+    }
+
+    const visited = new Array(n).fill(false)
+    function bfs(start,end,graph){
+        const startq = [start]
+        const endq = [end]
+        while(startq.length&&endq.length){
+            const slen = startq.length
+            for(let i = 0;i<slen;i++){
+                const scur = startq.shift()
+                if(visited[scur]) continue
+                if(endq.includes(scur)) return true
+                visited[scur] = true
+                const neighbors = graph[scur]
+                startq.push(...neighbors)
+            }
+
+            const elen = endq.length
+            for(let i = 0;i<elen;i++){
+                const ecur = endq.shift()
+                if(visited[ecur]) continue
+                if(startq.includes(ecur)) return true
+                visited[ecur] = true
+                const neighbors = graph[ecur]
+                endq.push(...neighbors)
+            }
+        }
+        return false
+    }
+    return bfs(source,destination,graph)
+};
+```
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">